1 引言
卫星导航在民用和军用领域均有较广泛的应用，由于卫星距接收机的距离达2～3万多公里，并且卫星发射功率只有几十瓦，所以到达地面接收机时的信号非常微弱，以GPS系统L1频率信号为例，到达地面时的信号功率只有-160 dBw，因此卫星导航接收机极易受到外界各类干扰的影响[1]，其中欺骗干扰是卫星导航系统面临的主要威胁之一。近年来不断有欺骗干扰成功欺骗GPS系统的例子出现，2011年伊朗利用美国无人机使用的GPS系统中的缺陷将其成功地欺骗至预设地点。Texas大学自2008年开始研究GPS欺骗干扰，并于2013年通过在游艇上实验成功将其欺骗偏离正常航线。2017年6月22日俄罗斯黑海卫星定位系统显示出错误的位置信息，英媒称该问题暗示俄罗斯可能在测试一种用于欺骗GPS的新系统。电子科技大学在2016年详细研究了生成式欺骗干扰并实现了对GPS系统的欺骗。可以看出欺骗攻击让人防不胜防，研究有效的欺骗干扰检测与抑制方法迫在眉睫[2- 6]。
矢量跟踪环路利用扩展卡尔曼的预测功能来提高矢量接收机对真实卫星信号的可预见性，目前基于矢量跟踪环路的抗欺骗干扰技术研究主要分为欺骗干扰检测与欺骗干扰抑制技术。基于矢量跟踪环路的欺骗干扰检测技术主要包括：DLR将波束形成算法与矢量跟踪环路相结合并对欺骗干扰进行检测[7]，该方法在跟踪环路中需要较多的相关器，因此复杂度较大；美国的伊利诺伊大学根据多个矢量接收机的辅助位置信息对欺骗干扰进行检测，该方法需要多个接收机，成本较高[8-12]。北京航空航天大学利用矢量跟踪通道的带宽信息对欺骗干扰进行检测，该方法对信号质量不敏感，在复杂的电磁环境中较稳健[13]。基于矢量跟踪环路的欺骗干扰抑制技术主要有：PLAN小组提出了根据相关器输出幅度的变化来检测欺骗干扰，然后利用矢量跟踪环路能够桥接被遮挡真实信号的特点，保证接收机不能跟踪上欺骗干扰，但是当接收机跟踪到的所有卫星信号被欺骗时该抑制方法将失效[14]。
基于现有的公开文献[15-17]，阵列天线技术在卫星导航抗干扰领域已有较广泛且深入的研究，为了提高矢量跟踪环路在复杂电磁环境下的稳健性，本文将阵列天线技术中的解重扩算法[18]和矢量跟踪环路紧耦合对生成式欺骗干扰进行检测和抑制，来提高矢量跟踪环路的抗欺骗干扰性能。首先根据预测的矢量跟踪环路参数重构参考信号；其次根据接收信号与参考信号的相关能量输出提出欺骗干扰检测算法；最后根据阵列接收信号与参考信号的相干累加结果提出欺骗干扰抑制算法。本文内容安排如下：第2节介绍阵列天线接收的数据模型，第3节介绍本文所提的欺骗干扰检测与抑制算法，第4节给出仿真结果，第5节总结全文。
2 数据模型及问题描述
考虑一个由M个阵元组成的均匀线阵，阵元间距为d，入射信号的波长为λ，取第一个阵元为参考点，如果有G个有用信号和G个欺骗干扰入射到均匀线阵上，其中有用信号的到达角度分别为θg(g=1,2,...,G)，欺骗干扰的到达角分别为
在远场窄带假设条件下，阵列接收信号可表示为
x(t)=xa(t)+xs(t)+e(t)=
(1)
其中x(t)=[x1(t),x2(t),...,xM(t)]T是M×1维阵列接收数据矢量；e(t)=[e1(t),e2(t),...,eM(t)]T是阵列接收噪声矢量，通常假设服从高斯分布；sg(t)是第g颗卫星信号的复包络；a(θg)是第g颗卫星信号的导向矢量，有如下形式
(2)
GPS信号sg(t)可表示为
(3)
其中Ag为信号功率；Dg(t)为导航数据位信息；Cg(t)表示第g颗卫星信号的C/A码；τg为接收到的卫星信号的扩频码相对于发射信号的时延； f0为载波频率，φg为载波初始相位。同理，与第g颗卫星信号的延迟相差Δτ的欺骗干扰可以表示为
(4)
其中
将公式(3)和公式(4)代入公式(1)中得到
exp[j(2πf0t+φg)]a(θg)+
(5)
基于公开的文献，生成式欺骗干扰可以增大接收机的定位误差，它的具体实施方式为[19-20]：欺骗干扰逐步和真实卫星信号保持同步，随着欺骗干扰功率的不断增加使跟踪环路偏离即时码跟踪点而成功欺骗接收机。下面以参考阵元、第g颗卫星信号为例分析生成式欺骗干扰对接收机的影响。
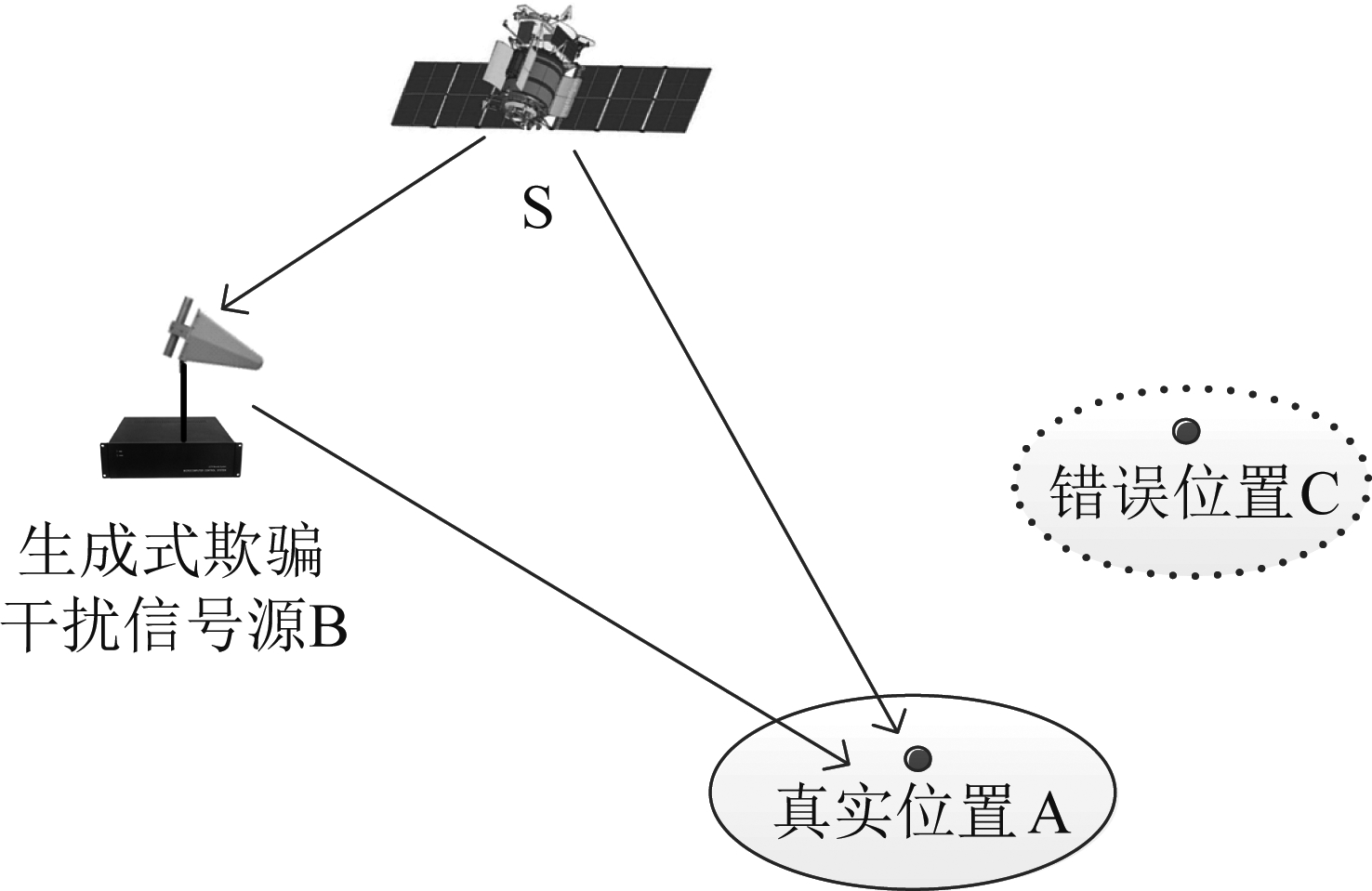
图1 生成式欺骗干扰示意图
Fig.1 Spoofing structure diagram
在相干累积时间为Tcoh时，第g颗卫星信号在第n毫秒与滞后码的相干累加结果为
Lg(n)=La(n)+Ls(n)=
(6)
其中R(Δτg)为第g颗卫星信号C/A码自相关函数，
为欺骗干扰与本地参考信号的相关函数；Δτg,Δf0分别为真实信号的码相位误差和载波频率误差，
分别为欺骗干扰的码相位误差和载波频率误差；
分别为真实信号和欺骗干扰的载波相位跟踪误差；e表示测量噪声分量；d′为1个码片的宽度。由于欺骗干扰引入的相关分量Ls(n)与欺骗干扰的延迟和功率有关，当欺骗干扰与真实卫星信号的时延间隔大于1.5个码片时Ls(n)为零，对接收机无影响。当欺骗干扰的延迟不断减小、功率不断增加时，相关分量Ls(n)会不断增加，在此期间欺骗干扰逐渐引入一定的码相位跟踪误差，从而使接收机的定位误差不断增大。如图2所示，本文从45 s开始对接收机实施欺骗，在无欺骗干扰的信号中加入欺骗干扰延迟逐渐减小、欺骗干扰功率逐渐增加的生成式欺骗干扰，在2 s之内将其逐步欺骗至一定的位置。
生成式欺骗干扰可以将接收机逐步引导至错误的位置，这种恶意的隐蔽式干扰很难被接收机察觉，本文将解重扩算法与矢量跟踪环路相结合提出一种欺骗干扰检测与抑制算法来提高矢量跟踪环路的抗欺骗干扰性能。
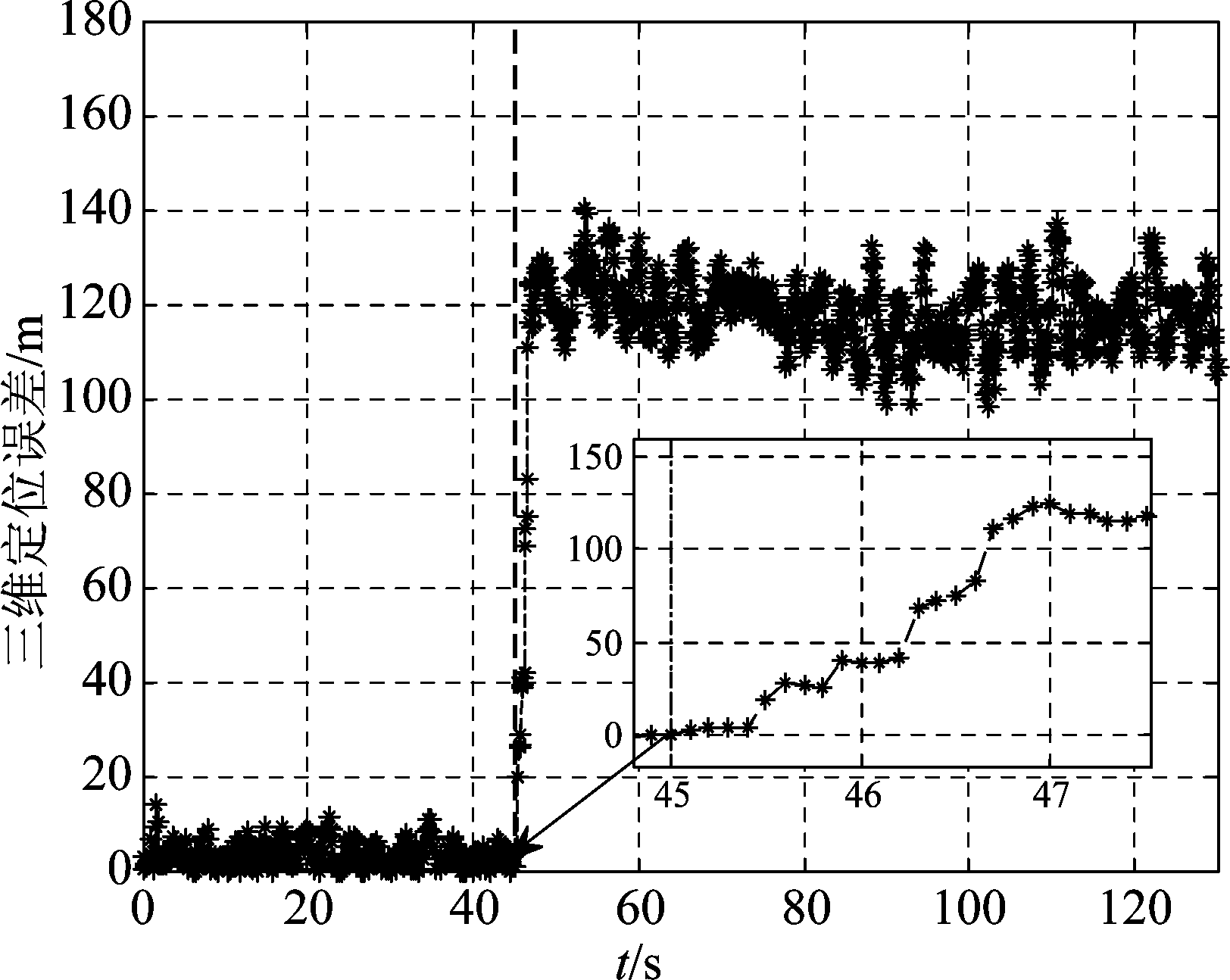
图2 模拟欺骗场景
Fig.2 Simulation of spoofing scenario
3 算法介绍
基于公开文献[1,18]，解重扩算法复杂度低，实现简单。该方法根据GPS解扩后的信息重构基于即时码的参考信号，通过阵列接收信号和参考信号的相干累加结果得到权矢量。解重扩算法具有高增益、高稳健的特点，可以提高卫星导航系统的抗干扰性能。本节将解重扩算法与矢量跟踪环路相结合对欺骗干扰进行检测与抑制，其处理流程如图3所示，下面以第g颗卫星为例对欺骗干扰检测与抑制算法分别展开介绍。
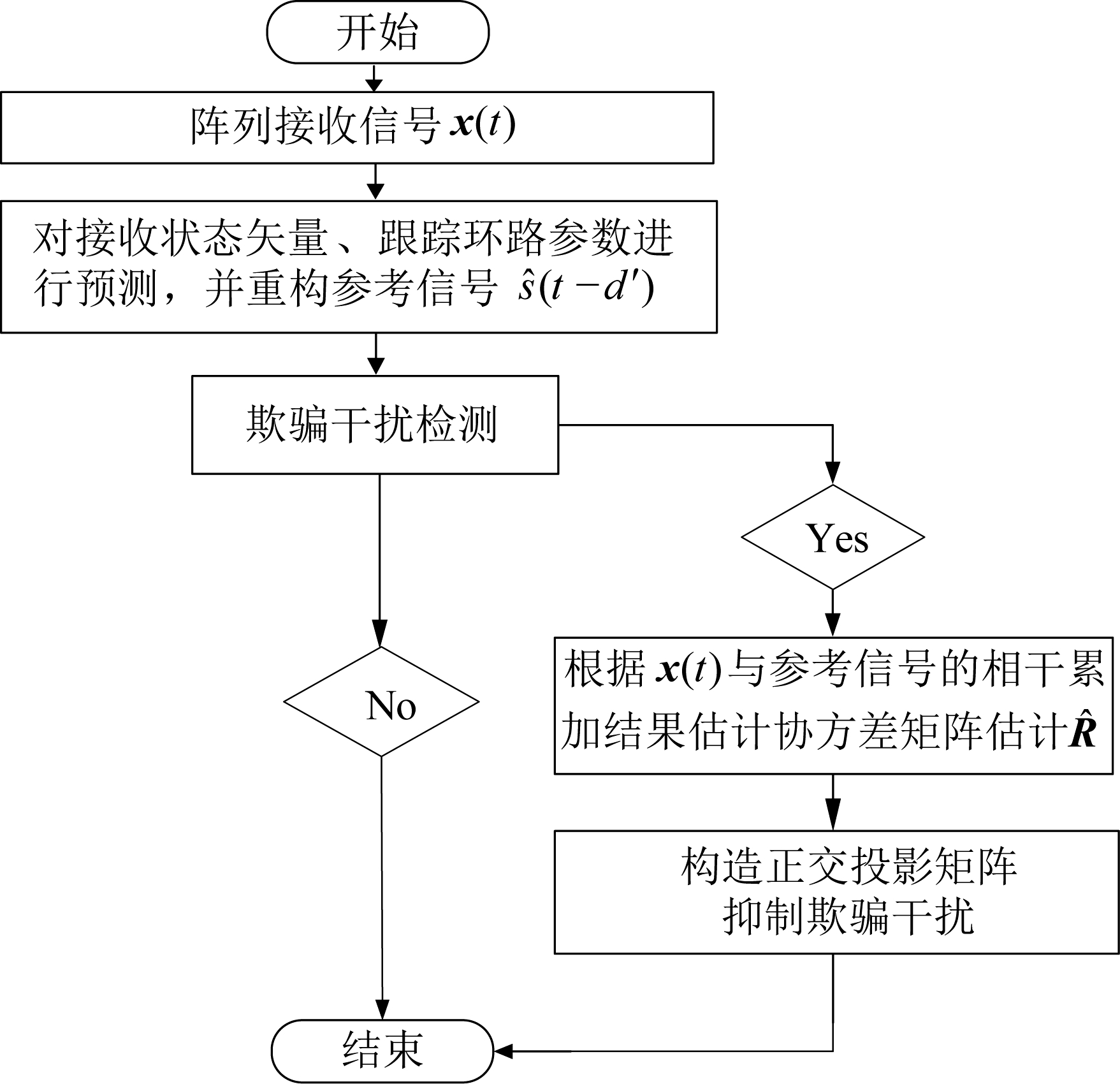
图3 欺骗干扰检测与抑制流程图
Fig.3 Flow chart for spoofing detection and suppression
本小节根据接收信号和基于远滞后码[14]的相干累加结果对欺骗干扰进行检测，下面以参考阵元为例对检测方法展开介绍。根据文献[21]可知，矢量跟踪环路利用卡尔曼滤波器的预测功能可以由前一时刻的信息预测得到当前时刻的跟踪环路参数，即载波频率
码相位
和载波相位
卡尔曼滤波器对跟踪环路参数的预测过程如下所示。
矢量跟踪环路的预测可以分为状态矢量的预测和跟踪环路参数的预测，将接收机的状态矢量定义为
其中
为接收机在ECEF坐标系中的三维位置坐标；c为光速；ctb为钟差；
为三维速度；ctd为钟漂。为了表述方便，给出以下定义
假设接收机在极短的一段时间Δt之内为匀速运动，根据前一时刻接收机的状态矢量X可以预测当前时刻的接收机状态矢量
因此，由
和当前时刻的星历信息可以预测得到第g颗卫星的伪距
与伪距率
即
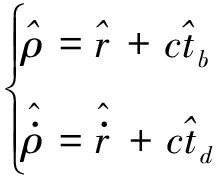
(7)
其中
表示第g颗卫星与接收机的几何距离，
表示第g颗卫星与接收机的距离对时间的导数，因此码频率、载波频率、码相位的预测值为：
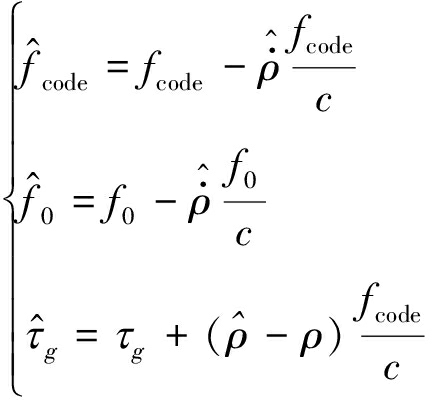
(8)
其中fcode表示C/A码的频率。根据以上预测的参数构造基于远滞后码[14]的参考信号
(9)
由C/A码的自相关特性可知，欺骗干扰存在时，参考阵元的接收信号与参考信号的相干累加结果为
VLg(n)=VLa(n)+VLs(n)=
(10)
其中VLa(n)表示参考阵元接收信号中的真实卫星信号La(n)与参考信号的相干累加结果，根据C/A码的互相关特性，由于真实卫星信号与参考信号之间的码片间隔大于一个码片，VLa(n)可近似为相关器输出噪声e；VLs(n)表示参考阵元接收信号中的欺骗干扰Ls(n)与参考信号的相干累加结果。因此根据参考阵元信号与远滞后码的相关能量构造欺骗干扰检测模型：
(11)
其中N是非相干累加的次数。由C/A码的自相关特性可知，矢量跟踪环路中出现欺骗干扰时，Ψ将会出现显著的相关峰值。基于公开资料[22]，Ψ的分布为2N个自由度的非中心χ2分布。无欺骗干扰时，检测统计量Ψ退化为2N个自由度的中心χ2分布。因此根据该检验统计量可以对生成式欺骗干扰进行检测。所提方法的检测门限根据恒定的虚警率给出，在判决门限取值为γ时，虚警率为：
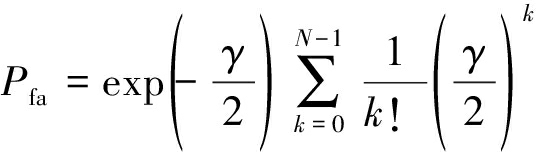
(12)
因此在恒虚警下γ的取值可以通过反解Pfa(γ)得到。基于以上分析，欺骗干扰检测模型如下所示：
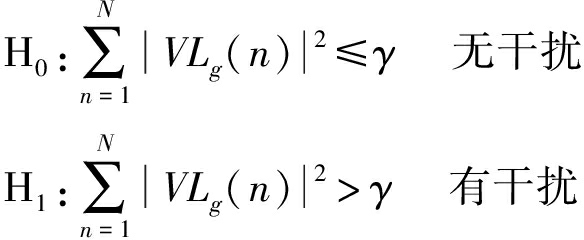
(13)
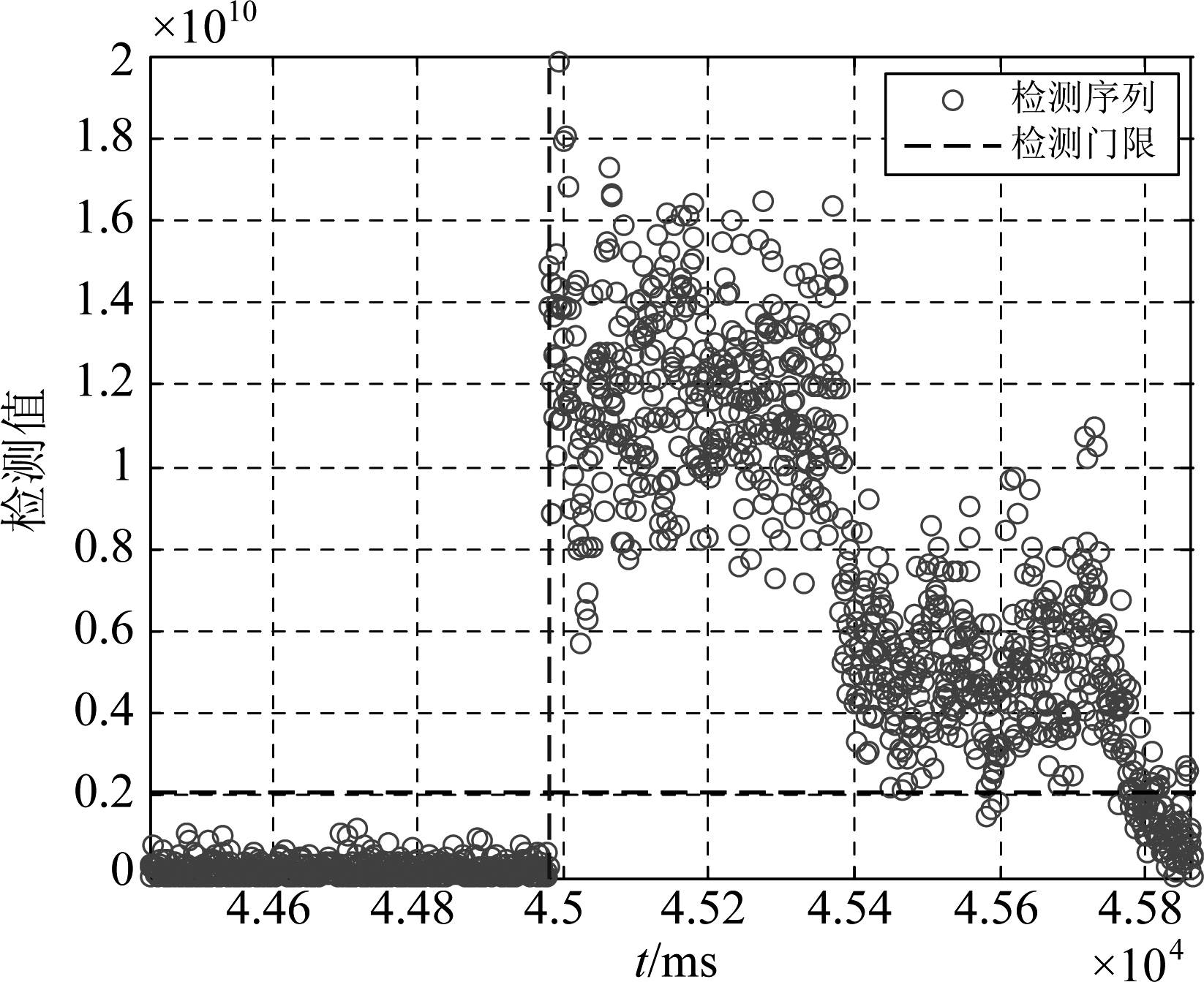
图4 检测统计量的变化
Fig.4 Change of detection statistics
图4是检测统计量Ψ受生成式欺骗干扰影响的示意图。本小节利用信号仿真器产生延迟不断发生变化的欺骗干扰(延迟由1400 ns-1200 ns-1000 ns- 800 ns不断发生变化)。通过该图可以看出生成式欺骗干扰通过引入额外的欺骗相关分量，从而导致检验统计量Ψ发生变化。本小节所提的欺骗干扰检测方法根据参考阵元与参考信号的相关能量输出检测欺骗干扰，出于算法普适性的考虑，以1/ 2码片为搜索步长、以远滞后码为参考基准，按照很远滞后码、远滞后码、滞后码的顺序在各码相位上逐一停留对检测统计量进行搜索检测，所提方法能够对落在检测门限之外的欺骗干扰进行检测。
对于检测到的欺骗干扰，本小节提出了基于阵列天线技术的欺骗干扰抑制方法，接下来对欺骗干扰抑制方法展开介绍。阵列接收信号与公式(9)中参考信号的相干累加结果为
(14)
取N毫秒数据的相干累加结果进行协方差矩阵估计，得到
(15)
其中
表示欺骗干扰与远滞后码的相关能量。对公式(15)中的协方差矩阵进行特征值分解，根据最大特征值对应的特征向量构造正交子空间P⊥：
(16)
根据该正交子空间对接收信号做正交投影可以抑制欺骗干扰。
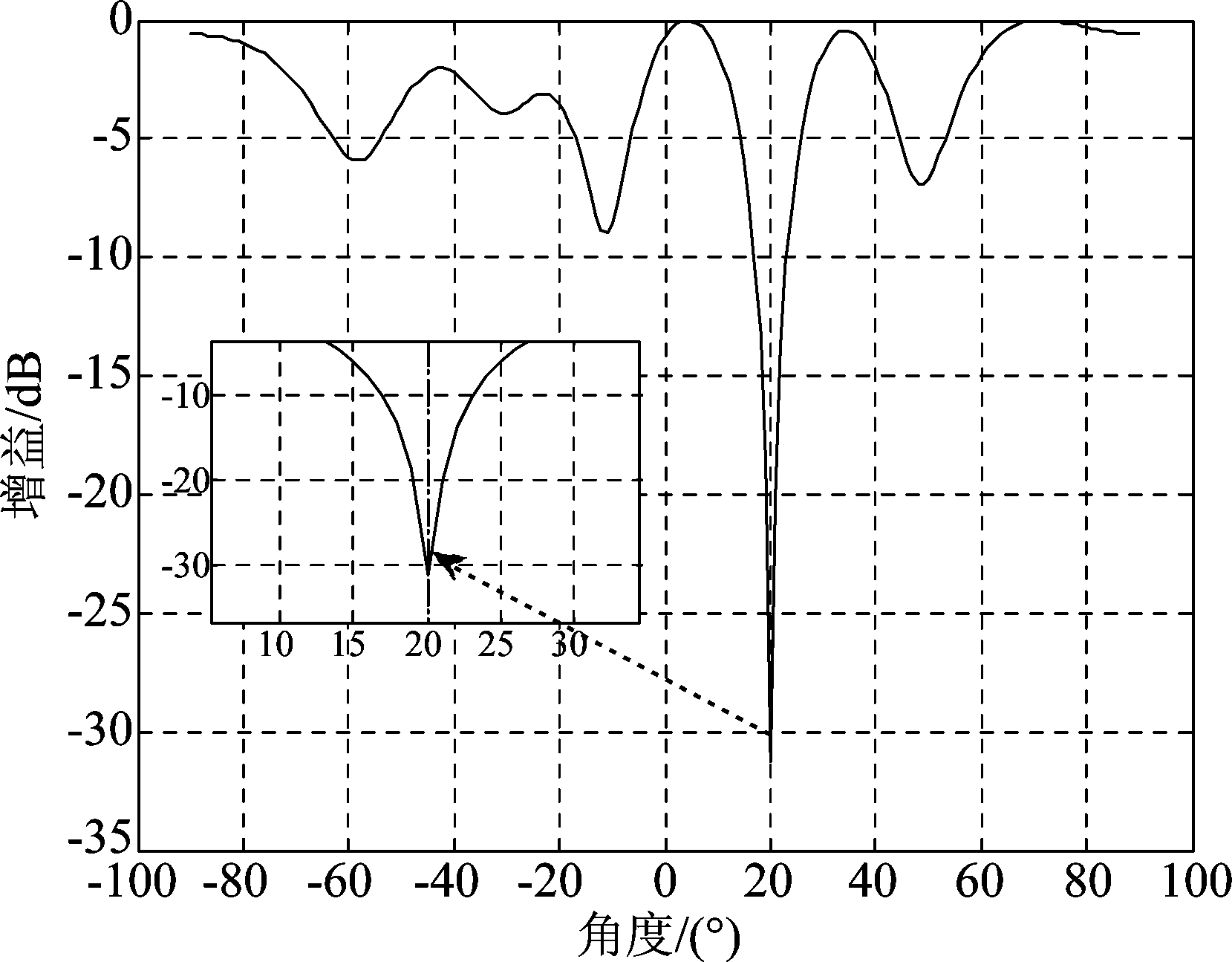
图5 波束图
Fig.5 Beam pattern
图5是本文所提欺骗干扰抑制算法的波束图，由该图可以看出所提方法可以在欺骗干扰来向上形成较深的零陷，从而可以抑制欺骗干扰。该仿真实验采用7阵元的线阵，使用信号仿真器产生PRN1,PRN3,PRN14,PRN20,PRN22五颗真实卫星信号和一个欺骗干扰。其中真实卫星信号来向分别为50°，35°,10°，-10°，-35°，GPS信号的SNR为-20 dB。欺骗干扰来向为20°，INR为-18 dB。
基于以上分析，可将所提方法对第g颗卫星信号的处理步骤(其余卫星信号采用相同的并行通道处理)概括如下：
步骤 1 根据跟踪环路预测的参数构造基于远滞后码的本地参考信号；
步骤 2 根据步骤1中的参考信号与接收信号的相干累加结果构造检验统计量得到欺骗干扰检测门限；
步骤 3 根据步骤2中的欺骗干扰检测模型检测欺骗干扰，无欺骗干扰则跳出步骤；有欺骗干扰进入下一步；
步骤 4 检测到欺骗干扰后，利用阵列接收信号与远滞后码的相干累加结果估计协方差矩阵，根据最大特征值对应的特征向量构造正交投影矩阵来抑制欺骗干扰。
本节所提欺骗干扰检测与抑制算法，在欺骗干扰和真实卫星信号来向未知的情况下，可以对欺骗干扰进行检测与抑制，具有盲自适应性。
4 仿真分析
本小节通过仿真实验分别从欺骗干扰延迟变化、欺骗干扰功率变化、欺骗干扰方向变化的角度对本文所提方法的有效性进行验证。仿真实验均采用7阵元的线阵，使用信号仿真器产生PRN1,PRN3,PRN14,PRN20,PRN22五颗真实卫星信号，来向分别为50°，35°,10°，-10°，-35°，GPS信号的SNR为-20 dB。
4.1 欺骗干扰延迟与功率变化时的抑制性能分析
使用GPS信号仿真器模拟生成式欺骗干扰场景：从45 s开始加入延迟和功率同时不断变化欺骗干扰(延迟由1400 ns-1200 ns-1000 ns- 800 ns不断变化；干噪比从-22 dB，-22 dB，-18 dB，-10 dB不断变化)，该欺骗干扰可以将接收机欺骗偏离正常位置。图6是矢量跟踪环路中的相关值在欺骗干扰的影响下不断发生变化的示意图，图7是传统的矢量跟踪环路(VTL)与本文所提方法进行对比的结果。
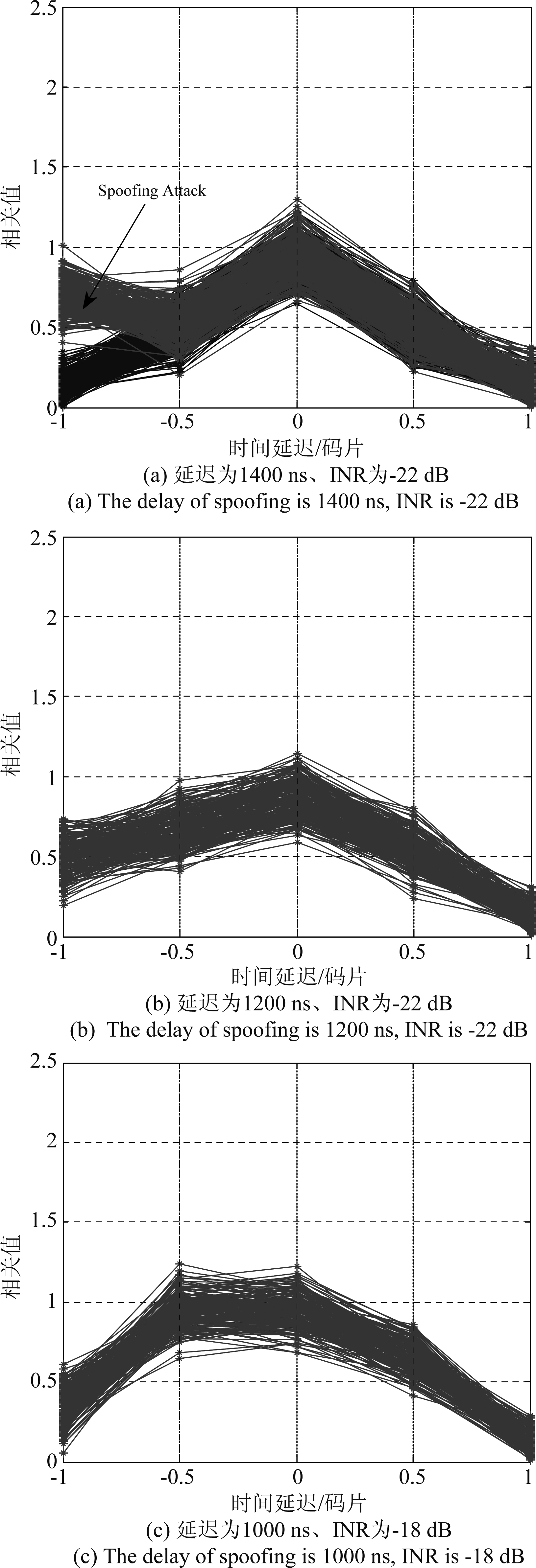
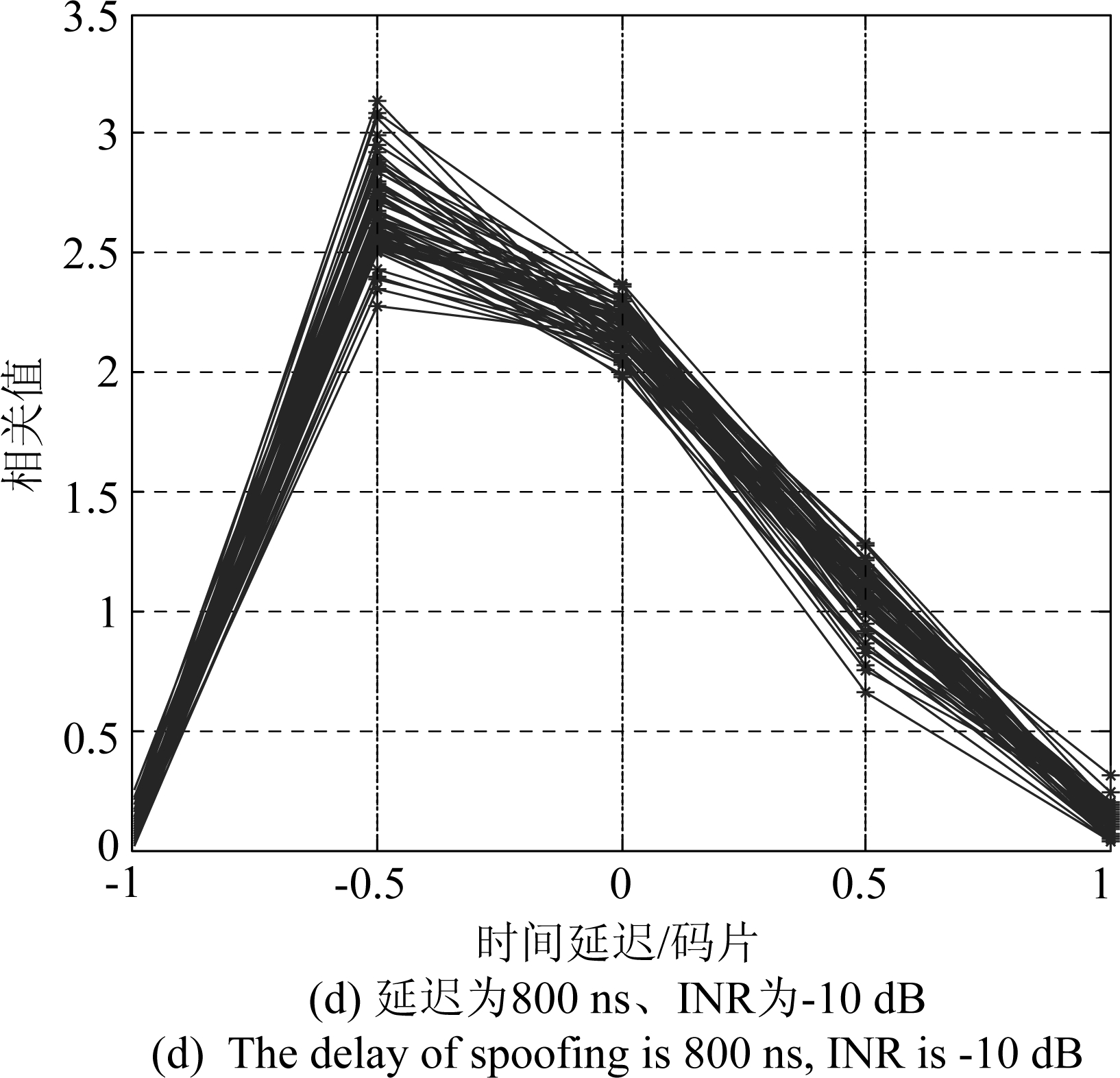
图6 相关值的变化
Fig.6 Change of correlation value
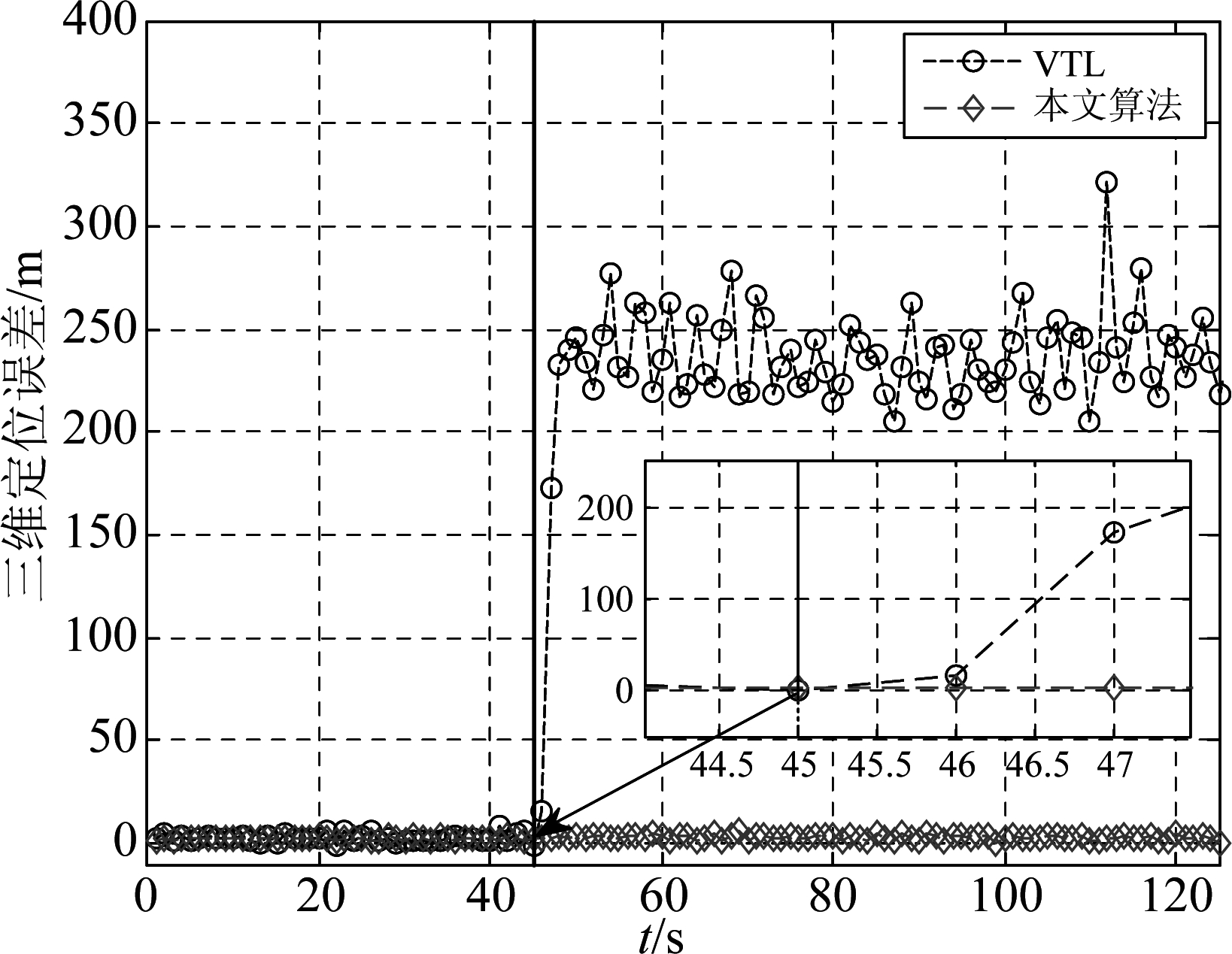
图7 对比结果
Fig.7 Comparison results
通过图6可知：在无欺骗干扰的情况下，相关值的形状接近等腰三角形，欺骗干扰导致其不断发生变化。由图6(a)可以看出，欺骗干扰的延迟为1400 ns(大于1个码片)，因此会对远滞后码的相关输出引入一定的相关分量，而对滞后码输出结果的影响较小；通过图7可以看出传统VTL的三维定位误差在45 s到45.4 s之内维持在正常工作范围之内，此时的欺骗干扰对接收机用户的定位结果影响较小。但是随着欺骗干扰延迟不断减小、功率不断增加，会对滞后码相关输出不断引入欺骗相关分量，因此图6(b)，6(c)，6(d)中的相关三角形不断发生畸变；由图7可以看出，接收机用户被该生成式欺骗干扰逐步欺骗至错误的位置。通过图7中的对比结果可以看出本文所提方法可以对欺骗干扰进行检测与抑制，从而保证接收机的三维定位误差维持在正常工作范围之内。
4.2 欺骗干扰方向变化时的抑制性能分析
使用GPS信号仿真器模拟生成式欺骗干扰场景：从45 s开始加入来向发生变化的欺骗干扰，其中欺骗干扰与真实卫星信号来向分别相差3°，6°，9°,12°,15°。图8是本文所提方法与传统矢量跟踪环路的三维定位误差的对比结果，表1是欺骗干扰来向不同的情况下，对抑制欺骗干扰后的三维定位误差进行10000次蒙特卡洛实验的统计结果。
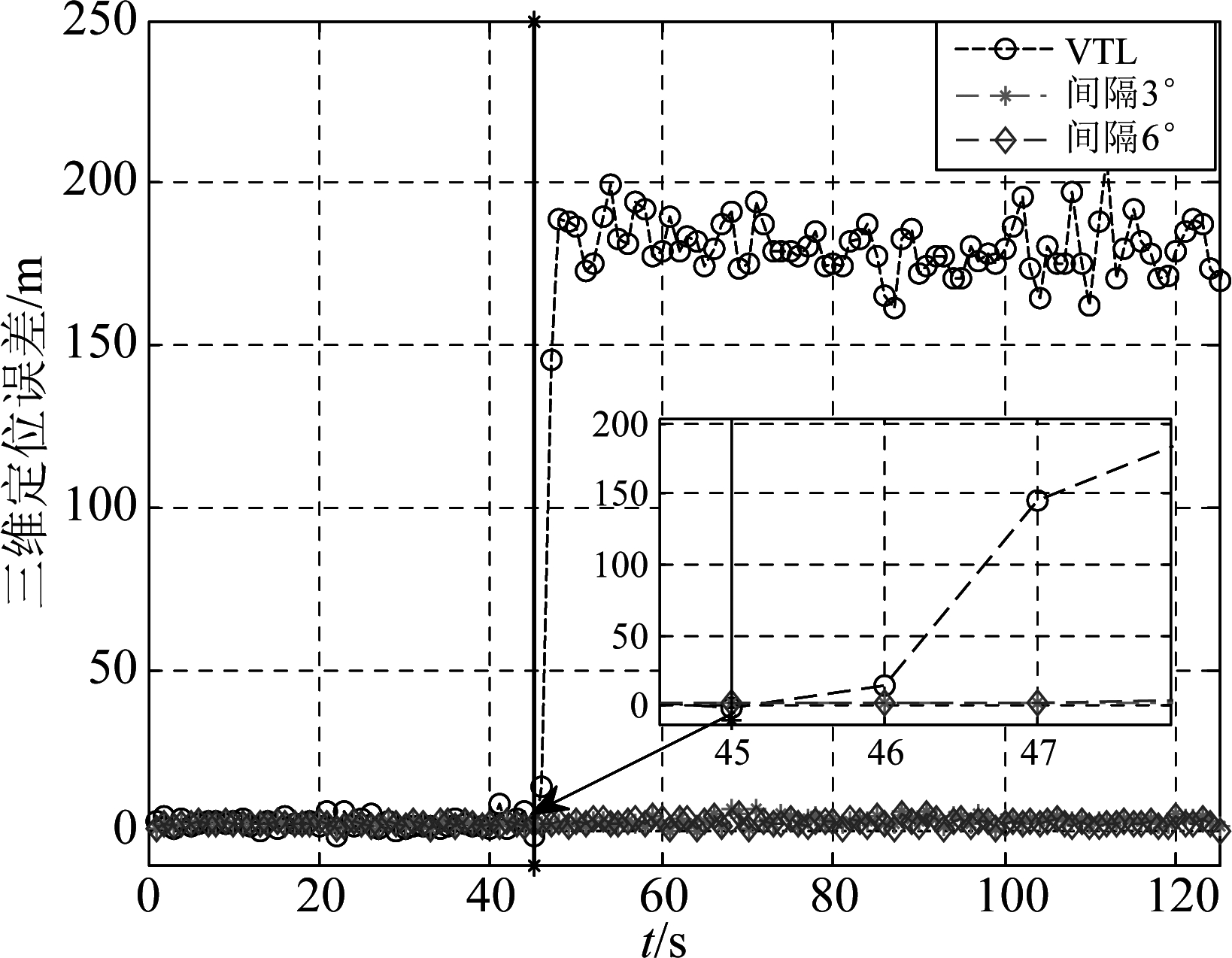
图8 定位误差对比结果
Fig.8 Comparison results of position errors
表1 定位结果的均方根误差
Tab.1 RMSE of position errors
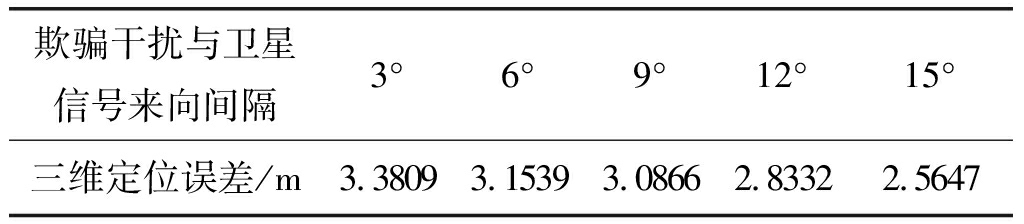
欺骗干扰与卫星信号来向间隔3°6°9°12°15°三维定位误差/m3.38093.15393.08662.83322.5647
通过图8可以看出本文所提方法对3°，6°来向的欺骗干扰均能在45 s时刻进行检测并抑制，保证接收机从45 s开始不受欺骗干扰的影响而正常工作；从整体来看，接收机的三维定位结果较平稳。由表1的统计结果可以看出，在欺骗干扰与真实卫星信号来向相差较近的情况下该方法仍然具有较小的定位误差；随着欺骗干扰与真实卫星信号的来向间隔逐渐增加，本文所提方法的处理效果不断提高。
4.3 被欺骗的卫星数目变化时的性能分析
使用GPS信号仿真器模拟生成式欺骗干扰场景：从45 s开始加入欺骗干扰，并且被欺骗的卫星数目不同。图9是传统矢量跟踪环路、本文所提算法、以及文献[14]中的抗欺骗干扰方法的三维定位误差的对比结果。
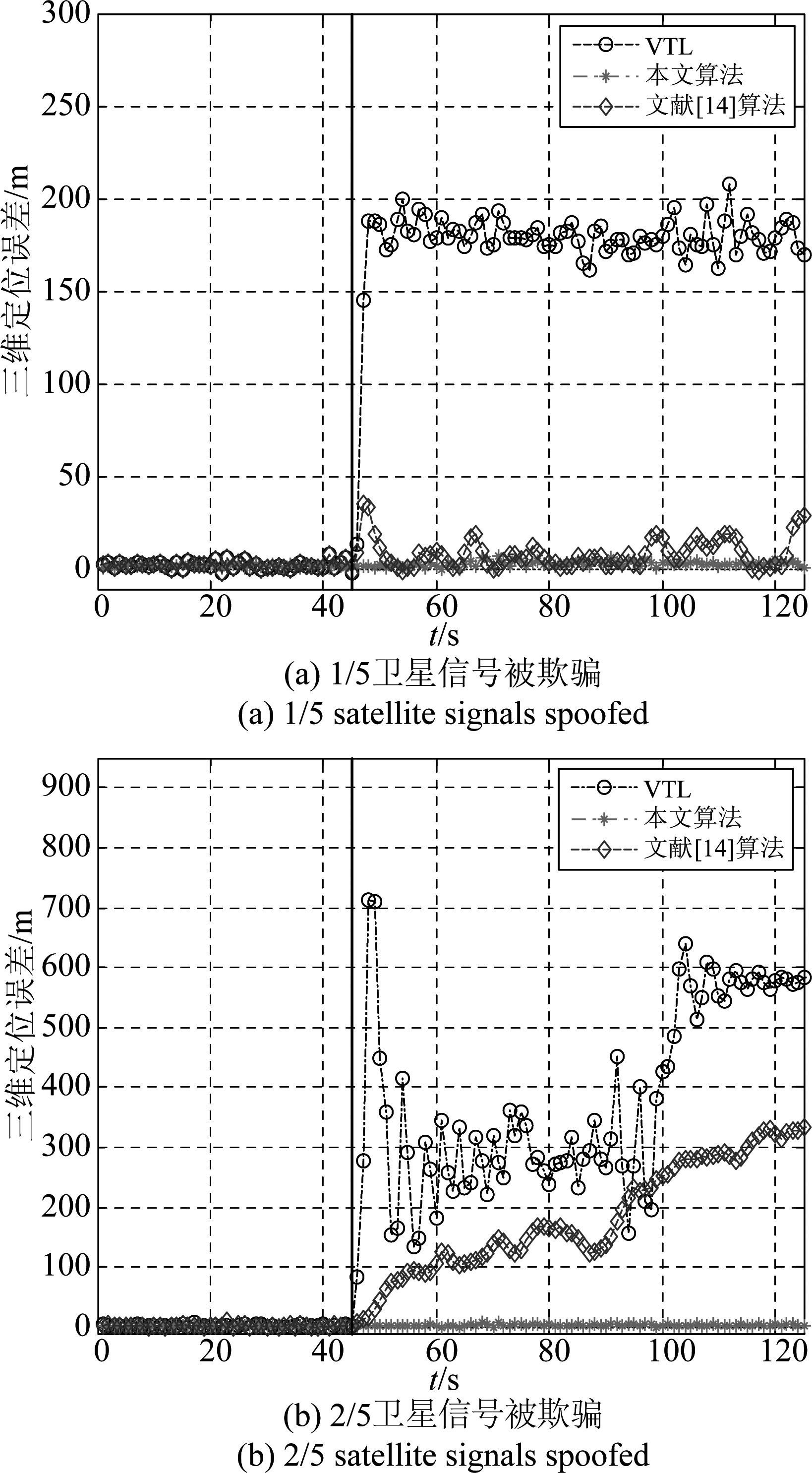
图9 定位误差对比结果
Fig.9 Comparison results of position errors
通过图9(a)可以看出，当5颗卫星信号中的1颗卫星信号被欺骗时，本文所提方法和文献[14]中的方法从45 s开始可以不受欺骗干扰的影响而保证接收机的定位误差维持在正常工作范围之内，但是本文所提算法的三维定位误差结果较文献[14]中的方法较平稳，且定位误差较小。通过图9(b)可以看出，当5颗卫星信号中的2颗卫星信号被欺骗时，本文所提算法仍然具有较稳健的定位性能，此时文献[14]中的算法效果不太好，这是由于GPS正常工作至少需要4颗卫星。通过以上对比结果可以看出，本文所提算法的定位性能较平稳。但是与文献[14]中的抗欺骗干扰方法相比，本文采用天线阵抑制欺骗干扰，成本偏高。
5 结论
针对矢量跟踪环路在复杂电磁环境下面临着被欺骗的风险，本文将阵列天线技术中的解重扩算法与矢量跟踪环路相结合来提高矢量跟踪环路的抗欺骗干扰性能。首先利用卡尔曼滤波器对跟踪环路的参数进行预测，并根据跟踪环路参数构造基于远滞后码的本地参考信号；其次根据参考阵元与参考信号的相干累加结果构造欺骗干扰检测模型；然后根据阵列接收信号与参考信号相干累加结果估计协方差矩阵，由协方差矩阵估计欺骗干扰的特征向量，通过该特征向量构造正交投影矩阵抑制欺骗干扰。理论分析和仿真实验得出以下结论：本文所提方法在欺骗干扰与卫星信号来向未知的情况下对生成式欺骗干扰具有较好的检测与抑制性能。
[1] 吴仁彪, 王文益, 卢丹，等. 卫星导航自适应抗干扰技术[M]. 北京: 科学出版社, 2015: 1-22.
Wu R B,Wang W Y,Lu D, et al. Adaptive Interference Mitigation in GNSS[M]. Beijing: Science Press,2015: 1-22. (in Chinese)
[2] Humphreys T E, Ledvina B M, Psiaki M L, et al.Assessing the Spoofing Threat: Development of a Portable GPS Civilian Spoofer[C]∥International Technical Meeting of the Satellite Division of the Institute of Navigation, 2008:2314-2325.
[3] Kerns A J, Shepard D P, Bhatti J A, et al. Unmanned Aircraft Capture and Control Via GPS Spoofing[J]. Journal of Field Robotics, 2014, 31(4):617- 636.
[4] 林成龙. 精准跟踪—让飞机永不失联[EB/OL]. http:∥www.caacnews.com.cn,2017- 08-21/ 2017-9-10.
Lin C L. Precise tracking-Let plane never lose touch[EB/OL]. http:∥www.caacnews.com.cn,2017- 08-21/ 2017-9-10.(in Chinese)
[5] 陈碧. GPS欺骗技术中的信号同步问题研究[D]. 成都: 电子科技大学, 2016.
Chen B. Research on signal synchronization in GPS spoofing technology[D]. Chengdu: University of Electronic Science and Technology of China,2016. (in Chinese)
[6] 陈碧, 郭承军.GPS欺骗干扰过程研究[J]. 科技通报, 2016, 32(10):164-169.
Chen B, Guo C J. Research on GPS deception jamming process[J]. Bulletin of Science and Technology,2016,32(10):164-169.(in Chinese)
[7] Cuntz M, Konovaltsev A, Meurer M. Concepts, Development, and Validation of Multiantenna GNSS Receivers for Resilient Navigation[J]. Proceedings of the IEEE, 2016, 104(6): 1288-1301.
[8] Chou D, Gao Grace Xingxin. Robust GPS-Based Timing for PMUs Based on Multi-Receiver Position-Information-Aided Vector Tracking[C]∥Proceedings of the 2015 International Technical Meeting of the Institute of Navigation, Dana Point, California, January 2015: 600- 607.
[9] Ng Yuting, Gao Grace Xingxin. Advanced Multi-Receiver Position-Information-Aided Vector Tracking for Robust GPS Time Transfer to PMUs[C]∥Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2015), Tampa, Florida, September 2015: 3443-3448.
[10] Chou D, Liang H, Gao G X. Robust GPS-Based timing for phasor measurement units: A Position-Information-Aided approach[J]. International Journal of Modelling Identification & Control, 2014, 24(1):62-74.
[11] Liang H, Work D B, Gao G X. GPS Signal Authentication From Cooperative Peers[J]. IEEE Transactions on Intelligent Transportation Systems,2015,16(4):1794-1805.doi: 10.1109/TITS.2014.2372000.
[12] Ng Y, Gao G. GNSS Multi-Receiver Vector Tracking[J]. IEEE Transactions on Aerospace & Electronic Systems, 2017, PP(99):1-1.
[13] Sun Z, Wang X, Feng S, et al. Design of an adaptive GPS vector tracking loop with the detection and isolation of contaminated channels[J]. GPS Solutions, 2016,21(7):1-13.
[14] Jafarnia-Jahromi A, Lin T, Broumandan A, et al. Detection and mitigation of spoofing attacks on a vector-based tracking GPS receiver[C]∥Proceedings of ION ITM, 2012, 2012: 790- 800.
[15] 包莉娜, 吴仁彪, 王文益,等. 两级结构的卫星导航压制式和欺骗式干扰联合抑制算法[J]. 信号处理, 2015,31(9): 1041-1045.
Bao L N, Wu R B, Wang W Y, et al. Two-step GPS interference suppression algorithm for spoofing and jamming[J]. Journal of Signal Processing, 2015,31(9): 1041-1045.(in Chinese)
[16] 王文益,彭敏英,吴仁彪.利用联合互质阵列的卫星导航抗干扰算法[J].信号处理,2015,31(9):1082-1086.
Wang W Y, Peng M Y, Wu R B. Interference Suppression by Utilizing Coprime Array for GNSS[J]. Journal of Signal Processing,2015,31(9):1082-1086.(in Chinese)
[17] 王璐, 李素姣, 张耀天, 等. 利用周期重复CLEAN的GNSS欺骗式干扰抑制算法[J]. 信号处理, 2015,31(12): 1636-1641.
Wang L, Li S J, Zhang Y T, et al. Spoofing Interference Suppression in GNSS Using Repeated CLEAN[J]. Journal of Signal Processing, 2015,31(12): 1636-1641.(in Chinese)
[18] 卢丹. 稳健的全球卫星导航系统抗干扰技术研究[D]. 西安：西安电子科技大学，2013.
Lu D. Robust Anti-jamming Techniques for Global Navigation Satellite System[D]. Xi’an: Xidian Univerisity, 2013.(in Chinese)
[19] Ioannides R T, Pany T, Gibbons G. Known Vulnerabilities of Global Navigation Satellite Systems, Status, and Potential Mitigation Techniques[J]. Proceedings of the IEEE, 2016, 104(6):1174-1194.
[20] Psiaki M L, Humphreys T E. GNSS Spoofing and Detection[J]. Proceedings of the IEEE, 2016, 104(6):1258-1270.
[21] Li F S, Wu R B, Wang W Y. The Anti-jamming Performance Analysis for Vector Tracking Loop[M]. China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume I: 665- 675. doi:10.1007/978-981-10- 0934-1_57.
[22] 姚铮, 陆明泉. 新一代卫星导航系统信号设计原理与实现技术[M]. 北京: 电子工业出版社, 2016: 114-151.
Yao Z, Lu M Q. Signal Design Principle and Implementation Technology of A New Generation of Satellite Navigation System[M]. Beijing: Electronic Industry Press, 2016: 114-151.(in Chinese)
