1 引言
图像超分辨率重构(Super-Resolution Reconstruction,SRR)是一种增强成像系统分辨率技术,该技术是从观察到的低分辨率图重建高分辨率图,为图像恢复出更多细节信息,提供更好的视觉效果图像。由于高分辨率图像中包含更多细节信息,SRR技术在视频监控、医学图像、遥感卫星、多径稀疏信道传输等各个领域具有重要现实意义和广泛应用价值[1-4],得到学术界高度关注[5-10]。然而,SRR技术是一个典型的病态逆过程[11-12],具有非常大的挑战性。
SRR方法研究经历了从频域转向空域以及从无训练样本到有训练样本的过程。最早SRR方法研究在频域中进行图像重构,通过设置截止频率方式恢复信息,但频域算法存在对噪声较为敏感的缺点[13]。基于非均匀插值的SRR方法是最直观通用的空域超分辨率重构方法,该方法通过在像素之间插入合适的像素值,实现图像分辨率提升[14]。然而,简单非均匀插值算法倾向于使图像变得平滑,同时会造成块状效应。后来,研究者通过在插值过程中引入图像先验信息来克服这一问题,但这种方式对图像视觉表现复杂度较为敏感,对于许多纹理或阴影图像,容易出现振铃效应。基于重建的SRR方法是对低分辨率图像进行一致性约束,并结合自然图像先验知识进行求解[15],该类算法能在先验信息充足条件下获得较好重构效果,但存在图像序列数目不充分导致重构效果退化的缺点。因此,传统SRR方法研究在实现条件上更加严苛,且对放大系数较为敏感,在有限条件下难以实现高质量图像重构[16]。基于机器学习SRR技术发展迅速,尤其是稀疏编码理论的发展为SRR方法研究带来了许多启发[17-22]。Timofte等[23]采用调整锚点的最近邻回归算法实现高质量高效超分辨率重构,同时为深度学习在超分辨率领域应用奠定了坚实的技术基础。目前,深度卷积神经网络(Deep Convolution Neural Network,DCNN)在计算机视觉问题中被广泛使用,Dong等[24]提出利用卷积神经网络对图像进行超分辨率重构(Super Resolution Using Convolutional Neural Networks, SRCNN),其利用卷积神经网络学习低分辨率到高分辨率的端到端映射关系,重构超分辨率图像。DCNN可实现端到端的学习架构,省去特征提取预处理过程和后续高分辨率图像块聚合过程,SRCNN算法的提出奠定了深度学习应用到超分辨率重构领域的基础。后来,Dong 等[24]在SRCNN方法基础上提出一种快速超分辨率(Fast Super-Resolution by Convolutional Neural Networks, FSRCNN)方法[25],该方法以低分辨率图像作为网络输入,通过减小特征图维度和卷积核尺寸,可减少网络训练参数,提高了网络运算速度。Shi等[26]提出一种利用亚像素卷积层的超分辨率(Super-Resolution Using Efficient Sub-Pixel CNN, ESPCN)重构方法,该方法在最后一层重新对特征图进行排列,以得到高分辨率图像,可大幅提高网络运算速度。He等[27]提出深度残差网络(Residual Network, ResNet),该网络采用残差块作为网络基本组成部分, 通过顺序累加残差可一定程度上解决DCNN随着深度增加而带来的网络退化问题,提高网络性能。在超分辨率中Kim等[28]引入更深网络,借鉴 ResNet思想减轻网络的学习“负担”,加速学习率,并构造适用于不同图像放大尺度的网络。近年,Lai等[29]提出基于级联卷积神经网路的拉普拉斯金字塔超分辨率重构方法(Laplacian pyramid super resolution network, LapSRN),该方法采用类似金字塔方式提取不同尺度图像特征,在每个子阶段利用残差策略训练网络,进而重构超分辨率图像。Lim等[30]利用深度残差网络进行超分辨率重构在NTIRE2017超分辨率挑战赛中拔得头筹。虽然以上网络取得了良好性能,但深层网络需要学习大量参数。与紧凑网络模型相比之下,深层网络需要更多的存储空间,难以推广到便携式设备中使用。
针对上述问题,本文提出一种可用于便携式设备的紧凑型多径残差卷积神经网络。与传统图像超分辨率方法不同,本文算法没有直接重建出高分辨率图像,而是通过网络学习到图像高频细节信息,并利用获得的高频信息和原始低分辨率图像重建出高分辨率图像。同时引入多径残差思想,采用多径结构及递归块连接方式,共享递归残差块所有参数,大大减少参数量。为使网络泛化能力更强,结构更紧凑,本文采用最大特征图(Max-Feature-Max, MFM)激活函数[31],可有效捕捉到紧凑表示及具有竞争性特征信息,实现低分辨率图像的超分辨率重构。
本文内容安排如下:第2部分阐述卷积神经网络基本理论知识;第3部分介绍本文采用的多径卷积神经网络以及最大特征图残差块;第4部分介绍实验结果;第5部分对本文进行总结和展望。
2 卷积神经网络
卷积神经网络(Convolution Neural Network, CNN)目前已成为图像处理领域的研究热点,在计算机视觉领域中被广泛使用。深度学习是一种端到端的学习算法,直接将图像输入到网络来学习目标特征,基于原始数据的表征学习算法,逐层进行特征提取和特征融合,随着网络不断加深,提取到的特征越抽象,越有利于实现后续的识别、重构等工作。典型CNN是一个多层的神经网络,能够高效高质地处理图像相关的机器学习问题。CNN主要由输入层、卷积层、池化层、全连接层和输出层组成,其结构如图1所示。
CNN权值共享结构类似于生物神经网络,卷积层中的神经元与其输入层的特征图进行局部连接,将该局部加权和传递给非线性函数,如修正线性单元(Rectified Linear Units, ReLU)函数,获得卷积层中每个神经元输出值。在同一个输入特征图和同一个输出特征图中,CNN权值共享,该网络通过权值共享减小模型复杂度,使网络更易于训练[32]。由于SRR是一病态逆问题,通常在求解高分辨率图像时需加入一个正则化项作为先验信息进行规范化约束,从而求得最优解,实现超分辨率重构。在传统方法中,该先验信息通过若干低分辨率和高分辨率图像对中学到,而基于深度学习的SRR通过神经网络直接学习分辨率图像到高分辨率图像的映射函数实现超分辨率重构[33]。本文设计了多径卷积神经网络结构,可自主学习图像特征,并引入最大特征图残差块,使网络能够直接学习SRR所需图像细节信息,使网络输出尽可能接近本地高分辨率图像,损失函数均方误差最小化。所提网络不仅能有效缓解深度网络难以训练问题,同时能够较好解决超分辨率病态逆问题。
3 本文方法
3.1 多径深度卷积神经网络结构
超分辨率卷积神经网络设计充分考虑低分辨率图像与高分辨率图像间关系,不仅可直接学习高分辨率图像与低分辨率图像的非线性映射关系,也可学习到从低分辨率图像中损失的细节信息。本文网络是由特征提取模块、一系列残差模块和重构模块构成,特征提取模块是通过一层卷积层中卷积核与输入图像进行卷积操作提取输入图像特征并输出特征图,由于大量图像细节经过多层卷积运算后消失,会导致网络训练性能下降的问题,此处本文引入多径结构模式学习局部残差学习(Local Residual Learning, LRL)方法缓解深度网络训练性能下降问题,以及加入全局残差学习(Global residual learning, GRL)方法充分利用低分辨率图像中的信息,通过卷积操作将估计的残差特征,并结合低分辨率信息重构高分辨率图像,所提多径卷积网络结构如图2所示。
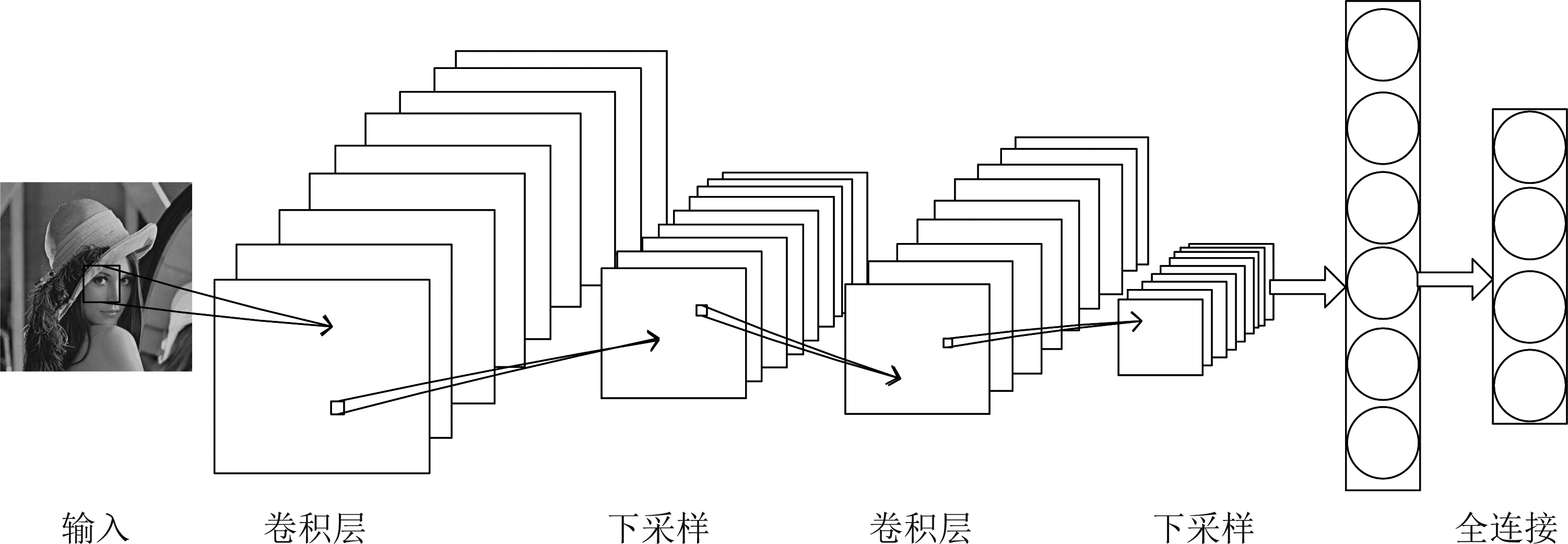
图1 卷积神经网络结构示意图
Fig.1 Diagram of convolutional neural network architecture
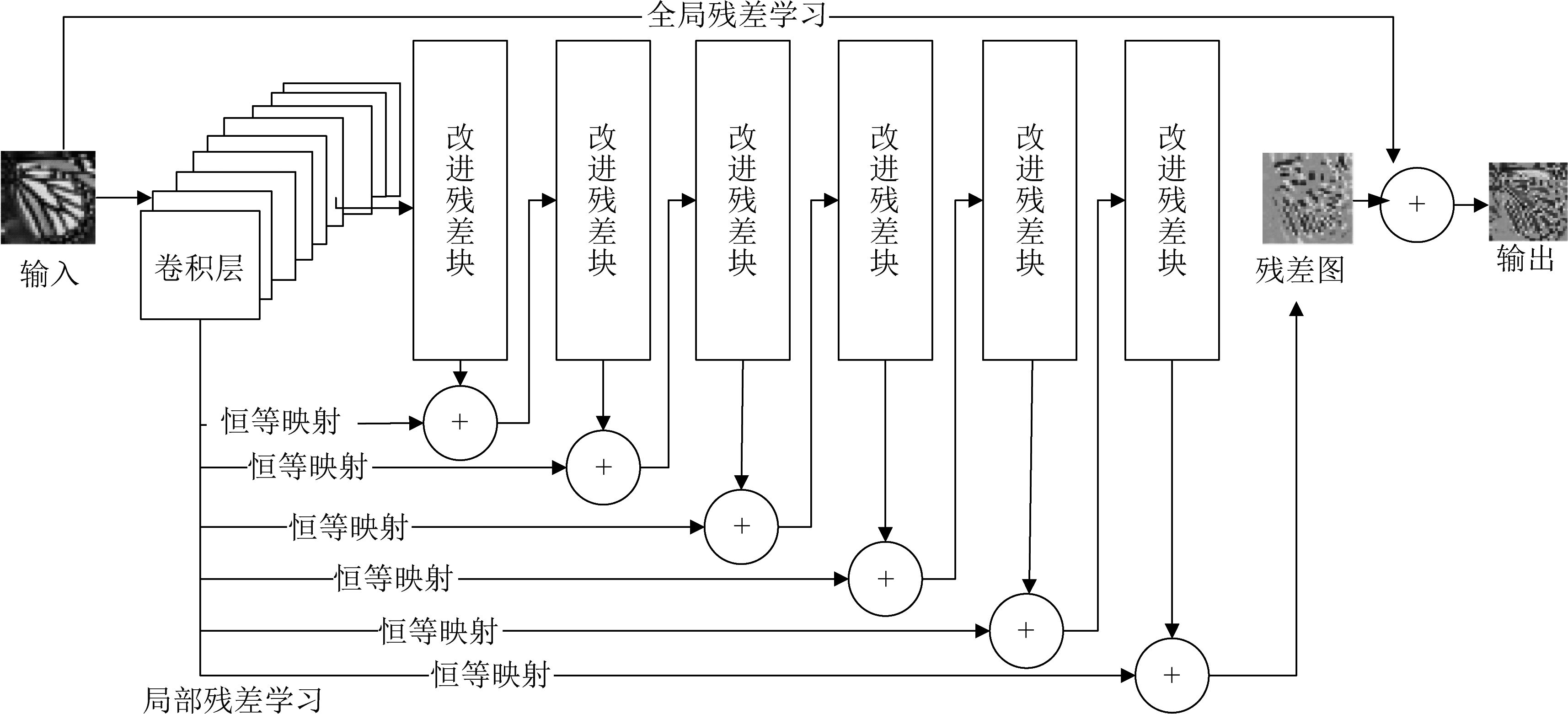
图2 多径深度卷积网络结构
Fig.2 Architecture of multi-path deep convolutional neural network
由图2可知,多径网络结构包括GRL和LRL两部分。本文中高分辨率图像由网络估计出的残差图像通过GRL分支与输入图像求和得到,而网络通过恒等映射分支所携带的丰富细节信息不断融合到主路径中。这种方式不仅可缓解深度网络难以训练问题,也有助于梯度流动。由于图像超分辨率重构是逐像素输出,相比数值输出,本文网络结构仅由卷积层构成,不考虑容易致使细节丢失的池化层。输入图像经过卷积层处理,卷积核尺寸为3×3,输出32张特征图,在改进残差块中进行训练。通过恒等映射分支携带的大量细节信息,补充到每一个残差块的输出特征图上。该递归式连接方式,可使每个残差块的权值共享,从而减小网络训练参数,在一定程度上缓解网络训练难度。
残差学习在传统线性网络结构基础上,引入捷径分支,以绕过相关层进行连接,经过求和方式融入到主路径。加入捷径分支后,训练过程中底层误差可通过捷径向上一层传播,减缓因层数过多造成的梯度消失现象,提高训练精度。同时,捷径引入并没有引入额外参数,不影响原始网络复杂度。整个网络仍可使用现有深度学习反馈训练求解。
残差网络是在链式模式中堆叠局部残差单元,每个残差单元由几个卷积层构成。链式残差模型如图3(a)所示,残差单元输出表示为:
HU=F(HU-1,WU)+HU-1
(1)
图像超分辨率重构中细节信息极为重要,为增强网络学习细节信息能力及有效避免过拟合现象,本文对残差网络连接方式进行改进,在残差网络中加入GRL,由于SRR输出和输入非常相似,GRL引入减小网络计算复杂度,显著提高网络训练效率。同时,为了增强每一个残差块输出的细节信息,将第一层卷积层输出特征补充到每一个残差块中,为与链式残差结构进行区分,这种改进型残差网络命名为多径残差结构。其结构示意图如图3(b)所示。将残差单元可定义为:
HU=F(HU-1,W)+H0
(2)
其中F表示残差单元的激活函数,H0是网络第一个卷积层的结果。由于残差单位是以递归方式学习的,所以权重设定W在递归块中的残差单位之间共享。
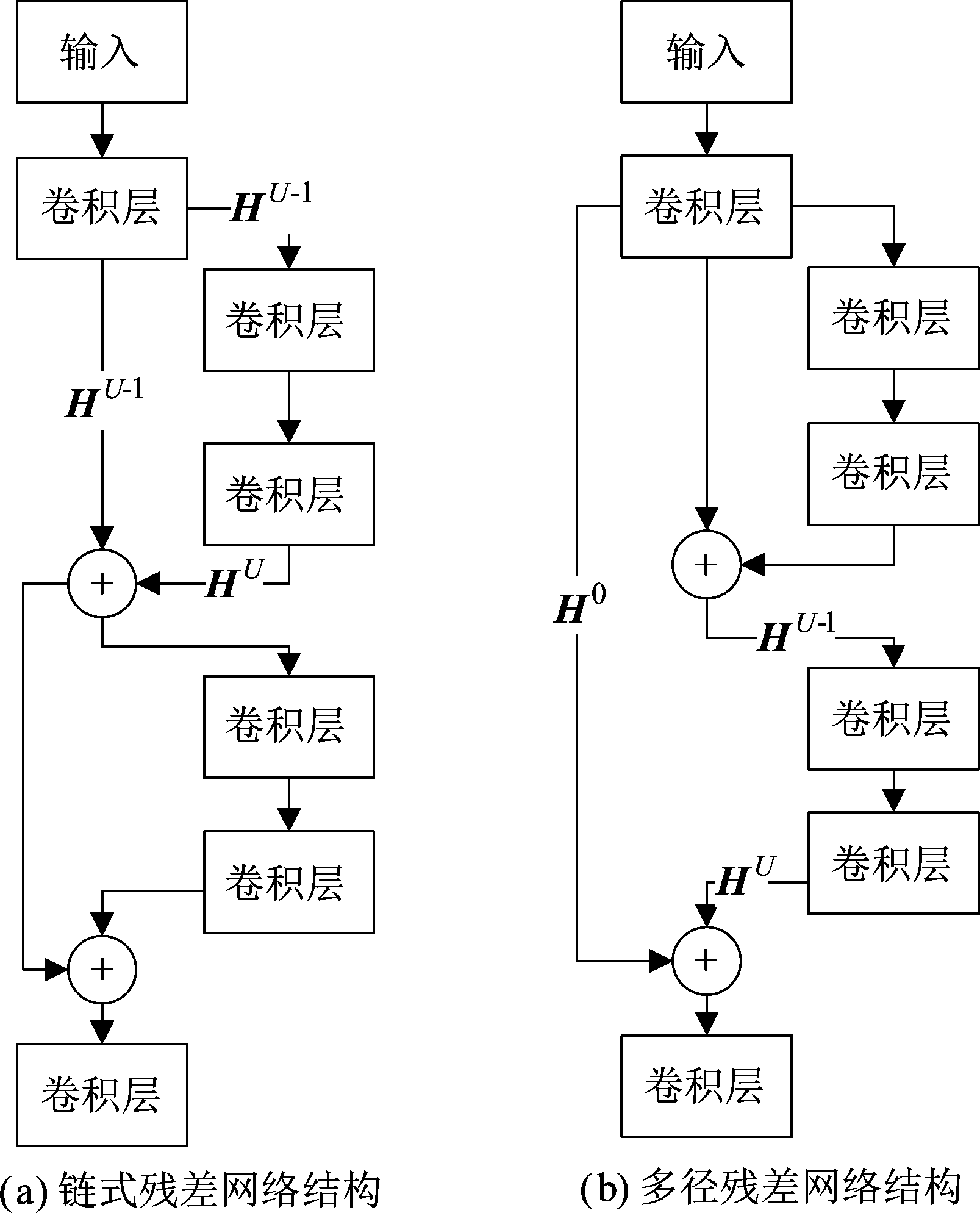
图3 残差结构示意图
Fig.3 Diagram of residual architecture
3.2 基于最大特征图的改进残差块
为了增强网络泛化能力,使网络结构更加紧凑,同时提高激活函数非线性性能,本文引入基于最大特征图激活函数,该激活函数在输入卷积层中选择两张特征图,并取相同位置较大的值,并提出一种基于最大特征图的改进残差块方法。MFM激活函数如图4所示。
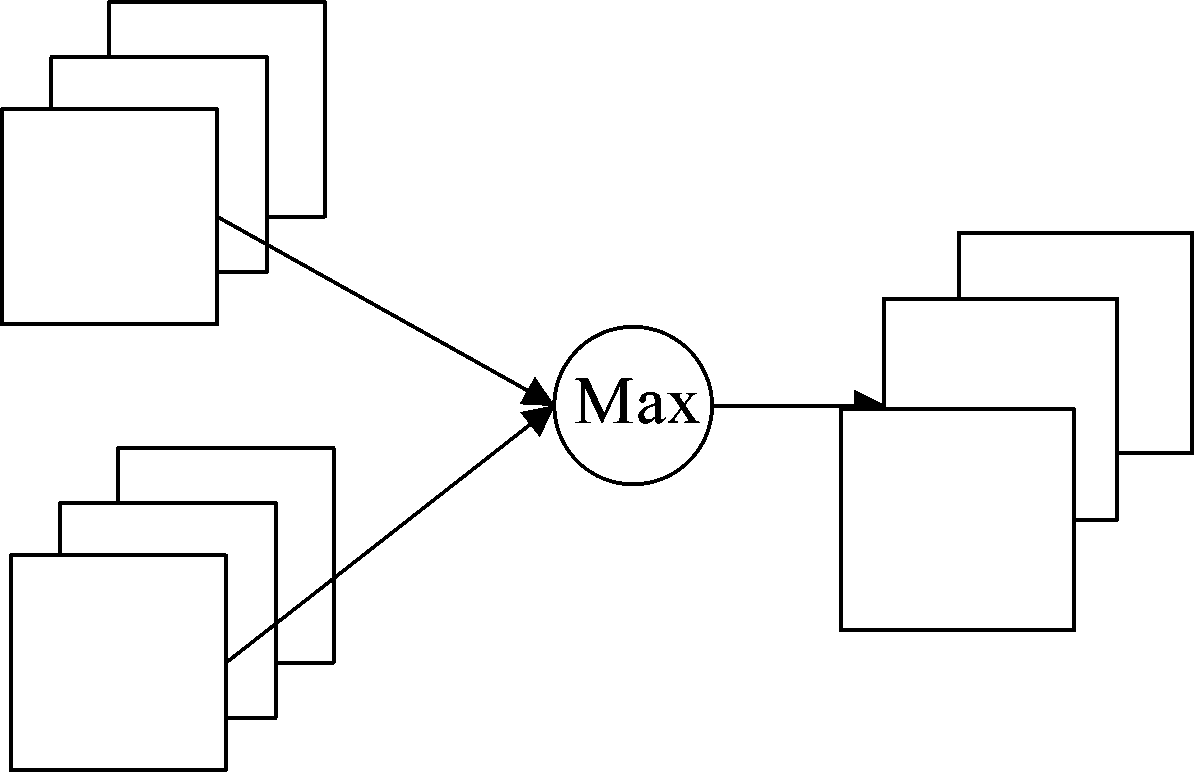
图4 MFM结构示意图
Fig.4 Diagram of MFM architecture
下面将对MFM和ReLU层的前向计算和后向梯度求解。
假设ReLU层的输入集为X,则输出集Y为
Y=max(0,X)
(3)
假设![]() 则ReLU层梯度为
则ReLU层梯度为
(4)
假设MFM层输入集为X,先把X等分成X1和X2两部分,再计算输出集Y,即
Y=max(X1,X2)
(5)
MFM层梯度为
(6)
其中,![]()
由公式(6)可看出,MFM激活层有一半梯度值为0,可得到稀疏梯度。MFM激活函数相比于ReLU函数,后者的特征是稀疏高维的。经过前者处理之后,可得到低维紧实特征,实现特征选择和降维效果。相比ReLU,MFM能使网络更紧凑。
残差块结构如图5(a),输入表示为Xi,恒等映射为H(Xi),残差映射定义为:
F(Xi+1)=H(Xi)+Xi
(7)
相比直接学习恒等映射H(Xi)=Xi,残差结构使网络训练更容易。随着深度网络不断发展,增加网络深度能够提升网络精度。为防止梯度爆炸或梯度弥散,进行规范初始化并引入批量正则化层(batch normalization, BN)方式,利用随机梯度下降(Stochastic Gradient Descent, SGD)方法使得反馈网络求解得以收敛,降低了网络灵活性。且层数较多时,梯度在传播过程中逐渐消失,反而会降低识别率。基于上述存在问题,本文提出基于最大特征图残差块,改进后残差块如下图5(b)所示。
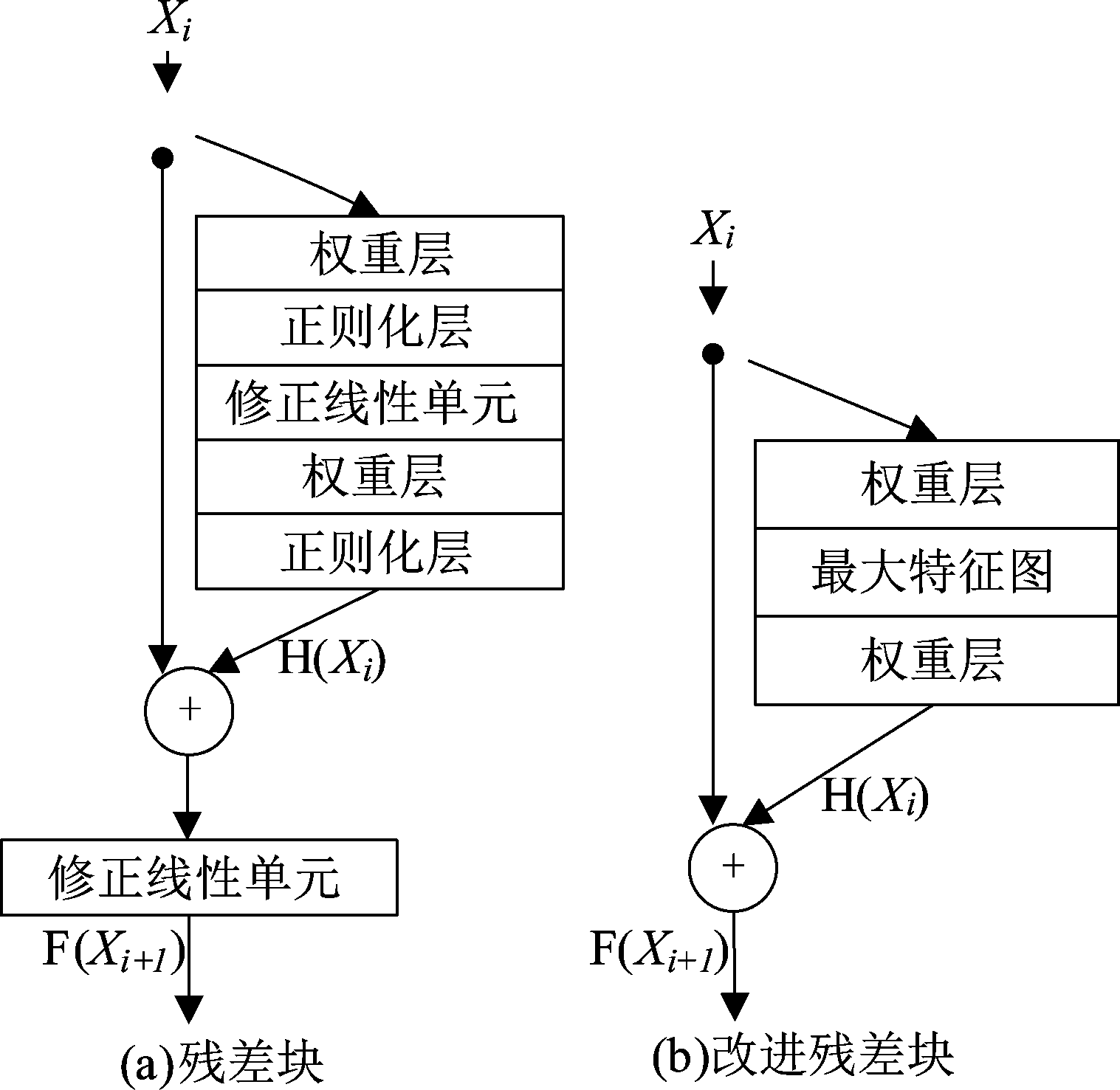
图5 基于最大特征图残差块
Fig.5 Based on Max-feature-Max residual block
由于BN层会致使部分细节信息丢失有价值信息,和消耗与卷积层等量内存,致使训练速度减慢。因而,本文采用去掉BN层,并采用多径结构方式,该方式能使网络更易收敛,并减轻网络深度导致的退化问题。卷积网络结构中采用ReLU激活函数时,存在当局部加权和为负数时激活后值为零导致丢失部分信息问题,及梯度消失问题。本文引入MFM激活函数,可有效克服上述两点问题,并能提高激活函数非线性性能,增强网络泛化能力,使网络结构更加紧凑。
4 实验结果与分析
4.1 实验参数设置
本文实验所用计算机配置为Xeon E3 CPU,NVIDIA GeForce GTX 980的GPU,内存为32G。实验平台搭载在win 10操作系统,Matlab R2015a,CUDA Toolkit 8.0,基于caffe框架[34]实现的。本实验初始学习率为0.01,学习率策略为“step”, 每进行20个epochs学习率下降10倍,权重衰减设置为0.001,采用SGD方法训练网络。
本文在Timofte数据集中进行超分辨率重构。为防止网络过拟合,采用尺度缩放和旋转两种方式对训练图像进行增强。具体地,对在数据集中每幅图像进行降采样,缩放到原图像尺寸的0.6、0.7、0.8、0.9倍。然后将数据集中图像按顺时针分别旋转90°、180°、270°。通过图像尺度缩放和旋转处理后,原数据库扩增20倍。
半监督学习(Semisupervised learning, SSL)方法已经被证明对于解决标签样本短缺是有效的通过一起使用大量的未标记样本来解决问题少量标记样本。然而,由于标签数据含有噪声,许多传统的SSL方法不具有鲁棒性。Du等[35]提出了一个基于最大相关熵准则(Maximum Correntropy Criterion, MCC)的鲁棒图形SSL方法去学习一个鲁棒而强大的泛化模型。基于图形的SSL框架通过实施,得到改进监督信息的正规化,这可以加强对标签的约束,从而确保预测的标签的每个群集都接近真实的标签。此外,MCC被引入到SSL框架来抑制标签噪声,减少噪声干扰,有利于后续超分辨率重构工作的顺利进行。本文超分辨率重构算法一种多标签的监督任务,异常标签在多标签情况下非常常见,并可能导致监督信息的偏倚,因此,Du等[36]提出一个基于MCC的鲁棒的多标签主动学习方法去解决该问题。该方法不仅可以构建强大查询模型去估计样本测量不确定性,也很好地表示多标签数据的相似性。
为获取输入网络初始高分辨率图像块及相应的本地高分辨率图像块,增强网络在不同尺度低分辨率图像的超分辨率重构效果,提高网络泛化能力,本文对增强后数据集进行预处理,过程如图6所示;与灰度图和RGB图像相比,高光谱图像(Hyperspectral Image, HSI)的光谱通道包含更丰富的信息,从而可以提供更多观测图像信息,然HSI总是受庞大的数据量和大量的冗余信息影响,这阻碍了其在很多方面的应用。HSI压缩是一种简单解决方式,但大多数传统的图像编码算法主要集中在空间维度上,不需要考虑光谱维度中的冗余。Du[37]提出一种基于图像块的低秩张量分解的新型HSI压缩和重构算法,该算法利用图像块张量间相似度进行压缩,且该方法优于传统的图像压缩方法和其他基于张量的方法。
本文图像预处理过程分为三个步骤,首先,提取原图像亮度通道图像,对图像亮度分量进行裁剪,并对裁剪后图像按不同尺度因子进行下采样。然后,将下采样后图像按照对应尺度进行上采样并生成初始高分辨率图像。最后,为匹配网络输入输出,将生成初始高分辨率图像及本地高分辨率图像按照步长21裁剪为31*31图像块。
4.2 实验结果分析
为验证本文所提图像超分辨率方法性能,实验在超分辨率重建领域中通用的测试集 Set5、Set14、BSD100上进行测试,并将测试结果与 Bicubic、A+[23]、SRCNN[24]、FSRCNN[25]、ESPCN[26]等主流方法进行对比。本文采用客观评价指标包括峰值信噪比(Peak Signal to Noise Ratio,PSNR)和图像的结构相似性(Structural Similarity,SSIM)。PSNR是对经过处理的图像与原图像进行对比得到误差定量计算,用来表征图像失真程度,PSNR越高,表明图像失真越小。SSIM用来表征处理后图像与原图结构相似性,其值越接近1,表明相似度越高,表明效果越好。表1展示了当训练集为91幅图像时,各方法分别在2倍、3倍、4倍图像尺度因子下,在Set5测试集上经超分辨率重建后PSNR值及SSIM值。
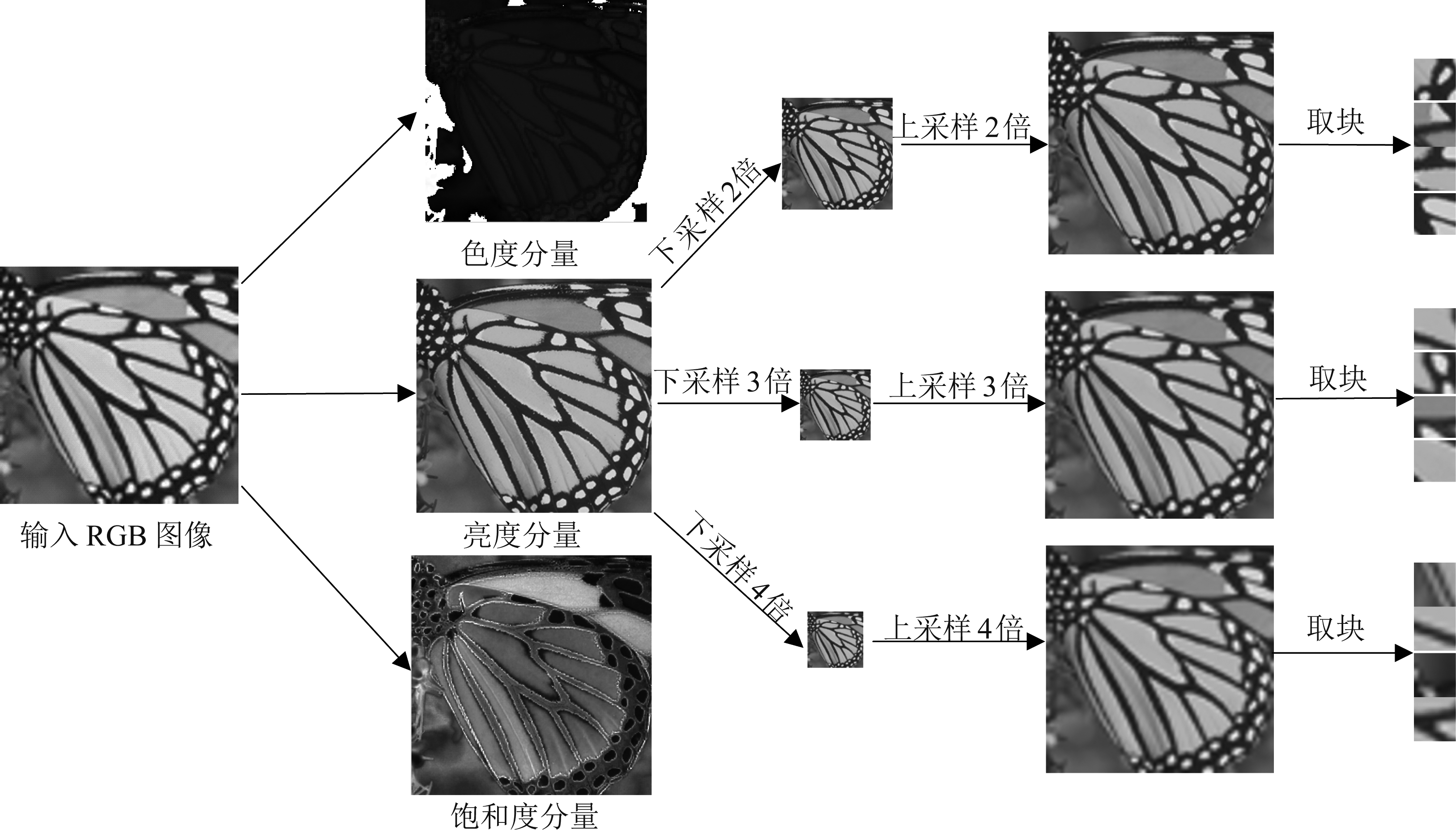
图6 图像预处理过程
Fig.6 Image pre-processing process
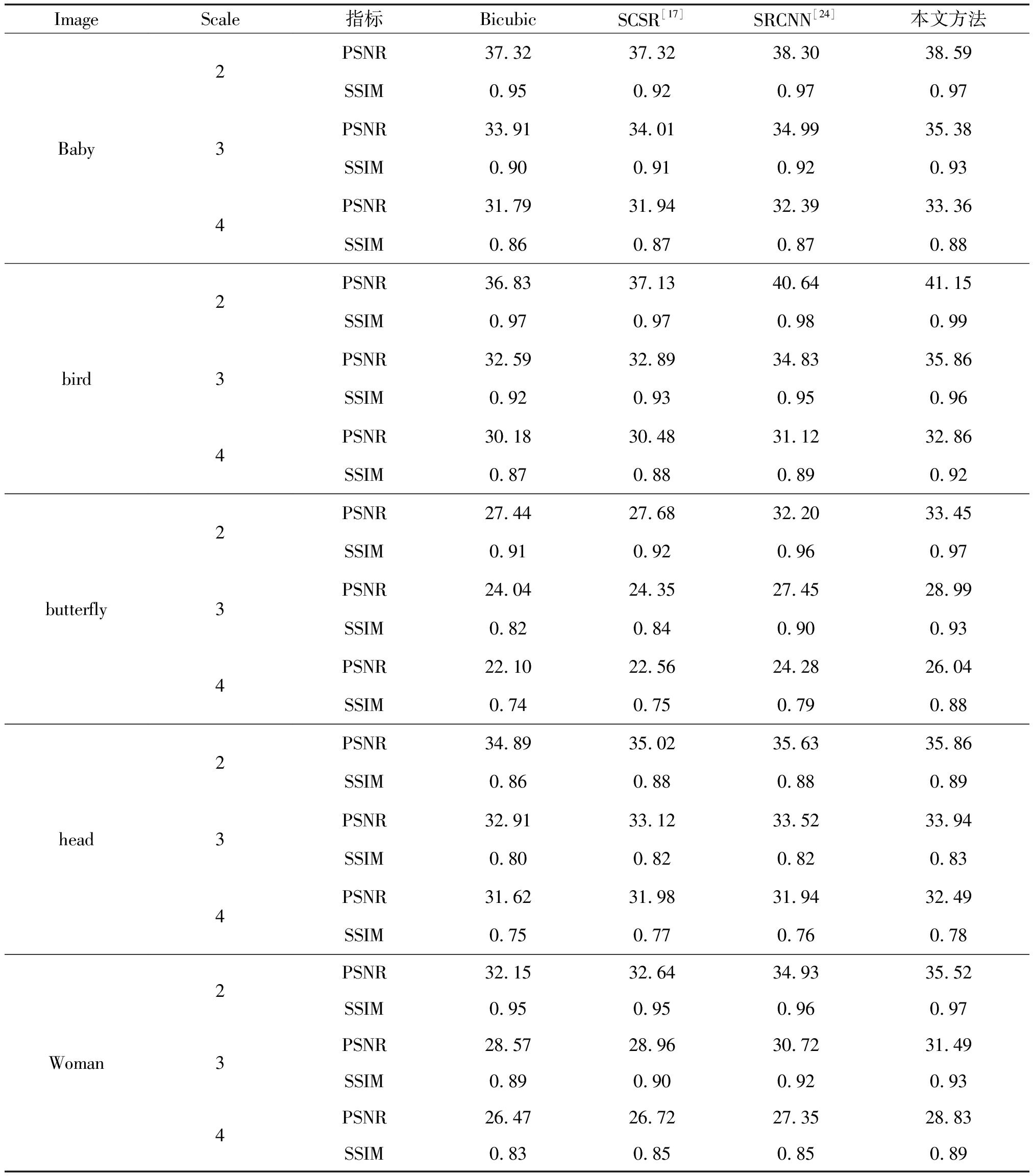
表1 超分辨率算法在Set5数据集上PSNR和SSIM对比
Tab.1 PSNR and SSIM comparison of super resolution algorithm on Set5 data set
ImageScale指标BicubicSCSR[17]SRCNN[24]本文方法Baby234PSNR37.3237.3238.3038.59SSIM0.950.920.970.97PSNR33.9134.0134.9935.38SSIM0.900.910.920.93PSNR31.7931.9432.3933.36SSIM0.860.870.870.88bird234PSNR36.8337.1340.6441.15SSIM0.970.970.980.99PSNR32.5932.8934.8335.86SSIM0.920.930.950.96PSNR30.1830.4831.1232.86SSIM0.870.880.890.92butterfly234PSNR27.4427.6832.2033.45SSIM0.910.920.960.97PSNR24.0424.3527.4528.99SSIM0.820.840.900.93PSNR22.1022.5624.2826.04SSIM0.740.750.790.88head234PSNR34.8935.0235.6335.86SSIM0.860.880.880.89PSNR32.9133.1233.5233.94SSIM0.800.820.820.83PSNR31.6231.9831.9432.49SSIM0.750.770.760.78Woman234PSNR32.1532.6434.9335.52SSIM0.950.950.960.97PSNR28.5728.9630.7231.49SSIM0.890.900.920.93PSNR26.4726.7227.3528.83SSIM0.830.850.850.89
表1将本文方法与SCSR方法和SRCNN方法这两种具有代表性超分辨率方法进行对比,从表1可看出,本文所提方法相比于传统基于样例学习方法具有更高的PSNR值和SSIM值,充分表明本文算法能够重建出与原图像结构更为相似的视觉效果图,处理效果更好,具有更好的图像超分辨率重构性能。
表2展示了当训练集为91幅图像时,各方法分别在2倍、3倍、4倍图像尺度因子下,在各测试集上图像经超分辨率重建后PSNR的平均值。
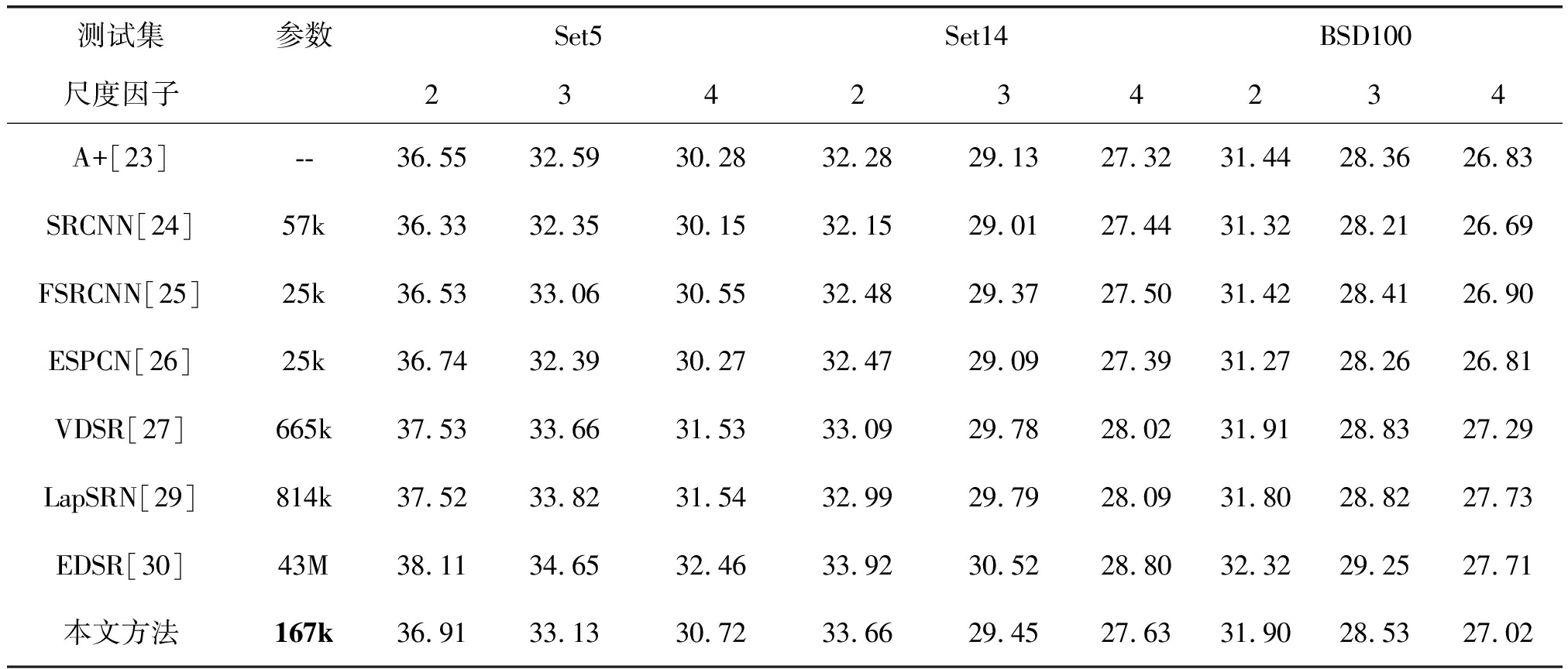
表2 超分辨率算法在Set5、Set14、B100数据集上PSNR平均值
Tab.2 Average PSNR comparison of super resolution algorithm on the Set5, Set14, B100 datasets
测试集参数Set5Set14BSD100尺度因子234234234A+[23]--36.5532.5930.2832.2829.1327.3231.4428.3626.83SRCNN[24]57k36.3332.3530.1532.1529.0127.4431.3228.2126.69FSRCNN[25]25k36.5333.0630.5532.4829.3727.5031.4228.4126.90ESPCN[26]25k36.7432.3930.2732.4729.0927.3931.2728.2626.81VDSR[27]665k37.5333.6631.5333.0929.7828.0231.9128.8327.29LapSRN[29]814k37.5233.8231.5432.9929.7928.0931.8028.8227.73EDSR[30]43M38.1134.6532.4633.9230.5228.8032.3229.2527.71本文方法167k36.9133.1330.7233.6629.4527.6331.9028.5327.02
从表2可看出,本文方法针对不同数据集进行超分辨率重构均能获得较好的实验效果,表明本文所提网络泛化能力较好。现有主流方法如SRCNN、FSRCNN、ESPCN、LapSRN、EDSR等方法需要分别针对不同尺度因子训练网络,网络利用率不高,可重用性差,而本文网络能够各数据集上超分辨率不同尺度,使网络适用多尺度超分辨率重构,具有可增强网络泛化能力的优点。此外,浅层网络具有参数少,易训练的优点,但感受野小,不利用充分利用图像上下文信息。深层网络能够带来更好的重构效果,但需要引入更多的训练参数,增大网络训练难度,本文方法能够极大减少参数量,同时保持较好的重构效果。
同时,在保持网络超参数设置不变,仅将网络结构调整为如图3所示的链式结构进行实验,重构效果如图7所示。
采用链式残差网络所重构图像效果很差,产生多重边缘纹理,在视觉上产生冲击,可能是训练方式、网络初始化方法、超参数设置等原因造成这一现象,后续工作有待进一步探究。
为了更直观显示本文方法与其他方法效果对比,图8展示了在尺度因子为3时,6幅测试集中,输入图像经过Bicubic、SRCNN与本文所提算法超分辨率重构后效果图,并取局部进行3倍放大后图像进行对比。与SRCNN算法相比,本文算法取得了效果上提升,处理结果较为清晰,边缘相对完整,边缘效果保持更好,锐度更强,恢复出的纹理信息更丰富,与原图相比,视觉效果更接近,这表明通过多径卷积神经网络模型学习残差信息更为有效。
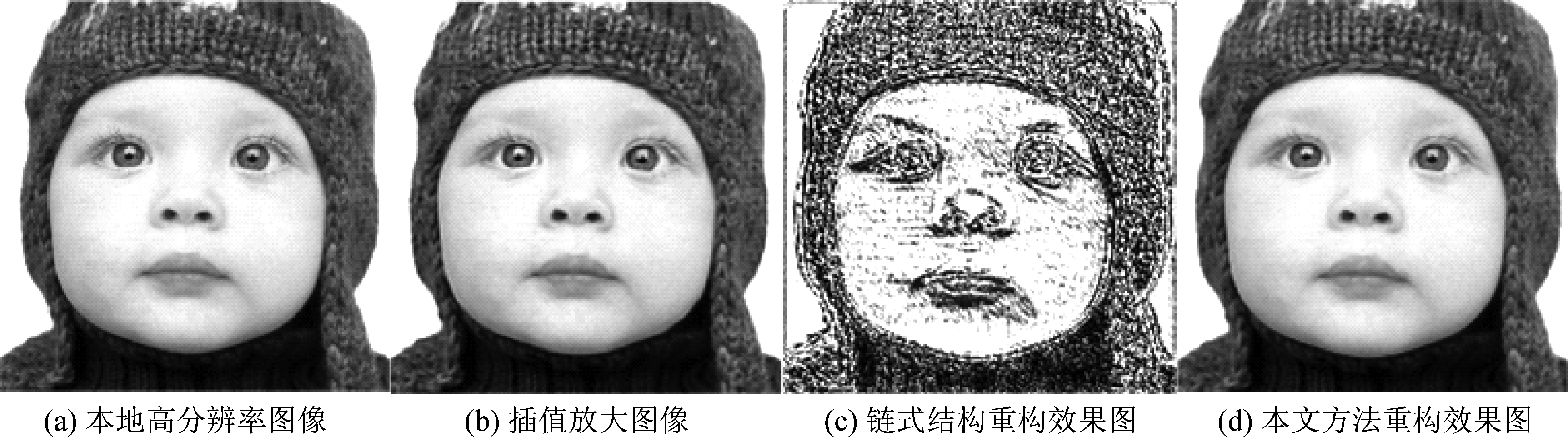
图7 链式结构与多径结构重构效果对比图
Fig.7 Comparison of chain structure and multipath structure reconstruction effect

图8 重构效果图
Fig.8 Subjective evalution effect
表3 不同激活函数性能比较
Tab.3 Performance comparison of various activation function
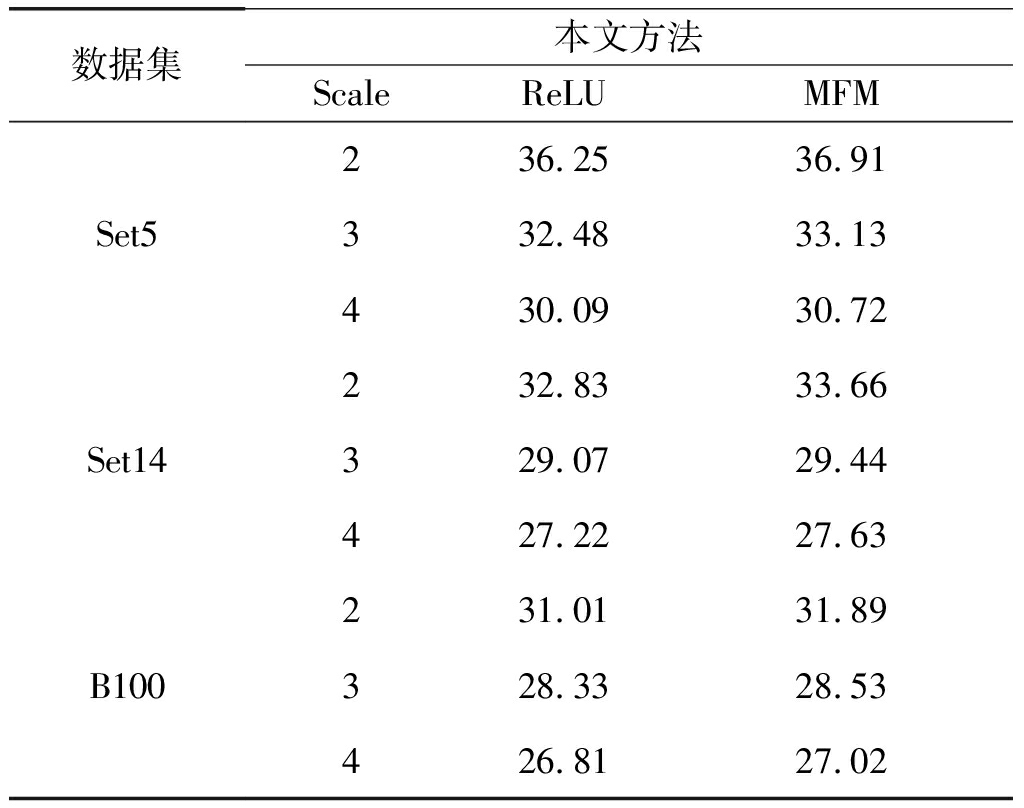
数据集本文方法ScaleReLUMFMSet5236.2536.91332.4833.13430.0930.72Set14232.8333.66329.0729.44427.2227.63B100231.0131.89328.3328.53426.8127.02
表3列出了采用ReLU激活函数与MFM激活函数对比结果。实验表明,采用MFM激活函数比采用ReLU激活函数效果要好,与ReLU激活函数相比,MFM具有拟合任意凸函数的特点,使得网络能收敛于更好的全局解。
5 结论
针对超分辨率重构现有方法存在的问题,本文提出可用于便携式设备的紧凑型多径残差卷积神经网络,并引入多径残差思想,增强网络细节信息。同时,采用递归块连接方式,共享递归残差块参数,大大了减少参数量。为使网络泛化能力更强,结构更紧凑,本文采用MFM激活函数,可有效捕捉到紧凑表示及具有竞争性特征信息,实现低分辨率图像的超分辨率重构。实验结果表明,本文方法具有良好的重构能力,图像清晰度和边缘锐度明显提高,在客观评价和主观视觉效果方面均优于当前主流的超分辨率重构方法,在未来的工作中,可为便携式高性能超分辨率重构奠定理论基础,以及将多径模型扩展到其他图像退化领域用于解决实际问题。
[1] Zou W W W, Yuen P C. Very Low Resolution Face Recognition Problem[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2012, 21(1):327-340.
[2] Shi W, Caballero J, Ledig C, et al. Cardiac Image Super-Resolution with Global Correspondence Using Multi-Atlas PatchMatch[C]∥Med Image Comput Comput Assist Interv, 2013:9-16.
[3] Thornton, Matthew W. Sub-pixel mapping of rural land cover features from fine spatial resolution remotely sensed imagery[J]. Investigative Ophthalmology & Visual Science, 2006, 32(5):1562-1568.
[4] 林格平,马晓川,鄢社锋,等. 无字典的超分辨率多径稀疏信道估计方法[J]. 信号处理, 2017,33(9): 1239-1247.
Lin Geping, Ma Xiaochuang, Yan Shengfeng, et al. Super-Resolution Multipath Sparse Channel Estimation With No Dictionary[J]. Journal of Signal Processing, 2017,33(9): 1239-1247.(in Chinese)
[5] Juefei X F, Savvides M. Single face image super-resolution via solo dictionary learning[J]. IEEE International Conference on Image Processing. IEEE, 2015, 2:2239-2243.
[6] Xiao J, Pang G, Zhang Y, et al. Adaptive shock filter for image super-resolution and enhancement[J]. Journal of Visual Communication & Image Representation, 2016, 40:168-177.
[7] Min L I, Cheng J, Xiang L E, et al. Super-Resolution Based on Sparse Dictionary Coding[J]. Journal of Software, 2012, 23(5):1315-1324.
[8] Zhang K, Tao D, Gao X, et al. Learning Multiple Linear Mappings for Efficient Single Image Super-Resolution[J]. IEEE Transactions on Image Processing, 2015, 24(3):846.
[9] 肖进胜, 刘恩雨, 朱力,等. 改进的基于卷积神经网络的图像超分辨率算法[J]. 光学学报, 2017(3):96-104.
Xiao Jinsheng,Liu Enyu,Zhu Li, et al. An Improved Image Super-resolution Algorithm Based on Convolution Neural Network[J]. Journal of Optics, 2017(3):96-104. (in Chinese)
[10] 王晓刚. 图像识别中的深度学习[J]. 中国计算机学会通讯, 2015, 11(8): 15-23.
Wang Xiaogang. Deep learning in image recognition[J]. Communications of the CCF, 2015, 11(8): 15-23 (in Chinese)
[11] 曾坤. 基于学习的单幅图像超分辨率重建的若干关键问题研究[D]. 厦门: 厦门大学, 2015.
Zeng Kun. Research on Some Key Problems of Super-resolution Reconstruction of Single Image Based on Learning[D]. Xiamen: Xiamen University, 2015. (in Chinese)
[12] 李展. 空间超分辨率图像重建算法研究[D]. 广州: 华南理工大学, 2012.
Li Zhan. Research on spatial super-resolution image reconstruction algorithm[D]. Guangzhou: South China University of Technology, 2012. (in Chinese)
[13] Fermuller J H, Wavelet-Based C. Super-Resolution Reconstruction: Theory and Algorithm[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2009, 31(4):649- 660.
[14] Sun J, Xu Z, Shum H Y.Image super-resolution using gradient profile prior[C]∥Computer Vision and Pattern Recognition 2008. Anchorage, AK, USA: IEEE, 2008:1- 8.
[15] Schultz R R, Stevenson R L.Video resolution enhancement[J]. Proc Spie, 1995:23-34.
[16] Yang J, Wright J, Huang T S, et al. Image super-resolution as sparse representation of raw image patches[C]∥Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition(CVPR), Anchorage, USA: IEEE, 2008: 1- 8.
[17] Yang J, Wright J, Shuang T. Image super-resolution via sparse represent-tation[J]. IEEE Transactions on Image Processing, 2010, 19(11):2861-2873.
[18] Yang J, Wang Z, Lin Z. Coupled dictionary training for image super-resolution[J]. IEEE Transactions on Image Processing, 2012, 21(8): 3467-3478.
[19] He L, Qi H, Zaretzki R, et al. Beta process joint dictionary learning for coupled feature spaces with application to single image super-resolution[C]∥Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Portland, USA: IEEE, 2013: 345-352.
[20] Timofte R, De V, Gool L V. Anchored neighborhood regression for fast example-based super-resolution[C]∥Proceedings of the IEEE International Conference on International Conference on Computer Vision(ICCV), Sydney, Australia: IEEE, 2013: 1920-1927.
[21] Zhu Y, Zhang Y, Yuille A, et al. Single image super-resolution using deformable patches[C]∥Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, USA: IEEE, 2014: 2917-2924.
[22] Zhu Y, Zhang Y, Bonev B, et al. Modeling deformable gradient com-positions for single-image super-resolution[C]∥Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition(CVPR), Boston, USA: IEEE, 2015: 5417-5425.
[23] Timofte R, De V, Gool L V. Anchored Neighborhood Regression for Fast Example-Based Super-Resolution[C]∥IEEE International Conference on Computer Vision. IEEE, 2014:1920-1927.
[24] Chao D, Loy C C, Kaiming H, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transaction on Pattern Analysis & Machine Intelligence, 2016, 38(2): 295-307.
[25] Dong C, Chen C L, Tang X. Accelerating the Super-Resolution Convolutional Neural Network[C]∥European Conference on Computer Vision. Springer: Cham, 2016:391- 407.
[26] Wenzhe S, Jose C, Ferenc H, et al.Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network[J]. Computer Vision and Pattern Recognition, 2016:1874-1883.
[27] He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[J]. Computer Vision and Pattern Recognition, 2015:770-778.
[28] Kim J, Lee J K, Lee K M.Accurate Image Super-Resolution Using Very Deep Convolutional Networks[J]. Computer Vision and Pattern Recognition, 2015:1646-1654.
[29] Lai W S, Huang J B, Ahuja N, et al. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution[C]∥IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2017:5835-5843.
[30] Lim B, Son S, Kim H, et al. Enhanced Deep Residual Networks for Single Image Super-Resolution[C]∥Computer Vision and Pattern Recognition Workshops. IEEE, 2017:1132-1140.
[31] Wu X, He R, Sun Z, et al. A Light CNN for Deep Face Representation with Noisy Labels[J]. Computer Science, arXiv preprint arXiv:1511.02683, 2015.
[32] 常亮, 邓小明, 周明全,等. 图像理解中的卷积神经网络[J]. 自动化学报, 2016, 42(9):1300-1312.
Chang Liang,Deng Xiaoming,Zhou Mingquan, el al. Convolutional Neural Networks in Image Understanding[J]. Journal of Automation, 2016, 42(9):1300-1312. (in Chinese)
[33] Taigw. 深度学习在图像超分辨率重建中的应用[EB/OL]. https:∥zhuanlan.zhihu.com /p/ 25532538?utm_source=tuicool&utm_medium=referral,2017- 03-22/ 2017-10-20.
Taigw. Application of Depth Learning in Image Super-resolution Reconstruction[EB/OL]. https:∥zhuanlan.zhihu.com/p/ 25532538?utm_source=tuicool&utm_medium=referral,2017- 03-22/ 2017-10-20. (in Chinese)
[34] Jia Y, Shelhamer E, Donahue J, et al. Caffe: Convolutional Architecture for Fast Feature Embedding[J].Eprint Arxiv, 2014:675- 678.
[35] Du B, Wang Z, Zhang L, et al. Robust and Discriminative Labeling for Multi-label Active Learning Based on Maximum Correntropy Criterion[J]. IEEE Transactions on Image Processing, 2017, PP(99):1-1.
[36] Du B, Tang X, Wang Z, et al. Robust Graph-Based Semisupervised Learning for Noisy Labeled Data via Maximum Correntropy Criterion[J]. IEEE Transactions on Cybernetics, 2018, PP(99):1-14.
[37] Du B, Zhang M, Zhang L, et al. PLTD: Patch-Based Low-Rank Tensor Decomposition for Hyperspectral Images[J]. IEEE Transactions on Multimedia, 2016, 19(1):67-79.



