1 引言
2006年,P.Antonik等学者首次提出了频率分集阵列(Frequency Diversity Array,FDA)雷达的概念[1],国内也称之为频控阵雷达[2],其可通过阵元间附加小的频偏控制实现距离-角度依赖波束。受益于这种独特波束,FDA雷达较传统相控阵和多输入多输出(Multiple Input Multiple Output,MIMO)雷达在波束综合[3- 8],高分辨成像[9-10],目标定位[11-14],距离模糊杂波和干扰抑制[15-16]等方面提供了更优的性能。
自适应波束形成作为该雷达研究中的难点问题,一直受到国内外学者的关注[17-19]。为降低波束域距离-角度耦合,文献[16]将FDA和MIMO技术结合起来并称之为FDA-MIMO雷达,该体制能同时利用FDA的距离波束特性和MIMO雷达的收发分集特性。文献[17]研究了基于MVDR的频率分集MIMO相控阵雷达距离依赖波束形成,理论上证明了该体制雷达较传统MIMO和相控阵雷达具有更优的波束性能;文献[18]分析了FDA-MIMO雷达频率增量误差对波束性能的影响,文献[15]对FDA-MIMO雷达距离欺骗干扰抑制问题进行了研究,且将最差性能最优波束形成算法扩展到该体制;而文献[19]则进一步将线阵FDA波束形成理论扩展到面阵并分析了其常规波束形成性能。虽然上述成果对FDA-MIMO雷达波束形成进行了较为深入的研究,但只考虑了回波数据包含信号的情况,并没有研究如何抑制目标到达角、阵列位置、幅相等误差对输出SINR带来的不利影响,而且对于如何解决距离波束栅瓣引起的周期性输出信干噪比(SINR)损失问题亦未深入。
为了提高频率分集雷达体制自适应波束形成的稳健性,本文在文献[15]和文献[19]的基础上,提出了一种频分子孔径MIMO雷达(Frequency Diverse Subaperturing MIMO,FDS-MIMO)阵列结构,并对该体制的自适应波束形成进行了深入研究。不同于已有成果,本文所采用的面阵频率分集阵列全维处理面临高维度和高计算复杂度问题,为此,本文基于所建立的信号模型,理论导出了基于等效载频的权向量分解解析解,提出了一种分解迭代的稳健波束形成新算法,通过将全维加权向量估计转化为一个循环迭代的降维权向量估计问题,有效提高了波束形成算法的运算效率和鲁棒性。同时,通过子孔径阵列间采用互质频偏实现了距离栅瓣的抑制,有效降低了传统方法存在的周期性输出SINR损失问题。
2 FDS-MIMO雷达信号模型
考虑一个平面频率分集雷达,如图1所示,其中
表示雷达坐标系。设第一个子阵首阵元(A点)为坐标原点和参考阵元。阵面由M×N个天线阵元组成,其中M和N表示沿x′轴和
轴方向的阵元个数,相应的阵元间隔分别为dx和
本文考虑非重叠子阵,面阵被划分为P×Q均匀长方形子阵,其中P和Q表示沿x′轴和轴方向的子阵个数,因此每个子阵沿x′轴和轴分别包含Kx=M/P和
个天线阵元。考虑实际中阵面往往是倾斜设置的,设倾斜角为β。该体制中每个子阵发射相同信号,子阵间信号相互正交且在子阵间设置一定的频偏,本文称之为FDS-MIMO雷达。此外,
表示目标坐标系,其中hr表示参考点与地面的高度。该坐标系中天线(m,n)的位置矢量为
(1)
其中,
本文用(θ,φ,r)即俯仰角,方位角和距离来表示目标的三维坐标位置,根据空间笛卡尔坐标转换关系,阵元(m,n)与参考点A沿雷达视线方向的距离差为
dmn(θ,φ)=Crr′mnar=(m-1)dxcos θcos φ+
(2)
其中,目标坐标系中雷达视线归一化方向矢量ar=r/r=(cos θcos φ, cos θsin φ, sin θ)T,而转换矩阵为
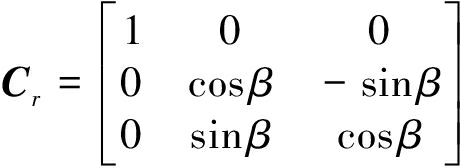
(3)
从而子阵(p,q)的阵内发射流形矢量可以写成
apq(θ,φ)=[ap(θ,φ)∘aq(θ,φ)]
(4)
其中,
阵间发射流行矢量为A(θ,φ),其中A(θ,φ)的第(p,q)个元素可以表示为
Apq(θ,φ)=
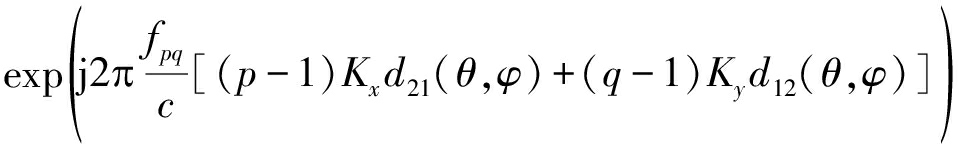
(5)
其中, fpq表示子阵(p,q)的发射载频,可以表示为
p=1,2,…,P;q=1,2,…,Q
(6)
其中,Δfx=Δf和
分别表示沿x′轴和轴的频偏,Δf为基础频偏。
假设子阵(p,q)发射的信号为
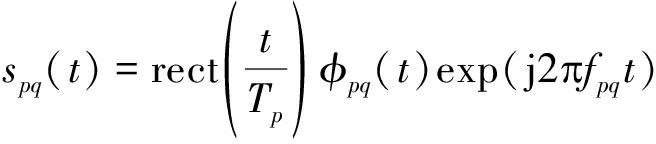
(7)
其中,Tp表示脉冲宽度,φpq(t)表示归一化能量波形即
考虑信号φpq(t)是相互正交的即[15]
(8)
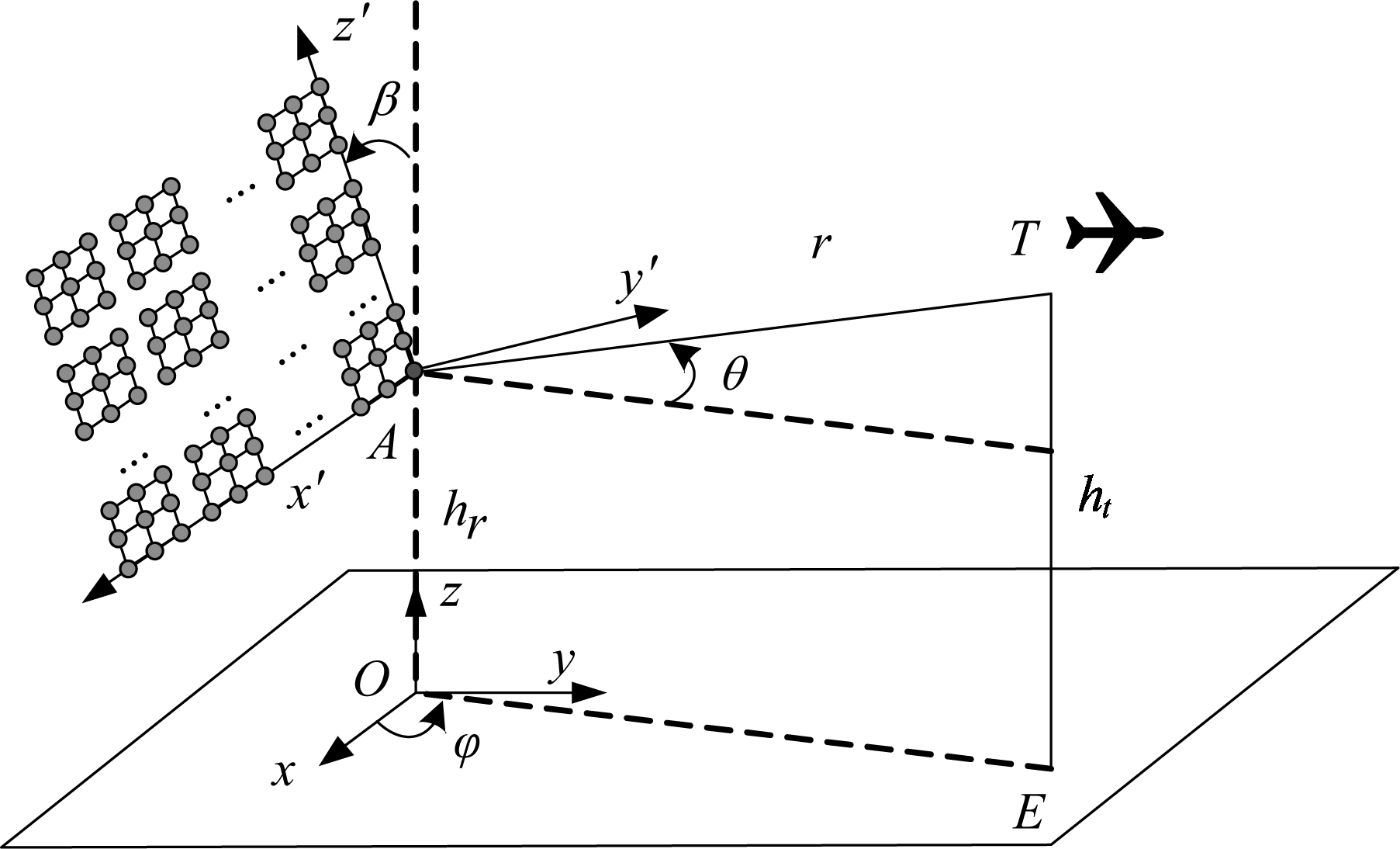
图1 FDS-MIMO雷达阵列结构示意图
Fig.1 Basic geometry of the FDS-MIMO radar
其中,τ表示任意时延。在点目标的假设下,所有子阵发射信号和可建模如下
(9)
其中,wpq是子阵(p,q)的加权向量。假设所有的子阵波束都指向(θ,φ),则非自适应波束形成权向量可以表示为
wpq=apq(θ,φ)/‖apq(θ,φ)‖F
(10)
因此(9)可以简化为
(11)
则第(m′,n′)个天线接收到的信号可以表示为
exp(j2πfpq(t-(τ0-τm′n′)))
(12)
其中,τ0=2r/c表示参考点与目标之间的双程时延,c表示光速,α是目标的散射系数,τm′n′=dmn(θ,φ)/c表示参考点和阵元(m′,n′)之间的传播时延。利用波形φm′n′(t)exp(j2πfm′n′t)对xm′n′(t)进行正交匹配滤波[7,15],可得第(m′,n′)个阵元的第(p,q)个通道的输出为
α·exp(j2πfpq(τm′n′-τ0))Apq(θ,φ, fpq)=
α′·Bm′n′(θ,φ)Apq(θ,φ, fpq)Rpq(r)
(13)
其中,
表示距离依赖导向矢量R(r)的第(p,q)个元素,α′=αexp(-j4πfcr/c),Bm′n′(θ,φ)=exp(j2πfpqτm′n′)。根据(13)可得四维接收数据可写成如下的张量形式
X0=α′·U(θ,φ,r)
(14)
其中,
发射-接收联合导向张量U(θ,φ,r)维数与X0相同。对张量X0按列进行拉直操作得
y=α′·νec[U(θ,φ,r)]
(15)
为简洁起见,记u(θ,φ,r)=νec[U(θ,φ,r)],假设远场存在一个期望信号和J个非相干干扰,接收的回波信号为
(16)
其中,α′0和α′j分别为目标和干扰的散射系数,n是与信号和干扰不相关的噪声。
3 提出的FDS-MIMO雷达分解迭代稳健波束形成算法
3.1 基于不确定集的稳健波束形成算法
最坏情况下性能最优算法(Worst-Case)是一种常用的波束形成算法,其通过定义导向矢量的不确定集和优化最坏情况下的性能来确定最优对角加载因子[20]。文献[15]将该方法扩展到FDA-MIMO雷达,其核心思想也是假定真实的导向矢量位于一个不确定的椭圆集内,并基于最差情况下的波束输出SINR最高为准则求解导向矢量,即
(17)
其中,
为假定的导向矢量,ue表示导向矢量误差向量,然而,不含信号的协方差矩阵R通常难以精确获得,一般利用采样协方差矩阵
来代替,其中
是快拍数。式(17)中非线性约束是非凸的[20],其等价于下面的凸优化问题:
s.t.wHud(θ0,φ0,r0)≥ε‖w‖+1
Im{wHud(θ0,φ0,r0)}=0
(18)
其中,权向量w可利用内点法求解。然而,由式(16)可知,本文FDS-MIMO雷达的权向量w维数很高,利用式(18)求解必然导致全维处理的计算复杂度高和快拍数需求大等问题[21]。
3.2 FDS-MIMO雷达权向量分解
考虑到
设
为系统等效载频,则式(13)中相位Bm′n′(θ,φ)=exp(j2πfpqτm′n′)≈exp(j2πfbτm′n′),产生的相位误差为
Δpq=2π(fb-fpq)τm′n′
(19)
其最大值为
(20)
更进一步,根据文献[22]的边界条件,max(Δpq)≤π/4=0.785时对系统性能的影响可忽略。
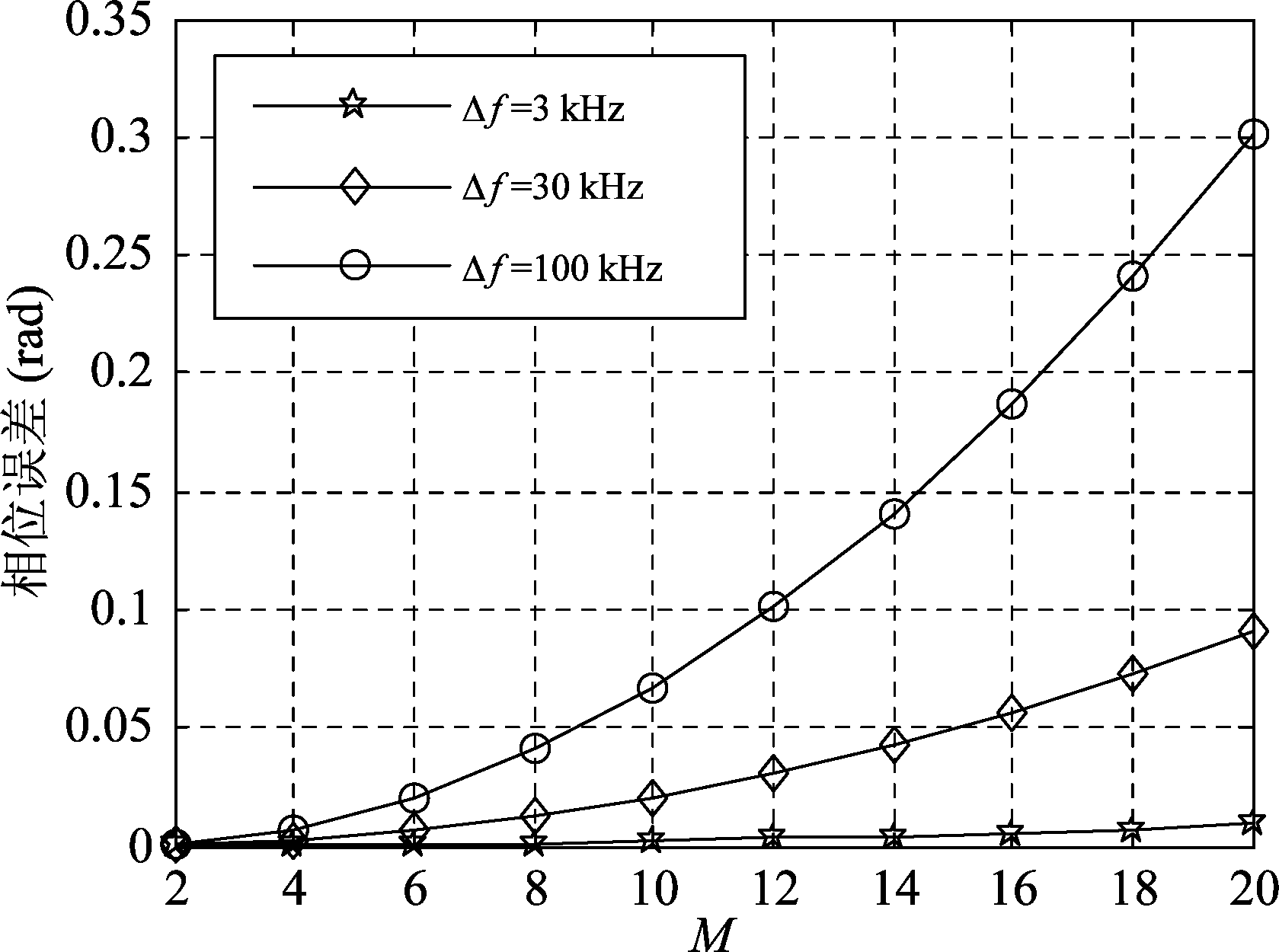
图2 三种频偏下不同阵列维数最大相位误差曲线
Fig.2 The maximal phase error versus array dimension under three kinds of frequency offsets
图2给出了三种频偏下不同阵列维数所产生的最大相位误差曲线,其中
目标位置为(10°,50°),阵列倾斜角β=10°。由图2可知阵元数越多、频偏越大对应的相位误差越大,但对于目前常用的频分MIMO雷达,仿真的参数条件下均可实现max(Δpq)≤π/4,这证实了等效载频的可行性。于是,通过上述近似,接收导向矩阵B(θ,φ)的第(m′,n′)个元素可进一步写成
Bm′n′(θ,φ)≈exp(j2πfb((m′-1)d21(θ,φ)+
(n′-1)d12(θ,φ))/c)
(21)
同理,可得发射阵间导向矢量的第(p,q)个元素Apq(θ,φ)可表示为
Apq(θ,φ)≈
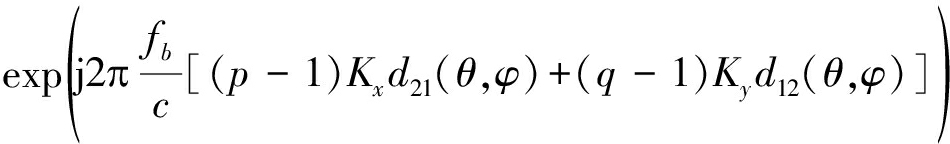
(22)
为方便后续分析,定义辅助向量F(γ,P)=[1,exp(jγ),…,exp(j(P-1)γ)]T,从而可得
FT(2πfbKxd21(θ,φ)/c,P)
(23)
B(θ,φ)=F(2πfbd12(θ,φ)/c,N)·
FT(2πfbd21(θ,φ)/c,M)
(24)
(25)
相应地,发射流形矢量可以表示为
AR(r,θ,φ)=R(r)⊙A(θ,φ)
F(-4πrΔfx/c+2πfbKxd21(θ,φ)/c,P)T
(26)
其中,⊙表示Hadamard乘积。从上式可知发射流形矢量不仅是角度依赖的,同时也是距离依赖的。对其按列进行拉直操作有
ar(r,θ,φ)=
F(-4πrΔfx/c+2πfbKxd21(θ,φ)/c,P)⊗
(27)
其中,⊗表示kronecker乘积,而将B(θ,φ)按列拉直操作则有
b(θ,φ)=νec[B(θ,φ)]=F(2πfbd21(θ,φ)/c,M)⊗
F(2πfbd12(θ,φ)/c,N)
(28)
于是阵列的发射-接收联合流行矢量可以写成如下的kronecker积形式
u(θ,φ,r)=F(-4πrΔfx/c+2πfbKxd21(θ,φ)/c,P)⊗
F(2πfbd21(θ,φ)/c,M)⊗F(2πfbd12(θ,φ)/c,N)
(29)
为表示方便,记u(θ,φ,r)=ap⊗aq⊗am⊗an。根据导向矢量u(θ,φ,r)的可分解性,权向量w也可以进行分解[23-24],于是全维权向量w可以表示为4个低维权向量的kronecker积形式
w=wp⊗wq⊗wm⊗wn=
(Ip⊗wq⊗wm⊗wn)wp=
(wp⊗Ip⊗wm⊗wn)wq=
(wp⊗wq⊗Ip⊗wn)wm=
(wp⊗wq⊗wm⊗Ip)wn
(30)
将上式代入式(18)可得对应的代价函数为
s.t. (wp⊗wq⊗wm⊗wn)Hu≥
ε‖wp‖‖wq‖‖wm‖‖wn‖+1
Im{(wp⊗wq⊗wm⊗wn)Hu}=0
(31)
3.3 FDS-MIMO雷达分解迭代稳健波束形成算法
虽然优化问题(31)是一个多元二次代价函数,难以直接求解,但如果固定其中三个变量,就可以转化为二次凸优化问题,此外易知4个低维权向量之间存在尺度模糊,为了不损失输出SINR的情况下消除这一模糊,可进行归一化处理,即‖wq‖=‖wm‖=‖wn‖=1。下面基于循环迭代的思想[25]求解式(31),若假定wq,wm和wn已知且范数为1,则根据式(30)和(31)可得如下关于wp的代价函数
(32)
其中,
表示降维后的协方差矩阵,Tp=Ip⊗wq⊗wm⊗wn,上式可以采用内点法快速求解。为简洁起见,直接给出wq,wm和wn的求解模型
ε‖wp‖‖wq‖+1
(33)
ε‖wp‖‖wm‖+1
(34)
ε‖wp‖‖wn‖+1
(35)
其中,
表示降维后的协方差矩阵与
定义方式一致,式(33)～(35)也可以采用内点法快速求解。综上所述,本文基于降维的分解四迭代稳健波束形成算法的流程可总结如下:
1)给定初始值wq(0),wm(0)和wn(0)并进行归一化使其范数为1;
2)将wq(i-1),wm(i-1)和wn(i-1)代入式(32)求解wp(i)(i=1,2,…);
3)将wp(i),wm(i-1)和wn(i-1)代入式(33)得到wq(i);
4)将wp(i),wq(i)和wn(i-1)代入式(34)计算wm(i);
5)将wp(i),wq(i)和wm(i)代入式(35)计算wn(i);
6)其中,步骤3)～5)求得的权向量要进行范数归一化处理,重复步骤2)～5),直到max{‖wq(i)-wq(i-1)‖,‖wm(i)-wm(i-1)‖,‖wn(i)-wn(i-1)‖}≤δ (0<δ≪1)迭代结束,此时的权向量估计为w=wp(i-1)⊗wq(i-1)⊗wm(i-1)⊗wn(i-1)。
3.4 提出方法性能分析与讨论
本节从两个方面讨论所提算法的性能。
(1)样本需要量和计算复杂度:由上述分析可知本文方法分别需要估计Mi×Mi, i=P,Q,M,N的4个协方差矩阵,由此可知所提算法的训练样本只需不小于max{P,Q,M,N}。全维Worse-Case算法需要估计的协方差矩阵为C×C(C=PQMN)维,由于采用了系统的全部自由度,样本数大于等于C时才能保证内点法正常工作。用内点法求解时,Worst-Case算法的计算复杂度为O(BP3Q3M3N3),其中B为迭代次数,一般需要10次左右[20],而本文算法求解4个低维的凸优化问题的运算量为O(B(P3+Q3+M3+N3)),其分解迭代次数一般为4～5次,可以看出到本文方法的运算量O(5B(P3+Q3+M3+N3))≪O(BP3Q3M3N3),因此与Worst-Case算法相比,本文方法的计算复杂度和训练样本需求都明显降低。
(2)SINR损失分析:当干扰源离目标很近时将会导致干扰抑制性能的损失,文献[15]定义了SINR损失来衡量,其定义为
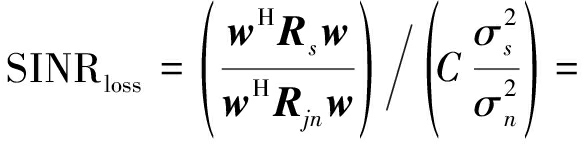
(36)
其中,Rs和Rjn分别为信号,干扰加噪声协方差矩阵,
为噪声功率,
可以看出当干扰被完全抑制的情况下SINRloss=1。由于基础频偏Δf对应的不模糊距离为c/(2Δf),一般情况下保证c/(2Δf)大于雷达可探测距离就可以避免距离模糊的出现,但是为了提高距离分辨率和抗干扰能力,通常需要增加频偏,比如设置
这将导致距离栅瓣的存在,从而产生周期性SINR损失。考虑单个从角度主瓣进入的干扰,可得
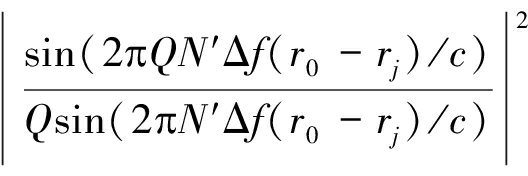
(37)
其中,
为干扰功率且
当干扰从波束距离维主瓣之外进入时SINRloss≤3 dB,根据频率分集阵列的波束具有距离周期性,从上式可以知道,当干扰从波束距离栅瓣进入时即rj=r0-Nuc/(2Δf)(Nu为整数),将会产生与从距离主瓣进入相当的性能损失,此时
这就意味着自适应波束形成器对干扰失去了抑制能力,这一点在文献[15]进行了分析,但并没有给出解决办法。为抑制文献[15]中波束距离栅瓣引起的周期性SINR损失问题,利用二维频分MIMO雷达增加的一个额外自由度,本文提出沿面阵两方向频偏均匀且互质的解决方案,即
其中Nx和
为互质整数,则有
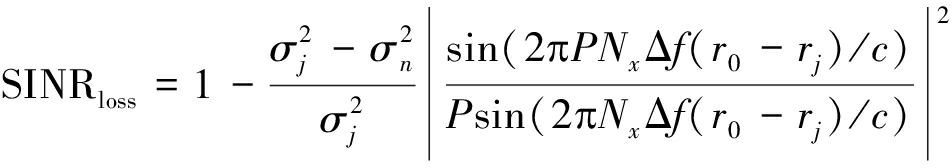
(38)
讨论 1 从式(37)中可知,均匀频偏条件下,波束域的距离周期性模糊会导致性能的严重损失,这是由于沿x′轴和轴方向的波束距离周期性相同引起的;由式(38)可知,得益于采用的互质频偏方案,只有当干扰在目标附近时才会导致较大的性能损失,即使干扰位于一个方向的波束距离栅瓣(ηx=1或
在另一方向也能进行干扰抑制
或ηx≈0),从而保证了在原来的栅瓣位置SINRloss≈1即干扰抑制性能几乎没有损失。
讨论1说明,采用互质频偏方案后,除非干扰在目标附近才会导致SINR严重损失,当干扰距离rj位于x′轴和轴方向的距离栅瓣位置时,不可能使得ηx=1且
同时成立,从而不会导致周期性SINR损失。此处采用反证法证明,假设干扰距离rj位于x′轴和轴方向的距离栅瓣位置时使得ηx=1且同时成立,根据ηx和
关于rj的周期值c/(2NxΔf)和
可得
rj-r0=Px·c/(2NxΔf)
(39)
(40)
由于只讨论雷达探测范围内的距离模糊问题,有Px∈(-Nx,Nx)和
从而有
(41)
根据Px和
的取值范围,以及Nx和的互质特性,式(41)只有唯一的解即
此时rj=r0,这说明只存在rj=r0使得ηx=1且
当干扰位于主瓣区域以外时,不存在其他干扰距离使得ηx=1且从而抑制了距离栅瓣导致的周期性SINR损失,至此讨论1证明完毕。
4 仿真实验与结果分析
为了验证本文所提算法的有效性,设FDS-MIMO雷达包含M×N=6×6个天线单元并划分为P×Q=3×3个子阵,倾斜角β=10°,载频fc=300 MHz,天线间距为半波长,基础频偏Δf=3 kHz,迭代停止门限δ=0.01。噪声建模为复高斯白噪声,目标位于{10°, 50°, 30 km},其散射系数服从Swerling-II模型[26]。同时,为了对比分析本文方法的性能,仿真实验添加了3种算法进行对比,分别是采样求逆算法(SMI);对角加载算法(LSMI),其加载量为噪声功率的10倍;以及文献[15]中采用的Worst-Cases算法。
仿真 1 导向矢量精确已知
假设波束主瓣指向目标,且主瓣中存在一个位于{10°, 50°, rj km}的干扰源,其中rj为干扰所在距离,对应的回波信噪比(SNR)为5 dB,干噪比(INR)为30 dB,快拍数为2C=648。本实验考察SINR损失随干扰距离的变化并验证所提出的互质频偏方案抑制周期性SINR损失的有效性,其中SINR损失由式(36)计算,权向量分别由SMI,LSMI,Worst-Case以及本文算法计算得到。考虑到快拍数有限导致协方差存在误差,Worst-Case以及本文算法中误差界选取ε=0.5。图3给出了SINR损失与干扰距离的关系曲线(OPT表示理论最优SINR输出),图中曲线由100次独立重复试验获得,且其中图3(a)中
图3(b)中
值得说明的是在该仿真参数条件下,3.3节中采用等效载频所带来的最大相位误差max(Δpq)≤1.06×10-3,该误差对后续性能分析的影响可以忽略。由图3可知:1)当采用均匀频偏时,由于波束栅瓣的距离周期性,输出SINR曲线存在明显的周期性损失,如rj=10 km, 20 km,这与文献[15]的结果是一致的。而采用本文提出的面阵两方向互质频偏后,只有干扰源距离与目标较近时才会产生严重的SINR损失,消除了均匀频偏存在的周期性SINR损失问题;2)因回波包含期望信号,在快拍数为2倍协方差矩阵维数时,SMI算法远远大于3 dB(波束距离维副瓣区域SINR损失约为30 dB)、LSMI和Worst-Cases算法SINR损失相对较低,而本文算法能够通过分解迭代得到与协方差矩阵匹配的权向量,实现了近似SINR最优。
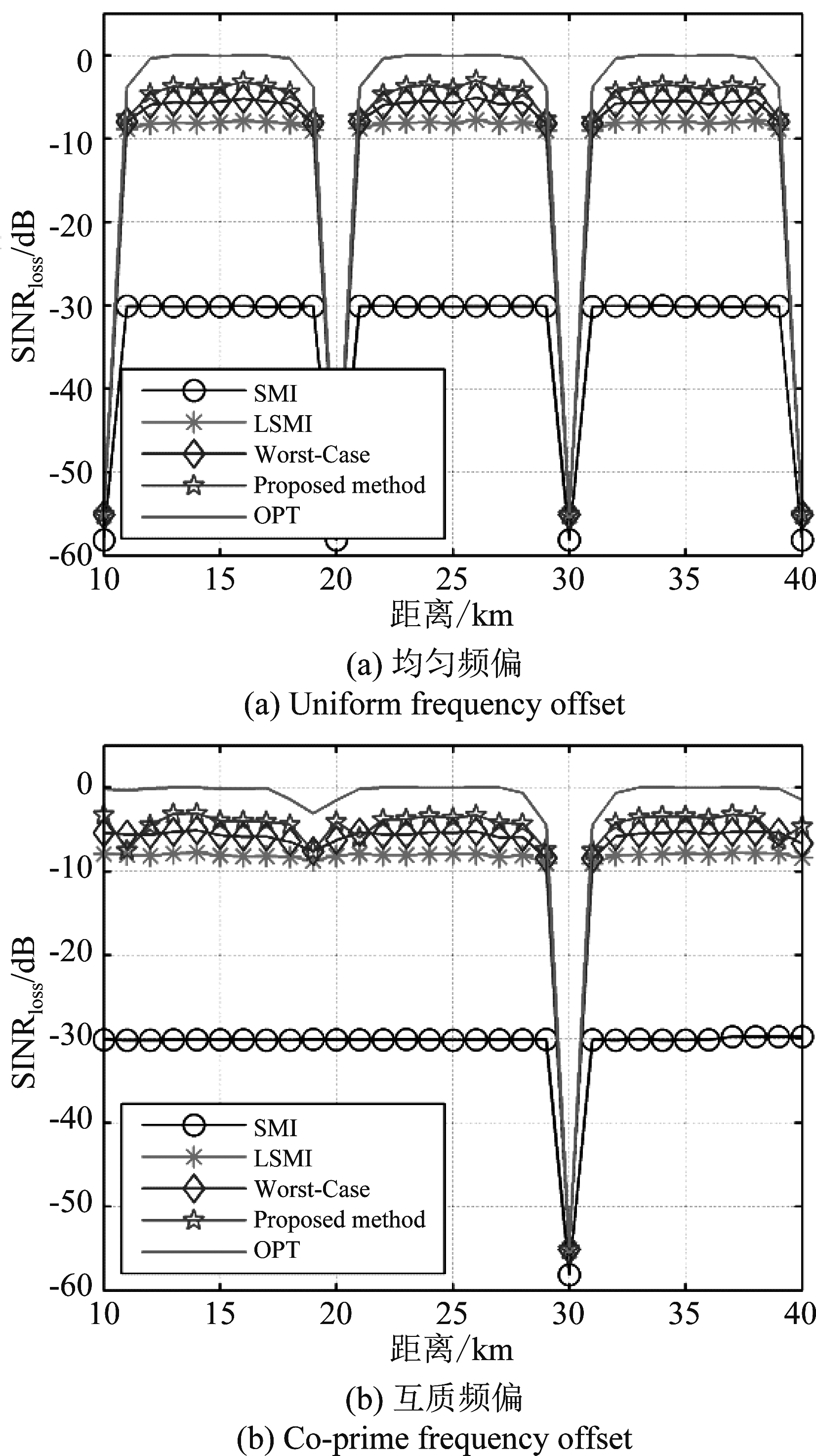
图3 SINR损失随干扰距离变化曲线
Fig.3 SINR loss versus the range of interference
仿真 2 导向矢量距离角度失配
本实验考察导向矢量失配情况下各算法输出SINR随SNR和快拍数变化情况。假设两个干扰分别位于{10°, 50°, 25 km}和{50°, 70°, 35 km},INR均为30 dB。假定的目标位置为{12°, 52°, 30.1 km},为比较的公平性,本文算法和Worst-Case均采用最佳球形不确定集值,即
其中u为指向{10°, 50°, 30 km}的真实导向矢量,ud为指向假定{12°, 52°, 30.1 km}处目标的导向矢量[27]。图4给出了导向矢量距离角度失配情况下各算法性能对比结果,且图4(a)中采用的快拍数为648,图4(b)中SNR为5 dB。从图4(a)中可以看出,低SNR下时四种算法性能差别不大,但随着SNR的增加,信号“自消”情况逐渐严重,导致SIM和LSMI算法性能远离理论最优值,而Worst-Case和本文算法能够根据不确定集求解权向量,具有更稳健的抗导向矢量失配能力,且本文提出的算法性能优于Worst-Case。另一方面,图4(b)表明由于信号“自消”,SMI和LSMI算法随着快拍数增加,性能并没有上升,其他算法随着快拍数增加性能逐渐改善。同时,在快拍数较少时,Worse-Case算法效果与SMI近似,劣于LSMI算法,而本文算法在不同快拍数情况下都优于其他方法,最接近理论最优值,这证实了本文算法的稳健性。
仿真 3 导向矢量随机失配
本试验在仿真2的基础上,考察导向矢量随机误差对算法性能的影响。设随机导向矢量误差服从零均值,方差为0.01的高斯分布,其他参数与仿真2一致。图5给出了导向矢量随机失配情况下各算法性能对比曲线,其中图5(a)中采用的快拍数为648,图5(b) SNR为5 dB。对比图4(a)和图5(a)可以看出在随机导向误差情况下Worst-Case算法受随机误差影响较大,性能有较大下降,而本文方法性能基本保持不变,其原因在于当导向矢量存在随机误差时,ε不再是最佳的球形不确定集值,特别是当ε小于实际的最佳值时,Worst-Case算法性能会明显下降,而本文的迭代算法能够通过迭代逐步收敛到真实的导向矢量,这也是本文算法抗随机误差更加稳健一个原因。此外,对比图4(b)和图5(b)可以看出在随机误差情况下,本文算法性能几乎不受影响,且明显优于其他3种方法,进一步证实了本文提出算法的稳健性。
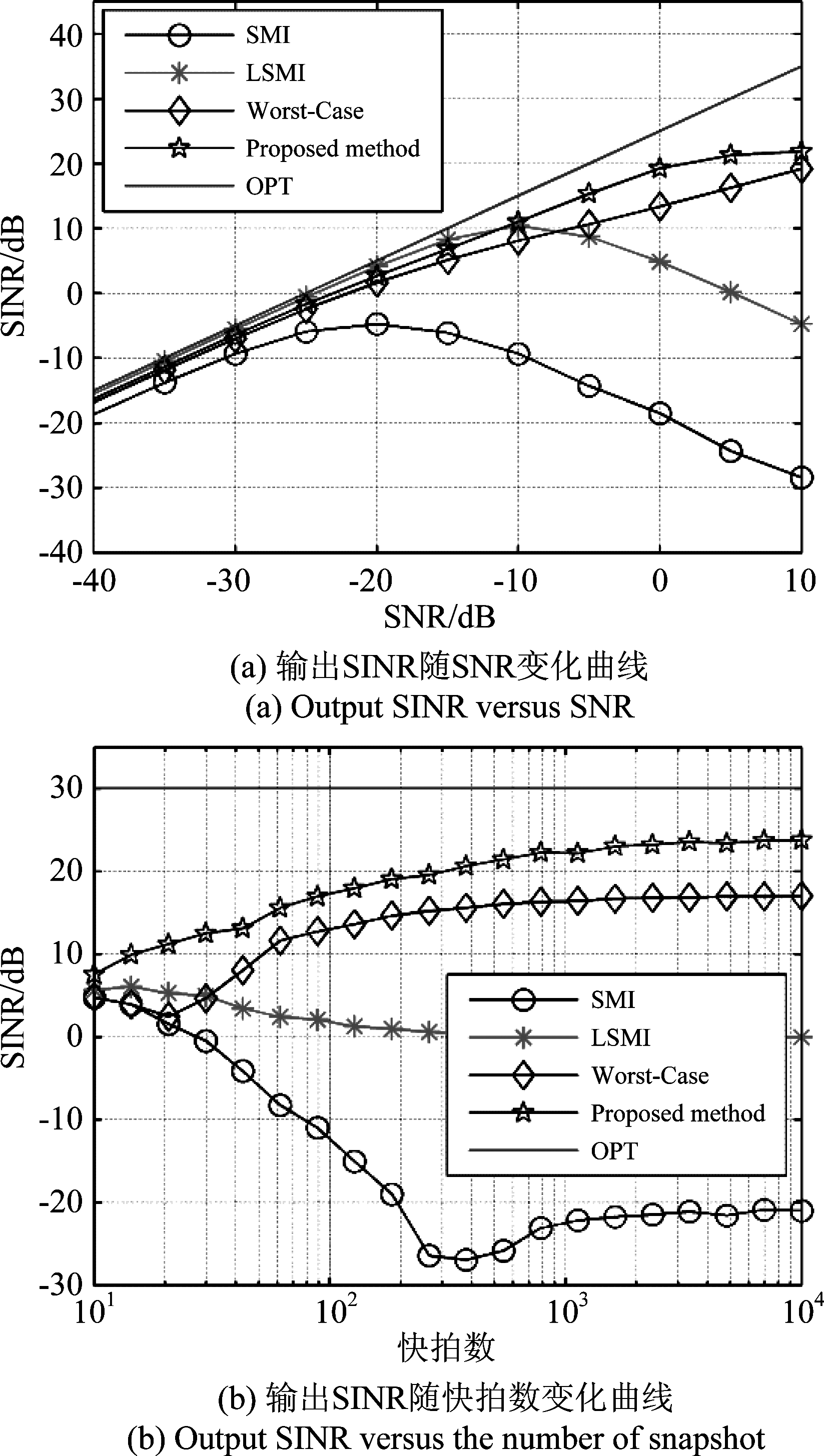
图4 导向矢量距离角度失配情况下各算法性能对比
Fig.4 Algorithms performance comparison under the steerig vector mismatch in range and angle
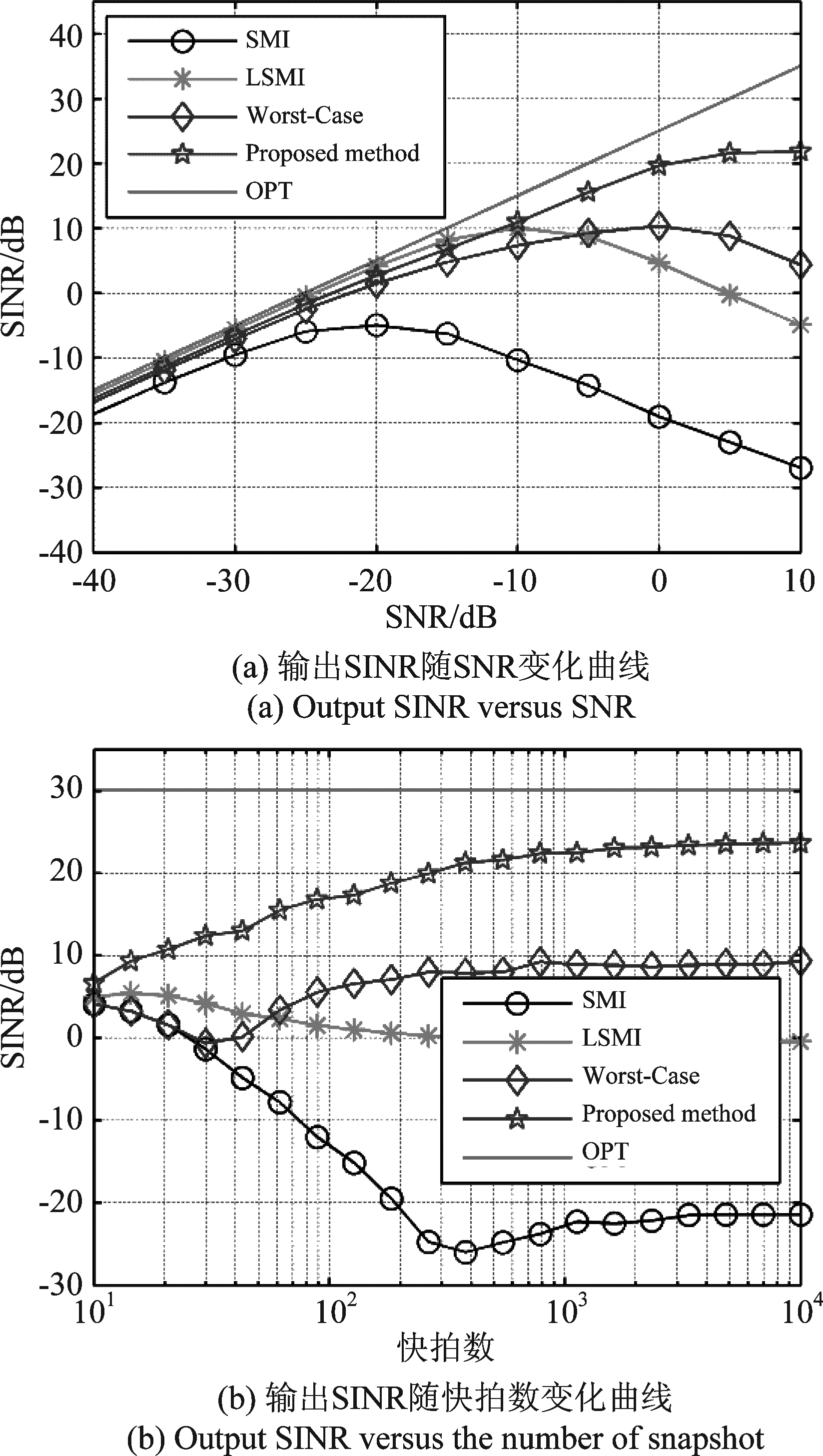
图5 导向矢量随机失配情况下各算法性能对比
Fig.5 Algorithms performance comparison under the random steerig vector mismatch
5 结论
针对频分MIMO雷达稳健波束形成问题,本文建立了米波频分子孔径MIMO雷达信号模型,理论导出了其导向矢量分解的解析表达式,并进一步提出了一种分解迭代稳健自适应波束形成算法。研究表明,通过将原始的全维问题转化为低维权向量的估计问题,较大的提高了计算效率。同时,本文算法能够有效抑制距离栅瓣带来的周期性SINR损失问题,且在导向矢量失配时较之传统全维算法具有更高更稳健的输出SINR。
[1] Antonik P, Wicks M C, Griffiths H D, et al. Frequency diverse array radars[C]∥Proceedings of IEEE Radar Conference, Verona, NY, USA, 2006: 215-217.
[2] 王文钦,邵怀宗,陈慧. 频控阵雷达:概念、原理与应用[J]. 电子与信息学报,2016, 38(4):1000-1011.
Wang Wenqin, Shao Huaizong, Chen Hui. Frequency Diverse Array Radar: Concept, Principle and Application[J].Journal of Eletronics & Information Tehnology, 2016, 38(4):1000-1011. (in Chinese)
[3] Wang W Q. Range-angle dependent transmit beampattern synthesis for linear frequency diverse arrays[J]. IEEE Transactions on Antennas Propagation, 2013, 61(8): 4073- 4081.
[4] Xu Y H, Shi X W, Xu J W, et al. Range-angle-dependent beamforming of pulsed frequency diverse array[J]. IEEE Transactions on Antennas Propagation, 2015, 63(7): 3262-3267.
[5] Yao A M, Wu W, Fang D G. Frequency Diverse Array Antenna Using Time-Modulated Optimized Frequency Offset to Obtain Time-Invariant Spatial Fine Focusing Beampattern[J]. IEEE Transactions on Antennas Propagation, 2016, 64(10): 4434- 4446.
[6] Khan W, Qureshi I M, Saeed S. Frequency diverse array radar with logarithmically increasing frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 499-502.
[7] Shao H Z, Dai J, Xiong J, et al. Dot-shaped range-angle beampattern synthesis for frequency diverse array[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1703-1706.
[8] Gao K D, Wang W Q, Chen H, et al. Transmit Beamspace Design for Multi-Carrier Frequency Diverse Array Sensor[J]. IEEE Sensors Journal, 2016, 16(14): 5709-5714.
[9] 王天云,陆新飞,丁丽,等. 基于贝叶斯压缩感知的FD-MIMO雷达Off-Grid目标稀疏成像[J]. 电子学报,2016,44(6): 1314-1321.
Wang Tianyun, Lu Xinfei, Ding Li, et al. Bayesian compressive sensing-based sparse imaging for Off-Grid Target in Frequency Diverse MIMO radar[J]. Acta Electronica Sinica, 2016, 44(6): 1314-1321. (in Chinese)
[10] Farooq J, Temple M, Saville M. Exploiting frequency diverse array processing to improve SAR image resolution[C]∥Proceedings of IEEE Radar Conference, Rome, Italy, 2008: 1-5.
[11] Xu J W, Liao G S, Zhu S H, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J].IEEE Transactions on Signal Processing,2015, 63(13): 3396-3410.
[12] Wang W Q, So H C. Transmit subaperturing for range and angle estimation in frequency diverse array radar[J]. IEEE Transactions Signal Processing, 2014, 62(8): 2000-2011.
[13] Wang W Q, Shao H Z. Range-angle localization of targets by a double-pulse frequency diverse array radar[J]. IEEE Journal on Selected Topics in Signal Processing, 2014, 8(1): 1-9.
[14] Li X X, Wang D W, Ma X Y. Three-Dimensional Target Localization and Cramér-Rao Bound for Two-Dimensional OFDM-MIMO Radar[J]. International Journal of Antennas and Propagation, 2017, 2017(1): 1-14.
[15] Xu J W, Liao G S, Zhu S H, et al. Deceptive jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015, 113: 9-17.
[16] Sammartino P F, Baker C J, Griffiths H D. Frequency diverse MIMO techniques for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201-222.
[17] Wang W Q. Phased-MIMO Radar with frequency diversity for range-dependent beamforming[J]. IEEE Sensors Journal, 2013, 13(4): 1320-1328.
[18] Gao K D, Shao H Z, Chen H, et al. Impact of frequency increment errors on frequency diverse array MIMO in adaptive beamforming and target localization[J]. Digital Signal Processing, 2015, 44: 58- 67.
[19] Jones A M, Rigling B D. Planar frequency diverse array receiver architecture[C]∥Proceedings of IEEE Radar Conference, Atlanta, GA, 2012: 145-150.
[20] Vorobyov S A, Gershman A B, Luo Z Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transations on Signal Processing, 2003, 51(2): 313-324.
[21] Reed I S, Mallett J D, Bren nan L E. Rapid convergence rate inadaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 853- 863.
[22] Wang W Q, So H C, Shao H Z. Nouniform frequency diversity array for range-angle imaging of targets[J]. IEEE Sensors Journal, 2014, 14(8): 2469-2476.
[23] 洪振清,张剑云. 一种降维的MIMO雷达MVDR波束形成算法[J]. 信号处理,2011, 27(8): 1184-1188.
Hong Zhenqing, Zhang Jianyun. A dimension-reduced MVDR beamforming algorithm for MIMO radar[J]. Signal Processing, 2011,27(8): 1184-1188. (in Chinese)
[24] 李敬军,姜永华,但波. MIMO雷达降维的低运算量波束形成方法[J]. 信号处理,2013, 29(11): 1590-1596.
Li Jingjun, Jiang Yonghua, Dan Bo. Dimension-reduced and low computation beamforming method in MIMO radar[J]. Journal of Signal Processing, 2013, 29(11): 1590-1596. (in Chinese)
[25] Feng D Z, Zheng W X, Cichocki A. Matrix-group algorithm via improved whitening process for extracting statistically independent sources from array signals[J]. IEEE Transations on Signal Processing, 2007, 55(3): 962-977.
[26] Cheng Y B, Yu R S, Hong G, et al. Multi-SVD based subspace estimation to imprve angle estiation accuracy in bitatic MIMO radar[J]. Signal Processing, 2013, 93: 2003-2009.
[27] 王昊,马启明. 修正主模抑制稳健自适应波束形成算法[J]. 电子与信息学报,2017, 39(11):2620-2626.
Wang Hao, Ma Qiming. Modified Dominant Mode Rejection Robust Adaptive Beamforming Algorithm[J].Journal of Electronics & Information Technology, 2017, 39(11):2620-2626. (in Chinese)
