1 引言
在无线通信中,自适应调制编码技术(Adaptive modulation and coding, AMC)常被用来解决信道容量无法充分利用的问题。该技术可以根据信道质量随时间的变化情况,对发射端的各项参数做出相应调整[1]。但在实际应用中,一般无法通过协议实现多方通信的同步,这使得相关控制信息有时不能准时或正确地传送到接收端,从而造成通信无法建立。因此接收端如何仅根据接收数据快速地盲识别出发送端所采用的参数,即信道编码识别也成为了一个非常重要的问题。随着认知无线电或认知通信的发展,信道编码识别将成为未来智能通信系统的重要功能之一[2]。
信道编码识别应用于AMC技术的接收端时,接收端通常已知发送端所有可能的编码参数组合。如4G LTE系统的物理层下行控制信道便是这种情况下的典型应用。对于上述领域的信道编码识别技术的研究,主要集中于卷积码的识别上。如文献[3]和文献[4]利用接收序列的软信息计算出每种编码候选的综合后验概率(syndrome posterior probability, SPP),并以SPP作为识别特征量来快速识别发送端使用的编码方式。文献[5]针对SPP计算复杂和存储困难的问题提出了采用对数似然比(log-likelihood ratio,LLR)的加权均值作为识别特征量的优化算法。文献[6]则提出利用似然差(likelihood difference, LD)代替LLR作为特征识别量的优化算法。
上述信道编码识别算法在进行信道译码前,都需要计算每个可能的编码候选的识别特征量,而其识别特征量的形式复杂,都包含大量指数和乘法运算。一方面识别特征量的计算复杂度较高,引入的额外延时较大。另一方面,识别特征量的计算需要引入大量的额外资源消耗,不利于在对硬件资源受限的应用场景中。针对上述问题,本文将信道译码与信道编码识别相结合,以信道最大似然译码中的参数最大欧氏距离作为识别特征量,对每个可能的编码候选进行识别。该算法无需引入额外的特征量计算过程,也无需相应的硬件资源消耗。一方面该算法原理简单,实现容易,便于应用在硬件资源受限的场景中。另一方面该算法也可以与已有的信道编码盲识别算法相结合以进一步加速接收端的译码流程。
2 系统模型
一般通信链路结构如图1所示。设信道编码前的信息序列为b=[b1,b2,…,bK],经过码率为K/N的编码后得到编码序列c=[c1,c2,…,cN]。若信号调制序列为s,经过AWGN信道后,在接收端的接收序列为r=s+w,其中w为噪声序列。软解调之后输出的软信息序列为l=[l1,l2,…,lN]。
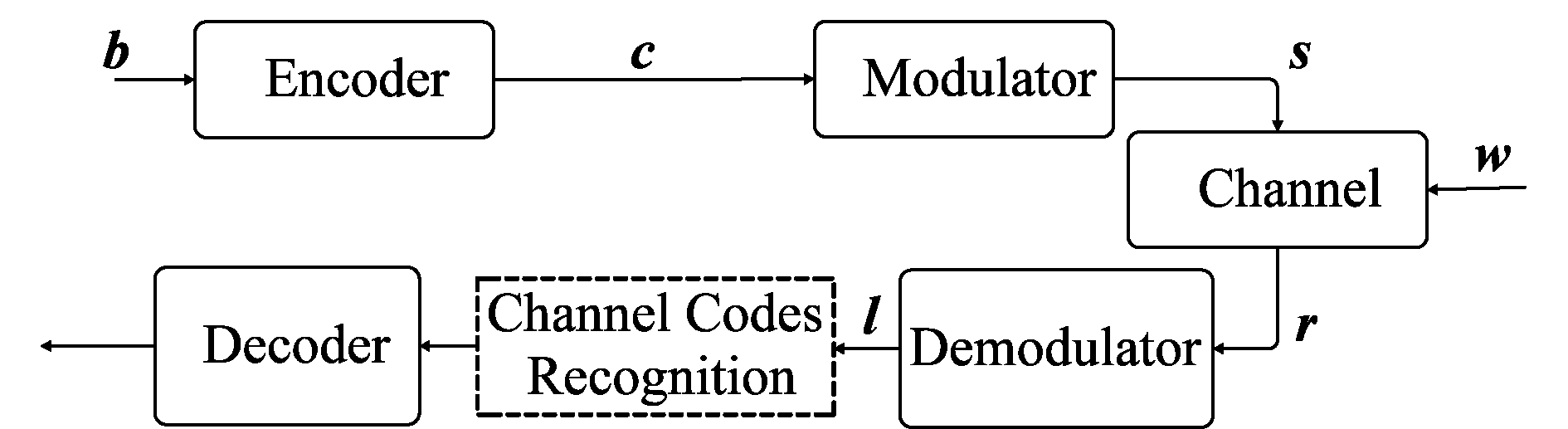
图1 一般通信链路结构
Fig.1 Structure of a general communication link
第i比特的软信息li表示为编码比特ci的后验概率对数似然比,即
(1)
控制信道的信息传输可靠性要求高,通常采用BPSK或QPSK调制方式[7]。在这种情况下,式(1)表示的比特软信息可以简单地通过将BPSK信号或者QPSK信号的同相和正交分量乘以CSI参数(Lc)得到[8],即
li=Lcri=c′i+w′i,i=1,2,...,N
(2)
其中Lc=4Es/N0,c′i∈{+1,-1},w′i~N(0,σ′)为归一化后的信道噪声。
在获得软信息序列l后,译码器开始信道译码。信道译码器的基本任务是根据一套译码规则,由接收序列的软信息序列l给出与发送的信息序列b最接近的估值序列![]() 由于b与编码码字c之间存在一一对应关系,等价于译码器根据l产生一个c的最接近估值序列
由于b与编码码字c之间存在一一对应关系,等价于译码器根据l产生一个c的最接近估值序列![]() 当输入为软信息时,最大似然译码的译码过程为根据输入软信息l在2K个码字集中寻找与l的欧氏距离最小的码字
当输入为软信息时,最大似然译码的译码过程为根据输入软信息l在2K个码字集中寻找与l的欧氏距离最小的码字![]()
设当前译码距离为n,软信息序列l与![]() 的最小欧氏距离emin为:
的最小欧氏距离emin为:
(3)
去除公共项即平方项,式(3)等价为
(4)
值得注意的是,此时![]() 与l对应最大欧氏距离
与l对应最大欧氏距离![]()
3 基于MLD的信道识别算法
3.1 算法原理
假设发送端所采用的信道编码参数候选集合为Ω={C1, C2, …, CM},该集合中共有M种编码方式。发送端依据信道条件等因素从候选集合Ω中选择一个合适的编码候选C来编码信息序列。接收端经过软解调得到软信息序列l后,开始尝试依据候选集合Ω中不同编码候选进行盲译码,直到找到发送端所采用的编码候选C并解码出所需信息序列。在进行信道译码时,本文所提信道编码识别算法将最大似然译码的参数emax做为识别特征量,对当前译码依据的编码候选的正确性进行识别,以提前终止无效的译码过程。下面通过推导说明其理论的正确性。
根据接收端当前译码采用的编码候选Ct与发送端所采用的编码候选C相同与否,有相同和不同两种情况,分别表示为假设H1和H0。
在假设H1下,译码结果正确时,有![]() 又有li=c′i+w′i,带入到式(4)可以得到
又有li=c′i+w′i,带入到式(4)可以得到
(5)
依据正态分布的可加性可知![]()
在假设H0下,发送端的编码序列c不满足译码器当前尝试的编码形式,对译码器而言可视为随机01序列[6],设为q=[q1,q2,…,qN],此时软信息序列变为l′=[l′1,l′2,…,l′N],l′i=q′i+w′i, i=1, 2,…, N。由于q无对应的有效码字,此时译码器将搜寻到与q最接近的有效码字![]() 此时emax变为
此时emax变为
(6)
其中q′i∈{+1,-1}。
设![]() 与q′前n项中有m个位置的数据不相同,即两者汉明距离为m。变换式(6)中数据累加的顺序,按照q′和
与q′前n项中有m个位置的数据不相同,即两者汉明距离为m。变换式(6)中数据累加的顺序,按照q′和![]() 对应位置的数据不相同的在前,相同的在后的顺序重新排列,式(6)变为
对应位置的数据不相同的在前,相同的在后的顺序重新排列,式(6)变为
(7)
同理于H1情况,依据正态分布的可加性可知,此时![]()
由此可知,接收端译码器译码到i=n时的最大欧氏距离emax可以表示为
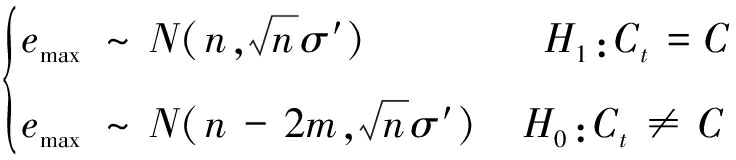
由此可以看出,参数emax在H1和H0两种不同的假设下的分布规律不同。利用上述不同,便可以将参数emax作为特征,以区分两种假设,即判断当前译码采用的编码候选的有效性。下面基于信道检测原理推导识别特征emax对应的识别特征量和检测阈值。
在对Ct进行识别时,会出现虚警和漏警两种错误。虚警错误将引入无效的译码环节,表征了信道编码盲识别算法的加速效果,虚警率越低算法加速效果越佳。漏警错误将使译码器无法得到正确的译码信息,如对于PDCCH的盲译码而言会造成整个子帧数据的丢失和丢包率的增加,反而大幅增加了系统的处理延时和功耗[10]。漏警表征了算法的可靠性,漏警概率越低则算法的可靠性越强。比较两种错误的影响,可以确定导致无法获得正确译码序列的漏警情况对于系统的影响更加严重。基于上述分析,本文采用奈曼-皮尔逊准则(Neyman-Pearson criterion,NP criterion),将漏警概率作为确定检测阈值的限制条件α以保证算法的可靠性,推导信道编码盲识别所需的识别特征量和判决阈值。
NP准则的表达式为
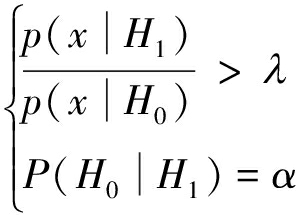
(8)
其中:λ为NP准则的判决阈值,α为系统限定的漏警概率。
emax在假设H0和H1下的条件概率分布函数为:
p(emax|H0)=
(9)
(10)
将式(9)和式(10)带入NP准则式(8)的判决公式中有:
(11)
式(11)可以化简为
(12)
此时NP准则式(8)转化为:
(13)
由上式可以发现,识别假设H0和H1的特征emax对应的识别特征量为其本身。
识别所需的检测阈值λ′可以通过将漏检概率设定为α得到,有
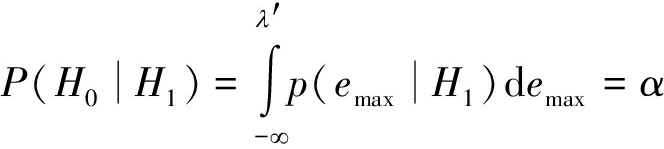
依据前文分析可知,在H1下![]() 相应的阈值λ′可以通过查找标准正态分布表计算得到:查找标准正态分布表得到(1-α)所对应的边界值λ0,λ′和λ0的关系如下:
相应的阈值λ′可以通过查找标准正态分布表计算得到:查找标准正态分布表得到(1-α)所对应的边界值λ0,λ′和λ0的关系如下:
(14)
依据NP准则式(13),在译码器译码深度到达n时,接收端可以依据emax对当前尝试的编码候选Ct进行信道编码的盲识别检测,当emax大于判决阈值λ′时,判定Ct=C,继续进行后续译码流程。反之则判定Ct ≠ C,放弃当前译码过程,开始对下一编码候选Ct+1的盲译码尝试。
上述识别算法的虚警概率可以表示为:
(15)
前文已知,在假设H0下![]() 将公式(15)归一化有
将公式(15)归一化有
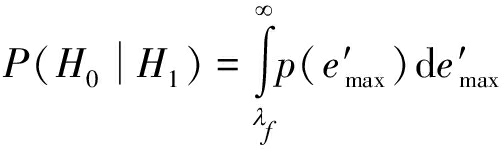
(16)
其中,e′max~N(0,1)且有
(17)
(18)
则某一m值下的虚警率可以依据式(16)和阈值λf,查找标准正态分布表计算得到。
3.2 算法运行流程
基于文献[3- 6]所提出识别算法(算法1)的接收端译码流程如图2所示。接收端在获取软信息序列l后,依次计算编码候选集Ω中各个候选的识别特征量函数Ft,直到计算完全部M个候选的特征量。图2中参数t表示候选集Ω中各个候选的序号,t=1,2,...,M。在计算完全部特征量后,接收端比较并选取候选集Ω中特征量最大值对应的编码候选作为识别算法预测的编码候选,即![]() 在获得预测的编码候选
在获得预测的编码候选![]() 后,译码器依据
后,译码器依据![]() 进行信道译码。译码后的结果通常采用CRC校验检测其正确性和完整性。若译码结果未通过CRC校验,则重新调整识别结果再依据新的识别结果进行信道译码等操作。
进行信道译码。译码后的结果通常采用CRC校验检测其正确性和完整性。若译码结果未通过CRC校验,则重新调整识别结果再依据新的识别结果进行信道译码等操作。
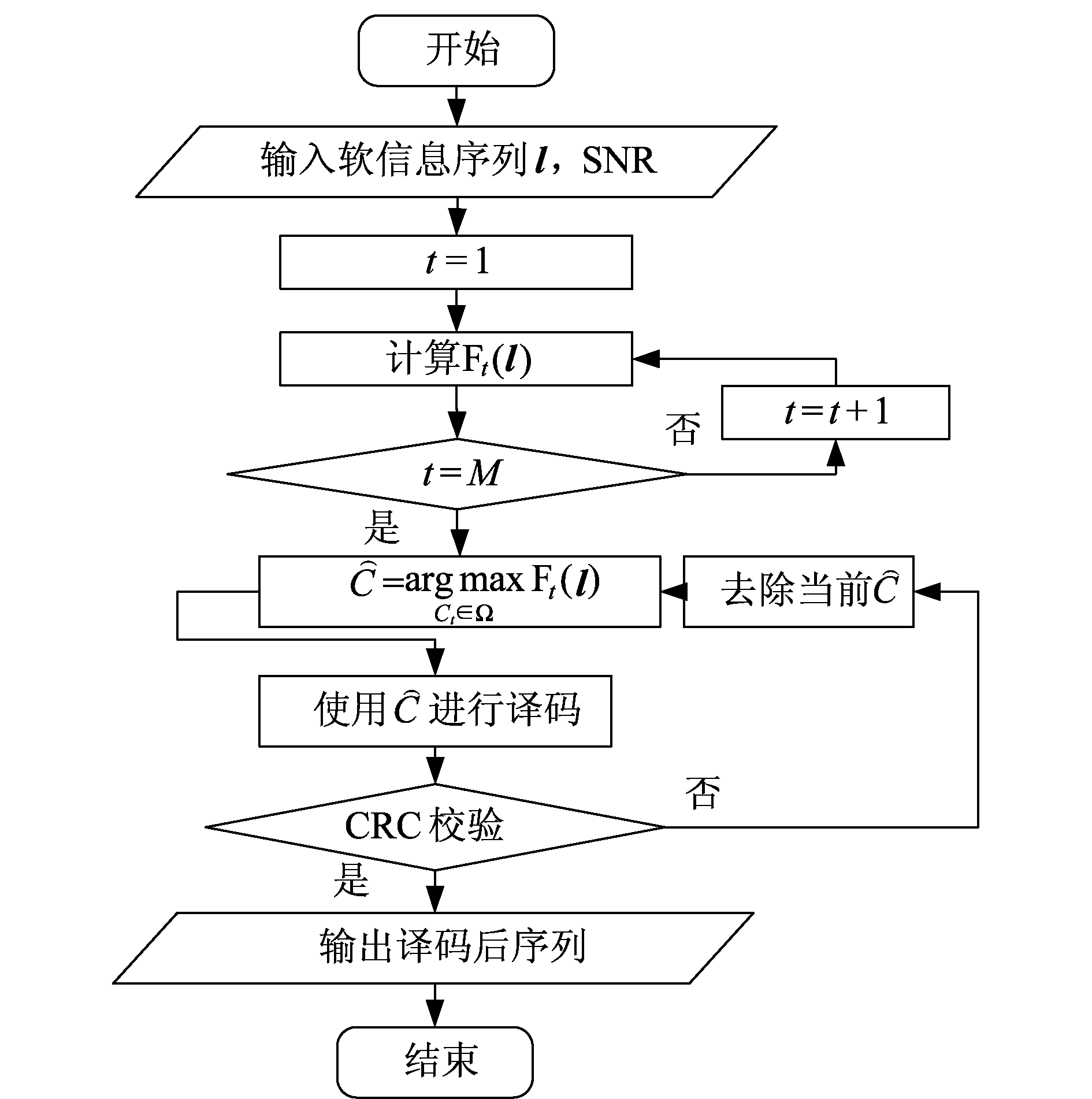
图2 算法1流程
Fig.2 The flowchart of algorithm 1
在上述盲译码流程中,接收端进行信道译码前需要计算所有候选的特征量,且其计算过程涉及双曲正切变换,计算过程复杂。一方面,计算过程的延时较大,另一方面,该过程的硬件实现困难。
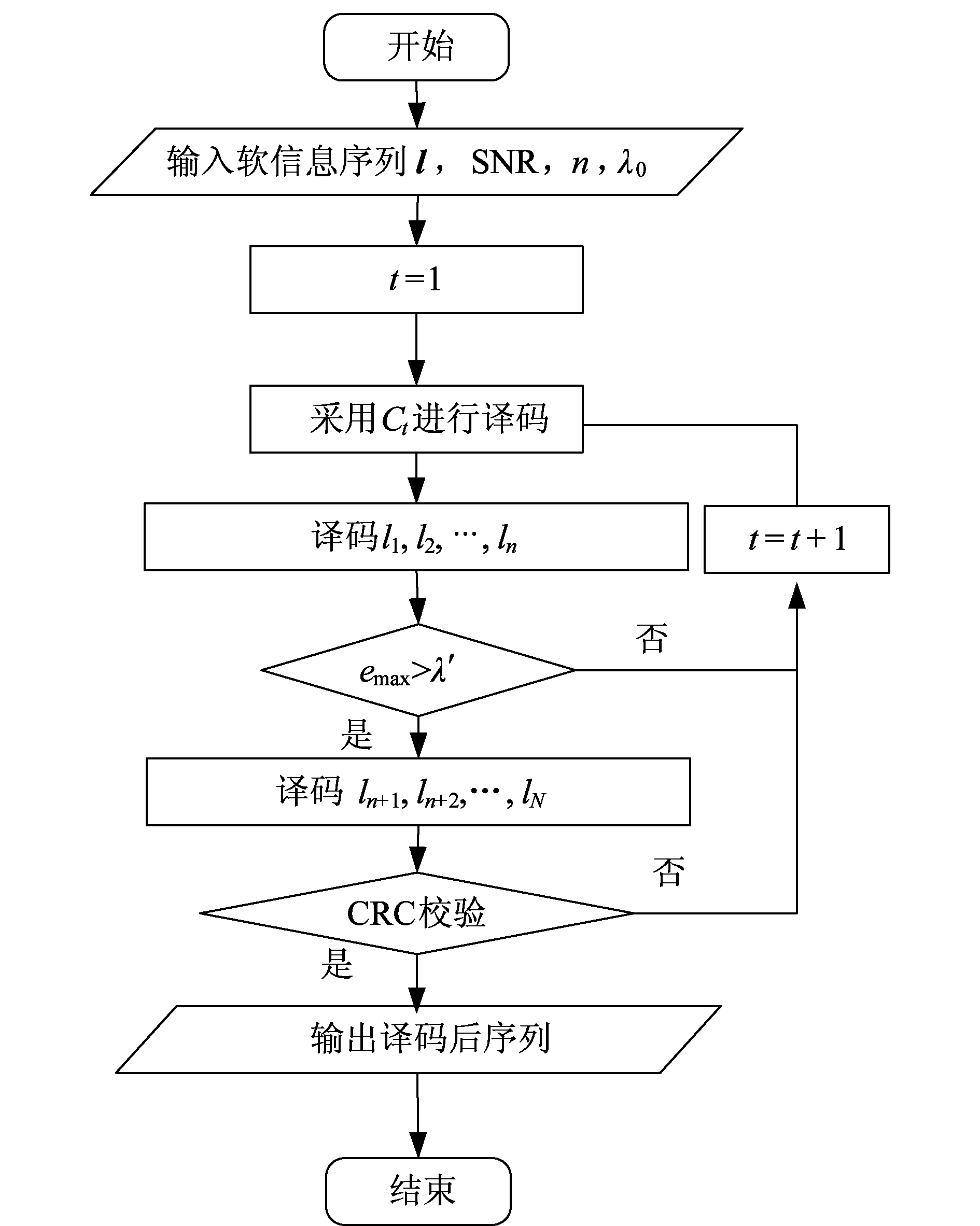
图3 算法2流程
Fig.3 The flowchart of algorithm 2
本文所提出的信道编码盲识别算法(算法2)与信道译码相结合,其盲译码流程如图3所示。在输入软信息l后,接收端开始依次尝试采用编码候选集Ω中各种编码候选Ct进行信道译码。在每次信道译码深度达到n时,接收端比较并得到当前译码器中的最大欧氏距离值emax。将emax与识别阈值λ′进行比较,若emax大于λ′则判定当前候选Ct为有效候选,接收端继续进行后续译码过程,直到获得完成的译码序列。在完成译码后对结果进行CRC校验,若未通过则表明检测算法出现错误,继续对下一候选进行译码和检测,直到获得正确的译码结果。
该算法相当于将依据某一编码候选进行部分信道译码的过程同时作为其识别特征量的生成过程。当通过识别检测时,译码器继续后续译码过程并获得译码信息。该方法无需对全部编码候选进行特征量求解。实现本文所提出的算法,只需要对译码器做出适当修改,在完整的译码过程中插入识别比较环节即可,其硬件实现难度远小于算法1。
3.3 算法实现
以咬尾卷积码的Viterbi译码器为例,最大似然译码的emax为译码过程中的最大路径度量(Path Metric, PM)。图4(a)和(b)分别给出了一般咬尾卷积码的Viterbi译码器[12]和加入本文提出算法的译码器的有限状态机(Finite-state machine, FSM)示意图。
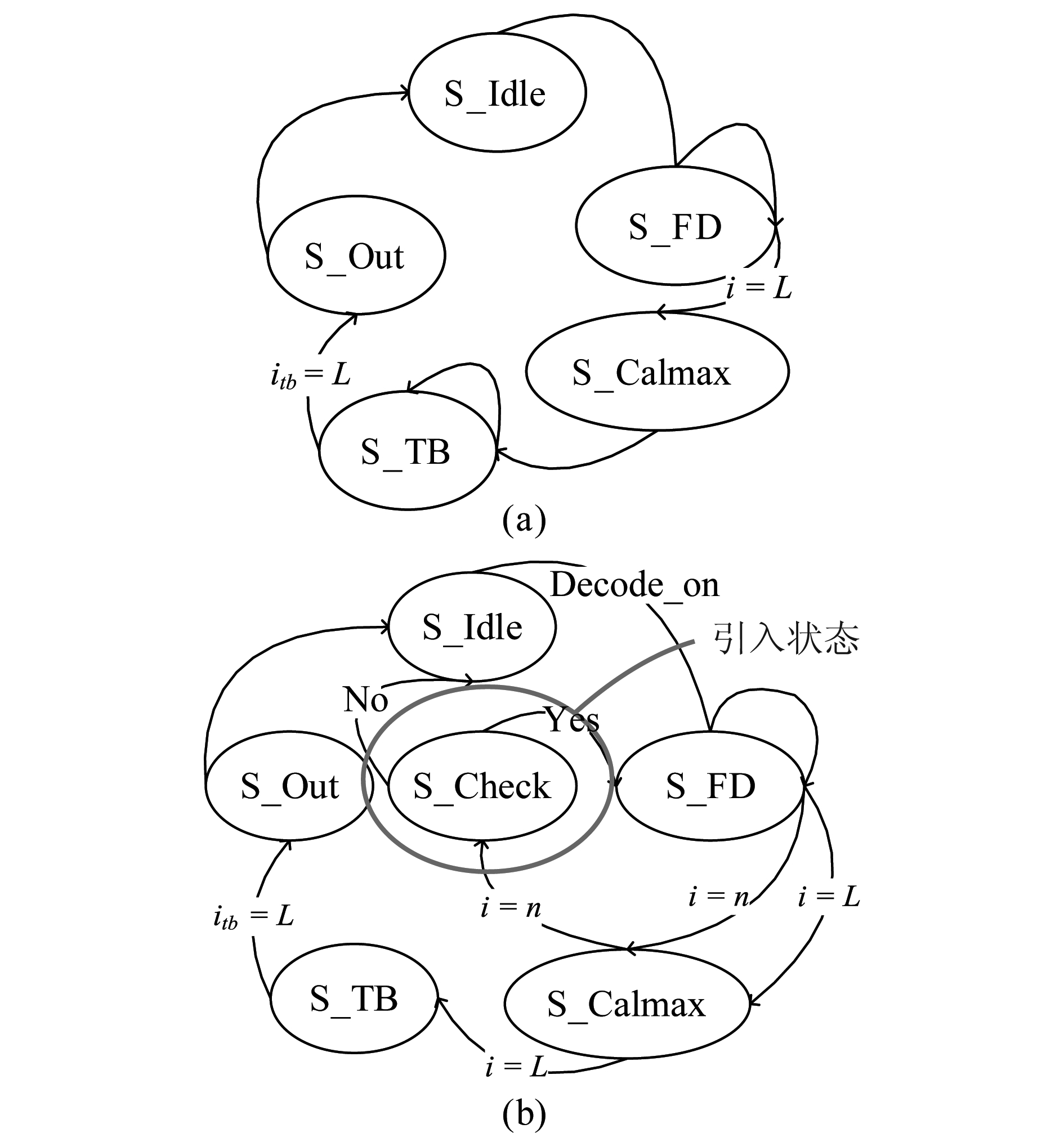
图4 (a) 一般咬尾Viterbi译码器的FSM,
(b)有信道编码盲识别的咬尾Viterbi译码器的FSM
Fig.4 (a) FSM of normal tail-biting Viterbi decoder,
(b) FSM of tail-biting Viterbi decoder with channel
code blind recognition
当接收到Decode_on信号时图4(b)所示的Viterbi译码器由初始状态(S_Idle)跳转到正向译码状态(S_FD)开始正向译码,依据输入软信息不断更新各个路径的路径度量。在译码深度达到信道编码盲识别所需的长度n时,译码器暂停正向译码,并跳转至最大PM计算状态(S_Calmax),计算当前的最大PM值。获得最大PM值后译码器进入识别检测状态(S_Check),对当前尝试的候选Ct进行识别检测。如果识别检测未通过则回到S_Idle等待开始下一次的译码,反之译码器回到S_FD状态继续后续正向译码流程。图4中S_TB状态表示回溯状态,S_Out表示译码结果输出状态。对比图4(a)基本Viterbi译码器FSM可以看出本文提出的信道编码盲识别算法仅额外引入了一个S_Check状态用以在译码深度达到n时对最大PM值进行识别检测。
4 仿真试验
本文的仿真部分以PDCCH的盲检为实例,产生仿真数据,分析所提出的信道识别算法在应用于PDCCH盲检这种典型的盲译码实例时,设定漏警α,译码长度n和信噪比SNR对于算法性能的影响。基于FPGA对图4所示的两种Viterbi译码器结构进行硬件实现,比较单纯的Viterbi译码器和具有信道编码识别功能的Viterbi译码器的硬件资源消耗,分析引入而不能问所提出的信道编码算法所需的资源消耗情况。
4.1 LTE的PDCCH盲检
在LTE系统的PDCCH中,基站在向小区内各个用户设备(user equipment, UE)发送下行控制信息(downlink control information, DCI)时,会依次依据每个UE的信道条件等因素从当前子帧的控制区域中选择一段未被其他UE的DCI占用的时频资源(称为PDCCH候选)来承载其DCI。PDCCH候选共有1至4四种聚合等级,分别对应72 bit,144 bit,288 bit和576 bit四种序列长度。
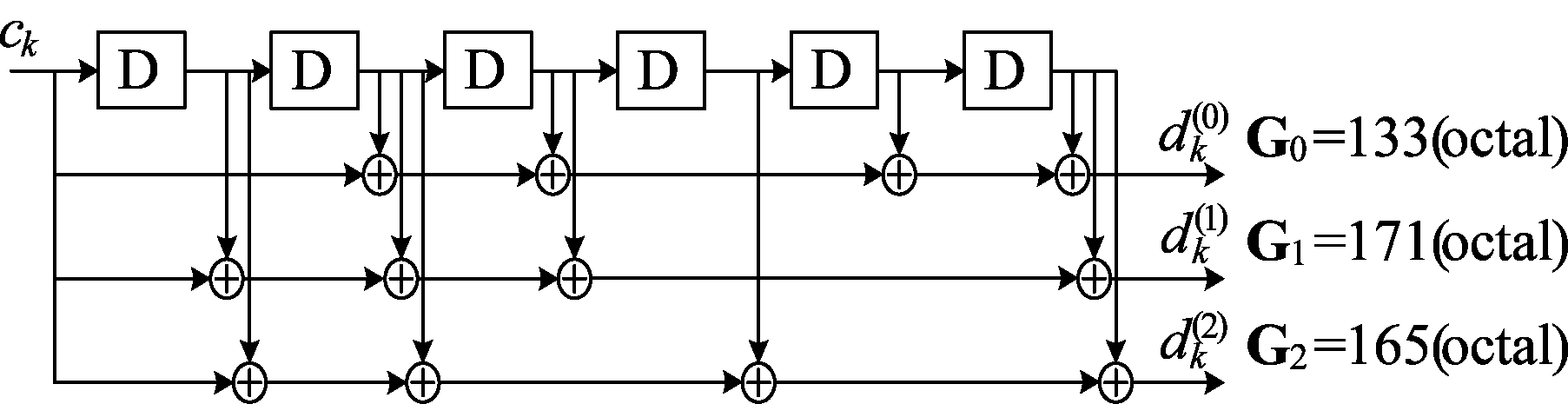
图5 码率1/3的咬尾卷积编码器
Fig.5 Rate 1/3 tail biting convolutional encoder
PDCCH固定采用图5所示的卷积编码器对DCI进行编码,然后通过重复或者打孔将其长度变更为所选择的PDCCH候选的长度。在接收端,UE采用盲检的机制依次对预先定义的PDCCH候选集中各个候选进行盲译码,直到通过CRC校验获取所需DCI。当前盲译码的PDCCH候选与基站所选择的候选相同时即H1的情况,接收序列r来自于有效的编码序列。当两者不同时即H0的情况,接收序列r将来自于自身或者其他用户的部分编码序列,又由于发送端加扰处理的影响,此时接收序列r可以看作来自01随机序列。
4.2 算法性能
基于上述分析进行如下实验:对应假设H1和假设H0分别产生有效数据测试组和无效数据测试组两组数据。有效数据测试组的信号序列采用PDCCH的信道编码方式进行卷积编码,无效数据测试组中为01随机序列,每一组测试数据包含10000个信号序列。测试序列采用QPSK调制并通过高斯白噪声信道(AWGN)传输。在生成测试数据后分别对两组数据进行信道编码盲识别测试。
本章对于算法的加速性能和可靠性即虚警率和漏警率进行评估。依据两种错误的含义,漏警率定义为有效数据测试组中被检测为无效测试序列的样本在该组中所占的比例。虚警率定义为无效数据测试组中被检测为有效序列的样本在该组中所占的比例。
首先对算法的漏警率进行仿真测试,结果如下。
图6分别给出了在不同信噪比SNR与译码长度n下,漏警率随系统设定的漏警率α的变化曲线。观察图6可发现,在信噪比条件较好和译码长度较长的情况下,仿真值与设定值相吻合,证明理论推导正确。同时也可以发现,在信噪比条件较差的情况下仿真值略高于设定值。出现上述偏离情况的原因是:在信噪比过低时,噪声的干扰已经大于信道编码的纠错能力,译码器译码结果出现错误,实际仿真中包含译码结果错误引入的漏警错误,故略高于理论值。对比相同SNR下不同译码长度n对应的三条曲线也可以发现,增加译码长度会使算法漏检仿真值更加贴近理论值,这与信道编码的纠错能力随着长度的增加而增加的特性相符合。
下面对算法的虚警率进行性能测试。式(17)为虚警概率表达式,虚警概率主要受阈值λf影响,随λf增大而减小。由式(18)可知虚警概率与设定漏警概率α,译码长度n,噪声功率σ′2,和![]() 与q′的汉明距离m这四个变量有关。但在每次译码过程中,距离值m值是未知且不可控的,难以依据公式推导出该识别算法精确的虚警概率。因此本文只对算法的虚警概率进行定性分析,并采用仿真的方法进行算法的性能测试。
与q′的汉明距离m这四个变量有关。但在每次译码过程中,距离值m值是未知且不可控的,难以依据公式推导出该识别算法精确的虚警概率。因此本文只对算法的虚警概率进行定性分析,并采用仿真的方法进行算法的性能测试。

图6 n=24,n=48,n=96时不同SNR下漏警率仿真值随理论值α的变化曲线
Fig.6 Missing alarm probability simulation value versus theoretical value α curves for
different SNR at n=24, n=48, n=96
假设![]() 与q′的差异均匀分布,即m与n呈正比关系,系数设为A。公式(18)可以转换为如下形式:
与q′的差异均匀分布,即m与n呈正比关系,系数设为A。公式(18)可以转换为如下形式:
由上式可以发现,增大设定漏警率α(λ0),增大空间信道的信噪比(σ′),增加译码长度n,都可以降低算法的虚警率,提高算法性能。下面分别分析这三者对于算法虚警率的影响。
图7给出了虚警率随漏警率α的变化曲线。对于一个检测算法,虚警率和漏警率存在折中关系,检测阈值的更改必然会导致其中一方的增加和另一方的减少,图7的性能仿真曲线体现出了这种转换关系。由章节3.2部分分析可知,虚警率表征了检测算法的加速效果,漏警率表征了检测算法的可靠性,故该方法在应用时需要依据系统对于可靠性和延时的需求来综合权衡参数α值的设定。
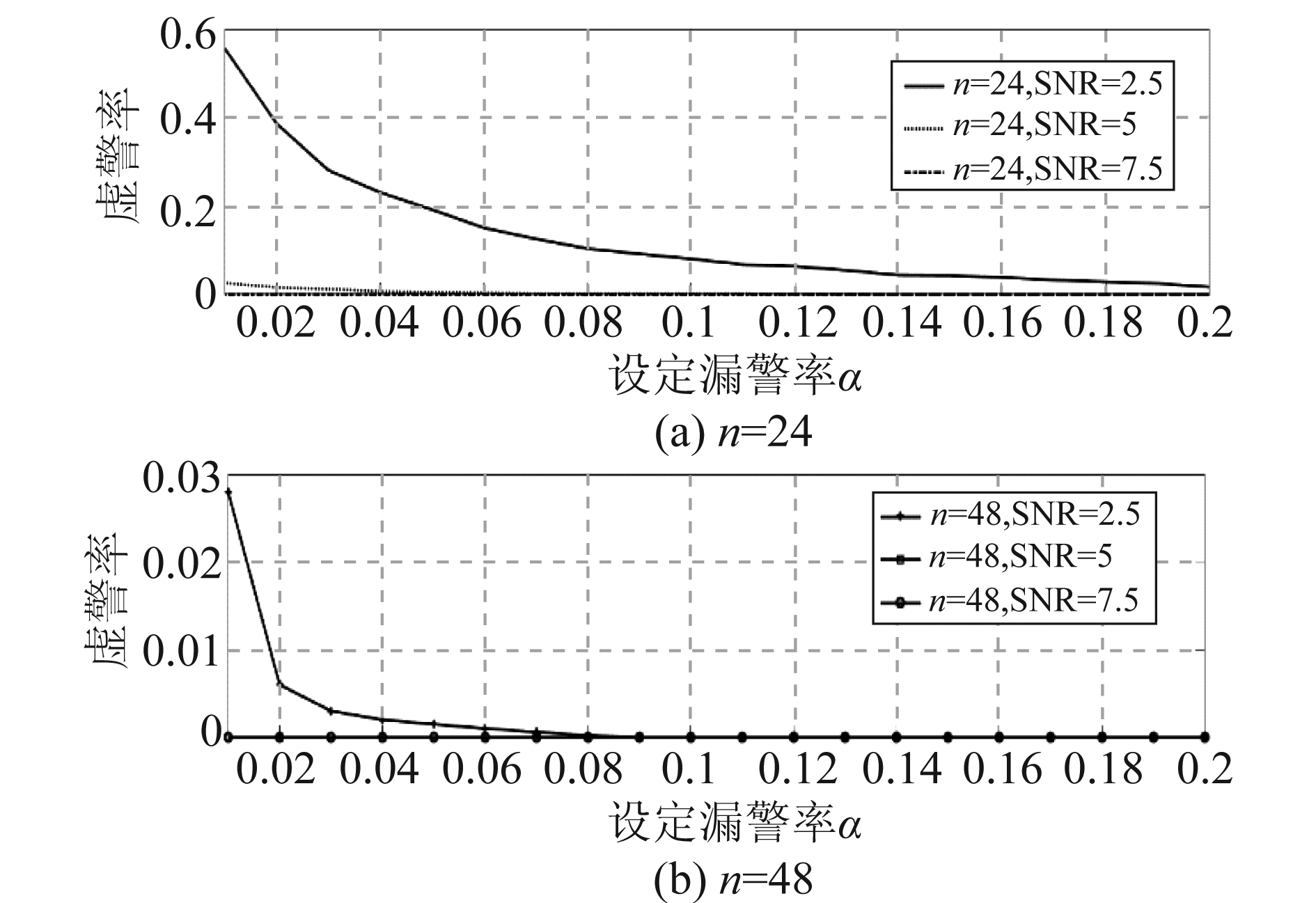
图7 n=24,n=48时不同SNR下虚警率随α的变化曲线
Fig.7 False alarm probability value versus α curves for
different SNR at n=24, n=48
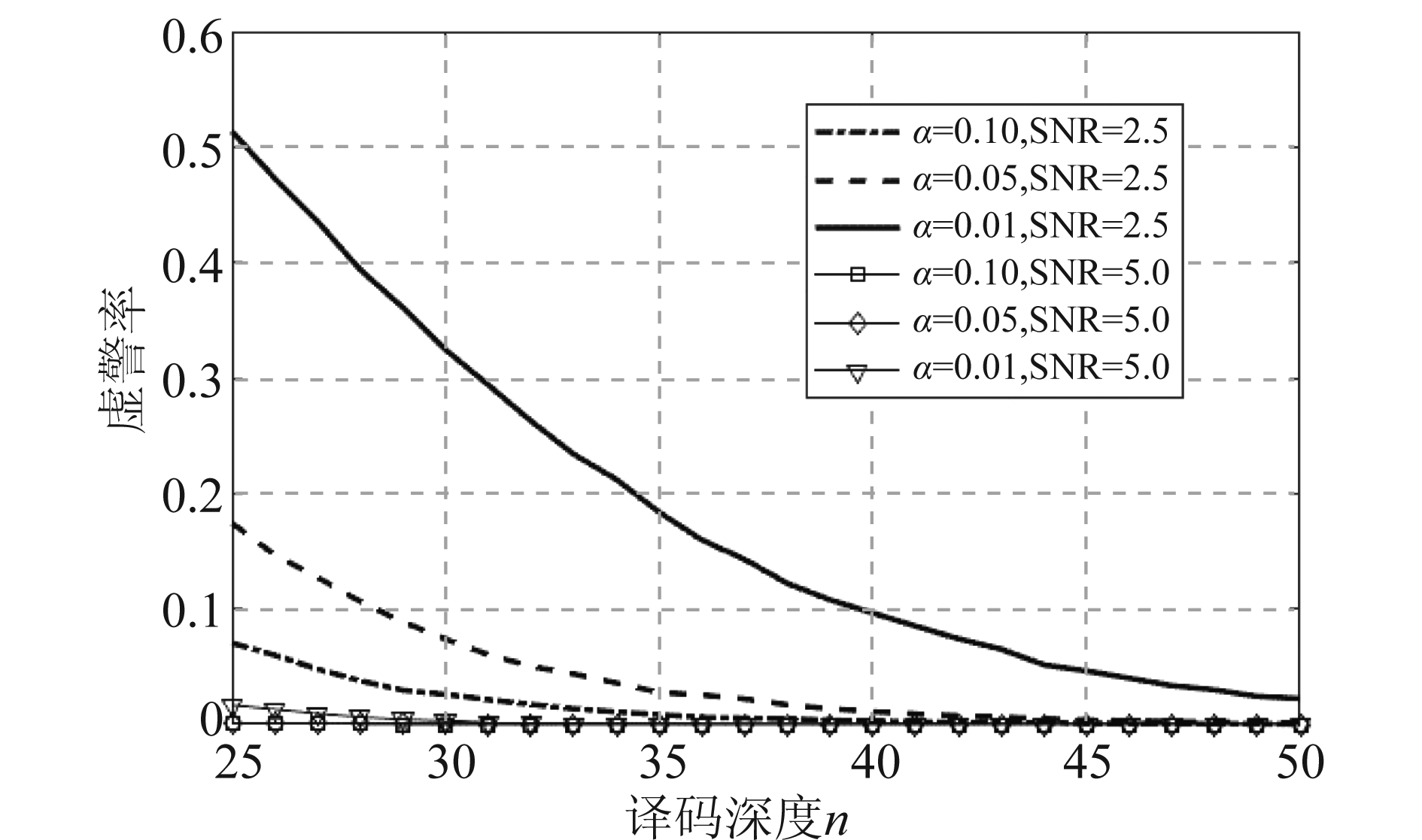
图8 不同的SNR和α下虚警率随n的变化曲线
Fig.8 False alarm probability value versus n
curves for different SNR and α
图8显示了虚警率随着译码深度n增加的变化曲线。译码深度n表示在Viterbi译码器正向译码时选择进行信道编码盲识别的时机,由图8可以看出增加译码深度n可以有效降低虚警率的发生,但识别检测所需的延迟增大,单次盲译码的加速效果变差。
最后分析信道条件SNR对于所提出的信道编码识别算法的影响。接收端的UE设备在进行咬尾卷积码的译码时,常采用循环译码的方式,将接收序列循环译码两到三次。这里本文选择直接在完成第一次循环译码时进行信道编码的盲识别,即n设为接收序列长度。这样对于无效候选的盲译码可以省去后续一到两次循环译码和回溯等操作,达到加速盲检过程的目的。图9给出了在设定α为0.001时四种不同译码长度n下盲识别算法的性能随信道条件SNR的变化曲线,分别对应4种不同聚合等级的PDCCH候选。信道条件是发送端选择PDCCH候选重要的参考因素,信道条件越差,所选取的PDCCH候选聚合等级越高。观察图9可以发现,随着检测译码距离n的增加,算法的性能曲线向左推移,算法的适用信道范围变大,随着信道条件的降低,基站所选择的PDCCH候选聚合等级增加,而本文所提出的识别算法适用的信道范围也会随之变大以适应信道条件的降低,如在系统漏警率为0.001时,对于n=24的情况,在SNR大于5.5时检测算法的虚警率已经小于0.1;n=48时相应检测性能的SNR下限已经减少至3 dB;而对于n=192的情况,在SNR=0.2 dB时所提算法的虚警率仍小于0.1。
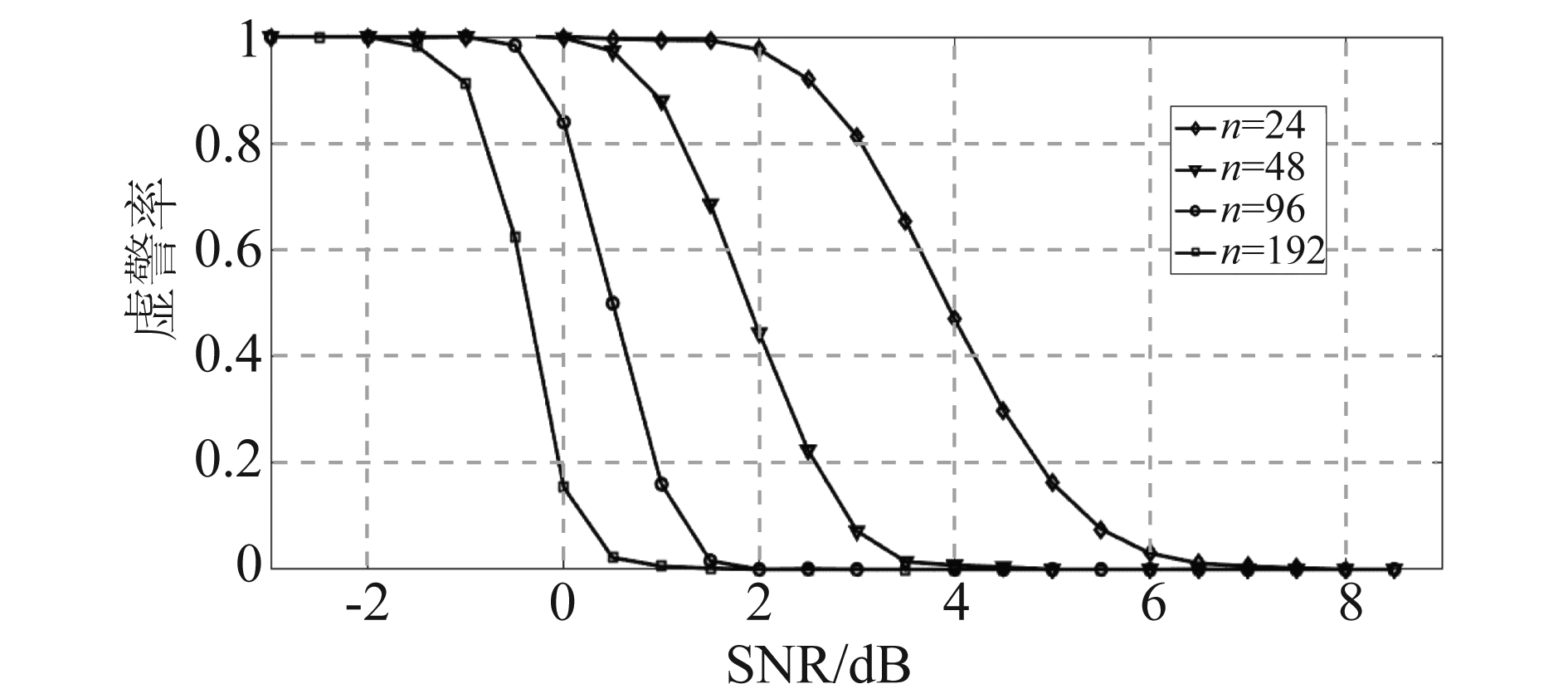
图9 不同的n下α=0.001时虚警率随SNR的变化曲线
Fig.9 False alarm probability versus SNR curves at
α=0.001 for different n
4.3 硬件实现开销分析
本文使用的硬件平台为Xilinx型号为xc7vx-485tffg1157-1的FPGA,利用Vivado 2016.2进行综合
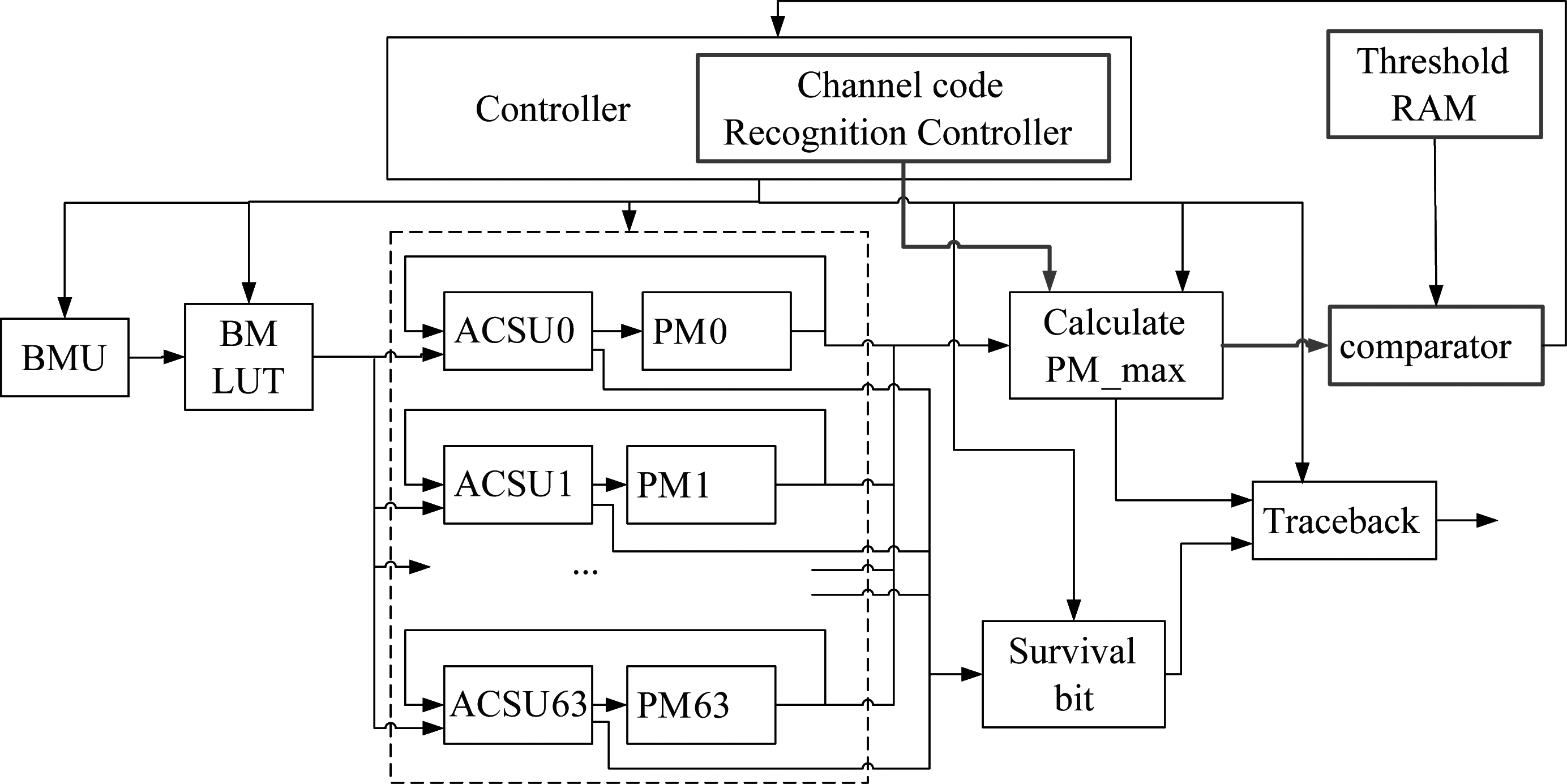
图10 咬尾卷积码的Viterbi译码器的实现框图
Fig.10 Implementation block diagram of Viterbi decoder for tail-biting convolutional code
分析。分别实现图4所示的两种Viterbi译码器结构,对应编码器结构如图5所示。其中图4(b)对应的Viterbi译码器的硬件结构如图10所示。图10中红色圈标记为与图4(a)相比多出的功能模块。译码器采用循环译码方式实现咬尾卷积码的译码,译码长度为2.5L,采用基-2结构,共64条路径度量,分支度量采用查表法,保存路径更新采用回溯法。
从图10可以看出,控制器模块中增加了信道编码识别控制器结构,该结构用于控制PM最大值模块在达到识别所需的译码深度n时计算当前最大PM值并将其输出用于识别检测。
由于本文所提出的信道盲识别算法是通过对标准的咬尾Viterbi译码器的改进实现的,所以其资源消耗表示为相较于原Viterbi译码器的资源增加量。两种方法硬件实现的资源消耗见表1。
表1 图4的两种Viterbi译码器结构的硬件资源消耗
Tab.1 Hardware resource of the two Viterbi decoder
structures in Fig.4
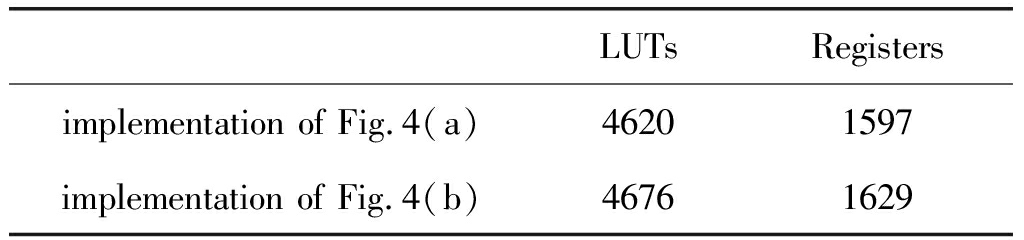
LUTsRegistersimplementation of Fig.4(a)46201597implementation of Fig.4(b)46761629
对比表1可以看出,采用本文所提出的方法的Viterbi译码器仅增加了56个LUTs和32个寄存器。LUTs资源仅增加1.21%,寄存器资源增加2.00%
由以上仿真与实现的结果可以看出,本文所提出的算法原理简单,实现容易,可以以较低的资源消耗为代价来实现性能良好的信道编码盲识别加速。该优势使得其更便于应用于硬件资源受限的应用中。
5 结论
本文针对目前的信道编码识别算法普遍需要额外计算识别特征量,延时高且不易硬件实现的问题,提出了一种基于最大似然译码的信道编码盲识别算法。该算法直接将译码器中的最大欧氏距离值作为特征量进行信道编码的识别,并提前终止无效译码尝试。以LTE中的PDCCH盲检为典型应用场景,通过仿真证明了理论推导的正确性、分析了算法性能,并对算法进行了硬件实现。实验结果表明本文所提方法原理简单,性能良好,便于应用在硬件资源受限的场景中。
参考文献
[1] Goldsmith A J, Chua S G. Adaptive coded modulation for fading channels[J]. Communications IEEE Transactions on, 1998, 46(5): 595- 602.
[2] 张永光, 楼才义. 信道编码及其识别分析[M]. 北京:电子工业出版社, 2010.
Zhang Y G, Lou C Y. Channel Coding and the Recognition Analysis[M]. Beijing:Publishing House of Electronics Industry, 2010. (in Chinese)
[3] Moosavi R, Larsson E G. A fast scheme for blind identification of channel codes[C]∥Global Telecommunications Conference. IEEE, 2011: 1-5.
[4] Moosavi R, Larsson E G. Fast blind recognition of channel codes[J]. IEEE Transactions on Communications, 2014, 62(5): 1393-1405.
[5] 魏刚, 张云冲, 戴旭初. 一种改进的信道编码盲识别算法[J]. 遥测遥控, 2016(2): 13-20.
Wei G,Zhang Y C,Dai X C.A Modified Algorithm for Blind Recognition of Channel Codes[J].Journal of Telemetry, Tracking and Command,2016(2):13-20. (in Chinese)
[6] Yu P, Peng H, Li J. On blind recognition of channel codes within a candidate set[J]. IEEE Communications Letters, 2016, 20(4): 736-739.
[7] Tech.Rep.“Physical channels and modulation”,3GPP Technical Specification Group Radio Access Network, Evolved Universal Terrestrial Radio Access (E-UTRA), TS 36.211 V10.7.0[OL]. https:∥portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2425, Mar. 2013.
[8] Tosato F, Bisaglia P. Simplified soft-output demapper for binary interleaved COFDM with application to HIPERLAN/ 2[C]∥IEEE International Conference on Communications. IEEE, 2002: 664- 668 vol.2.
[9] 王新梅, 肖国镇. 纠错码:原理与方法[M]. 西安:西安电子科技大学出版社, 1991.
Wang X M, Xiao G Z. Error correcting codes: Principles and methods[M].Xi’an: Xidain University Press, 1991. (in Chinese)
[10] Bai D, Lee J, Kim S, et al. Near-Optimal Contraction of Voronoi Regions for Pruning of Blind Decoding Results[J]. IEEE Transactions on Communications, 2015, 63(6): 1963-1974.
[11] Chen F T, Zheng W Q, Lv N. FPGA implementation of PDCCH blind detection algorithm in TD-LTE[J]. Advanced Materials Research, 2014, 926-930: 3616-3620.



