1 引言
运动单站定位通过单个运动观测站来对目标辐射源进行截获、测量并获得目标的位置信息。运动单站定位系统与多站定位系统相比,不需要大量的通信数据传输,具有结构简单、设备灵活等优点,因此对航海和航空、卫星定位预警、引导反辐射武器、电子侦察等许多民用、军用领域都有着广阔的应用前景[1]。
传统的运动单站定位一般采用两步定位体制,即使单站观测器与辐射源之间发生相对几何位置的变化,在位置变化的过程中通过多次测量获得目标的信息数据[2],然后进行参数估计,最后得出目标的位置估计,其中的参数估计有多种方法,如对波达方向(Direction of Arrival,DOA)[3]、 到达时间(Time of Arrival, TOA)[4]、 到达时间差(Time Difference of Arrival, TDOA)[5]、到达频差(Frequency Difference of Arrival)[6]、多普勒频差(Differential of Doppler, DD)[7]的估计及联合估计[8-9]等。然而,两步定位体制也存在着一些问题。由信息论的角度来讲,从接收到的原始数据到获得最后结果,每增加一步处理流程,会难以避免造成一定的信息损失,导致定位精度受到影响,难以得到最优的估计结果。近些年来,随着数据传输速度及计算机性能的提高,以Weiss和Amar为代表的一些国内外学者提出了一种新的无源定位方法,即单步定位算法,又称直接定位算法(Direct Position Determination, DPD)[10]。该类定位方法的基本理念是从接收到的数据中直接得到目标辐射源的位置,而不需要进行参数估计。Weiss在文献[10]中提出了基于阵列信号处理的静止多站DPD算法。而后部分学者又将DPD算法应用到运动多站方向,提出了基于多普勒与时延的运动多站DPD方法[11],以及基于多普勒的运动多站DPD方法[12-13]。Oispuu又利用单个运动天线阵列提出了针对多目标的DPD算法[14]。通过大量实验可以验证,在低信噪比条件下,DPD方法比传统两步定位方法具有更高的定位精度。
然而,对于运动单站定位问题,DPD算法目前的研究仍然有很大的拓展空间。本文借鉴DPD算法的基本理念,提出了一种基于多普勒的运动单站直接定位算法。该算法去除参数估计步骤,从接收数据中直接提取目标位置信息,并通过二维格网型空间索引以获取目标的位置估计。此外,本文还分析推导了算法的CRLB、理论误差及运算量。仿真结果表明,与两步定位算法相比,DPD算法能够有效抑制噪声影响,目标位置估计定位精度大幅提高,算法估计性能更加逼近CRLB。
2 问题描述与定位模型
如图1所示,假设存在一个静止目标辐射源,位置向量为p0,发射信号s(t)带宽为W,载频为fc。某运动观测站在K个观测间隙内对辐射源的数据进行采样,每个观测间隙的观测时间为T,用pk和vk(k=1,...,K)表示观测站在第k个观测间隙内的位置与速度。

图1 目标直接定位示意图
Fig.1 Sketch map of direct localization for target
则观测站在t时刻接收到的数据模型为
rk(t)=bksk(t)ej2πft+nk(t)
(1)
式中:
(1)bk表示信号在第k个观测间隙到达观测站的传播系数;
(2)nk(t)表示均值为0,方差为σ2的高斯噪声;
(3)f表示观测站在第k个观测间隙接收到的信号频率,可以表示为
f=fc·(1+μk(p))
(2)
式中, μk(p)表示目辐射源与观测站相对运动而产生的多普勒效应,可表示为
(3)
式中c表示电磁波的传播速度。
由于fc为已知量,则通过数字下变频处理后得到的信号频率为
(4)
则式(1)可表示为
rk(t)=bksk(t)ej2πfkt+nk(t)
(5)
假设观测站在第k个观测间隙内采样时间间隔为Ts,采样快拍次数为Ns,将式(5)用向量形式表示
rk=bkFksk+nk
(6)
式中
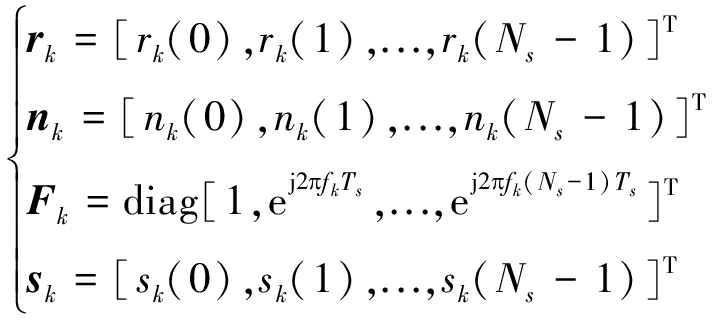
(7)
3 算法推导
通常对目标位置的估计可以视为利用接收数据rk估计出辐射源位置坐标p0。对式(6)可以将对辐射源定位的问题转化为通过构造代价函数求解,则目标位置的最小均方误差估计为下列代价函数的最小值
(8)
使上式最小的bk的估计可以由下式得到
bk=[(Fksk)H(Fksk)]-1×(Fksk)Hrk=(Fksk)Hrk
(9)
不失一般性,对任意的k,假设
‖s‖2=1
(10)
将式(9)与式(10)代入式(8),可以得到
(11)
注意到:‖rk‖2与参量无关,则Q(p)的最小化可以通过最大化![]() 来实现
来实现
(12)
式中
(13)
3.1 未知信号
当传输信号是未知时,则式(12)的最大值转化为选择与sk对应的Vk的最大特征值,结果为
(14)
式中,Vk 的维度是Ns×Ns,当采样率增大时,进行特征值分解求取特征值所需的计算量也将快速增大。
一般地,对于一个矩阵A,其表达式AAH与AHA的非零特征值是等价的,因此,对于式(13),可令
(15)
即有Ns×Ns矩阵Vk可以用L×L维矩阵![]() 代替,其中,L为观测站数目,在本文讨论的运动单站定位中即为1×1矩阵,则对比式(13)与式(15)可以得出结论,当L≪Ns时,采用式(15)会大幅降低计算量。
代替,其中,L为观测站数目,在本文讨论的运动单站定位中即为1×1矩阵,则对比式(13)与式(15)可以得出结论,当L≪Ns时,采用式(15)会大幅降低计算量。
最后,通过进行二维格网型空间索引,求出式(14)的最大值,其所对应的坐标值即为辐射源的位置坐标,即有
(16)
3.2 已知信号
假设传输信号是已知的,则式(12)可以表示为
(17)
其中
Sk=diag{sk}
(18)
则式(17)可被简化为
(19)
同理,目标位置p0的估计值可以通过二维格网型空间索引得到,表达式如下
(20)
4 算法分析
4.1 克拉美罗界(CRLB)推导
对于参数估计问题,CRLB为任何无偏估计量的方差的下限,由此,可以估计算法的理论性能标准。本文中,设J为系统的Fisher信息矩阵(Fisher Information Matrix, FIM),则由文献[15]可得
![]()

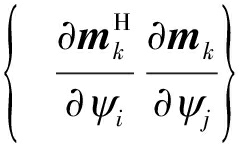
(21)
式中ψi表示第i个未知参数向量的元素,在本文中,参数向量为辐射源的二维位置向量,则ψi=ψ1=x, ψj=ψ2=y。另外
mk bkFksk
bkFksk
(22)
对于式(21),运用链式求导法则可得
(23)
式中
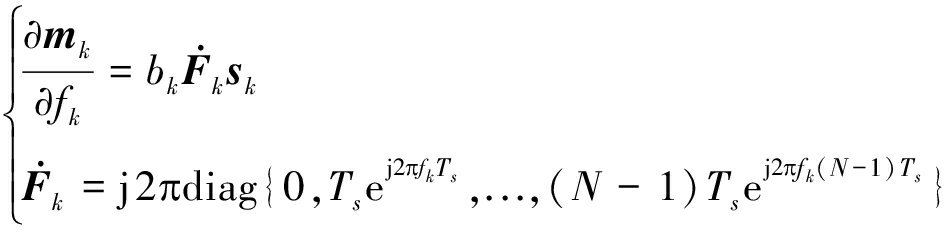
(24)
令![]() 由式(2)和(3)可得
由式(2)和(3)可得
(25)
则
(26)
同理
(27)
式中,φ表示观测站运动速度方向与目标连线的夹角,θ表示x方向与目标连线的夹角,dk表示观测平台与目标的距离。
综上,FIM信息矩阵可由式(28)给出
![]()

![]()
(28)
4.2 误差分析
由于DPD算法不需要参数估计这一步骤,因此可以避免参数误差带来的定位失真。到目前为止,本文以上所做分析都建立在假设接收到理想的多普勒频率的基础上。然而,在实际观测过程中,多普勒可能无法准确测量,导致按照理想模型进行推导所得到的辐射源位置可能会不准确。
加入误差分析时,将式(1)修改为带误差的数据模型
(29)
式中:![]() 表示模型中带误差的多普勒频率测量值。
表示模型中带误差的多普勒频率测量值。
定义Δfk为多普勒的真实值与测量值之差
(30)
假设Δτ与为Δf零均值高斯分布,则其协方差可表示为
E[Δf(Δf)T]=Qf
(31)
式中:Qf为对角矩阵,矩阵元素为误差方差![]() 重新进行第三章节的推导,可以得到类似式(14)的位置估计结果
重新进行第三章节的推导,可以得到类似式(14)的位置估计结果
(32)
式中![]()
4.3 计算量分析
对于未知信号,当采用式(15)进行运算时,计算vk需要N次乘法运算,计算共轭矩阵![]() 约需0.5N次运算,由3.1节可知,
约需0.5N次运算,由3.1节可知,![]() 为1×1矩阵,则将其代入式(14)进行特征值分解需要1次乘法运算。设网格点数为Mg,则总的计算量为MgK(1+0.5N+N)≅1.5MgKN。
为1×1矩阵,则将其代入式(14)进行特征值分解需要1次乘法运算。设网格点数为Mg,则总的计算量为MgK(1+0.5N+N)≅1.5MgKN。
对于已知信号,由于Fk与Sk都是对角矩阵,则计算![]() 的值需要2N次乘法运算,而求取共轭矩阵
的值需要2N次乘法运算,而求取共轭矩阵![]() 的值,又需要进行0.5N2次乘法运算,则总的计算量为MgK(2N+0.5N2)≅0.5MgKN2。
的值,又需要进行0.5N2次乘法运算,则总的计算量为MgK(2N+0.5N2)≅0.5MgKN2。
5 仿真实验
首先,定义均方根误差为:
(33)
仿真参数设置:假设存在一个静态发射源,发射载频fc=0.5 GHz,带宽为300 kHz的高斯信号,其传播速度c为光速。观测站与目标位置分布如图2所示,辐射源位置为(2500 m, 2500 m),观测站沿y=500 m向x轴正方向移动,其速度为300 m/s,观测间隔为3.33 s,且观测次数设定为10次。
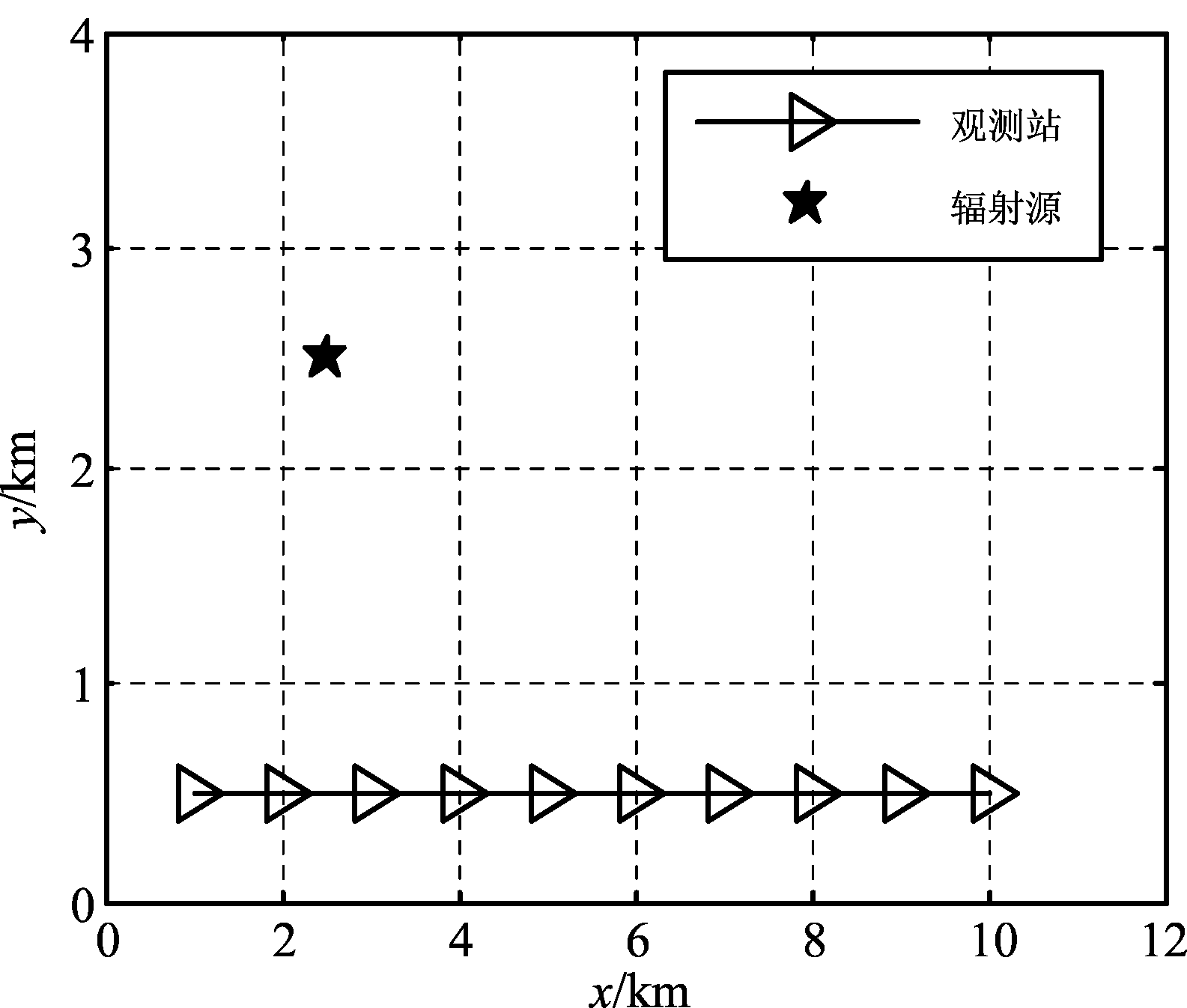
图2 目标辐射源与观测站间的地理位置关系示意图
Fig.2 Sketch of the relationship between the
radiation source and the observation station
5.1 算法的估计精度性能对比
为考察不同算法位置估计精度,本文采用本文提出的运动单站DPD算法与文献[7]提出的迭代频差两步定位算法(DD)进行仿真对比。
(1)将每个观测间隙内的样本点数设为100,载波频率fc=0.5 GHz,如图3(a)所示为不同算法在不同信号条件下目标位置估计均方根误差随信噪比的变化曲线;
(2)将信噪比设为0 dB,载波频率fc=0.5 GHz,图3(b)所示为不同算法在不同信号条件下目标位置估计均方根误差随每个观测间隙内样本点数的变化曲线;
(3)将信噪比设为0 dB,每个观测间隙内的样本点数设为100,图3(c)所示为不同算法在不同信号条件下目标位置估计均方根误差随载波频率的变化曲线。
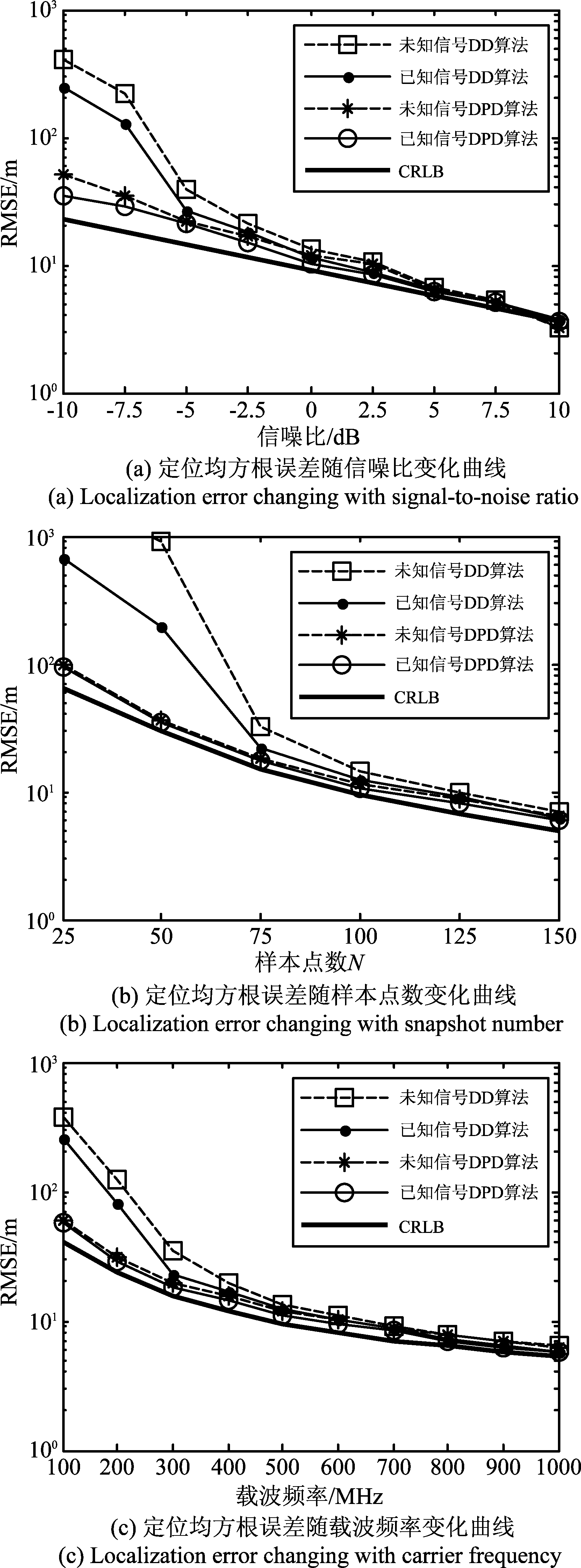
图3 定位均方根误差随信噪比、
样本点数和载波频率的变化曲线
Fig.3 Localization error changing with SNR,
snapshot number and carrier frequency
从图中可以得出以下结论:
(1)DPD算法的定位性能要明显优于两步定位算法,能够较好地逼近CRLB,这是由于DPD算法能够充分利用接收数据提供的信息,从而使位置估计精度整体提升;
(2)随着信噪比、样本数据量与载波频率的提高,不同算法的RMSE均有所降低,并且与CRLB的下降趋势一致。相比于两步定位算法,在低信噪比、低样本数据量与相对低频条件下,本文DPD算法具有更高的定位精度;
(3)与未知信号相比,已知信号能够增加数据信息量,在利用更多信息的情况下,各算法的估计性能有所提高,但就整体而言,两种DPD算法性能差异并不大。
5.2 多普勒测量误差对估计性能的影响
图4表示在给定信噪比为20 dB、样本点数为50和载波频率fc=0.5 GHz的情况下,多普勒测量误差对不同算法定位性能的影响。从图中可以看出,多普勒测量误差对于DPD算法定位性能的影响程度与4.2节理论值差距不大,并远小于两步定位算法。这是由于在两步定位过程中,误差经过参数估计可能会被放大,然后定位解算步骤又会进一步引入误差,最终导致的估计偏差较大。而DPD算法不需要参数估计这一步骤,因此避免了参数误差带来的定位失真。
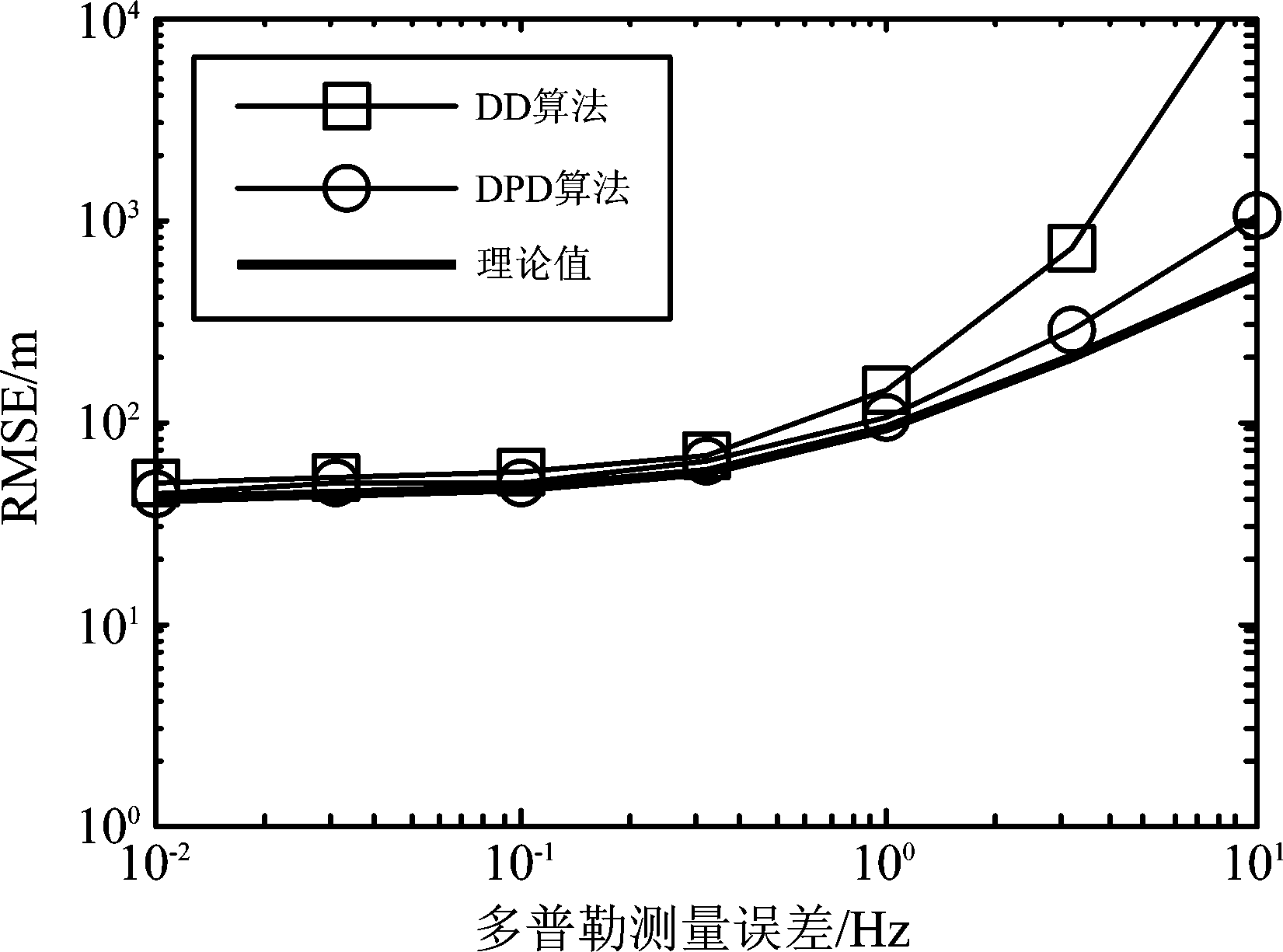
图4 多普勒测量误差对估计性能的影响
Fig.4 The effect of Doppler measurement
error on estimation performance
6 结论
针对利用传统运动单站算法对目标定位性能不够理想的问题,笔者提出了一种利用多普勒的运动单站直接定位算法,将直接定位算法引入到运动单站定位系统中,并分析推导了新算法的CRLB、理论误差与计算量。仿真实验表明:较之传统的运动单站定位算法,本文DPD算法能够较好地抑制噪声的影响,提高定位精度,尤其在低信噪比、低样本数据量以及相对低频条件下仍能逼近CRLB;在已知信号条件下,算法定位精度有所提高;多普勒测量误差对DPD算法定位性能的影响远小于两步定位算法。
参考文献
[1] 李鹏. 对固定辐射源的单站无源定位技术[J]. 电子科技, 2013, 26(9):61- 64.
Li Peng. The passive positioning technology for fixed radiant in single station[J]. Electronic Science and Technology, 2013, 26(9):61- 64. (in Chinese)
[2] 秦明峰, 郝青儒, 范广伟. 运动单站无源定位性能分析[J]. 无线电工程, 2014(4):50-53.
Qin Mingfeng, Hao Qingru, Fan Guangwei. Analysis on Passive Localization Performance of Moving Single Observer[J]. Radio Engineering, 2014(4):50-53. (in Chinese)
[3] Wang D, Zhang L, Wu Y. The structured total least squares algorithm research for passive location based on angle information[J]. Science in China, 2009, 52(6):1043-1054.
[4] Oh D, Kim S, Yoon S H. Two-Dimensional ESPRIT-Like Shift-Invariant TOA Estimation Algorithm Using Multi-Band Chirp Signals Robust to Carrier Frequency Offset[J]. IEEE Transactions on Wireless Communications, 2013, 12(7):3130-3139.
[5] Yang K, An J, Bu X, et al. Constrained Total Least-Squares Location Algorithm Using Time-Difference-of-Arrival Measurements[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3):1558-1562.
[6] Sun M, Ho K C. An Asymptotically Efficient Estimator for TDOA and FDOA Positioning of Multiple Disjoint Sources in the Presence of Sensor Location Uncertainties[J]. IEEE Transactions on Signal Processing, 2011, 59(7):3434-3440.
[7] 杨洁,刘聪锋.迭代频差定位算法及其性能分析[J].西安电子科技大学学报:自然科学版,2013,40(5):8-14.
Yang Jie, Liu Congfeng. Iteration FDOA location algorithm and its performance analysis[J]. Journal of Xidian University, 2013,40(5):8-14. (in Chinese)
[8] Yeredor A, Angel E. Joint TDOA and FDOA Estimation: A Conditional Bound and Its Use for Optimally Weighted Localization[J]. IEEE Transactions on Signal Processing, 2011, 59(4):1612-1623.
[9] Ho K C, Chan Y T. Geolocation of a known altitude object from TDOA and FDOA measurements[J]. IEEE Transactions on Aerospace & Electronic Systems, 1997, 33(3):770-783.
[10] Weiss A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5):513-516.
[11] Weiss A J. Direct Geolocation of Wideband Emitters Based on Delay and Doppler[J]. IEEE Transactions on Signal Processing, 2011, 59(6):2513-2521.
[12] Amar A, Weiss A J. Localization of Narrowband Radio Emitters Based on Doppler Frequency Shifts[M]. IEEE Transactions on Signal Processing, 2008, 56(11):5500-5508.
[13] 王鼎,尹洁昕,吴志东,等. 一种基于多普勒频率的恒模信号直接定位方法[J]. 航空学报,2017,38(9):284-297.
Wang Ding, Yin Jiexin, Wu Zhidong,et al. A direct localization method for constant modulus source based on Doppler frequency shifts[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9):284-297.(in Chinese)
[14] Oispuu M, Nickel U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal Processing, 2010, 90(12):3056-3064.
[15] Van T, Harry L. Optimum Array Processing: Part IV of Detection, Estimation and Modulation Theory[M]. New York:Wiley-Interscience, 2002.


