1 引言
根据美国航空数据网站Flightstats列出的2016年全球航空公司延误率排名显示,中国四家航空公司航班延误时长排世界前十,可见我国航班延误问题十分严重。虽然民航总局和各机场、航空公司针对航班延误问题都采取了一定的应急措施,但事后的状况料理效果有限。航班延误预测可使相关部门提前知晓可能延误的时间,做好应对措施并进行航班计划和机位指派的优化,具有重要的现实意义[1]。
国内外已有大量学者投入到航班延误预测的工作中[2-3]。文献[4]考虑同一架飞机的连续航班情况,利用贝叶斯网络进行航班延误波及分析,可反映连续航班延误原因分布及波及分布。文献[5]提出一种针对机场繁忙时段的航班延误免疫预测算法,可针对一天不同时段繁忙程度的差异性,自适应调整算法中的检测参数。以上方法虽都取得了较高的正确率,但都没有考虑到气象因素对航班延误预测的影响。可研究表明气象因素对于航班延误预测十分重要,在诸多影响原因中占比例较大,融入气象数据有利于正确率的进一步提高[6]。
当融入更多特征后,不可避免地导致数据量增大。一方面可基于大数据挖掘更多有效信息,以提高预测正确率[7];另一方面又将导致运算量的成倍增长,使传统数据处理方式和预测算法面临计算瓶颈。例如,文献[8]采用支持向量机算法进行航班延误预测,同时考虑航空网络信息扩展特征,降低预测误差。但受数据处理能力限制,需要采用PCA(Principal Component Analysis)方法对扩展特征后的数据进行有效降维。随着大数据技术的快速发展,并行计算框架已作为应对计算瓶颈的有效手段应用于诸多行业[9-11]。文献[10]在Spark并行计算框架基础上,采用大规模机器学习进行药物靶目标识别;文献[11]利用改进的并行化聚类算法辨识电力系统的不良数据。这些应用都表明使用大数据处理技术可有效增强模型的数据处理能力并增强算法效果。但较少有人基于大数据平台进行航班延误预测。文献[12] 率先采用深度学习方法预测机场延误状态,使用长短时记忆网络(long short term memory,LSTM)考虑时间维度特征,但该模型没有克服深度加深时模型无法收敛的难题,且实现的是机场延误状态的预测,并没有给出单个航班的延误时间范围。
本文基于Spark并行架构进行了航班延误数据和气象数据的融合,并使用并行化随机森林算法[13]构建航班延误预测模型。可在无需数据降维的情况下挖掘海量航班延误数据中的数据特征,并通过并行化计算快速进行到港航班延误等级预测。
2 数据预处理
航班延误预测模型的整个流程都在Spark并行计算框架中完成,原始航班数据和气象数据存于Hadoop分布式文件系统(Hadoop Distributed File System,HDFS),每步输出的中间数据以数据框的形式存储于集群内存,可快速进行算法迭代和后续的数据再利用。
2.1 数据定义
为方便后文叙述,现对数据定义如下:
定义 1 航班数据F中包含〈C,So,Sd,Ao,Ad,tsd,tad,tsa,taa〉,其中,C代表航空器型号,So代表起飞机场所在州;Sd代表目的机场所在州;Ao代表起飞机场;Ad代表目的机场;tsd代表计划起飞时间;tad代表实际起飞时间;tsa代表计划到达时间;taa代表实际到达时间。
定义 2 气象数据O中包含〈A,t,T,H,Wd,Ws,P,S,V〉,其中,A代表观测站所在机场;t代表观测时间;T代表温度;H代表湿度;Wd代表风向;Ws代表风速;P代表气压;S代表天空状况;V代表能见度。
定义 3 在数据融合时,考虑航班到达前n个小时内目的机场气象数据,其定义如下
Wd,n=〈O(Ad,tsa),…,O(Ad,tsa-nh)〉
(1)
其中,O(Ad,tsa)代表目的机场Ad在到达时间tsa的气象数据;O(Ad,tsa-nh)代表目的机场Ad在到达时间tsa向前追溯n个小时后所在时刻的气象数据。
定义 4 航班离港延误时间DD(F)定义为实际起飞时间和计划起飞时间的差值:
DD(F)=F.tad-F.tsd
(2)
定义 5 航班到港延误时间AD(F)定义为实际到达时间和计划到达时间的差值:
AD(F)=F.taa-F.tsa
(3)
定义 6 给定一次航班F和时间阈值Th,若AD(F)≥Th则判定航班延误,否则判为不延误。
2.2 数据融合
首先,需要完成数据清洗和标准化。在样本量足够大的情况下,数据清洗时直接对数据中有空值的航班数据和气象数据删除。同时本文只关注延误数据,因此对于数据集中取消和改航数据进行过滤处理,并依据起飞机场所在州和目的机场所在州进行各州州时转换,保证全部时间的时区一致。
由于航班数据和气象数据分别具有不同的量纲和标识方式,因此对名义变量进行编码,编码采用频次统计的方式,每一变量中出现频次最高的变量值编码为0,其次为1,依次类推。这种编码方式可保证特征的稀疏性,增强鲁棒性。最后对所有特征按公式(4)进行标准化处理。
(4)
其中xi表示变量值,E[x]表示变量的均值,Var[x]代表变量的方差,![]() 表示标准化后的变量值。
表示标准化后的变量值。
数据融合之前需将航班数据和气象数据建立关联,以保证信息的时空一致性。空间维度上以航班数据中的目的机场和气象数据中的观测站所在机场确定相同位置;时间维度上以航班计划到达时间和气象观测时间作为关联参数。数据融合过程在Spark并行架构中使用数据框和Spark sql程序自动完成,底层以Map和Reduce过程实现。
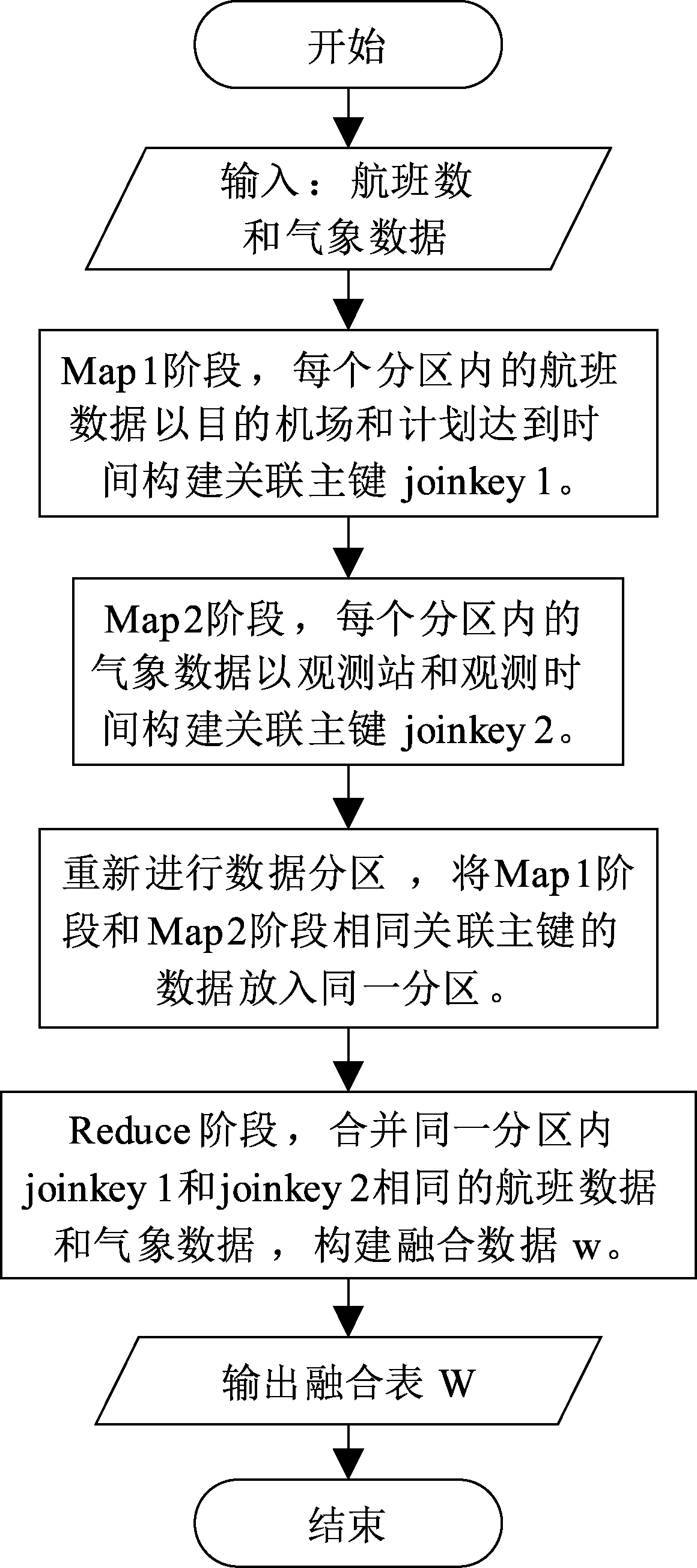
图1 数据融合
Fig.1 Data fusion
数据融合过程如图1所示。首先在Map阶段对不同分区数据建立关联主键,航班数据以Ad和tsa作为关联主键,气象数据以A和t作为关联主键;构建主键后依据主键将数据分区(Partition),将相同主键数据放入同一Partition;最后在Partition内进行Reduce操作,完成气象数据和航班数据的融合。当考虑到达机场n个小时的气象数据时,将公式(1)中定义的Wd,n-1输入Map1中,Map2中关联主键变为Ad和tsa-nh,Reduce阶段输入不变,从而得到Wd,n。
3 并行化随机森林算法
本文的航班延误预测模型采用并行化随机森林算法进行分类预测。模型训练时,使用HDFS将融合后数据均匀分布于集群机器中。然后利用训练集构建决策树,用测试集进行分类能力评估,如图2所示。
在训练基决策树时采用并行化的训练方式,每步中间数据以数据框形式存储。为尽可能利用Spark并行框架的计算优势,本文采用并行树策略和并行切分策略两种优化方法,如图3所示。
表1 并行化随机森林算法
Tab.1 Parallel random forest algorithm

输入:原数据集D;基决策树算法F;基学习器数T,子空间属性数d′。过程:1.t=1,2,3,…,T do2. Dt=RS(D,m)随机从D中有放回地抽取含m个样本的采样集;3. dt=RS(D,d′)从所有属性中随机选择d′个不同属性;4. D′t=Mapdt(Dt)D′t仅包含dt中的属性;5. a∗=Mapa∈dt(D′t,a)选取最优划分属性;6. ht=F(D′t)7.H(x)=Reduce ht输出:随机森林模型H(x)。
(1)并行树策略。传统单机构建随机森林时,采用深度优先方式递归调用,逐个生成树。在并行框架下,可在训练数据时将数据缓存于不同分区,采用广度优先策略。每个分区的数据单独训练一棵基决策树,每棵树的训练互不影响,之后进行聚合形成随机森林模型。此时,随机森林模型构建时间等于单个决策树的生成时间。
(2)并行切分策略。在进行基决策树分类器的属性切分时,传统对连续特征属性所有值进行排序再分裂的方法在分布式环境下并不可行。因为大量且高维数据情况下将产生高额计算代价和通信开销,算法效率低下。因此,将多个分区并行进行属性划分,根据分裂准则选取最优分裂点,并转化为根据最优分裂点划分的分区。最后再将每个分区选择的最优分裂点聚合,选出全局最优分裂点。
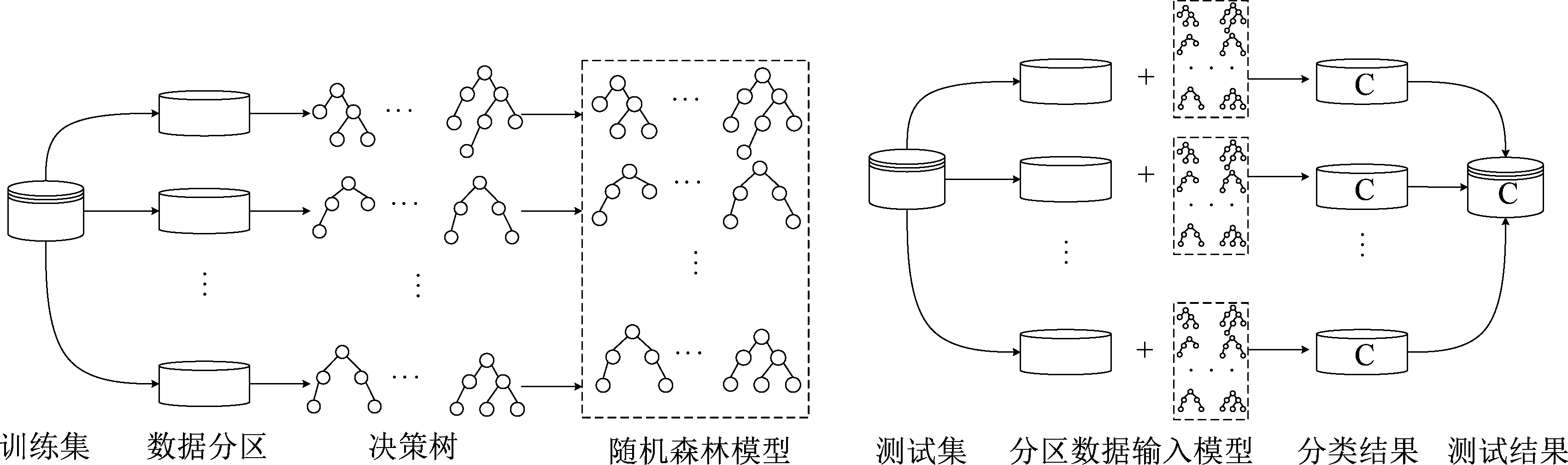
图2 航班延误预测模型
Fig.2 Flight delay prediction model

图3 并行策略
Fig.3 Parallel strategy
并行化后的算法原理如表1所示。首先,给定一个原始数据集D,使用自助采样法进行T次有放回采样,生成T个包含m个样本的采样集Dt,并将每个采样集存储于不同分区;然后同时使用各个分区数据训练基决策树,训练时假设每个样本有d个属性,则在训练基决策树的每个结点时先从该结点的属性集合中随机选择包含d′个属性的子集dt,再从dt中按并行切分策略选择一个最优属性进行划分;最后返回每个基决策树的训练结果ht并按公式(5)进行聚合计算。
(5)
其中,arg max f(x)表示当f(x)取最大时x的取值,Y代表类别集合,y代表预测样本的实际类别。
在步骤5中选取划分属性时,数据集D′t的纯度使用基尼指数(Gini index)度量。
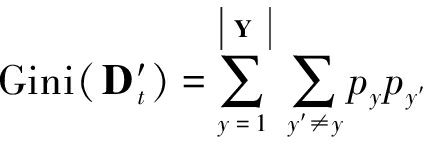
(6)
其中,py表示样本集合D′t中第y类样本所占比例,py′代表第y′类样本所占比例,y,y′=1,2,…,|Y|。Gini(D′t)反映了数据集D′t中随机抽取两个样本其类别标记不一致的概率。Gini(D′t)越小则数据集D′t的纯度越高。
假定离散属性a有V个可能的取值,使用a对样本D′t进行划分,会产生V个分支结点,其中第ν个分支结点包含了D′t中所有在特征a上取值为aν的样本,记为![]() tν。特征a∈dt的基尼指数可通过公式(7)计算。
tν。特征a∈dt的基尼指数可通过公式(7)计算。
(7)
在每次划分时,按公式(8)计算数据不纯度减少程度。
ΔGini(a)=Gini(D′t)-Gini_index(D′t,a)
(8)
选取划分后基尼指数降低最大的特征作为最优划分特征,即:
(9)
在测试时同样将多个分区的数据并行输入随机森林模型同时测试,从而提高算法效率。由于采用自助采样法进行抽样,每个决策树的训练样本Dt中包含原数据集D中63.2%的样本,则剩下的约36.8%样本则可作为图2模型中的测试集使用各基学习器进行预测。另Hoob(x)表示预测函数,则有:
(10)
4 实验
本文模型使用数据为美国交通运输统计局(Bureau of Transportation Statistics,BTS)提供的航班准时表现数据(Airline On-Time Performance Data,AOTP)和美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的本地气候质量监控数据(Quality Controlled Local Climatological Data,QCLCD)[12]。从AOTP中提取一次航班的所有信息,包括起飞和降落时间、航空器型号、起飞机场、目的机场、起飞城市、目的城市等,构建航班数据。从QCLCD中提取每个航班计划到达时刻目的机场的天气情况、温度、能见度、湿度、风速、风向等信息,构建气象数据。
其中,AOTP包含从1987年至今的航班数据,QCLCD包含美国1600个气象观测站的气象数据,气象数据每小时进行一次更新。本文使用两个数据源中2015-2016年数据,数据信息如表2所示。
表2 数据源信息
Tab.2 Data source information

数据源数据维度AOTP103 405 986×44QCLCD11 235 340×48
实验环境为包括一个主节点和四个从节点的Spark集群,集群的调度模式为standalone[14]。每台计算机的硬件配置为内存8GB,处理器6核。软件配置为操作系统Centos6.5,并安装Hadoop2.6.3和Spark2.0版本。本模型采用深度为16,决策树个数为50的随机森林模型。
4.1 模型正确率和召回率
由于航班延误预测是偏分类问题,如将大部分航班判为不延误,虽然模型正确率很高但是没有实际预测意义。因此引入延误召回率作为模型衡量指标。
预测结果混淆矩阵如表3所示。实际为延误预测也为延误的航班为真正例(true positive,TP),实际为延误预测为不延误的为假反例(false negative,FN),实际为不延误预测也为不延误的为真反例(true negative,TN),实际为不延误预测为延误的为假正例(false positive,FP)。
表3 预测结果混淆矩阵
Tab.3 Confusion matrix of prediction results
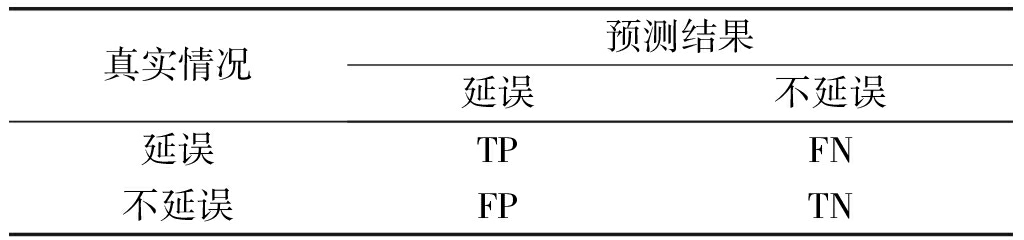
真实情况预测结果延误不延误延误TPFN不延误FPTN
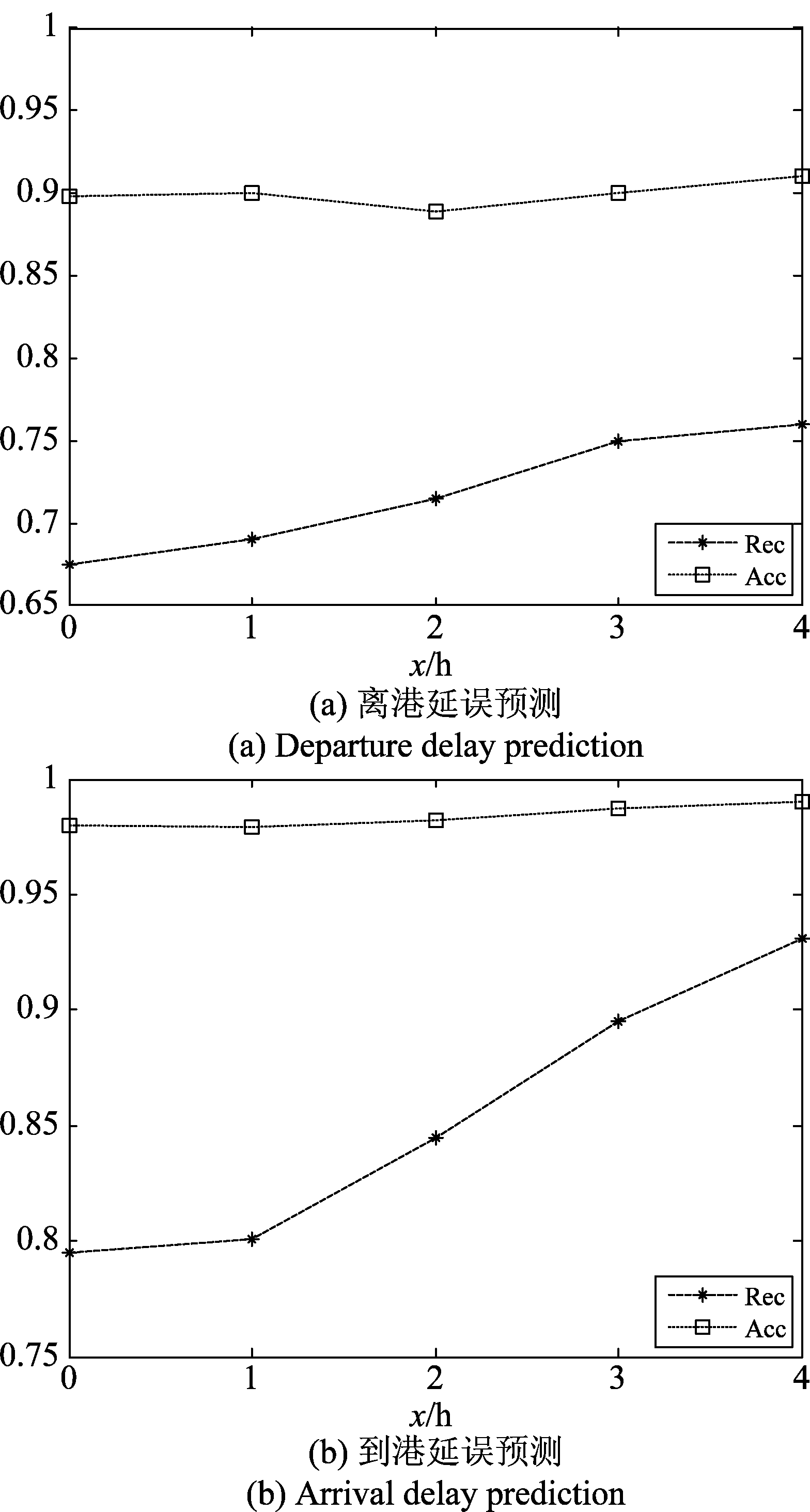
图4 考虑气象因素时预测性能变化
Fig.4 Predicts performance changes when considering
weather factors
正确率Acc用以衡量所有判断正确的航班数占总航班数的百分比,按如下公式计算:
(11)
航班延误预测召回率Rec代表延误航班判断正确数量占总延误航班数的百分比,按公式(12)计算。
(12)
取Th为60,融合不同小时的天气数据后,Acc和Rec变化曲线如图4所示。在不考虑气象因素时,正确率就已达到90%以上,但召回率却相对较低。这是由于航班延误预测属于偏分类问题,有大量样本预测为不延误。这也说明了引入召回率作为衡量指标的重要性。
随着考虑气象因素小时数的增加,离港延误预测和到港延误预测的正确率变化不大,但召回率都显著提高,且到港延误预测的提升优于离港延误预测。这一方面验证了高维气象特征对衡量指标的重要影响,另一方面说明了起飞和降落受气象因素影响程度的差异性。
分别选取Th=15、30、45、60时,Acc和Rec变化曲线如图5所示。随着阈值的增大,离港延误预测和到港延误预测正确率和召回率提高,且趋势基本一致。当Th=15时,离港延误预测可取得73.05%的召回率和90.1%的正确率;到港延误预测可取得83.2%的召回率和93.7%的正确率。当在Th=60时,离港延误预测可取得84.8%的召回率和95.4%的正确率;到港延误预测可取得93.1%的召回率和99.0%的正确率。当阈值增加时,不延误样本和延误样本的不均衡比例减小,模型性能得以进一步提高。
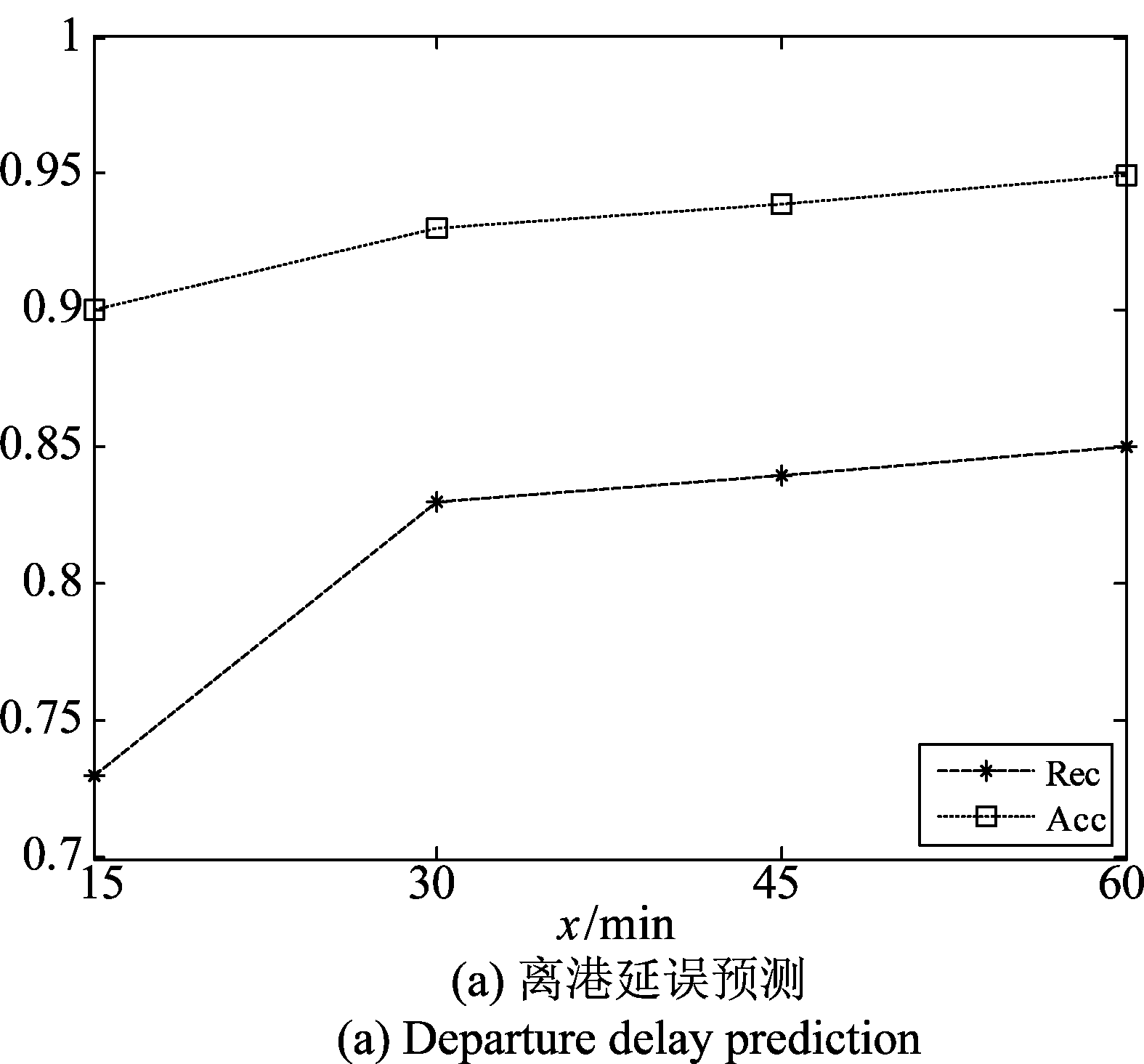
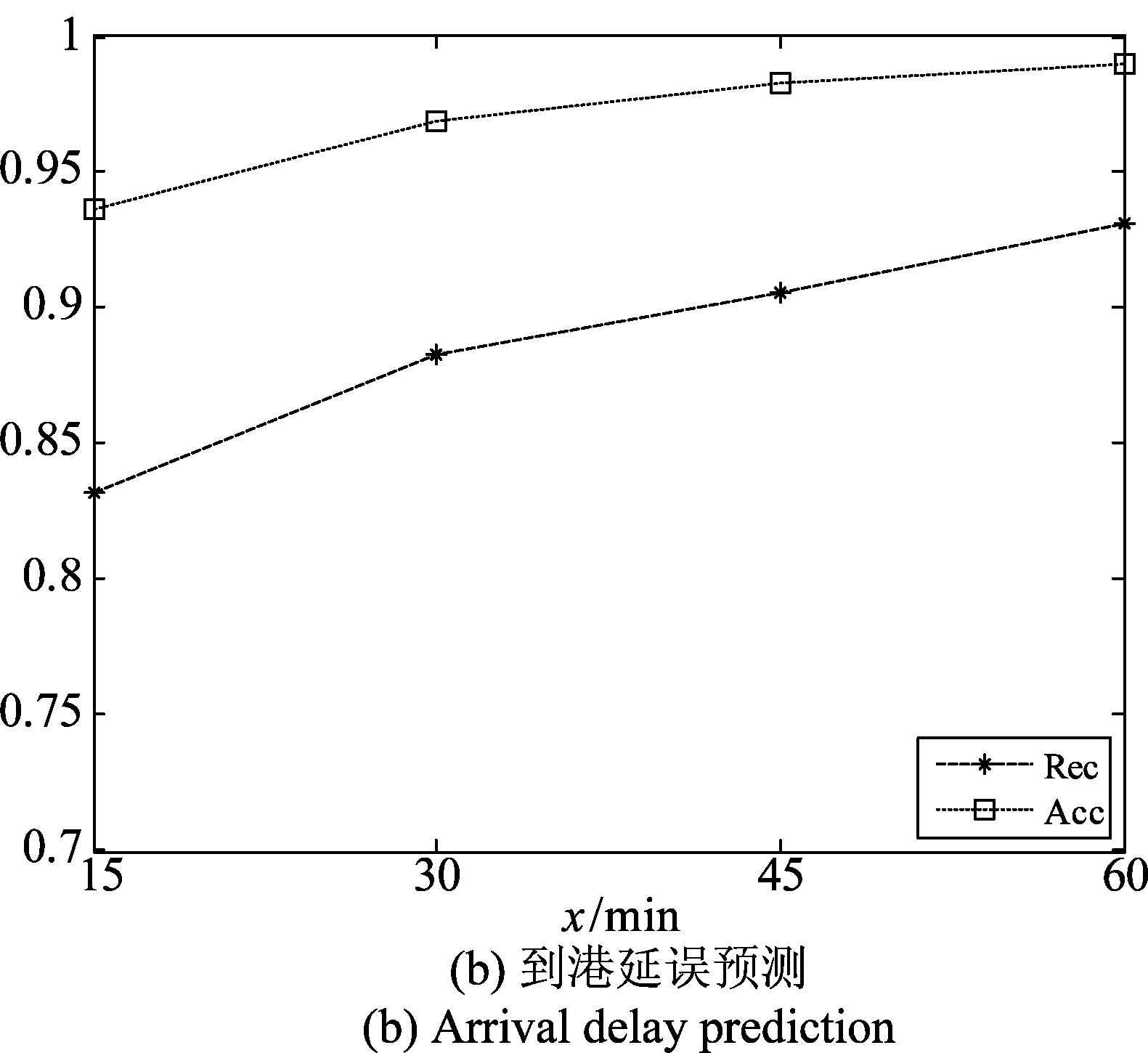
图5 不同阈值对预测性能影响
Fig.5 Influence of different thresholds on prediction Performance
4.2 泛化误差性能
使用分类强度s、决策树之间的相关性ρ以及ρ/s2比率度量随机森林测试时的泛化误差性能。随机森林各决策树之前相关性越小,单个决策树强度越高,则ρ/s2越小,代表随机森林性能越好。
分类强度定义为:
(13)
其中,K代表测试样本中样本数量。s衡量了测试集中将样本分类正确的平均票数和错分为其他类的平均票数之最小差值,s越大分类器性能越好。
相关性定义为:
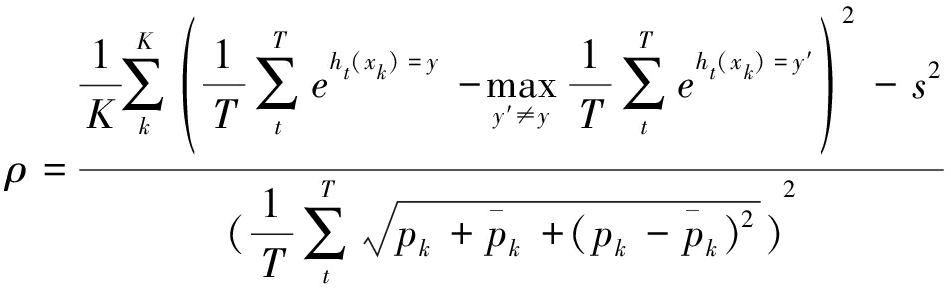
(14)
其中,
(15)
(16)
(17)
即![]() 表示除真实类外得票数最高的类别。ρ表征了各决策树之间的关联程度,ρ越小,各决策树生成过程越独立,模型泛化性能越强。
表示除真实类外得票数最高的类别。ρ表征了各决策树之间的关联程度,ρ越小,各决策树生成过程越独立,模型泛化性能越强。
表4给出了本文模型的泛化误差性能。可以看出本文模型各个决策树之前关联性较弱,且每个决策树的分类性能较好,具有较好的泛化误差性能。
表4 泛化误差性能
Tab.4 Generalization error performance

sρρ/s20.7780.2720.450
4.3 特征分析
取Th为60,融合到港时刻前3个小时的天气数据后,分别去除某个气象特征的数据进行到港延误预测,并和使用全部气象特征进行预测的结果进行比对,则查全率会有不同程度的下降变化。用下降百分比表征此特征对于延误预测的影响程度,如图6所示。
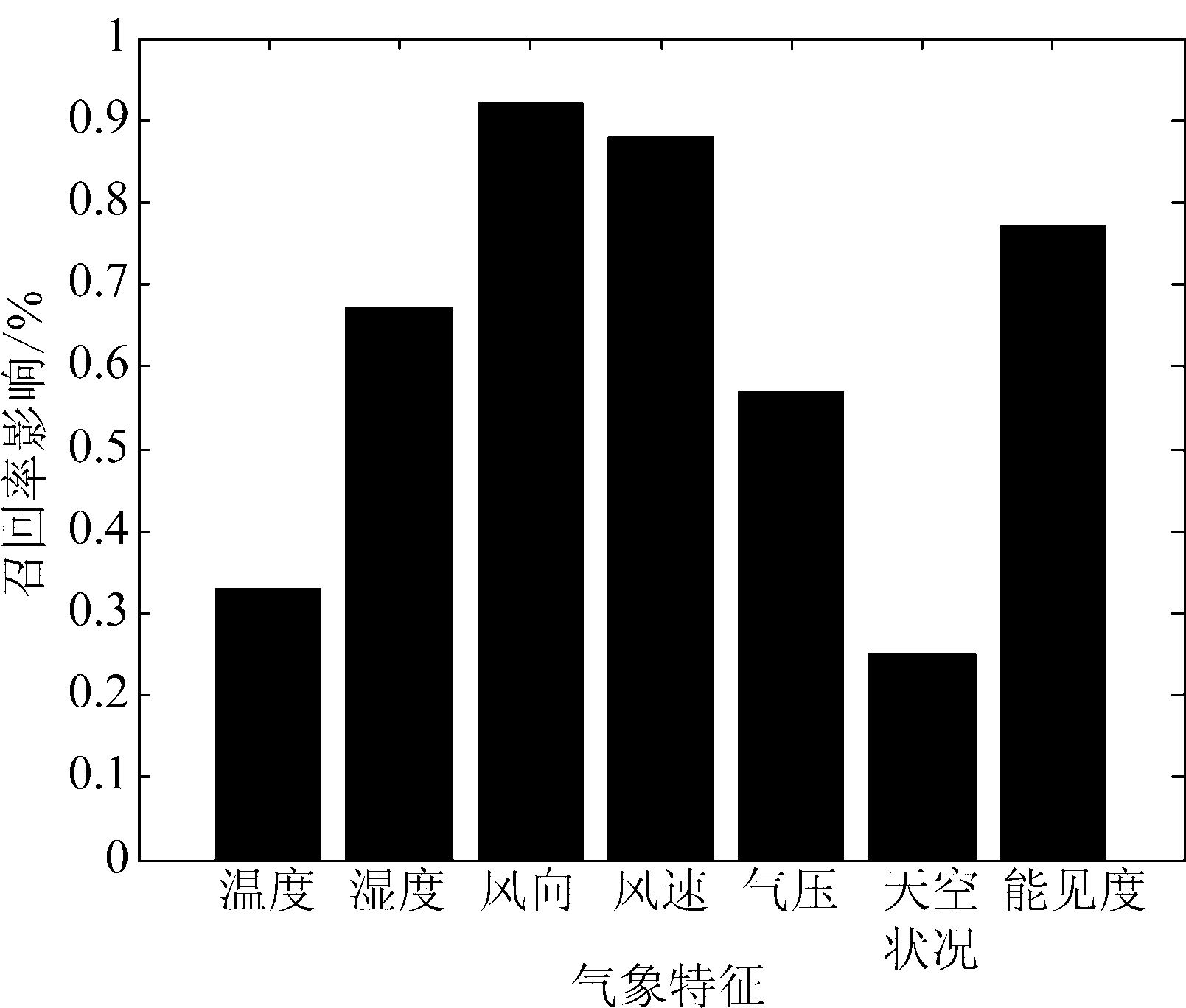
图6 气象特征分析
Fig.6 Analysis of meteorological features
从实验结果可以看出,风向、风速和能见度对延误预测影响较大,湿度和气压其次。从实际情况分析,风速和风向的变化会引起风切变等气象情况,使飞机无法起降。同时,降雨、降雪和风暴等极端恶劣天气也都伴随着风向、风速和能见度的改变。
4.4 加速比
为验证模型可扩展性和并行化优势,实验采用加速比作为指标,用以衡量同一数据集下增加节点时算法的表现。加速比是指同一任务在单处理器系统和并行处理器系统中运行消耗的比率,其计算公式为:
Ssp=Ts/Tp
(18)
其中Ts表示单机环境下串行算法的运行时间,Tp表示在p个相同节点上计算所需时间。Ssp越大表明并行计算消耗时间越少,并行效率和性能提升越高。
航班延误预测模型的加速比变化曲线如图7所示。随着云集群节点数的增加,实验的运行时间减小,Ssp皆大于1且持续增加。理想情况下随节点数的增加,加速比应呈成倍变化趋势。但节点数越大实际运行情况和理想情况差距越大,这主要是由于集群间通信时IO开销逐渐增大导致。
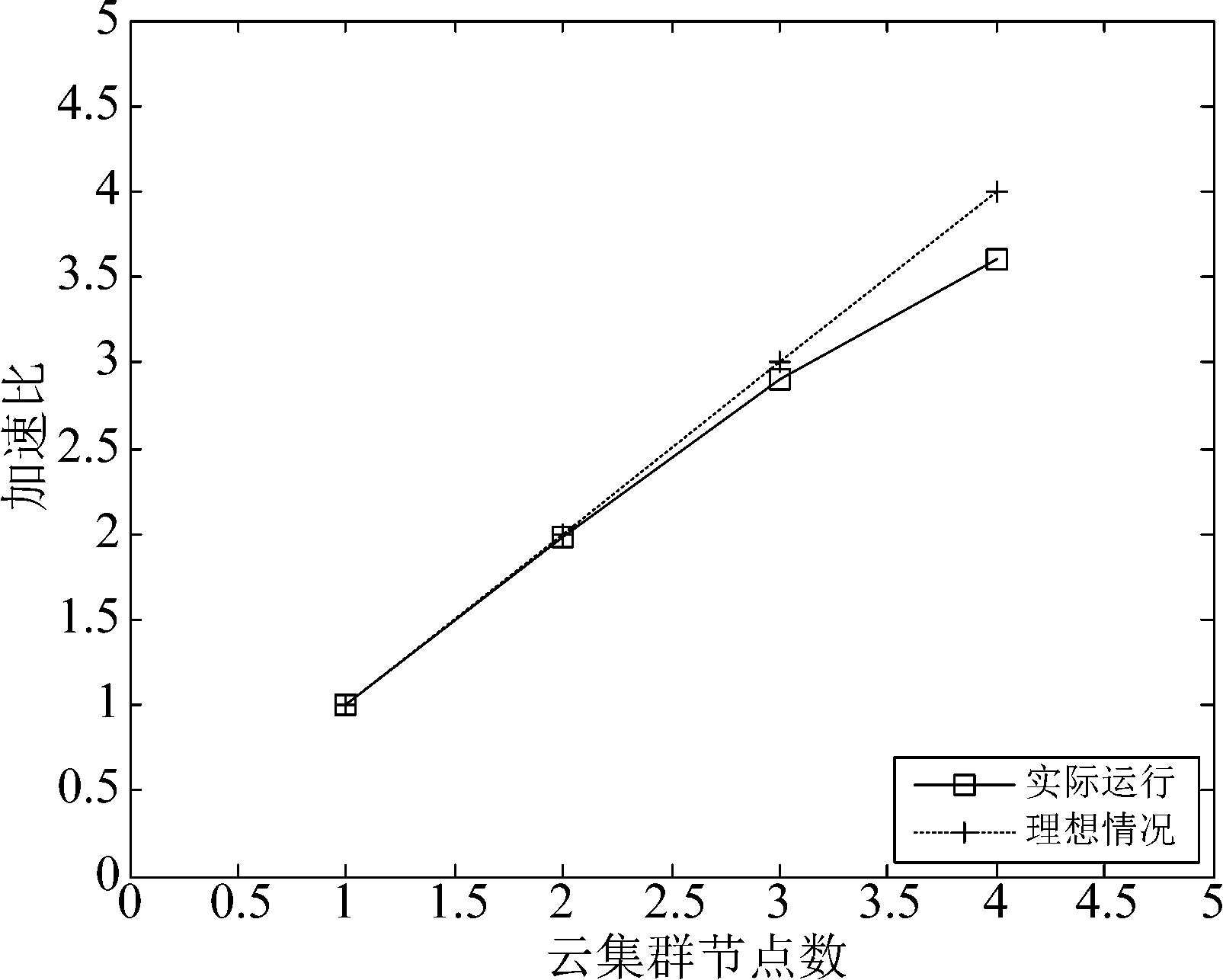
图7 加速比
Fig.7 Speedup
实际运行情况虽未达到理想化标准,但仍成线性变化,因此可以预期,对更大规模的数据进行并行化处理时,加速比性能会进一步提升。实验结果表明本文模型具有良好的可扩展性。
5 结论
本文提出了基于Spark并融合气象数据的航班延误预测模型,通过考虑单个航班到达目的机场时刻的气象数据,提高了航班延误预测的正确率和查全率;并在Spark并行计算架构上利用并行化随机森林算法进行模型生成,克服了海量高维数据的计算难度。实验表明该模型加入气象数据后,预测效果明显增强,且使用并行化算法后,提高了数据处理能力,满足了航班延误预测模型处理海量高维数据的需求,具有十分重要的应用价值。
参考文献
[1] 李军会, 朱金福, 陈欣. 基于航班延误分布的机位鲁棒指派模型[J]. 交通运输工程学报, 2014, 14(6): 74- 82.
Li Junhui, Zhu Jinfu, Chen Xin. Robust assignment model of airport gate based on flight delay distribution[J]. Journal of Traffic and Transportation Engineering, 2014, 14(6): 74- 82.(in Chinese)
[2] 程华, 李艳梅, 罗谦, 等. 基于C4.5决策树方法的到港航班延误预测问题研究[J]. 系统工程理论与实践, 2014, 34(s1): 239-247.
Cheng Hua, Li Yanmei, Luo Qian, et al. Study on flight delay with C4.5 decision tree based prediction method[J]. System Engineering-Theory & Practice, 2014, 34(s1): 239-247.(in Chinese)
[3] 罗赟骞, 陈志杰, 汤锦辉, 等. 采用支持向量机回归的航班延误预测研究[J]. 交通运输系统工程与信息, 2014, 15(1): 143-149.
Luo Yunqian, Chen Zhijie, Tang Jinhui, et al. Flight delay prediction using support vector machine regression[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 15(1): 143-149.(in Chinese)
[4] 曹卫东, 贺国光. 连续航班延误与波及的贝叶斯网络分析[J]. 计算机应用, 2009, 29(2): 606- 610.
Cao Weidong, He Guoguang. Bayesian networks analysis for sequence flight delay and propagation[J]. Journal of Computer Applications, 2009, 29(2): 606- 610.(in Chinese)
[5] 丁建立, 王曼, 曹卫东, 等. 面向机场时段差异的航班延误免疫预测算法[J]. 计算机工程与设计, 2015, 36(4): 1037-1041.
Ding Jianli, Wang Man, Cao Weidong, et al. Immune prediction algorithm of flight delay for hub airport in different periods[J]. Computer Engineering and Design, 2015, 36(4): 1037-1041.(in Chinese)
[6] Khanmohammadi S, Tutun S, Kucuk Y. A new multilevel input layer artificial neural network for predicting flight delays at JFK airport[J]. Procedia Computer Science, 2016,95:237-244.
[7] Rebollo J J, Balakrishnan H. Characterization and prediction of air traffic delays[J]. Transportation Research Part C: Emerging Technologies, 2014, 44:231-241.
[8] 罗谦, 张永辉, 程华, 等. 基于航空信息网络的枢纽机场航班延误预测模型[J].系统工程理论与实践, 2014, 34(S1):143-150.
Luo Qian, Zhang Yonghui, Cheng Hua, et al. Study on flight delay prediction model based on flight networks[J]. Systems Engineering-Theory & Practice, 2014, 34(s1):143-150.(in Chinese)
[9] 刘宏波, 李玉, 林文杰,等. 并行MCMC算法的SAR影像分割[J]. 信号处理, 2016, 32(8): 998-1006.
Liu Hongbo, Li Yu, Lin Wenjie, et al. SAR image segmentation with parallel MCMC algorithm[J]. Journal of Signal Processing, 2016, 32(8): 998-1006.(in Chinese)
[10] Harnie D, Saey M, Vapirev A E, et al. Scaling machine learning for target prediction in drug discovery using apache spark[J]. Future Generation Computer Systems, 2017, 67:409- 417.
[11] 孟建良, 刘德超. 一种基于Spark 和聚类分析的辨识电力系统不良数据新方法[J]. 电力系统保护与控制, 2016, 44(3): 85-91.
Meng Jianliang, Liu Dechao. A new method for identifying bad data of power system based on Spark and clustering analysis[J]. Power System Protection and Control, 2016, 44(3): 85-91.(in Chinese)
[12] Kim Y J, Choi S, Briceno S, et al. A deep learning approach to flight delay prediction[C]∥IEEE. 2016 IEEE/AIAA 35th Digital Avionics Systems Conference. New York: IEEE, 2016: 1- 6.
[13] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.
[14] Zaharia M, Chowdhury M, Das T, et al. Resilient distributed datasets: a fault-tolerant abstraction for in-memory cluster computing[C]∥Usenix Conference on Networked Systems Design and Implementation. Lombard: Usenix Association, 2012:2-2.


