1 引言
物理层安全技术能够直接利用无线信道的随机性来保证信息的安全传输,与传统的上层加密编码方案对比,可有效降低无线通信系统的复杂度和能耗[1-2]。Wyner在[3]中原创性地针对窃听信道模型提出了物理层安全的概念。作为一种有效的协作加扰策略,目的端加扰方案允许目的节点在不影响合法信息接受质量的同时发射人工噪声从而降低无线通信系统被窃听的风险[4]。
自干扰(Self-Interference, SI)的存在是制约全双工(Full-Duplex, FD)技术发展的重要因素。近年来,自干扰消除(Self-Interference Cancellation, SIC)技术发展迅猛,能够将自干扰抑制到-110 dB。被动自干扰消除技术利用路径损耗、交叉极化和天线的方向性达到自干扰抑制的目的[5- 6]。主动自干扰消除技术则通过自干扰的相关信息在模拟或数字域进行自干扰抑制工作[7]。
文献[8]将全双工技术应用到目的端加扰系统,总结了全双工目的端加扰方案的优越性。在多输入多输出(Multi-Input Multi-Output, MIMO)窃听模型中,为最大化安全自由度,文献[9]给出了最优收发天线分配方案并设计了预编码矩阵。在单输入多输出(SIMO)通信系统中,文献[10]优化了全双工目的端加扰系统的发射和接收波束形成方案。
文献[11]为最大化无线携能通信系统的可达速率,提出了一种基于功率分配能量采集技术的天线模式切换算法。在双向全双工无线通信系统中,文献[12]基于天线模式切换技术分别设计了信源端和目的端天线选择策略。文献[13]将天线模式切换技术推广到了双向全双工MIMO无线通信系统,用于提升系统的可达速率性能。为提升全双工中继无线通信系统的性能表现,文献[14]提出了一种中继处天线模式切换和机会式信源选择的联合优化策略。
完全不同于以上文献中的固定工作模式天线设置,本文所考虑的多天线目的节点采用天线模式切换技术根据全局信道状态信息动态地选取一簇天线工作在人工噪声发射模式,剩余天线工作在信息接收模式。本文的主要贡献总结如下:
(1)为获取最大的可达安全速率,本文基于贪婪搜索天线模式切换和最优功率分配策略设计了一种针对全双工目的端加扰无线通信系统的两步走联合优化方案。
(2)在假设合适的收发天线集和已确定的前提下,通过分析优化目标函数关于功率分配因子的凹凸性及引用凸优化理论中的KKT条件,推导出最优功率分配因子闭合表达式。
符号释义:本文中,(·)T代表转置,(·)H表示共轭转置, {·}为求数学期望符号,|·|为求模符号,‖·‖表示求弗罗贝尼乌斯范数符号
{·}为求数学期望符号,|·|为求模符号,‖·‖表示求弗罗贝尼乌斯范数符号![]() 代表均值为μ方差为σ2的复高斯分布。黑斜体小写字母表示向量,如, v。黑斜体大写字母表示矩阵,如,I。
代表均值为μ方差为σ2的复高斯分布。黑斜体小写字母表示向量,如, v。黑斜体大写字母表示矩阵,如,I。
2 系统模型
图1给出了全双工目的端加扰无线传输系统模型。该系统模型由一个信源节点(S)、一个全双工目的节点(D)和一个窃听节点(E)组成。S、D和E三个节点配置的天线数分别为:1根、ND根和1根。值得注意的是,![]() 和
和![]() 分别代表包含NDt根发射天线和NDr根接收天线的发射天线集合和接收天线集合,有NDt+NDr=ND成立,其中ND代表节点D处天线总数。假设所有信道链路均为块衰落瑞利信道,即信道在一个相干时间内保持平稳并且在不同的相干时间相互独立。信道S→D、S→E和D→E分别表述为hSD=[hS1,hS2,…,hSNDr]T、gSE和gDE=[g1E,g2E,…,gNDtE]。其中,hSi表示节点S到集合
分别代表包含NDt根发射天线和NDr根接收天线的发射天线集合和接收天线集合,有NDt+NDr=ND成立,其中ND代表节点D处天线总数。假设所有信道链路均为块衰落瑞利信道,即信道在一个相干时间内保持平稳并且在不同的相干时间相互独立。信道S→D、S→E和D→E分别表述为hSD=[hS1,hS2,…,hSNDr]T、gSE和gDE=[g1E,g2E,…,gNDtE]。其中,hSi表示节点S到集合![]() 中第i根接收天线之间的信道参数,gjE代表集合
中第i根接收天线之间的信道参数,gjE代表集合![]() 中第j根发射天线到节点E之间的信道参数,有i=1,…,NDr和j=1,…,NDt成立。所有信道参数皆为服从独立同分布的零均值循环对称复高斯随机变量,平均信道增益分别为
中第j根发射天线到节点E之间的信道参数,有i=1,…,NDr和j=1,…,NDt成立。所有信道参数皆为服从独立同分布的零均值循环对称复高斯随机变量,平均信道增益分别为![]() 和
和![]() 节点S和节点D的发射功率分别为PS和PD。限制系统总发射功率为P=PS+PD,且有PD=(1-α)P和PS=αP成立。其中,α为信源发射功率和系统总发射功率的比值,即功率分配因子。值得注意的是,对系统总发射功率的限制在很多已有文献中十分常见,如文献[4,10,15-16,25]。
节点S和节点D的发射功率分别为PS和PD。限制系统总发射功率为P=PS+PD,且有PD=(1-α)P和PS=αP成立。其中,α为信源发射功率和系统总发射功率的比值,即功率分配因子。值得注意的是,对系统总发射功率的限制在很多已有文献中十分常见,如文献[4,10,15-16,25]。
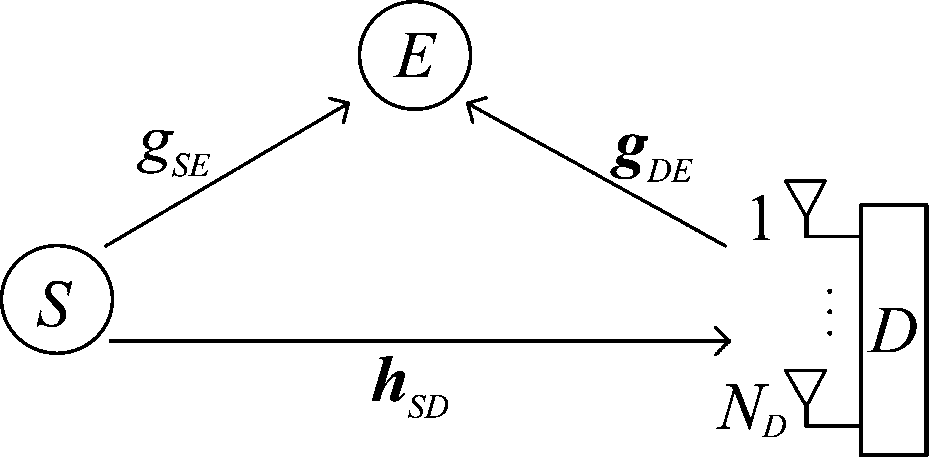
图1 全双工目的端加扰无线传输系统模型图
Fig.1 System model of the FD destination-based jamming secure transmission scheme
基于全双工目的端加扰策略,节点D能够在使用NDr根天线接收节点S发送的信息的同时使用剩余的NDt根天线广播人工噪声。通过使用自干扰消除技术,节点D可以将自干扰强度抑制到噪声级。因此,本文忽略节点D处的自干扰对系统性能的影响。在以信息论为导向的可达安全速率研究中,完全自干扰消除是一种被广泛使用的假设[17]。假设节点S和节点D已知信道S→D的信道状态信息(Channel State Information, CSI)。为最大化接收信噪比(Signal-to-Noise Ratio, SNR),节点D采用最大比合并策略接收信号,具体表示为:
![]()
(1)
其中,![]() 为S所发送之有用信息
为S所发送之有用信息![]() 表示节点D处的加性高斯白噪声(Additive White Gaussian Noise, AWGN)。
表示节点D处的加性高斯白噪声(Additive White Gaussian Noise, AWGN)。
节点D处广播的人工噪声表示为一个零均值方差为![]() 的复高斯随机变量ν。假设节点E是一个主动窃听节点,节点S和节点D已知窃听信道CSI[18-20]。为最大化人工噪声对节点E的干扰作用,节点D采用最大比发射策略广播人工噪声。节点E的接收信号可表示为:
的复高斯随机变量ν。假设节点E是一个主动窃听节点,节点S和节点D已知窃听信道CSI[18-20]。为最大化人工噪声对节点E的干扰作用,节点D采用最大比发射策略广播人工噪声。节点E的接收信号可表示为:
gSExS+‖gDE‖ν+nE
(2)
其中,![]() 代表节点E处的AWGN。
代表节点E处的AWGN。
基于式(1)和式(2),可分别计算出节点D和节点E处的SNR如下:
(3)
![]()
(4)
其中有,![]() 和γSE=|gSE|2。
和γSE=|gSE|2。
3 可达安全速率分析
本节将建立最大化全双工目的端加扰无线传输系统可达安全速率的优化问题,并通过天线模式切换和最优功率分配联合优化方案解决所建立的优化问题。
本系统中,可达安全速率数学表达式如下[21]:
RS=max{0,log2(1+γD)-log2(1+γE)}=
max{0,log2(Λ)}
(5)
其中,定义为:
![]()
(6)
为最大化系统的可达安全速率,可建立优化问题P1数学模型如下:
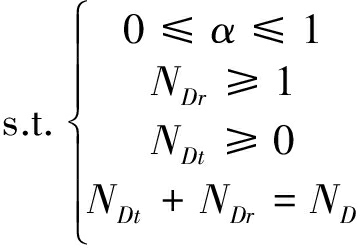
(7)
对数函数log是增函数,在给定收发天线集合的前提下,优化问题P1等效于优化问题P2[22]。
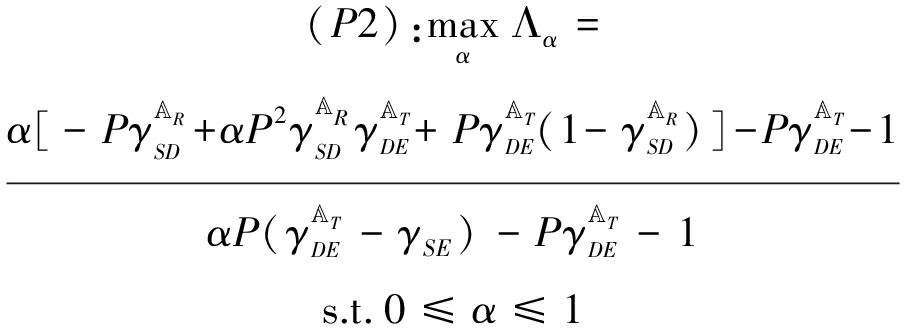
(8)
值得注意的是,优化问题P2是一个关于变量α的非线性凹凸性不定的函数,使问题变得数学上无解,这个性质将在下文定理中加以证明。为了使优化问题P2可解,本文设计了一种两步走的联合优化策略:第一步,对任意给定的合适收发天线集合,求取相应的本地最优功率分配因子![]() 第二步:将
第二步:将![]() 代入本文设计的天线模式切换方案,最终得到最优收发天线集合与对应的全局最优功率分配因子。下面的引理有助于求取最优功率分配因子闭合表达式。
代入本文设计的天线模式切换方案,最终得到最优收发天线集合与对应的全局最优功率分配因子。下面的引理有助于求取最优功率分配因子闭合表达式。
引理:对任意给定的收发天线集合,当![]() 时,正安全速率在0<α≤1上总是存在,且此时可达安全速率表示为:
时,正安全速率在0<α≤1上总是存在,且此时可达安全速率表示为:
RS=log2(Λ),0≤α≤1
(9)
当![]() 时,可达安全速率可表示为:
时,可达安全速率可表示为:
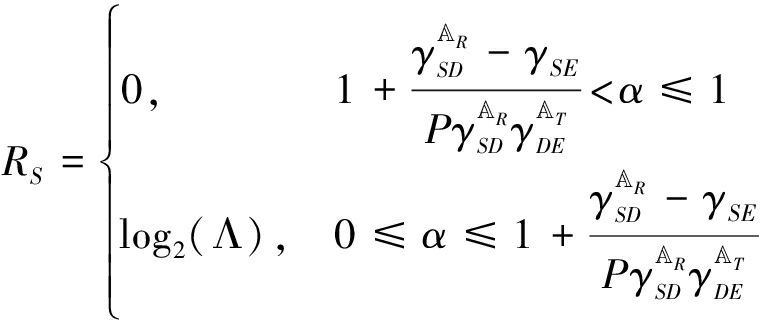
(10)
当![]() 时,可达安全速率始终有RS=0,0≤α≤1。
时,可达安全速率始终有RS=0,0≤α≤1。
证明:见附录。
3.1 最优功率分配方案
下面的定理将在任意给定合适的收发天线集合的前提下,给出系统最优功率分配因子的闭合表达式[23-24,26]。
定理:对任意给定合适的收发天线集,当Γ<0时,式(6)是关于α的严格凹函数,当Γ≥0时,是α的凸函数。其中,![]() 最优功率分配因子的闭合表达式如下:
最优功率分配因子的闭合表达式如下:

(11)
其中,
![]()
![]()
(12)
证明:见附录。
3.2 穷举天线模式切换方案
基于上文定理,在任意给定合适的收发天线集合条件下,结合式(3)、式(4)、式(6)和式(11),可以给出代入最优功率分配因子闭合式后的优化目标函数为:
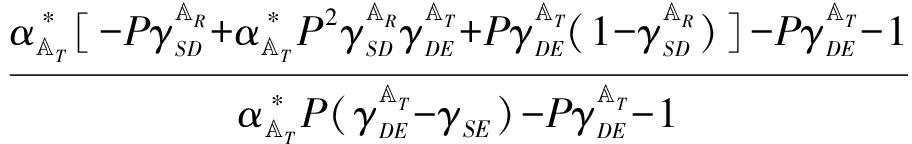
(13)
在实际应用场景中,目的端天线的总数量是有限的,可以应用穷举搜索的方法从所有适合的收发天线集合堆中找出最优的收发天线集合。
3.3 贪婪天线模式切换方案
对于任意给定的发射天线集合![]() 对应的接收天线集合记为
对应的接收天线集合记为![]() 其中,an表示目的端所有ND根天线中工作于接收模式的天线标签,集合
其中,an表示目的端所有ND根天线中工作于接收模式的天线标签,集合![]() 是集合
是集合![]() 的补。本文中,有关系
的补。本文中,有关系![]() 和
和![]() 成立,其中符号card(·)表示对集合取势。记目的端有
成立,其中符号card(·)表示对集合取势。记目的端有![]() 根天线工作于发射模式的最大优化目标函数为:
根天线工作于发射模式的最大优化目标函数为:
![]()
(14)
将发射天线集合初始值设置为空集,并记为![]() 此时,目的端没有任何天线工作于发射模式,所以系统应将所有的功率分配给信源,也就是有,α=1。计算初始的优化目标函数并记为
此时,目的端没有任何天线工作于发射模式,所以系统应将所有的功率分配给信源,也就是有,α=1。计算初始的优化目标函数并记为![]() 当任一根天线切换到发射模式,记为
当任一根天线切换到发射模式,记为![]() 在每次迭代操作中,从集合
在每次迭代操作中,从集合![]() 选出来切换到发射模式的天线都是任意的。本方案的核心思想是,当有任意一根天线从接收模式切换到发射模式时,检测优化函数
选出来切换到发射模式的天线都是任意的。本方案的核心思想是,当有任意一根天线从接收模式切换到发射模式时,检测优化函数![]() 是否有增益产生。方案将在集合
是否有增益产生。方案将在集合![]() 内只有一根天线剩余时终止,同时输出对应的最优值
内只有一根天线剩余时终止,同时输出对应的最优值![]() 和
和![]() 贪婪天线模式切换方案可总结如下:
贪婪天线模式切换方案可总结如下:

贪婪天线模式切换方案1. Begin2. 初始化:设置初始发射天线集合为 optT=⌀,初始功率分配因子为α=1。计算初始优化变量并记为Λmax T。3. FORi=1:ND-14. 对任一根集合 R中的天线an,设置合适的发射天线集合为 T= T∪[an],同时有 R= R\[an]。根据式(11)计算出所有可能的α∗ T,根据式(13)计算出所有可能的ΛT。5. 基于式(14),在所有可能的Λ T中获取最大值并记为Λmax T,同时获取相对应的本地最优发射天线集合并记为 locT。6. IFΛmax T≥Λ optT7. optT= locT;8. T= locT;9. ELSE10. T= locT;11. END IF12. END FOR13. 输出: optT、 optR、α∗ optT和Λ optT。14.END
4 仿真与讨论
本节将给出应用本文所提天线模式切换和最优功率分配联合优化方案的全双工目的端加扰无线传输系统可达安全速率的Monte Carlo性能仿真并给出对应的分析和讨论。假设各信道的平均信道增益分别为ΩSD=ΩDE=ΩSE=1。为凸显本文所提联合优化方案的性能优越性,给出了采用固定收发天线方案的传统目的端加扰方案的可达安全速率性能仿真。其中,传统目的端加扰方案的接收天线数目与发射天线数目一致[10]。

图2 平均可达安全速率在不同目的端加扰方案下随P变化的趋势
Fig.2 Average achievable secrecy rate versus P for different destination-based jamming schemes
图2给出了不同目的端加扰方案的平均可达安全速率对比结果。图2中,所有目的端加扰方案的天线总数皆设置为ND=10。其中,两个传统目的端加扰方案的收发天线数俱为NDt=NDr=5。没有应用最优功率分配方案的传统目的端加扰方案的功率分配因子固定为α=0.3。应用最优功率分配方案的传统目的端加扰方案的功率分配因子设置为式(11)。由图2可得,穷举天线模式切换方案的性能最优。本文所提贪婪天线模式切换方案平均可达安全速率性能与穷举天线模式切换方案很接近。贪婪天线模式切换方案的平均可达安全速率性能表现远远优于两种传统目的端加扰方案,凸显了天线模式切换技术在优化系统天线分配和提升系统空间自由度利用效率方面的优势。同时,没有应用最优功率分配方案的传统目的端加扰方案的平均可达安全速率性能表现逊色于应用最优功率分配方案的传统目的端加扰方案,揭示了最优功率分配方案在提升系统性能方面的优越性。
图3为不同目的端加扰方案平均可达安全速率在P=20 dB条件下随ND的变化趋势图。两种传统目的端加扰方案的功率分配因子设置与图2相同。由图3可知,当ND较小时(如ND≤4),贪婪天线模式切换方案的性能与最优的穷举天线模式切换方案几乎一致。随着ND增大,贪婪天线模式切换方案性能逐渐弱于最优的穷举天线模式切换方案。由图可得,贪婪天线模式切换方案在所有的ND上,平均可达安全速率性能都远优于传统目的端加扰方案。
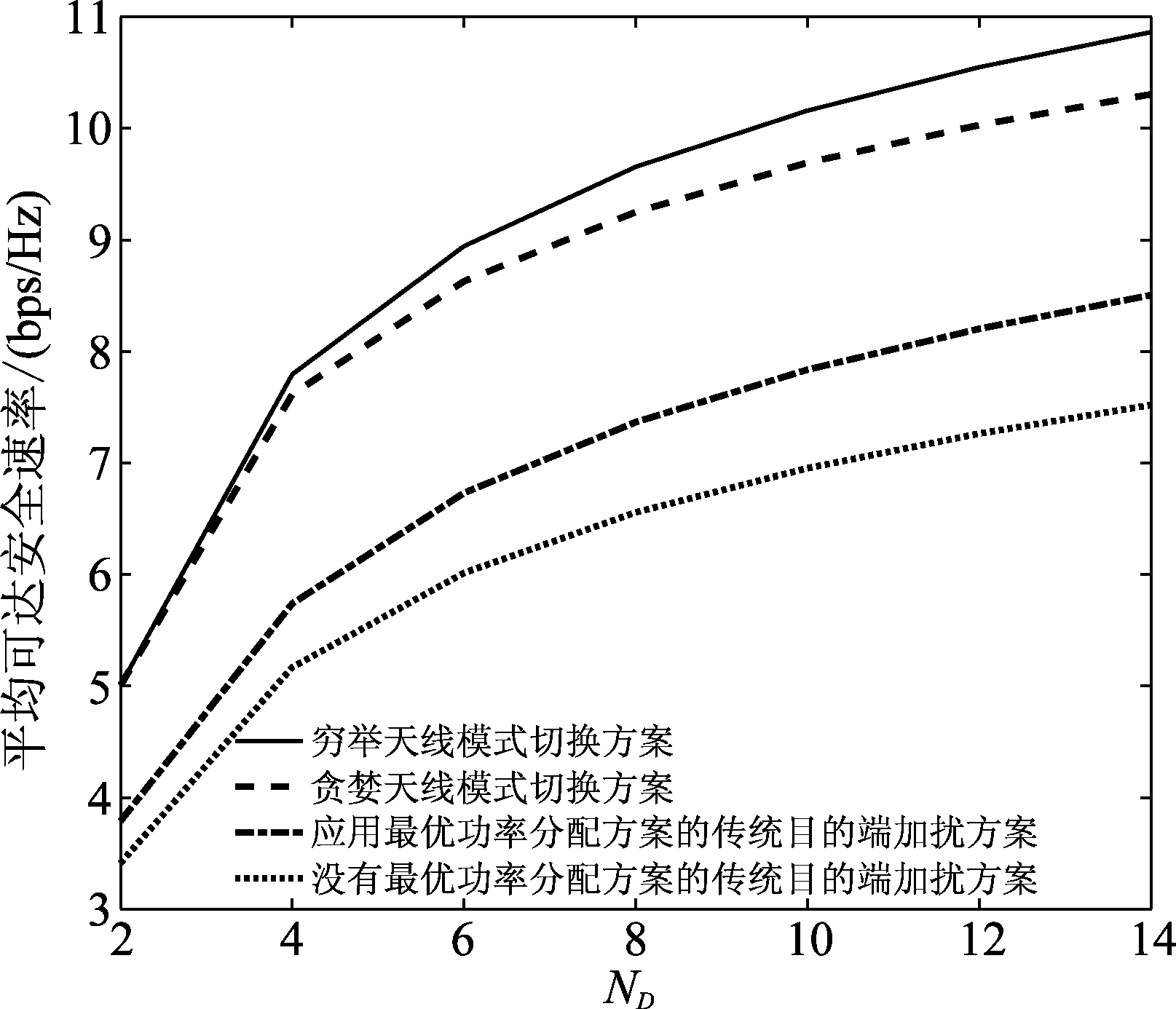
图3 平均可达安全速率在不同目的端加扰方案下随ND变化的趋势
Fig.3 Average achievable secrecy rate versus ND for different destination-based jamming schemes
5 结论
针对全双工目的端加扰无线通信系统的性能指标可达安全速率,提出了一种次优的联合优化方案。在目的端天线工作模式未预定义的场景中,联合优化方案具体表现为两部走的优化策略。第一步,基于全局信道状态信息,推导出适用于任何收发天线集组合的最优功率分配因子闭合表达式。第二步,结合最优功率分配方案,设计了一种基于贪婪搜索的天线模式切换方案。仿真结果显示应用本文联合优化方案的目的端加扰系统可达安全速率性能表现明显优于传统的目的端加扰方案。
附录
引理之证明
在任意给定合适的收发天线集前提下,正可达安全速率只有当Λ严格大于1,也就是,γD>γE的情况下存在。进一步,我们有:
![]()
(15)
上式可改写为:
![]()
(16)
式(16)便是本系统正可达安全速率存在的充分必要条件。
当![]() 时,式(16)在区间0<α≤1上一定成立,此时正可达安全速率在区间0<α≤1上总是存在。本文中,功率分配因子一定为非负值,即α≥0。为满足上述条件,对式(16)加以如下限制:
时,式(16)在区间0<α≤1上一定成立,此时正可达安全速率在区间0<α≤1上总是存在。本文中,功率分配因子一定为非负值,即α≥0。为满足上述条件,对式(16)加以如下限制:
(17)
上式可化简为:![]()
当![]() 时,正可达安全速率只在区间
时,正可达安全速率只在区间![]() 上存在。由式(5),当
上存在。由式(5),当![]() 时将可达安全速率置零。
时将可达安全速率置零。
当![]() 时,不满足系统约束条件α≥0。因此,正可达安全速率在区间0<α≤1上一定不存在。进一步有,RS=0,0≤α≤1。
时,不满足系统约束条件α≥0。因此,正可达安全速率在区间0<α≤1上一定不存在。进一步有,RS=0,0≤α≤1。
证明完毕。
定理之证明
式(6)关于功率分配因子α的二阶偏导数可表示为:
![]()
(18)
其中,
(19)
由式(19)可知,Θ是非负值变量。因此,式(18)的正负完全取决于变量Γ,亦即式(6)关于变量α的凹凸性不定,且仅取决于变量Γ的正负性。
当变量Γ≥0时,式(6)是关于功率分配因子α的凸函数。进一步得:
(20)
由上文引理可知,此时正可达安全速率在区间0≤α≤1上一定不存在。因此,当变量Γ≥0时,根据式(5),可达安全速率在区间0≤α≤1上被强制为零。所以,这种情况下没有最优功率分配问题存在,不参与优化问题的讨论。
当变量Γ<0时,式(6)是关于功率分配因子α的严格凹函数。进一步得:
(21)
由引理可得,当![]() 时,总有RS=0,0≤α≤1成立。因此,在条件
时,总有RS=0,0≤α≤1成立。因此,在条件![]() 下,没有最优功率分配问题存在,同样不参与优化问题的讨论。
下,没有最优功率分配问题存在,同样不参与优化问题的讨论。
当![]() 时,式(6)是关于α的严格凹函数。可应用KKT条件来确定最优功率分配因子。
时,式(6)是关于α的严格凹函数。可应用KKT条件来确定最优功率分配因子。
对本系统,有如下拉格朗日方程成立:
L(α, μ)=Λ-μ(α-1)
(22)
其中, μ≥0是与α相关联的拉格朗日乘子。
用以求取最优功率分配因子的KKT条件可具体表示为下述三个条件限制:
![]()
(23)
μ(α-1)=0
(24)
α-1≤0
(25)
式(23)中的∂Λ/∂α具体表达式为:
![]()
(26)
其中,变量Φ表达式如下:
(27)
上述KKT条件共存在两组解。其一:α1=1且μ=∂Λ/∂α|α=1。其二:0<α<1且μ=0。
当μ=0且![]() 时,通过解∂Λ/∂α=0可得两个根分别为:
时,通过解∂Λ/∂α=0可得两个根分别为:
![]()
(28)
(29)
其中,变量 Ψ如式(12)所示。式(28)和式(29)的取值与![]() 息息相关,下文将讨论它们之间取值的具体对应关系。
息息相关,下文将讨论它们之间取值的具体对应关系。
当![]() 时,式(28)中
时,式(28)中![]() 且
且![]() 此时,易知α2>1。
此时,易知α2>1。
当![]() 时,式(28)分子部分为非负值,又此时分母部分小于零,因此有α2<0。
时,式(28)分子部分为非负值,又此时分母部分小于零,因此有α2<0。
由上述分析可知,在μ=0且![]() 条件下,α2不可能落在区间[0,1]内,因此α2不是合适的最优解,弃之。
条件下,α2不可能落在区间[0,1]内,因此α2不是合适的最优解,弃之。
进一步地,最优功率分配因子的确定依赖于对式(6)单调性的分析。
当![]() 时,式(26)可被改写为:
时,式(26)可被改写为:
![]()
(30)
上式的正负只取决于![]()
当![]() 时,由上文易知α2>1,因此
时,由上文易知α2>1,因此![]() 当
当![]() 时,α2<0,有
时,α2<0,有![]() 成立。由此,在α3≥1条件下,式(26)在区间α∈(0,1]上为非负值,此时最优功率分配因子为α*=1。在α3<1条件下,式(26)在区间α∈(0,α3]上非负,在区间α∈(α3,1]上为正值,此时,最优功率分配因子为α*=α3。总之,当
成立。由此,在α3≥1条件下,式(26)在区间α∈(0,1]上为非负值,此时最优功率分配因子为α*=1。在α3<1条件下,式(26)在区间α∈(0,α3]上非负,在区间α∈(α3,1]上为正值,此时,最优功率分配因子为α*=α3。总之,当![]() 时,最优功率分配因子的具体表达式为:α*=min(α3,1)。
时,最优功率分配因子的具体表达式为:α*=min(α3,1)。
当μ=0且![]() 时,∂Λ/∂α=0只有唯一解为:
时,∂Λ/∂α=0只有唯一解为:
![]()
(31)
式(26)可以展开成下述形式:
(32)
当α4>1时,α-α4<0,式(32)在区间α∈(0,1]上为正值,此时最优功率分配因子为α*=1;当α4≤1时,式(32)在区间α∈(0,α4]上非负,在区间α∈(α4,1]上为正值,此时最优功率分配因子为α*=α4。总之,当![]() 时,最优功率分配因子的具体表达式为:α*=min(α4,1)。
时,最优功率分配因子的具体表达式为:α*=min(α4,1)。
当![]() 时,式(6)在区间
时,式(6)在区间![]() 上是关于α的凹函数。又易知当
上是关于α的凹函数。又易知当![]() 或α=0时,Λ=1。因此,此时最优功率分配因子是在区间
或α=0时,Λ=1。因此,此时最优功率分配因子是在区间![]() 中,且满足∂Λ/∂α=0的一点。由上文可知,当
中,且满足∂Λ/∂α=0的一点。由上文可知,当![]() 时,α*=α3。当
时,α*=α3。当![]()
最终,最优功率分配因子的闭合表达式可表述为式(11),证毕。
参考文献
[1] Zhao R, Lin H, He Y C, et al. Secrecy Performance of Transmit Antenna Selection for MIMO Relay Systems With Outdated CSI[J]. IEEE Transactions on Communications, 2018, 66(2):546-559.
[2] Zhao R, Yuan Y, Fan L, et al. Secrecy Performance Analysis of Cognitive Decode-and-Forward Relay Networks in Nakagami-m Fading Channels[J]. IEEE Transactions on Communications, 2017, 65(2):549-563.
[3] Wyner A D. The wire-tap channel[J]. Bell Labs Technical Journal, 2014, 54(8):1355-1387.
[4] Zhao R, Huang Y, Wang W, et al. Ergodic Achievable Secrecy Rate of Multiple-Antenna Relay Systems With Cooperative Jamming[J]. IEEE Transactions on Wireless Communications, 2016, 15(4):2537-2551.
[5] 谭星, 赵睿, 王聪,等. 协作干扰下的非可信中继与全双工目的节点系统的遍历安全容量分析[J]. 信号处理, 2017,33(5):732-740.
Tan Xing, Zhao Rui, Wang Cong, et al. Ergodic Secrecy Capacity of Untrusted Relay and Full Duplex Destination Systems with Cooperative Jamming[J]. Journal of Signal Processing, 2017,33(5):732-740. (in Chinese)
[6] 聂志巧, 赵睿, 方嘉佳,等. 基于功率分配能量采集的全双工放大转发中继系统[J]. 信号处理, 2017, 33(4):641- 648.
Nie Zhiqiao, Zhao Rui, Fang Jiajia, et al. Amplify-and-Forward Full-Duplex Relaying Systems with Power Splitting-Based Energy Harvesting[J]. Journal of Signal Processing, 2017, 33(4):641- 648. (in Chinese)
[7] Li Y, Zhao R, Fan L, et al. Antenna Mode Switching for Full-Duplex Destination-Based Jamming Secure Transmission[J]. IEEE Access, 2018, PP(99):1-1.
[8] Li W, Ghogho M, Chen B, et al. Secure Communication via Sending Artificial Noise by the Receiver: Outage Secrecy Capacity/Region Analysis[J]. IEEE Communications Letters, 2012, 16(10):1628-1631.
[9] Li L, Chen Z, Zhang D, et al. A Full-Duplex Bob in the MIMO Gaussian Wiretap Channel: Scheme and Performance[J]. IEEE Signal Processing Letters, 2015, 23(1):107-111.
[10] Zheng G, Krikidis I, Li J, et al. Improving Physical Layer Secrecy Using Full-Duplex Jamming Receivers[J]. IEEE Transactions on Signal Processing, 2013, 61(20):4962- 4974.
[11] Zhou Z, Peng M, Zhao Z, et al. Joint Power Splitting and Antenna Selection in Energy Harvesting Relay Channels[J]. IEEE Signal Processing Letters, 2014, 22(7):823- 827.
[12] Zhou M, Cui H, Song L, et al. Transmit-Receive Antenna Pair Selection in Full Duplex Systems[J]. IEEE Wireless Communication Letters, 2014, 3(1):34-37.
[13] Jang S, Ahn M, Lee H, et al. Antenna Selection Schemes in Bidirectional Full-Duplex MIMO Systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(12):10097-10100.
[14] Li R, Gao H, Long W, et al. Joint Relay Transmit-Receive Antenna Selection and Opportunistic Source Selection Strategy for Full-Duplex Relaying[M]. International Conference on Telecommunications, 2014:37- 41.
[15] Zhao R, Lin H, He Y C, et al. Impacts of outdated CSI for secure cooperative systems with opportunistic relay selection[J]. Science China Information Sciences, 2017, 60(6):069303.
[16] Fan L, Zhao R, Gong F K, et al. Secure Multiple Amplify-and-Forward Relaying over Correlated Fading Channels[J]. IEEE Transactions on Communications, 2017, PP(99):1-1.
[17] Chen G, Yu G, Xiao P, et al. Physical Layer Network Security in the Full-Duplex Relay System[J]. IEEE Transactions on Information Forensics & Security, 2015, 10(3):574-583.
[18] Wu H, Tao X, Han Z, et al. Secure Transmission in MISOME Wiretap Channel With Multiple Assisting Jammers: Maximum Secrecy Rate and Optimal Power Allocation[J]. IEEE Transactions on Communications, 2017, 65(2):775-789.
[19] Khisti A, Wornell G W. Secure Transmission With Multiple Antennas—Part II: The MIMOME Wiretap Channel[J]. IEEE Transactions on Information Theory, 2010, 56(11):5515-5532.
[20] Krikidis I, Ottersten B. Secrecy sum-rate for orthogonal random beamforming with opportunistic scheduling[J]. IEEE Signal Processing Letters, 2013, 20(2):141-144.
[21] Vilela J P, Bloch M, Barros J, et al. Wireless Secrecy Regions With Friendly Jamming[J]. IEEE Transactions on Information Forensics & Security, 2011, 6(2):256-266.
[22] Jing Y, Jafarkhani H. Network Beamforming Using Relays With Perfect Channel Information[J]. IEEE Transactions on Information Theory, 2009, 55(6):2499-2517.
[23] Li C, Yang H J, Sun F, et al. Approximate Closed-Form Energy Efficient PA for MIMO Relaying Systems in the High SNR Regime[J]. IEEE Communications Letters, 2014, 18(8):1367-1370.
[24] Li C, Sun F, Cioffi J M, et al. Energy Efficient MIMO Relay Transmissions via Joint Power Allocations[J]. IEEE Transactions on Circuits & Systems II Express Briefs, 2014, 61(7):531-535.
[25] Li C, Liu P, Zou C, et al. Spectral-Efficient Cellular Communications With Coexistent One-and Two-Hop Transmissions[J]. IEEE Transactions on Vehicular Technology, 2016, 65(8):6765- 6772.
[26] Li Y, Zhao R, Tan X, et al. Secrecy Performance Analysis of Artificial Noise Aided Precoding in Full-Duplex Relay Systems[C]∥GLOBECOM 2017-2017 IEEE Global Communications Conference. IEEE, 2017:1- 6.



