1 引言
近些年来随着移动终端的大量普及，移动数据流量呈现爆发式地增长，专家预计2020年的数据流量将是当前数据流量的几千倍，因此第五代移动通信将面临巨大的挑战。大规模MIMO作为5G的关键技术之一，它能够充分利用无线空间的维度资源，改善频谱效率和能量效率[1-2]。在大规模MIMO系统中，基站配置数十根甚至上百根天线，它可以跟大量的用户终端通信，并且每个用户终端通常配置多根天线。一般来说，获取精确的信道状态信息(CSI Channel State Information)对于大规模MIMO系统的通信过程是至关重要的[3- 4]。得益于TDD模式的互易性，基站可以根据上行链路导频序列的训练结果来获取下行链路的CSI[5]。尽管如此，训练中的导频开销还是会随着总的用户天线数的增加而急剧地增长。另外在多小区系统中，小区之间导频序列的复用也会产生小区间的干扰，这种现象被称为导频污染[6]。
在大规模MIMO系统中，尽管可以利用TDD的互易性，训练过程中的导频开销还是会随着用户总的天线数的增加而急剧地增长，这使得CSI的获取变得具有挑战性[7]。由于大规模MIMO信道空间具有渐进正交性，文献[8]、文献[9]使用改进的盲信道估计算法消除矩阵模糊度，从而减小导频污染的影响，但是盲信道估计算法的复杂度较高，在实际的大规模MIMO系统中一般难以应用。文献[10]将指数相关模型应用在大规模MIMO信道估计中并加以分析，具体来说，文献[10]利用指数相关模型去构建信道自相关矩阵，仿真结果表明了天线间相关系数和导频长度对系统平均均方误差(MSE Mean Square Error)的影响程度。大规模MIMO信道在角度域和时延域具有稀疏性，文献[11]采用压缩感知的方法去估计大规模MIMO稀疏信道，其优点是在减小导频开销的同时保证了一定的信道估计性能。为了优化导频位置，文献[12]提出一种基于最小化完全块相关值的导频优化准则以及相应的导频搜索算法，仿真结果表明了利用此优化方法获取导频可以明显地减小信道估计误差。针对已经存在的大规模MIMO MMSE(Minimum Mean Square Error)信道估计方法需要完美已知小区间的大尺度衰落系数，文献[13]提出一种改进的大规模MIMO MMSE信道估计方法，该方法不需要预先知道小区间的大尺度衰落系数。文献[13]假设信道是平坦衰落的，文献[14]在文献[13]的基础之上，研究时变的频率选择信道下的多小区大规模MIMO TDD系统下的信道估计问题。针对大规模MIMO FDD(Frequency Division Duplexing)系统前向链路导频训练阶段存在巨大的反馈开销问题，文献[15]将信道矩阵分成稀疏矢量部分和密集矢量部分，稀疏矢量部分采用CS(Compressed Sensing)技术去估计，而密集矢量部分采用LS(Least Square)信道估计算法去估计。通过这种分割，可以减小导频开销和提高信道子空间的追踪性能。
文献[10]仅考虑了用户端单天线的情况，这在5G通信系统中并不能满足通信需求，同时指数相关模型虽能反映天线间的相关系数对大规模MIMO信道估计的影响，但是模型的构建稍显简单。本文在文献[10]的基础之上，重点研究大规模MIMO信道估计和导频开销问题，提出了一种联合波束域分解和SVD的大规模MIMO信道估计方法。将用户端天线数扩展到5G环境中实际的M根而非原文的1根，同时应用文献[16]的波束域分解方法，简化模型，将SVD引入从而进一步降低[10]中LMMSE(Linear Minimum Mean Square Error)算法复杂度。仿真结果表明，本文方法较[10]进一步减小了信道估计误差以及降低了导频开销。
本文的组织结构如下：第2节引入大规模MIMO上行链路系统模型；第3节引入大规模MIMO信道模型，分别介绍了指数相关模型和基于波束域分解的信道模型；第4节基于上面的讨论，给出了联合波束域分解和SVD的大规模MMO信道估计方法，同时推导出估计误差协方差矩阵闭式表达式；第5节是数值仿真，验证上述推论；第6节总结全文。
本文使用的符号定义如下：矩阵和矢量分别用大写和小写的粗体字母表示，比如X和x。(·)T,(·)*,(·)H分别表示矩阵的转置、共轭、共轭转置，‖·‖2表示二阶范式。I代表合适维度的单位矩阵，
表示变量x的期望。假设x服从高斯分布，且u和J是复高斯随机变量x的均值和协方差矩阵，则有
2 系统模型
考虑一个单小区的TDD系统，包含一个基站和K个用户，基站配置N根天线，假设基站侧天线是均匀线性阵列(ULA Uniform Linear Array)，K个用户随机并且均匀地分散在小区内部，每个用户配备M根天线，如图1所示。假设信道是块衰落的，并且上下行链路采用的是TDD协议，因此在充分利用信道的互易性之后，可以持续性地获得CSI去监测上行链路的状态信息。假设各个用户的信道估计是相互独立的，则在第k个用户发送导频数据之后，基站端的接收信号可以表示为
y=hx+n
(1)
其中
表示基站和用户之间的物理信道，
表示来自用户的发射信号，
表示信号传输过程中的噪声，且假设
同时定义信号功率
信道的协方差矩阵可以表示为：
(2)
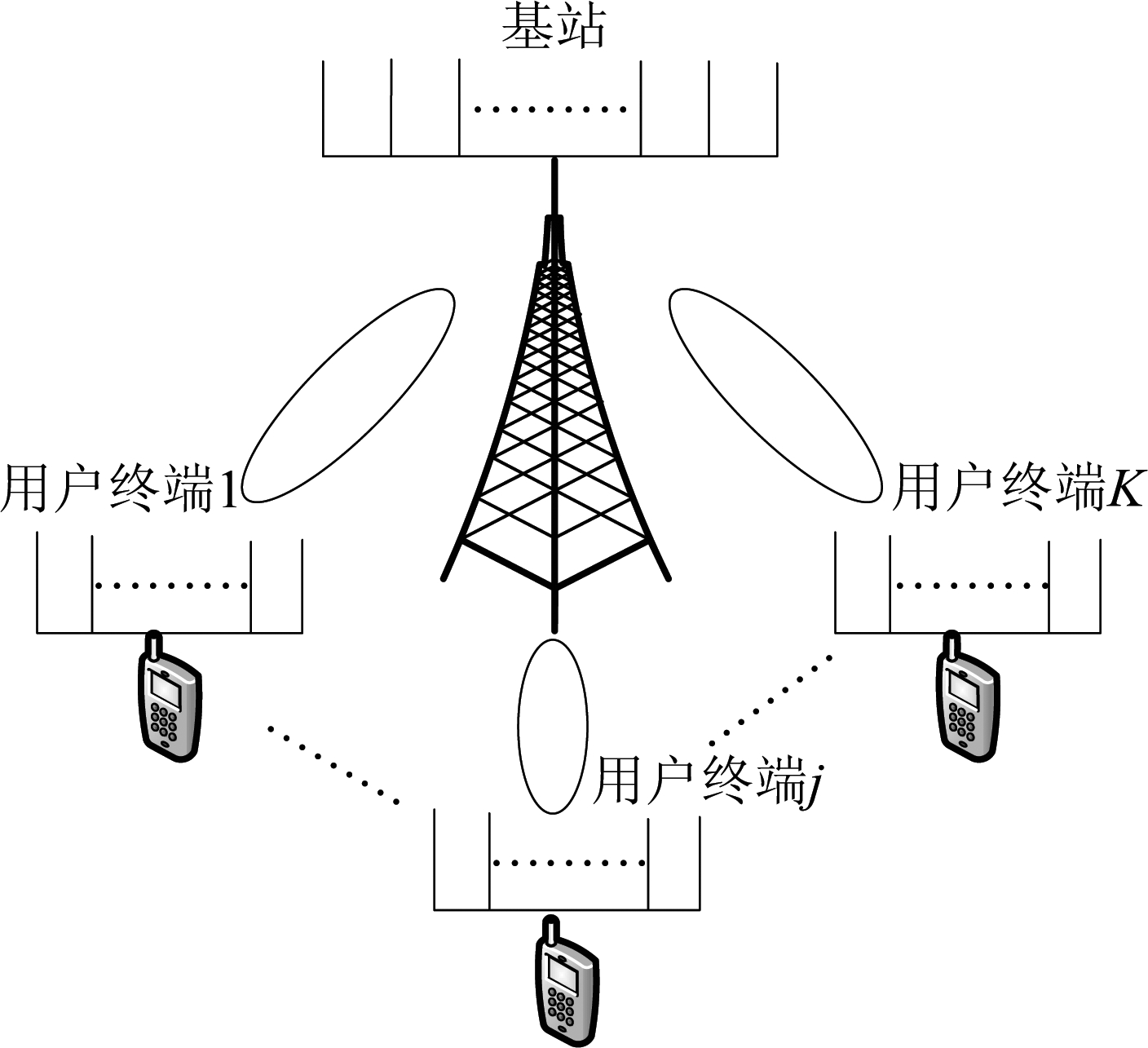
图1 包含一个基站和K个用户的单小区系统
Fig.1 A single cell system that contains a base station and K users
3 信道模型
3.1 指数相关模型
指数相关模型是一个单参数的模型，可以被用于研究天线间相关性对MIMO信道容量的影响。当天线阵列中的天线是等间距分布的时候，它构建的信道协方差矩阵是有可能存在的[17]。文献[10]利用指数相关模型去研究天线间的相关系数对大规模MIMO信道估计的影响，具体来说，可以通过指数相关模型去构建大规模MIMO信道自相关矩阵，构建规则如下[10,17]：
(3)
其中i是行标， j是列标，α是每一条链路的衰落因子，r表示天线间的相关系数。
3.2 基于波束域分解的信道模型
对于大规模MIMO系统而言，获取实时并且精确的CSI是非常困难的，文献[16]在基站侧的BDMA(Beam Domain Multiple Access)传输过程中采用统计的CSI而非瞬时的CSI，可大大降低获取精确CSI的难度，因此BDMA的方法可用在对CSI要求比较高的环境中，比如高铁、航空器等。本文运用波束域分解的方法，一方面降低了获取精确CSI的难度；另一方面，将混合信道分解成多个单用户大规模MIMO信道可以降低系统的导频开销[16]，接下来针对单用户的大规模MIMO系统进行波束域信道建模。
假设只考虑电波传播信道模型在水平维度的到达角和离去角，基站周围没有强烈的信号散射，基站和用户之间总共有L条路径，则第k个用户信号在第l条传播路径上相应的大规模MIMO上行链路信道矩阵可以表示为[16,18]：
(4)
其中al,k是第l条传播路径的衰减系数，上标u表示上行链路，dl,k表示发射天线和接收天线之间的距离，λ是载波波长，dl,k/λ～U(0,1)，θl,k表示到达角AOA(Angel of Arrival)，φl,k表示离去角AOD(Angel of Departure)
是接收天线阵列响应矢量，并且满足
是发射天线阵列响应矢量，并且满足‖et(φl,k)‖2=1，表示如下[19]：
(5)
其中θ～U(0,π)，N表示天线数目，d表示均匀线性阵列的天线间距，我们定义ro=d/λ为天线间距波长比去度量天线间的相关强度。
假设信道是宽带信道，发射信号在经过OFDM(Orthogonal Frequency Division Multiplexing)调制之后，第k个用户信号在第i个子载波上的信道响应矩阵可以表示为：
(6)
其中τl,k表示第l条路径的传播时延。由于θl,k是接收信号的抽样值，则不同方向的接收信号彼此之间是相互正交的，而基站可以完美地分离这些正交的方向性信号[20]，可得如下推论：
(7)
同理在用户端有如下推论：
(8)
在上述推论的基础上，式(6)可以被重写为：
(9)
其中
表示发射天线阵列响应矩阵，
表示接收天线阵列响应矩阵，并且Vk、Ik近似为单位矩阵；
表示波束域信道矩阵，具体形式如下[16]：
(10)
其中Pr,n表示AOA最接近θn,k的所有路径的集合，Pt,m表示AOD最接近φm,k的所有路径的集合，则信道自相关矩阵可以表示为：
(11)
4 基于波束域分解-SVD的信道估计
在获得信道自相关矩阵Rh之后，将发射的导频信号x与接收信号y做对比，可以估计出当前的CSI。LMMSE准则作为一种经典的信道估计准则被文献[10]采用，因此我们首先将LMMSE准则应用到本文场景去估计h。假设发射的是正交导频序列且导频序列是等功率分配的，根据经典的LMMSE算法，h的最优线性估计量表示如下[21]：
(12)
由式(1)可得接收信号y的协方差矩阵为：
(13)
在得到Ry之后，将式(13)带入(12)得
(14)
则h的估计误差协方差矩阵为：
(15)
由于Ry是对称阵，所以
也是对称阵，故
将式(1)代入式(15)里得，具体推导过程见附录。
(16)
将式(11)代入式(16)中可得波束域信道建模下的估计误差协方差矩阵为：
(17)
观察式(14)，发现在获取
的过程中需要求Ry的逆，而矩阵的逆运算一般复杂度比较高。尤其在大规模MIMO系统中，当基站天线数目非常多的时候，Ry的阶数会很大，由此带来的运算量会相当大。基于这一点，本文在从波束域建模信道的同时，对LMMSE算法的求逆运算进行优化，这样在减小导频开销的同时可以进一步降低算法的复杂度。通过式(11)获得Rh之后，对Rh进行SVD运算如下，考虑到Rh是对称阵，则SVD等价于特征值分解。
(18)
根据SVD理论，U是酉矩阵，满足UUH=I。在此基础上，重新推导式(14)如下：
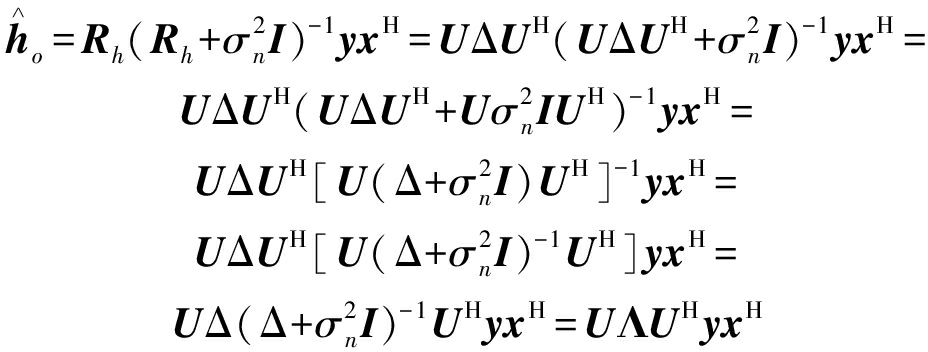
(19)
其中
由于Λ和Δ都是对角阵，设Λ的主对角线元素为Λk，Δ的主对角线元素为Δk，则Λk和Δk满足如下关系式：
(20)
由于文献[10]采用的是LMMSE信道估计算法，本文采用的是经过SVD优化后的信道估计算法。由文献[22]可知，LMMSE算法复杂度Ο(N3)，经过SVD优化后的LMMSE算法复杂度Ο(N2)。现对式(12)和式(19)进行详细的算法复杂度分析，也即是对文献[10]和本文的信道估计算法复杂度分析如下：
表1 两种信道估计算法复杂度比较
Tab.1 Complexity comparison of two channel estimation algorithms
文献[10]信道估计算法复杂度(复乘次数)本文信道估计算法复杂度(复乘次数)Rh+σ2nINSVD运算Ο(N2)(Rh+σ2nI)-1Ο(N3)UΛNpRh(Rh+σ2nI)-1N3UΛUHN2p
从表1中可以看出，文献[10]信道估计算法整体复杂度为N+Ο(N3)+N3，本文信道估计算法整体复杂度为Ο(N2)+Np+N2p。与文献[10]相比，本文算法大大降低了运算复杂度。在得到优化后的信道估计量
之后，重新推导式(16)可得优化后的Rerror如下：
+UΛUHyxHxyHUΛHUH}
(21)
将式(1)带入(21)中得，具体推导过程见附录：
UΛUHyxHxyHUΛHUH}=
UΔUH-UΔUHUΛHUH-UΛUHUΔUH+
(22)
则平均均方误差可以表示为：
(23)
其中ν是导频序列的长度，同时定义相关估计误差如下：
(24)
综合第2节、第3节的内容，下面给出联合波束域分解和SVD的信道估计方法在多用户大规模MIMO系统上行链路传输中的实现流程。
联合波束域分解和SVD的信道估计方法1.通过用户调度,不同的用户对应不相重叠的波束,多用户的大规模MIMO信道可以分解成多个彼此正交的单用户大规模MIMO信道[16]。2.波束域信道建模(a) 通过式(4)构建大规模MIMO上行链路信道矩阵hul,k,其中AOA和AOD的公式参考式(5),然后对信号进行调制,本文采用的是OFDM。(b)根据AOA和AOD的特性得到推论(7)、(8),然后重写式(6),并获得波束域信道矩阵h^i,k,信道自相关矩阵Rh。3.SVD(a)根据经典的LMMSE算法,推导出本文场景下的最优信道估计量h∧。将步骤2中得到的Rh代入式(16),得到估计误差协方差矩阵Rerror。(b)对步骤2中得到的Rh进行SVD运算,推导出优化后的信道估计量h∧o。将h∧o代入式(16),得到优化后的估计误差协方差矩阵R′error。(c)进行算法复杂度分析,并定义MSEavg和MSErela以便仿真分析。
5 仿真与性能分析
在本节中，我们给出一些仿真例子去验证本文提出的联合波束域分解和SVD信道估计方案的优越性。仿真实验平台是Matlab，采用蒙特卡罗仿真独立进行1000次实验获得Rh。本文采用的是正交导频序列，仿真参数与文献[10]相同，设置SNR=0 dB，通过控制导频和噪声的功率可以改变信噪比，AOA和AOD服从[0,π]均匀分布。
首先我们研究当相关系数变化时，相关估计误差MSErela随导频长度的变化关系，仿真中设定基站天线数N=64，仿真结果如图2、图3所示。图2显示了文献[10]所提出的信道估计方案的性能曲线，图3显示了本文所提出的信道估计方案的性能曲线。由于文献[10]假定每个用户终端都是单天线的，所以在仿真时设定M=1；而本文假定用户终端是多天线的，所以在仿真时设定M=4。从图2、图3中均可以看出：随着导频长度的不断增大，MSErela的值在不断减小，这说明信道估计精度在不断提高；不同之处在于当相关系数r增大时，信道估计误差会变小；当天线间距波长比ro减小时，信道估计误差会变小。从物理意义上来说，这是因为随着r增大，天线间的相关性会增强；而ro减小表明天线间距在减小，天线间的相关性在增强，当这种相关性被合理地利用时，信道估计的精度得以提高。
图2 当r变化时，相关估计误差随导频变化曲线
Fig.2 When r changes, the correlation estimation error varies with the pilot curve
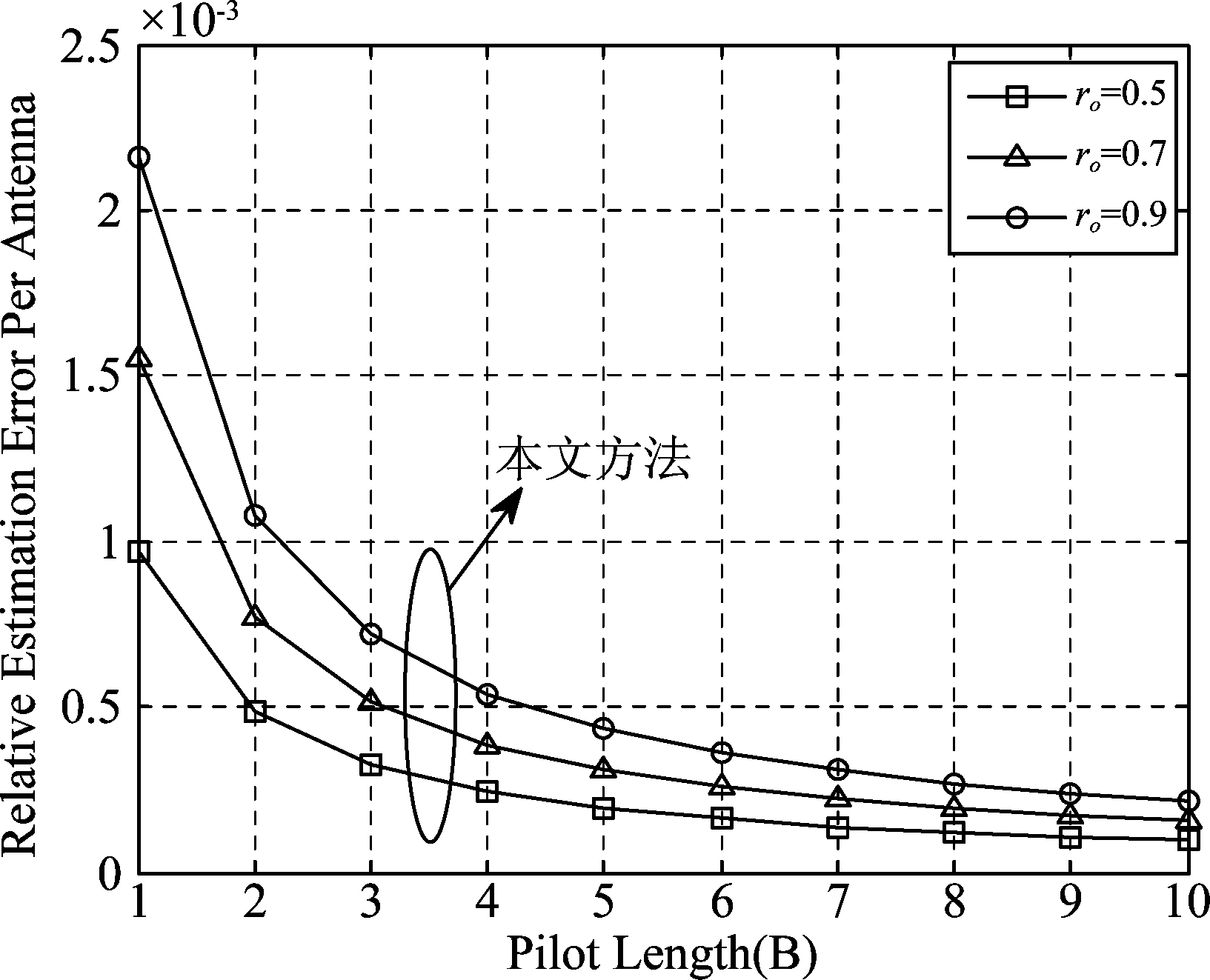
图3 当ro变化时，相关估计误差随导频变化曲线
Fig.3 When ro changes, the correlation estimation error varies with the pilot curve
从图2、图3的数值结果中可以看出：在信道估计精度方面，本文所提出的基于波束域分解-SVD信道估计方案的相关估计误差要远小于文献[10]中的方案。当使用长度更短的导频序列时，可以达到或者超过文献[10]中方案的信道估计精度，这说明本文方案相比文献[10]在一定程度上也减小了导频开销。
图4、图5揭示了当基站天线数变化时，相关估计误差MSErela随导频长度的变化关系。仿真时设定基站天线数N=32、64、128。同前面一样，当仿真文献[10]中的方案时设定M=1，同时设定相关系数r=0.5、0.7；仿真本文方案时设定M=4，同时设定天线间距波长比ro=0.5、0.7。图4显示了文献[10]所提出的信道估计方案的性能曲线，图5显示了本文所提出的信道估计方案的性能曲线。从图4、图5的数值结果中可以看出：本文所提方案在这种场景下的相关估计误差仍远小文献[10]中的方案；同时我们从图5中发现在导频数量比较少的情况下，基站侧配置不同天线数对应的相关估计误差差别较大。但是随着导频长度逐渐增大，当基站侧天线数变化时，相关估计误差不会有显著变化。这说明了在实际的大规模MIMO TDD系统中，信道估计的精度近似独立于基站的天线数。
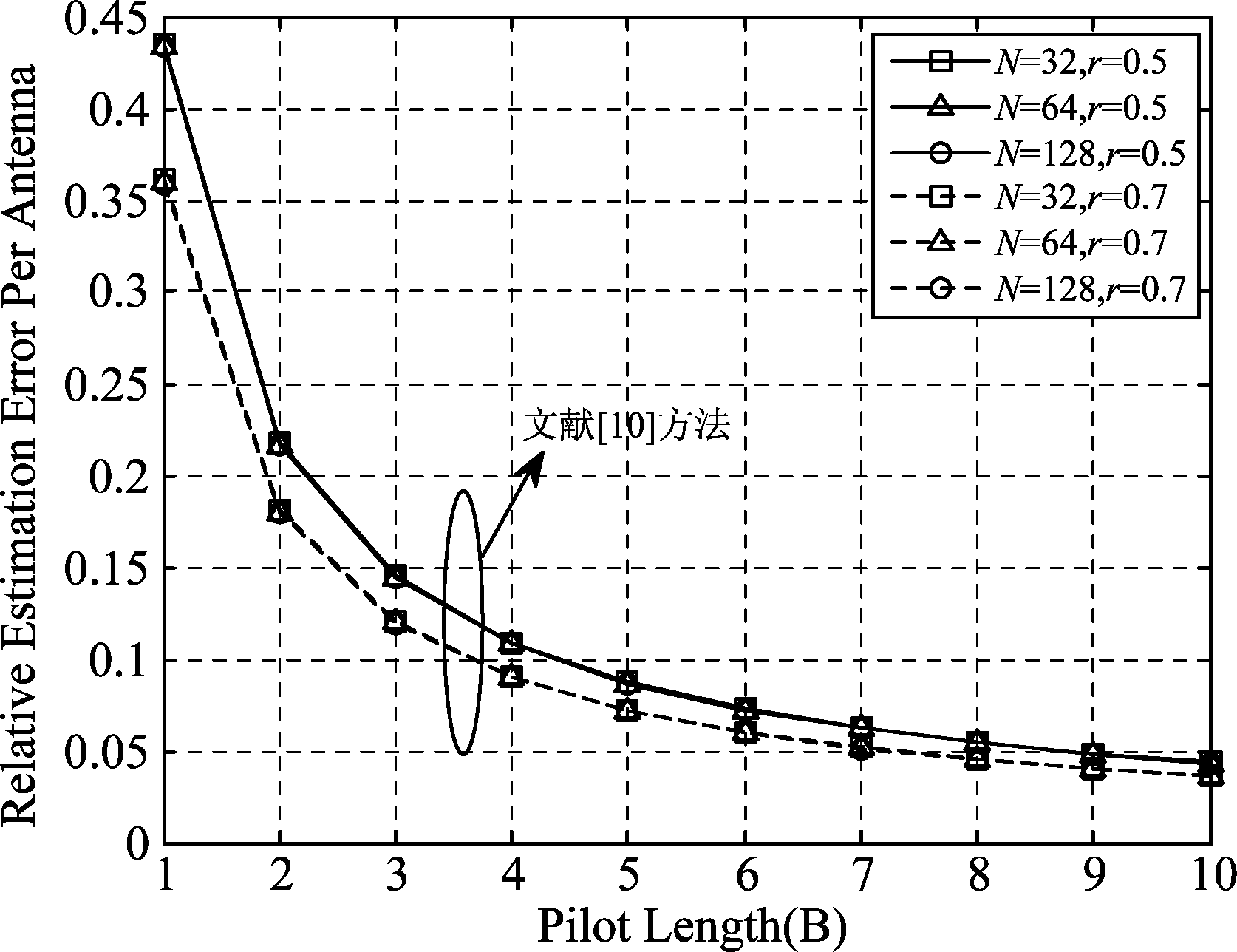
图4 当N,r同时变化时，相关估计误差随导频变化曲线
Fig.4 When N and r change at the same time, the correlation estimation error varies with the pilot curve
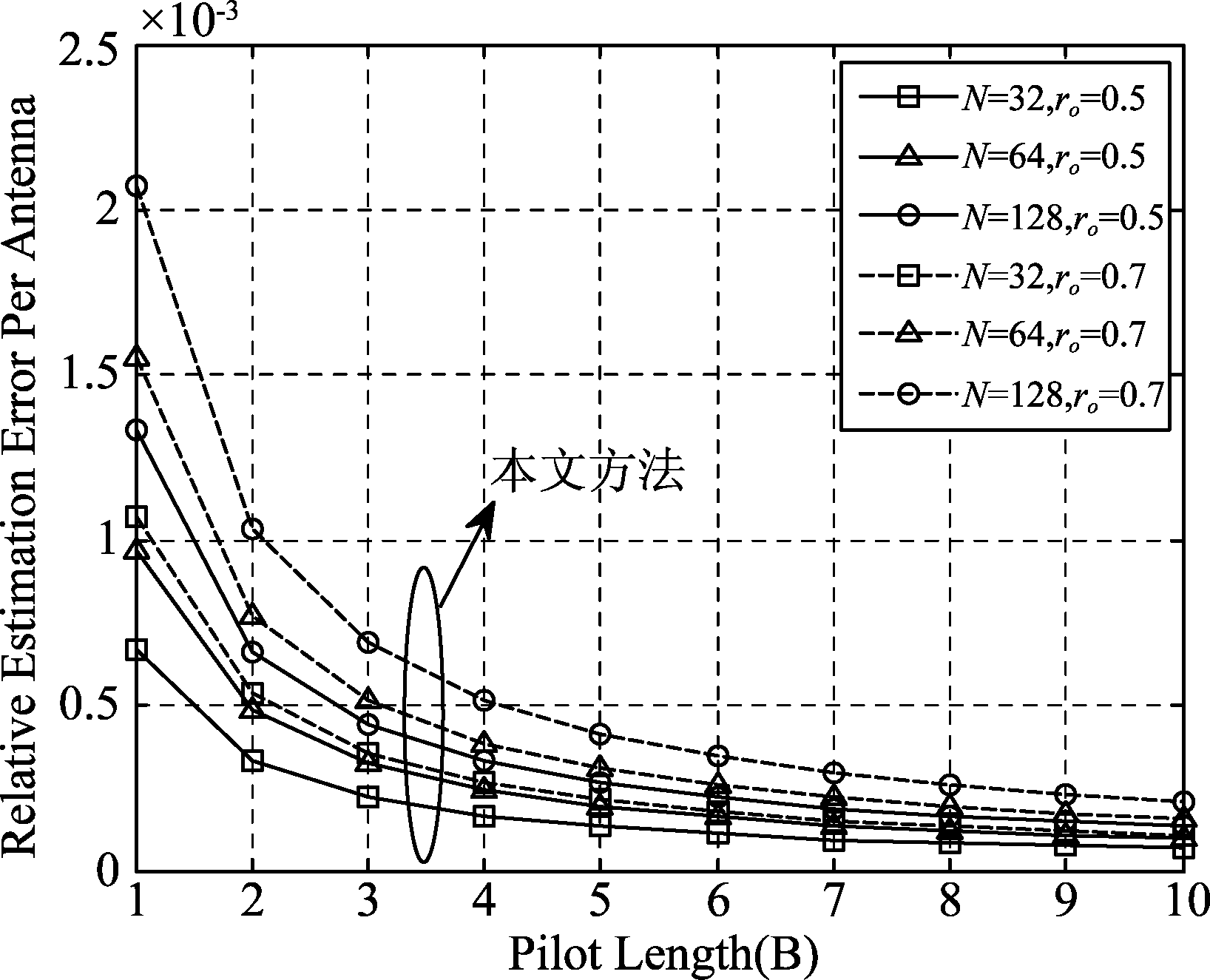
图5 当N,ro同时变化时，相关估计误差随导频变化曲线
Fig.5 When N and ro change at the same time, the correlation estimation error varies with the pilot curve
图6显示了当用户端天线变化时，相关估计误差MSErela随导频长度的变化关系。仿真时设定基站天线数N=64，用户端天线数M=2、4、8。从图6中可以看出：随着导频数量的逐渐增多，增大用户端天线数，相关估计误差没有发生显著变化。这说明了在实际的大规模MIMO TDD系统中，信道估计的精度近似独立于用户端的天线数。
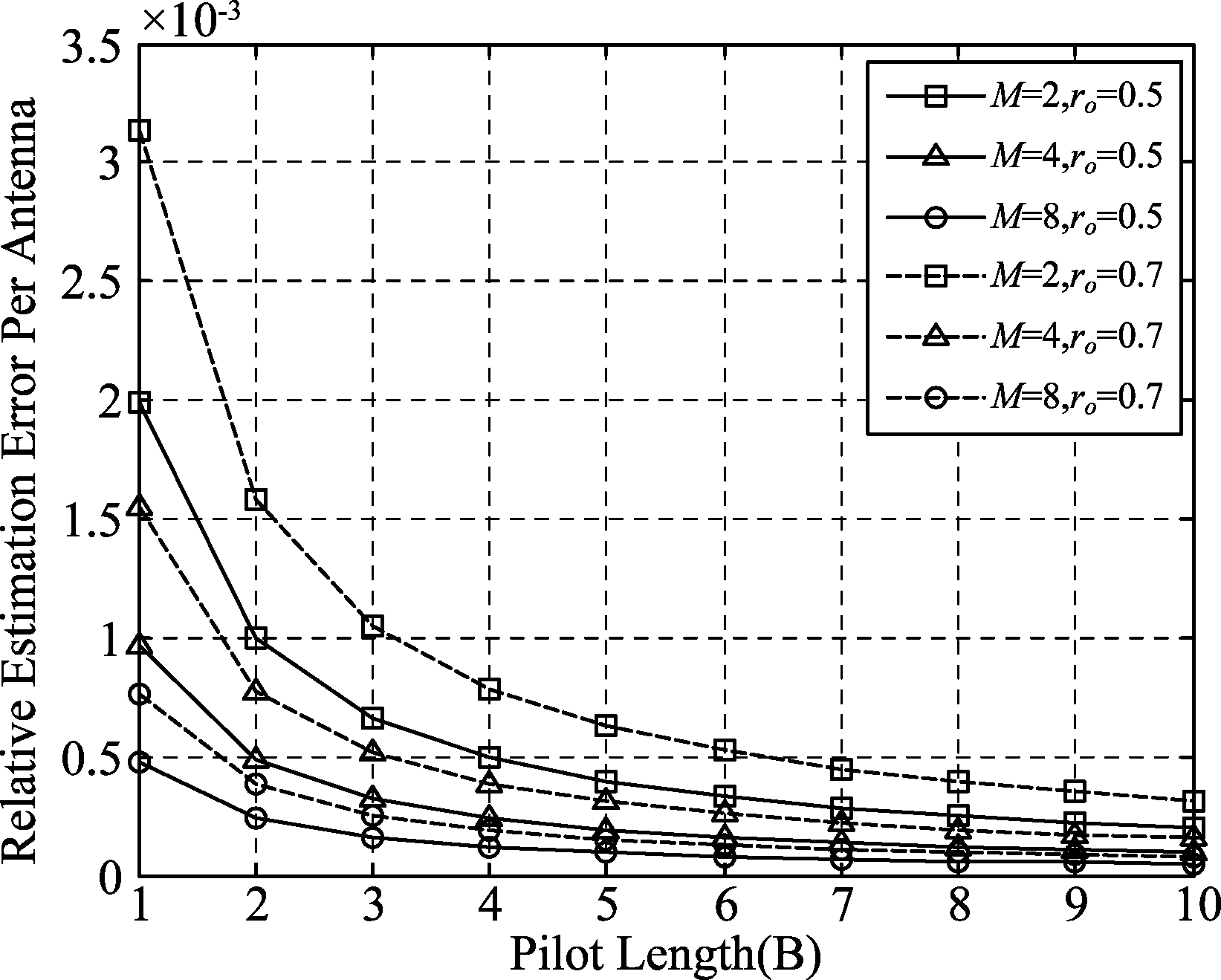
图6 当M变化时，相关估计误差随导频变化曲线
Fig.6 When M changes, the correlation estimation error varies with the pilot curve
6 结论
本文主要研究了多用户大规模MIMO系统上行链路传输的信道估计和导频开销问题。应用波束域分解中的波束域信道建模理论来构建信道自相关矩阵，同时针对LMMSE算法中矩阵求逆运算复杂度较高的问题，我们对获取的信道自相关矩阵进行SVD运算。综合两种技术提出了联合波束域分解和SVD的信道估计算法，并推导出了估计误差协方差矩阵的闭式表达式。仿真结果显示，不管是在信道估计误差方面还是导频开销方面，本文提出的信道估计方案的性能都要优于文献[10]中的信道估计方案。最后，我们验证了在TDD模式下，信道相关估计误差近似独立于基站天线数和用户端天线数。
附录A
公式(16)推导过程如下：
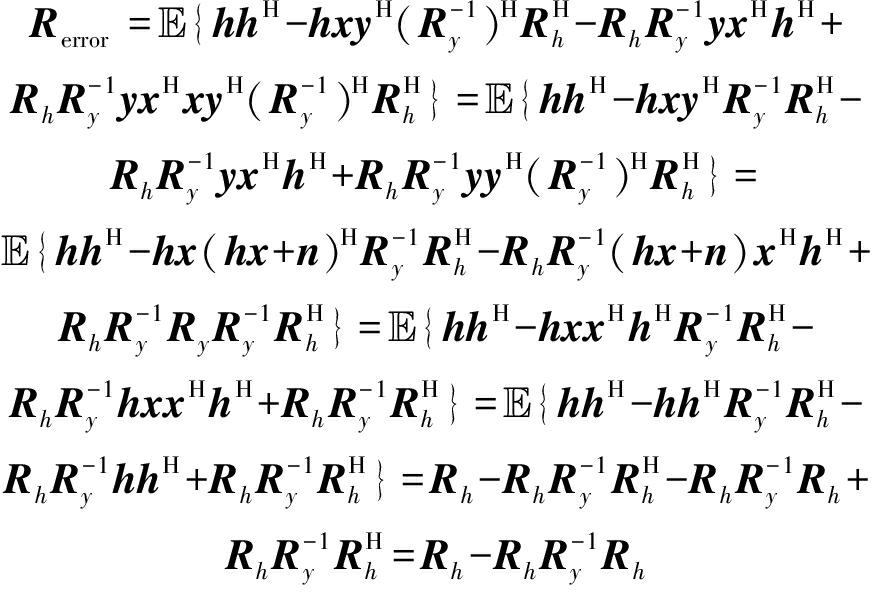
(A.1)
公式(22)推导过程如下：
UΛUH(hx+n)xHhH+UΛUHyxHxyHUΛHUH}=
UΛUHhhH+UΛUHyyHUΛHUH}=Rh-RhUΛHUH-UΛUHRh+UΛUHRyUΛHUH=Rh-RhUΛHUH-
UΔUHUΛHUH-UΛUHUΔUH+
UΔUH-UΔΛHUH-UΛΔUH+
(A.2)
参考文献
[1] Kamga G, Xia Minghua, Aissa S. Spectral-Efficiency Analysis of Regular-and Large-Scale (Massive) MIMO With a Comprehensive Channel Model[J]. Vehicular Technology, IEEE Transactions on, 2017, 66(6): 4984- 4996.
[2] Liu Zujun, Du Weimin, Sun Dechun. Energy and Spectral Efficiency Tradeoff for Massive MIMO Systems With Transmit Antenna Selection[J]. Vehicular Technology, IEEE Transactions on，2017, 66(5): 4453- 4457.
[3] Kong Chuili, Zhong Caijun, Jin Shi, et al. Multipair full-duplex massive MIMO relaying with low-resolution ADCs and imperfect CSI[C]∥IEEE International Conference on Communications (ICC). Paris: IEEE, 2017: 1- 6.
[4] Chen Junting, Yin Haifan, Laura C, et al. Feedback Mechanisms for FDD Massive MIMO With D2D-Based Limited CSI Sharing[J]. Wireless Communications, IEEE Transactions on，2017, 16(8): 5162-5175.
[5] Jiang Xiwen, Florian K, Luc D. How accurately should we calibrate a Massive MIMO TDD system?[C]∥IEEE International Conference on Communications Workshops (ICC). Kuala Lumpur: IEEE, 2016: 706-711.
[6] Li Jiamin, Wang Dongming, Zhu Pengcheng, et al. Downlink Spectral Efficiency of Distributed Massive MIMO Systems with Linear Beamforming under Pilot Contamination[J]. Vehicular Technology, IEEE Transactions on，2017, PP(99): 1-1.
[7] Wang Qian, Jing Yindi. Performance Analysis and Scaling Law of MRC/MRT Relaying With CSI Error in Multi-Pair Massive MIMO Systems[J]. Wireless Communications, IEEE Transactions on, 2017, 16(9): 5882-5896.
[8] Ngo H Q, Larsson E G. EVD-based channel estimation in multicell multiuser MIMO systems with very large antenna Arrays[C]∥IEEE International Conference on Acoustics，Speech and Signal Processing (ICASSP). Kyoto: IEEE，2012: 3249-3252．
[9] Muller RR, Vehkapera M, Cottatellucci L. Blind pilot decontamination[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 773-786.
[10] Albdran S, Alshammari A, Atiqur Rahman Ahad M, et al. Effect of Exponential Correlation Model on Channel Estimation for Massive MIMO[C]∥IEEE International Conference on Computer and Information Technology (ICCIT). Dhaka: IEEE, 2016: 80- 83.
[11] Masood M, Afify L H, Al-Naffouri T Y. Efficient Coordinated Recovery of Sparse Channels in Massive MIMO[J]. Signal Processing, IEEE Transactions on, 2015, 63(1): 104-118.
[12] 何雪云, 梁天, 赵彦. 大规模MIMO-OFDM系统结构化压缩感知信道估计中导频优化方法研究[J]. 信号处理，2017, 33(1): 87-94.
He Xueyun, Liang Tian, Zhao Yan. Optimizing Pilots for Structured Compressive Sensing Based Channel Estimation in Massive MIMO-OFDM Systems[J]. Journal of Signal Processing, 2017, 33(1): 87-94.(in Chinese)
[13] Khansefid A, Minn H. On Channel Estimation for Massive MIMO With Pilot Contamination[J]. IEEE Communication Letters, 2015, 19(9): 1660-1663.
[14] Felipe A. P. De Figueiredo, Fabbryccio A. C. M. Cardoso, Ingrid Moerman, et al. Channel Estimation for Massive MIMO TDD Systems Assuming Pilot Contamination and Frequency Selective Fading[J]. IEEE Access, 2017(5): 17733-17741.
[15] Han Y, Lee J, Love D. Compressed Sensing-Aided Downlink Channel Training for FDD Massive MIMO Systems[J]. Wireless Communications, IEEE Transactions on, 2017, 65(7): 2852-2862.
[16] Sun Chen, Gao Xiqi, Jin Shi, et al. Beam Division Multiple Access Transmission for Massive MIMO Communications[J]. Communications, IEEE Transactions on, 2015, 63(6): 2170-2184.
[17] Loyka S L. Channel capacity of MIMO architecture using the exponential correlation matrix[J]. IEEE Communications Letters, 2001, 5(9): 369-371.
[18] Tse D, Viswanath P. Fundamentals of Wireless Communication[M]. New York, NY, USA: Cambridge Univ. Press, 2005.
[19] Mezghani A, Swindlehurst A L. Blind estimation of sparse multi-user massive MIMO channels[J]. arXiv:1612.0013lvl, Dec. 2016.
[20] Sayeed A. Deconstructing multi-antenna fading channels[J]. Signal Processing, IEEE Transactions on, 2002, 50(10): 2563-2579.
[21] 郑心如. 大规模MIMO系统导频设计和信道估计技术研究[D]. 南京: 东南大学, 2015.
Zheng Xinru. Pilot design and channel estimation for massive MIMO systems[D]. Nanjing: Southeast University, 2015.(in Chinese)
[22] Savaux V, Lou⊇t Y. LMMSE channel estimation in OFDM context: a review[J]. IET Signal Processing, 2017, 11(2): 123-134.
