1 引言
随着无线通信网络的快速发展,智能设备越发普及,相应的移动数据量呈指数式增长,用户体验急需提升[1]。为满足上述需求,许多新技术诸如小区超密集部署技术和协作多点技术应运而生。然而,在考虑如何增大数据传输速率的同时,也应该从经济和生态的角度关注由此带来的能量消耗问题[2]。
传统的蜂窝系统对处理普遍存在的小区间干扰及海量数据传输与处理等问题显得有些力不从心,近年来,基于集中式处理的分布式天线系统(DAS: distributed antenna systems)、云无线接入网络(C-RAN, cloud radio access network)在学术界和工业界得到广泛关注[3]。DAS/C-RAN是基于集中计算处理的绿色实时无线接入网络,利用集中处理器的高处理能力可以有效克服小区间干扰及进行高效的资源分配与用户调度。其网络架构由三个部分组成,分别是对信号进行集中式处理的基带单元(BBU, baseband unit),远端射频头(RRHs, remote radio heads),以及连接BBU和RRH的低延迟前端链路。在实际的通信系统中,为增大用户端的数据速率,要求前端链路能够适应大比特率传输的要求,这就增加了集中式处理系统架构的实现复杂度。因此,怎样在集中式处理系统网络中设计前端压缩预编码策略成为目前学术界的一大研究热点[4]。
在上行链路中,通过在BBU中进行用户信息集中预编码,能显著提升传统蜂窝网络的吞吐量[5],该方法同样适用于下行链路。然而将所有无线设备的信息在BBU进行集中处理再通过前端链路传送至RRH的方式,无形中增大了前端链路的传送负担。由于DAS/C-RAN前端链路容量有限,考虑RRHs和BBU之间的功能分区。为增强DAS/C-RAN的性能,考虑将传统的所有基带信息均在BBU处理的方式替换为在BBU和RRHs之间进行联合处理的方式。因此,针对DAS/C-RAN下行链路,通常有两种预编码压缩策略。传统的DAS/C-RAN解决方案称为先预编码后压缩(CAP, compression after precoding),在该策略中,BBU集中进行预编码操作,然后通过前端链路将预编码信号量化并转发给各RRH[6]。在另一种称之为先压缩后预编码(CBP, compression before precoding)的策略中,BBU通过计算得到预编码矩阵,前端链路对预编码矩阵进行量化,并将量化后的预编码矩阵和各RRH对应的用户信息共同传递给RRH簇,最后各RRH在接收到消息后对其服务的用户进行预编码[7]。
目前,许多研究人员从不同角度研究DAS/C-RAN发送策略。文献[8]针对用户加权和速率最大化问题,从RRH发送功率约束角度出发,通过主导最小化(MM, majorization minimization)算法进行优化。文献[6]在此基础上,加入了前端链路容量限制,提出了能有效求解用户加权和速率最大化问题的优化迭代算法。文献[9]则考虑在发送功率限制和满足用户服务质量的前提下,最小化系统总功率消耗。文献[10]旨在最大化系统能效,但考虑的是用户速率固定时的系统功率消耗最小化问题。值得注意的是,无处不在的通信需求势必会伴随着大幅的能量消耗,并产生一定的生态影响和经济影响。然而,上述工作仅涉及加权和速率最大化问题和总功率消耗最小化问题。为了在下行集中式处理网络中实现节能传输,需要平衡好用户和速率和总功率消耗两者间的关系。
针对集中式处理网络的下行链路,本文拟研究CBP策略的预编码矩阵和量化噪声矩阵的联合设计。在每个RRH发送功率受限,前端链路容量受限和用户特定速率约束条件下,最大化系统能效。由于目标函数是分式形式,分子上的功率表达式中含有离散的指示函数,且前端容量和用户可获得的速率表达式均非凸,使得原始问题是非凸的,难以直接求解。因此,通过采用分式规划和逐次凸近似的方法[11-16],将原始问题转化为凸优化问题,并提出了一种能有效求解该近似问题的二层迭代算法。数值仿真结果验证了所提算法的有效性,相较于传统的和速率最大化(Max-SR, maximum sum rate)准则和总功率消耗最小化(Min-P, minimum power consumption)准则,能效最大化(Max-EE, maximum energy efficiency)准则具有更好的能效性能。且CBP策略的RRH调度的用户较少时,能效性能较优。
2 系统模型
考虑由L个RRH、K个用户及一个中央处理器组成的集中式处理(DAS/C-RAN)下行网络,![]() 和
和![]() 分别表示RRH集合和用户集合。第l个RRH的发射天线数为Nl,第k个用户的接收天线数为Bk,总的发射和接收天线数分别为
分别表示RRH集合和用户集合。第l个RRH的发射天线数为Nl,第k个用户的接收天线数为Bk,总的发射和接收天线数分别为![]() 和
和![]() 假设所有的用户信息在BBU中均已知,且所有的RRH通过各自的前端链路连接到BBU。信道的相干周期为T,则第k个用户接收到的维数为Bk×T的信号可以表示为
假设所有的用户信息在BBU中均已知,且所有的RRH通过各自的前端链路连接到BBU。信道的相干周期为T,则第k个用户接收到的维数为Bk×T的信号可以表示为
Yk=HkX+Nk
(1)
其中,Hk=[Hk,1,…,Hk,L]表示块衰落信道,Hk,l表示从第l个RRH到第k个用户的维数为Bk×Nl的信道矩阵,Nk表示维数为Bk×T的噪声矩阵,且每个元素服从均值为0,方差为1的循环对称复高斯分布![]() 表示RRHs的发送信号集合,Xl表示第l个RRH发射的维数为Nl×T的信号。对于X的生成,这里考虑先将预编码矩阵量化,再对用户信息进行预编码的方式,即CBP策略。
表示RRHs的发送信号集合,Xl表示第l个RRH发射的维数为Nl×T的信号。对于X的生成,这里考虑先将预编码矩阵量化,再对用户信息进行预编码的方式,即CBP策略。
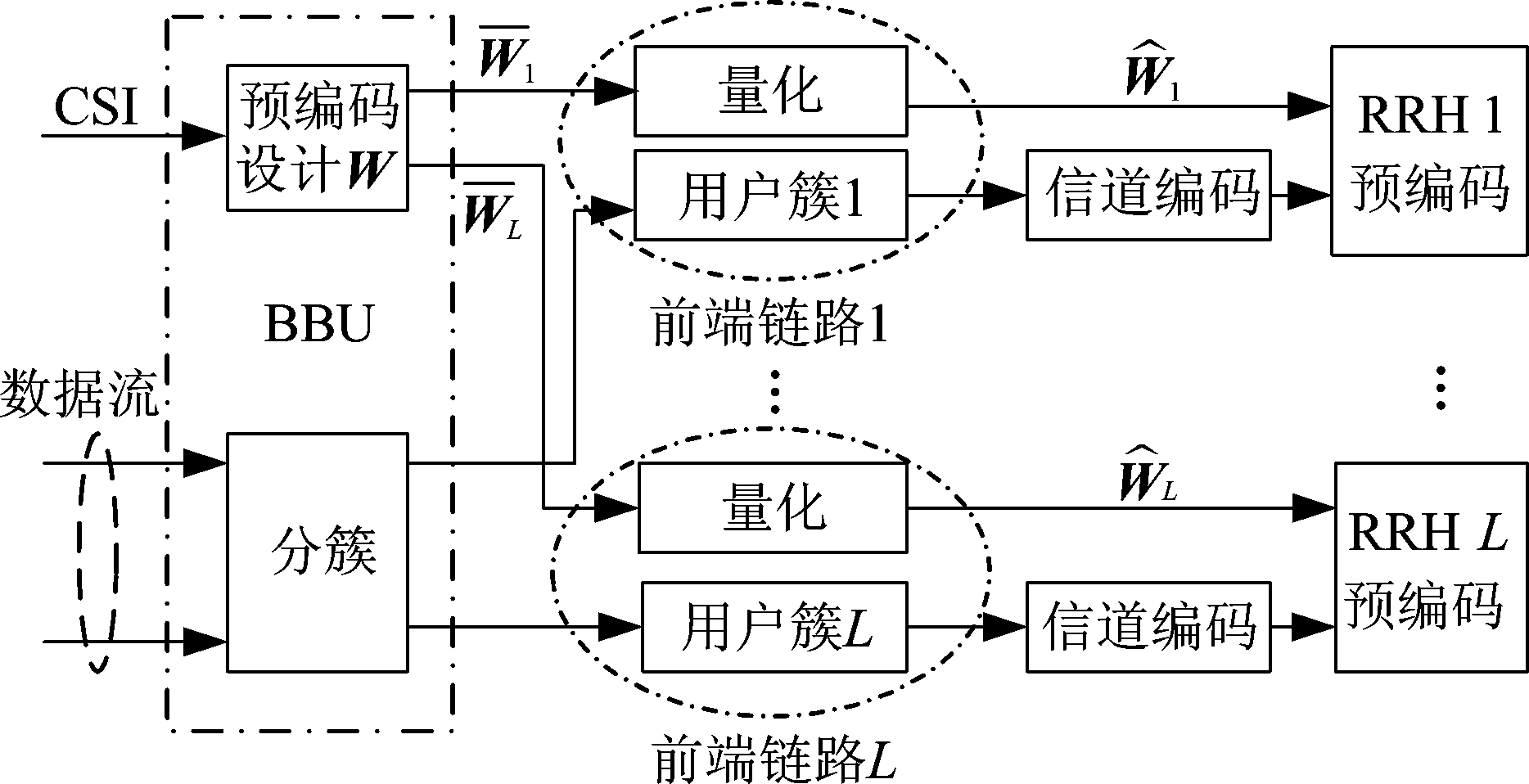
图1 DAS/C-RAN下行链路的CBP策略
Fig.1 CBP strategy for the downlink of the DAS/C-RAN
CBP策略的系统实现框图如图1所示,预编码矩阵和用户信息独立地从BBU传送至RRH。令Sk表示第k个用户信道编码后维数为Mk×T的信号,并假设所有用户的数据流总数为![]() 且满足M≤min(N,B)。不失一般性,Sk所有的元素均服从
且满足M≤min(N,B)。不失一般性,Sk所有的元素均服从![]() 令
令![]() 表示第l个RRH服务的用户簇,
表示第l个RRH服务的用户簇,![]() 表示
表示![]() 中的第m个用户,
中的第m个用户,![]() 表示第l个RRH包含的所有用户数据流总数。BBU首先产生一个对应于第l个RRH的维数为
表示第l个RRH包含的所有用户数据流总数。BBU首先产生一个对应于第l个RRH的维数为![]() 的预编码矩阵
的预编码矩阵![]() 再通过前端链路量化后传送给第l个RRH。经过量化后的预编码矩阵为
再通过前端链路量化后传送给第l个RRH。经过量化后的预编码矩阵为![]() 其中
其中![]() 表示独立于
表示独立于![]() 的噪声矩阵,且服从均值为0,方差为Ωl的循环对称复高斯分布。因此,所有RRH组成的维数为N×M的预编码矩阵可以表示为
的噪声矩阵,且服从均值为0,方差为Ωl的循环对称复高斯分布。因此,所有RRH组成的维数为N×M的预编码矩阵可以表示为
(2)
其中,![]() 和
和![]() 分别表示在BBU中形成的预编码矩阵和量化噪声矩阵
分别表示在BBU中形成的预编码矩阵和量化噪声矩阵![]() 表示维数为MVl×M的矩阵,其中
表示维数为MVl×M的矩阵,其中![]() 是维数为
是维数为![]() 的矩阵,且除了
的矩阵,且除了![]() 到
到![]() 列包含一个单位阵外其余元素全为0。也就是说,一旦
列包含一个单位阵外其余元素全为0。也就是说,一旦![]() 那么与第l个RRH和第k个用户相关的预编码项W(l,k)为0。
那么与第l个RRH和第k个用户相关的预编码项W(l,k)为0。
对于每个用户来说,除了有用信息外,将其他用户对其产生的干扰信号和噪声都视为干扰信息。因此,第k个用户可获得的速率表达式为:
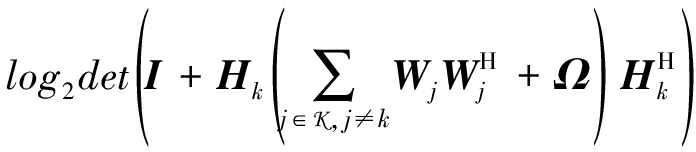
(3)
其中,W=[W1,…,WK],且Wk表示对应于第k个用户的维数为N×Mk的预编码矩阵,Ω=diag(Ω1,…,ΩL) 表示量化噪声矩阵。此外,根据速率失真理论[17],在第l个RRH上用来传送量化信号的速率可以计算为
(4)
其中,El表示维数为N×Nl的矩阵,且除了![]() 到
到![]() 行包含一个单位阵外其余元素全为0。
行包含一个单位阵外其余元素全为0。
3 问题描述
考虑DAS/C-RAN下行链路中的先压缩再预编码方案,即CBP策略,在RRH发送功率受限,前端链路容量受限和保证用户服务质量要求的条件下,最大化系统的能效。该问题可以表述为
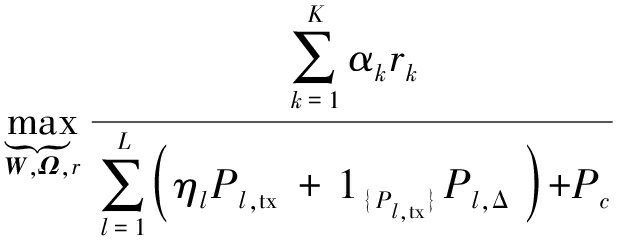
(5a)
(5b)
(5c)
(5d)
(5e)
其中,(5b),(5c)和(5d)分别表示前端容量限制,发送功率限制和用户特定速率限制。(5e)表明一旦第k个用户不在第l个RRH的服务用户簇中,相对应的预编码项设为0。rk表示第k个用户的速率,ηl≥1和αk≥0分别表示第l个RRH的功率放大器的倍数和第k个用户的优先权![]() 表示第l个RRH的发送功率。1{x}是指示函数,定义为
表示第l个RRH的发送功率。1{x}是指示函数,定义为
(6)
Pl,Δ=Pl,active-Pl,sleep和![]() 是两个常量,其中P0表示基本功率消耗,Pl,active和Pl,sleep分别表示第l个RRH处于活跃状态和睡眠状态所需的最小功率消耗。Cl,max,Pl,max和rk,min分别表示第l条前端链路的最大容量,第l个RRH的最大发送功率和第k个用户的最小目标速率。
是两个常量,其中P0表示基本功率消耗,Pl,active和Pl,sleep分别表示第l个RRH处于活跃状态和睡眠状态所需的最小功率消耗。Cl,max,Pl,max和rk,min分别表示第l条前端链路的最大容量,第l个RRH的最大发送功率和第k个用户的最小目标速率。
对于给定的用户速率,通常考虑的准则是最小化功率消耗[10],但是难以达到最优的系统能效。功率消耗最小化问题可以表示为
(7)
s.t. (5b),(5c),(5d),(5e)
同样的,另一个传统的准则是最大化加权和速率[6],该问题可以表示为
(8)
s.t. (5b),(5c),(5d),(5e)
我们主要考虑基于能效最大化准则下问题(5)的求解。然而,由于目标函数(5a)是分式形式,且功率消耗项中包含有指示函数,导致问题(5)非凸,无法直接求解,下面将针对上述问题设计有效的算法。
4 问题求解及算法设计
这一部分的主要目标是求解问题(5)。首先通过分式规划将目标函数转化为参数化减法形式,然后采用逐次凸近似方法将原始问题转化为可求解的形式,最后提出了一种能有效求解该近似问题的二层迭代优化算法。
问题(5)中的目标函数可视为一个非线性分式规划,根据分式规划和减式线性规划间的关系可得到有效化简[18]。通过引入辅助变量ρ,目标函数重写为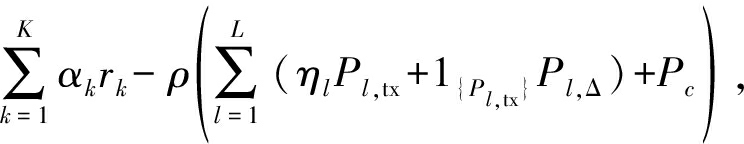 当存在ρ使得该式等于0时,这个ρ就是所求的最大能效。因此,对于固定的参数ρ,原始优化问题可以转换成以下形式:
当存在ρ使得该式等于0时,这个ρ就是所求的最大能效。因此,对于固定的参数ρ,原始优化问题可以转换成以下形式:
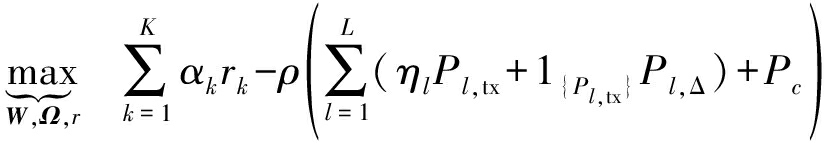
(9)
s.t. (5b),(5c),(5d),(5e)
接下来,我们将关注上述转换后的优化问题,并由此提出一种二层迭代算法以有效求解问题(5)。在每次外层迭代中,通过梯度优化算法更新参数ρ,在每次固定ρ的内层迭代中,求解问题(9)。
由于目标函数中的指示函数以及Cl(W,Ω)和Rk(W,Ω)表达式的非凸特性,问题(9)的求解仍然十分艰巨。因此退而求其次,采用逐次凸近似的方法获得问题(9)的次优解。首先,我们利用重加权‖·‖1范数得到指示函数的近似形式,即
(10)
其中, μl是引入的另一个辅助变量,通过下式进行逐次迭代更新:
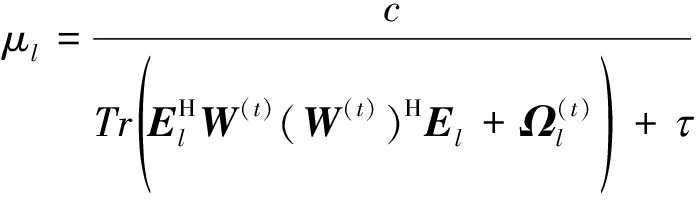
(11)
其中,W(t)和![]() 分别表示第t次迭代的预编码矩阵和对应于第l个RRH的量化噪声矩阵,τ和c是两个常量。这里我们选取c=1/ln(1+τ-1),且τ是一个趋于零的正实数,目的是为了保证算法1的收敛性[10]。但值得注意的是,式(11)中的重加权因子不唯一,若选取得当,指数函数和反三角函数同样可达到目的[19-20]。显然,若本次迭代时
分别表示第t次迭代的预编码矩阵和对应于第l个RRH的量化噪声矩阵,τ和c是两个常量。这里我们选取c=1/ln(1+τ-1),且τ是一个趋于零的正实数,目的是为了保证算法1的收敛性[10]。但值得注意的是,式(11)中的重加权因子不唯一,若选取得当,指数函数和反三角函数同样可达到目的[19-20]。显然,若本次迭代时 较小,则下次迭代时μl就会变大,从而进一步减小下一次迭代时的发送功率
较小,则下次迭代时μl就会变大,从而进一步减小下一次迭代时的发送功率![]() 也就是说, μl的作用是驱使RRH处于睡眠状态。
也就是说, μl的作用是驱使RRH处于睡眠状态。
针对(5b)和(5d)表达式的非凸特性,接下来我们将分别推导得到Cl(W,Ω)和Rk(W,Ω)的凸近似函数[21],并使得原问题变为一个凸问题。令![]() 此时Cl(W,Ω)和Rk(W,Ω)重新定义为
此时Cl(W,Ω)和Rk(W,Ω)重新定义为![]() 和
和![]()
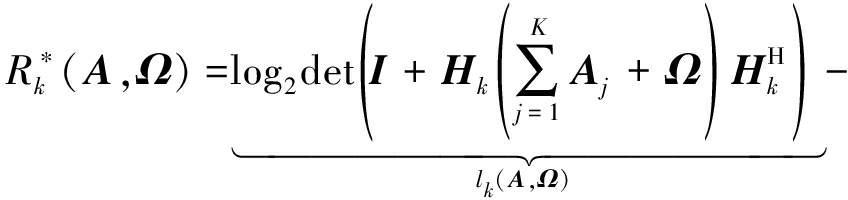
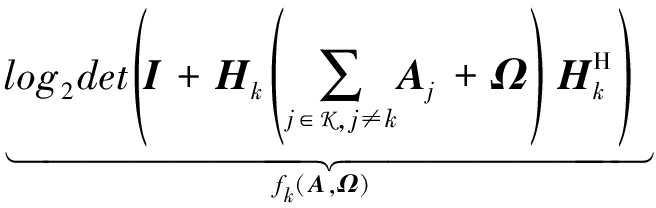
(12)
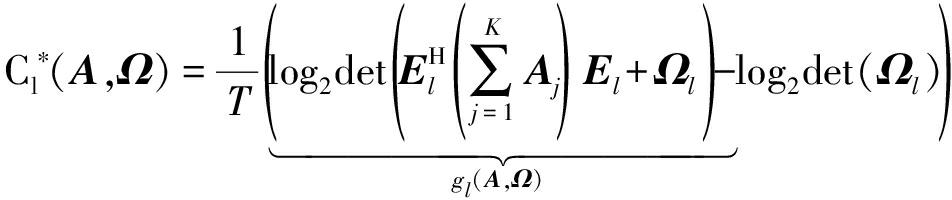
(13)
我们的目标是寻找![]() 的凹下界和
的凹下界和![]() 的凸上界。由于fk(A,Ω)和gl(A,Ω)均非凸,首先得到fk(A,Ω)和gl(A,Ω)这两者分别在点
的凸上界。由于fk(A,Ω)和gl(A,Ω)均非凸,首先得到fk(A,Ω)和gl(A,Ω)这两者分别在点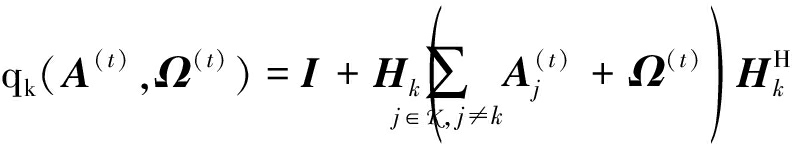 和点
和点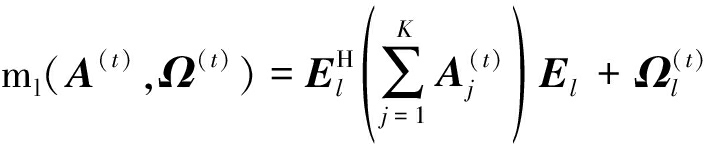 处的凸上界为:
处的凸上界为:
fk(A(t+1),Ω(t+1))≤fk(A(t),Ω(t))+Tr![]() (qk(A(t),Ω(t))-1 (qk(A(t+1),Ω(t+1))-qk(A(t),Ω(t)))
(qk(A(t),Ω(t))-1 (qk(A(t+1),Ω(t+1))-qk(A(t),Ω(t)))![]() =fk(A(t),Ω(t))-Bk+Tr
=fk(A(t),Ω(t))-Bk+Tr![]() (qk(A(t),Ω(t)))-1 qk(A(t+1),Ω(t+1))
(qk(A(t),Ω(t)))-1 qk(A(t+1),Ω(t+1))![]()
![]()
(14)
gl(A(t+1),Ω(t+1))≤gl(A(t),Ω(t))+Tr![]() (ml(A(t),Ω(t)))-1 (ml(A(t+1),Ω(t+1))-ml(A(t),Ω(t)))
(ml(A(t),Ω(t)))-1 (ml(A(t+1),Ω(t+1))-ml(A(t),Ω(t)))![]() =gl(A(t),Ω(t))-Nl+Tr
=gl(A(t),Ω(t))-Nl+Tr![]() (ml(A(t),Ω(t)))-1ml(A(t+1),Ω(t+1))
(ml(A(t),Ω(t)))-1ml(A(t+1),Ω(t+1))![]()

![]()
(15)
其中,A(t)和Ω(t)分别表示第t次迭代的预编码协方差矩阵和量化噪声矩阵,A(t+1)和Ω(t+1)分别表示第(t+1)次迭代的预编码协方差矩阵和量化噪声矩阵。经过(14)和(15)的变换,式(12)和(13)已经分别变成了我们想要的凹下界和凸上界形式。为了进一步减小优化过程中的复杂度,还可以将lk(A,Ω)进行线性凸近似,得到在点![]() 的凹下界为:
的凹下界为:
lk(A(t+1),Ω(t+1))≥Tr(Jkpk(A(t+1),Ω(t+1)))+
(16)
其中,Re{x}表示复数x的实部,![]()
完成上述函数的凸近似后,将式(10),(14),(15),(16)分别带入问题(9)中相应的部分,在固定参数ρ时,问题(9)可以转化为以下形式:
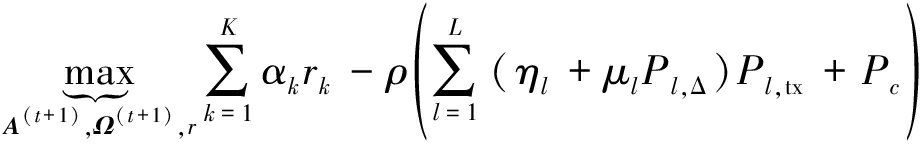
(17)
为方便起见,问题(17)中省去了对矩阵A(t+1)秩的限制,而优化问题最终要获得的是预编码矩阵W(t+1),这可通过随机技术由A(t+1)计算得到。假定矩阵![]() 的SVD分解形式为
的SVD分解形式为![]() 那么第k个用户的预编码矩阵可以表示为
那么第k个用户的预编码矩阵可以表示为![]() 其中Vk是一个维数为N×Mk的随机矩阵,且所有的元素满足均匀分布或高斯分布[22]。
其中Vk是一个维数为N×Mk的随机矩阵,且所有的元素满足均匀分布或高斯分布[22]。
利用内点法[23]很容易就能求解问题(17),内层迭代结束后,根据式(18)通过Dinkelbach算法更新参数ρ就能完成外层迭代[11,24],即
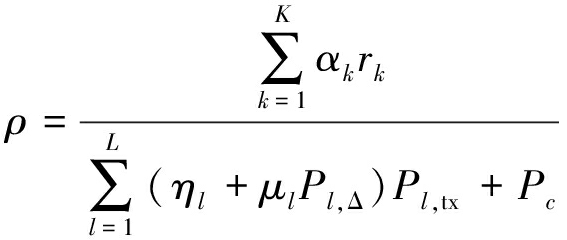
(18)
本文提出的求解问题(5)的能效设计算法可归纳为算法1,其中f(t)和f(t+1)分别表示式(17)在第t次迭代和在第(t+1)次迭代时的目标函数值。值得注意的是,文献[13]保证了给定参数ρ时式(17)这个内层迭代收敛,而分式规划和单调有界定理也保证了更新参数ρ的外层迭代收敛,因此算法1收敛[14]。
所提出的算法包含一个二层迭代,对于固定参数ρ,内层迭代可以利用内点算法进行优化求解[23],而对于外层迭代只需要通过式(18)更新参数ρ即可,因此算法1的复杂度主要在于步骤3中问题(17)的求解。该问题的复杂度是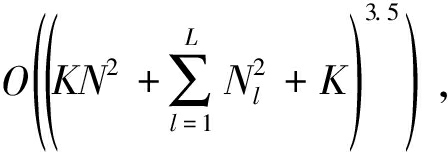 若算法1达到收敛所需的迭代次数为T1,则总的算法复杂度为
若算法1达到收敛所需的迭代次数为T1,则总的算法复杂度为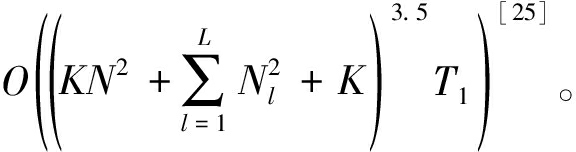

算法1 Max-EE优化算法1. 令t=0,f(t)=0,并设置初始矩阵{A(t)k}Kk=1和Ω(t)Z。2. 根据式(11)和(18),由A(t)和Ω(t)计算得到μ(t)和ρ(t)。3. 根据ρ(t),μ(t),A(t)和Ω(t),求解问题(17),得到相应的最优值A∗,Ω∗和r。4. 根据式(11),由A∗和Ω∗计算得到μ∗,并根据A∗,Ω∗和r计算得到f(t+1)。5. 若满足f(t+1)-f(t)<ξ,其中ξ是一个任意小的正实数,则更新A(t+1)=A∗,Ω(t+1)=Ω∗,μ(t+1)=μ∗,并转到步骤6;否则,更新A(t)=A∗,Ω(t)=Ω∗,μ(t)=μ∗,f(t)=f(t+1),并回到步骤3。6. 根据式(18),由A(t+1)和Ω(t+1)计算得到ρ(t+1)。7. 若满足ρ(t+1)-ρ(t)<ξ,输出最优的A(t+1)和Ω(t+1);否则,令t=t+1,并回到步骤3。
5 仿真结果
这一部分,我们针对C-RAN下行链路中的CBP策略,通过Matlab仿真分析了所提的Max-EE算法与已有Max-SR[6]和Min-P[10]算法的性能。考虑一个由L=4个RRH和K=4个单天线用户组成的C-RAN网络,每个RRH安装有Nl=2根天线,并假定所有的RRH和用户都随机分布在边长为1000 m的正方形区域内,如图2所示。从第l个RRH到第k个用户的信道Hk,l由下面的方程生成:
(19)
其中,Gk,l表示小尺度衰落系数,并服从均值为0和方差为1的高斯分布。θk,l表示大尺度衰落系数,表达式为10lg(θk,l)=-38lg(dk,l)-34.5+ςk,l,其中dk,l表示从第l个RRH到第k个用户的距离,ςk,l表示均值为0和标准偏差为8 dB的对数正态阴影衰落,噪声为-100 dBm/Hz。所有的RRH和前端链路分别具有相同的最大发送功率Pl,max=P和最大容量Cl,max=C。每个RRH处于活跃状态和睡眠状态所需要消耗的最小功率分别为Pl,active=10.6 W和Pl,sleep=5 W,基本功率消耗为P0=20 W。功率放大器倍数,加权因子,常数τ和c分别设置为ηl=2.8,αk=1,τ=10-5和c=1/ln(1+τ-1)[10]。由于CBP策略的RRH可以根据一定的调度准则进行用户调度,这里假设距离每个RRH最近的Nc个用户作为其需要服务的用户簇。
图2 RRHs和用户随机分布在正方形区域中的C-RAN网络
Fig.2 The architecture of the C-RAN with RRHs and users randomly distributed in a square area
图3说明了在几次随机信道实现下算法1的收敛情况,随机信道的产生依赖于式(19)。由图可见,算法1的能效随着迭代次数产生了一个非递减的序列,且在有限次迭代后收敛到一个稳定值,验证了所提算法的收敛性。
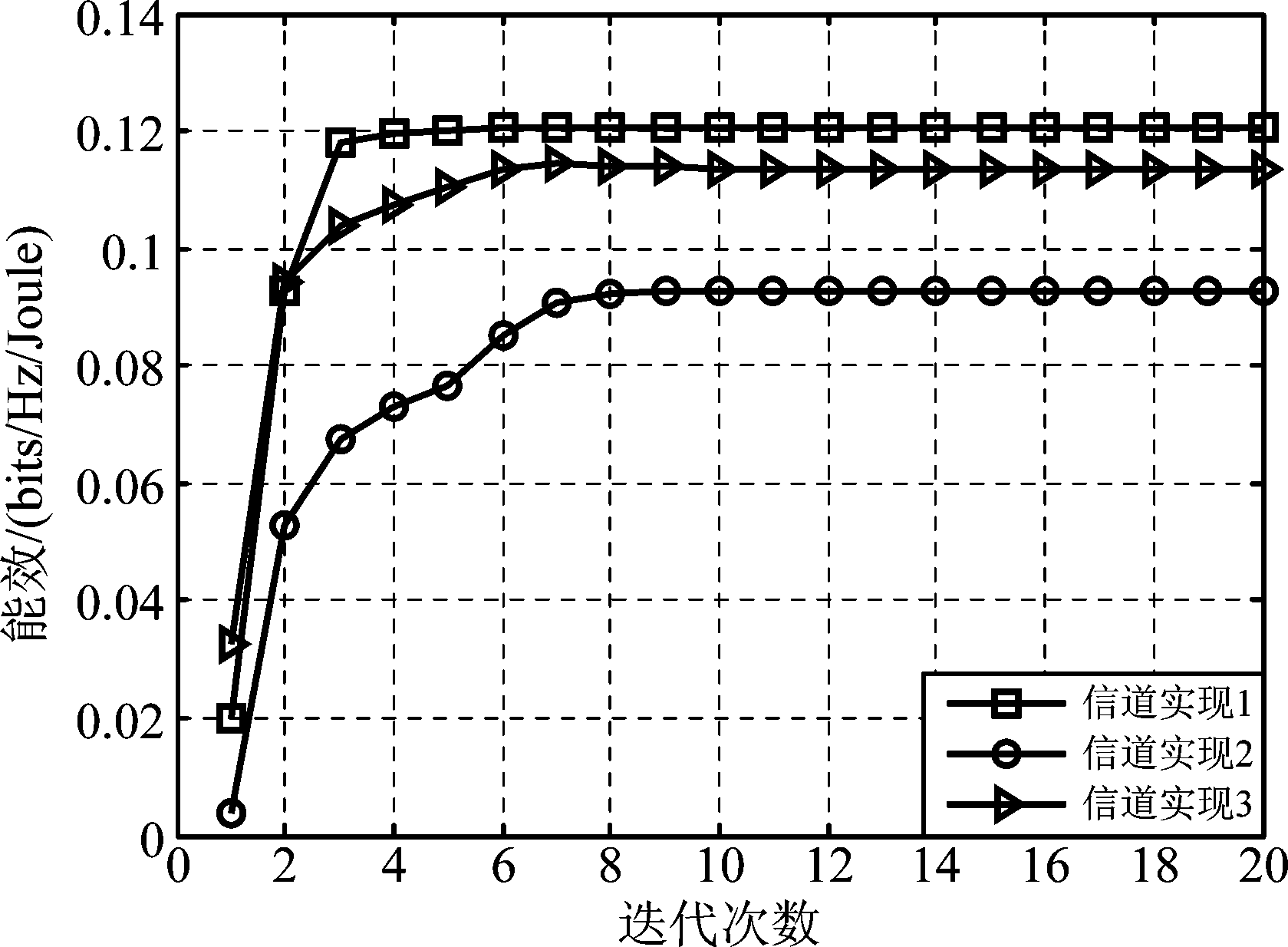
图3 算法1迭代性能,Nc=2,C=5 bits/s/Hz,P=8 dB, T=10
Fig.3 The iterative performance of Algorithm 1 with Nc=2,C=5 bits/s/Hz,P=8 dB, T=10
图4在不同的RRH功率限制下,分析了在Max-EE、Max-SR和Min-P这三种准则下CBP策略的能效性能。数值仿真结果表明,对于本文所提的Max-EE算法,在低功率区域内,能效逐渐增大,然而在中高功率区域,能效趋于稳定。对于Max-SR准则,为实现和速率最大化,需要消耗几乎全部的发送功率,且用户速率的提高使得约束条件5(b)中用来传送预编码矩阵的容量减小,因此能效随着功率呈现减小的趋势。而对于Min-P准则,能效始终保持平稳。
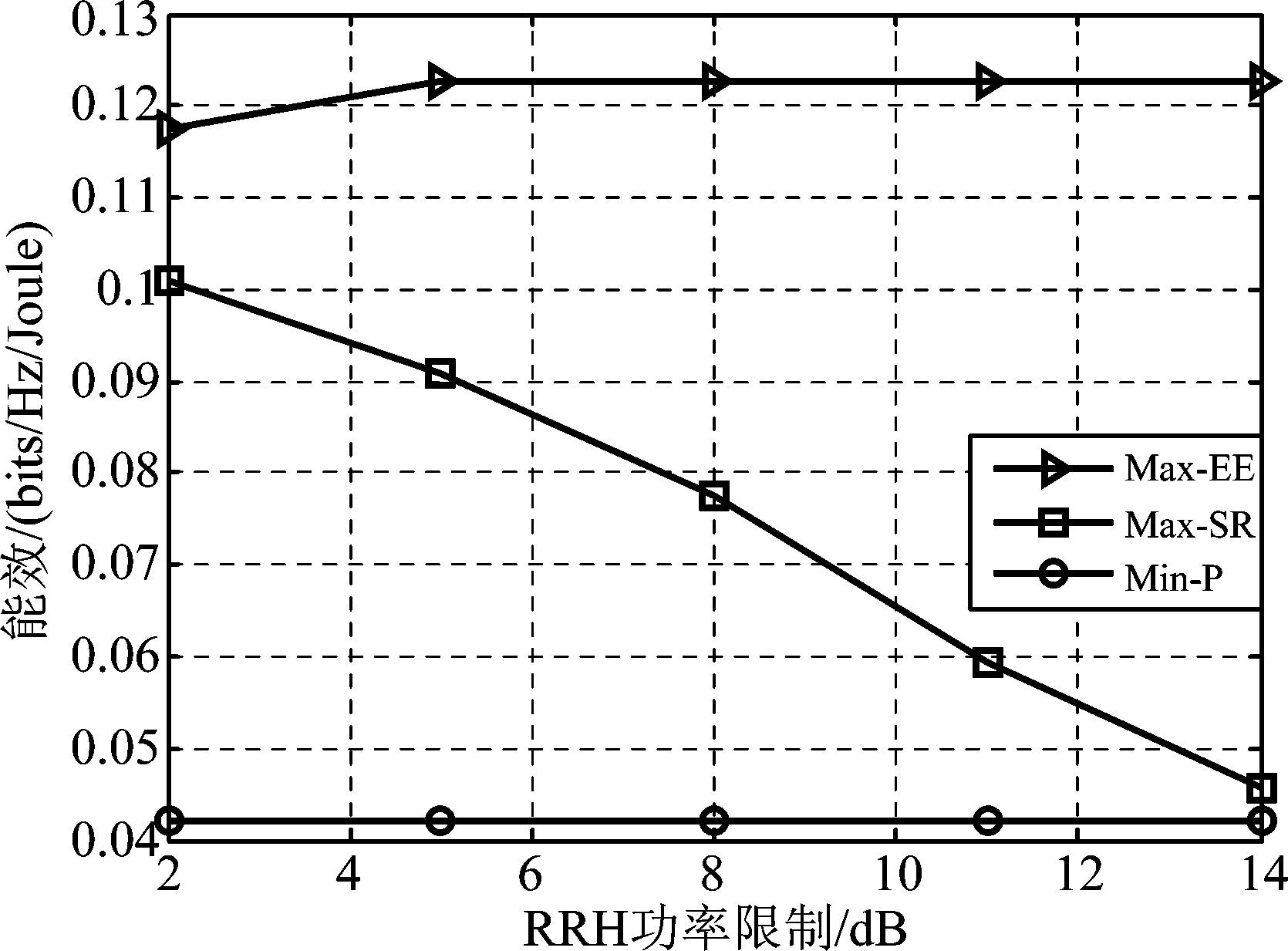
图4 CBP策略的能效性能,Nc=2,C=5 bits/s/Hz,T=10
Fig.4 The energy efficiency of CBP strategy with Nc=2,C=5 bits/s/Hz,T=10
图5在不同的前端容量限制下,比较了基于三种准则下CBP策略的能效性能。仿真分析表明,在低前端容量区域能效逐渐增加,然而在中高前端容量区域能效保持恒定值不变。这是由于在低容量限制区域,容量的增加放宽了约束条件5(b)的影响,但是中高容量限制区域,此时RRH消耗了所有的发送功率给用户传送预编码信号,因此容量限制条件作用不大。
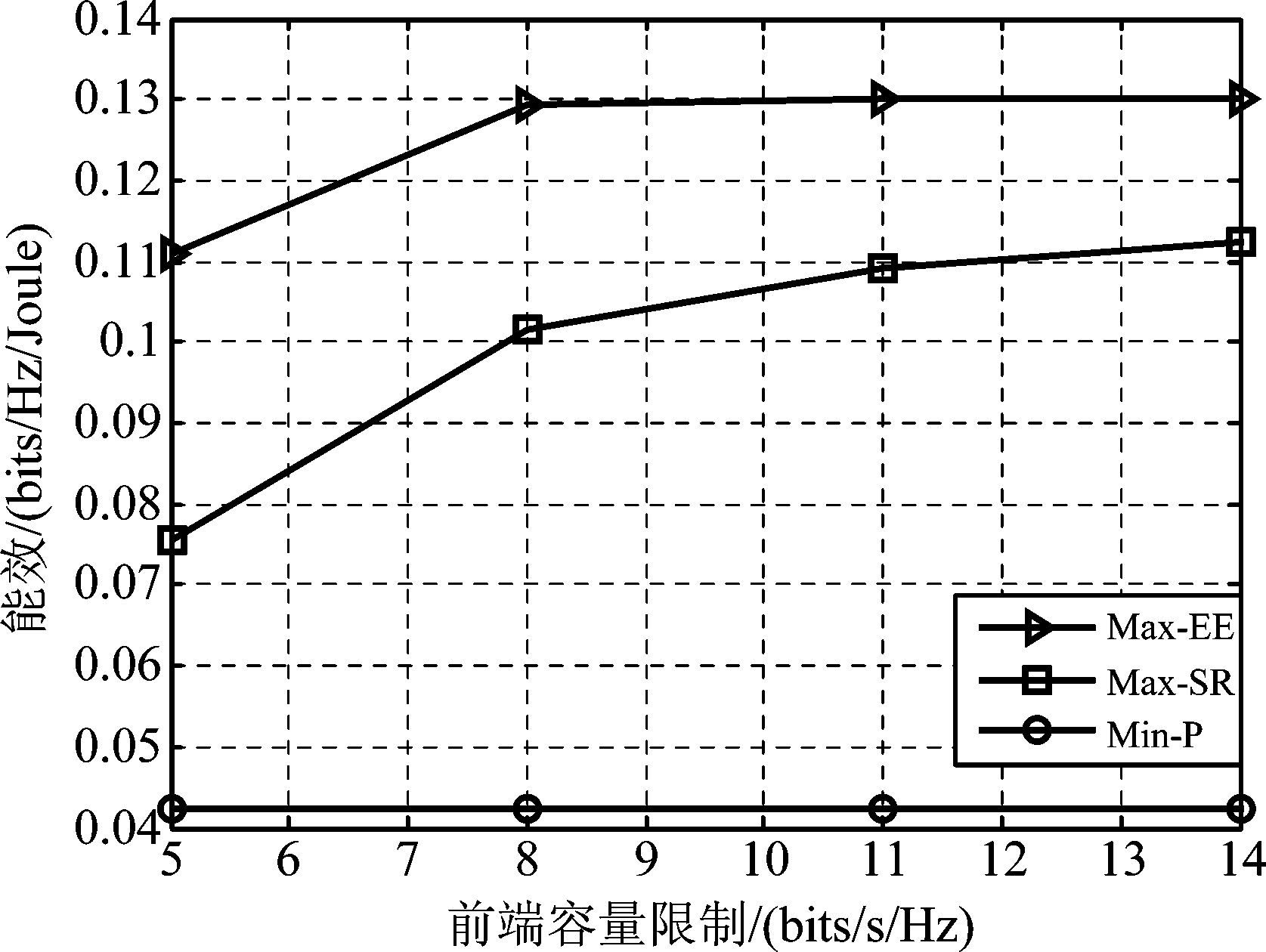
图5 CBP策略的能效性能,Nc=2,P=8 dB,T=10
Fig.5 The energy efficiency of CBP strategy with Nc=2,P=8 dB,T=10
图6说明了在本文所提的Max-EE准则下,信道相干周期和RRH进行调度的用户数对CBP策略能效性能的影响。可以看到能效随着相干周期T的增大而逐渐增大,这是由于对CBP策略而言,在同一个信道相干周期中预编码矩阵只需要传送一次,在减小能量损耗的同时增大了系统能效。且当RRH调度的用户数较少时,能效性能也有大幅提升,这是因为较小的调度用户数,减弱了对应于每个RRH的链路容量开销,从而增大了系统能效。
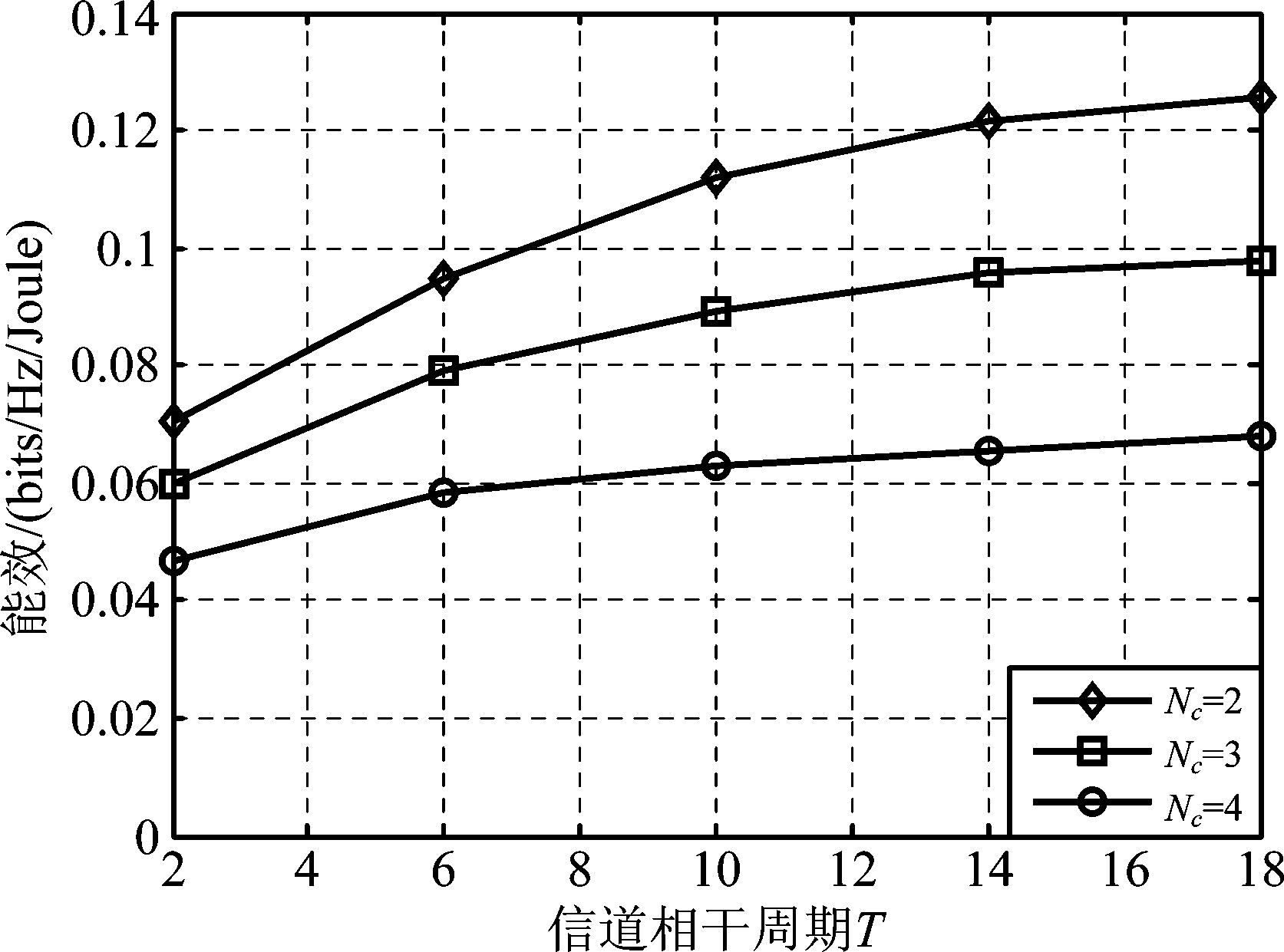
图6 CBP策略的能效性能,C=5 bits/s/Hz,P=8 dB
Fig.6 The energy efficiency of CBP strategy with C=5 bits/s/Hz,P=8 dB
6 结论
本文研究了集中式处理下行链路系统中CBP策略的能效设计。为求解该非凸问题,首先利用分式规划和逐次凸近似的方法,将原始问题转化为凸优化问题,然后提出了一种有效的二层迭代优化算法。大量的Matlab数值仿真结果表明,从能效的角度,所提的Max-EE算法优于传统的Max-SR和Min-P算法。当CBP策略的RRH进行调度的用户数较少时,能效性能较好。
参考文献
[1] Andrews J G, Buzzi S, Wan C, et al. What will 5G be?[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1065-1082.
[2] Shi Y, Zhang J, Letaief K B, et al. Group sparse beamforming for green cloud-RAN[J]. IEEE Transactions on Wireless Communications, 2014, 13(5): 2809-2823.
[3] Rao X, Lau V K N. Distributed fronthaul compression and joint signal recovery in cloud-RAN[J]. IEEE Transactions on Signal Processing, 2015, 63(4): 1056-1065.
[4] Samardzija D, Pastalan J, MacDonald M, et al. Compressed transport of baseband signals in radio access networks[J]. IEEE Transactions on Wireless Communications, 2012, 11(9): 3216-3225.
[5] Zhou Y, Yu W. Optimized backhaul compression for uplink cloud radio access network[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1295-1307.
[6] Kang J, Simeone O, Shamai S, et al. Fronthaul compression and precoding design for C-RANs over ergodic fading channels[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5022-5032.
[7] Chae C B, Bahk S. Before/after precoded massive MIMO in cloud radio access networks[C]∥IEEE International Conference on Communications Workshops, Budapest, Hungary, 2016: 169-173.
[8] Park S H, Simeone O, Sahin O, et al. Joint precoding and multivariate backhaul compression for the downlink of cloud radio access networks[J]. IEEE Transactions on Wireless Communications, 2013, 61(22): 5646-5658.
[9] Dhifallah O, Dahrouj H, Al-Naffouri T Y, et al. Joint hybrid backhaul and access links design in cloud radio access networks[C]∥IEEE 82nd Vehicular Technology Conference, Boston, MA, USA, 2015: 1-5.
[10] Dai B, Yu W. Energy efficiency of downlink transmission strategies for cloud radio access networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 1037-1050.
[11] Dinkelbach W. On nonlinear fractional programming[J]. Management Science, 1967, 13(7): 492-498.
[12] He S, Huang Y, Yang L, et al. Coordinated multicell multiuser precoding for maximizing weighted sum energy efficiency[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 741-751.
[13] He S, Huang Y, Jin S, et al. Coordinated beamforming energy efficient transmission in multicell multiuser systems[J]. IEEE Transactions on Communications, 2013, 61(12): 4961-4971.
[14] Wang J, Feng W, Chen Y, et al. Energy efficient power allocation for multicell distributed antenna systems[J]. IEEE Communications Letters, 2016, 20(1): 177-180.
[15] Li Y, Fan P, Beaulieu N C, et al. Cooperative downlink max-min energy-efficient precoding for multicell MIMO networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(11): 9425-9430.
[16] Nguyen K G, Tran L N, Vu Q D, et al. Distributed energy efficiency fairness optimization by ADMM in multicell MISO downlink[C]∥IEEE International Conference on Communications, Kuala Lumpur, Malaysia, 2016: 1- 6.
[17] Gamal A E, Kim Y -H. Network Information Theory[M]. Cambridge University Press, 2011.
[18] He S, Huang Y, Jin S, et al. Energy efficient coordinated beamforming design in multicell multicast networks[J]. IEEE Communications Letters, 2015, 19(6): 985-988.
[19] Candes E J, Wakin M B, Boyd S P, et al. Enhancing sparsity by reweighted  1-minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877-905.
1-minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877-905.
[20] Zhou H, Tao M, Chen E, et al. Content-centric multicast beamforming in cache-enabled cloud radio access networks[C]∥IEEE Global Communications Conference, San Diego, CA, USA, 2015: 1- 6.
[21] Rubio J, Pascual-Iserte A, Palomar D P, et al. Joint optimization of power and data transfer in multiuser MIMO systems[J]. IEEE Transactions on Signal Processing, 2017, 65(1): 212-227.
[22] Yu H, Lau V K N. Rank-constrained schur-convex optimization with multiple trace/logdet constraints[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 304-314.
[23] Boyd S, Vandenberghe L. Convex Optimization[M]. Cambridge University Press, 2004.
[24] Schaible S. Fractional programming. ii, on dinkelbach’s algorithm[J]. Management Science, 1976, 22(8): 868- 873.
[25] Zhou Y, Yu W. Fronthaul compression and transmit beamforming optimization for multi-antenna uplink C-RAN[J]. IEEE Transactions on Signal Processing, 2017, 64(16): 4138- 4151.



