1 引言
随着数码相机的普及使得近景影像的获取十分便捷,因此,基于近景影像的三维重建也成为摄影测量和计算机视觉领域研究的热门话题,其中关键核心问题即影像匹配[1-3]。现有点匹配算法,如SIFT[4]、ASIFT[5]、SURF[6]等算法已经非常成熟,可获取可靠的同名点。但这些方法得到的结果往往是稀疏的匹配点集,难以胜任高精细三维建模的需求,故基于影像的密集匹配变得十分必要的。目前常用的方法是基于静态区域约束的密集匹配。该类方法将影像划分成多个独立区域并结合多种约束条件完成匹配。文献[7- 8]利用N个种子点和Voronoi方法将图像划分成N个区域,利用SSD等约束完成区域内像素点的匹配、文献[9-10]利用稀疏匹配结果进行Delaunay三角网的构建,在同名三角网的区域里进行匹配、文献[11]利用Markov网络作为区域约束引导匹配传播,用贝叶斯置信度传播算法完成网格中逐像素的匹配。该类方法约束区域大小是固定的,不能随着匹配点的增加而动态更新约束范围,不能有效利用过程数据,约束较为固定。另一种是渐进传播约束的密集匹配,常用的渐进三角网传播策略,文献[12]提出一种自适应三角形约束的影像可靠匹配方法,与上述固定区域约束相比,该方法提出了一种动态更新三角形的匹配传播策略,将匹配过程中产生新的同名点不断插入到初始三角网中,时时更新优化三角形用于进一步约束后续点匹配。但该方法利用三角网内已有的特征点进行匹配,本质上仍属于稀疏匹配范畴,且时时更新三角网算法较为复杂,计算量大。文献[13]提出一种近景影像三角网内插点密集匹配方法,该方法认为理想状态下,同名三角形的重心即为同名点,后续再经过彩色信息相似性约束和极线约束进行筛选。该方法对于视差变化小的近景影像,或者视频序列影像效果较为理想,对于视差变化较大的近景影像难以适用。针对上述问题,本文提出一种简单有效的迭代三角网约束的近景影像密集匹配算法。该方法以初始同名点构建的Delaunay三角网作为匹配基础,以左影像三角形重心作为匹配基元,综合多重约束确定右影像上的同名点。迭代过程中整体构网,以三角形面积为间接约束,以是否有新的同名点产生为直接约束作为迭代停止的条件,取得较好的密集匹配结果。
2 算法原理
本文首先利用SIFT算法对左、右影像进行匹配,并采用RANSAC方法对匹配结果进行错误剔除,得到初始同名点。利用初始同名点构建左、右影像上同名Delaunay三角网,通过目视检测同名三角网的一致性进一步剔除误匹配点,确保初始同名三角网的正确性;然后依次以左影像上三角形重心作为匹配基元加密匹配,匹配过程中综合利用同名三角形区域约束、核线约束确定右影像匹配候选点集,利用灰度相关约束确定最终同名点;对于上述过程未匹配到同名点的重心点,在确定同名三角形相似度的条件下,通过仿射变换和重心约束确定同名点;最后结合已有同名点及新匹配得到的同名点,整体构建Delaunay三角网,迭代匹配,直到新构建的三角网内所有三角形面积都小于一定阈值为止,迭代停止。
2.1 左、右影像上同名三角网的构建
利用初始同名点构建左、右影像上同名三角网是本文算法加密匹配的基础。利用初始稀疏点建立的三角网中的三角形要尽量达到角度和边长接近正三角形,理论证明,Delaunay三角网是有限点集中的、且唯一存在的局部等角三角网。因此本文选择Delaunay三角网作为初始网型。在以三角网作为区域约束的匹配传播中,应确保左、右影像上同名三角网的关系是一一对应的,即两张影像上同名三角网内同名三角形的顺序要一致,同名三角形的顶点对应关系要一致。本文以左影像作为基准,对左影像上的初始同名点严格按照Delaunay准则构建初始三角网,依次得到每个三角形的顶点索引。对应右影像上,则根据左影像上三角形的顶点索引及其对应的右影像上的同名点直接构建对应的同名三角网。
2.2 同名三角形约束下的重心点匹配
2.2.1 匹配基础
研究以同名三角形作为匹配基础,以三角形重心点作为密集匹配基元,匹配过程中涉及三角形重心、面积、以及三角形相似性等基本理论,因此,首先对上述基础理论进行简单介绍。
(1)三角形重心
三角形的重心点是三条边中线的交点,其点位必然在三角形内。假定某一三角形顶点坐标分别为A(xA,yA)、B(xB,yB)、C(xC,yC),其重心点P坐标为:
![]()
(1)
(2)三角形面积
三角形面积S可利用海伦公式求得:
(2)
其中l=(l1+l2+l3)/3,l1、l2、l3分别为三角形三边的边长。
(3)三角形相似性
定义左影像中的某一三角形的特征向量为Tri=[l1,l2,l3,cos(θ),A,B,C],其中三角形三边边长满足l1≤l2≤l3关系,cos(θ)为三角形最大角的余弦值[14]。A,B,C,为三角形三个顶点坐标。对应的右影像上同名三角形特征向量为![]() 则两三角形的相似性计算公式如下[15]:
则两三角形的相似性计算公式如下[15]:
![]()
(3)
当T△=1时,认为两三角形完全相似。
2.2.2 多重条件约束下重心点匹配
对左影像上任一三角形的重心点P,如图1(a)所示,将其作为匹配基元进行匹配,确定其在右影像上的同名点的具体过程如下:
假定理想状态下,根据同名点一定位于同名三角形内的原理,首先将候选点搜索范围定位于右影像上对应的同名三角形内。
然后根据同名点必定位于同名核线上这一原理,根据文献[16]中基于共面条件的核线求解方法计算左影像重心点P在右影像上的核线,进一步将候选点的搜索范围限定到同名三角形内的同名核线上,如图1(b)所示,减小了搜索范围,提高了算法的运行效率。
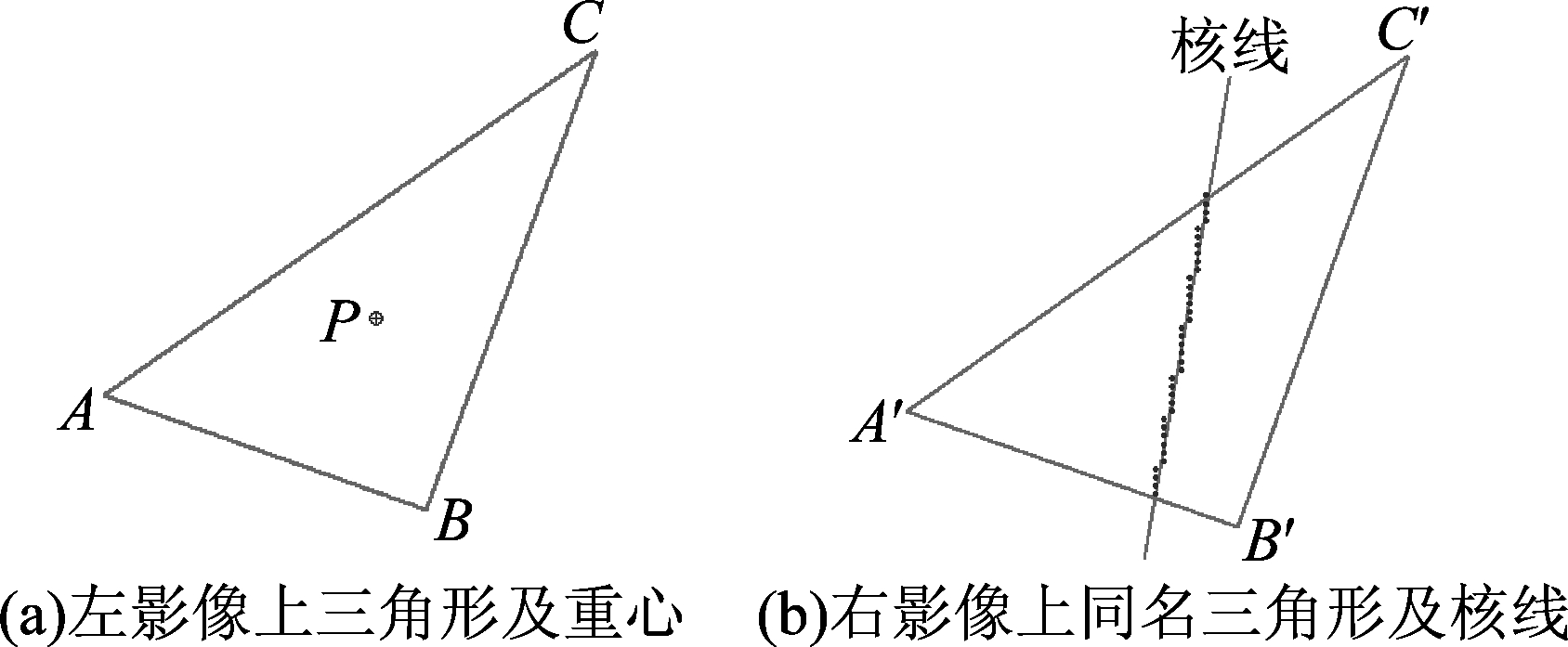
图1 同名三角形和核线约束匹配候选点
Fig.1 Matching candidates by triangle and epipolar constraints
依次遍历同名三角形内同名核线段上的候选点,利用灰度相似性约束确定最终的同名点;该过程根据公式(4)分别计算左影像上重心点P与右影像上所有候选之间的灰度相关系数ρ[17],选取相关系数最大且大于一定阈值Tρ的候选点作为P点的同名点。实验过程中相关系数阈值Tρ=0.75。
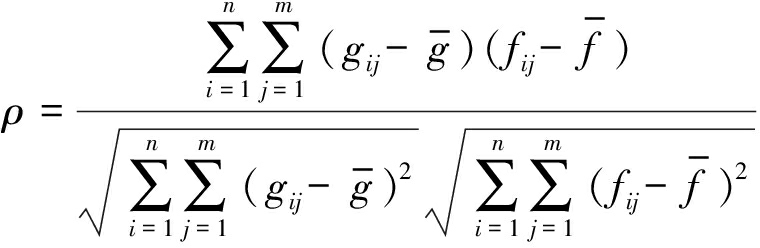
(4)
式中gij、 fij分别表示左、右影像上以重心点P和搜索范围内单个像素为中心建立的相关窗口内第i行第j列像素的灰度值,相关窗口大小为n×m,本文设置为![]() 和
和![]() 分别为相关窗口内所有像素灰度平均值。
分别为相关窗口内所有像素灰度平均值。
2.3 迭代三角网约束密集匹配
2.3.1 具体步骤
迭代三角网约束密集匹配算法实现整体流程如图2所示,具体步骤如下:
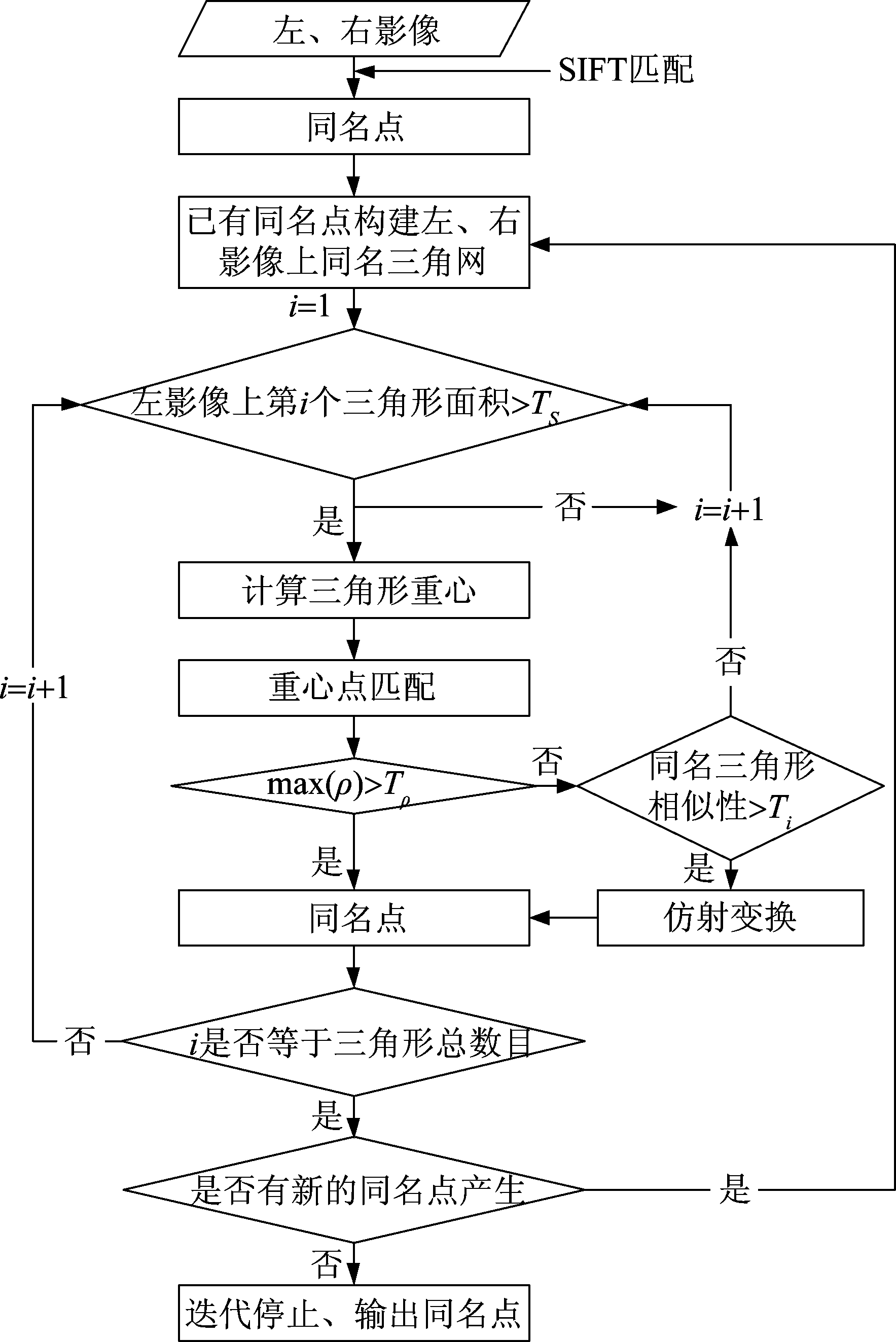
图2 迭代三角网密集匹配流程图
Fig.2 Flowchart of dense matching by iterative triangle network
步骤1 利用已有同名点构建同名Delaunay三角网。
步骤2 依次遍历左影像上三角网中所有三角形,对每一个三角形按照步骤3进行处理,然后转到步骤5。
步骤3 判断三角形面积是否大于给定的阈值TS?如果大于,计算三角形重心并按照2.2.2所述原理对其进行匹配,得到新的匹配点。对于相关系数不满足阈值未匹配到同名点的重心点,进行步骤4。
步骤4 判断左、右影像上同名三角形的相似性,如果相似性大于一定阈值Ti,首先根据左、右影像上同名三角形对应的三个顶点坐标和六参数仿射变换公式(5)计算仿射变换参数[18]:
x′=a0+a1x+a2y
y′=b0+b1x+b2y
(5)
其中,a0、a1、a2、b0、b1、b2表示仿射变换的六参数,x和y表示左影像上三角形顶点坐标,x′和y′表示右影像上同名三角形对应的顶点坐标。然后根据求得的参数和公式(5),将左影像上的重心点映射至右影像上,将其作为左影像上三角形重心点的同名点。
步骤5 判断是否有新增的匹配点?是,转到步骤1;否,则停止迭代。图3分别为局部影像的初始三角网、迭代两次之后的中间三角网、以及最终的三角网,从中可以看出三角网逐步加密的效果。
2.3.2 迭代停止条件
本文同时选取三角形面积和同名点数目作为迭代停止条件。条件一:理想状态下,三角网中每个三角形面积都小于阈值,迭代停止;条件二:在实际匹配过程中,如果存在任一三角形重心点未匹配成功,会导致该三角形的面积永远大于阈值,条件一约束失败,会反复循环迭代匹配。因此匹配过程中,在三角形面积约束迭代的基础上,同时增加了同名点数目作为迭代停止条件,通过判断当前匹配是否有新的同名点增加作为迭代终止条件。满足上述任一条件,停止迭代。且条件一满足,条件二同时满足,反之条件二满足,条件一未必满足。假定K为新增同名点数目,初始值为1,具体程序实现如下:
⑴ K=1;
⑵ while K
⑶ if三角网内每个三角形面积<TS
⑷ K=0;迭代停止;
⑸ else
⑹ 大于面积阈值的三角形重心依次进行匹配;
⑺ if有新匹配点产生
⑻ K=1;继续迭代;
⑼ else
(10) K=0;停止迭代;
(11) end
(12) end
(13) end
3 实验结果及分析
3.1 本文算法密集匹配结果
实验在3.30GHz Intel Core i5- 4590 CPU、4G内存的电脑上进行,采用MATLAB2016a平台完成算法实现。实验影像来自网上公开的影像库数据,从中选取三组不同类型的近景影像对作为实验数据,分别如图4(a)、图4(b)、图4(c)所示。三组影像大小分别为680像素×850像素、600像素×800像素和512像素×768像素。其中,图4(a)所示立体像对

图3 三角网约束匹配传播
Fig.3 Matching propagation by Delaunay
之间存在较大的旋转变化,且纹理较丰富;图4(b)所示建筑物立体像对存在一定的尺度变化,且纹理较为单一;图4(c)所示立体像对存在视角变化,影像上存在重复纹理。本文首先采用SIFT匹配算法对图4所示三组影像对进行匹配实验,并采用RANSAC方法对匹配结果进行检核,剔除错误的匹配,得到初始可靠的同名点。然后利用初始可靠同名点构建Delaunay三角网,得到左、右影像上初始同名三角网,作为后续密集匹配的基础。三组影像初始同名三角网构建分别如图5(a)、图5(b)、图5(c)所示。从中可以看出,初始三角网基本覆盖立体像对重叠区域或基本覆盖建筑物主体部分。但由于初始同名点数目较少,初始三角网较为稀疏,且形状不规则,存在部分狭长三角形。通过本文迭代三角网约束加密匹配后,得到最终同名三角网分别如图6(a)、图6(b)、图6(c)所示,对应的同名点分别如图7(a)、图7(b)、图7(c)所示,鉴于文章篇幅,仅对TS=50的结果图进行显示。从中可以看出,经过本文算法密集匹配后,初始三角网得到了加密,优化,且同名点均匀分布。

图4 原始实验影像
Fig.4 Original stereo image pairs

图5 初始三角网
Fig.5 Initial Delaunay TIN

图6 TS=50密集匹配后生成的三角网
Fig.6 Final Delaunay TIN of dense matching by TS=50


图7 TS=50密集匹配得到的同名点
Fig.7 Final corresponding points of dense matching by TS=50
图8为面积阈值TS分别取50、40、30、20条件下三组实验影像密集匹配结果统计图,分别从同名点数目、三角网数目、迭代循环次数、运行时间四个方面进行统计。从中可以看出,①相比较初始SIFT匹配结果,密集匹配后同名点及三角网数目大幅度增多;②对于每组实验影像,随着面积阈值的减小,同名点数目、三角网数目、运行时间逐次递增,其中图4(a)同名点数目增加幅度最大,TS=20时同名点数目从初始1614增加到23575,提高了13倍,大大提高了匹配点的数量;③随着面积阈值的递减,初始循环次数无规律可言,这是由于本文算法迭代过程中对同名点整体构网,部分三角形具备不固定性,而当迭代次数开始递增时,说明网型开始趋于规整;④运行时间上,图4(b)影像所用时间最少,图4(a)影像所用时间最长,这与影像大小、同名点的数目与迭代的次数均相关,整体可以看出,本文算法具有较高的运算效率。
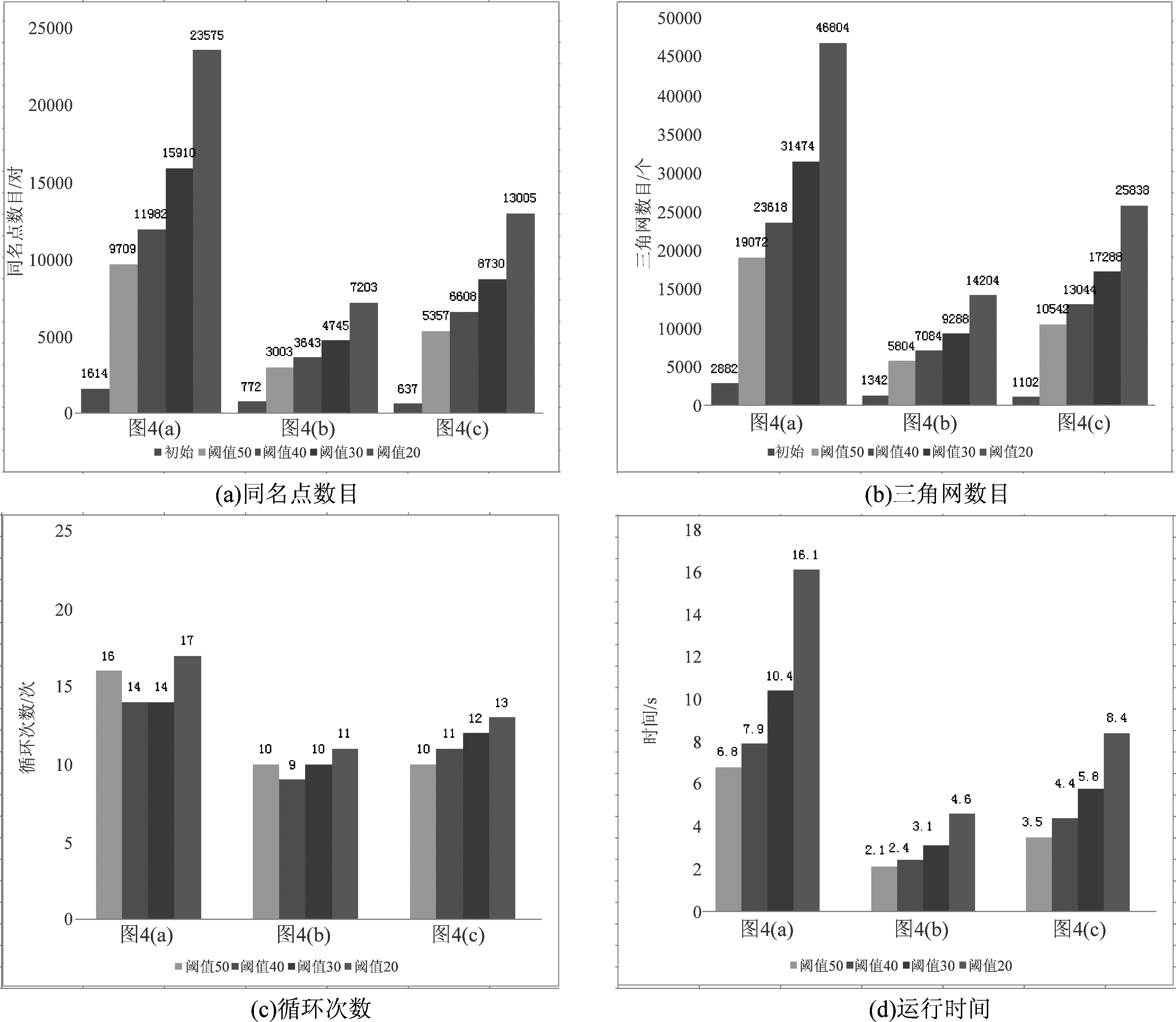
图8 不同面积阈值条件下密集匹配结果统计
Fig.8 Statistics of the result of dense matching by different threshold values
图9为不同面积阈值条件下三组实验影像匹配正确率统计图,实验过程中结合RANSAC方法与目视判断对匹配结果进行错误判读。从中可以看出,图4(a)影像匹配正确率高于图4(b)、图4(c)影像,这主要是由于后两组影像存在尺度变化、纹理单一且重复等问题。此外,随着面积阈值的减小,匹配的正确率随之降低,原因在于本文算法利用三角网作为匹配传播和区域约束的载体,因此随着面积阈值的减小,迭代次数的增加,产生的错误传播及累积现象。后续可以通过对上一次匹配结果进行错误剔除再进行下一次迭代匹配,减少错误传播,提高匹配正确率。
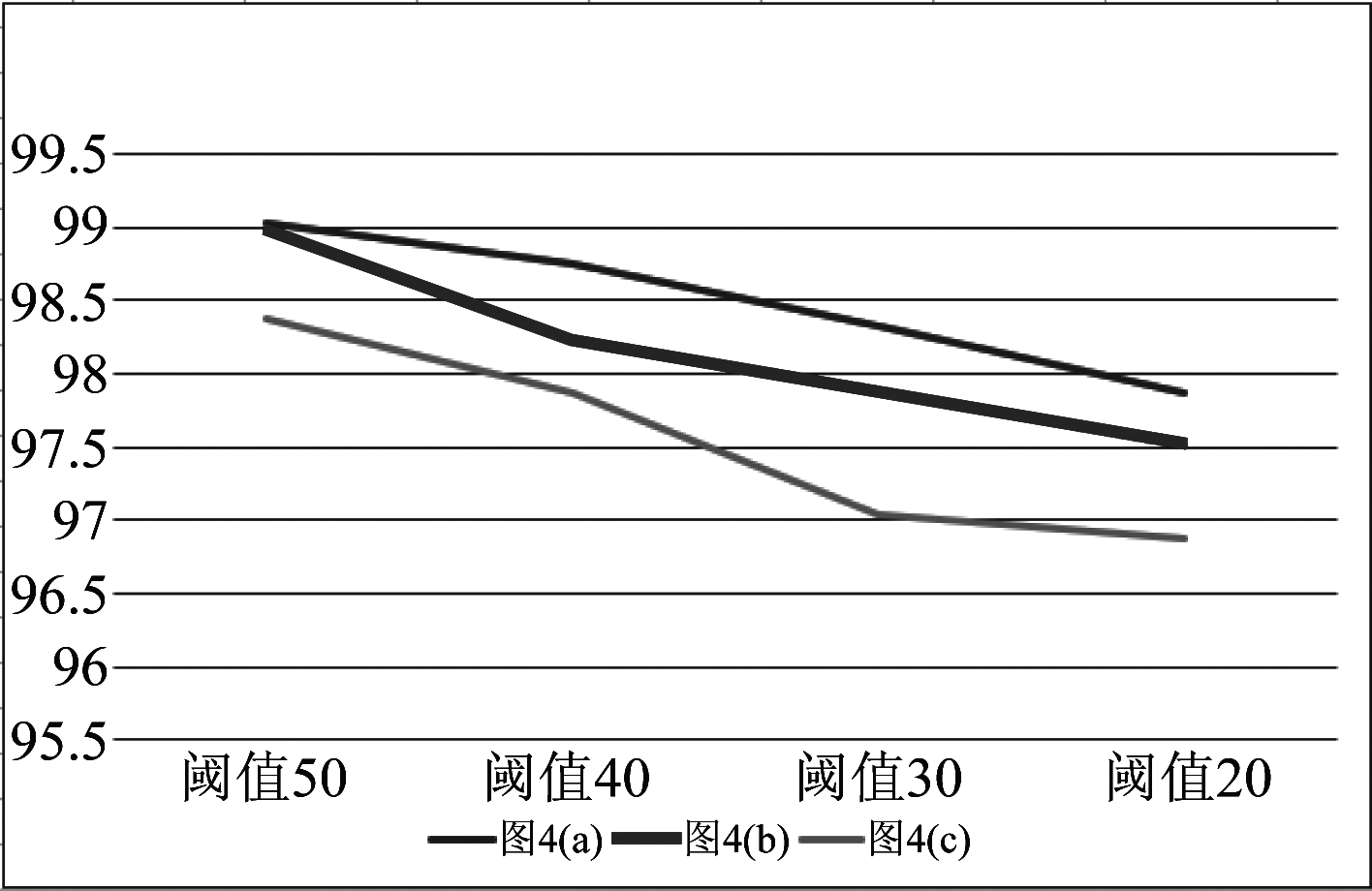
图9 不同面积阈值条件下密集匹配正确率
Fig.9 The accuracy of dense matching by different threshold values
综上所述,本文算法对存在旋转、尺度变化、视角变化、重复纹理的近景影像,都能取得可靠的密集匹配结果,具有较好的适应性。较传统的稀疏匹配,密集匹配结果能更好地反映近景影像场景的细节信息,可为后续基于影像的高精度三维建模提供较好的基础数据。
3.2 不同算法对比分析
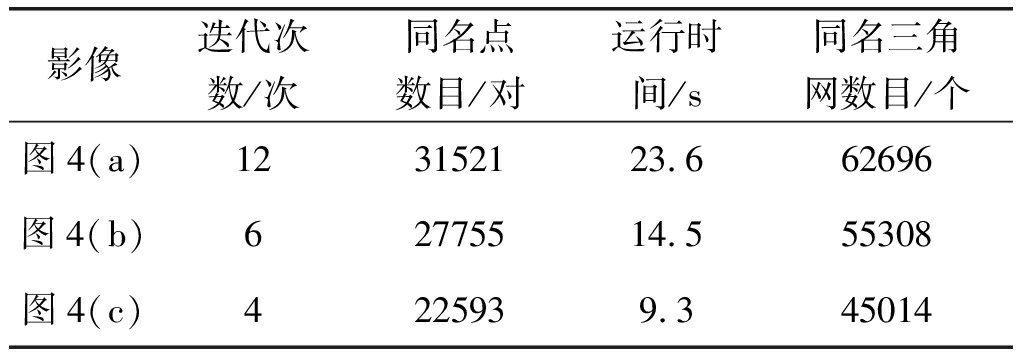
为了进一步验证本文算法的有效性,本文还实现了文献[13]中的密集匹配方法。文献[13]同样采用三角网内插点渐进匹配方法,与本文算法不同的是,该算法假定左、右影像上同名三角形的重心点即为同名点,在此基础上,通过多波段灰度相关和极限约束进行验证,剔除非同名点。实验过程中涉及与本文相同的数据或参数,如初始同名点、相关窗口大小、相关系数阈值等设置均与本文相同。针对图4中三组实验影像,文献[13]密集匹配结果统计如表1所示。根据同名点数目及后续运行速度,匹配过程中人工设置迭代次数,在迭代次数少于本文算法的情况下,运行时间、同名点数目及其对应三角网的数目均多于本文算法。但是从图10密集匹配得到的同名三角网来看,部分同名点簇团状分布,均匀性差,这是由于一些面积较大的同名三角形重心未满足约束条件,匹配失败,而面积较小的三角网则不断的渐进匹配。进而可以验证本文算法增加虚拟同名点的必要性及结合面积和同名点作为约束迭代终止条件的优越性。
表1 文献[13]密集匹配结果统计
Tab.1 The statistical results of dense matching in reference[13]
影像迭代次数/次同名点数目/对运行时间/s同名三角网数目/个图4(a)123152123.662696图4(b)62775514.555308图4(c)4225939.345014
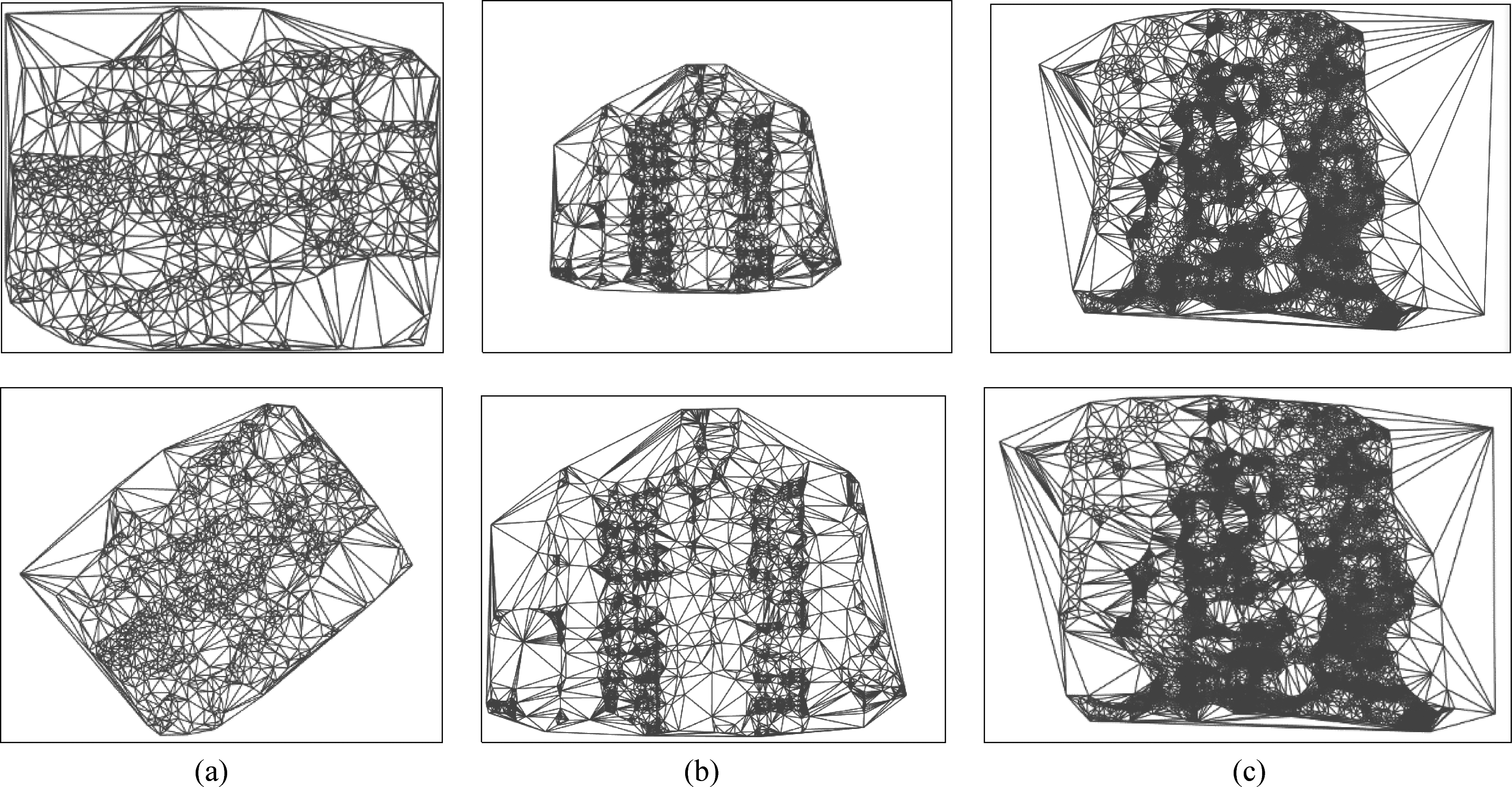
图10 文献[13]密集匹配得到的同名三角网
Fig.10 Corresponding Delaunay TIN of dense matching in reference[13]
4 结论
针对传统稀疏匹配难以满足高精度三维建模需要,本文提出一种简单有效的迭代三角网约束的近景影像密集匹配算法。该方法利用SIFT匹配获取初始同名点构建初始Delaunay三角网,将其作为匹配基础。以三角形重心作为匹配基元进行加密匹配,匹配过程中综合利用多重约束条件确定最终同名点。每次迭代匹配过程中,依次遍历三角网中所有的三角形进行匹配,将新产生的同名点和初始同名点整体进行构网。迭代过程中,以三角形面积为间接约束,以是否有新的同名点产生为直接约束作为迭代停止的条件。针对不同类型的近景影像对进行匹配实验,验证了本文算法对存在旋转、尺度变化、视角变化、重复纹理的近景影像都具有较好的适应性,均能取得可靠的密集匹配结果,为后续精细的三维建模提供有利的基础数据。
但该类基于同名三角形约束的影像匹配算法对于景深变化较大、且视角变化较大的复杂地物的近景影像的适用性有待进一步验证,后续将针对该类型的影像数据进行针对性研究。
参考文献
[1] 耿英楠.立体匹配技术的研究[D].长春:吉林大学,2014.
Geng Yingnan.Research on Stereo Matching Algorithms[D]. Changchun: Jilin University,2014.(in Chinese)
[2] Marr D, Poggio T. A Computational Theory of Human Stereo Vision[J]. Readings in Cognitive Science, 1988, 204(1156):534-547.
[3] Mayhew J E W, Frisby J P. Psychophysical and Computational Studies Towards a Theory of Human Stereopsis[J]. Artificial Intelligence,1981, 17(1):349-385.
[4] Lowe D G.Distinctive Image Features form Scale-in-variant Keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[5] Morel J M, Guo Y. ASIFT:A New Framework for Fully Affine Invariant Comparison[J]. Siam Journal on Imaging Science,2009,2(2):438- 469.
[6] Herbert B, Andreas E. SURF: Speeded Up Robust Features[J]. Computer Vision and Image Understanding,2008,110(3): 346-359.
[7] Aurenhammer F, Voronoi Diagrams-A Survey of A Fundamental Geometric Data Structure[J]. ACM Computing Surveys,1991,23(3):345- 405.
[8] Tang L, Tsui H T, Wu C K. Dense Stereo Matching Based on Propagation With a Voronoi Diagram[C]∥Proceedings of India Conference on Computer Vision, Graphics and Image ProcessingⅢ, 2002: 230-240.
[9] Tsai V J D. Delaunay Triangulation in TIN Creation: An Overview and a Linear-time Algorithm[J]. International Journal of Geographical Information Science,1993,7(6):501-524.
[10] 李文龙.SURF算法和Delaunay三角网算法相结合的遥感图像匹配技术的研究与实现[D].上海:华东理工大学,2013.
Li Wenlong. SURF Algorithm and Delaunay Triangulation Algorithm Combining Remote Sensing Image Matching Technology Research and Implementation[D]. Shanghai: East China Institute of Technology,2013.(in Chinese)
[11] Sun J, Zheng N N, Shum H Y. Stereo Matching Using Belief Propagation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(7):787- 800.
[12] 朱庆,吴波,赵杰.基于自适应三角形约束的可靠影像匹配方法[J].计算机学报,2005,28(10):1734-1739.
Zhu Qing,Wu Bo,Zhao Jie. A Reliable Image Matching Method Based on Self-adaptive Triangle Constraint[J].Chinese Journal of Computers,2005,28(10):1734-1739.(in Chinese)
[13] 朱红,宋伟东,杨冬,等. 近景影像三角网内插点密集匹配方法[J].测绘科学,2016,41(4):19-23.
Zhu Hong,Song Weidong,Yang Dong,et al. Dense Matching Method of Inserting Point into the Delaunay Triangulation for Close-range Image[J].Science of Surveying and Maping, 2016,41(4):19-23.(in Chinese)
[14] 窦慧丽.基于Delaunay三角剖分的指纹匹配算法[D].长春:吉林大学,2004.
Dou Huili. Fingerprint Matching Algorithm Based on Delaunay Triangulation[D]. Changchun: Jilin University,2004.(in Chinese)
[15] 吴波.自适应三角形约束下的立体影像可靠匹配方法[D].武汉:武汉大学,2006.
Wu Bo. A Reliable Stereo Image Matching Method Based on the Self-adaptive Triangle Constraint[D]. Wuhan: Wuhan University, 2006.(in Chinese)
[16] 来春风.数字近景影像稠密匹配方法研究[D].南京:南京师范大学,2012.
Lai Chunfeng.A Dissertation Submitted in Partial Fulfillment of the Requirements For the Degree of Master of Science[D]. Nanjing: Nanjing Normal University,2012.(in Chinese)
[17] 王竞雪,宋伟东,韩丹,等. 边缘视差连续性约束的航空影像特征线匹配算法[J].信号处理,2015,31(3):364-371.
Wang Jingxue,Song Weidong,Han Dan,et al.Feature Line Matching Algorithm for Aerial Image based on Continuity Constraint of Edge Parallax[J].Journal of Signal Processing,2015,31(3):364-371.(in Chinese)
[18] 朱红,宋伟东,谭海,等. Delaunay三角网优化下的小面元遥感影像配准算法[J].信号处理,2016,32(9):1032-1038.
Zhu Hong,Song Weidong,Tan Hai,et al. A Tiny Facet Primitive Remote Sensing Image registration Algorithm Based on Optimized Delaunay Triangulation[J].Journal of Signal Processing,2016,32(9):1032-1038.(in Chinese)


