1 引言
脑肿瘤是一种高危疾病,仅在 2015 年美国确诊的新发脑肿瘤病例大约23000例[注] http:∥www.ucancer.org。目前有效的治疗方案是通过核磁共振成像(Magnetic Resonance Imaging,MRI)确定脑肿瘤位置和大小信息。鉴于脑肿瘤形状复杂,大小和位置具有随机性,类型差异大等因素,目前还没有很好的分割算法能够满足临床需要,不同专家手动分割脑肿瘤[1]图像的结果也有很大差异,而且人工成本较高。因此,研究准确的全自动脑肿瘤分割算法非常重要[2]。
脑肿瘤自动分割技术一直以来都是研究热门方向,尤其是多模式脑肿瘤图像分割[3-4],脑肿瘤分割目的是检测肿瘤区域的位置和范围,在不同模式MRI图像中,这些肿瘤区域可以通过和正常区域比较识别出来。MRI包含多种模式图像,主要有FLAIR、T1C和T2等,如表1所示,在FLAIR模式中肿瘤与正常组织灰度差异明显,肿瘤呈高亮度,脑脊液呈低亮度。在T1C模式中,虽然部分肿瘤区域呈低亮度,与有些正常组织灰度差异不明显,但是边界纹理特征区别明显。而T2模式无论灰度及纹理特征都有一定的差异。3种模式图像可以为肿瘤分割提供部分不相关且互补的信息,为充分利用每个模式的图像信息,本文采用线性融合的方式来预处理不同模式的图像。
分割脑肿瘤的算法有很多,其中阈值算法、聚类算法和形变模型算法[5-7]是比较常用的算法。阈值算法最早用于脑肿瘤图像分割,其中OTSU[8]算法是一种自动适应阈值算法,能够有效避免固定阈值带来的误差,但是不适用于复杂的脑肿瘤图像;文献[9]针对于脑肿瘤这种复杂的图像提出一种用于多区域图像分割的局部模糊阈值(Fuzzy threshold,FTH) 算法,但是阈值算法对像素空域信息考虑不足,导致阈值类算法分割不能有效解决脑肿瘤分割问题。
模糊聚类是适合脑肿瘤图像分割的一类算法,尤其是模糊C均值(Fuzzy C-means, FCM)算法,但由于医学图像信息复杂,边缘不清晰,因此,种子点选取对聚类结果影响很大,且FCM算法难以利用图像的空域信息,本身计算复杂。文献[10]提出快速FCM(Fast FCM, FFCM)算法改进计算速度问题;针对空间信息不足的问题,文献[11]使用空间FCM(Spatial FCM, SFCM)算法分割图像,有效利用空间信息之间的相关性;文献[12]使用K近邻的聚类方法,结合简单的特征向量得到不错的效果,然而无法得到连续区域的分割结果。
水平集也是一种常用的分割算法,属于形变模型算法这一类,但是脑肿瘤组织灰度不均匀,脑肿瘤组织之间没有明显的边界,采用这类算法容易出现边缘泄露的问题。因此文献[13]提出将模糊聚类与水平集方法相结合(Fuzzy Clustering with Level Set Methods, FCLSM)算法有效解决水平集算法边缘问题,但是FCLSM算法容易陷入局部最优解。文献[14]提出距离正则化水平集算法(Distance Regularized Level Set Evolution, DRLSE),距离正则化效应消除了对重新初始化的需要,从而避免初始化引起的局部误差,但是边界效果较差;文献[15]提出一种混合水平集算法,混合水平集算法利用边界和区域信息来实现鲁棒和准确的分割,但初始值需要手动选取。
针对传统FCM算法耗时长和水平集算法对初始值依赖的缺陷,本文提出一种全自动改进的多模式脑肿瘤图像混合分割算法,首先对多模式脑肿瘤图像进行预处理,预处理包括中值滤波、归一化处理和线性融合,线性融合之后得到预处理图像,进而对预处理图像进行FFCM[10]分割得到欠分割图像,之后欠分割图像作为混合水平集算法的初始轮廓,最后利用混合水平集算法[15]修正欠分割图像存在的边界问题,将FFCM与还和水平集两种方法相结合,一方面可以加速混合水平集算法的速度,另一方面也弥补了FFCM算法分割不足的问题,有效改进各自的缺陷。
2 基本理论
2.1 基于直方图的FFCM理论
FFCM的核心思想是计算每一个像素强度值的隶属度和聚类中心,使得聚类内耗费函数的方差和迭代误差最小,耗费函数的值是像素到聚类中心2范数测度的加权累积和。FFCM聚类分割算法是将数据通过模糊C均值理论分为c类,对于像素为M×N图像(M,N为图像的宽和高),假设{hi,i=1,2,…,n;n=M×N}是图像直方图中的像素强度值构成的集合。{νj, j=1,2,…,c}是聚类中心构成的集合,且μj(hi)是hi隶属于j类的隶属函数,于是FFCM的目标函数为:
(1)
且
0≤μj(hi)≤1 ∀i, j
式中,![]() 代表2范数,b为大于1的常数,控制聚类结果的模糊度。为计算Jf的最小值,使得
代表2范数,b为大于1的常数,控制聚类结果的模糊度。为计算Jf的最小值,使得
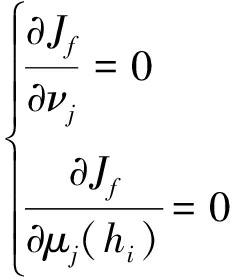
(2)
由式(1)与式(2)可以推导出
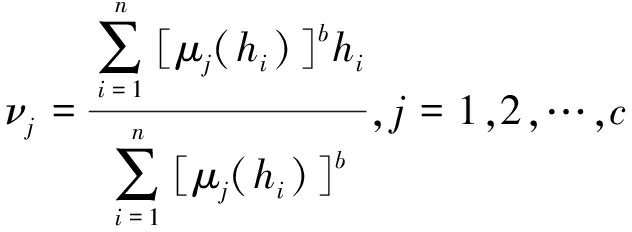
(3)
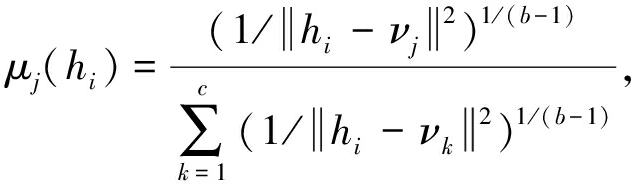
i=1,2,…,n; j=1,2,…,c
(4)
迭代式(3)与式(4)若满足迭代终止条件,t>T或![]() 则停止,其中t表示迭代次数,T代表最大迭代次数。算法结束后,按最大隶属度对像素进行分类,若μj(hi)>μj(hk),则将hi归为第j类区域,k=1,2,…,c;i≠k。
则停止,其中t表示迭代次数,T代表最大迭代次数。算法结束后,按最大隶属度对像素进行分类,若μj(hi)>μj(hk),则将hi归为第j类区域,k=1,2,…,c;i≠k。
2.2 混合模型水平集原理
水平集方法是将低维曲线表示为高维曲面的零水平集。任意时刻,只要知道水平集函数就可求出其零水平集曲线。与粒子模型[17]和参数模型[18]相比,水平集算法能有效解决尺寸问题。
由于脑肿瘤的MRI图像极为复杂,本文使用混合水平集[15]算法来弥补FFCM算法在边界上的不足和图像中的漏洞。嵌入函数φ的零集用于表示活动轮廓C={X1φ(X)=0},轮廓内/外的点具有正/负φ值。需要最小化函数定义为:
(5)
其中I为待分割图像,![]() 为与图像梯度相关的边界特征图(g可以是递减函数,如
为与图像梯度相关的边界特征图(g可以是递减函数,如![]() 式中c为控制斜率),H(φ)为赫维赛德函数,Ω为图像域,α和β是预定义权重以平衡两项。μ为指示目标对象的灰度级下限的预定义参数。
式中c为控制斜率),H(φ)为赫维赛德函数,Ω为图像域,α和β是预定义权重以平衡两项。μ为指示目标对象的灰度级下限的预定义参数。
![]() 为指向曲线外部的法向量。因此活动轮廓的显性曲线进化偏微分方程为:
为指向曲线外部的法向量。因此活动轮廓的显性曲线进化偏微分方程为:
(6)
式中曲率![]() 为内积。由于只有曲线的几何变化在分割中是感兴趣的,所以由式(6)可以注意到曲线上的所有点都在法线方向上移动。式(6)第一项是描述目标对象内部的曲线部分的扩展运动和外部部分的收缩运动的传播项,第二项是平流项,描述由g的梯度引起的向量场中的曲线移动,以将曲线吸引到目标对象的边界,第三项描述由梯度特征映射g加权的曲率流,作用是平滑边界支持弱的部分的曲线。
为内积。由于只有曲线的几何变化在分割中是感兴趣的,所以由式(6)可以注意到曲线上的所有点都在法线方向上移动。式(6)第一项是描述目标对象内部的曲线部分的扩展运动和外部部分的收缩运动的传播项,第二项是平流项,描述由g的梯度引起的向量场中的曲线移动,以将曲线吸引到目标对象的边界,第三项描述由梯度特征映射g加权的曲率流,作用是平滑边界支持弱的部分的曲线。
在水平集中,![]() 和
和![]() 描述相同的曲线变化[15],若φ是有符号距离函数,即
描述相同的曲线变化[15],若φ是有符号距离函数,即![]() 水平集嵌入函数随时间变化的导数为:
水平集嵌入函数随时间变化的导数为:
(7)
3 实验与结果分析
为更好验证本文提出的改进多模式脑肿瘤图像混合分割算法的有效性,目前使用最为广泛的在线图库是BRATS 2015[注] https:∥www.smir.ch/BRATS/Start2015,图库中给出病人的FLAIR,T1,T2,T1C四种已按照标准大脑配准图像,即每种模式像素的同一坐标对应大脑中的同一个位置。数据量大并且提供四种数据模式,为了验证本文算法,本文随机选取47例带有脑肿瘤的FLAIR、T2、T1C和金标准图像,图像均来自于不同的肿瘤图像。
3.1 评价指标
在脑肿瘤图像分割领域,Jaccard系数、相似系数(Dice)和recall是最常用的评价标准。表达式如下
(8)
(9)
(10)
式中S表示分割结果的二值图像,G表示金标准的二值图像,N(·)表示对图像中真值统计求和。
3.2 算法框架
图1是本文提出的改进的多模式脑肿瘤图像混合分割算法框架,首先输入FLAIR、T2和T1C三种模式的MRI图像,由于图像存在噪声,采用中值滤波对图像进行滤波处理,滤波图像使用FFCM聚类算法进行聚类,聚类数c=10,聚类一方面对图像归一化,另一方面能够有效保留区域信息,防止细小漏洞;因为图像已经按照标准大脑配准,之后将每一个像素点的灰度值按照线性比例FLAIR∶T2∶T1C=5∶4∶1融合得到预处理图像,然后使用FFCM算法分割预处理图像,设置阈值自动提取灰度值较大的区域,得到肿瘤欠分割图像,最后使用混合水平集[15]分割欠分割图像得到分割图像,最后评价分割结果。
表1是算法部分步骤的结果。从表1中可以看出,图像经过线性融合之后,边界变得更明显,预处理图像经过FFCM和自动阈值之后得到欠分割图像,与金标准进行对比Dice=0.9540,并且欠分割图像存在过多的漏洞,边界还存在明显的不足;因此将欠分割图像作为混合水平集的初始区域,可以有效弥补混合水平集对于初始值的依赖,经过混合水平集合得到分割图像,其Dice=0.9775提升明显,边界明显更接近金标准图像,并且单张图像时间为0.72 s,实时性较高。
为测试出合适的线性融合比例,本文通过40组比例测试,经过对比和实验观察,部分测试结果如表2所示,表2是部分线性融合比例,由于从表1中可以看出,FLAIR和T2的边界信息更好,所以表2
列出的是FLAIR和T2占比例较高的分割结果,从结果中看出融合比例为FLAIR∶T2∶T1C=5∶4∶1时效果最佳,因此本文的选择的融合比例为FLAIR∶T2∶T1C=5∶4∶1。
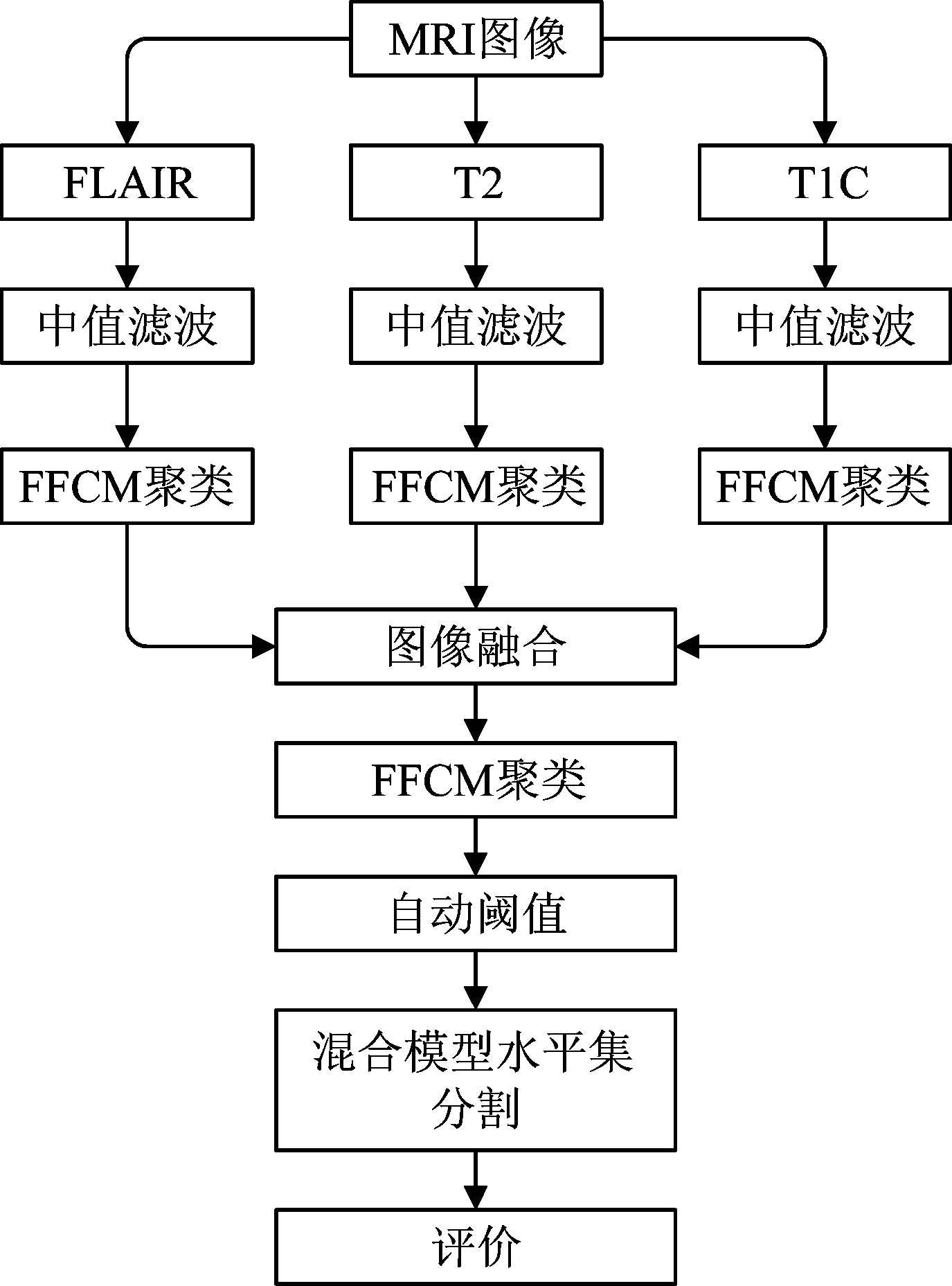
图1 本文分割算法框架
Fig.1 Segmentation algorithm framework in this paper
表1 本文脑肿瘤分割主要步骤
Tab.1 The main steps of brain tumor segmentation in this paper
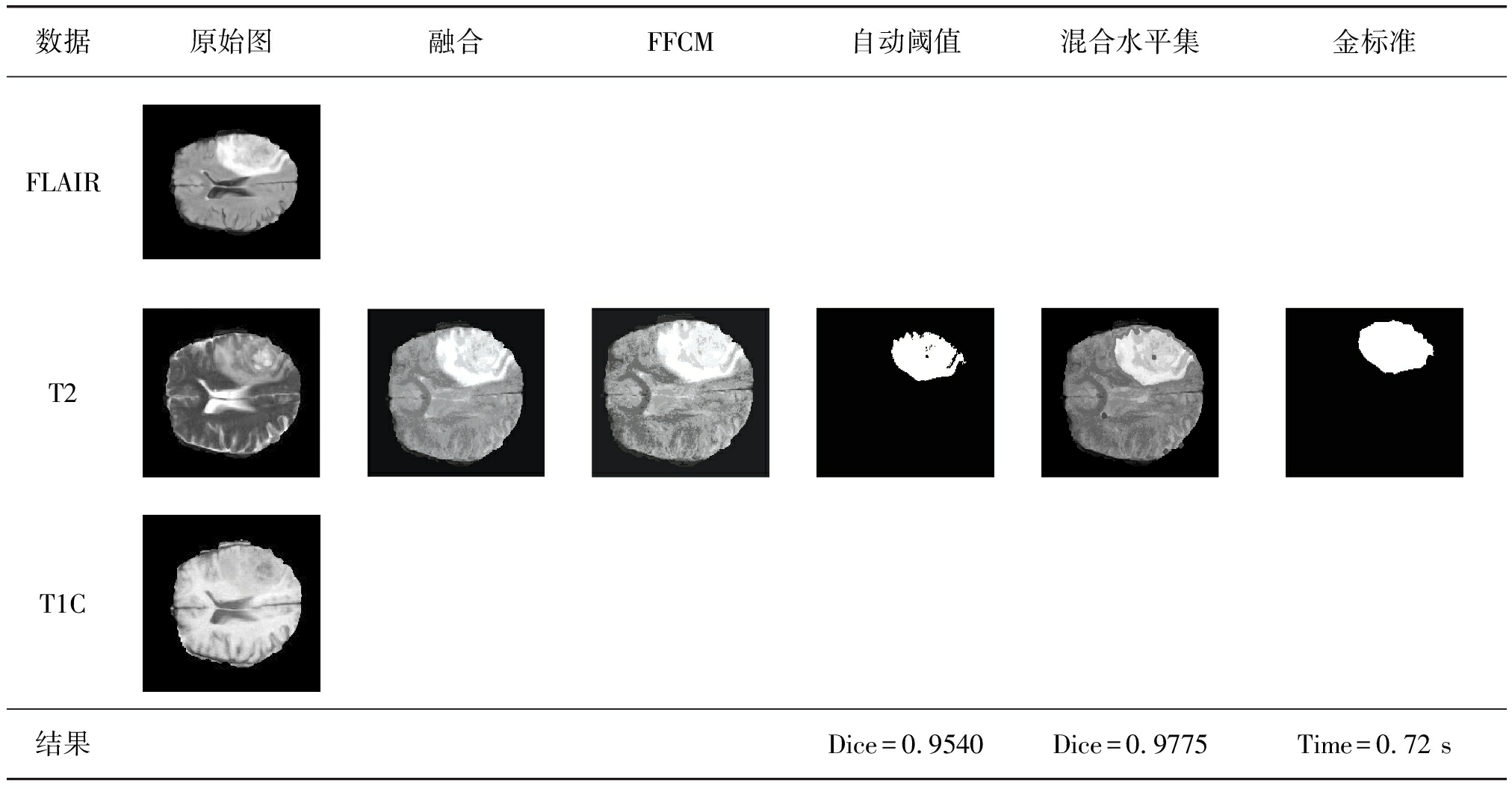
数据原始图融合FFCM自动阈值混合水平集金标准FLAIRT2T1C结果Dice=0.9540Dice=0.9775Time=0.72 s
表2 47例图像不同比例的处理结果
Tab.2 The processing result of 47 images in different proportion

FLAIR∶T1C∶T29∶0∶18∶0∶27∶1∶27∶0∶36∶0∶46∶1∶36∶1∶25∶0∶55∶1∶45∶2∶35∶1∶34∶2∶3平均Dice0.840.860.860.870.880.860.860.840.900.870.870.89平均Jaccard0.750.770.770.790.790.770.780.750.820.790.790.81平均recall0.850.850.870.850.860.840.870.790.890.880.860.89
3.3 对比和讨论
为了验证本文所使用的多模式图像的有效性,本文分别与使用单模式图像的分割结果和其他同类算法结果进行对比。表2分别列出了FLAIR、T2和T1C三种单模式和本文融合的结果;表3分别与阈值类算法:OTSU[8]算法和FTH[9]算法;模糊聚类算法:FCM算法、FFCM[10]算法、SFCM[11]算法和KNN[12];水平集类算法:FCLSM[13]算法、DRLSE[14]算法和混合水平集算法[15]进行对比,同时与有类似框架文献[16]对比。在表3中,为了保证对比条件一致,所有算法使用图像均为线性融合之后的预处理图像。
表3和表4列出了相应算法处理47例脑肿瘤图像的结果,其中参数Jaccard、Dice和recall所对应的列是分割47例脑肿瘤图像得到的平均值,最后一列是分割47例脑肿瘤图像所使用的总时间,单位为s。在表3中本文论证多模式图像的融合的优越性能,从FLAIR、T2和T1C三种单模式的分割参数Jaccard、Dice和recall对比中,本文提出的改进的多模式脑肿瘤图像混合分割算法虽然耗时比单模式长,但是Dice达到0.90,Jaccard达到0.82,recall达到0.89,明显高于其他单模式的分割。
表3 47例肿瘤图像单模式的处理结果
Tab.3 The processing result of 47 single modal images
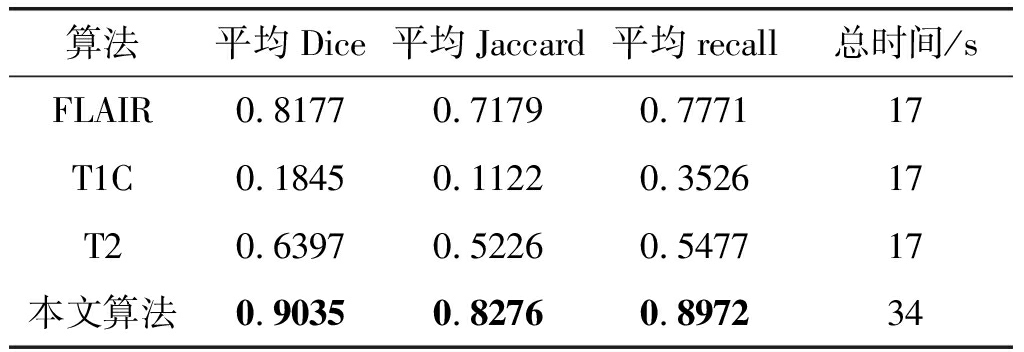
算法平均Dice平均Jaccard平均recall总时间/sFLAIR0.81770.71790.777117T1C0.18450.11220.352617T20.63970.52260.547717本文算法0.90350.82760.897234
在表4中,本文提出的全自动化算法与同类算法进行比较,包括阈值算法、聚类算法和水平集算法,从结果来看本文算法耗时比较短,仅比OTSU算法和FFCM算法慢,但是本文算法在效果上,平均Dice、Jaccard和recall均是最高的;与同类混合算法比较,本文的性能也优于同类算法。为了验证本文算法的有效性,本文提出的算法与Havaei[19]提出的KNN算法和Pereira[20]提出的多模态三维神经网络模型算法等权威结果比较,本文算法的Dice=0.90,Havaei[19]的Dice=0.85,Pereira[20]的Dice=0.88,本文算法的Dice明显优于两位学者提出的算法。
表4 47例图像不同算法的结果
Tab.4 The result of 47 images in different algorithm
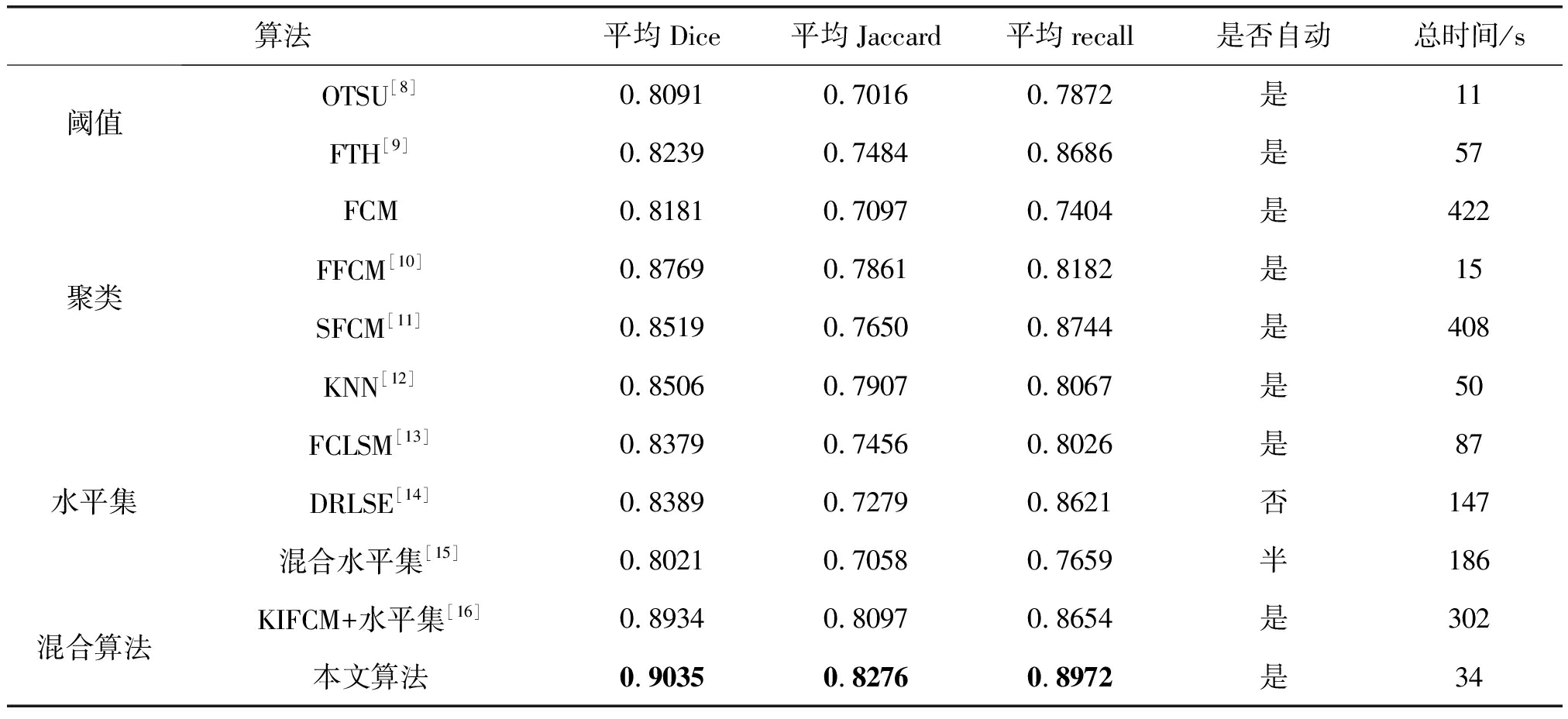
算法平均Dice平均Jaccard平均recall是否自动总时间/s阈值OTSU[8]FTH[9]0.80910.82390.70160.74840.78720.8686是是1157聚类FCMFFCM[10]SFCM[11]KNN[12]0.81810.87690.85190.85060.70970.78610.76500.79070.74040.81820.87440.8067是是是是4221540850水平集FCLSM[13]DRLSE[14]混合水平集[15]0.83790.83890.80210.74560.72790.70580.80260.86210.7659是否半87147186混合算法KIFCM+水平集[16]本文算法0.89340.90350.80970.82760.86540.8972是是30234
为验证本文算法的稳定性,在图2中,本文的47例脑肿瘤图像与其他算法进行单独比较,每一个框的下标是算法名称,框中的直线为该算法平均值,框的大小代表算法稳定性,框越大,算法稳定性越差,框内的折线图是47例脑肿瘤图像的Dice所画。本文算法为第一个框,从图2中可看出本文算法稳定性高于其他算法,分割47例脑肿瘤图像整体的波动较小,并且整体性能高于其他算法,平均的Dice达到0.90。
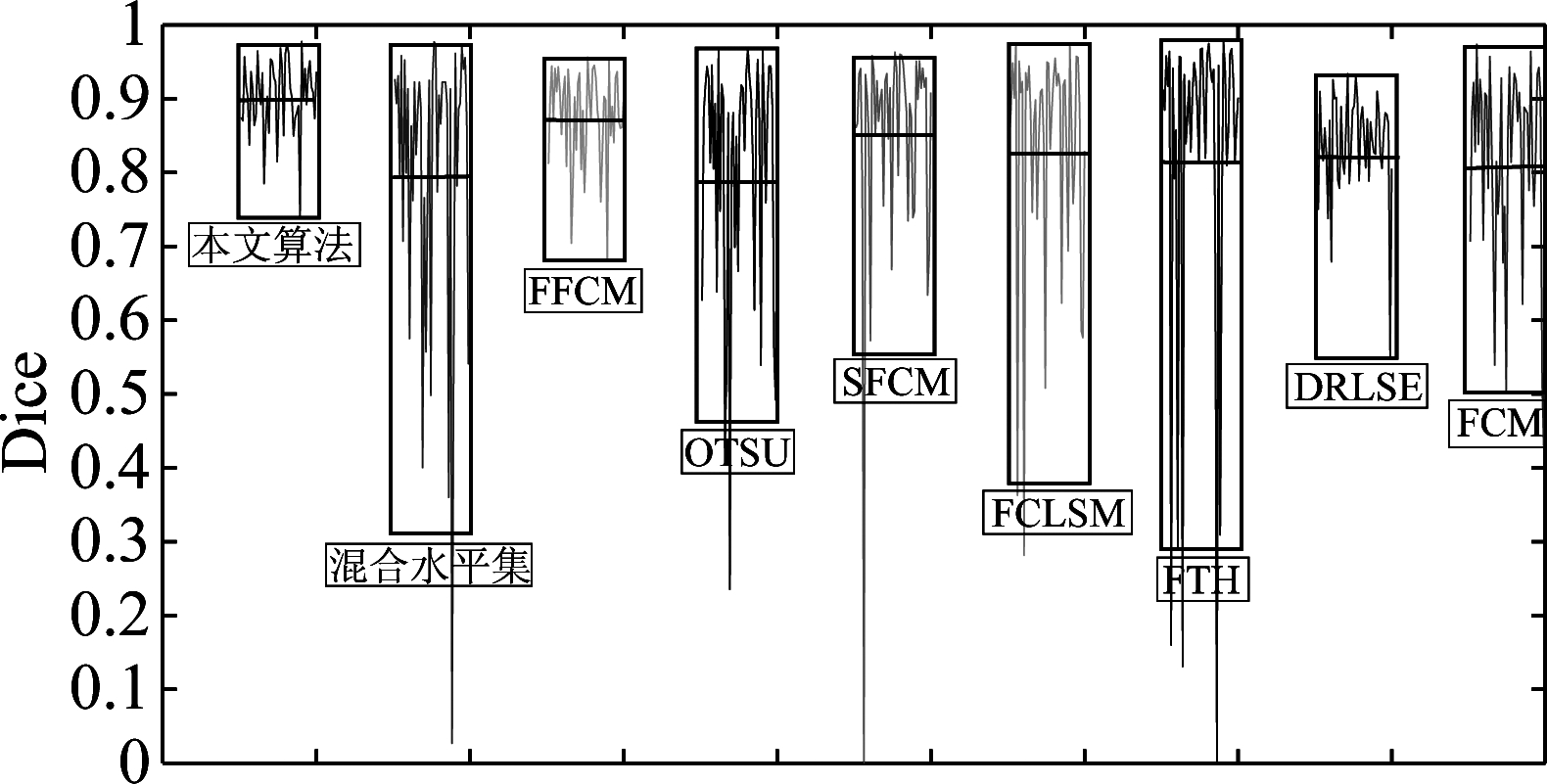
图2 47例脑肿瘤图像分割的Dice
Fig.2 The Dice of 47 brain tumor image segmentation
4 结论
本文提出一种全自动改进的多模式脑肿瘤图像混合分割算法,首先对多模式图像进行中值滤波,滤波后的多模式图像分别进行FFCM聚类,聚类一方面对图像归一化,另一方面能够有效保留区域信息,防止细小漏洞;为利用不同模式图像的优势,本文采用线性融合的方式,融合比例为:FLAIR∶T2∶T1C=5∶4∶1,融合之后的图像为预处理图像,之后预处理图像进行FFCM聚类,聚类图像通过自动阈值分割得到一个欠分割图像,为弥补图像边界问题,采用混合水平集算法,同时将FFCM分割的欠分割图像作为水平集的初始轮廓输入,一方面加快了分割的速度,另一方面也提高了分割的精度。分割图像与金标准对比,平均Dice达到0.90;与同类算法对比,经本文算法得到的Dice、Jaccard和recall最佳,实时性较好,稳定性较高。
实验结果表明,本文提出改进的多模式脑肿瘤图像混合分割算法具有稳定性好,实时性高,准确性高等优点,对脑肿瘤图像分割研究有一定的意义,且能满足医学的临床需要。
参考文献
[1] Luo S, Li R, Ourselin S. A new deformable model using dynamic gradient vector flow and adaptive balloon forces[J]. Aprs Workshop on Digital Image Computing, 2003:9-14.
[2] Harati V, Khayati R, Farzan A. Fully automated tumor segmentation based on improved fuzzy connectedness algorithm in brain MR images[J]. Computers in Biology & Medicine, 2011, 41(7):483- 492.
[3] Njeh I, Sallemi L, Ayed I B, et al. 3D multimodal MRI brain glioma tumor and edema segmentation: A graph cut distribution matching approach[J]. Computerized Medical Imaging & Graphics the Official Journal of the Computerized Medical Imaging Society, 2015, 40:108-119.
[4] Zhao X, Wu Y, Song G, et al. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation[J]. 2017.
[5] Khurana S, Garg ML. MRI based Brain Tumor Segmentation Methods: A Critical Review[J]. International Journal of Advance research in Computer Science and Management Studies, 2015, 3(4):432- 446.
[6] Menze B H, Jakab A, Bauer S, et al. The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS)[J]. Medical Imaging IEEE Transactions on, 2015, 34(10):1993-2024.
[7] Gordillo N, Montseny E, Sobrevilla P. State of the art survey on MRI brain tumor segmentation[J]. Magnetic Resonance Imaging, 2013, 31(8):1426-38.
[8] Jeevitha A J A, Narendran P N P. BTS (Brain Tumor Segmentation) Based on Otsu Thresholding[J]. PARIPEX-INDIAN JOURNAL OF RESEARCH, 2012, 2(2):53-55.
[9] Aja-Fern ndez S, Curiale A H, Vegas-S
ndez S, Curiale A H, Vegas-S nchez-Ferrero G. A local fuzzy thresholding methodology for multi-region image segmentation[J]. Knowledge-Based Systems, 2015, 83(1):1-12.
nchez-Ferrero G. A local fuzzy thresholding methodology for multi-region image segmentation[J]. Knowledge-Based Systems, 2015, 83(1):1-12.
[10] Tian J, Huang Y, Tian J. Histogram Constraint Based Fast FCM Cluster Image Segmentation[C]∥IEEE International Symposium on Industrial Electronics. IEEE Xplore, 2007:1623-1627.
[11] Sedaaghi M H. Segmentation of pomegranate MR images using spatial fuzzy c-means (SFCM) algorithm[J]. Proc Spie, 2011, 8285(9):170-177.
[12] Havaei M, Jodoin P M, Larochelle H. Efficient Interactive Brain Tumor Segmentation as Within-Brain kNN Classification[C]∥International Conference on Pattern Recognition, 2014:556-561.
[13] Li B N, Chui C K, Chang S, et al. Integrating spatial fuzzy clustering with level set methods for automated medical image segmentation[J]. Computers in Biology & Medicine, 2011, 41(1):1-10.
[14] Li C, Xu C, Gui C, et al. Distance Regularized Level Set Evolution and Its Application to Image Segmentation[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2010, 19(12):3243-3254.
[15] Zhang Y, Matuszewski B J, Shark L K, et al. Medical Image Segmentation Using New Hybrid Level-Set Method[C]∥Bio-Medical Visualization, 2008. MEDIVIS'08. Fifth International Conference. IEEE, 2008:71-76.
[16] Abdel-Maksoud E, Elmogy M, Al-Awadi R. Brain tumor segmentation based on a hybrid clustering technique[J]. Egyptian Informatics Journal, 2015, 16(1):71- 81.
[17] Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models[J]. International Journal of Computer Vision, 1988, 1(4):321-331.
[18] Precioso F, Barlaud M, Blu T, et al. Robust real-time segmentation of images and videos using a smooth-spline snake-based algorithm[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2005, 14(7):910-924.
[19] Havaei M, Jodoin P M, Larochelle H. Efficient Interactive Brain Tumor Segmentation as Within-Brain kNN Classification[C]∥International Conference on Pattern Recognition, 2014:556-561.
[20] Pereira S, Pinto A, Alves V, et al. Brain Tumor Segmentation using Convolutional Neural Networks in MRI Images[J]. IEEE Transactions on Medical Imaging, 2016, 35(5):1240-1251.


