1 引言
在频率选择性衰落信道中,无线通信系统常用均衡技术消除符号间的干扰[1-2]。如果是时变[3- 4]信道,并且接收机不知道信道信息,则接收机很难精确估计出发送端发送的数据符号。在时变频率选择性衰落信道下,具有近似最优信道估计的接收机可以更精确的估计信号信息。
对于时变频率选择性衰落信道,性能最优的接收机有很高的复杂度,而现有的次最优迭代接收机性能与最优估计性能有较大差距,且复杂度较高。文献[5]中使用最小均方滤波器,这种滤波器是线性信道估计器并且是模块化设计,各模块用启发式的方式连接,在每次迭代中分别进行信道估计和数据均衡,即用从信道估计器得到的信道估计值估计数据,再用数据检测值估计信道,没有考虑信道抽头和数据符号之间的相关性。文献[6]使用最大似然准则进行数据检测,复杂度太高。进行联合信道估计和数据检测一个简单的方法是把信道估计嵌入到数据检测的过程中,基于这种思想文献[7]提出了可调节软输入软输出检测技术。在文献[7]的基础上,文献[8]提出了贝叶斯结构期望最大化检测器,即在最大后验概率估计器中嵌入一个卡尔曼估计器实现联合信道估计和数据均衡,和前面介绍的几种接收机相比,它具有较低的复杂度和较高的性能。文献[9]中提出的非线性卡尔曼滤波器(EKF)是在滤波器中嵌入延时以便消除先验信息干扰,使均衡器输出似然函数,与文献[8]相比,它有更好的性能。在延时较小的情况下,文献[9]具有较低的复杂度,但性能较差。以上算法设计的迭代接收机的思想是先进行模块化设计,然后把译码器、解调器和均衡器等各模块以启发式的方式连接,其性能与最优估计相差较大,且复杂度高。
消息传递算法在特定的因子图上按照一定的消息更新规则和消息调度机制迭代地求解变量的近似局部后验概率密度的一类算法。用消息传递算法设计的迭代接收机同样包括信道估计、均衡、解调和译码等功能,但抛弃了传统模块化设计的方法,把整个接收机看成一个有机的整体,在系统全局函数分解的因子图上求解待估计变量的边缘后验函数,这样设计出的迭代接收机考虑了系统中所有的未知变量及其关系。消息传递算法在迭代接收机设计方面有广泛的应用,本文使用的迭代接收机联合了置信传播(BP)[10]、期望传播(EP)[11]和平均场(MF)[12]。MF算法处理因子图中的非线性因子节点时具有一定的优势,降低了迭代接收机的计算复杂度。本文将联合BP-EP-MF的消息传递算法应用到频率选择性慢衰落信道估计中,比文献[9]中的EKF信道估计器的性能高、复杂度略低,而且收敛速度加快。
下文用*和T分别表示共轭和转置。CN(x;mx,Vx) 表示一个多变量复高斯概率密度分布函数,向量mx表示均值,矩阵Vx表示方差。当a为常数时, f(x)=ag(x)表示成f(x)∝g(x)。
2 信号模型及其因子图表示
2.1 信号传输模型
针对频率选择性慢衰落信道,本文使用位交织编码调制发射系统。符号位向量b编码后表示为c,码字向量c交织后进行正交相移键控调制(QPSK),调制符号用d表示。导频符号t由QPSK星座图中的值随机产生。符号x包含t和d,x被发送到频率选择性慢衰落信道。接收机接收到的信号用y表示。
(1)
其中hi=[hi,L-1,hi,L-2,…,hi,0]T表示时变信道抽头系数,并且满足0≤k≤L-1。当向量si=[xi-L+1,xi-L,…,xi]T中的元素都是导频时,定义![]() 其余的sj定义
其余的sj定义![]() 并且满足
并且满足![]() 和
和![]() 加性复高斯白噪声wi的均值为0,方差为σ2。
加性复高斯白噪声wi的均值为0,方差为σ2。
2.2 信道模型
假设hi是随机瑞利衰落信道,且满足均值为0的复高斯多变量随机过程[9]。根据信道的基带频谱和时间自相关函数[9],可知信道模型可以用自回归(AR)过程表示。由于这里主要考虑信道估计,所以用低阶的AR模型就足够了。
(2)
ρ表示AR过程的阶数, 本文ρ取1,u的方差γ和系数A通过解Yule-Walker方程得出[13]。
根据公式(2)可得信道的概率模型为:
p(h1…hi…hI)=p(hI1hI-1)…p(hi1hi-1)…
p(h21h1)p(h1)
(3)
p(hi1hi-1)=CN(hi;Ahi-1,γ)
(4)
2.3 因子分解与因子图
一个目标分解成几个子目标相乘的形式叫做因子分解,本文是把一个多变量的复杂全局联合后验概率密度函数分解成若干个简单局部函数的乘积形式。在频率选择性慢信道通信系统中,根据全局联合后验概率密度函数的因子分解建立信道的因子图模型,使系统中的未知变量及关系清楚地表示在因子图中。
联合后验概率密度函数p(b,c,d,s,h1y)因子分解如下:
fhi(hi,hi-1)×fX(x,c,b)
(5)
当i<1和i>N时,xi等于0。根据公式(5)得到的因子图模型如图1。
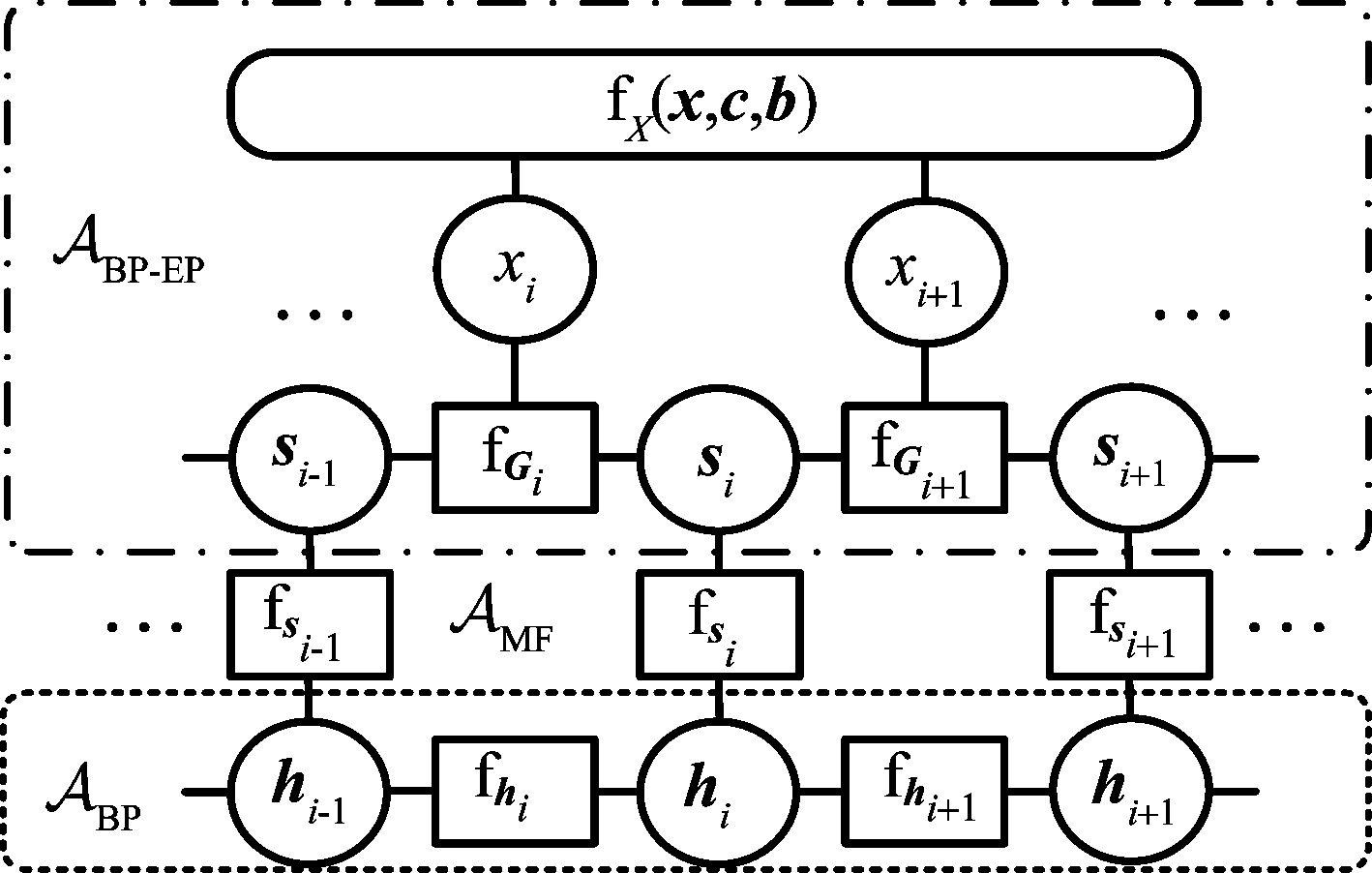
图1 BP-EP-MF模型因子图
Fig.1 The factor graph of BP-EP-MF model
每个因子的表达式如下:
fGi(si,si-1,xi)=δ[si-(Gsi-1+exi)]
(6)
(7)
fhi(hi,hi-1)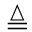 p(hi1hi-1)
p(hi1hi-1)
(8)
由文献[11]可以知道GL×L=[0(L-1)×1IL-1;01×L]和e=[01×(L-1)1]T,并且G=G′G″,G″=[IL-10(L-1)×1]T,G′=[0(L-1)×1IL-1]。
3 基于BP-MF-EP联合消息传递算法的迭代均衡器
迭代均衡器在第一次迭代的时候只用导频进行信道估计,第二次迭代开始用所有的数据符号和导频符号进行联合信道估计和数据均衡,所以存在一部分消息要分别计算![]() 和
和![]() 时更新的消息。
时更新的消息。
消息传递算法的更新规则见参考文献[14]。因为信道信息未知,所以在图1中的因子节点{fsi,∀i} 是非线性的。根据消息传递算法的特点,选择用MF处理非线性因子节点。如图所示,将因子图分成三个部分:BP-EP子图、MF子图和BP子图。相应地,因子节点被分成三个不相交的集合:![]() 和
和![]() 且
且![]() 下面详细地介绍每个部分传递的消息。
下面详细地介绍每个部分传递的消息。
3.1 MF子图传递的消息
(1)当![]() 时,根据MF消息更新规则,fsi到hi传递的消息如下:
时,根据MF消息更新规则,fsi到hi传递的消息如下:
(9)
当![]() 时,根据MF消息更新规则,fsi到hi的消息更新如下:
时,根据MF消息更新规则,fsi到hi的消息更新如下:
(10)
均值和方差分别为:
(11)
(12)
si的置信![]() 的计算方法在BP-EP部分介绍。
的计算方法在BP-EP部分介绍。
(2)根据MF消息更新规则,fsi到si传递的消息mfsi→si如下:
(13)
均值和方差分别为:
(14)
(15)
hi的置信![]() 的计算方法在BP部分介绍。
的计算方法在BP部分介绍。
3.2 BP子图传递的消息
BP子图选择的消息传递机制是前向后向算法,故BP子图需要计算前向、后向和输出的消息。
3.2.1 前向消息
(1)假设hi-1到fhi的消息是![]() 所以根据BP消息更新规则,fhi到hi传递的消息更新如下:
所以根据BP消息更新规则,fhi到hi传递的消息更新如下:
(16)
均值和方差分别为:
(17)
(18)
(2)当![]() 时,根据BP消息更新规则,利用公式(10)计算hi到fhi+1传递的消息:
时,根据BP消息更新规则,利用公式(10)计算hi到fhi+1传递的消息:
nhi→fhi+1(hi)∝mfhi→hi(hi)mfsi→hi(hi)
(19)
均值和方差分别为:
(20)
(21)
当![]() 时,根据BP消息更新规则,利用公式(11) 计算hi到fhi+1更新的消息:
时,根据BP消息更新规则,利用公式(11) 计算hi到fhi+1更新的消息:
nhi→fhi+1(hi)∝mfhi→hi(hi)mfsi→hi(hi)
(22)
均值和方差分别为:
(23)
(24)
3.2.2 后向消息
(1)假设hi+1到fhi+1的消息是![]() 所以根据BP消息更新规则,fhi+1到hi传递的消息如下:
所以根据BP消息更新规则,fhi+1到hi传递的消息如下:
(25)
均值和方差分别为:
(26)
(27)
![]() 时,根据BP消息更新规则,利用公式(10)计算hi到fhi传递的消息:
时,根据BP消息更新规则,利用公式(10)计算hi到fhi传递的消息:
nhi→fhi(hi)∝mfhi+1→hi(hi)mfsi→hi(hi)
(28)
均值和方差分别为:
(29)
(30)
当![]() 时,根据BP消息更新规则,利用公式(11) 计算hi到fhi的消息:
时,根据BP消息更新规则,利用公式(11) 计算hi到fhi的消息:
nhi→fhi(hi)∝mfhi+1→hi(hi)mfsi→hi(hi)
(31)
均值和方差分别为:
(32)
(33)
3.2.3 输出消息
根据MF消息更新规则,从hi到MF子图的消息是hi的置信。
b(hi)=mfsi→hi(hi)mfhi→hi(hi)mfhi+1→hi(hi)
(34)
均值和方差分别为:
(35)
(36)
3.3 BP-EP子图传递的消息
BP-EP子图的消息计算需要MF子图输出的连续高斯消息和解调器输出的离散消息。为了降低复杂度,文献[11]采用EP算法把解调器输出的离散消息近似成连续的高斯消息。
假设:![]() 和
和![]()
(1)在文献[11]中详细地介绍消息![]() 和
和![]() 的计算方法。根据MF消息更新规则,从si到MF子图的消息应该是si的置信。计算结果如下:
的计算方法。根据MF消息更新规则,从si到MF子图的消息应该是si的置信。计算结果如下:
b(si)=mfGi→si(si)mfGi+1→si(si)mfsi→si(si)
(37)
均值和方差分别为:
(38)
(39)
(2)fGi到xi传递的消息如下
(40)
均值和方差分别为:
(41)
(42)
4 消息传递机制
在第一次迭代时仅使用导频进行信道状态估计,然后在以后的迭代中用导频和数据符号进行联合均衡和信道估计。消息更新机制总结如下:
初始化消息nhi→fhi+1(hi)∝CN(hi;0,1/L)、mfGi+1→si(si)∝CN(si;0,∞) 和nhi→fhi(hi)∝CN(hi;0,1/L)。
在第一次迭代的时候消息更新顺序如下:
![]() 用公式(22)更新nhi→fhi+1(hi)和mfhi→hi(hi)=nhi-1→fhi(hi-1)。
用公式(22)更新nhi→fhi+1(hi)和mfhi→hi(hi)=nhi-1→fhi(hi-1)。
![]() 用公式(31)更新nhi→fhi(hi)和mfhi+1→hi(hi)=nhi+1→fhi+1(hi+1)。
用公式(31)更新nhi→fhi(hi)和mfhi+1→hi(hi)=nhi+1→fhi+1(hi+1)。
在第二次及以后的迭代中消息更新顺序如下:
(1)i=![]() Ny;更新mfGi→si(si)和nsi→fGi+1(si)。
Ny;更新mfGi→si(si)和nsi→fGi+1(si)。
(2)i=Ny+![]() -
-![]() 2;更新mfGi+1→si(si) 和nsi→fGi(si)。
2;更新mfGi+1→si(si) 和nsi→fGi(si)。
(3)i=![]() Ny;用公式(37)和(10)更新b(si) 和mfsi→hi(hi)。
Ny;用公式(37)和(10)更新b(si) 和mfsi→hi(hi)。
(4)i=![]() Ny;用公式(16)和(22)更新mfhi→hi(hi)和nhi→fhi+1(hi)。
Ny;用公式(16)和(22)更新mfhi→hi(hi)和nhi→fhi+1(hi)。
(5)i=Ny:-![]() 1;用公式(25)和(31)更新mfhi+1→hi(hi)和nhi→fhi(hi)。
1;用公式(25)和(31)更新mfhi+1→hi(hi)和nhi→fhi(hi)。
在以上每次迭代完之后都要更新以下消息:
(1)i=![]() Ny;用公式(37)和(10)更新b(si)和mfsi→hi(hi)。
Ny;用公式(37)和(10)更新b(si)和mfsi→hi(hi)。
(2)i=![]() Ny;更新mfGi→si(si)和nsi→fGi+1(si)。
Ny;更新mfGi→si(si)和nsi→fGi+1(si)。
(3)i=Ny+![]() -
-![]() 2;更新mfGi+1→si(si)和nsi→fGi(si)。
2;更新mfGi+1→si(si)和nsi→fGi(si)。
(4)i=![]() Ny;更新mfGi→xi(xi)。
Ny;更新mfGi→xi(xi)。
5 仿真结果和复杂度分析
这一部分讨论在频率选择性慢衰落信道下,本文所提出的联合消息传递算法迭代接收机在信道估计中的性能和复杂度。
5.1 性能比较
在仿真中,每一个数据块设置1000个比特,使用码率R=1/ 2的(23,35)8 卷积码。调制之后,每15个信息符号之前插入10个导频符号。由于加入了导频,所以在仿真中要考虑导频对信噪比的影响。瑞利衰落信道抽头数量设置为L=3,每一个抽头的功率等于1/L。信道抽头基于Bello模型[9],根据文献[15]中的方法生成,多普勒归一化速率设置为fDTs=0.001。仿真结果如图2所示,![]() 标记的仿真线为本文所提算法的结果。
标记的仿真线为本文所提算法的结果。
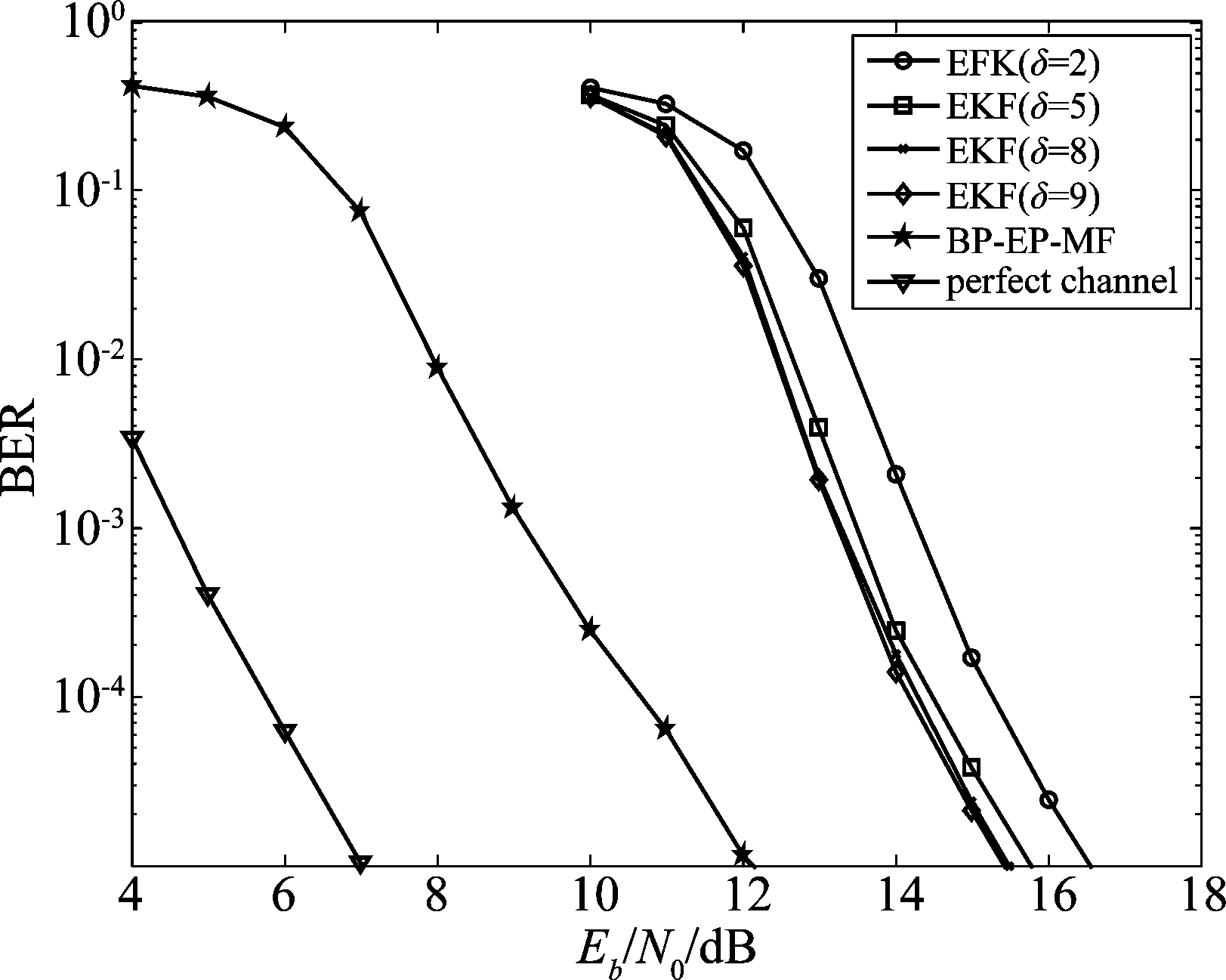
图2 SNR与BER的关系曲线图
Fig.2 Performance of BER versus SNR
在图2中可以清楚地看出,当误码率(BER)等于10-5,EKF均衡器中取δ=8和δ=9时,联合消息传递算法均衡器比EKF均衡器性能提高约3.5 dB;EKF均衡器中δ=5时,联合消息传递算法均衡器比EKF均衡器性能提高约3.8 dB; EKF均衡器中δ=2时,联合消息传递算法均衡器比EKF均衡器性能提高约4.5 dB。当误码率(BER)等于10-5,联合消息传递算法均衡器比已知信道信息时的性能差5 dB。从图中可以看出随着延时δ的增加,EKF均衡器性能改善很小,δ=8和δ=9的性能接近。
在图3中仿真了SNR=13 dB时,不同的均衡器随着迭代次数增加的收敛情况。BP-EP-MF均衡器在第三次迭代时就已经收敛,明显比EKF均衡器收敛速度快。从图4中,可以看出BP-EP-MF均衡器在不同信噪比情况下,五次迭代后基本都已经收敛。
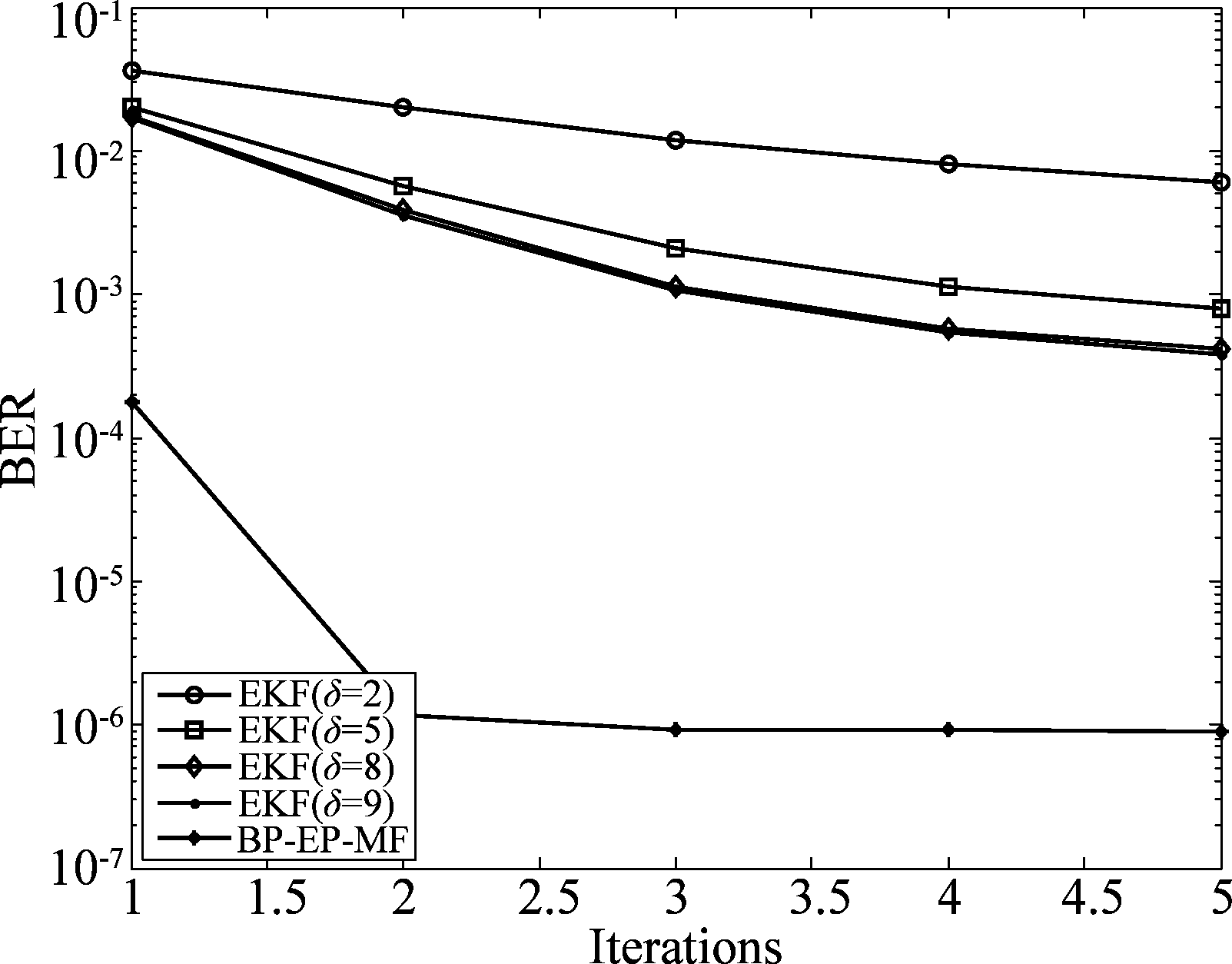
图3 迭代次数与BER的关系曲线图
Fig.3 Performance of BER versus Iterations
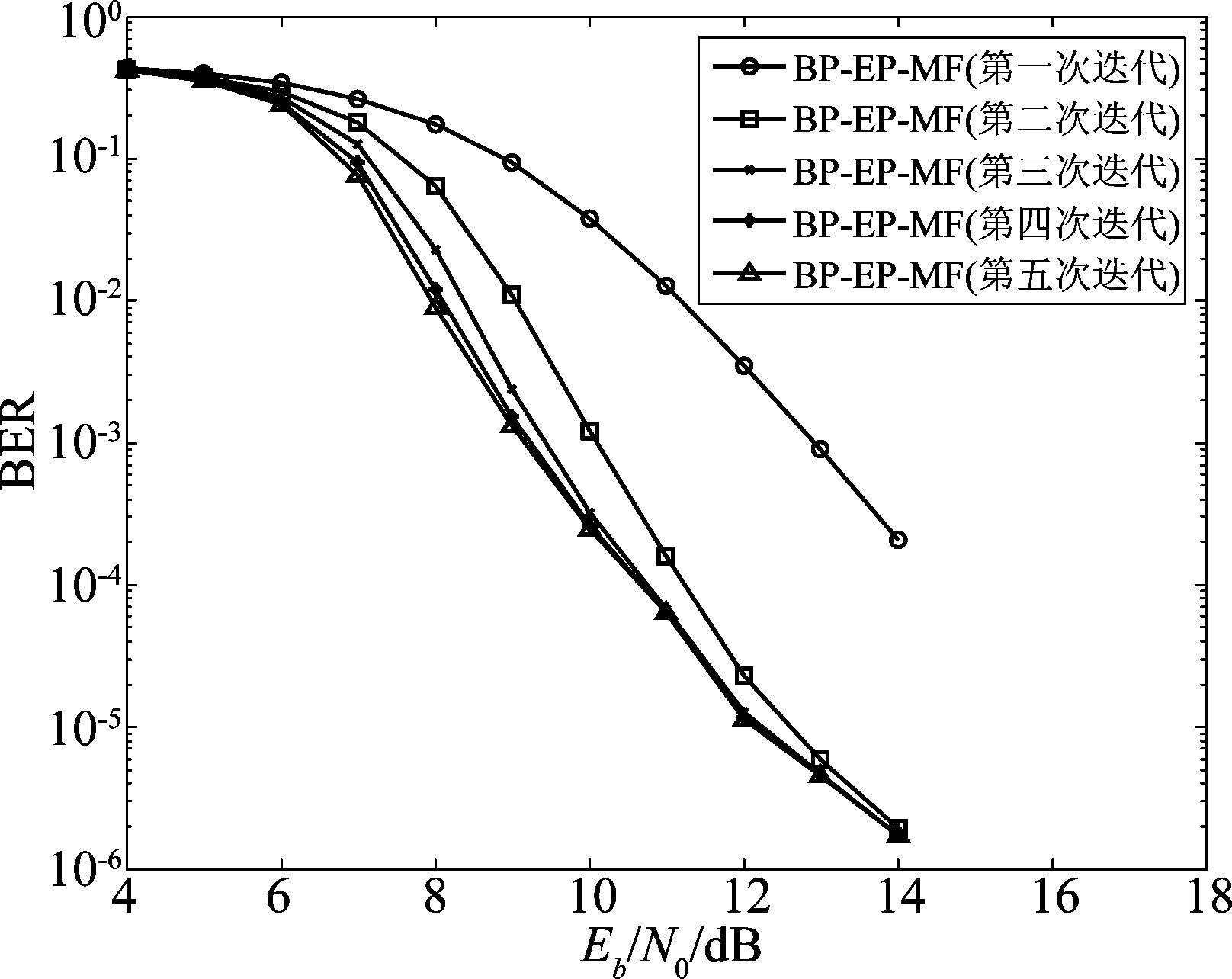
图4 SNR与BER的关系曲线图
Fig.4 Performance of BER versus SNR
5.2 复杂度比较
联合消息传递算法在(10)、(13)、(16)、(22)、(25)、(37)和(40)的计算中存在L维矩阵求逆,则复杂度为![]() 由文献[8]可知EKF算法的复杂度为
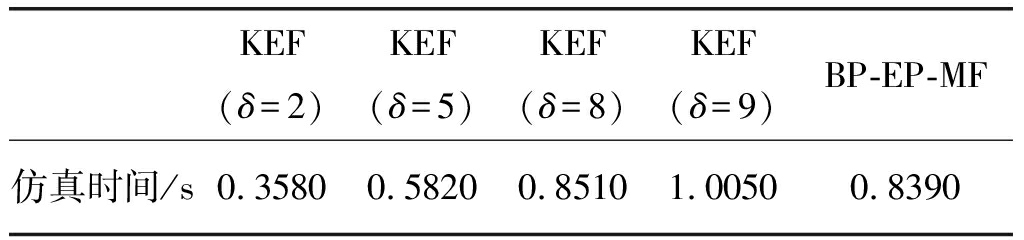
由文献[8]可知EKF算法的复杂度为![]() 表1中给出了不同均衡器在同一台电脑中的仿真时间,每次仿真取一帧数据,五次迭代。从表中可以看出BP-EP-MF算法比KEF(δ=2)的仿真时间多了约134.44%,比KEF(δ=5)的仿真时间多了约44.16%,比KEF(δ=8)的仿真时间少了约1.41%,比KEF(δ=9)的仿真时间少了约16.52%。
表1中给出了不同均衡器在同一台电脑中的仿真时间,每次仿真取一帧数据,五次迭代。从表中可以看出BP-EP-MF算法比KEF(δ=2)的仿真时间多了约134.44%,比KEF(δ=5)的仿真时间多了约44.16%,比KEF(δ=8)的仿真时间少了约1.41%,比KEF(δ=9)的仿真时间少了约16.52%。
表1 信道估计算法运行时间
Tab.1 Running time comparison of different algorithms
KEF(δ=2)KEF(δ=5)KEF(δ=8)KEF(δ=9)BP-EP-MF仿真时间/s0.35800.58200.85101.00500.8390
6 结论
针对频率选择性慢衰落信道,现有的迭代接收机性能与最优估计性能有较大差距,且复杂度高,本文提出了BP-EP-MF迭代接收机。文中用概率密度函数表示信道模型,便于全局后验概率密度函数因子分解,建立因子图模型。因子图模型可以在图中清楚表示出系统中的所有的未知变量及关系,包括信道抽头和数据符号的相关性。因子图中的非线性因子节点选择MF算法处理降低复杂度。仿真结果表明,本文针对频率选择性慢信道提出的BP-EP-MF迭代接收机在性能方面大幅提升,在复杂度方面略微降低,而且收敛速度加快。
参考文献
[1] Arjmandi H,Movahednasab M, Gohari A. ISI-Avoiding Modulation for Diffusion-Based Molecular Communication[J]. IEEE Transactions on Molecular, Biological and Multi-Scale Communications, 2017, 3(1):48-59.
[2] Colavolpe G, Germi G. On the application of factor graphs and the sum-product algorithm to ISI channels[J]. IEEE Transactions on Communications, 2005, 53(5): 818- 825.
[3] Zhang Jianchun, Ma Xiaobing, Zhao Yu. A Stress-Strength Time-Varying Correlation Interference Model for Structural Reliability Analysis Using Copulas and Practice[J]. IEEE Transactions on Reliability, 2017, 66(2):351-365.
[4] 赵知劲,吴棫. OFDM时变信道的粒子流滤波估计算法[J].信号处理,2016,32(2):244-251.
Zhao Zhijin, Wu Yu. The estimation algorithm of OFDM time-varying channel using particle flow filtering[J]. Journal of Signal Processing, 2016,32(2):244-251. (in Chinese)
[5] Song S, Singer A C, Sung K. Soft input channel estimation for turbo equalization[J]. IEEE Transactions on Signal Processing, 2004, 52(10):2885-2894.
[6] Chugg K M, Polydoros A. MLSE for an unknown channel-Part I: Optimality considerations[J]. IEEE Transactions on Communications, 1996, 44(7): 836- 846.
[7] Anastasopoulos A, Chugg K M. Adaptive soft-input soft-output algorithms for iterative detection with parametric uncertainty[J]. IEEE Transactions on Communications, 2000, 48(10): 1638-1649.
[8] Nissila M, Pasupathy S. Adaptive Bayesian and EM-based detectors for frequency-selective fading channels[J]. IEEE Transactions on Communications, 2003, 51(8):1325-1336.
[9] Li Xin, Wong Tan F. Turbo Equalization with Nonlinear Kalman Filtering for Time-Varying Frequency-Selective Fading Channels[J]. IEEE Transactions on Wireless Communications, 2007, 6(2):691-700.
[10] Dong Jingru, Yin Hang, Wang Sijia. An Improved Message Passing Schedule of BP-Based Decoding Algorithm for LDPC Codes[C]∥IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), 2016:480- 484.
[11] Sun Peng, Zhang Chuanzong, Wang Zhongyong, et al. Iterative receiver design for ISI channels using combined belief-and expectation-propagation[J]. IEEE Signal Processing Letters, 2015, 22(10):1733-1737.
[12] 崔建华, 王忠勇,王法松,等. 无线网络中基于变分消息传递的分布式写作定位算法[J].信号处理, 2017, 33(5): 661- 668.
Cui Jianhua, Wang Zhongyong, Wang Fasong, et al. Distributed cooperative localization algorithm based on Variational massage passing for wireless networks[J]. Journal of Signal Processing, 2017, 33(5): 661- 668. (in Chinese)
[13] Haykin S. Adaptive Filter Theory[M]. Upper Saddle River: Prentice Hall, 1996:105-150.
[14] Kschischang F, Frey B, Loeliger H A. Factor graphs and the sum-product algorithm[J]. IEEE Transactions on Information Theory, 2001, 47(2): 498-519.
[15] Jakes W C. Microwave Mobile Communications[M]. New York: John Wiley & Sons, 1974:11-79.



