1 引言
DS_CDMA(Direct sequence code division multiple access)被广泛地应用于无线通信领域。由于其具有抗干扰能力强、抗衰落性好、保密隐蔽性好等优点, 在航天、卫星测控、导航、军事通信中得到广泛的应用。
非合作侦察中，需要对通信方的信号进行盲接收并提取信息，或对各个用户的通信行为进行实时的监控，首先需要估计出用户数，然后进一步进行码元分析或网络通信行为特征的分析。由于信道的传输损耗(如：随机时延或者多径效应等)，各用户信号在信道中传输时扩频码可能并不完全正交。并且随着天线技术的发展，方向性增强，非合作方的接收信号普遍比合作方的接收信号弱。即需要研究在扩频码元非完全正交、低信噪比的条件下，DS_CDMA系统的快速用户数估计。现行用于系统用户数估计的方法主要有两大类：(1)信息论的方法。传统的信息论方法：Schwartz and Rissanen提出的MDL(Minimum description length criterion)方法和Akaike 提出的AIC(Akaike information Criterion)方法[1]，最早是为了用于阵列信号的信源个数分析，适用于信号与噪声子空间区分较为明显的信源数目分析，不能直接用于DS_CDMA系统用户数估计。随后Shahrokh Valaee等人提出了PDL(Predictive description length)算法，其估计准确率有所提升，但在信噪比低时效果不佳。PDL算法在信噪比为-3 dB时，仅有20%的识别率[2]。(2)假设检验方法。由Veniamin A.Bog等人提出了不变量估计方法。Qing Mou，Ping Wei等人将其用于DS_SS(direct sequence spread spectrum)信号，信噪比较高时估计准确率较高，但信噪比在-8 dB以下时，用户数估计只有10%的准确率[3]。该算法计算量大、时间长，不适用于实时快速的检测，实际运用中可能由于参数设置的偏差，导致估计有较大的偏差，主观因素影响较大。
针对DS_CDMA系统特点，本文提出了一种基于特征值一阶变化率的DS_CDMA用户数估计算法。算法先对数据进行相位非同步的解调处理，解决信息论方法不适用于DS_CDMA系统用户数估计的问题；再通过移位相关，估计出失步点，再提取数据矩阵；最后奇异值分解提取特征值。针对传输中码元不完全正交的情形以及噪声的相似性，采用特征值的变化量作为估计的参量。为快速充分的利用奇异值分解的特征值进行用户数估计，本文选用一阶变化率作为变化量度量，再按照信息论准则对其进行用户数估计。仿真实验表明，本文算法在适用范围和灵敏度方面均有较大提升。
2 DS_CDMA多用户估计算法
2.1 DS_CDMA系统模型
DS_CDMA下行链路中，多个用户同时进行通信，通信信号为BPSK短码扩频信号，则接收机的接收信号为：
(1)
yi(t)=Ai×di(t-T0)×pi(t-nTc)×
cos(ω0t+θi)
(2)
其中，Y(t)表示接收机接收的射频信号；yi(t)表示第i个用户发射的信号； di(t-kT0)表示第i个用户的第k个信息码元；pi(t-nTc)表示第i个用户的扩频序列的第n个码片；Ai为第i个用户的衰落因子；τi为第i个用户随机时延；ω0为载波频率；n0(t)表示零均值加性高斯白噪声；T0表示的是信息码元持续时间；Tc表示的是扩频序列一个码片持续时间,其满足T0=N×Tc。
2.2 算法理论分析
假定已经估计出信号的载波频率
码元宽度T0，伪码长度N。
经典信息论方法中，均是直接对中频信号进行采样，以码元内某个采样点或多个采样点均值作为码片值。但由于其调制有载波，抽样得到的码片值不仅与消息码元有关，也与抽样位置有关，即不同位置抽样值不同。并且若采样频率与载波频率不是整数倍关系，即使对相同码元的抽样值也有差别。
信息论关于特征值分解可以分离出信号和噪声子空间的证明[1],只是证明载波频率不同的非扩频信号可以通过特征值分解估计信号源个数。即使后来关于扩频信号的特征分解可以区分出信号和噪声的证明[2,8-11]，只是证明了基带扩频信号的可分解性，没有明确证明：中频扩频信号采样值可以通过奇异值分解区分信号和噪声。
而对于中频信号而言，采样率不同或采样位置不同，奇异值分解的结果差异较大。因此，本文首先对接收机中频A/D采样的信号进行预处理，去除载波。
首先对接收的信号进行相位非同步的解调，将信号降到基带再进行采样。设用于解调的载波信号为：
为任意值，解调后的信号为：
(3)
若载波估计准确即
则载波相位的未同步分量对于信号幅度的影响因子cos(θi-θ0)和信号传输过程中各用户信号衰减因子Ai均为常量，为便于分析，将其等效为一个衰减因子
虽然这种衰减会影响估计结果，由于噪声的高斯性，可以通过累积方式来抑制噪声，放大信号。
对解调信号Y*(t)进行带宽为2/Tc的低通滤波，再以码速率1/Tc采样，将各个码片抽样点按列构成如下消息矩阵：
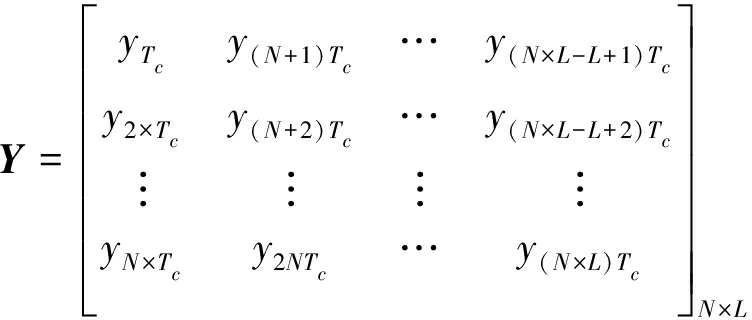
(4)
其中，Y为基带抽样信号构成的消息矩阵，yk×Tc表示的是第k个码片的抽样值；依据短码扩频信号的模型[1-2,8-9]，消息矩阵可以等价为：Y=H×D+S，其中
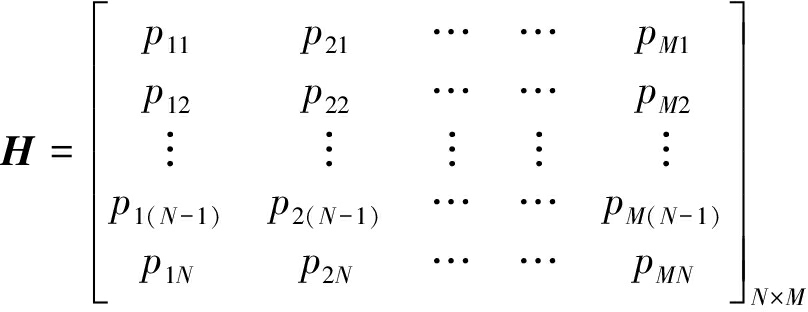
(5)
(6)
其中，H为扩频序列矩阵，第i列表示第i个用户的扩频序列；D为消息矩阵， di, j表示第i个用户的第j个消息码元。S为高斯白噪声矩阵。
实际系统中各用户通信起止时间一般不同，则接收信号中各用户信息码元存在错位，不完全对准。且对接收信号提取一个持续时间为码元周期T0的样值点时，实际却可能包含两个码元，即包含前一个码元后半部分和后一个码元的前半部分。这就使得Y中的每一列含有不同码元。故本文选取消息矩阵Y中的N*行和P*列形成矩阵
满足M≤N*≤N，M≤P*≤P)，使得矩阵Y*的每一列属于同一个信息码元。
为了保证Y*中各列的样值点均属于同一码元，需要在提取Y*之前对失步点进行粗估计。本文选用了M Sun,LX Tian关于失步点估计的方法，即循环移位估计[5]。该算法计算量小，耗时较短，满足快速计算要求。循环移位方法流程：对接收信号取持续时间为一个扩频周期的样值点，对此段信号进行移位自相关，再对相关值求和,最后作出各个移位点对应的相关值图像，各个峰值点即为各个用户码元粗略起始点估计。本文算法只需取一段不含有相关峰值的N*个样值点，构成Y*第一列，然后隔一个扩频周期取相同位置的N*个样值点构成Y*。
对
求相关矩阵G:
G=(Y*)H×Y*=D*H×HH×H×D*+δ2I
=D*H×D*+δ2I
(7)
对矩阵G进行奇异值分解。在扩频序列完全正交的条件下，提取出的特征值按从大到小排列理论上满足[1-2,12]:
λ1≥λ2≥λ3…≥λM≥λM+1=λM+2…=λN
(8)
经典信息论估计方法就是基于噪声子空间特征值相同的条件，进行的用户个数判断。但由于实际中信道带宽有限的原因，抽样所得的扩频序列不可能保证完全正交，并且各用户扩序列的不完全对准以及传输中噪声影响都会使得抽样所得的扩频码元正交性进一步减弱，信号会扩散到噪声子空间中，导致噪声子空间特征值也不相同，即λM+1≥λM+2…≥λN。由于噪声的高斯性，其变化率基本保持一致，并且相对于信号子空间伪随机的特征值变化率有明显差异。因此，本文选取特征值的变化量作为信息论准则的衡量参数。为了简化计算，本文选用L个一阶变化率作为一次度量，然后按照如下的信息论准则进行信源数目估计：
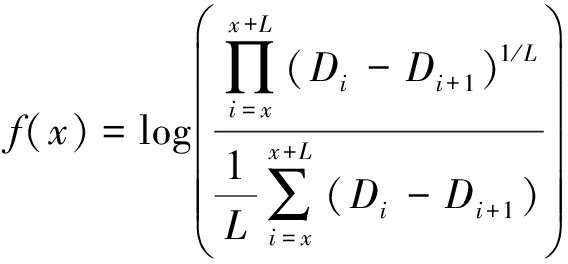
(9)
对于式(9)， L个特征值变化率Di越是类似， f(x)值越小，并且在L个特征值变化率Di完全相同时， f(x)达到最小值。当L个变化率均属于噪声子空间时，其变化率基本一致， f(x)值较小；而L个变化率含有信号子空间的值时，其变化率波动较大， f(x)值较大。本文算法从f(x)的函数值最后一个点开始搜索，以连续高速上升的初始点对应的x值作为估计值，信号源个数M=x-1。如图1是13个用户的信号数目估计效果图，以图中的标注点x=14为估计点，估计的用户个数为M=14-1=13个。
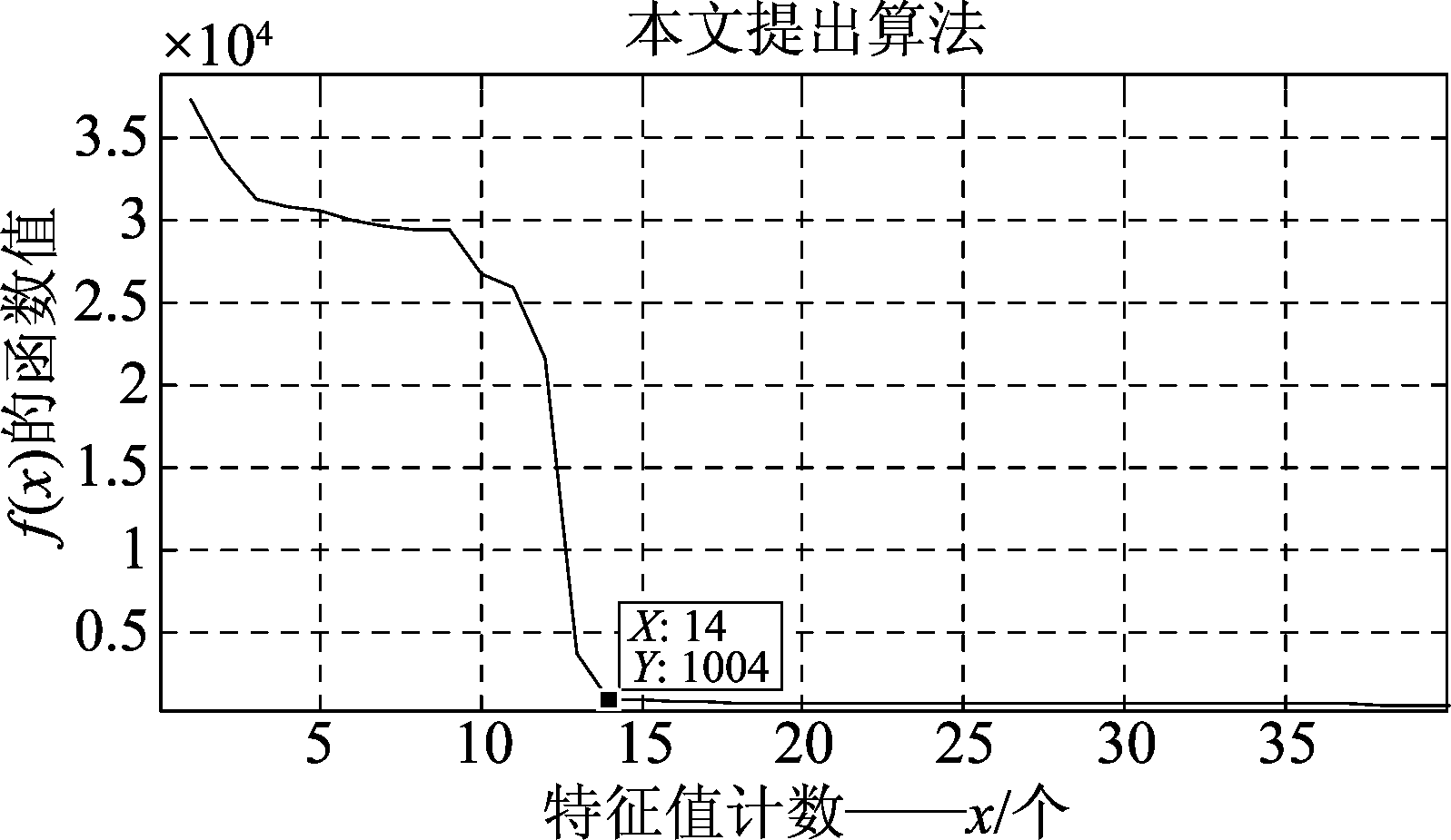
图1 13个用户的信号数目估计
Fig.1 Estimate of the number of signals from 13 users
2.3 算法流程：
(1)对于接收机中频A/D采样输出的信号，通过信号检测估计出其载波频率ω0，码元宽度T0，伪码长度N。
(2)相位非同步解调。用估计出的载波信号：C=cos(ω0t+θ0)，θ0取任意[0～2π]，对接收信号进行解调。
(3)低通滤波，码速率采样。对信号进行带宽为2/Tc的低通滤波，再以码片速率1/Tc进行抽样得到基带扩频序列y(k×Tc),k∈1,2,3,…。
(4)失步点估计，构造矩阵取持续时间为T0的一段样值点，对此段信号进行依次移位，再自相关求和，做出移位点与相关值的图像。找峰值之间间距最大的两个连续峰，在这两个峰之间，取N*个连续码片样值点作为第一列，每隔一个码元周期取相同位置 N*个连续码片样值点，构成各列，形成矩阵满足M≤N*≤N，M≤P*≤P)。
(5)求相关阵G=(Y*)H×Y*,对矩阵G进行奇异值分解，提取出特征值，构成向量D1×p*=[D1,D2,…,Di]。
(6)求特征值一阶变化率向量
本文取长度L为P*/4)。依次对于第x个值，以式(9)求取函数值f(x),x=[1,2,…,i-1-L]。从f(x)的函数值最后一个点开始搜索，找出连续快速上升的起始点对应的x值，估计信号源个数为M=x-1。对于其中连续快速上升起始点的搜寻方法，取噪声的特征值变化率的2倍作为阈值
(本文取最后10个特征值变化率，以其均值的3倍作为阈值Q)，从最后一个特征值开始搜索，当出现连续两个特征值变化率的绝对值均大于阈值Q时，即以先搜索到的大于阈值的点作为连续高速上升的初始点。
3 实验验证
实验1 实验条件：用户个数为13个，扩频码长N为1023的均衡Gold序列[13]，载波频率24 MHz，码元速率为6×106 Baud，采样频率96 MHz。噪声为高斯白噪声，信噪比SNR为0 dB。三次实验分别为：(1)各用户使用同一载波且均同步；(2)各用户载波初相位随机且均同步；(3)各用户载波相位随机并且各用户不同步。比较本文算法、PDL、AIC修正算法以及不变量检测算法的估计性能。仿真实验中，行数N*和列数P*分别选取200和600，使用的数据占据时长约为100 ms,本文提出的算法估计用户数所使用的平均时长为1.1 s(文中不考虑信号检测估计载波频率、码速率的时间)。进行1000次蒙特卡罗仿真实验，各算法估计准确率如表1所示。
表1 不同载波初相、同步和非同步条件下，各估计算法的准确率
Tab.1 The accuracy of each estimation algorithm under different initial carrier phase,synchronous and non-synchronous conditions
实验条件本文算法PDLAIC-modify不变量检测载波初相相同、同步95%94%89%93%载波初相随机、同步94%91%80%89%载波初相随机、不同步92%83%77%86%
由统计结果可见，本文算法在同步和非同步情况下均可以较好的识别出系统中用户的个数。在特殊情况下，若用于解调的载波初相位与某一实际信号的相位差非常接近π/ 2，使得衰减因子cos(θi-θ0)几乎为零，可能需要通过大量数据累计来放大信号，数据较少可能会出现估计信号数比实际信号数少一个。实际中可通过独立重复实验估计用户个数，克服估计随机性。
实验2 实验条件: 用户个数为20个，载波频率相同，相位随机且各用户均不同步。其余信号参数与实验1相同。观察随着信噪比降低各个算法的估计准确率。仿真实验中，行数N*和列数P*分别选取200和600，使用数据占据的时长约为100 ms，本文提出的算法估计用户数所使用的平均时长为1.1 s。统计1000次独立实验中估计结果准确的次数。不同信噪比条件下，各算法的估计准确率如表2所示。
表2 不同信噪比条件下，各个算法的用户数估计准确率
Tab.2 The accuracy of estimation versus SNR for the proposed algorithm, AIC and PDL algorithms
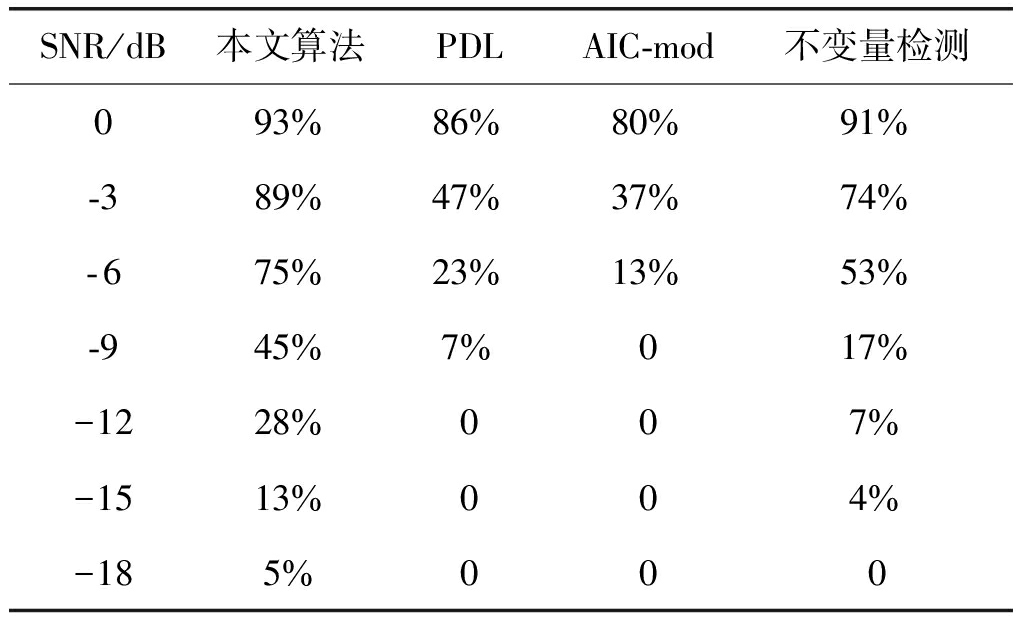
SNR/dB本文算法PDLAIC-mod不变量检测093%86%80%91%-389%47%37%74%-675%23%13%53%-945%7%017%-1228%007%-1513%004%-185%000
可以发现随着信噪比降低，偏差会逐步加大。通过进一步实验发现，估计准确率与码元的采样位置有一定关系，如果采样点在码元的边界处，由于码间串扰等因素影响，采样值可能有较大误差。由于实际系统中普遍存在失步现象，各个用户码元不可能对准，接收机采样点无法对准所有用户码元的中间位置，所以估计有一定偏差。在低信噪比条件下，可以通过增加数据长度P*来提升估计准确率。
实验3 实验条件:各个用户载波相位随机，且非同步。其余信号参数均与实验1相同(SNR=0 dB)。观察随着用户个数变化本文算法的估计准确率。进行1000次蒙特卡罗仿真，统计结果如表3所示。
表3 不同用户个数条件下，本文算法的估计准确率
Tab.3 The accuracy of estimation versus the number of users for the proposed algorithm
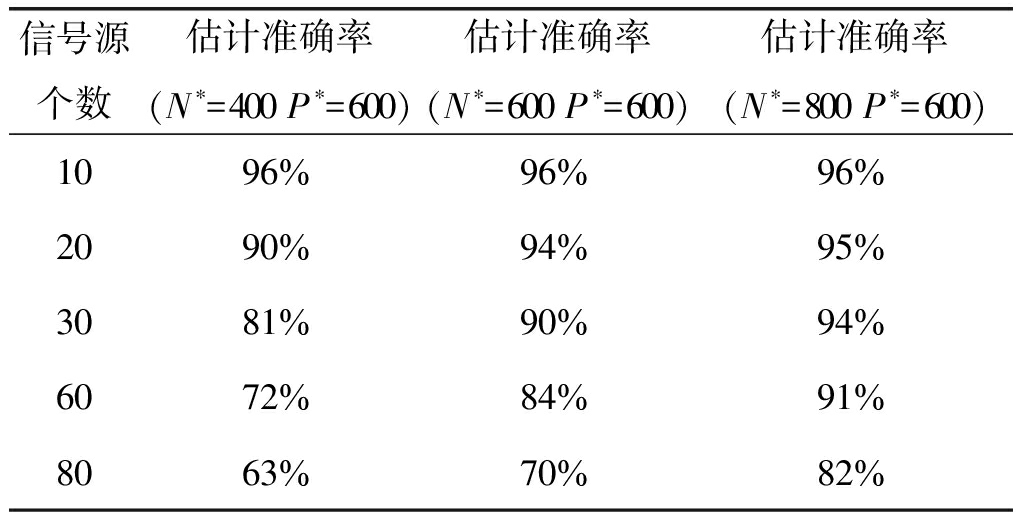
信号源个数估计准确率(N∗=400 P∗=600)估计准确率(N∗=600 P∗=600)估计准确率(N∗=800 P∗=600)1096%96%96%2090%94%95%3081%90%94%6072%84%91%8063%70%82%
结果统计发现：随着用户个数增加，起初估计准确率几乎保持不变；当用户个数增长到一定门限值时，用户估计准确率会随着用户个数的增加而快速下降。并且随着N*的增大，这个门限值就越高，用户数的估计就越准确。实验3使用的数据时长约为150～200 ms，本文算法估计用户数所使用的平均时长为1.7 s。随着信号源的个数的增加，码元之间的正交性减弱，同时噪声的影响增大。实际在通过增加N*，牺牲时间来增加使用数据数量，提升估计准确率。
实验4 实验条件: 用户个数为10个，载波频率24 MHz，码元速率为6×106 Baud，采样频率96 MHz。噪声为高斯白噪声，信噪比SNR为0 dB。假设估计的用户载波频率存在偏差，观察随着估计载波频率的变化本文算法的估计准确率。进行100次蒙特卡罗仿真，统计结果如图2所示。
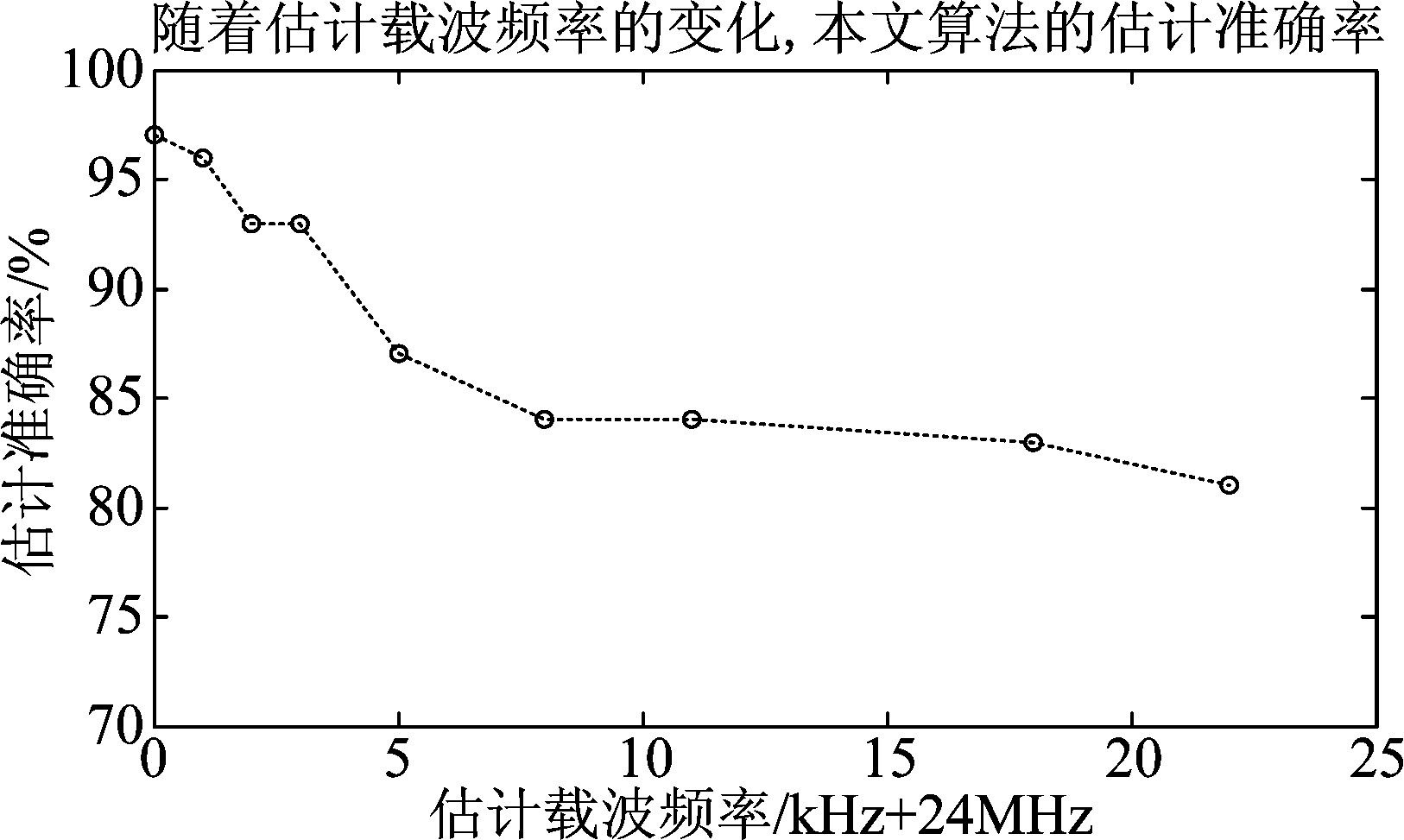
图2 随着估计载波频率的变化，本文算法的估计准确率
Fig.2 The accuracy of the algorithm in this paper versus the estimation of carrier frequency
由实验4可以发现，当频偏较小时，频偏相对于数据预处理的影响较小。随着频偏继续增大，准确率降低之后趋于稳定。实际操作中，如果频率偏差在较小的范围内，由于码元速率远高于因估计不准确导致的残余载波的频率，因此对每个码元持续时间T0内的抽样值带来较小的误差。故小频偏对算法性能影响较小。并且实际的载波估计算法可以将载波估计误差控制在5 kHz范围内。
4 结论
本文针对DS_CDMA系统的快速多用户估计，先对信号进行相位非同步的解调处理，提升样值点的可靠性；然后进行失步点估计，保证使用各用户同一个码元的数据构造矩阵；再进行奇异值分解；最后采用基于特征值一阶变化率的信息论方法进行用户数估计。仿真实验表明，本文算法可以在2 s内快速估计出系统用户的个数，并且在同步和非同步系统中均具有较好的估计效果，也适用于扩频码元一定程度上非正交的情况。较于其他算法，在信噪比为-6～-12 dB时，估计准确率提升15%～20%。该算法在非合作通信信号侦察中，具有较好的应用前景。
参考文献
[1] Wax M, Kailath T. Determining the number of signals by information theoretic criteria[C]∥Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP. IEEE, 1984:232-235.
[2] Valaee S，Shahbazpanahi S. Detecting the number of signals in wireless DS-CDMA networks[J]. Communications IEEE Transactions on, 2008, 56(7):1189-1197.
[3] Mou Q, Wei P, Tai H M. Invariant detection for QPSK DS-SS signals[J]. Signal Processing, 2010, 90(5):1720-1729.
[4] Kay S M, Gabriel J R. Optimal invariant detection of a sinusoid with unknown parameters[J]. Signal Processing IEEE Transactions on, 2002, 50(1):27- 40.
[5] Sun M, Tian L X. Blind synchronization and sequences identification in CDMA transmissions[C]∥Military Communications Conference, 2004.Milcom 2004.IEEE, 2004,Vol.3:1384-1390.
[6] Zhen J, Qin D, Wang Z. Method of determining number of wideband signals based on Bootstrap technique[C]∥International Conference on Communications and NETWORKING in China, 2015:365-370.
[7] Farsi N, Escrig B, Hamza A. Estimation of the number of signals based on a sequence of hypothesis test and random matrix theory[C]∥Complex Systems. IEEE, 2016.
[8] Fishler E, Grosman M, Messer H. Determining the Number of Discrete Alphabet Sources from Sensor Data[J]. Eurasip Journal on Advances in Signal Processing, 2005, 2005(1):1-9.
[9] 熊伟杰. 直扩信号盲估计技术研究[D]. 成都：电子科技大学, 2015.
Xiong Weijie.Study on blind estimation technology of DS signal[D]. Chengdu: University of Electronic Science and Technology, 2015. (in Chinese)
[10] 牟青. 直接序列扩频信号的截获分析研究[D]. 成都：电子科技大学, 2010.
Mou Qing.Study on Intercept Analysis of Direct Sequence Spread Spectrum Signal[D]. Chengdu: University of Electronic Science and Technology, 2010. (in Chinese)
[11] 程皓. 低截获直扩信号参数盲估计方法研究[D]. 成都：电子科技大学, 2007.
Cheng Hao. Research on Blind Estimation Method for Low Intercept Direct Sequence Signal[D]. Chengdu: University of Electronic Science and Technology, 2007. (in Chinese)
[12] Horn R A, Johnson C R. Matrix Analysis[J]. Graduate Texts in Mathematics, 2012, 169(8):1-17.
[13] 田日才, 迟永钢，等. 扩频通信[M]. 北京：清华大学出版社, 2014.
Tian Ricai, Chi Yonggang, et al. Spread spectrum communication[M]. Beijing: Tsinghua University Press, 2014. (in Chinese)
