1 引言
BPSK(Binary Phase Shift Keying)信号是数字通信中经常采用的调制信号。它具有较高的频带利用率、较强的抗噪声干扰能力和具备展宽信号带宽的优势,难于探测[1]。因此,相移键控经常应用于军事通信、低截获概率雷达信号,并且它也是和扩频技术结合最成熟的调制技术。
对于作为非合作方的第三方无线电监测,由于接收到的信号往往都比较弱,因此对微弱BPSK信号的盲检测是一个重要课题。当前,相移键控信号的盲检测有很多方法,如文献[2-3]采用高阶累积量和循环谱的检测方法,文献[4]采用联合频谱估计与循环矩的检测方法,文献[5]采用最大自然准则估计方法,文献[6]采用基于星座图的检测方法,文献[7]采用随机共振相移键控信号参数估计方法,以及早期采用的各种时频分析检测方法等。这些方法大部分需要在信噪比大于0 dB才能取得良好效果,对于信噪比低于-10 dB的微弱相移键控信号检测,很多方法效果不明显。
自混沌理论应用于微弱信号检测以来,由于其可在较低信噪比下检测出微弱信号的存在,受到了越来越多研究者的重视。在实际应用中,常常采用Duffing系统作为产生混沌现象的非线性系统。Duffing振子对与系统策动力同频率的小信号具有敏感性,而对高斯噪声信号具有极强免疫力,因此,利用Duffing振子在混沌态到周期态的分岔行为,可以判断出强噪声中是否存在微弱周期信号。
在Duffing振子检测微弱信号理论和方法的研究方面,文献[8]提出变尺度微弱信号检测方法,解决不同频率下的参数确定问题。文献[9-10]提出从周期态向混沌态的逆向相变检测方法,减少相变过渡带的影响。文献[11]提出策动力移相法用于消除检测盲区,构造基于类Halmiton系统的检测统计量作为系统状态量化判断标准。文献[12]提出了利用哈密顿量构造统计量的定量判别方法,有利于在短时间内进行判决。文献[13]将小波变换与Duffing振子结合检测微弱信号,达到了一定效果。文献[14]基于van der Pol-Duffing振子进行微弱信号检测,在-45 dB信噪比下仍可以检测出信号。文献[15]可以实现对多频率信号的检测。文献[16]提出适应步长型检测方法,提高弱信号检测性能。这些文献资料主要是针对周期弱信号检测的。
在Duffing振子检测相移键控信号的研究方面,文献资料比较少,主要原因在于信号与Duffing系统的频差以及信号本身相位的变化会导致Duffing系统相图呈现复杂的状态。文献[17]对采用Duffing振子检测相移键控信号进行了研究,可以在-28 dB信噪比下取得较好效果,但不能应用于盲检测。文献[18]建立了识别相移键控信号识别模型,但它们只针对信号频率与Duffing系统内置信号频率同频的情况。文献[19]建立了基于Duffing振子的相移键控信号调制识别算法,但同样需要知道载频频率的先验知识,并且信噪比要求较高(-5 dB以上)。
本文在研究Duffing振子周期信号检测基础上,指出Duffing系统策动力(内置信号)之间与输入信号之间的频差和相差将使系统将进入周期性混沌状态,而对BPSK信号,系统将进入间歇性混沌状态。本文采用时序图法表征间歇性混沌状态,并利用改进的S变换算法提取时序输出包络以提高系统状态判断准确性,分析了方程控守频带范围,最后通过正相振子和反相振子检测方程建立了微弱BPSK信号盲检测模型并进行了仿真实验。
2 Duffing振子微弱周期信号检测
2.1 频率相位匹配时检测原理
考虑Holmes型Duffing方程[20]:
(1)
式中,k为阻尼率;-x+x3为非线性恢复力,由于Duffing方程中具有此非线性项,使得方程具有丰富的非线性动力学特性[21];Fcos(ωt)为系统内置信号也即系统策动力,F表示内置信号幅值,ω表示内置信号角频率也即振子的固有频率。方程(1)也可写为:
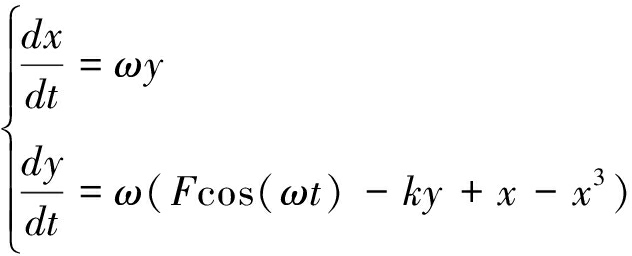
(2)
研究Duffing方程动力学过程,Duffing振子相轨迹具有如下特性:固定k值,1)当F=0时,相轨迹从任意初始值开始的演化轨道收敛到焦点(±1,0)中的一个;2)当F≠0时,F较小,相轨迹逐渐收敛到两个焦点之一。随着F的增大,相轨迹由周期逐渐演化为混沌运动,并在较大范围内保持混沌运动。当F大于某一个阈值Fr(Fr称为临界值)时,系统相轨迹由混沌态跃迁为大尺度周期态。
在方程(2)中取参数k=0.5,初始值x(0)=0,y(0)=x′(0)=0,采样速率fs=40 MHz,采样点数10000点,内置信号频率f=ω/(2π)=1 MHz,采用四阶Runge-Kutta算法对微分方程进行求解,去除暂态后得到系统的相轨迹。当F=0.825时,系统处于混沌态,如图1(a)所示;当F=0.826时,系统处于大尺度周期态,如图1(b)所示。从图形可以看出,系统参数F的微小变化将引起系统状态从混沌态到周期态的跃迁。因此,F=0.825认为是系统状态改变的临界值Fr。
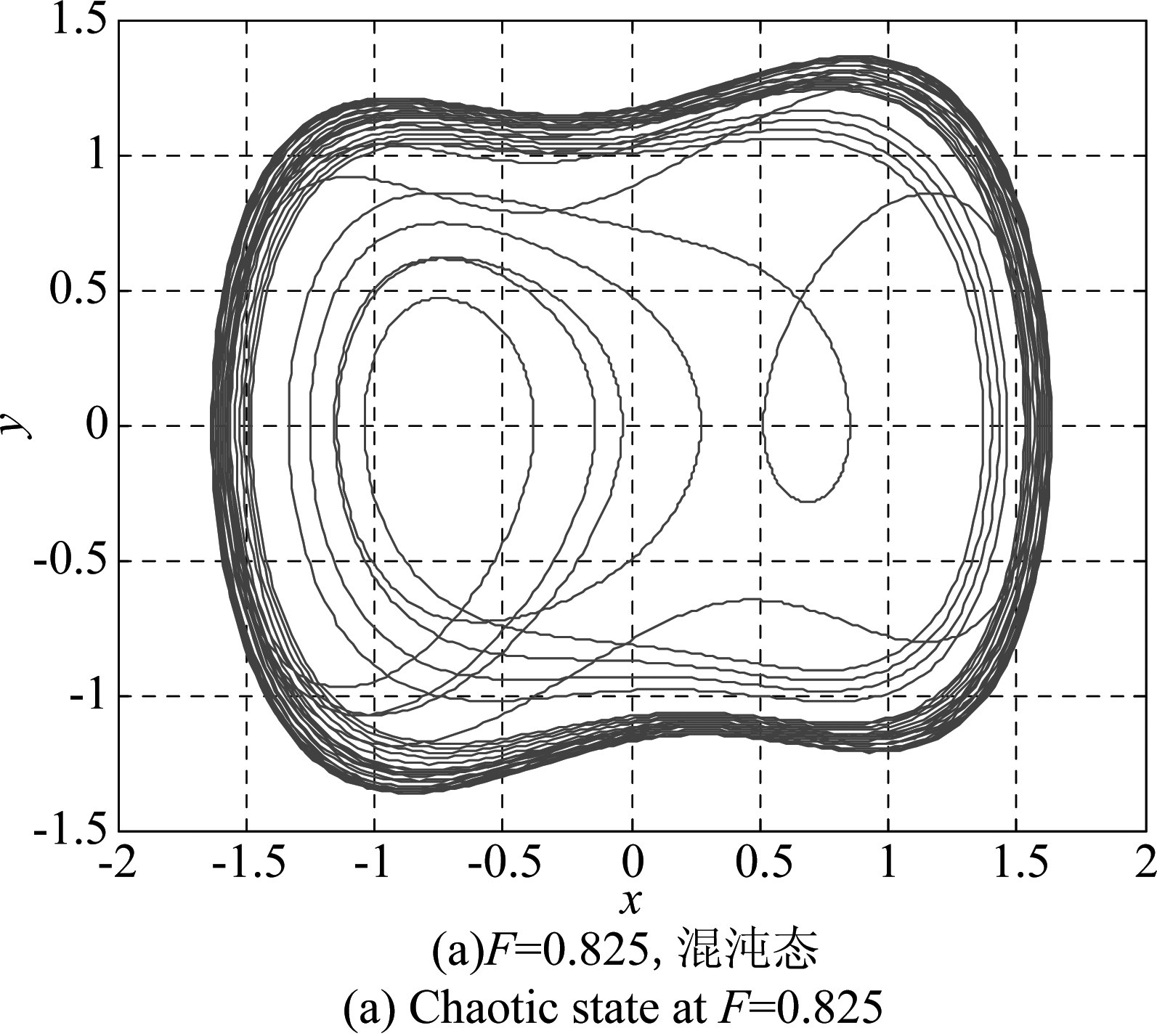

图1 Duffing振子混沌态和周期态相轨迹分布
Fig.1 Phase trajectory distributions of chaotic and periodic state
在对弱信号检测时,系统内置信号幅值设定为临界值Fr,将含有高斯白噪声n(t)的待测信号s(t)作为周期驱动力的摄动输入到系统中,则弱信号检测模型为:
Frcos(ωt)+s(t)+n(t)
(3)
当待测信号中包含同频的微弱周期小信号且与参考信号相位一致时,叠加后的策动力幅值将超过临界值,系统发生正向相变,进而判断待测信号中微弱周期信号的存在。
取s(t)=0.01cos(2πfct), fc=1 MHz,噪声为高斯白噪声,SNR=-30 dB。Duffing系统实验参数同图1,可以得到Duffing系统在Fr=0.825处的相轨迹输出如图2所示,系统处于周期态,判断存在微弱信号。
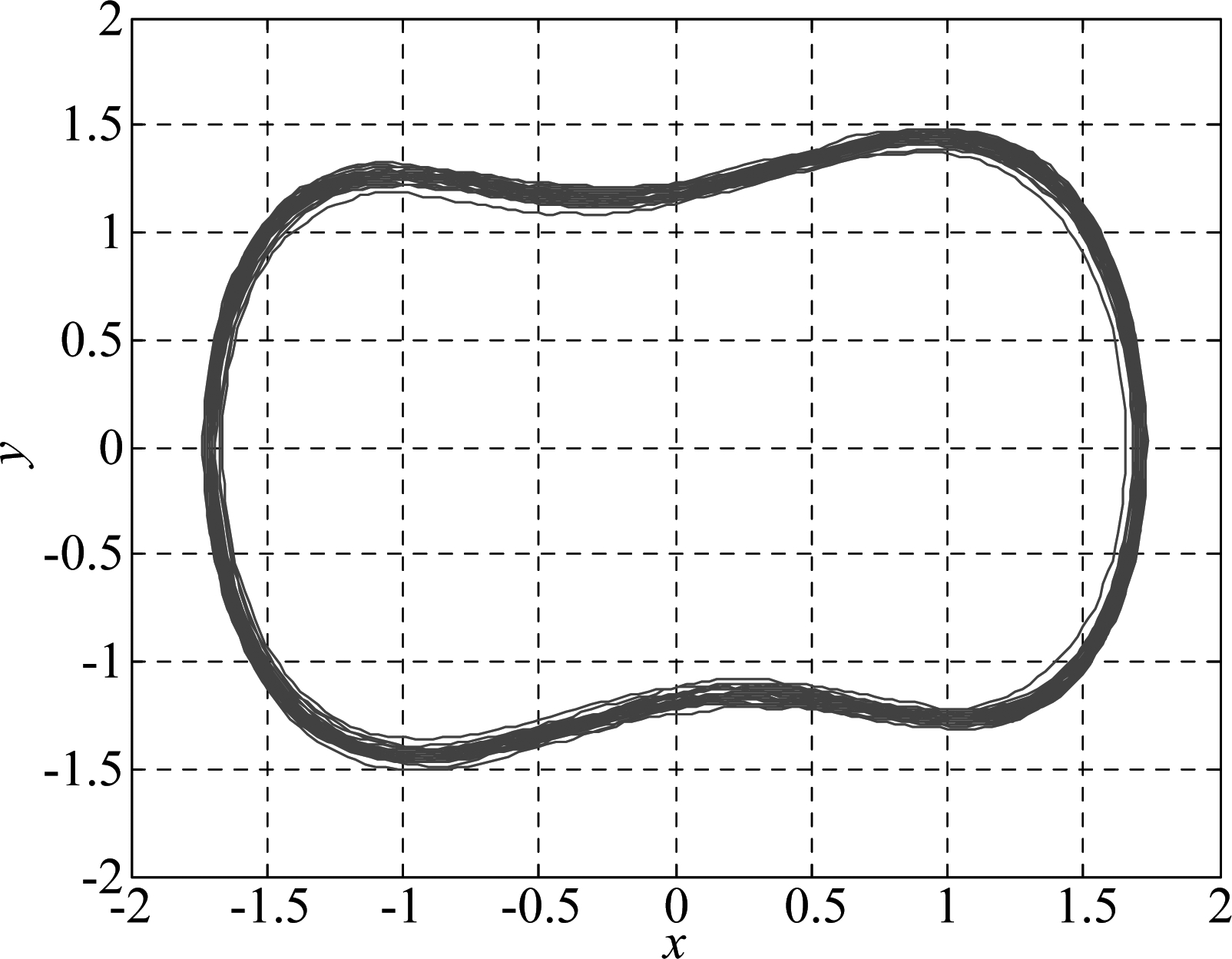
图2 匹配输入信号的Duffing系统相图
Fig.2 Phase figure of Duffing system with the matched input signal
2.2 频率相位不匹配对Duffing系统相图影响分析
考虑一般情况,输入信号Input为:
Input=s(t)+n(t)=Acos((ω+Δω)t+φ)+n(t)
(4)
即待检信号s(t)与Duffing系统内置信号存在频差Δω和相位差φ,A为待检信号幅度。此时,在临界门限下,Duffing系统周期驱动力r(t)可以写为:
r(t)=Frcos(ωt)+Acos((ω+Δω)t+φ)=
B(t)cos(ωt+θ(t))
(5)
其中,
(6)
(7)
现在,只考虑微弱信号情况,即A≪Fr,A/Fr→0,则有:
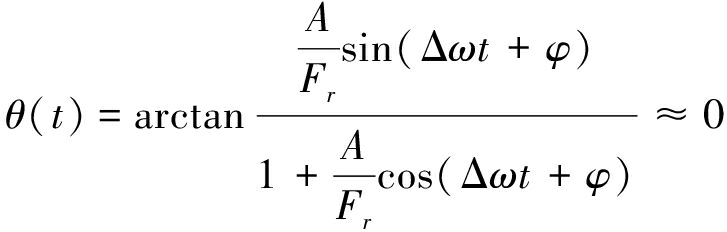
(8)
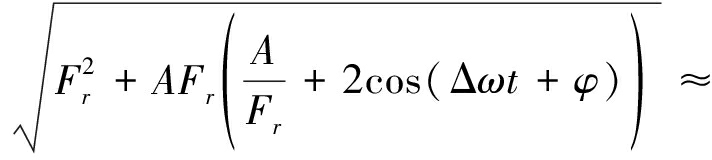
(9)
对于未知频率相位信号,大部分存在频差1Δω1≠0和相差φ≠0。由式(9)可以得出:
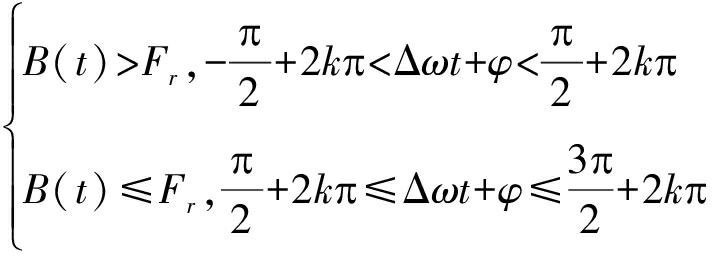
(10)
当![]() 时,输入信号幅度B(t)大于系统临界值Fr,系统处于周期态;当
时,输入信号幅度B(t)大于系统临界值Fr,系统处于周期态;当![]() 时,输入信号幅度B(t)小于等于系统临界值Fr,系统处于混沌态。令Δω=2πΔf,B(t)将以周期2π/1Δω1(即1/1Δf1)大于和小于临界值Fr,使得Duffing系统也将以周期1/1Δf1在周期态和混沌态之间转换,且周期态和混沌态持续时间都为π/1Δω1(即1/(21Δf1)),系统进入周期性混沌状态。
时,输入信号幅度B(t)小于等于系统临界值Fr,系统处于混沌态。令Δω=2πΔf,B(t)将以周期2π/1Δω1(即1/1Δf1)大于和小于临界值Fr,使得Duffing系统也将以周期1/1Δf1在周期态和混沌态之间转换,且周期态和混沌态持续时间都为π/1Δω1(即1/(21Δf1)),系统进入周期性混沌状态。
可见,频差1Δω1的存在,将使得Duffing系统相轨迹处于一个不稳定的状态中,系统相图一会处于周期态,一会处于混沌态。随着频差1Δω1的增大,相轨迹状态变化周期减小,在周期态和混沌态之间切换的频率加快。
仿真实验如下。取频差Δf=Δω/(2π)=5 kHz,为简化讨论,令相差φ=0,其他实验条件同上。得到Duffing系统相图如图3所示。
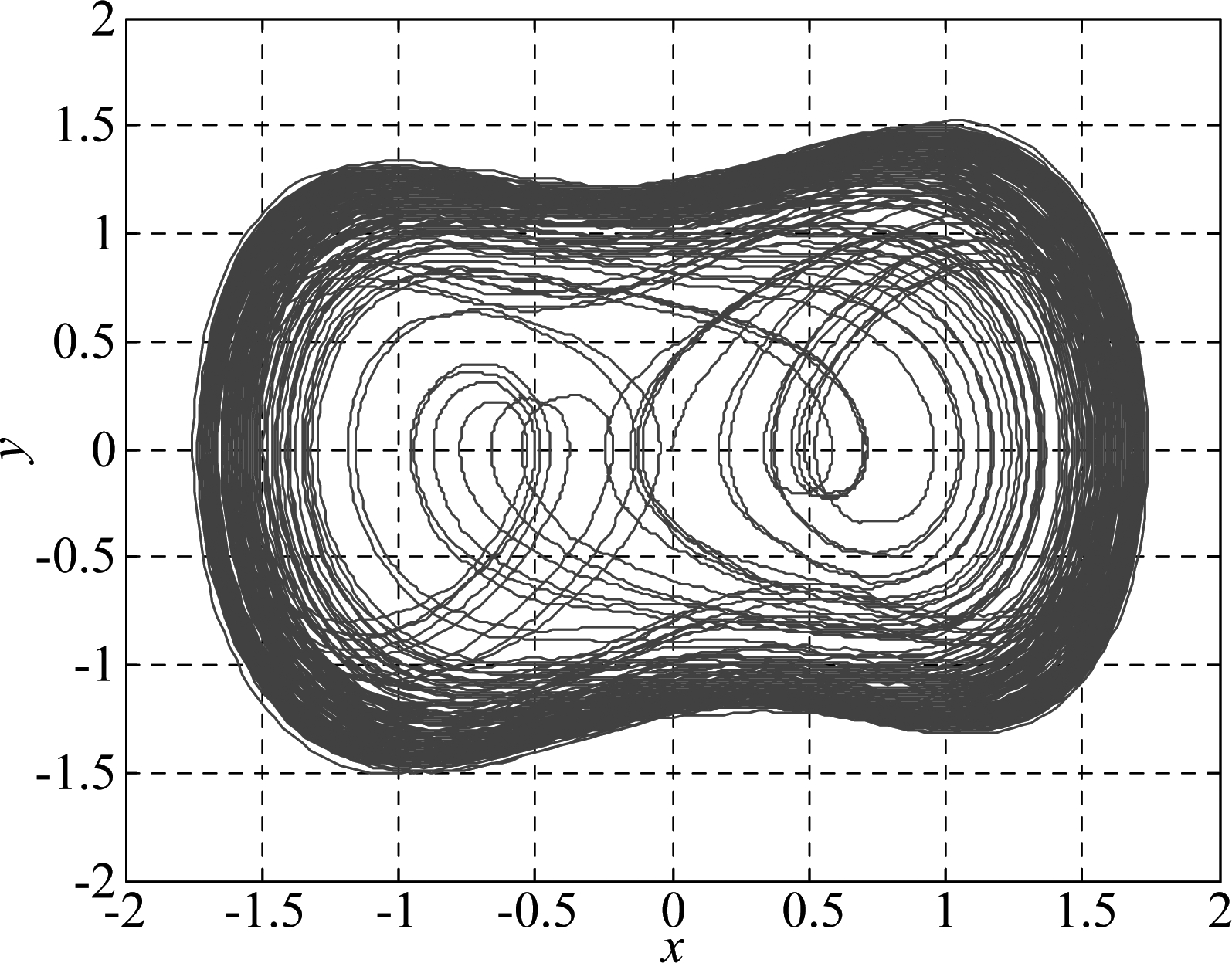
图3 Δω≠0,φ=0时Duffing系统相图
Fig.3 Phase figure of Duffing system at Δω≠0, φ=0
以1/4周期(即![]() 对系统相图进行分段得到的分段Duffing系统相轨迹演化如图4所示。
对系统相图进行分段得到的分段Duffing系统相轨迹演化如图4所示。
从图3可以看出,在整个采样时间内,系统相图呈混沌态,似乎检测不出有待检信号的存在。但由图4,Duffing系统相轨迹演化实际上以1/4周期(即![]() 周期性呈现混沌态和周期态。图4只给出了一个周期内的变化情况,如果继续分析下一周期,会得到同样的结果。对频率相位不匹配的微弱周期信号检测,主要判断系统是否处于周期性混沌状态。
周期性呈现混沌态和周期态。图4只给出了一个周期内的变化情况,如果继续分析下一周期,会得到同样的结果。对频率相位不匹配的微弱周期信号检测,主要判断系统是否处于周期性混沌状态。
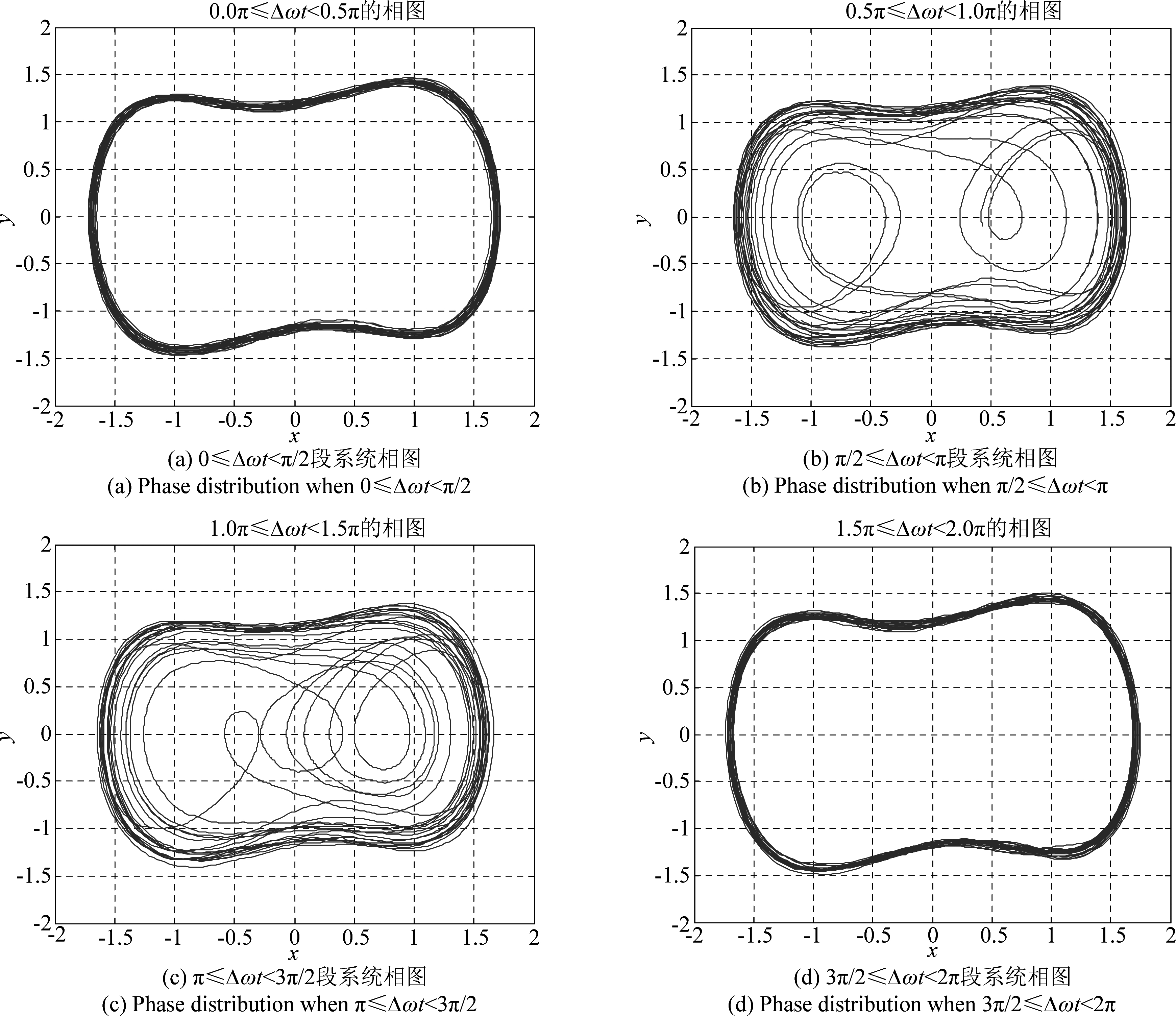
图4 Δω≠0,φ=0时Duffing系统分段相图
Fig.4 Segment phase figures of Duffing system at Δω≠0, φ=0
综合以上两点,可以看出,对于任意的待检信号s(t)=Acos((ω+Δω)t+φ),当信号s(t)与Duffing系统内置信号存在频差Δω和相位差φ时,相差φ只会影响系统是处于周期态还是混沌态,但系统相图的状态是稳定的;而频差Δf将使系统相图处于周期性混沌的不稳定状态当中,相轨迹演化一会儿处于混沌态,一会儿处于周期态,并以周期1/1Δf1交替出现,周期态和混沌态持续时间相同,为tspan=1/(21Δf1)。
3 Duffing振子微弱BPSK信号盲检测模型
3.1 BPSK信号
相移键控是利用载波的相位变化来传递数字信息,而振幅和频率保持不变。双极性BPSK信号的时域表达式可以表示为[1]:
(11)
若BPSK信号“1”码和“-1”码等概率出现,可以得到BPSK信号的功率谱密度为:
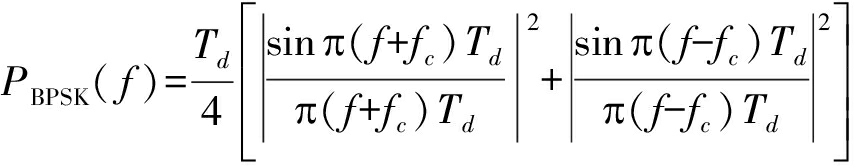
(12)
式中,Td为基带信号码元周期。
从式(12)可以看出,BPSK信号的功率谱中无载波分量,实际上是抑制载波的调制信号,从频谱上直接分析是否存在微弱BPSK信号是比较困难的。
3.2 基于S变换时序图法混沌状态判别
对微弱BPSK信号的盲检测,由于不知道BPSK信号的频率,并且其相位在不断变化当中,在频偏和相位的双重影响下,此时Duffing系统相图处于不具有周期性的间歇性混沌状态。因此,对微弱BPSK信号Duffing系统状态的判别,需要密切和时间关联,这样才能准确判断系统在某一时刻是处于周期态还是混沌态,进而判断微弱信号的存在。
对混沌特性的判定,目前通常采用的方法主要包括相平面法、Lyaponov指数法和时序图法[18]。
相平面法就是得到混沌系统运动轨迹图像,如上面分析所采用,然后对相图进行图像识别,判断系统是处于周期态还是混沌态。系统是一段时间内的整体轨迹。
Lyaponov指数法是采用Lyaponov指数来表征系统在相空间中相邻轨道间收敛或发散的平均指数率。对一维映射xn=f(xn),Lyaponov指数定义为[22]:
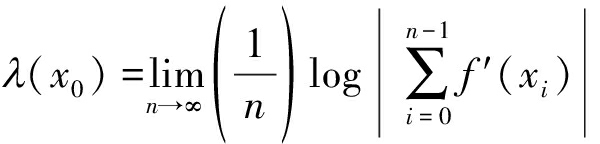
(13)
可见,Lyaponov指数是沿轨道长期平均的结果,是一种整体特征。
时序图法是指混沌系统在混沌态和周期态具有不同的输出时对应的不同时序图,其反应了在不同时间Duffing系统输出。因此,这种方法更适合反映间歇性混沌在各个时间的状态。
可以得到在混沌态和周期态下Duffing系统输出x的时序图如图5所示,实验条件同图1。

图5 Duffing振子混沌态和周期态时序图
Fig.5 Sequence diagram of chaotic and periodic state
从图5看出,当系统处于混浊临界状态时,系统并没有固定的周期。当系统跃变到大尺度周期状态时,系统拥有了固定的周期。这些差别,直接在频率域上分析很难区分,但混沌态和周期态对Duffing系统输出的包络产生了比较明显的影响,在混沌态下,Duffing系统输出包络起伏较大,而在周期态下,包络恒定。为了更清晰反应时序输出包络的变化,本文采用S变换来直接提取Duffing系统输出时序包络。
S变换是在连续小波变换和短时傅里叶变换基础上发展起来的一种时频分析方法,同其他时频方法相比,具有多分辨特性、无交叉项、计算速度快等特点[23-25]。
信号h(t)的S变换定义为:
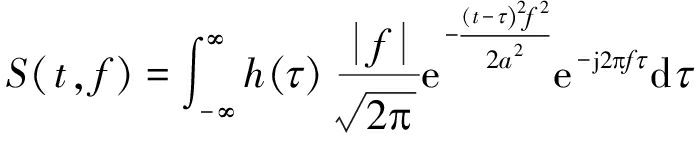
(14)
式中,a为常数。S变换对应的窗函数为:
(15)
其中![]() 为尺度因子。
为尺度因子。
S变换离散变换形式为:
(16)
其中k=0,1,…,N-1;n=1,…,N-1。N为采样点数。为了进一步提高运算速度,采用文献[25]提出的改进离散S变换算法提取Duffing系统输出时序包络。
仿真实验如下。
(1)无频差
BPSK信号仿真在式(11)中取A=0.01, fc=1 MHz,码元速率fd=1/Td=40 kHz,采样速率fs=40 MHz,采样点数N=10000,噪声为高斯白噪声,SNR=-30 dB,Duffing系统参数设置同图2。S变换中,为了更好提取f=1 MHz的Duffing系统时序输出包络和反映包络变化,窗函数w(t)在f=1 MHz处的时窗宽度取为4.68 μs。此时,BPSK信号与Duffing系统内置频率同频,可以得到Duffing系统时序输出和在f=1 MHz处S变换包络提取结果如图6所示。

图6 无频差BPSK信号Duffing振子输出时序图及包络
Fig.6 Sequence diagram and envelope of Duffing system output with no frequency difference
从图6可以看出,当输入信号与Duffing系统内置信号频差Δf=0时,Duffing系统状态在输入信号调制码元为“1”时,呈周期态;为“-1”时,呈混沌态。值得注意的是,此时,Duffing系统输出状态不具有周期性,是间歇性混沌状态。而系统状态在Duffing系统输出时域波形包络上进行了体现,周期态时,包络恒定,混沌态时,包络起伏较大。据此可以判断系统的状态。
对比图6(a)和(c),系统在周期态和混沌态之间进行状态转换时,存在过渡带。文献[9-10]对于减少过渡带影响进行了论证。
(2)有频差
当输入信号与Duffing系统内置信号频差Δf≠0时,一方面,信号相位的变化会使系统处于间歇性混沌状态,调制码元为“1”时,系统处于周期态;“-1”时,会使系统处于混沌态。另一方面,频差的影响也将使系统以周期![]() 交替出现混沌态和周期态。两方面的影响,从而使得系统状态输出比较复杂,间歇性混沌状态比Δf=0时更加突出和明显。
交替出现混沌态和周期态。两方面的影响,从而使得系统状态输出比较复杂,间歇性混沌状态比Δf=0时更加突出和明显。
图7给出了在BPSK信号频率fc=1.005 MHz,其他实验条件同上情况下,Duffing系统时序输出和在f=1 MHz处S变换包络提取结果。可以看出,虽然由于频差的影响,BPSK信号Duffing系统输出状态变复杂,但仍然可以分辨出系统的间歇性混沌状态。
Duffing系统间歇性混沌状态是判断有无BPSK信号存在的重要依据,其主要受两个因素影响。一是相位变化速率,即码元速率的影响。一般来说,频差引起的周期态或混沌态持续时间![]() 与调制信号码元长度
与调制信号码元长度![]() 满足2tspan>td,即1Δf1<fd,可以得到清晰的Duffing系统状态图。二是频差的影响。输入信号与Duffing系统内置信号频差越小,对间歇性混沌状态的贡献越小;频差越大,贡献越大。频差太大,将使混沌态和周期态持续时间很短,无法找到持续一段时间的恒定包络,不能判断系统状态。文献[26]表明,当
满足2tspan>td,即1Δf1<fd,可以得到清晰的Duffing系统状态图。二是频差的影响。输入信号与Duffing系统内置信号频差越小,对间歇性混沌状态的贡献越小;频差越大,贡献越大。频差太大,将使混沌态和周期态持续时间很短,无法找到持续一段时间的恒定包络,不能判断系统状态。文献[26]表明,当![]() 时,有规则的周期混沌现象才可以被辨认出来。因此,Duffing系统识别BPSK信号的工作带宽B=21Δf1应该满足:
时,有规则的周期混沌现象才可以被辨认出来。因此,Duffing系统识别BPSK信号的工作带宽B=21Δf1应该满足:
B
(17)
由以上讨论,相较于相平面法和Lyaponov指数法反应的是一段时间内的整体特征,时序图法来表示BPSK信号的Duffing系统状态并利用S变换提取输出时序包络,可以较好反映出Duffing系统在每个时刻的状态,对于分析间歇性混沌状态是一个很好的工具。而且,时序图法的运算速度比另外两种方法较快,具有较高的效率。
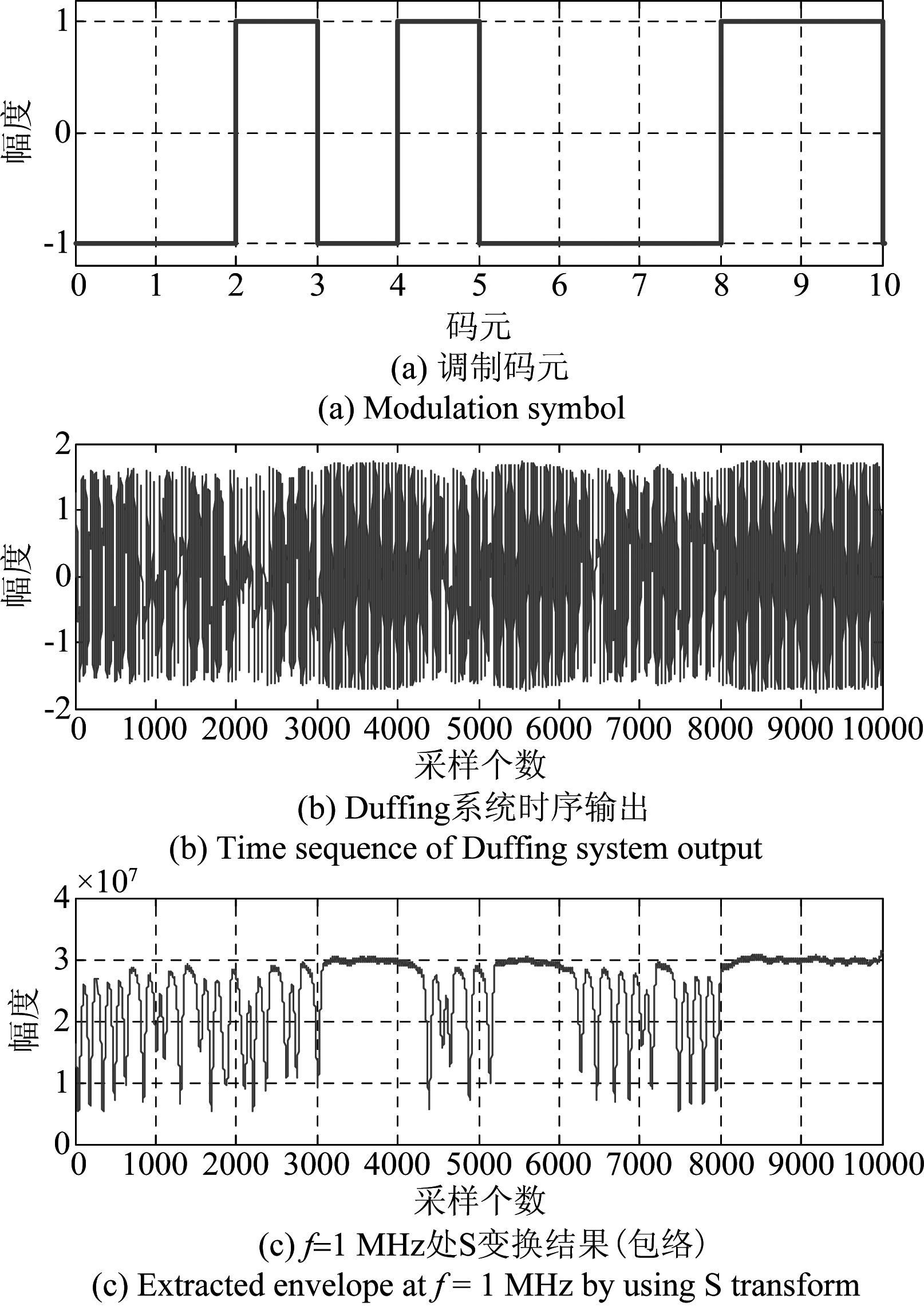
图7 有频差BPSK信号Duffing振子输出时序图及包络
Fig.7 Sequence diagram and envelope of Duffing system output with frequency difference
3.3 微弱BPSK信号盲检测模型
对于方程(3),在有微弱周期信号输入但与Duffing系统内置频率相位相反时,系统处于混沌态。对这类信号建立检测方程如下:
Frcos(ωt+π)+s(t)+n(t)
(18)
对比方程(3)和方程(18),两者区别在于将Duffing系统内置信号反相,称方程(3)为正相振子检测方程,方程(18)为反相振子检测方程。
与对方程(3)的分析类似,我们同样可以得出反相振子检测方程在频差和相差影响下的Duffing系统相轨迹演化与正相振子检测方程相同。区别在于,当Duffing系统有摄动信号输入时,如果正相方程处于周期态,则对应时段反相方程处于混沌态;反之亦反。
在检测存在相位反相变化的微弱BPSK信号时,将方程(3)和方程(18)系统输出状态结合,更加有利于判断Duffing系统输出状态,从而判断系统输入中是否有待检信号。建立单通道微弱PSK信号盲检测模型如图8所示。
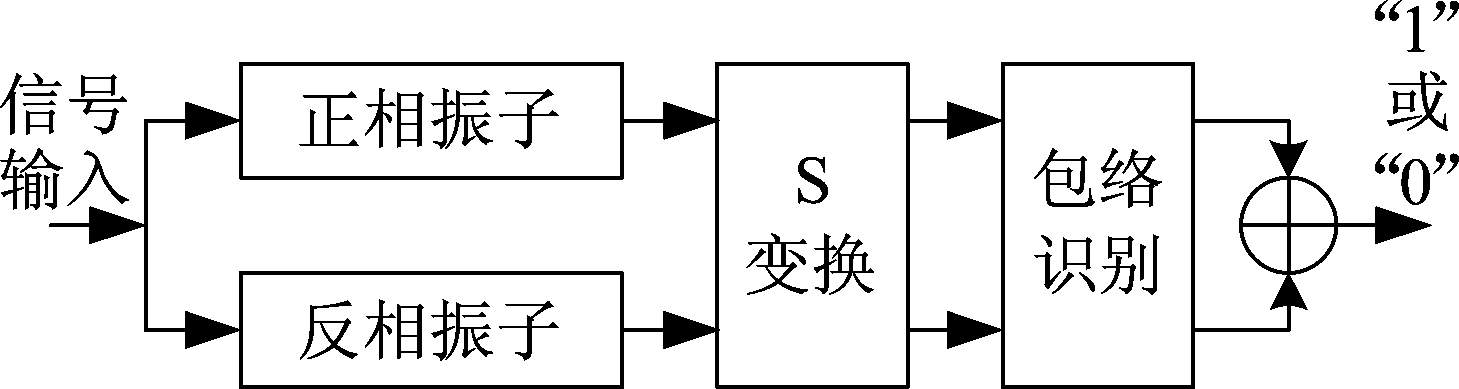
图8 单通道微弱BPSK信号盲检测模型
Fig.8 One-channel blind detection model of the weak BPSK signal
在检测时,根据式(17)确定检测模型控守频段,取其中心频率作为Duffing系统正相和反相振子内置频率,S变换对正相和反相振子输出时序在内置频率上提取包络,包络识别算法根据幅度离散情况,判断是否有周期态存在,存在周期态,输出“1”,否则输出“0”,最后对正相和反相两路输出进行“或”运算。系统输出“1”,则判断控守带宽内有微弱BPSK信号存在,否则判断为无。
为进一步验证模型盲检测效果,仿真接收机中频信号频率为1 MHz,控守带宽为80 kHz,BPSK信号采样速率40 MHz,采样点数10000点,信道噪声为高斯白噪声。采用图8模型对BPSK信号进行盲检测,Duffing系统参数设定同上。仿真实验以信噪比进行分组,信噪比在-15 dB到-35 dB范围内取步进为5 dB,在-35 dB至-45 dB范围内取步进为1 dB,共15组实验。每组进行100次仿真实验,每次实验时BPSK信号幅度在0.001~0.020之间(确保信号微弱性)、码元速率在5~40 kHz之间以及载频在0.960~1.040 MHz随机选取。在图8所示模型中输入含有高斯白噪声的微弱BPSK信号,Duffing系统输出“1”为正确识别,输出“0”为错误识别,统计每组实验中的正确识别次数和错误识别次数,并计算检测概率和错误概率,得到随输入信号信噪比变化的检测概率和错误概率如图9所示。可以看出,在信噪比大于-41 dB时,检测概率大于错误概率,系统在信噪比大于-40 dB时,可以稳定实现对微弱BPSK信号的盲检测。
在接收机接收到的整个频段范围内判断是否有微弱BPSK信号存在时,可以将处理频段分为n个通道,每个通道控守的带宽为B,采用每个通道分段控守,实现对整个频段的全覆盖。Duffing振子盲检测微弱BPSK信号模型如图10所示。任一通道内有相图状态输出“1”,则判断在对应通道内有微弱信号存在。
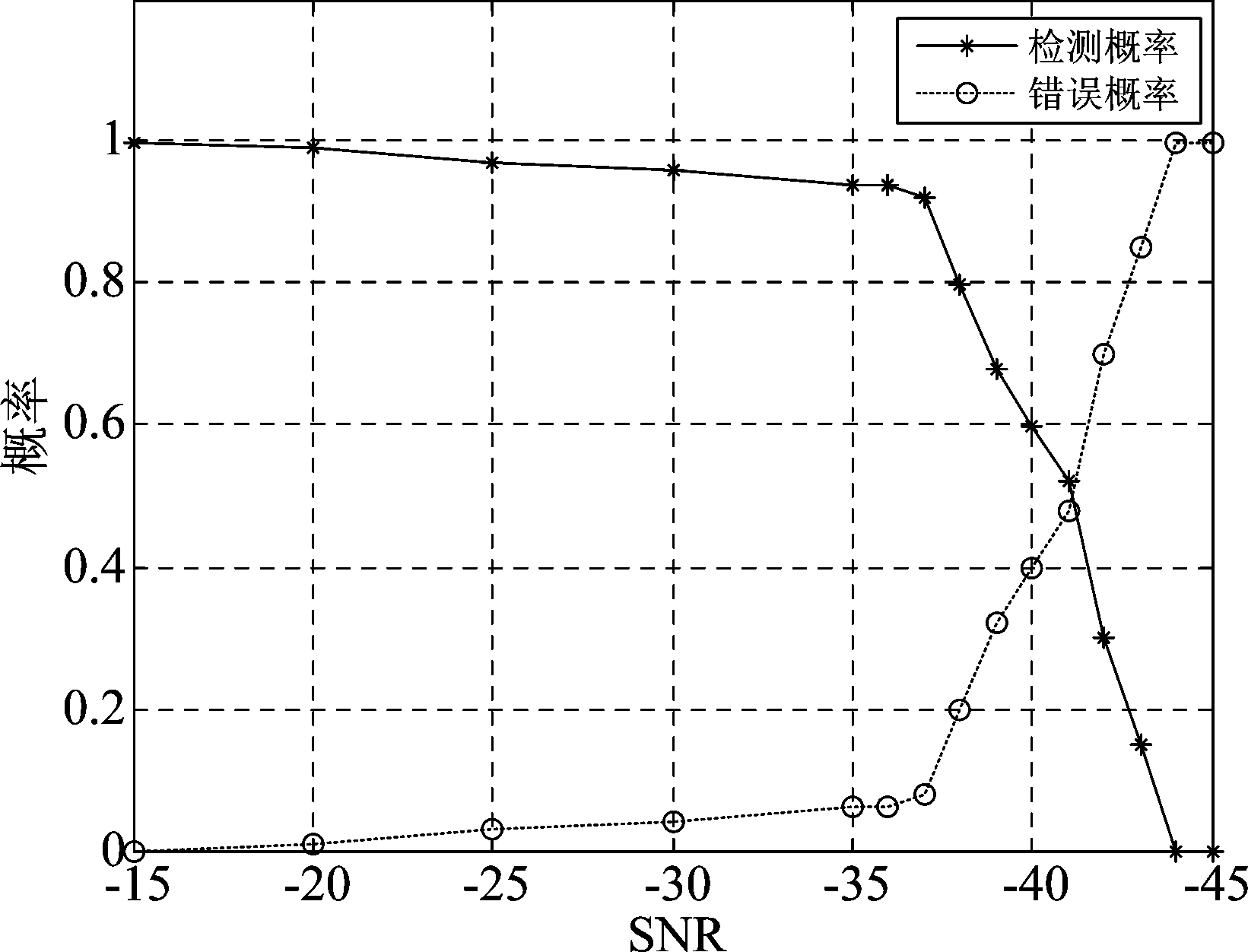
图9 检测概率和错误概率随信噪比变化图
Fig.9 Figure of probability of detection and error by changing of SNR
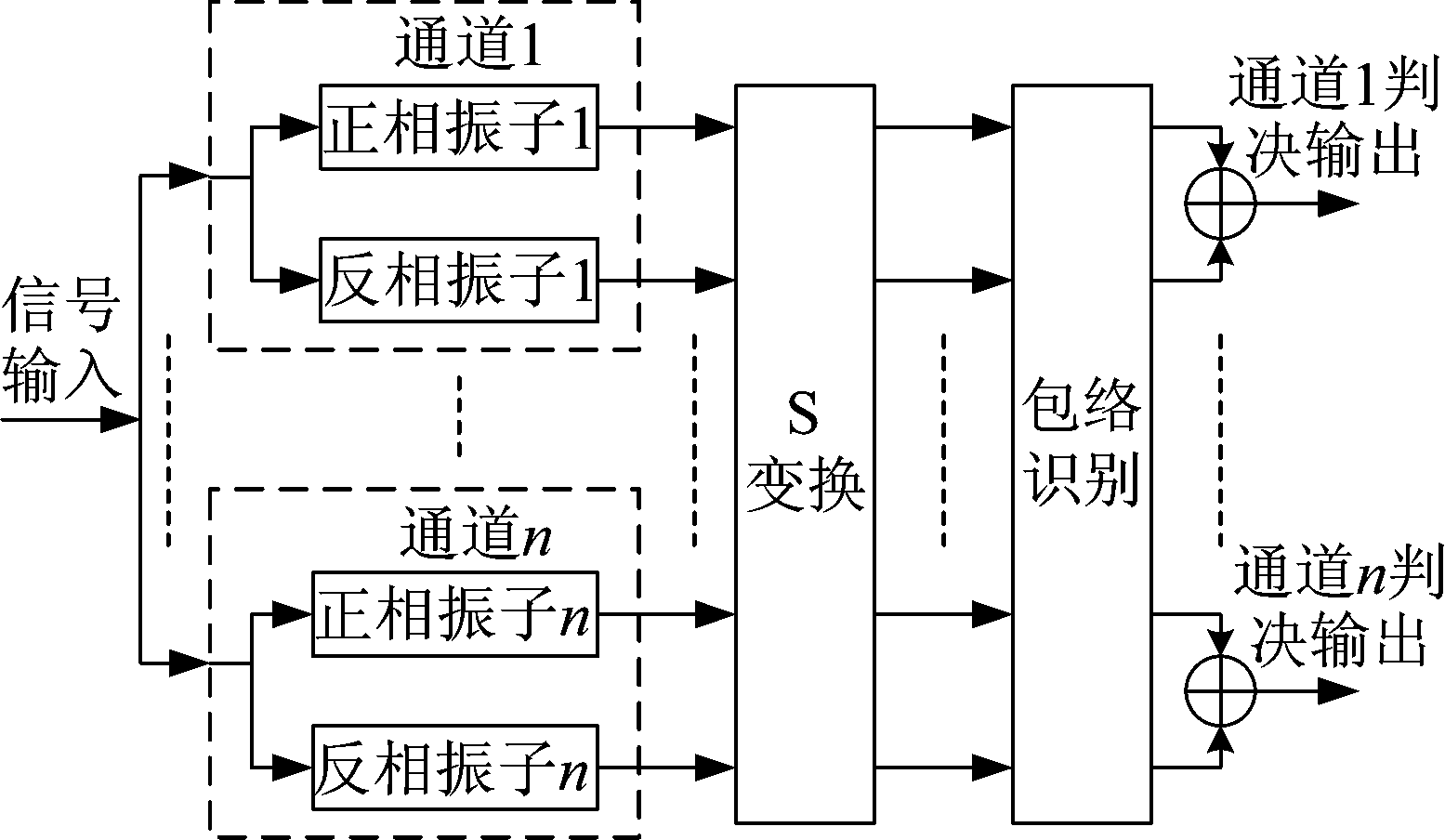
图10 基于Duffing系统和S变换微弱BPSK信号盲检测模型
Fig.10 Blind detection model of weak BPSK signals by using Duffing oscillator and S transform
4 结论
本文从Duffing振子微弱信号检测基本原理出发,分析了周期信号与Duffing系统内置信号存在频差和相差时,对Duffing系统相轨迹演化的影响。针对微弱BPSK信号盲检测问题,指出由于没有BPSK信号先验载波知识和信号本身相位变化,将引起Duffing系统间歇性混沌发生。为了更好反应间歇性混沌状态变化,采用时序图法并引入S变换提取时序输出包络来判别混沌状态,并分析了检测方程确定的控守频带范围。通过建立正相振子和反相振子检测方程,提出了基于Duffing振子和S变换的微弱BPSK信号盲检测模型,并通过仿真实验,验证了模型的有效性和可行性。基于Duffing振子和S变换微弱BPSK信号盲检测模型的建立,对于搜索和探测强噪声中的未知微弱BPSK信号,具有重要的理论和应用价值,拓展了Duffing振子在信号检测领域的应用范围。
参考文献
[1] 樊昌信, 曹丽娜. 通信原理[M]. 第6版. 北京: 国防工业出版社, 2010: 188-212.
Fan Changxin, Cao Lina. Communication Theory[M]. Sixth Edition. Beijing: National Defense Industry Press, 2010: 188-212. (in Chinese)
[2] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法[J]. 电子与信息学报, 2016, 38(3): 674- 680.
Zhao X W, Guo C X, Li J C. Mixed Recognition Algorithm for Signal Modulation Schemes by High-order Cumulants and Cyclic Spectrum[J]. Journal of Electronics & Information Technology, 2016, 38(3): 674- 680. (in Chinese)
[3] 郑鹏, 张鑫, 刘锋, 等. 基于循环谱的MPSK信号盲检测[J]. 计算机仿真, 2012, 29(4): 130-133.
Zheng P, Zhang X, Liu F, et al. Blind detection of MPSK Signals Based on Cyclic Spectrum[J]. Computer Simulation, 2012, 29(4): 130-133. (in Chinese)
[4] 吴涛, 狄旻珉, 黄国策. 联合频偏估计与循环矩的MPSK信号调制识别算法[J]. 仪表技术与传感器, 2014, 12: 102-104.
Wu T, Di M M, Huang G C. Joint Frequency Offset Estimation and Cyclic Moments MPSK Signal Modulation Recognition Algorithm[J]. Instrument Technique and Sensor, 2014, 12: 102-104. (in Chinese)
[5] Antonio A. Efficient Maximum-Likelihood Based Clock and Phase Estimators for OQPSK Signals[J]. IEEE Trans. on Comm., 2015, 63(7): 2647-2657.
[6] 王婷婷, 龚晓峰. 基于星座图的PSK、QAM信号联合识别算法应用[J]. 计算机应用研究, 2015, 32(7): 2116-2118.
Wang T T, Gong X F. Application of joint signal recognition on PSK and QAM based on constellation[J]. Application Research of Computers, 2015, 32(7): 2116-2118. (in Chinese)
[7] Zhen Yafeng, Duan Chaowei. The Application of Stochastic Resonance in Parameter Estimation for PSK Signals[C]∥2015 IEEE International Conference on Communication Software and Networks (ICCSN), Chengdu,China,2015:166-172.
[8] 赖志慧, 冷永刚, 孙建桥, 等. 基于Duffing振子的变尺度微弱特征信号检测方法研究[J]. 物理学报, 2012, 61(5): 050503.
Lai Z H, Leng Y G, Sun J Q, et al. Weak characteristic signal detection based on scale transformation of Duffing oscillator[J]. Acta Phys. Sin., 2012, 61(5): 050503. (in Chinese)
[9] 刘海波, 吴德伟, 戴传金, 等. 基于Duffing振子的弱正弦信号检测方法研究[J]. 电子学报, 2013, 41(1): 8-12.
Liu H B, Wu D W, Dai C J, et al. A new weak sinusoidal signal detection method based on Duffing oscillators[J]. Acta Electronica Sinca, 2013, 41(1): 8-12. (in Chinese)
[10] 刘海波, 吴德伟, 金伟, 等. Duffing振子微弱信号检测方法研究[J]. 物理学报, 2013, 62(5): 050501.
Liu H B, Wu D W, Jin W, et al. Study on weak signal detection method with Duffing oscillators[J]. Acta Phys. Sin., 2013, 62(5): 050501. (in Chinese)
[11] 牛德智, 陈长兴, 班斐, 等. Duffing振子微弱信号检测盲区消除即检测统计量构造[J]. 物理学报, 2015, 64(6): 060503.
Niu D Z, Chen C X, Ban F, et al. Blind angle elimination in weak signal detection with Duffing oscillator and construction of detection statistics[J]. Acta Phys. Sin., 2015, 64(6): 060503. (in Chinese)
[12] 魏恒东, 甘露, 李立萍. 基于哈密顿量的Duffing振子微弱信号检测[J]. 电子科技大学学报, 2012, 41(2): 203-207.
Wei H D, Gan L, Li L P. Weak signal detection by Duffing oscillator based on Hamiltonian[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(2): 203-207. (in Chinese)
[13] Jiang Yu, Zhu Hua, Li Z. A new compound faults detection method for rolling bearings based on empirical wavelet transform and chaotic oscillator[J]. Chaos, Solitons and Fractals, 2016, 89: 8-19.
[14] Zhao Zhihong, Yang Shaopu. Application of van der Pol-Duffing oscillator in weak signal detection[J]. Computers and Electrical Engineering, 2015, 41: 1- 8.
[15] Zhao Wenli, Zhao Jingxiao, Huang Zhenqiang, et al. Weak signal detection technology based on Holmes Duffing oscillator[J]. Procedia Engineering, 2012, 29: 1796-1802.
[16] 丛超, 李秀坤, 宋扬. 一种基于新型间歇混沌振子的舰船线谱检测方法[J]. 物理学报, 2014, 63(6): 064301.
Cong C, Li X K, Song Y. A method of detecting line spectrum of ship-radiated noise using a new intermittent chaotic oscillator[J]. Acta Phys. Sin., 2014, 63(6): 064301. (in Chinese)
[17] 毕红博, 尹成群, 黄怡然, 等. 基于Duffing振子检测PSK信号方法的研究[J]. 信息技术, 2008, 4: 121-123.
Bi H B, Yin C Q, Huang Y R, et al. Study on detection method of PSK signal based on Duffing oscillator[J]. Information Technology, 2008, 4: 121-123. (in Chinese)
[18] 马腾跃. 多节点监测系统微弱信号检测算法研究[D]. 北京: 北京邮电大学, 2015.
Ma T Y. Research on detection method of weak signal in spectrum monitoring system[D]. Beijing: Beijing University of Post and Telecommunications, 2015. (in Chinese)
[19] 靳晓艳, 周希元. 一种基于特定Duffing振子的MPSK信号调制识别算法[J]. 电子与信息学报, 2013, 35(8): 1882-1887.
Jin X Y, Zhou X Y. A Modulation Classification Algorithm for MPSK Signals Based on Special Duffing Oscillator[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1882-1887. (in Chinese)
[20] 李月, 杨宝俊. 混沌振子系统(L-Y)与检测[M]. 北京: 科学出版社, 2007: 20.
Li Y, Yang B J. Chaotic oscillator (L-Y) and detection[M]. Beijing: Science Press, 2007: 20. (in Chinese)
[21] 刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社, 2004: 132-135.
Liu B Z, Peng J H. Nonlinear Dynamics[M]. Beijing: High Education Press, 2004: 132-135. (in Chinese)
[22] Peitgen H, Jurgens H, Saupe D. Chaos and Fractals-New Frontiers of Science[M].Second Edition.Springer, 2004: 660.
[23] Huang Zhonglai, Zhang Jianzhong, Zhao Tiehu, et al. Synchrosqueezing S-Transform and Its Application in Seismic Spectral Decomposition[J]. IEEE Trans. on Geoscience and Remote Sensing, 2016, 54(2): 817- 825.
[24] Hamed Hasanvand, Amir Parastar, Behrooz Arshadi, et al. A comparison between S-transform and CWT for fault location in combined overhead line and cable distribution networks[C]∥21st IEEE Electrical Power Distribution Conference, 2016: 70-74.
[25] 吴彦华. 改进的离散S变换快速算法与连续小波变换算法性能分析[J]. 信号处理, 2012, 28(7): 973-979.
Wu Yanhua. Compare of the performance between the improved discrete S transform fast algorithm and CWT[J]. Signal Processing, 2012, 28(7): 973-979. (in Chinese)
[26] 徐艳春. 基于混沌振子的微弱光电信号检测技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
Xu Yanchun. Study of weak photo-electric signal detection based on chaotic oscillator[D]. Harbin: Harbin Institute of Technology, 2010. (in Chinese)