1 引言
GNSS(Global Navigation Satellite System)信号到达用户接收机时极其微弱,其信号强度在-160 dBW左右,极易受到各类干扰的影响。其中,欺骗式干扰与真实卫星信号在时间域和频率域都具有相同的格式,是一种故意的干扰。此外,由于欺骗式干扰的功率远低于接收机噪声水平,传统的干扰抑制方法不能很好地工作。因此,需要针对欺骗式干扰的特点利用新的方法对它进行有效地抑制,保障GNSS接收机的定位、导航、授时正确[1-7]。
在现有的欺骗式干扰抑制方法中,多天线技术利用欺骗式干扰和真实卫星信号空间特性的差异在空域上把欺骗式干扰和真实卫星信号区分开,从而进行欺骗式干扰的抑制。加拿大Calgary大学PLAN实验室的Saeed Daneshmand等人利用欺骗式干扰来自空间同一个方向的特点,在空间能量最大的方向设置零陷来抑制欺骗式干扰,该方法不需要对阵列进行校准,因此可以作为一个单独的模块安装在接收机中[8]。Konovaltsev等人提出一种改进的联合欺骗检测和姿态估计算法,通过波束形成技术在估计得到的欺骗式干扰来向上置零陷来抑制欺骗式干扰,并通过仿真和实采实验验证了欺骗式干扰抑制的性能[9]。多天线技术在欺骗式干扰抑制中已被证明是非常有效的方法,然而它的干扰抑制能力受自由度限制,而且多天线间通道误差的存在将降低阵列处理性能。
合成阵列避免了传统天线阵列的上述问题,其核心思想是把移动天线接收到的时间采样信号转换成空间采样信号,通过单个天线运动形成合成阵列的多个虚拟阵元,并同时处理不同时间点不同空间位置上的采样信号。合成阵列不存在通道一致性问题,同时,天线运动可以形成更大的孔径,使阵列的空间分辨率更高,因而来向估计和干扰抑制性能将更好。近年来,在卫星导航领域应用合成阵列的研究正逐渐开展。加拿大Calgary大学PLAN实验室的A.Broumandan等人基于轨迹精确可控的运动天线利用UCA-MUSIC算法对较大功率的压制式干扰进行了来向估计[10]。该实验室也提出了基于ESPRIT算法的AOA估计方法,并对真实的CDMA信号进行了测试,在合成阵列的ESPRIT算法中,唯一的限制是阵元双动的平移不变性,此外,考虑到窄带信号假设的影响,合成阵列的孔径应设定在几米以内[11]。该实验室还研究了GNSS信号的合成阵列稳健波束形成算法,比较了多种波束形成方法的性能,但是,该方法需要已知GNSS信号的来向[12]。佛罗里达大学的Andrey Soloviev,俄亥俄大学的Frank van Graas以及空军研究实验室的Mikel Miller研究了利用GPS天线运动合成大的天线孔径产生窄波束的特点来进行干扰消除[13]。
上述方法均是卫星信号和本地码相关之后再进行处理,属于基于相关域的方法,因此均需要改变接收机的结构,复杂度较高。此外,上述方法没有针对欺骗式干扰进行专门的研究。本文针对欺骗式干扰,在数据域直接处理,在不需要改变普通接收机结构的前提下,提出一种利用合成阵列进行GNSS欺骗式干扰抑制的方案。文章的结构组织如下,第二部分推导了合成阵列接收数据模型,第三部分给出了数据域欺骗式干扰抑制的方法,第四部分为仿真实验,第五部分为本文的总结。
2 数据模型
考虑一个轨迹精确可控的天线沿直线匀速运动如图1所示。
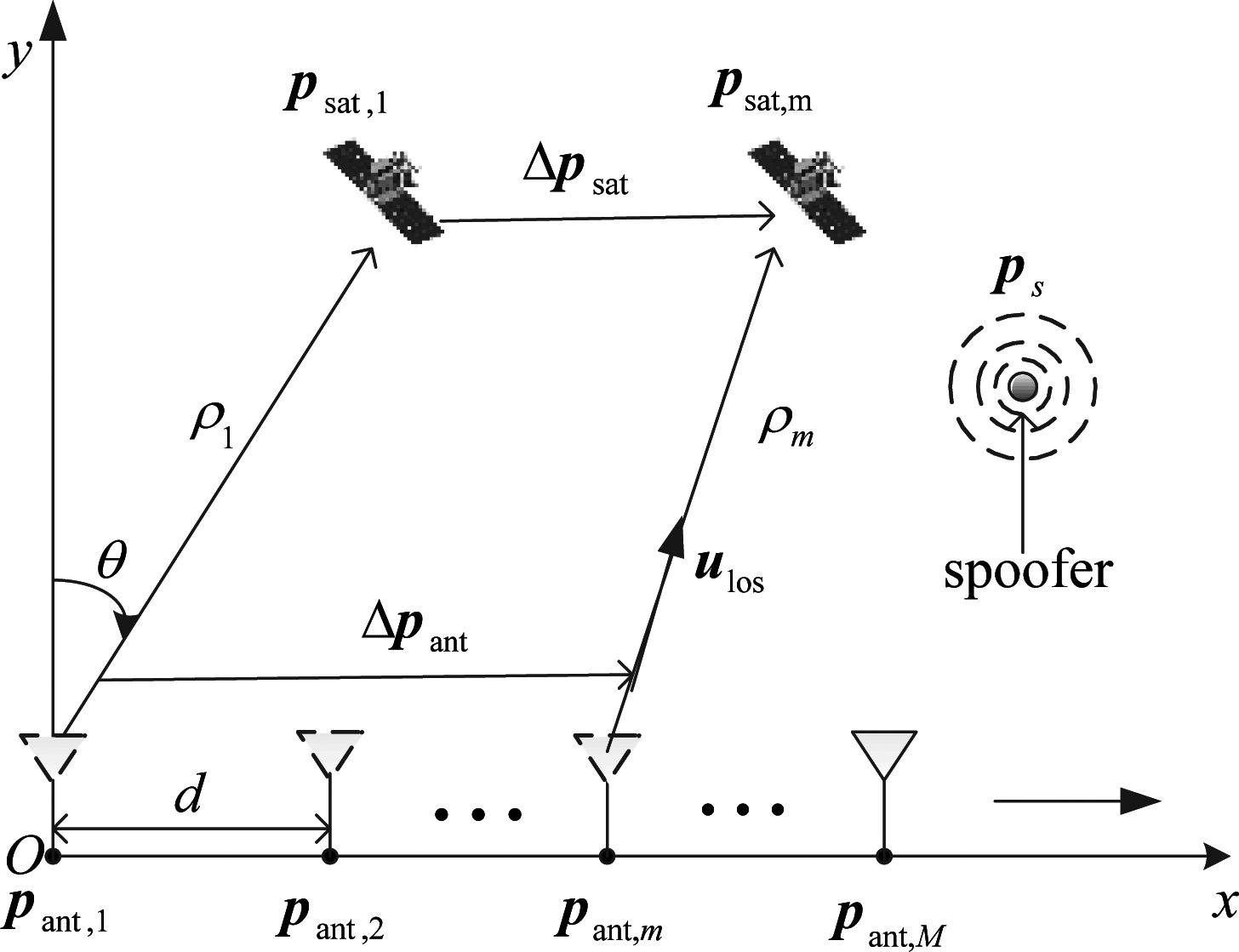
图1 合成阵列示意图
Fig.1 Synthetic array schematic diagram
图1中x轴正方向表示单天线的运动方向,pant,1、pant,m表示天线在t1时刻和tm时刻的位置矢量,m表示第m个虚拟阵元,M表示虚拟阵元数,d表示两个相邻虚拟阵元之间的距离,一般取半波长。y轴为阵元运动方向的法线方向, psat,1和psat,m分别表示卫星在t1时刻和tm时刻的位置矢量,ps表示欺骗式干扰的位置矢量, ρ1和ρm分别表示t1时刻和tm时刻卫星和天线之间的距离,θ表示卫星信号入射角度。
令t1时刻天线接收的卫星信号为
s(t1)=Ad(t1-τ)c(t1-τ)exp(jωRF(t1-τ))
(1)
A表示卫星信号的幅度,d(t)、c(t)分别代表卫星信号的导航电文和扩频码,ωRF表示射频角频率,则tm时刻天线接收的卫星信号可写作
s(tm)=Ad(tm-τ-Δτm)c(tm-τ-Δτm)
exp{jωRF(tm-τ-Δτm)}=
Ad(tm-τ-Δτm)c(tm-τ-Δτm)
exp{jωRF(tm-τ)+Δφm)}
(2)
其中,tm=t1+(m-1)ΔT,ΔT表示相邻虚拟阵元的时间间隔。假设ΔT为C/A码周期的整数倍(本文取1 ms),且假设导航电文不翻转,此时各阵元接收到的信号包络不发生变化,因此,两个虚拟阵元的接收信号只差一个相位为Δφm的指数项,即式(2)可写为
s(tm)=Ad(tm-τ-Δτm)c(tm-τ-Δτm)
exp{jωRF(tm-τ-Δτm)}=Ad(t1-τ)
c(t1-τ)exp{jωRF(tm-τ)}×exp(jΔφm)
(3)
令Δτm和Δφm表示卫星和天线相对运动过程中,tm时刻与t1时刻天线接收到该颗卫星的码延迟之差和载波相位之差,Δτm和Δφm可以写成如下形式
(4)
Δφm=-ωRFΔτm=-2π(ΔPsv-ΔPant)·ulos/λRF=
Δφsv,m+Δφant,m
(5)
其中,ΔPsv=Psv,m-Psv,1、ΔPant=Pant,m-Pant,1分别表示由t1时刻至tm时刻卫星和天线的位置变化矢量,![]() 表示径向矢量。Δφsv,m=-2πΔPsv·ulos/λRF和Δφant,m=2πΔPant·ulos/λRF分别表示由卫星运动及天线运动引入的相位差,c表示信号传播速度。定义卫星运动引入的多普勒角频率
表示径向矢量。Δφsv,m=-2πΔPsv·ulos/λRF和Δφant,m=2πΔPant·ulos/λRF分别表示由卫星运动及天线运动引入的相位差,c表示信号传播速度。定义卫星运动引入的多普勒角频率![]() 则卫星运动引入的相位差Δφsv,m=-ωd,sv(m-1)ΔT。
则卫星运动引入的相位差Δφsv,m=-ωd,sv(m-1)ΔT。
因此,tm时刻天线接收的卫星信号可重新写作
s(tm)=s(t1)·exp(jΔφsv,m)·
exp(-jωd,sv(m-1)ΔT)
(6)
图2利用高保真卫星信号仿真器仿真了运动天线和静止天线接收的卫星信号多普勒频率的变化情况,其中,运动天线为沿轨迹精确可控的轨道以20 m/s的速度作匀速直线运动。
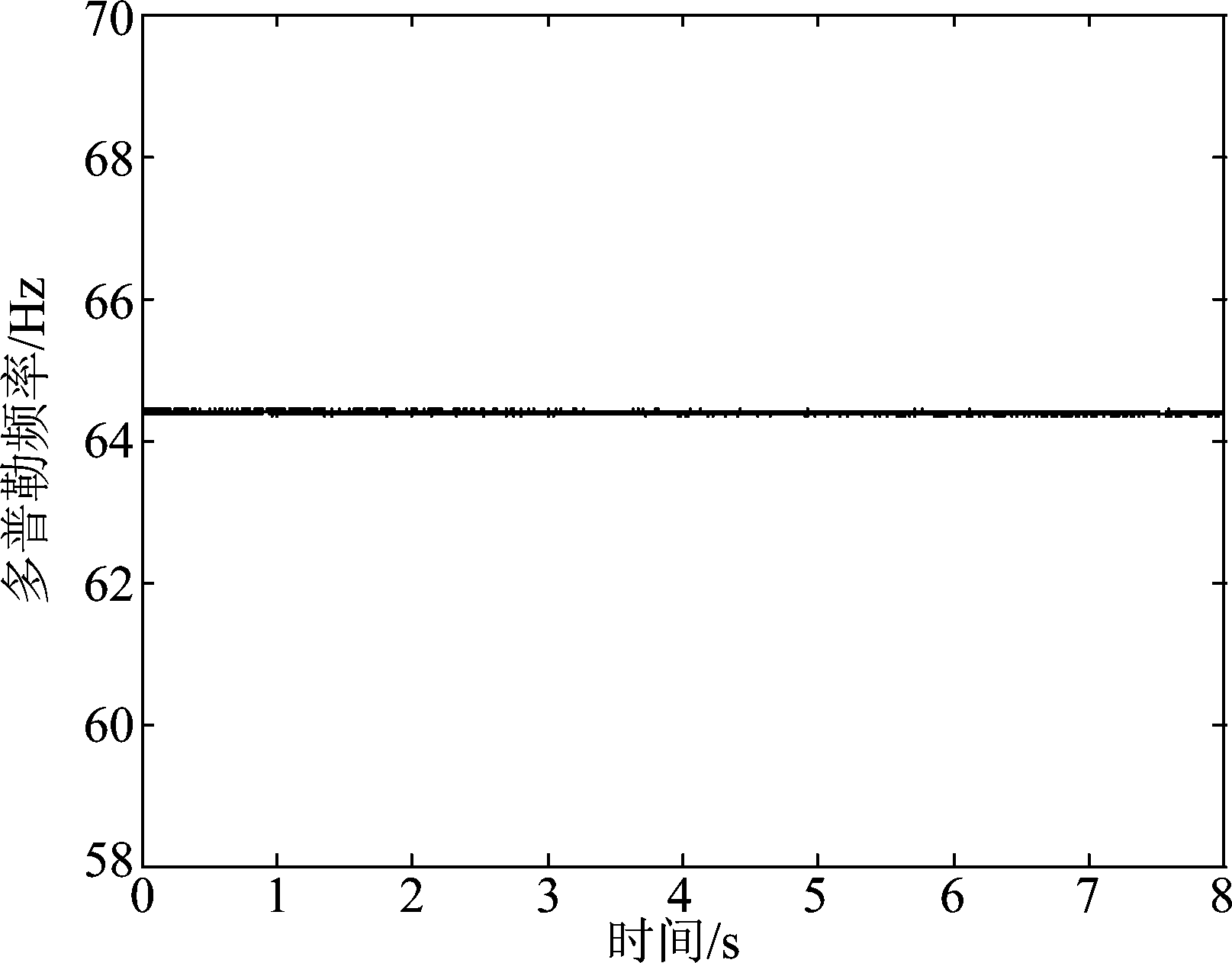
图3 仅由天线运动引起的多普勒频率
Fig.3 Doppler frequency due to antenna motion
由图2可见,短时间内当天线固定不动时,多普勒频率(此时仅由卫星运动引起)呈线性变化,运动天线的多普勒频率也呈线性变化且变化趋势与静态天线相同,两者差值表示由天线运动引起的多普勒变化,且值为常数(如图3所示),该值与天线的运动速度有关。因此,由天线运动引起的相位Δφant,m呈线性变化,和传统阵列中阵列流型矢量的相位项类似。
3 数据域欺骗式干扰抑制
数据域欺骗式干扰抑制方案分为以下几个模块:合成阵列数据接收模块、干扰来向估计模块、天线权值计算模块以及欺骗式干扰抑制模块,如图4所示。
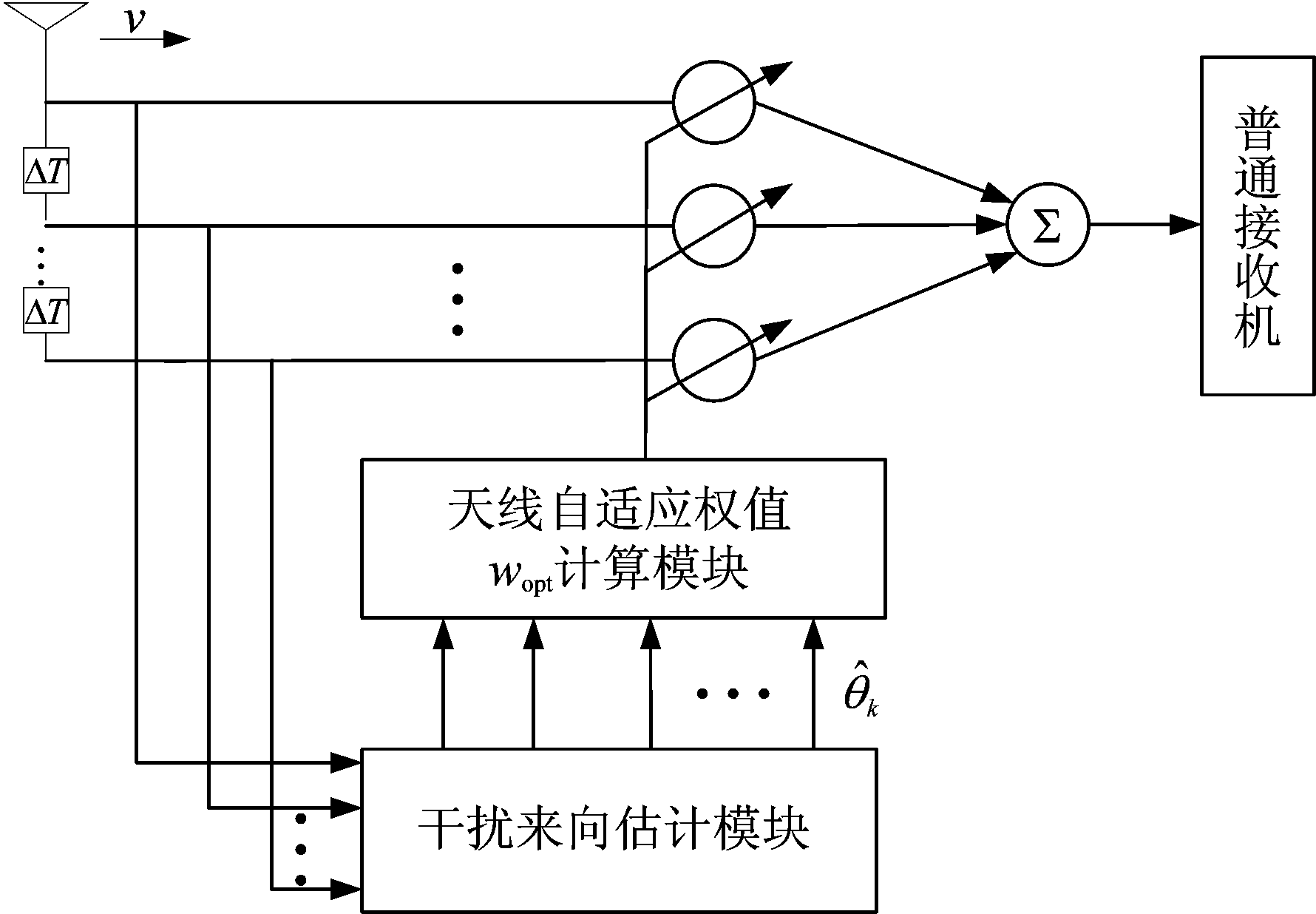
图4 数据域欺骗式干扰抑制算法原理框图
Fig.4 Block diagram of spoofing interference suppression algorithm in data domain
3.1 合成阵列接收数据
合成阵列数据接收模块由单个天线沿精确可控的固定轨迹匀速直线运动形成,天线在运动过程中接收卫星信号和欺骗式干扰信号,相邻两个虚拟阵元以ΔT为时间间隔接收采样信号。在ΔT时间间隔内的快拍数用字母N表示,在存在欺骗式干扰环境下,将单天线接收的信号经下变频和A/D采样后的数字中频信号写成矢量形式,即可得到合成阵列的信号模型
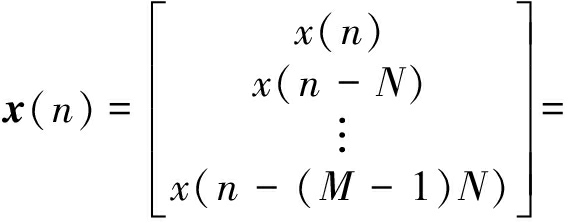
(7)
其中,式(7)右边的接收信号包括三个部分,第一部分表示接收到的真实卫星信号,P为真实卫星信号的个数,sp表示真实卫星信号,![]() 表示第p个真实卫星信号的导向矢量,
表示第p个真实卫星信号的导向矢量,![]() 表示由第p颗卫星运动引起的第m个虚拟阵元与参考阵元之间接收信号的相位差。第二部分表示欺骗式干扰信号,Q为欺骗式干扰源的个数, jq表示欺骗式干扰信号,由于欺骗干扰源位置固定,因此Dq为单位阵,此时合成阵列虚拟阵元接收到的欺骗式干扰的相位差只由天线运动决定,表现为欺骗式干扰的导向矢量
表示由第p颗卫星运动引起的第m个虚拟阵元与参考阵元之间接收信号的相位差。第二部分表示欺骗式干扰信号,Q为欺骗式干扰源的个数, jq表示欺骗式干扰信号,由于欺骗干扰源位置固定,因此Dq为单位阵,此时合成阵列虚拟阵元接收到的欺骗式干扰的相位差只由天线运动决定,表现为欺骗式干扰的导向矢量![]() 第三部分e1(n)为噪声信号。
第三部分e1(n)为噪声信号。
3.2 干扰来向估计模块
在得到合成阵列接收数据模型的基础上,把合成阵列接收到的中频采样信号送入干扰来向估计模块中分别利用MUSIC算法和RELAX算法进行干扰来向估计。
3.2.1 利用MUSIC算法估计干扰来向
多重信号分类(Multiple Signal Classification, MUSIC)是最为经典的高分辨率来向估计算法,是一种基于矩阵特征分解的方法,通过在空域内进行一维谱峰搜索得到信源DOA的估计值。已知信号源的个数,MUSIC算法的步骤归纳如下:
根据接收到信号的N个快拍数据计算信号协方差矩阵R的估计值
(8)
N表示ΔT时间间隔内的快拍数,代入合成阵列接收数据模型(7)可得
(9)
其中,Pa、Ps分别表示真实信号功率、欺骗式干扰功率;σ2表示噪声功率;Lq表示第q个欺骗式干扰源转发的PRN个数。考虑到欺骗式干扰相对真实卫星信号的码延迟通常大于一个码片,且它们之间的空间相关性较弱,因此上式的表达中略去了真实卫星信号和欺骗式干扰相关后的结果。
从式(9)可以看到,值LqPs大于Pa,因此大特征值对应的特征矢量构成的是欺骗式干扰子空间,当已知欺骗式干扰源的个数时,把剩下的特征值对应的特征矢量看作噪声子空间UN,得到阵列空间谱函数为![]() 当θ为欺骗式干扰的来向角时,由于欺骗式干扰子空间和噪声子空间的正交性,此时谱函数的分母无限接近0,因此MUSIC伪谱搜索图中的峰值对应的角度即为欺骗式干扰的来向。
当θ为欺骗式干扰的来向角时,由于欺骗式干扰子空间和噪声子空间的正交性,此时谱函数的分母无限接近0,因此MUSIC伪谱搜索图中的峰值对应的角度即为欺骗式干扰的来向。
(10)
本方案中,MUSIC算法需要已知欺骗式干扰源数目从而构造噪声子空间,此外,欺骗式干扰和真实卫星信号的功率接近且均远低于噪声的特点会使得MUSIC算法可能无法准确获得噪声子空间而导致性能变差。因此MUSIC算法在当前应用背景下性能不够理想。此时考虑利用不需要知道信号源数目以及对信噪比不敏感的RELAX算法进行干扰来向估计。
3.2.2 利用RELAX算法估计干扰来向
合成阵列接收数据模型式(7)可以写成![]() 其中I=P+Q表示信号源的个数,
其中I=P+Q表示信号源的个数,![]() 泛指接收信号的导向矢量,si(n)表示接收信号的波形。在最小二乘的意义下可以通过使以下代价函数最小来估计θi和si(n)。
泛指接收信号的导向矢量,si(n)表示接收信号的波形。在最小二乘的意义下可以通过使以下代价函数最小来估计θi和si(n)。
(11)
上述最小二乘方程很难直接求解,解决此问题的常用方法是松弛算法,如RELAX算法[14-16]。RELAX算法把复杂的多维优化问题转化为一系列一维优化问题,在估计出一个信号之后,RELAX算法把该信号减去作为新的xk(n)来估计下一个信号,在得到下一个信号的估计值后,RELAX算法会把新估计出的信号作为已知量减去重新估计第一个信号,重复上述过程反复迭代直到所有的信号估计值都实际收敛,从而得到全部欺骗干扰源的来向
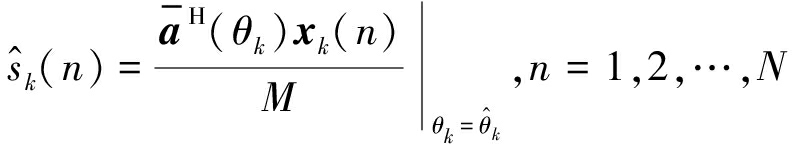
(12)
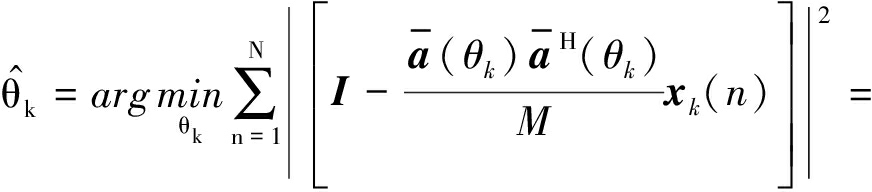
(13)
RELAX算法对信噪比的变化不敏感且能准确分辨出两个来向相近的信号,然而算法过程需要多次迭代运算,计算较复杂[14]。
3.3 天线权值计算和干扰抑制模块
在权值计算模块中,利用上述方法估计出所有欺骗干扰源的来向后,就可以构造得到天线自适应权矢量
wopt=(I-A(θ)AH(θ)/M)·g
(14)
其中,![]() 为欺骗式干扰的阵列流型,g=[1 0 … 0]T。将单天线合成阵列接收信号进行加权后即可得到无欺骗式干扰的数据
为欺骗式干扰的阵列流型,g=[1 0 … 0]T。将单天线合成阵列接收信号进行加权后即可得到无欺骗式干扰的数据
(15)
把处理后的数据送入普通接收机中即可得到正确的导航结果。
4 仿真实验
实验中运动天线沿精确可控轨迹匀速直线运动形成包含10个虚拟阵元的合成阵列,相邻虚拟阵元时间间隔ΔT=1 ms,阵元间距为GNSS信号波长的一半d=λ/2。真实卫星信号为PRN1、PRN3、PRN22、PRN25,入射角度分别为0°、10°、-10°、-40°,SNR=-20 dB。两个欺骗式干扰源均由PRN1、PRN3、PRN22、PRN25的转发信号组成。
为了说明干噪比对RELAX和MUSIC两种算法性能的影响,在INR=-18 dB以及INR=-10 dB条件下,比较了欺骗式干扰在入射角度间隔分别为两个波束宽度,一个波束宽度以及2/3个波束宽度条件下的来向估计性能。本次实验中固定其中一个欺骗式干扰源的来向为20°,另一个欺骗式干扰源的来向随着所设干扰源来向间隔的变化而变化。
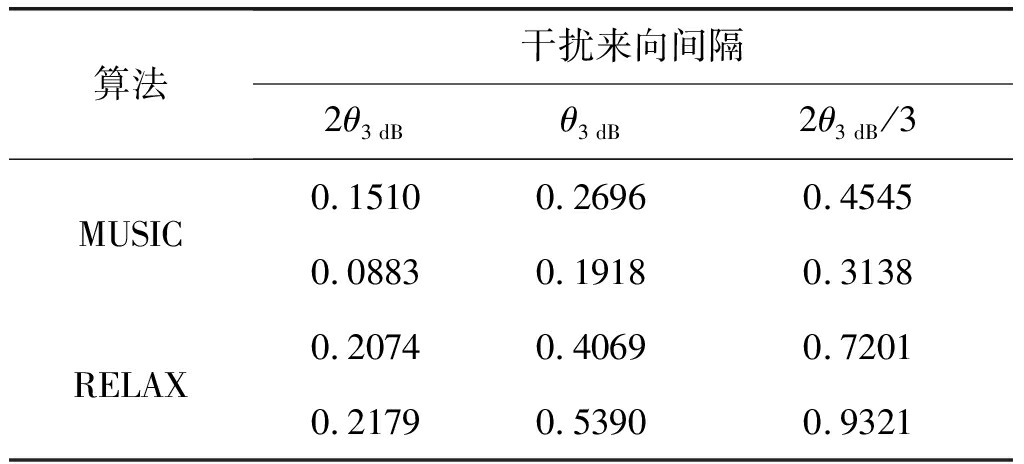
表1 INR=-10 dB干扰来向估计值均方根误差(度)
Tab.1 RMSE of Interference DOA estimation under INR=-10 dB
算法干扰来向间隔2θ3 dBθ3 dB2θ3 dB/3MUSIC0.15100.26960.45450.08830.19180.3138RELAX0.20740.40690.72010.21790.53900.9321
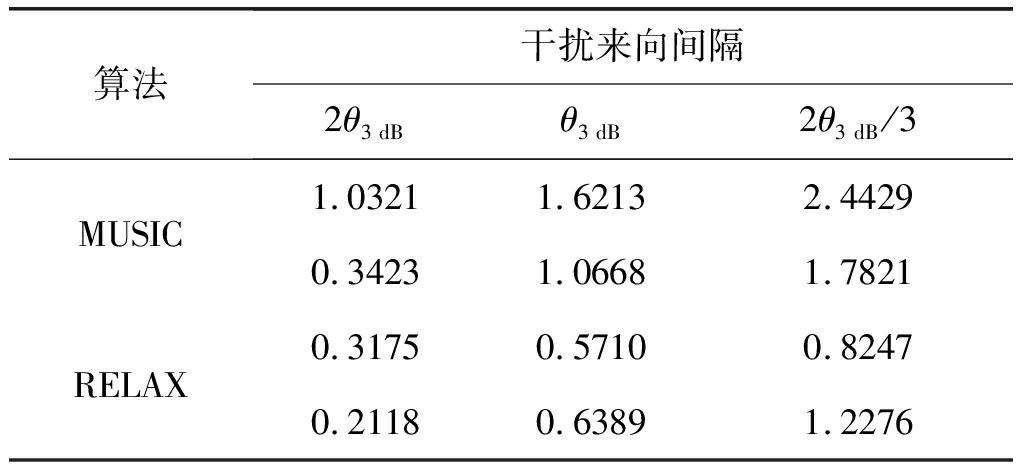
表2 INR=-18 dB干扰来向估计值均方根误差(度)
Tab.2 RMSE of Interference DOA estimation under INR=-18 dB
算法干扰来向间隔2θ3 dBθ3 dB2θ3 dB/3MUSIC1.03211.62132.44290.34231.06681.7821RELAX0.31750.57100.82470.21180.63891.2276
由表1可以看出,当干噪比INR=-10 dB时,随着干扰来向间隔逐渐减小,两种算法的干扰来向估计性能均变差,且MUSIC算法在该干噪比下的干扰来向估计性能要比RELAX算法好;当把欺骗式干扰的干噪比降为INR=-18 dB,如表2所示,随着干扰来向间隔逐渐缩小,两种算法的干扰来向估计性能均变差,然而在该干噪比下,RELAX算法的干扰来向估计性能要优于MUSIC算法,其中MUSIC算法的来向估计性能随着干噪比的降低而严重下降,RELAX算法的来向估计性能随着干噪比的降低下降缓慢,体现出了RELAX算法对干噪比不敏感的特点。在公开的文献中,欺骗式干扰的功率值一般设定为比真实卫星信号大2 dB左右,从而保障欺骗式干扰能成功的欺骗地面接收机,因此,可以看到在本章数据域欺骗式干扰抑制方案中,RELAX算法是一种更好的选择。
下面给出上述两种算法在干噪比为-18 dB条件下干扰抑制的性能,以干扰间隔为两个波束宽度为例,天线方向图如图5所示。
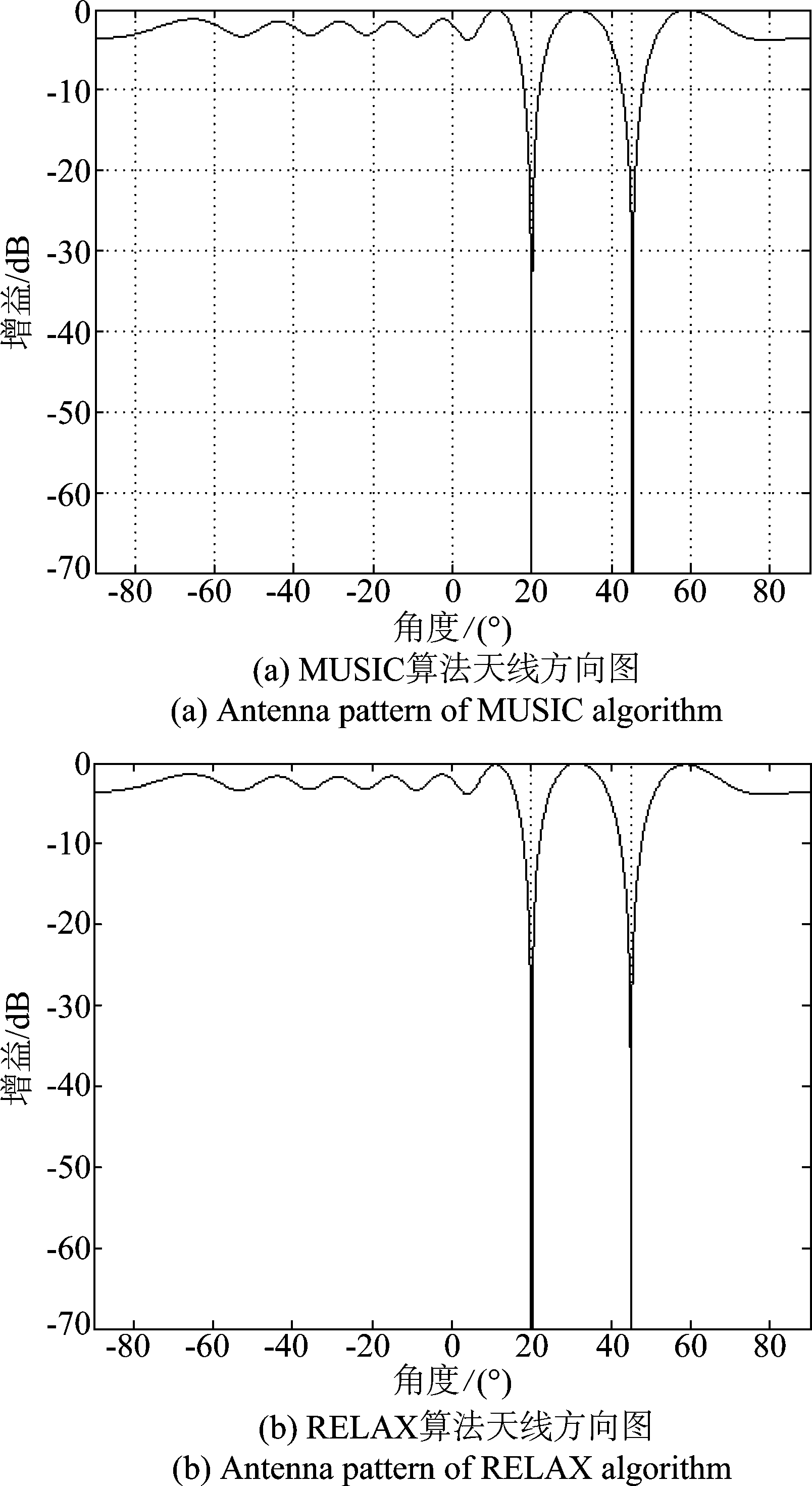
图5 天线方向图
Fig.5 Antenna pattern
可以看到,采用MUSIC算法和RELAX算法抑制干扰时,阵列天线在两个欺骗式干扰来向上均形成了较深的零陷,保证能把欺骗式干扰抑制掉。在其他方向上的天线增益较为平坦,保证真实卫星信号能以很小的损失通过。下面以PRN1为例,通过PRN1的二维搜索结果图来给出本文算法下欺骗式干扰抑制前后的效果。
图6(a)可以看出,欺骗式干扰抑制前,接收机二维搜索捕获结果中存在三个明显的相关峰,由于转发式欺骗干扰功率高于真实卫星信号功率,因此两个较高的峰对应欺骗式干扰相关峰,较低的峰对应真实卫星信号相关峰。利用本文所提合成阵列欺骗式干扰抑制算法进行干扰抑制后的捕获结果如图6(b)、(c),可以看出欺骗式干扰均已被成功抑制,接收机此时可以正常捕获到真实卫星信号。
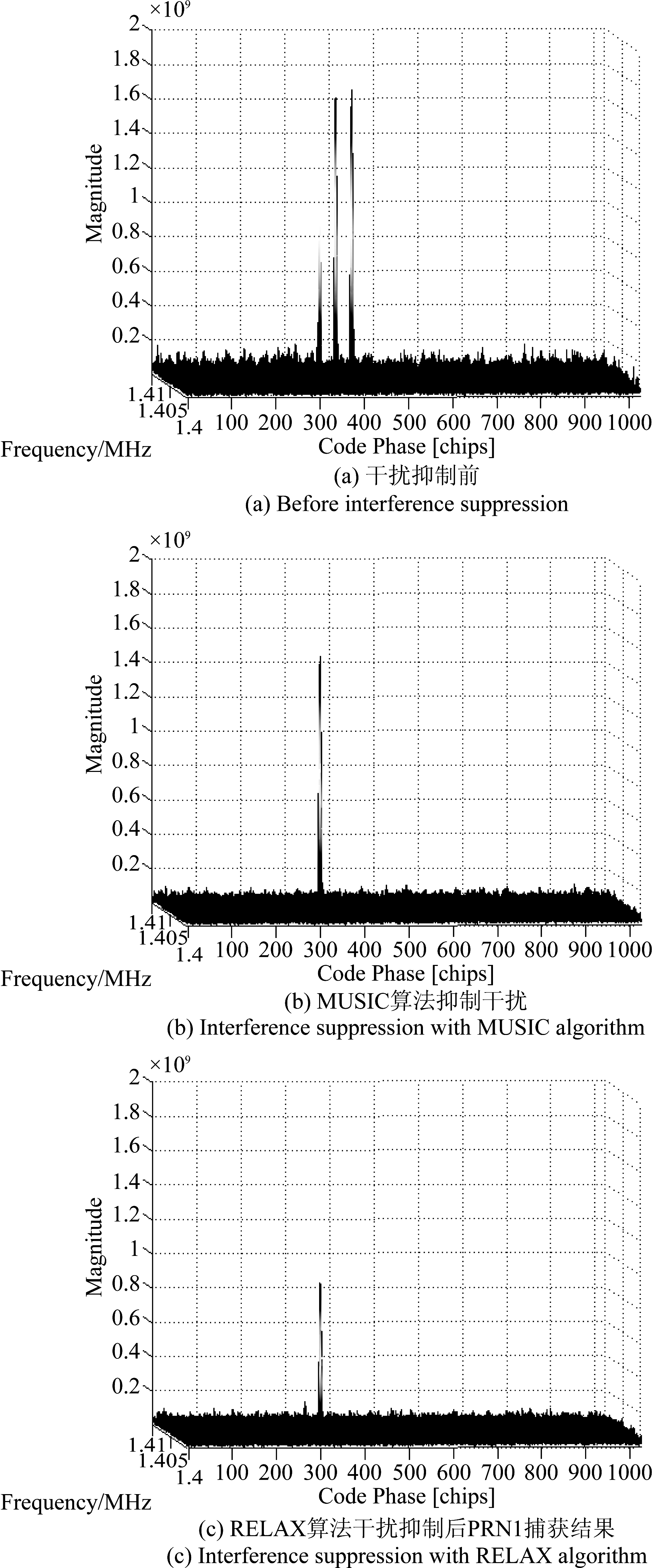
图6 PRN1捕获结果对比
Fig.6 Acquisition results comparison of PRN1
5 结论
本文基于合成阵列的场景,提出了一种欺骗式干扰抑制方案,首先分析了存在欺骗式干扰的环境下合成阵列的接收信号模型,文中利用RELAX算法和MUSIC算法估计了多个欺骗式干扰来向,并在该方案中比较了这两种方法的来向估计性能,在干扰来向估计之后通过构造合成阵列自适应权向量来抑制欺骗式干扰并从接收机捕获结果比较了这两种算法的干扰抑制性能。上文所述方法针对天线运动轨迹精确可控,即合成阵列的阵列流型已知的情况,不考虑天线运动误差的影响,而在实际应用中,由阵元运动引起的位置误差是不可避免的,因此为了体现合成阵列的优点需要对阵元运动引起的位置误差进行补偿,关于合成阵列运动误差补偿的问题将在下一步工作中进行。
参考文献
[1] 刘春保. 卫星导航系统脆弱性评估与对策[J]. 卫星应用, 2015(4): 49-54.
Liu Chunbao. Vulnerability Assessment and Countermeasure of Satellite Navigation System[J]. Satellite Applications, 2015(4): 49-54. (in Chinese)
[2] 辛洁, 赵伟, 张之学,等. 卫星导航系统发展及其军事应用特点分析[J]. 导航定位学报,2015(4):38- 43.
Xin Jie, Zhao Wei, Zhang Zhixue, et al. Development of GNSS and Characteristic Analysis of Military Application[J]. Journal of Navigation and Positioning, 2015(4): 38- 43. (in Chinese)
[3] 王群. 四大卫星导航系统及其特点[J]. 国防科技, 2015(1): 40- 43.
Wang Qun. Four satellite navigation systems and their characteristics[J]. National Defense Science and Technology, 2015(1): 40- 43. (in Chinese)
[4] 成跃进. 现代卫星导航定位系统发展介绍[J]. 空间电子技术, 2015(1): 17-25.
Cheng Yuejin. The Development Intro of Satellite Navigation and Positioning System[J]. Space Electronic Technology, 2015(1): 17-25. (in Chinese)
[5] 卢丹. 稳健的全球导航卫星系统抗干扰技术研究[D]. 西安: 西安电子科技大学, 2013.
Lu Dan. Robust Anti-jamming Techniques for Global Navigation Satellite System[D]. Xi’an: XiDian Univerisity, 2013.(in Chinese)
[6] Shen Jun, Ma Jiaqing, Yang Jian. Updated on Development of BeiDou Navigation Satellite System[C]∥Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2015), Tampa, Florida, USA, 2015: 1264-1290.
[7] Connor L. Brashar. An Analysis of Near-band Harmful Interference on Civilian GPS Receivers[C]∥Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2016), Portland, Oregon, 2016: 3123-3132.
[8] Daneshmand S, Jafarnia-Jahromi A, Broumandan A, et al. A Low-Complexity GPS Anti-Spoofing Method Using a Multi-Antenna Array[C]∥Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 2012: 1233-1243.
[9] Konovaltsev A, Cuntz M, Haettich C, et al. Autonomous Spoofing Detection and Mitigation in a GNSS Receiver with an Adaptive Antenna Array[C]∥Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2013), Nashville, TN, USA, 2013: 2937-2948.
[10] Broumandan A, Lin Tao, Moghaddam A, et al. Direction of Arrival Estimation of GNSS Signals Based on Synthetic Antenna Array[C]∥Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, 2007: 728-738.
[11] Ali Broumandan, John Nielsen, Gérard Lachapelle. Practical Results of High Resolution AOA Estimation by the Synthetic Array[C]∥Proceeding of IEEE Vehicular Technology Conference’08 Fall, Calgary, Alberta, Canada, Sep.21-24, 2008.
[12] Lin Tao, Ali Broumandan, John Nielsen, et al. Robust Beamforming for GNSS Synthetic Antenna Arrays[C]∥Proceedings of the 22th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, 2009:387- 401.
[13] Andrey Soloviev, Frank van Graas, Sanjeev Gunawardena, et al. Synthetic Aperture GPS Signal Processing: Concept and Feasibility Demonstration[C]∥Proceedings of the 2009 International Technical Meeting of the Institute of Navigation, Anaheim, CA, 2009: 851- 863.
[14] Li Jian, Petre Stoica. Efficient mixed-spectrum estimation with applications to target feature extraction[J]. IEEE Transactions on Signal Processing, 1996, SP- 44(2): 281-295.
[15] Li Jian, Zheng Dunmin, Petre Stoica. Angle and waveform estimation via RELAX[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 1077-1087.
[16] Liu Zhengshe, Li Jian. Implementation of the RELAX algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(2): 657- 664.





