1 引言
无线频谱是不可再生的宝贵资源,提高频谱利用率是无线通信的主要目标。但传统的固定频谱分配政策使得频谱利用率极其低下,也就是说,存在很多授权频谱空缺,而绝大部分未授权频谱却过于拥挤。认知无线电(Cognitive Radio,CR)的出现就是解决这一问题[1-2]。在CR系统中,频段上主用户(Primary User,PU)的活动情况由认知用户(Secondary User,SU)时刻感知,即频谱感知技术[3-5]。传统的频谱感知算法很适合在高斯噪声背景检测,但在实际信道中存在人为因素和自然因素,背景噪声大都为非高斯噪声(如Alpha分布噪声、Laplace分布噪声、混合高斯噪声等),这类噪声较高斯噪声而言具有更为厚重的拖尾,从而导致传统检测器的性能大大退化甚至失效[6-7]。
由于实际环境中的PU、噪声及信道的先验信息是很难提前获取,所以利用接收数据的采样协方差矩阵的盲检测器已受到越来越多学者的关注。文献[8]提出了最大最小特征值之比(MME)算法,首先通过计算求出采样协方差矩阵,接着再根据随机矩阵理论(RMT)求得采样协方差矩阵的最大特征值和最小特征值[9-11]之比为统计量进行判决,在噪声不确定性影响下,MME算法的检测性能明显优于能量检测算法(ED)。文献[12]提出一种改进的NMME算法,首先是对接收信号的采样协方差进行估计,接着根据RMT进行最小特征值分解[13],计算统计量,正是由于该算法门限值比传统的MME更小,所以其检测性能优于传统的MME。文献[14]提出了协方差绝对值算法(CAV),该算法根据接受信号的采样协方差推导出检测概率与判决门限的表达式,当噪声不确定存在时,检测概率明显高于ED算法。文献[15]提出了能量最小特征值(EME),研究了接收数据的采样协方差的最小特征值分布特性,检测统计量采用接受信号的平均能量与最小特征值之比,与ED算法不同,门限和噪声能量无关,因此其检测性能比ED优越。文献[16]提出DMM算法,对接收信号相关矩阵进行特征值分解,得到算法的统计量,并且可以动态地设定门限以及克服噪声不确定度的影响,DMM算法性能明显优于ED算法。这些算法在高斯噪声背景下的频谱感知中得到了很好的应用,但当背景为非高斯噪声时,这些算法感知性能降低甚至失效。
目前,分数低阶统计量在非高斯噪声下的频谱检测得到了推广。因此,本文利用分数低阶矩对数据预处理来改进传统的MME算法,并分别在Alpha噪声和Laplace噪声下对提出的算法进行了仿真分析。分析结果表明:相较于传统的MME,本文提出的改进算法有优越的感知性能,且在克服噪声不确定性影响的同时实现了盲感知。
2 频谱感知系统
2.1 系统模型
在CR系统中,假设有I个非授权用户正在感知空闲频谱。这I个非授权用户在特定的时间内对授权用户发射机发出的信号进行搜集,然后将最终搜集到的SU信号的观测向量发送给融合中心进行最终决策,融合中心来判断此时频谱是否空缺。为此,可以将频谱感知原理的数学模型表示为:
(1)
式(1)中,zi(j)表示第i个SU在第j个时刻的接收信号,其中i∈{1,2,3,4,…,I}, j∈{1,2,3,4,…,J}。wi(j)表示在观测过程中第i个SU在第j个时刻的背景噪声,本文分别采用Alpha分布和Laplace分布拟合非高斯噪声。s(j)为PU在第j个时刻的发射信号,且与噪声wi(j)相互独立,在本文中s(j)均采用Gaussian信号进行模拟仿真。hi表示信道增益。H0和H1有以下两种意义:H0表示授权用户没有使用该频段,H1表示授权用户此时正在使用该频段。在H0情况下,该频段可以被SU接入进行通信,但是在H1情况下,SU不可接入或快速退出该频段,以免严重地干扰PU的正常通信。
2.2 非高斯噪声模型
在许多通信领域中所遇到的噪声大多为非高斯分布。目前适应性较强的非高斯噪声模型有Alpha分布[17-18]和Laplace分布[19-20]等,Alpha分布是仅有地满足中心极限定理的一种广义高斯分布,Laplace分布可有效地模拟通信领域中的脉冲噪声。
2.2.1 Alpha稳定分布噪声
Alpha稳定分布可以很好地模拟CR环境中的噪声,如大气噪声,电话线路中的干扰噪声[21]等等。Alpha稳定分布最重要的特性是有厚尾以及稳定的概率分布。基于特征函数的表示为:
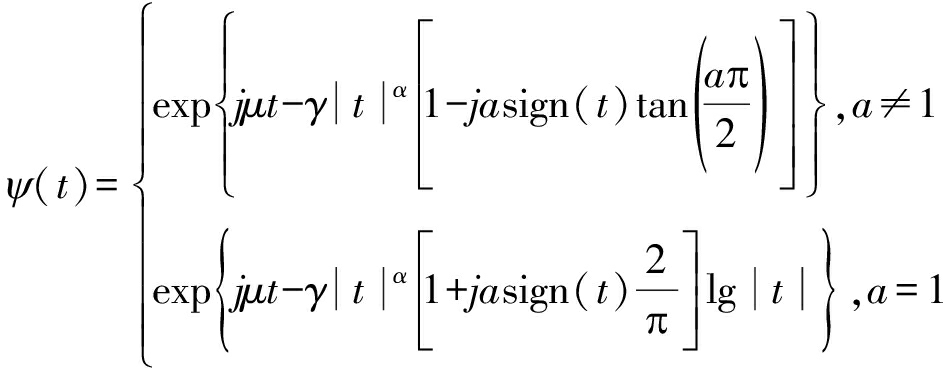
(2)
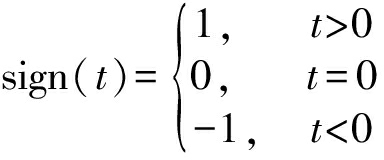
(3)
式(2)中,a、γ、 μ、α分别为对称、尺度、位置参数以及特征指数。从图1中可以看出,α可以控制整个分布的拖尾程度,其值越小,表示拖尾越严重,非高斯性则会越强,越容易导致虚警,从而不能高效利用频谱资源。反之,α值越大,拖尾越薄弱,而非高斯性越弱,越不易导致虚警,使得频谱资源利用率提高。
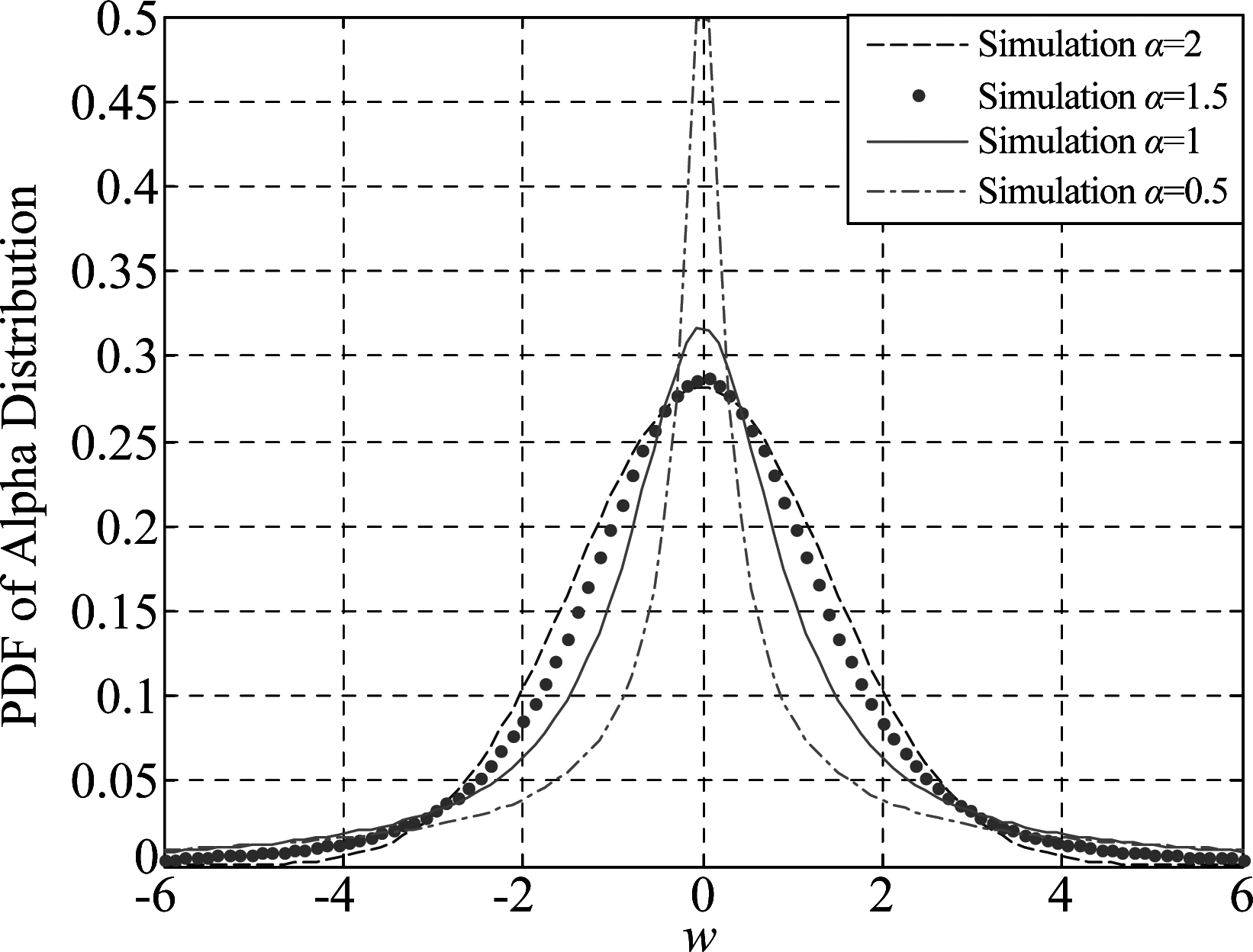
图1 Alpha分布的PDF
Fig.1 PDF of the Alpha distribution
当w~Sα(γ,β,a)时,Alpha分布有以下非常重要的性质:
(4)
由式(4)表明,α<2的Alpha分布不存在有限的二阶矩,只有分数低阶矩(p<α<2)存在,所以传统的基于二阶矩的方法如能量检测、协方差矩阵等检测方法均不再适用。
2.2.2 Laplace分布噪声
Laplace分布噪声可以很好地模拟多用户之间的干扰在超带宽无线系统中,同时在航天和无线电环境下的信号处理得到了广泛使用。Laplace分布是一种广义高斯噪声,它所含参数少,利于计算。其概率密度函数(PDF)可以表示为:
(5)
式(5)中,u和b分别为位置参数及尺度参数。图2中反应了不同的b对Laplace分布的PDF的影响。在图中可以看到,当b越小,拖尾衰减越快,则对应的分布拖尾越薄弱,非高斯性越弱,能够充分利用频谱资源。反之,当b越大,拖尾衰减缓慢,拖尾变得厚重,非高斯性增强,无法充分使用频谱资源。
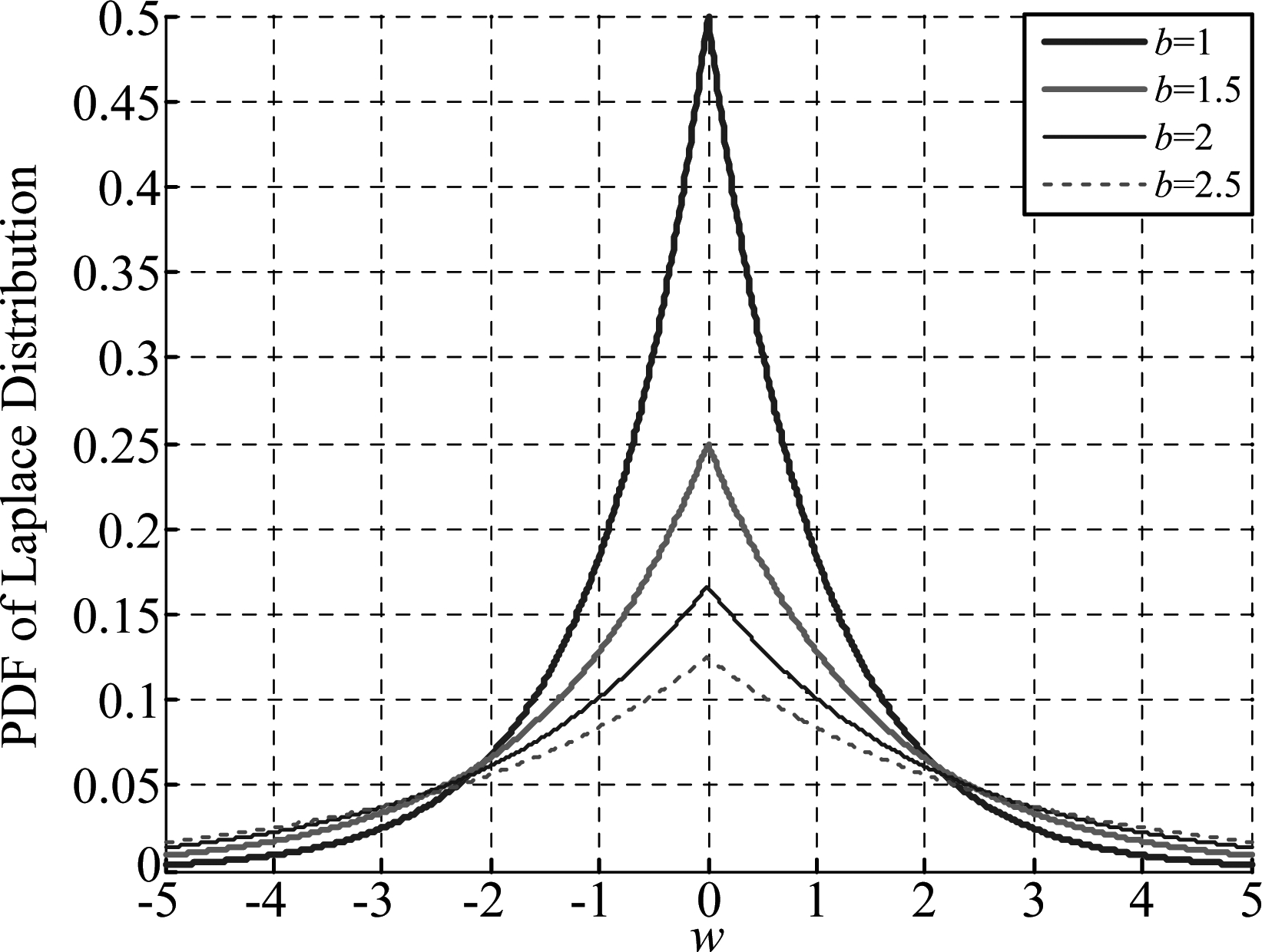
图2 Laplace分布的PDF
Fig.2 PDF of the Laplace distribution
3 基于分数低阶矩协方差MME检测的频谱感知算法
3.1 传统的MME算法
文献[15]提出的MME能够克服噪声不确定度的影响,在高斯背景噪声下是一种很好的盲检测算法。根据接收信号矩阵定义采样协方差矩阵:
(6)
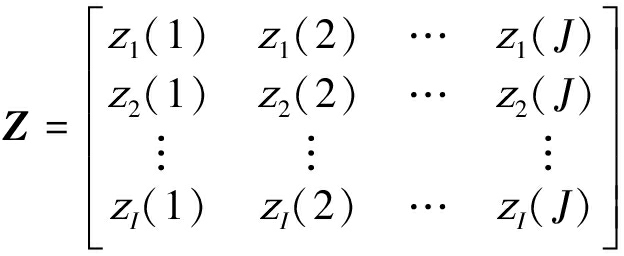
(7)
当只有噪声存在时,Rz(J)转换为Rw(J),且Rz(J)近似服从Wishart矩阵[9],根据RMT求得矩阵的最大特征值,再结合最小特征值的渐进值推导出MME算法的虚警概率表达式:
(8)
式(8)中,![]() 同时可以得到门限的表达式为:
同时可以得到门限的表达式为:
(9)
由文献[15]可知传统的MME算法在高斯噪声背景下有很好的检测性能,但当背景噪声为非高斯分布时,依据RMT求得采样协方差矩阵的最大最小特征值不再适用,这将导致传统MME算法在非高斯噪声分布下感知性能衰退甚至失效。
3.2 改进MME算法以及步骤
3.2.1 改进的MME算法
传统的MME算法在高斯噪声背景下有优越的检测性能,而实际CR场景大多为非高斯噪声,这使得MME性能减退甚至失效,且由于Alpha分布没有二阶统计量或能量谱,但可对采样数据进行预处理转换。为此,本文采用分数低阶矩对观测数据进行预处理,获得分数低阶矩协方差矩阵,再对分数低阶矩协方差矩阵进行最大最小特征值分解。本文将z(j)转换为式(10),它通过分数幂运算降低非高斯噪声的过大样本值,从而可以提高感知性能,并且调节p值可进一步优化感知性能。
(10)
依据统计量可以定义分数低阶协方差矩阵[18]为:
(11)
在实际CR中,观测数据的协方差矩阵很难获知,所以定义采样信号的分数低阶协方差矩阵为:
(12)
式(12)中,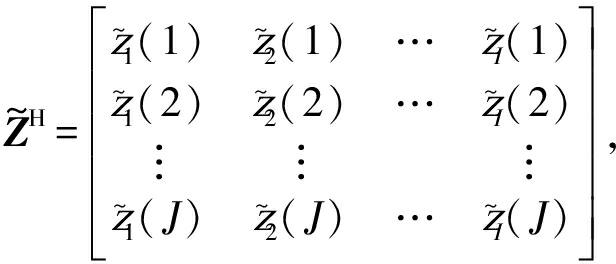 求得矩阵
求得矩阵![]() 的最大最小特征值之比作为统计量:
的最大最小特征值之比作为统计量:![]() 依据统计量T与判决门限
依据统计量T与判决门限![]() 对应的关系来判断PU的存在与否,倘若
对应的关系来判断PU的存在与否,倘若![]() 表示PU存在,授权频段不可侵犯使用;反之,
表示PU存在,授权频段不可侵犯使用;反之,![]() 说明PU不存在,授权频段空缺,可接入占用。
说明PU不存在,授权频段空缺,可接入占用。
3.2.2 改进MME算法的计算步骤
(1)首先对观测数据做分数低阶运算,可得到![]() 然后组成矩阵
然后组成矩阵![]()
(2)接着求采样信号的分数低阶协方差矩阵为:![]()
(3)获得![]() 最大最小特征值分别为:
最大最小特征值分别为:![]() 和
和![]()
(4)依据虚警概率的要求,本文仿真取Pfa=0.1,求得判决门限![]()
(5)判断过程,如果![]() 信号存在;否则,信号不存在。
信号存在;否则,信号不存在。
4 仿真分析
本节采用10000次的Monte Carlo仿真,PU信号采用服从均值为零的高斯分布,根据文献[7]虚警概率Pfa≤0.1。本文仿真在Pfa=0.1情况下进行改进算法与传统MME算法的检测性能比较。其中Alpha噪声参数取值分别为:a=0,γ=1, μ=0,α=1;Laplace噪声参数取值分别为:![]()
4.1 改进的MME与传统MME在不同噪声下的性能比较
图3取J=200,I=5,SNR=-10 dB,在非高斯噪声背景下给出Pfa与γ的关系。从图3中可以看出,当噪声为Alpha分布时,α=1,p=0.2;α=0.6,p=0.1,Pfa随着感知门限γ的增大而减小。同样在噪声为Laplace分布,p=0.2和p=0.1时,改进算法的Pfa也是随着γ值的增大而减小。特别地,当Pfa=0.1时,感知门限γ如表1所示。
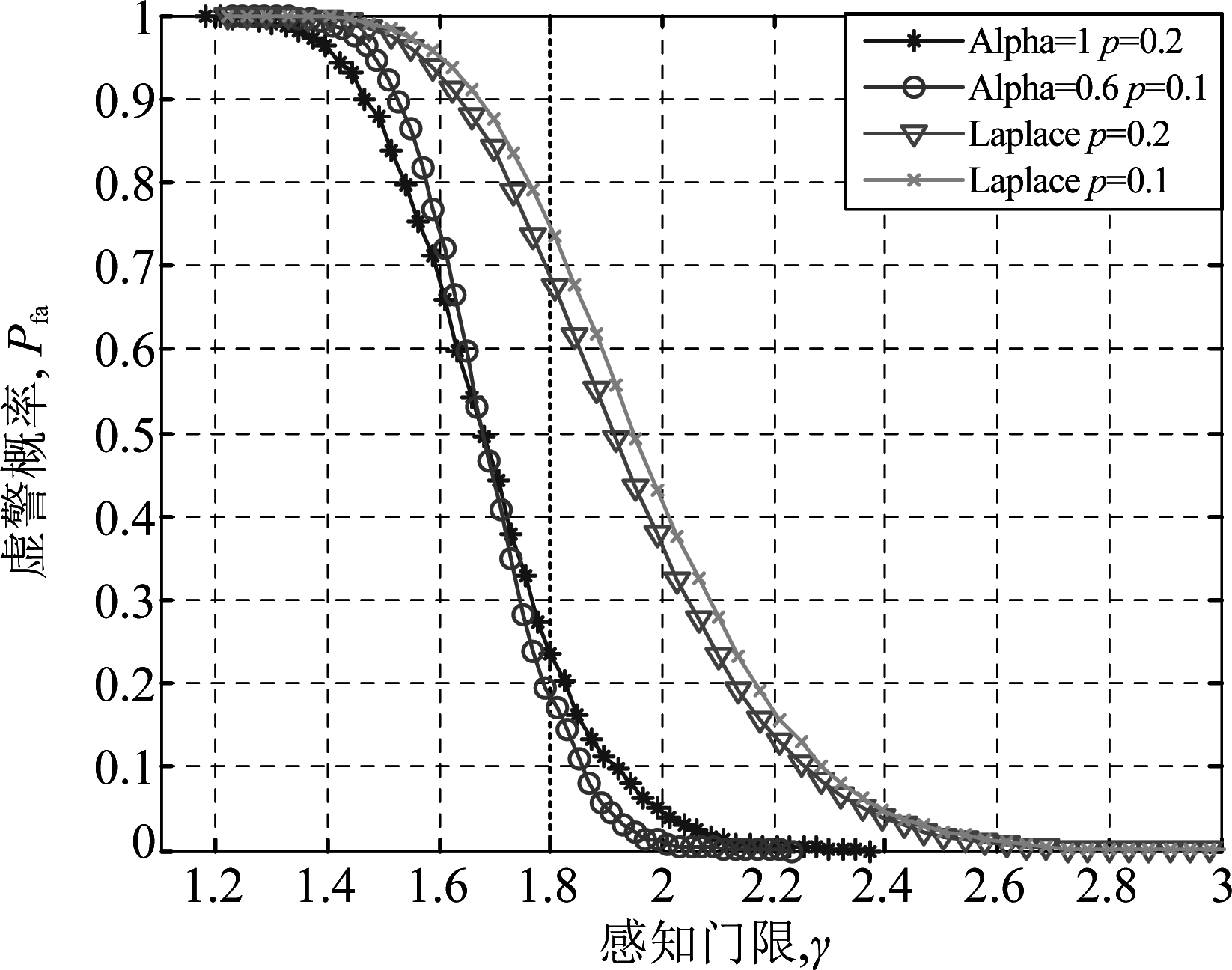
图3 虚警概率Pfa与感知门限γ的关系
Fig.3 Probability of false alarm versus sensing threshold
表1 感知门限
Tab.1 Sensing threshold
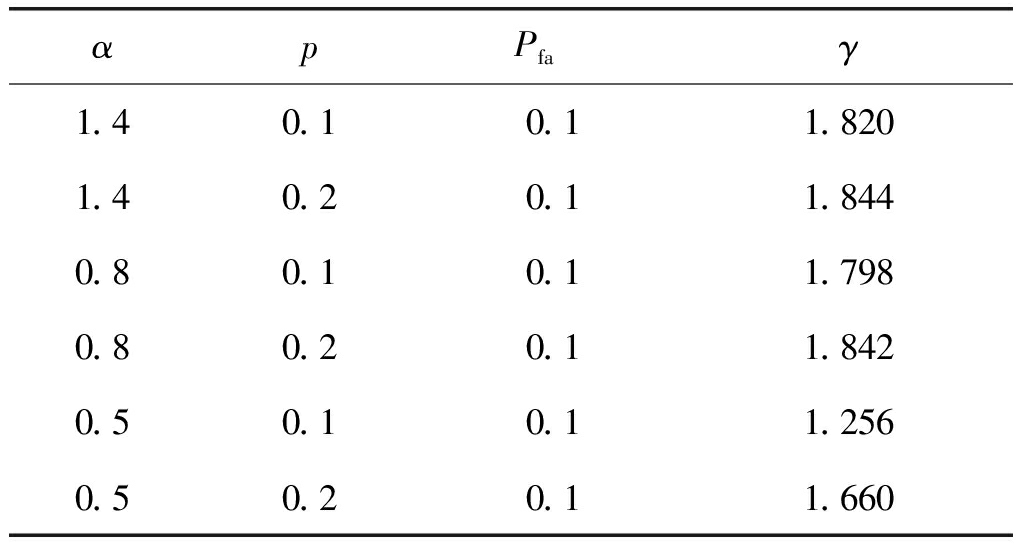
αpPfa γ1.40.10.11.8201.40.20.11.8440.80.10.11.7980.80.20.11.8420.50.10.11.2560.50.20.11.660
图4取J=200,I=5,SNR=-5 dB,在Alpha噪声分布和Gaussian噪声分布下,本文提出的改进算法与传统的MME算法的检测概率Pd与虚警概率Pfa的ROC比较。从图4可以看出,传统的MME算法在Gaussian噪声分布下性能最优,在Pfa=0.1时,传统MME的Pd达到0.97,而改进的算法在Gaussian噪声下且阶数p=0.2时仅达到0.78,表明改进算法不适用于高斯噪声分布。但是当背景噪声为Alpha分布时,当Pfa=0.1时,传统MME的Pd仅有0.1,传统MME检测性能完全失效,而改进算法性能却有很大提高,在Pfa=0.1且p=0.1时的Pd达到0.86,同时随着p值的减小,Pd值在提高,表明改进的算法可以在Alpha分布下使用,且具有较好的检测性能。

图4 检测概率Pd与虚警概率Pfa的ROC曲线
Fig.4 ROC curves of the probability of false alarm and detection
图5取J=200,I=5,SNR=-10 dB,在Laplace分布噪声下,本文改进的算法与传统MME算法的ROC比较。从图5可以看出,在Laplace分布噪声下,在Pfa=0.1时,传统MME算法的Pd仅仅达到0.36,而此时改进算法的Pd在p=0.2时高达0.90,改进算法的感知性能相比于传统MME明显提高。在p=0.8时,Pd=0.68;p=0.6时,Pd=0.83;p=0.4时,Pd=0.89;可以看出随着p值的减小,改进算法检测效果越好。即噪声为Laplace分布时,本文提出的改进算法的感知性能远优于传统MME算法。
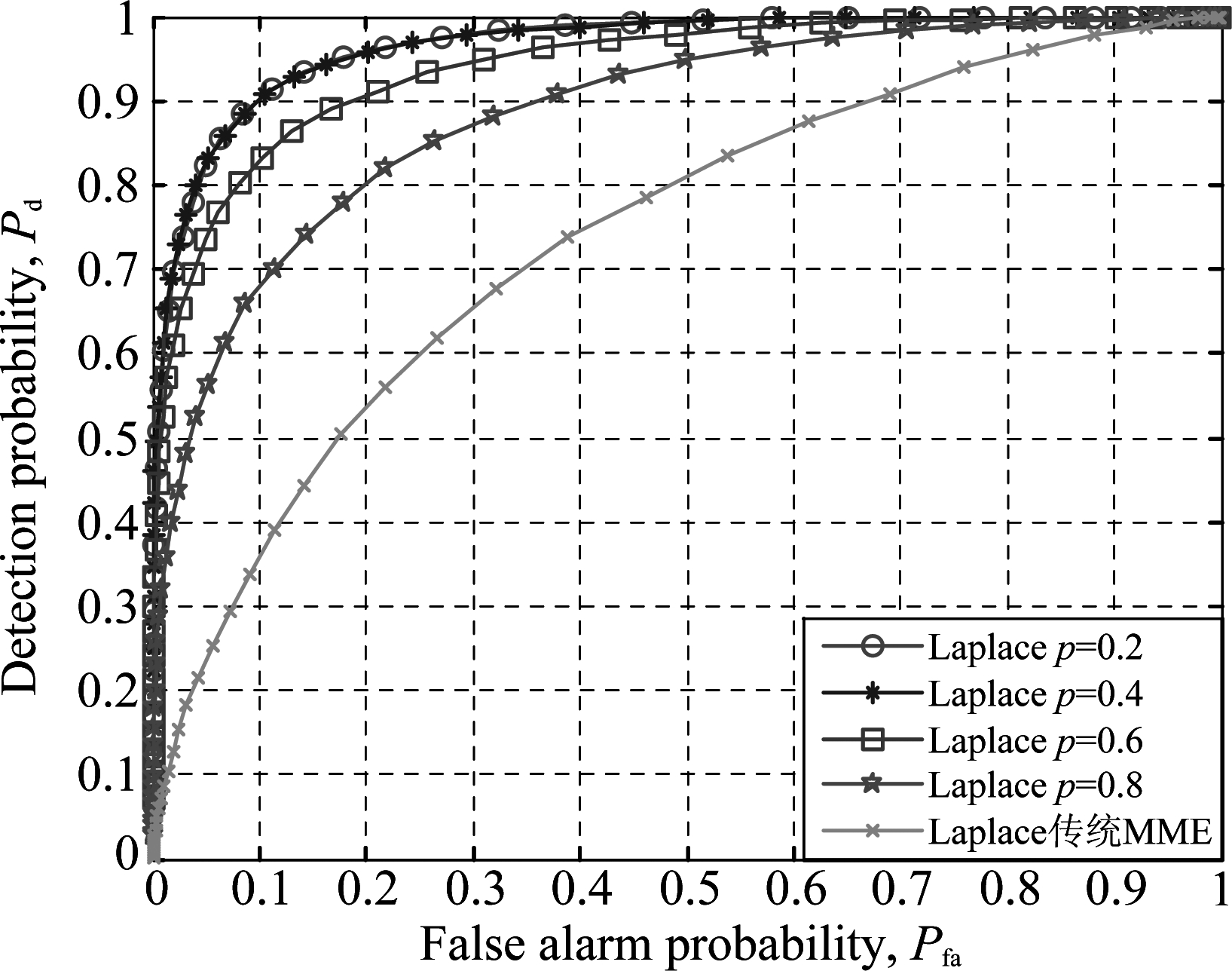
图5 Laplace噪声下,改进算法与传统MME算法的ROC比较
Fig.5 ROC of improved algorithm compares to traditional MME for Laplace
图6取J=200,I=5,SNR=-10 dB,当噪声方差和背景噪声改变时,检测概率Pd与阶数p的关系。从图6可以看出,当背景噪声为Alpha分布时,在0<p<0.8且SNR=-10 dB时,改进的算法感知性能优于传统的MME算法,检测概率由0.1提高到了0.44,且当SNR增加时,感知性能明显提高。当背景噪声为Laplace分布时,在0<p<1且SNR=-10 dB时,传统MME的Pd=0.40,而改进算法的Pd可达到0.91。很明显,在非高斯噪声分布下,本文改进的算法能有效减小这些具有脉冲性的噪声样本幅值,进而可以降低虚警概率,提高检测概率,从而提高了频谱利用率。
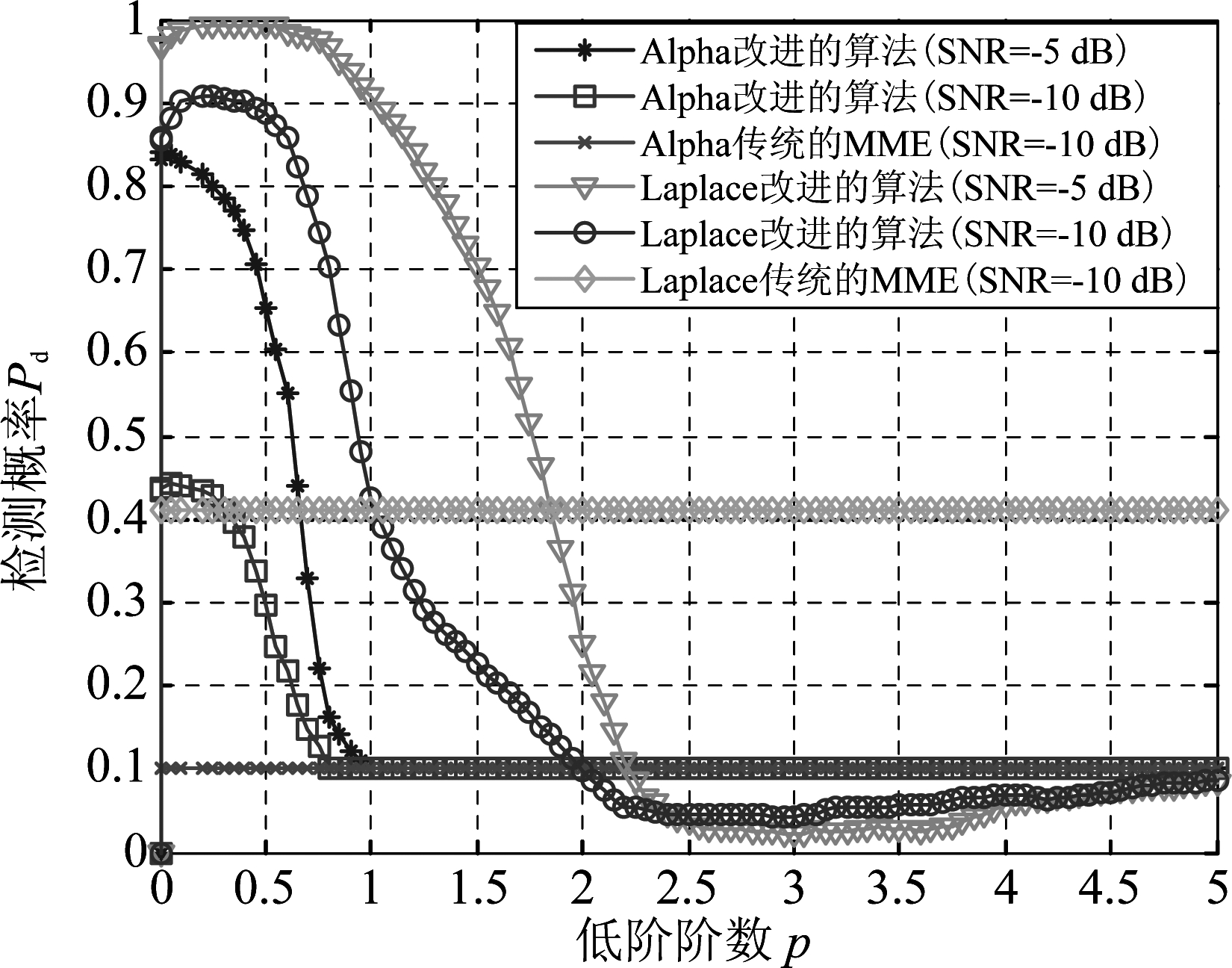
图6 检测概率Pd与阶数p的关系
Fig.6 Probability of detection versus p
图7取J=200,I=5,Pfa=0.1,改进算法与MME在非高斯噪声下Pd与信噪比SNR的关系。从图4~5中可以看出,当噪声为Lapalce分布,SNR从-15 dB增加到-10 dB时,改进的算法在p=0.2时候的Pd值从0.53上升到0.89,可知,无论CR环境如何变化,只要SNR增加,改进算法的感知性能都能有所提高。但当噪声为Alpha分布时,在SNR为-12 dB时,改进的算法在p=0.2时候的Pd值低于0.3,感知性能较差,而当SNR低于-9 dB时,在Alpha分布下改进算法Pd值总大于传统的MME的Pd值,即改进的算法在非高斯噪声情况下感知性能明显优于传统的MME算法。
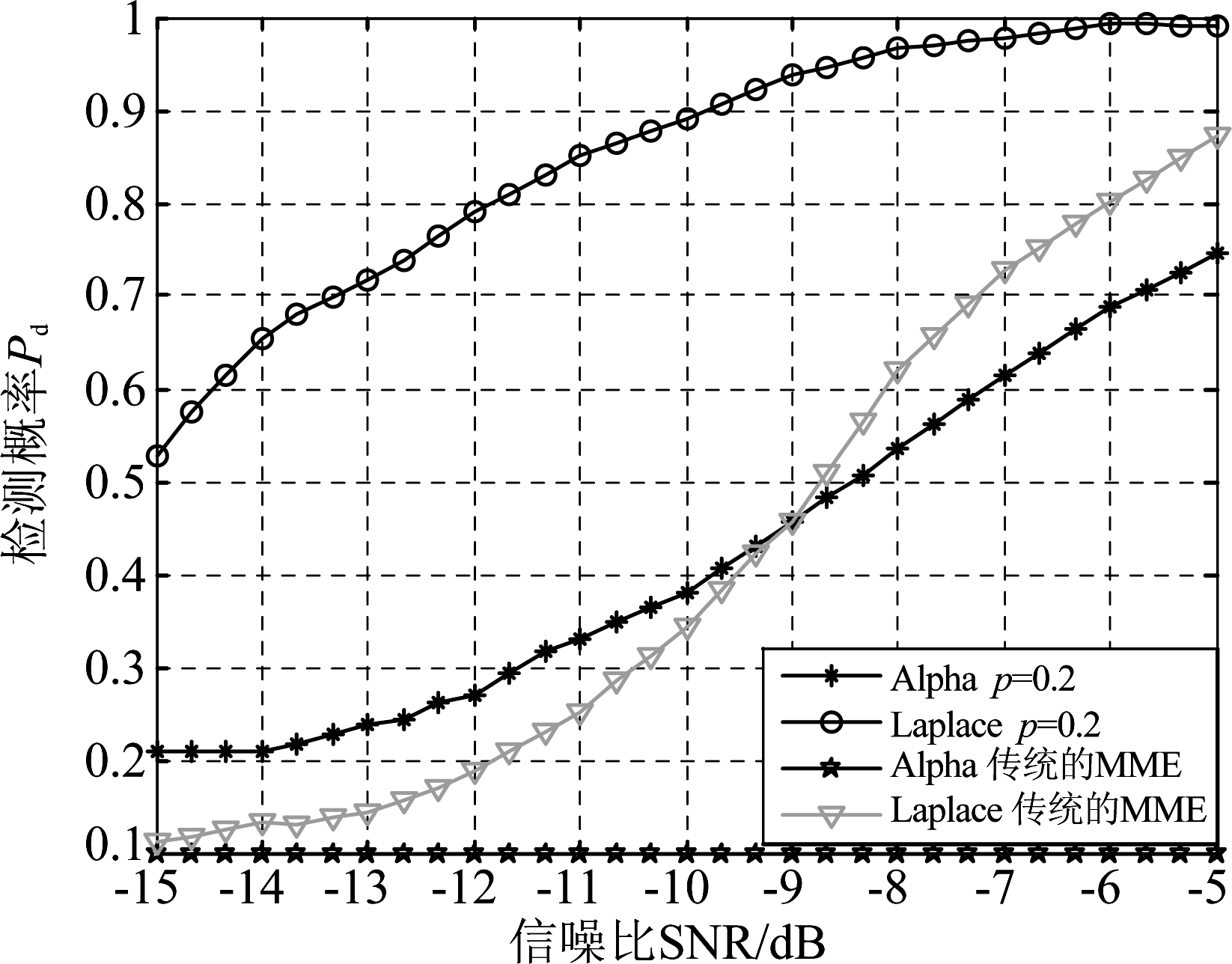
图7 检测概率Pd与信噪比SNR的关系
Fig.7 Probability of detection versus SNR
5 结论
本文提出非高斯噪声中基于分数低阶矩协方差MME检测的频谱感知算法。其中非高斯噪声选用了Alpha分布和Laplace分布,在其严重的厚尾的特性下,传统的MME算法检测性能减退甚至失效,为此采取分数低阶矩采样协方差降低非高斯特性。仿真结果表明,相较于传统的MME算法,本文提出的改进算法有优越的检测性能,不仅可以克服噪声不确定性还能实现盲感知。
参考文献
[1] Hwang I, Lee J W. Cooperative Spectrum Sensing With Quantization Combining Over Imperfect Feedback Channels[J]. IEEE Transactions on Signal Processing, 2016, 65(3):721-732.
[2] Jia M, Gu X, Guo Q, et al. Broadband Hybrid Satellite-Terrestrial Communication Systems Based on Cognitive Radio toward 5G[J]. IEEE Wireless Communications, 2016, 23(6):96-106.
[3] Bhardwaj P, Panwar A, Ozdemir O, et al. Enhanced Dynamic Spectrum Access in Multiband Cognitive Radio Networks via Optimized Resource Allocation[J]. IEEE Transactions on Wireless Communications, 2016, 15(12):8093- 8106.
[4] Grissa M, Yavuz A, Hamdaoui B. Preserving the Location Privacy of Secondary Users in Cooperative Spectrum Sensing[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(2):418- 431.
[5] 王凡, 卢光跃. 利用LMS的频谱感知算法[J]. 信号处理, 2016, 32(5):543-548.
Wang F, Lu G Y. Spectrum Sensing Method Using LMS[J]. Journal of Signal Processing, 2016,32(5): 543-548.(in Chinese)
[6] Zhu X, Champagne B, Zhu W P. Rao test based cooperative spectrum sensing for cognitive radios in non-Gaussian noise[J]. Signal Processing, 2014, 97(7):183-194.
[7] 朱晓梅, 蒋培, 包亚萍. 高斯混合噪声环境中基于分数低阶矩的频谱感知算法研究[J]. 信号处理, 2015,31(8):968-974.
Zhu X M, Jiang P, Bao Y P. Spectrum Sensing for Cognitive Radio Under Gaussian Mixture Noise Using Fractional Lower Order Moments[J]. Journal of Signal Processing, 2015,31(8): 968-974.(in Chinese)
[8] Zeng Y, Liang Y C. Maximum-Minimum Eigenvalue Detection for Cognitive Radio[C]∥International Symposium on Personal, Indoor and Mobile Radio Communications. IEEE, 2007:1-5.
[9] Tulino A M, Verdú S. Random Matrix Theory and Wireless Communications[J]. Communications & Information Theory, 2004, 1(1):1-182.
[10]Johnstone I M. On the Distribution of the Largest Eigenvalue in Principal Components Analysis[J]. Annals of Statistics, 2001, 29(2): 295-327.
[11]贺亚晨, 赵文静, 刘畅,等. 基于最大特征值的拟合优度检验频谱感知算法[J]. 信号处理, 2017,33(3A):33- 40.
He Y C, Zhao W J, Liu C, et al. A Novel Spectrum Sensing Method Using Goodness of Fit Test based on Maximum Eigenvalue[J]. Journal of Signal Processing, 2017,33(3A): 33- 40.(in Chinese)
[12]弥寅, 卢光跃. 基于特征值极限分布的合作频谱感知算法[J]. 通信学报, 2015, 36(1):84- 89.
Mi Y, Lu G Y. Cooperative spectrum sensing algorithm based on limiting eigenvalue distribution[J]. Journal on Communications, 2015, 36(1): 84- 89.(in Chinese)
[13]Penna F, Garello R, Spirito M A. Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in Wishart matrices[J]. IEEE Communications Letters, 2012, 13(7):507-509.
[14]Zeng Y, Liang Y C. Spectrum-Sensing Algorithms for Cognitive Radio Based on Statistical Covariances[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4):1804-1815.
[15]Zeng Y, Liang Y C. Eigenvalue based Spectrum Sensing Algorithms for Cognitive Radio[J]. IEEE Transactions on Communications, 2008, 57(6):1784-1793.
[16]王颖喜, 卢光跃. 基于最大最小特征值之差的频谱感知技术研究[J]. 电子与信息学报, 2010, 32(11):2571-2575.
Wang Y X, Lu G Y. DMM Based Spectrum Sensing Method for Cognitive Radio Systems[J]. Journal of Electronics and Information Technology, 2010, 32(11): 2571-2575.(in Chinese)
[17]Zhu X, Zhu W P, Champagne B. Spectrum sensing based on fractional lower order moments for cognitive radios in α-stable distributed noise[J]. Signal Processing, 2015, 111(C):94-105.
[18]Luo J, Wang S, Zhang W. Stochastic signal detection based on changeable fractional lower order moments in alpha stable noise[C]∥IEEE International Conference on Signal Processing, Communications and Computing. IEEE, 2016:1-5.
[19]Bao Y, Zhu Y, Zhu X, et al. A spectrum sensing method based on fractional lower order moments in weakly correlated Laplace noise[C]∥Asia-Pacific Signal and Information Processing Association Summit and Conference. IEEE, 2015:892- 896.
[20]Gao R, Li Z, Li H, et al. Absolute Value Cumulating Based Spectrum Sensing with Laplacian Noise in Cognitive Radio Networks[J]. Wireless Personal Communications, 2015, 83(2):1-18.
[21]Stuck B W, Kleiner B. A Statistical Analysis of Telephone Noise[J]. Bell Labs Technical Journal, 2013, 53(7):1263-1320.



