1 引言
直线匹配是指采用一定的匹配算法在两幅或者多幅覆盖同一区域或同一地物的影像上寻找同名特征线,建立不同影像上同名特征线的对应关系。利用影像上的直线信息重建人工地物三维模型在摄影量测和计算机视觉领域中有着重要的研究意义,其中直线匹配是其关键科学问题之一。
国内外学者针对直线匹配已开展了大量的研究。现有方法研究重心主要包括以下两个方面:一是搜索范围约束,常用的约束条件有核线约束[1-3]、三焦张量约束[4-5]、单应矩阵约束[6-7]、同名点约束[8-11]、三角网约束[12]等,已有的约束条件都需要先验知识或者较为严格的已知条件;二是直线段描述子的建立,结合已有的约束条件,传统直线段特征描述子多利用直线段本身的几何属性[13-14],如方向、长度、距离、重复性等。这类简单的几何属性受限于直线提取结果的影响,对于提取结果存在断裂及遮挡影像而言,匹配正确率较低。除此之外,直线邻域窗口的灰度信息也常被用于描述和匹配直线特征。结合核线约束,Schmid等[15]利用直线邻域窗口的灰度相关作为匹配测度对短基线影像的直线进行匹配。结合三角网约束,张云生等提出移动窗口的自适应直线相关方法[16],有效解决位于纹理断裂处的直线匹配问题。这类直接利用窗口灰度相关对于序列影像或者短基线的影像比较适用,但难以适应视角尺度变化较大的影像。因此,为提高描述子的可靠性,目前直线描述子多利用直线邻域区域内像素灰度直方图、梯度、均值、方差等信息。在无任何约束条件下,王志衡等提出了3个具有平移、旋转、光照不变性的均值-标准差描述子[17]。首先定义直线平行支撑域并将其分解为一系列平行线,分别选择灰度均值、梯度幅值均值、梯度均值三种不同特征建立直线描述矩阵,通过计算描述矩阵行向量的均值和标准差构建直线描述子。在此基础上,Wang等进一步提出了MSLD均值-标准差直线描述子(Mean-Standard Deviation Line Descriptor, MSLD)[18],与上述三个描述子不同的是,MSLD描述子通过统计像素支撑域内每个子区域4个方向的梯度向量构建描述子矩阵,进一步提高现有描述子的可区分性及鲁棒性,但现有研究局限于单一尺度拍摄的影像之间,对尺度变化较于敏感。相似于MSLD描述子,Zhang等[19]提出了LBD(Line Band Descriptor)描述子,首先将直线支撑域分为若干个与直线平行的子区域,通过统计每个子区域内4方向梯度向量构建直线描述子,该描述子在直线的局部邻域基础上引入了全局和局部高斯权重系数,匹配效果良好。但是由于同一直线在不同影像上提取结果的差异,直接利用不同影像上直线构建支撑域为非对应区域,对于复杂地物影像,匹配可靠性较弱。相似于SIFT点描述子[20],缪君等提出一种仿射不变的直线描述子用于直线匹配[21],该描述子在构建过程中考虑到不同影像间尺度变化及直线上点的对应关系,但是仅利用直线上的点构建描述子,舍弃直线邻域范围内的点,对于复杂地物影像,可靠性有待提高。
因此,针对不同类型影像直线匹配过程中直线描述子的稳定性,本文提出了一种结合区域仿射变换的MSLD直线描述子(MSLD Descriptor Combined Regional Affine Transformation, RAT_MSLD)用于直线段匹配。该描述子构建过程中,首先结合核线约束对目标直线及候选直线构建对应的同名直线支撑域,再通过仿射变换统一两个灰度支撑域的大小,最后利用仿射变换后的直线支撑域构建MSLD描述子用于后续匹配,匹配过程中结合三角网约束及核线限定搜索范围确定候选直线,提高匹配的可靠性。
2 算法原理
本文采用结合区域仿射变换的MSLD描述子进行直线段匹配的整体流程如图1所示。该算法在已有SIFT匹配获取初始可靠同名点基础上,对左、右影像上提取的直线段进行匹配。在初始匹配阶段,利用初始同名点构建的同名三角网约束目标直线的候选匹配直线;在匹配第二阶段,首先对左影像上目标直线构建直线平行支撑域,并根据左影像上目标直线两端点及其平行支撑域四角点的核线确定候选直线对应区域及其平行支撑域;然后对两直线支撑域分别进行仿射变换,以目标直线支撑域大小确定仿射变换后两直线支撑域的大小;对仿射变换后得到两直线支撑域,分别构建MSLD直线描述子;最后依据MSLD描述子,结合欧式距离和最邻近比值(Nearest neighbor distance ratio, NNDR)方法确定同名直线。
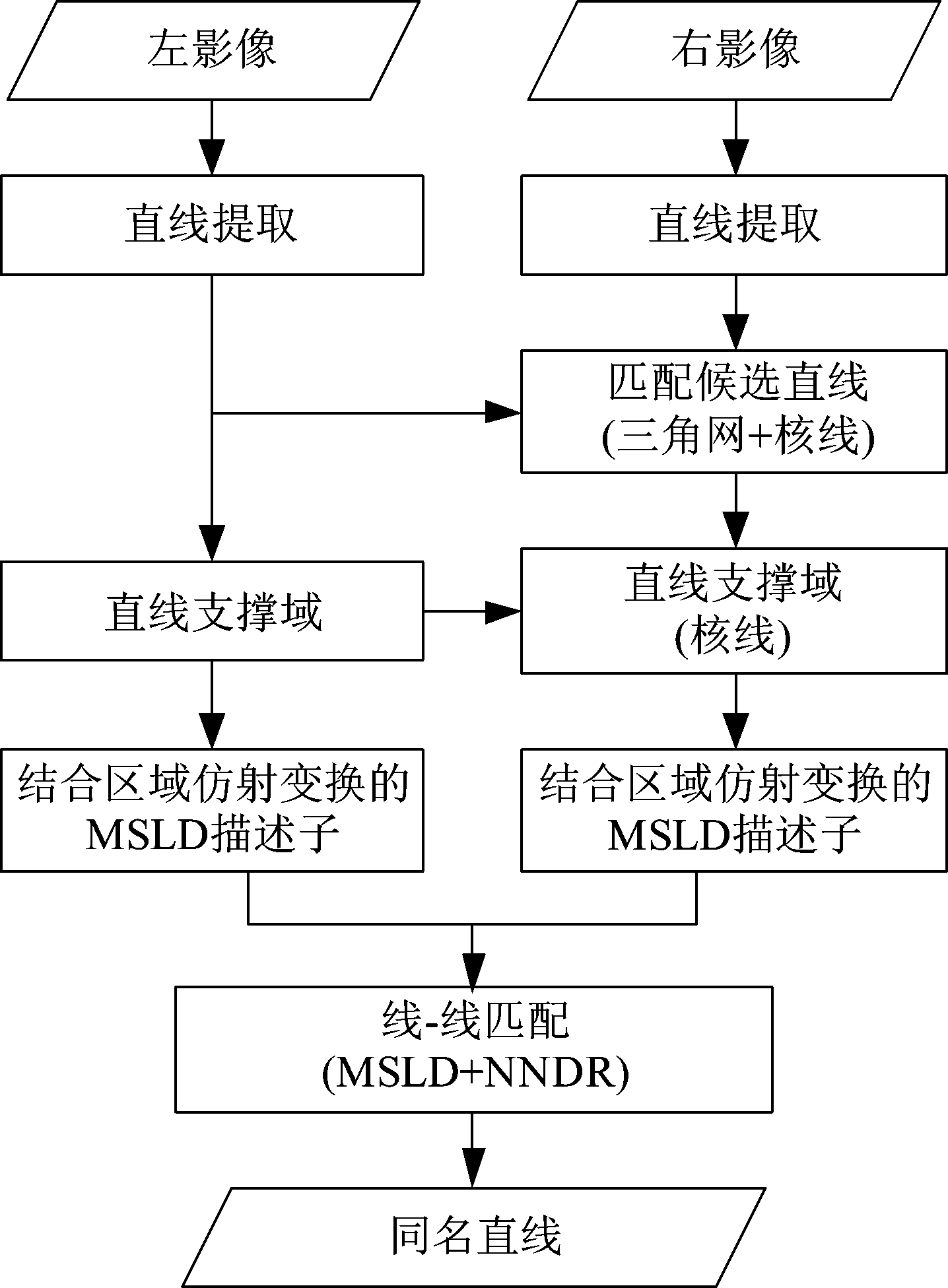
图1 直线匹配流程图
Fig.1 Flowchart of line matching
2.1 三角网约束
利用已有SIFT匹配得到的所有同名点构建左、右影像上的同名三角网。首先对左影像上的同名点按照Delaunay准则构建三角网,然后根据左影像上每个三角形的顶点索引及其对应的右影像上的同名点直接构建右影像上对应的同名三角网。三角网约束直线匹配即指同名直线经过同名三角形。对左影像上任一待匹配的目标直线,首先判断其经过的三角形,对应的右影像上同名三角形内经过的直线为候选直线。如图2所示,图2(a)是左影像上直线L经过的三角形,图2(b)中L1、L2、L3、L4为右影像上同名三角形内经过的直线,为L的匹配候选直线。三角网约束在很大程度上减少了匹配的搜索范围,降低错误匹配概率并缩短了匹配时间。
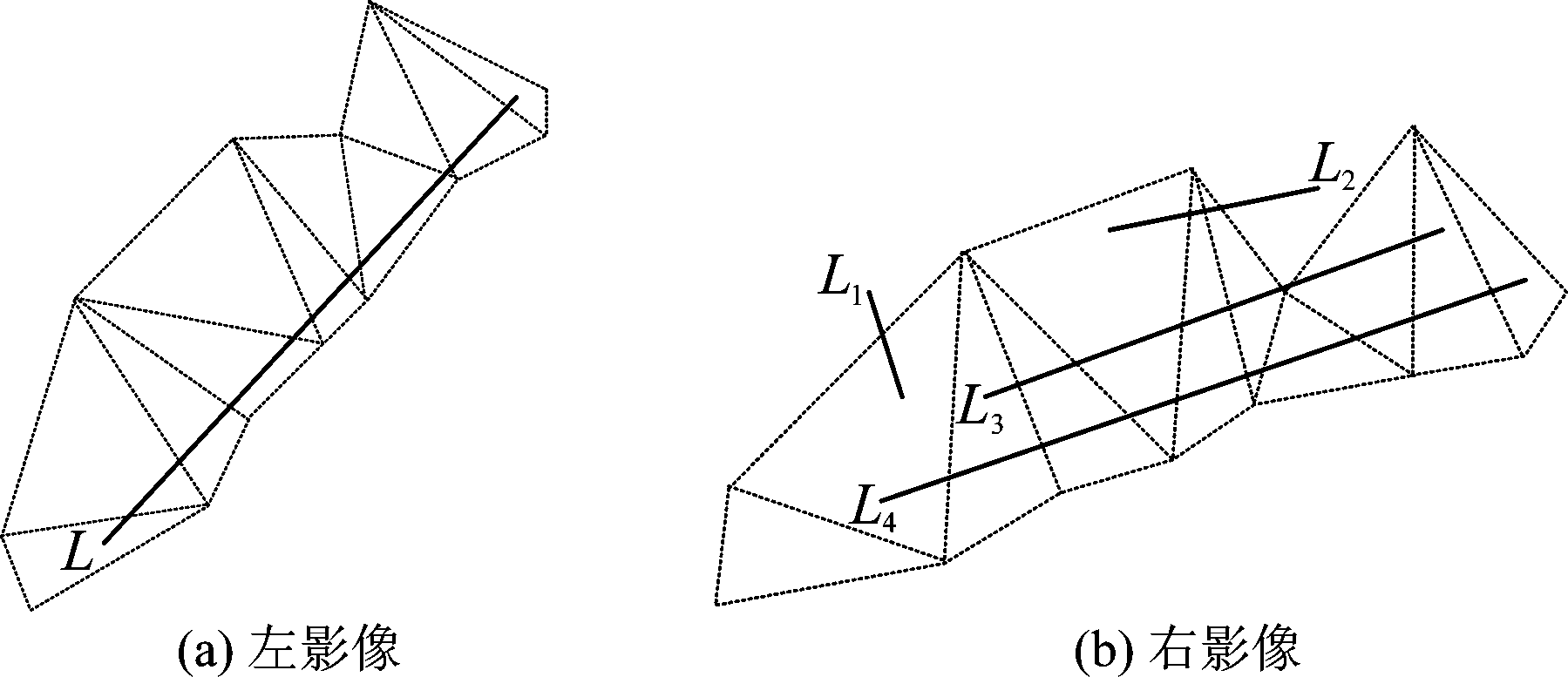
图2 三角网约束
Fig.2 Triangle constraint
2.2 描述子
2.2.1 MSLD描述子
Wang等提出MSLD直线描述子[18],对任一给定直线L,首先将直线上所有像素的平均梯度方向确定为直线的法方向d⊥,沿着法方向逆时针旋转至其垂直的方向即为直线方向dL。对直线L上每个像素点,以其为中心沿d⊥和dL方向建立矩形区域,被定义为像素支持域(Pixel Support Region, PSR)。沿直线方向dL上每个像素定义的像素支持域PSR依次被表示为G1,G2,...,GN,假设L包含N个像素。为了增加描述子的可区分性,每个PSR沿着d⊥方向划分为M个互不重叠且大小相同的子区域Gi=Gi1∪Gi2∪...∪GiM,i∈[1,n],如图3所示,每个PSR被分为3个子区域,即M=3。
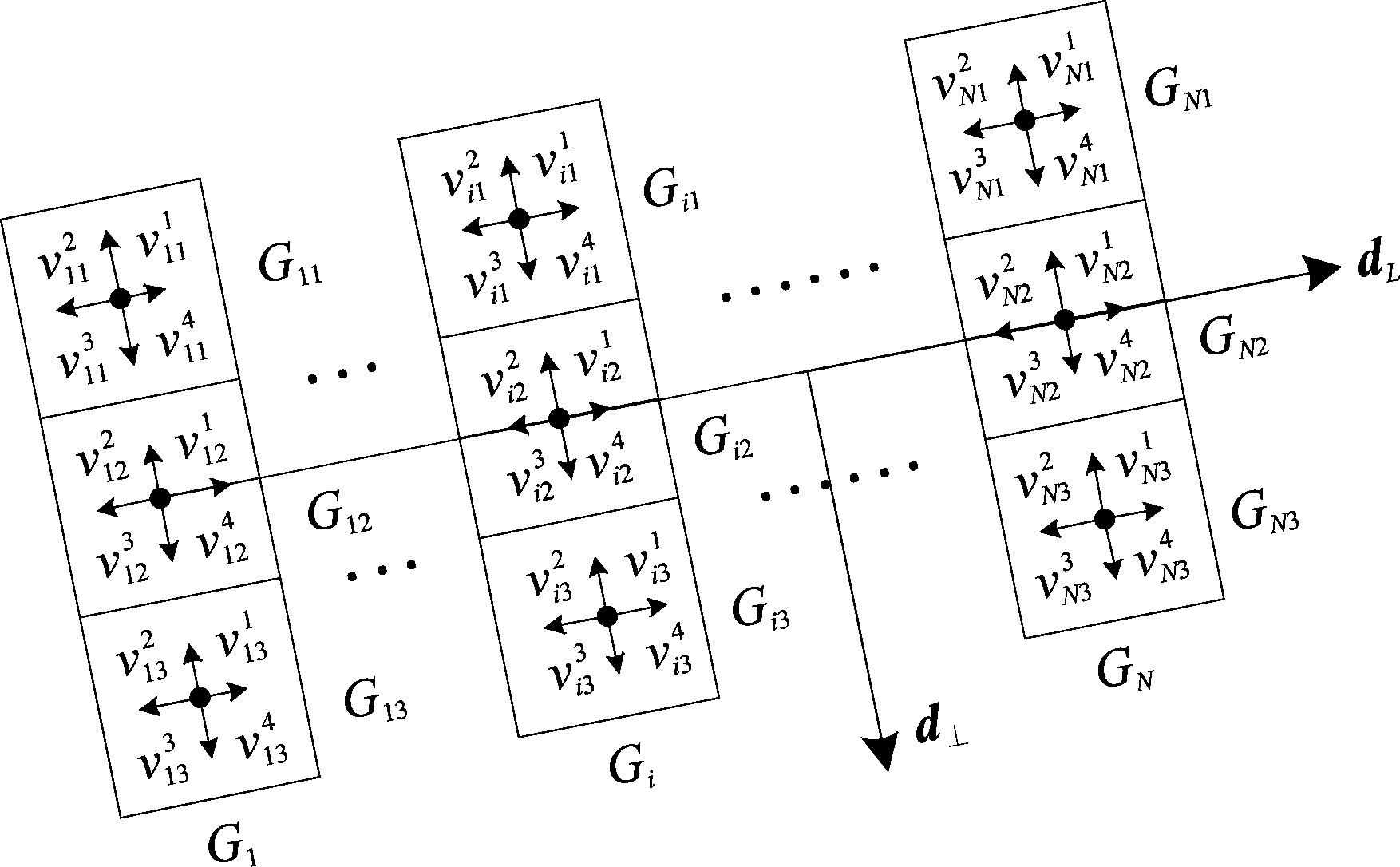
图3 MSLD描述子的构建
Fig.3 MSLD construction
相似SIFT特征描述子思想,对各个子区域Gij统计4方向的梯度向量,4方向分别为d⊥、dL方向及其反方向,如图3每个子区域内所示的4方向,得到一个4维的特征向量:
(1)
在计算所有子区域特征向量后,将其构成直线L的梯度描述子矩阵(Gradient Description Matrix, GDM),即得到4M×N大小的矩阵,表示如下:
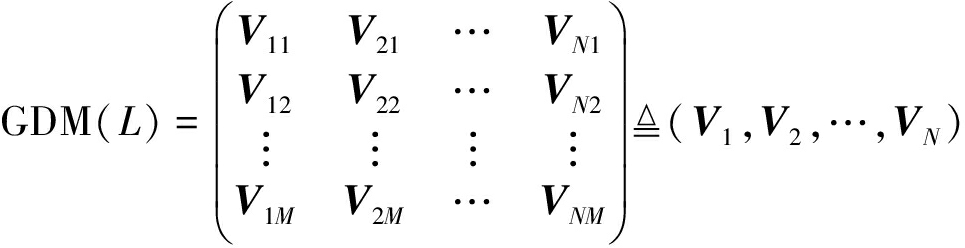
(2)
为了使直线描述子维数不受直线长度的影响,对GDM矩阵按行向量计算均值和标准差并将其作为直线描述子,称之为均值-标准差描述子(MSLD),MSLD构建过程如下:
M(GDM(L))=Mean{V1,V2,...,VN}∈R4M
(3)
S(GDM(L))=Std{V1,V2,...,VN}∈R4M
(4)
为了使描述子具有光照不变性,分别对均值和标准差向量进行归一化处理,得到由归一化后的均值和标准差向量构成的8M维的直线描述子:
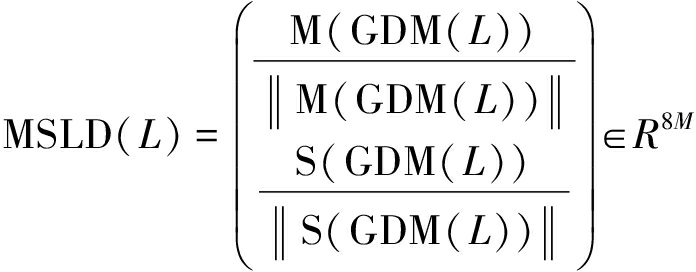
(5)
2.2.2 结合区域仿射变换的MSLD描述子
2.2.2.1 核线约束
对满足2.1三角网约束的候选直线进一步利用核线对其进行约束。匹配过程中,利用已知同名点,采用基于共面条件的相对定向线性变换算法(Realtive Orientation Linear Transformation, RLT)实时计算核线[22]。分别计算目标直线L两端点在右影像上核线,得到如图4(b)中Ha和Hb所示核线,保留位于核线范围内的候选直线用于后续匹配,如图4(b)中L1、L2、L3、L5所示。同时以目标直线为基准,其核线与候选直线交点为假定重叠部分的端点,对于交点不在直线段范围内的候选直线,后续构建直线支撑域过程中将其延长至端点处,如图4(b)中L3延长端点至a′、b′。

图4 核线约束
Fig.4 Epilolar constrant
2.2.2.2 构建直线支撑域
为了构建MSLD描述子,对目标直线和候选直线分别建立直线支撑域。如图5所示,对左影像上目标直线构建直线支撑域,L为影像上长度为l的一条直线段,定义以L为中心轴,宽度为w=2r+1的矩形区域为L的直线支撑域。为了确保同名直线支撑域为对应的同名区域,根据左影像上目标直线支撑域四角点及候选直线重叠段端点确定右影像上候选直线支撑域。如图所示,分别计算目标直线支撑域四角点1、2、3、4点在右影像上的核线,得到核线H1、H2、H3、H4。核线与过候选直线端点并与候选直线垂直的直线交点为对应的候选直线支持区四角点1′、2′、3′、4′。
2.2.2.3 RAT_MSLD描述子构建
由于左、右影像上目标直线支撑域和候选直线支撑域位置、方向、尺度、大小不一,不利于后续描述子构建,因此对目标直线和候选直线的直线支撑域分别进行仿射变换,统一二者的方向、尺度及大小。仿射变换后矩形支撑域的四边分别与影像的像素坐标系平行,原点在其左上角点处,其长度和宽度与目标直线支撑域的长度和宽度相同。仿射变换采用6参数仿射变换公式,如公式(6),其中x、y为仿射变换后灰度区域的像素坐标,x′、y′为原影像上像素坐标,a0、a1、a2、b0、b1、b2为变换参数。利用支撑域四角点的坐标计算仿射变换参数,最终得到仿射变换后灰度区域用于构建MSLD描述子。
x=a0+a1x′+a2y′
y=b0+b1x′+b2y′
(6)
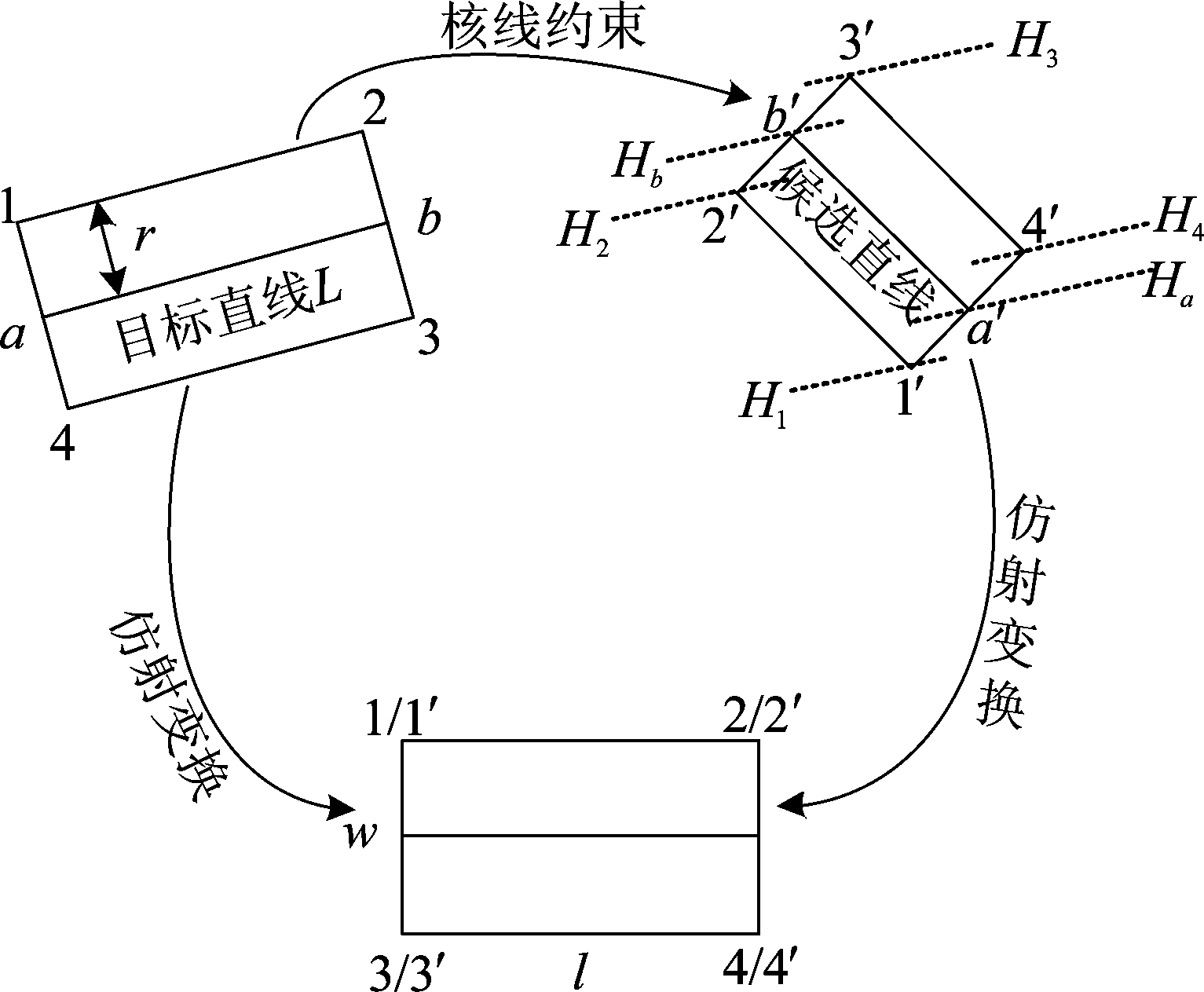
图5 直线支撑域确定及仿射变换
Fig.5 Line support region and Affine Transform
鉴于本文首先对利用核线确定左右影像上直线对应关系,并对其构建支撑域进行仿射变换,因此,不需对直线定义d⊥和dL方向,直接对仿射变换后的以直线为中心线的灰度区域进行像素支持域划分及其子区域的划分。对各个子区域Gij分别统计0、90、180、360四方向的梯度特征向量用于后续MSLD描述子构建。根据文献[17],匹配过程中,选择M=9,子区域大小为![]() 5。
5。
2.3 线-线匹配
结合MSLD描述子,本文采用欧式距离作为直线匹配测度,计算目标直线与候选直线间描述子的欧式距离D,如果D小于给定阈值TD,且最小欧式距离与次最小欧式距离的比值NNDR小于阈值TN,则认为与目标直线描述子有最小欧式距离的候选直线为最终的同名直线。
3 实验与分析
为了验证本文结合区域仿射变换MSLD描述子的有效性,选取六组具有代表性的近景影像用于直线匹配实验,如图6所示,图6(a)~(f)分别为尺度(scale)变化、尺度变化结合影像模糊、不同时相不同相机不同尺度影像、光照(light)变化、旋转(rotation)变化,视角(view)变化影像对。影像大小分别如表1所示。本文算法匹配结果如图6(g)~(r)所示,其中红色线为正确匹配直线,蓝色线为错误匹配直线。
为了对比分析,本文还采用文献[18]中MSLD描述子和文献[1]中传统灰度相关对图6所示六组影像进行直线匹配。实验在相同直线提取结果条件下,在三角网及核线约束确定相同候选直线的条件,采用不同的描述子用于相似性约束确定匹配同名直线。其中,灰度相关阈值为0.75,MSLD和本文结合区域仿射变换MSLD参数阈值一样,其中TD=1.2,TN=0.8。本文涉及所有直线匹配实验均采用左、右影像上直线提取结果中长度大于20的直线段用于匹配实验。鉴于篇幅,仅对本文RAT_MSLD描述子的匹配结果进行显示。对匹配结果进行人工目视判读,三种算法直线匹配结果统计如表1所示,表中MN(Matching Number)表示匹配直线的总数目,CM(Correct Matching)表示正确匹配数目,CR(Correct Ratio)表示匹配正确率,Time为算法执行时间。
本文首先对尺度变化影像进行直线匹配实验,图6(a)所示两张影像之间尺度约为1∶1.5,左、右影像上满足条件的直线数目分别为742、383条,采用本文RAT_MSLD描述子共得到同名直线171对,匹配结果全部正确。采用灰度相关和MSLD描述子匹配分别得到53、79对同名直线,正确率分别为98.1%、98.7%。进一步,对存在尺度变化及模糊效果的一组影像进行匹配实验,如图6(b)所示,两张影像之间尺度约为1.3∶1,左、右影像上满足条件的直线数目分别为555、286条,采用灰度相关、MSLD描述子、本文RAT_MSLD描述子匹配分别得到58、93、97对同名直线,正确率分别达到93.1%、94.6%、98.9%。此外,另任意选取两张不同时相不同大小不同相机不同尺度的影像进行匹配实验,如图6(c)所示,两张影像之间尺度约为1.2∶1,左、右影像上满足条件的直线数目分别为330、152条,其中灰度相关当阈值为0.75时匹配结果为0,匹配失败,MSLD描述子和本文RAT_MSLD描述子匹配分别得到17、34对同名直线,正确率分别达到82.3%、97.0%。采用三种描述子对三组影像进行匹配实验,实验结果表明本文RAT_MSLD描述子能够获取最多数目的匹配直线,且保持最高的正确率。同时,针对不同类型的尺度影像,本文描述子均能得到可靠的匹配结果。
采用灰度相关、MSLD描述子、本文RAT_MSLD描述子分别对图6(d)所示光照变化影像、图6(e)所示的旋转变化影像、图6(f)所示视角变化影像进行直线匹配实验,匹配结果统计如表1所示,从中可以看出,灰度相关匹配得到的直线数目相对较多,其中错误也较多,MSLD描述子及本文RAT_MSLD描述子匹配结果相对稳定,本文算法结果正确率也较高。
通过六组影像实验结果对比分析,灰度相关匹配受影像类型及相关系数阈值影响较大,当阈值统一设定为0.75时,存在尺度变化影像的匹配结果较少,其他影像匹配结果较多且错误也较多,说明该描述子不适于尺度变化影像,此外,相同阈值不适用于所有影像,考虑针对不同类型影像设置不同的相关系数阈值能提高结果的正确率;在相同匹配基础及相同阈值条件下,与本文RAT_MSLD描述子相比,MSLD描述子对尺度变化影像匹配得到的直线数目相对较少,但除图6(c)影像外,其他五组影像匹配结果的正确率均能达到94%以上,结果表明该描述子对尺度影像有一定的适应性,但是针对各种不同类型的尺度影像匹配的稳定性有待进一步加强;除图6(f)影像外,本文RAT_MSLD描述子对其他五组影像均获得最高的正确率,对于图6(f)影像,本文RAT_MSLD描述子匹配正确率低于MSLD描述子匹配结果,但本文RAT_MSLD描述子匹配得到的同名直线数目多于MSLD算子。结果表明,针对不同类型影像进行直线匹配,本文结合区域仿射变换的MSLD描述子均具有一定的稳定性。
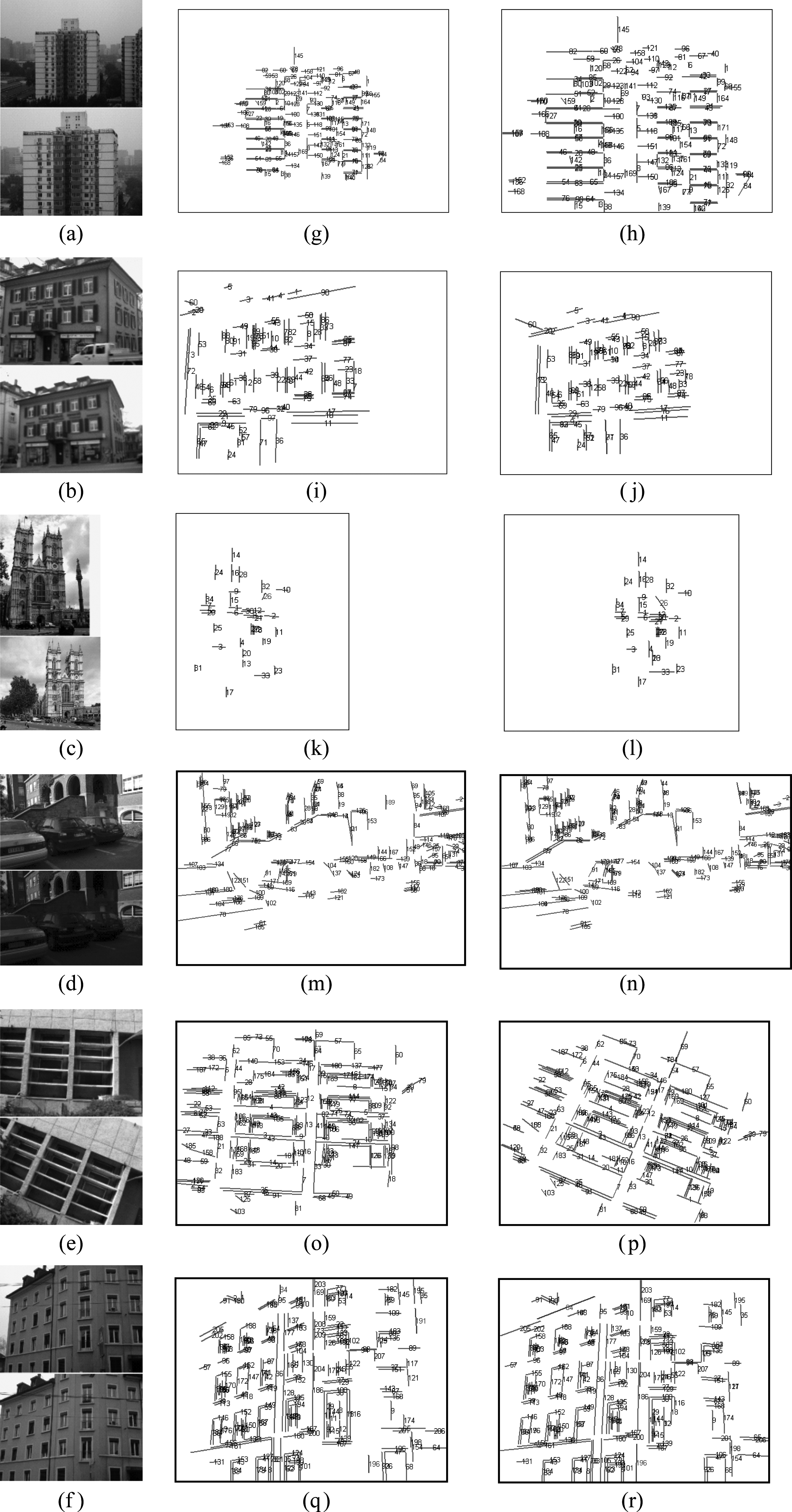
图6 实验影像
Fig.6 Test images and line matching results by algorithm proposed in this paper
表1 采用不同描述子直线匹配结果
Tab.1 Line matching result by different descriptor
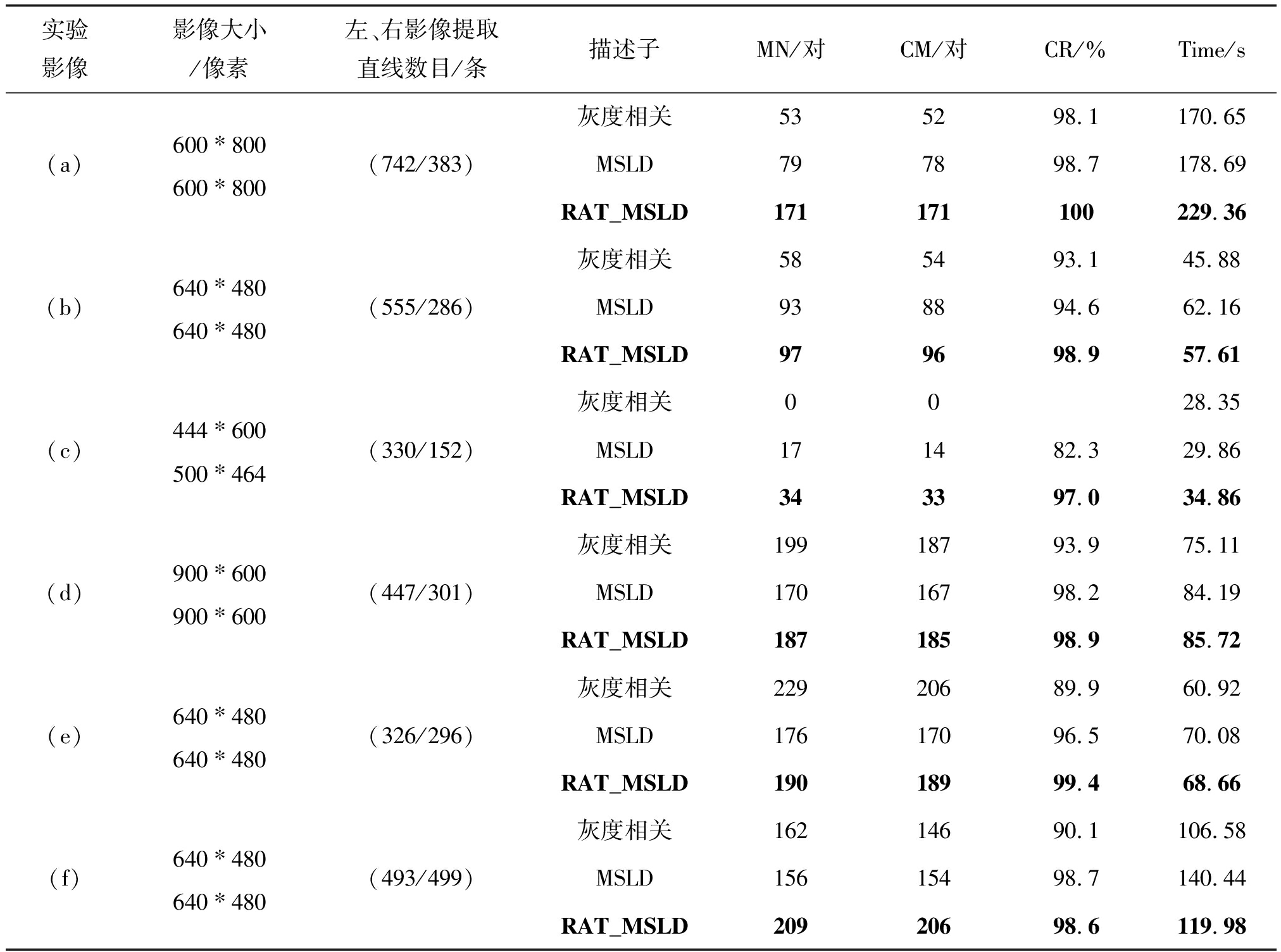
实验影像影像大小/像素左、右影像提取直线数目/条描述子MN/对CM/对CR/%Time/s(a)600∗800600∗800(742/383)灰度相关535298.1170.65MSLD797898.7178.69RAT_MSLD171171100229.36(b)640∗480640∗480(555/286)灰度相关585493.145.88MSLD938894.662.16RAT_MSLD979698.957.61(c)444∗600500∗464(330/152)灰度相关0028.35MSLD171482.329.86RAT_MSLD343397.034.86(d)900∗600900∗600(447/301)灰度相关19918793.975.11MSLD17016798.284.19RAT_MSLD18718598.985.72(e)640∗480640∗480(326/296)灰度相关22920689.960.92MSLD17617096.570.08RAT_MSLD19018999.468.66(f)640∗480640∗480(493/499)灰度相关162146 90.1106.58MSLD15615498.7140.44RAT_MSLD20920698.6119.98
此外,从三种描述子匹配运行的时间来看,与计算统计梯度信息的MSLD描述子和RAT_MSLD描述子相比,单纯利用窗口灰度信息的灰度相关匹配所需时间最少;针对不同实验影像,对MSLD描述子和RAT_MSLD描述子匹配所需时间进行比较,结果不一。这主要是由于直线长度不一致导致直线支撑域构建过程中所需时间不一致。在直线长度一致的情况下,理论上RAT_MSLD描述子匹配所需时间要多于MSLD描述子运行时间。但是MSLD描述子涉及的直线长度为左、右影像上提取直线的原始长度,而RAT_MSLD描述子涉及直线长度完全取决于左影像上提取直线的长度。因此,对于同一组实验影像而言,左影像上提取到的长直线相对较少,右影像上提取到的长直线相对较多的情况下,MSLD描述子匹配效率可能会低于RAT_MSLD描述子的匹配效率。
4 结论
针对直线匹配过程中现有直线描述子的稳定性,本文在已有MSLD描述子基础上,提出了一种结合区域仿射变换的MSLD直线描述子用于直线段匹配,并选取六组具有代表性的影像对进行匹配实验。与现有的MSLD描述子相比,本文利用核线约束确定左、右影像上对应的同名支撑域,加强描述子的有效性,提高直线匹配的正确率;通过对直线支撑域进行仿射变换,统一直线支撑域大小,实现不同尺度影像上直线的可靠匹配。结果表明,对于不同类型的实验影像,本文算法具有较好的稳定性及鲁棒性。但本文算法在构建直线平行支撑域过程中需利用核线确定候选直线对应端点及其支撑域四角点,因此对于存在较多与核线平行的直线特征的影像,有待进一步研究。
参考文献
[1] Schmid C,Zisserman A.The Geometry and Matching of Lines and Curves Over Multiple Views[J].International Journal of Computer Vision,2000,40(3):199-233.
[2] 曾凡洋,钟若飞,宋杨,等.车载全景影像核线匹配和空间前方交会[J].遥感学报,2014,18(6):1230-1236.
Zeng Fanyang,Zhong Ruofei,Song Yang,et al.Vehicle Panoramic Image Matching based on Epipolar Geometry and Space Forward Intersection[J]. Journal of Remote Sensing,2014,18(6):1230-1236.(in Chinese)
[3] 吴军,姚泽鑫,程门门.基于SIFT与SGM的倾斜航空影像密集匹配[J].遥感学报,2015,19(3):431- 442.
Wu Jun,Yao Zexin,Cheng Menmen.Airborne Oblique Stereo Image Dense Matching by Integrating SIFT and SGM Algorithm[J].Journal of Remote Sensing,2015,19(3):431- 442.(in Chinese)
[4] Hartley R.A Linear Method for Reconstruction from Lines and Points[C]∥Proceedings of the IEEE International Conference on Computer Vision,Cambridge, MA, USA,IEEE,1995,25(5):882- 887.
[5] 陆丽娜.基于三焦点张量的多视图目标三维重建[D].南京:南京航空航天大学,2010.
Lu Lina.Multiple-view 3D Reconstruction based on Trifocal Tensor[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010.(in Chinese)
[6] 付洋.基于2D单应矩阵约束的图像匹配方法[J].首都师范大学学报:自然科学版,2015,36(3):73-77.
Fu Yang.Image Matching Method Based on 2D Homography Matrix Constrain[J].Journal of Capital Normal University: Natural Science Edition,2015,36(3):73-77.(in Chinese)
[7] 王竞雪,宋伟东,韩丹,等.边缘视差连续性约束的航空影像特征线匹配算法[J].信号处理,2015,31(3):364-371.
Wang Jingxue,Song Weidong,Han Dan,et al. Feature Line Matching Algorithm for Aerial Image based on Continuity Constraint of Edge Parallax[J].Journal of Signal Processing, 2015,31(3):364-371.(in Chinese)
[8] Fan Bin,Wu Fuchao,Zhang Yihu.Line Matching Leveraged By Point Correspondences[C]∥IEEE Conference on Computer Vision and Pattern Recognition,San Francisco, CA, USA,IEEE,2010:390-397.
[9] Fan Bin,Wu Fuchao,Zhang Yihu.Robust Line Matching through Line-Point Invariants[J].Pattern Recognition,2012,45(2):794- 805.
[10]梁艳, 盛业华, 张卡,等.利用局部仿射不变及核线约束的近景影像直线特征匹配[J].武汉大学学报:信息科学版,2014,39(2):229-233.
Liang Yan,Sheng Yehua,Zhang Ka,et al. Linear Feature Matching Method based on Local Affine Invariant and Epipolar Constraint for Close-range Images[J].Geomatics and Information Science of Wuhan University, 2014,39(2):229-233.(in Chinese)
[11]王竞雪,宋伟东,王伟玺.同名点及高程平面约束的航空影像直线匹配算法[J].测绘学报,2016,45(1):87-95.
Wang Jingxue,Song Weidong,Wang Weixi.Line Matching Algorithm for Aerial Image based on Corresponding Point and Z-Plane Constraints[J].Acta Geodaetica et Cartographica Sinica,2016,45(1):87-95.(in Chinese)
[12]Wu Bo,Zhang Yunsheng,Zhu Qing.Integrated Point and Edge Matching on Poor Textural Images Constrained by Self-adaptive Triangulations[J].ISPRS Journal of Photogrammetry and Remote Sensing,2012,68(1):40-55.
[13]黄良明,彭立中,程民德.利用几何代数进行线段模型匹配和运动估计[J].中国图象图形学报,2001,6(3):270-274.
Huang Liangming,Peng Lizhong,Cheng Minde.Matching and Estimating Motion of Line Model Using Geometric Algebra[J].Journal of Image and Graphics,2001,6(3):270-274.(in Chinese)
[14]朱红,宋伟东,杜北,等.重合度约束的近景影像直线匹配算法[J].信号处理,2015,31(8):912-917.
Zhu Hong,Song Weidong,Du Bei,et al. Straight Line matching Algorithm of Close-Range Images based on Overlap Constraint[J].Journal of Signal Processing,2015,31(8):912-917. (in Chinese)
[15]Schmid C,Zisserman A.Automatic Line Matching Across Views[C]∥IEEE International Conference on Computer Vision and Pattern Recognition,San Juan, Puerto Rico, USA,IEEE,1997:666- 671.
[16]张云生,朱庆,吴波,等.一种基于三角网约束的立体影像线特征多级匹配方法[J].武汉大学学报:信息科学版,2013,38(5):522-527.
Zhang Yunsheng,Zhu Qing,Wu Bo,et al.A Hierarchical Stereo Line Matching Method Based on a Triangle Constraint[J]. Geomatics and Information Science of Wuhan University,2013,38(5):522-527.(in Chinese)
[17]王志衡,吴福朝.均值-标准差描述子与直线匹配[J].模式识别与人工智能,2009,22(1):32-39.
Wang Zhiheng,Wu Fuchao.Mean-Standard Deviation Descriptor and Line Matching[J].Pattern Recognition and Artificial Intelligence,2009,22(1):32-39.(in Chinese)
[18]Wang Zhiheng,Wu Fuchao,Hu Zhangyi.MSLD:A Robust Descriptor for Line Matching[J].Pattern Recognition,2009,42(5):941-953.
[19]Zhang Lilian,Reinhard Koch. An Efficient and Robust Line Segment Matching Approach Based on LBD Descriptor and Pairwise Geometric Consistency[J].Journal of Visual Communication and Image Representation,2013,24(7):794- 805.
[20]Lowe D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision,2004,60(2):91-110.
[21]缪君,储珺,张桂梅.一种仿射不变的直线描述子与直线匹配[J].电子学报,2015,43(12):2505-2512.
Miao Jun,Chu Jun,Zhang Guimei.An Affine Invariant Line Descriptor and Line Matching[J].Acta Electronca Sinica,2015,43(12):2505-2512.(in Chinese)
[22]来春风.数字近景影像稠密匹配方法研究[D].南京:南京师范大学2012.
Lai Chunfeng.A Dissertation Submitted in Partial Fulfillment of the Requirements For the Degree of Master of Science[D].Nanjing:Nanjing Normal University,2012.(in Chinese)



