1 引言
天基预警雷达是以卫星为载荷平台的雷达,雷达观测不受空域和地理条件的限制,能够实现对全球范围内全天时、全天候监视,对现代军事具有重要意义[1]。一方面,相对于传统的地面和机载雷达,天基预警雷达处于大气层外,具有极大地探测范围,可以比地面和机载雷达更早地发现目标,预警时间更早；另一方面,由于天基预警雷达的载体处于地球空间轨道,与地球不在同一个惯性系,而空中目标和地球处于一个惯性系,这就造成了雷达和目标处于不同的惯性系,并且两者距离大,导致跟踪的误差大,对目标跟踪算法提出了更高的要求。
对于天基预警雷达系统而言,雷达和目标处于不同的惯性系,状态方程和观测方程不在同一个坐标系中,转换的过程为非线性[2]。转换测量卡尔曼滤波算法[3- 4]利用坐标转换实现了线性化,文献[5]在三维空间中推导了转换坐标卡尔曼滤波算法,得到了测量值已知条件下的测量误差协方差表达式, 但是,这种去偏转换的方法引入了额外的误差,结果不够精确。文献[6]针对传统的量测转换方法在互距离测量误差增大时性能下降的问题,提出一种基于卡尔曼滤波预测的无偏量测转换方法,并结合无迹变换估计转换量测方差,取得了较好的跟踪效果。文献[7]提出了一种目标匀速运动时,均方意义下的最优估计卡尔曼滤波算法,并且给出了无偏转换测量误差协方差的简化方法。
本文从天基预警雷达特殊体制出发,建立了天基预警雷达模型,一方面,采用了UCM无偏变换[8]将雷达的东北天极坐标[9]的测量值转换到ECEF直角坐标系[10]中,并应用文献[11]中的求容积法的思想,代替传统的UT变换[12],将ENZ极坐标系下测量误差的协方差转换到ECEF极坐标系中,另一方面,引入了一个噪声协方差调整系数,自适应调整协方差Q和R的大小,最后通过蒙特卡罗仿真实验验证了本文提出的算法跟踪效果优于传统算法。
2 天基预警雷达跟踪模型
2.1 几何运动模型
假设地球是一个规则的均匀球体,半径Re=6378.14 km,雷达载体卫星平台处于圆形近地轨道,轨道高度800 km,轨道倾角37° 如图1所示,目标状态方程建立在地心固连(Earth-Centered and Earth-Fixed,ECEF)直角坐标系下,坐标原点O位于地心,XOY平面位于赤道面,X轴指向格林尼治子午圈,Z轴指向北极点。雷达观测方程建立在东北天(East-North-Zenith,ENZ)极坐标系下,坐标原点为天基雷达平台O′,EO′N平面为基准面,东向轴(E轴)为极轴。雷达的载体平台绕地球做圆周运动,卫星星下点为P,轨道高度H,雷达与目标的距离为r。
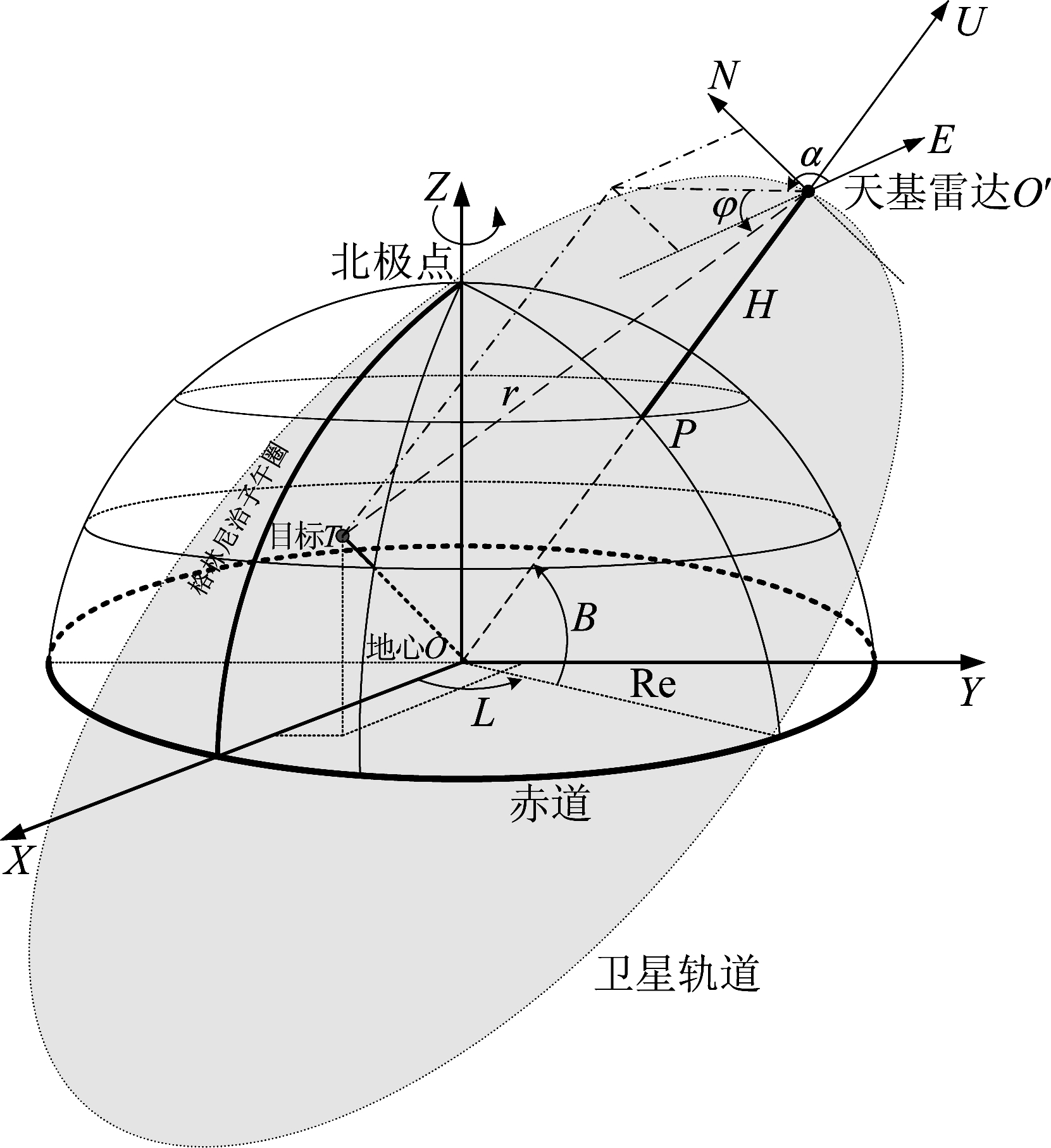
图1 天基预警雷达几何模型
Fig.1 Geometrical motion model of Space-based early warning radar
2.2 跟踪系统模型
目标的状态方程和转换后的观测方程建立在地球的地心固连直角坐标系中,可以表示为：
(1)
式中,X(k)代表系统的状态量,Z(k+1)代表系统转换的观测量,F(k)为系统的状态转移矩阵,H(k)为量测矩阵,W(k)、V(k)为零均值高斯白噪声,协方差矩阵分别为Q(k)和Rm(k)。
设目标在雷达的东北天极坐标系下的观测量为Z(k)=[r(k),θ(k),φ(k)]T,量测协方差矩阵
其中r(k)为目标与雷达之间的距离,θ(k)为目标的方位角,φ(k)为目标的俯仰角；目标在雷达的东北天直角坐标系下的观测量为Zen(k)=[xen(k),yen(k),zen(k)]T；将东北天极坐标系下的量测值转化到地心固连直角坐标系下为Zec(k)=[xec(k),yec(k),zec(k)]T,转化的方法如下：
第一步：通过UCM无偏转换将量测值Z(k)从雷达的东北天极坐标系转化到东北天直角坐标系下为Zen(k)
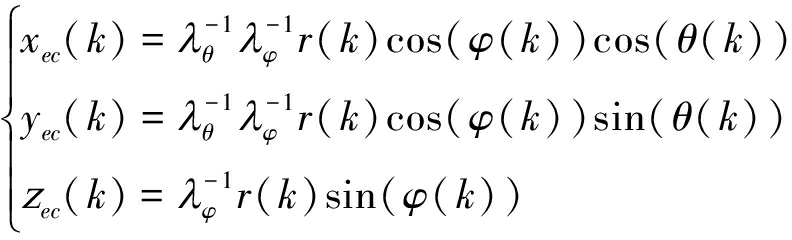
(2)
式中,
对转换量求数学期望,由式(3)可知偏差为0：
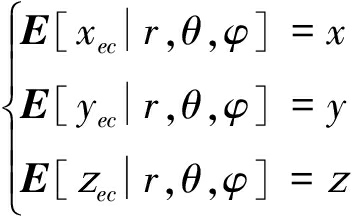
(3)
第二步：将天基雷达量测值Zen(k)从东北天直角坐标系转化到Zec(k)地心固连直角坐标系下。
(4)
式中：
Tcn=
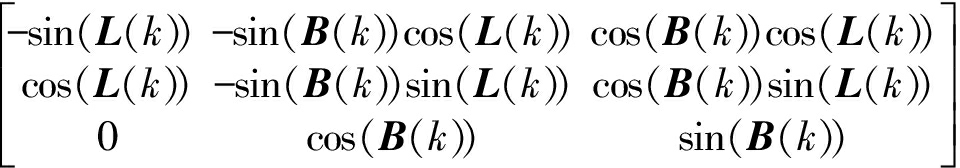
O′(L(k),B(k),H(k))为卫星在地理坐标系[13]下的位置,L(k)表示卫星的经度,B(k)表示卫星的维度,H(k)表示卫星的高度；卫星的位置在地心固连直角坐标系下表示为
则转换方程为：
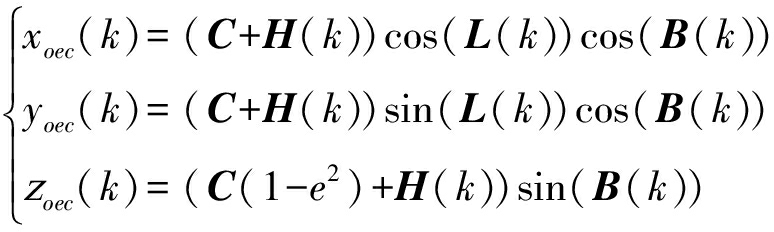
(5)
式中,C=Ea/(1-e2sin2B(k))1/ 2,Ea=6378137.0表示赤道半径,e代表地球偏心率,e2=0.0066943799013。
第三步：求转换后的测量误差协方差矩阵。
采用观测量求解转换后的测量误差协方差会带来较大的误差[14],文献[15]提出了一种利用UT变换求解转换后的测量误差协方差矩阵的方法,该方法的思想是通过对非线性函数的概率密度分布进行近似,将状态量近似为高斯随机变量,通过一系列的确定的样本来逼近状态的后验概率密度,与传统的线性化转换方法相比,UT变换的随机线性化包含了状态空间中的多点信息,具有比传统的线性化方法更高的精度。但是,一方面,UT变换容易出现“维数灾难”,导致计算量随着维度的增加呈现几何指数增长,引起计算量问题；另一方面,UT变换存在着权值参数初始化的问题,并且权值的初始化也会直接影响最终的结果。对此问题,本文引入了求容积法的思想,与传统的UT变换相比,不仅采样点数更少,而且也没有权值参数的初始化问题,计算的过程更简单快速,具体方法步骤如下：
步骤1 在东北天极坐标系下求解Z(k)的容积点ξi以及其对应的权值ωi
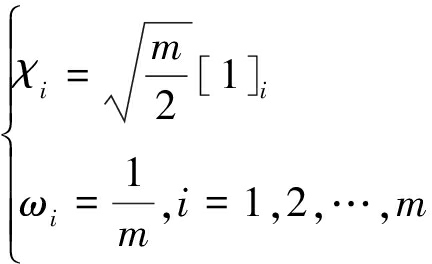
(6)
(7)
式中,m=2n,n为Z(k)的维数,R代表雷达东北天极坐标系下的测量协方差矩阵,其中[1]=[In×n,-In×n],I表示n维单位矩阵,[1]i是其中的第i列向量。
步骤2 利用第一步,第二步将ξi转换到地心固连直角坐标系下,得到转换后的容积点
步骤3 求解地心固连直角坐标系下的测量值容积点的均值Zm(k)和协方差Rm(k)。
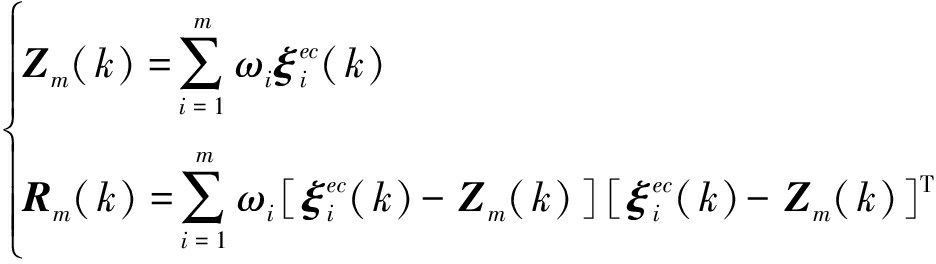
(8)
2.3 噪声协方差矩阵Q和R的自适应调整
在卡尔曼滤波器中,卡尔曼增益K对滤波结果的好坏起到了十分重要的作用,当目标处于非机动状态时,较小的卡尔曼增益能够起到良好的降噪效果,而较大的卡尔曼滤波增益能够对目标的机动作出快速反应[16]。计算K的过程也是卡尔曼滤波算法中至关重要的一步,其取值受到协方差矩阵Q和R的影响,特别是Q的取值：较大的Q值会减小观测值对滤波结果的影响,较小的Q值会使滤波结果过分依赖观测值,引入模型噪声,导致滤波发散。通常来说,K的取值与Q正比,与R成反比。
天基预警雷达跟踪的空中目标往往存在着机动,例如战斗机为了规避雷达的跟踪,往往会进行一系列机动,这些目标机动影响着滤波器的性能,甚至引起滤波发散,导致滤波的新息急剧发生变化,因此,可以利用新息序列来对目标的机动进行检测。
在卡尔曼滤波器中,状态量X和过程噪声协方差P的一步预测量可以表示为：
(9)
P(k+1|k)=F(k)P(k|k)FT(k)+Q
(10)
新息序列可以表示为υ(k),新息协方差矩阵表示为S(k)：
(11)
S(k)=E[υ(k)υT(k)]=HP(k+1|k)HT+R
(12)
那么新息的平方和定义为ε(k)：
ε(k)=υT(k)υ(k)
(13)
其中,新息的平方和ε(k)的数学期望等于新息的协方差矩阵S(k)的对角线元素和。由于目标机动会导致新息的实际值大于理论值,定义噪声协方差调整系数为α
α(k)=ε(k)(trace(S(k))-1
(14)
式中,trace(•)代表求矩阵的对角线元素之和。
调整之后的噪声协方差矩阵可以表示为
(15)
3 自适应转换测量卡尔曼滤波
天基预警雷达的目标状态方程建立在地球的地心直角坐标系下,观测方程建立在卫星的东北天极坐标系下,使天基预警雷达的跟踪问题变成了一个非线性的跟踪问题,转换测量卡尔曼滤波算法通过将雷达的极坐标观测值转换到直角坐标系下,使该问题变成了一个线性估计的问题。但是,一方面,天基预警雷达的目标与雷达的距离较大,远距离跟踪的情况下误差也随之变大；另一方面,目标的机动以及不良的观测信息都会导致滤波结果变坏,甚至发散。
本文针对上述问题,首先,采用了无偏转换的方法,降低了坐标转换带来的转换误差；其次,针对滤波发散的问题,引入一个噪声协方差调整系数,实时调整噪声协方差Q和R的大小,提高了滤波的精度,算法的流程如下：
1)初始化。
首先建立状态方程和观测方程
(16)
在k时刻,在利用第一步、第二步,将雷达东北天极坐标系下的观测量Z(k)转换到地球大地直角坐标系下,得到转换观测量Zm(k)和其转换测量协方差矩阵Rm(k)。
2)状态量和观测量的一步预测。
根据k时刻的状态量X(k),生成状态的一步预测量
以及观测量的一步预测
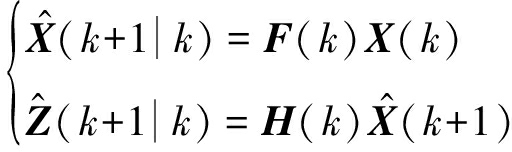
(17)
3)生成一步预测协方差矩阵P和新息的协方差矩阵S。
P(k+1|k)=F(k)P(k|k)FT(k)+Q′(k)
(18)
S(k+1)=E[υ(k+1)υT(k+1)]=
(19)
式中,
为新息序列,
为k时刻噪声协方差调整系数。
4)更新卡尔曼滤波增益。
K(k+1)=P(k+1|k)HT(S(k+1))-1
(20)
5)更新状态量X和协方差矩阵P。
X(k+1)=X(k+1|k)+K(k+1)υ(k+1)
(21)
P(k+1)=[I-K(k+1)H]P(k+1|k)
(22)
6)更新噪声协方差调整系数为α。
α(k+1)=ε(k+1)(trace(S(k+1))-1
(23)
算法的主要流程如图2所示。
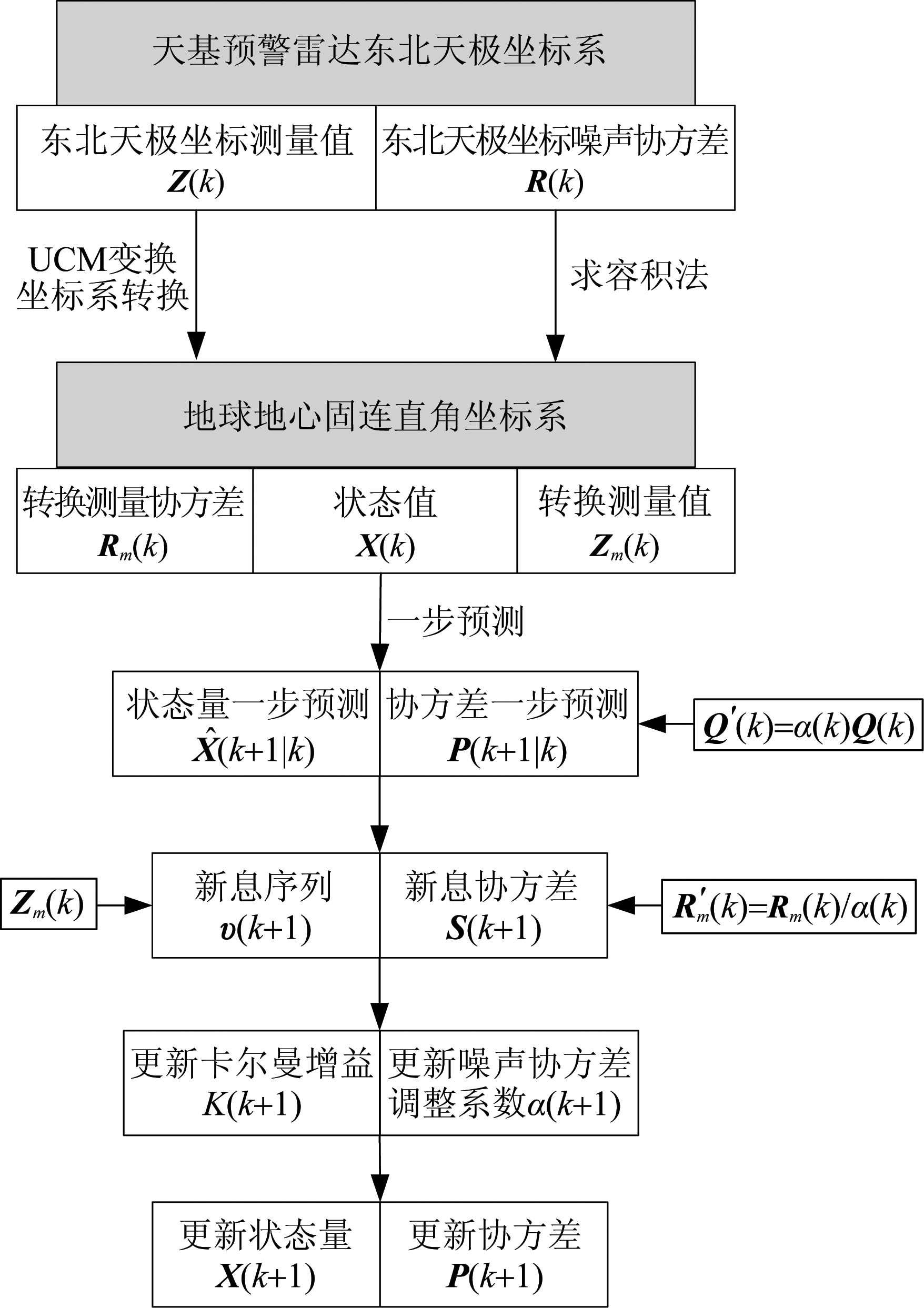
图2 自适应转换测量卡尔曼滤波算法流程
Fig.2 The process of adaptive converted measurement Kalman filtering algorithm
4 仿真分析
为了检验本文所提算法的有效性,运用蒙特卡罗仿真实验来对算法的性能进行检验,设置了几种典型的机动运动场景。
目标的运动形式采用战斗机的两种典型机动形式：蛇形机动和俯冲机动[17]。蛇形机动是战斗机的一种比较常用的机动方式,它一般发生在战斗机被敌方雷达跟踪的情况下,用来脱离雷达跟踪；俯冲机动包含一系列的复杂的高强度机动方式,通常在战斗机进行末端攻击时采用这种机动方式。文献[18]指出第三代战斗机最大升限一般为15000～20000 m,本文中飞机最高飞行高度为12000 m。
天基预警雷达运动的圆形轨道高度800 km,轨道倾角37°,卫星在轨运行速度7446 m/s,飞行方向自西向东,卫星初始位置(68.59°,16.78°,800 km),雷达的东北天极坐标系测量协方差为R(k)=diag(502,10-8,10-8),采样周期0.5 s。仿真中目标的运动模型采用Singer模型,机动频率的初始值设定为αs=1/ 20,初始设定的最大机动加速度为amax=35 m/s2,最大概率为Pmax=0.75,最小概率为P0=0.25。目标的初始协方差矩阵为P=diag(50,1,0.01,50,1,0.01,50,1,0.01)。在给定的初始条件下,分别采用传统的UT-UCMKF算法、混合坐标系下的非线性滤波UKF算法、以及本文给出的算法进行蒙特卡罗仿真,次数为500次,定义仿真中的位置均方根误差(Root Mean Square Error,RMSE)为：
RMSE=
式中,N为蒙特卡罗仿真次数,x(k)、y(k)、z(k)表示目标的真实坐标位置；
表示目标位置的蒙特卡罗仿真实验估计值,同理可以得到速度的RMSE。
场景1 弱机动条件下算法性能
本文设定的蛇形机动发生在水平面内,目标运动方式主要表现为一系列的加速运动,目标在地心固连直角坐标系下的初始状态：
(1397.89 km,358.97 m/s,0 m/s2,5349.92 km,0 m/s,0 m/s2,3173.86 km,0 m/s,0 m/s2)
仿真的总时长为105 s,目标在0～25 s内做匀速直线运动；在25～40 s做匀加速机动,加速度矢量为(0 m/s2,10 m/s2,0 m/s2)；在41～55 s做匀加速机动,加速度矢量为(0 m/s2,-30 m/s2,0 m/s2)；在55～75 s做匀加速机动,加速度矢量为(0 m/s2,30 m/s2,0 m/s2)；在75～85 s做匀加速机动,加速度矢量为(-20 m/s2,26.2 m/s2,0 m/s2)；在85～105 s做匀速直线运动。仿真结果如图3、图5所示。
从仿真结果可知,在目标的机动性不强的情况下,本文所提出的算法性能明显优于传统的算法UT-UCMKF以及非线性滤波算法UKF。图4中,未调整噪声协方差,滤波开始阶段,由于初始化误差,三种算法都出现了比较严重的发散情况,本文所提算法的误差与UKF算法的误差接近,但明显优于UT-UCMKF；图5中,加入噪声协方差调整系数之后,本文算法和UT-UCMKF算法的滤波发散的情况得到了明显的改善,收敛速度更快,算法的性能明显更优。
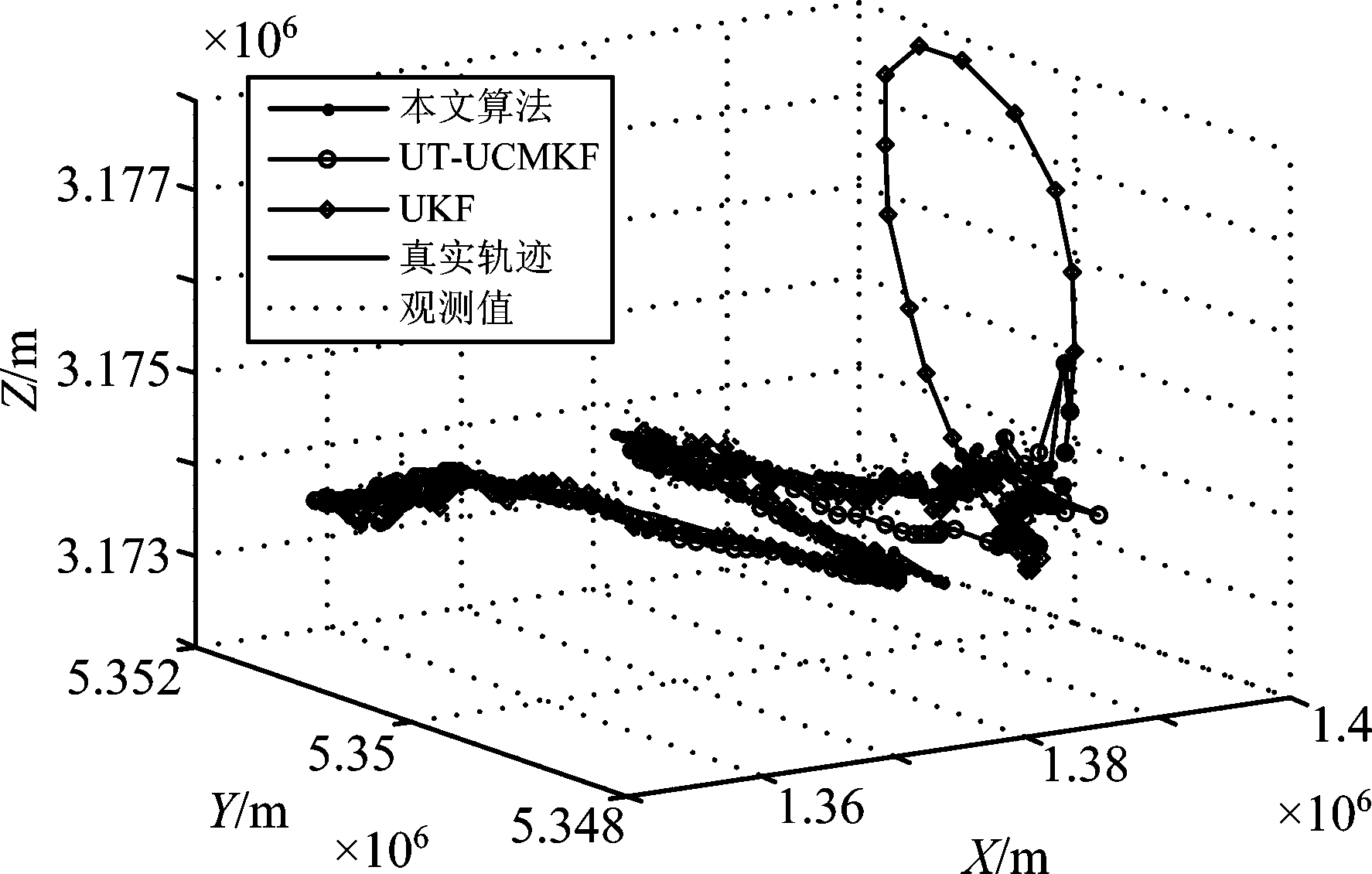
图3 场景1跟踪滤波轨迹
Fig.3 The filtering trace of scene one
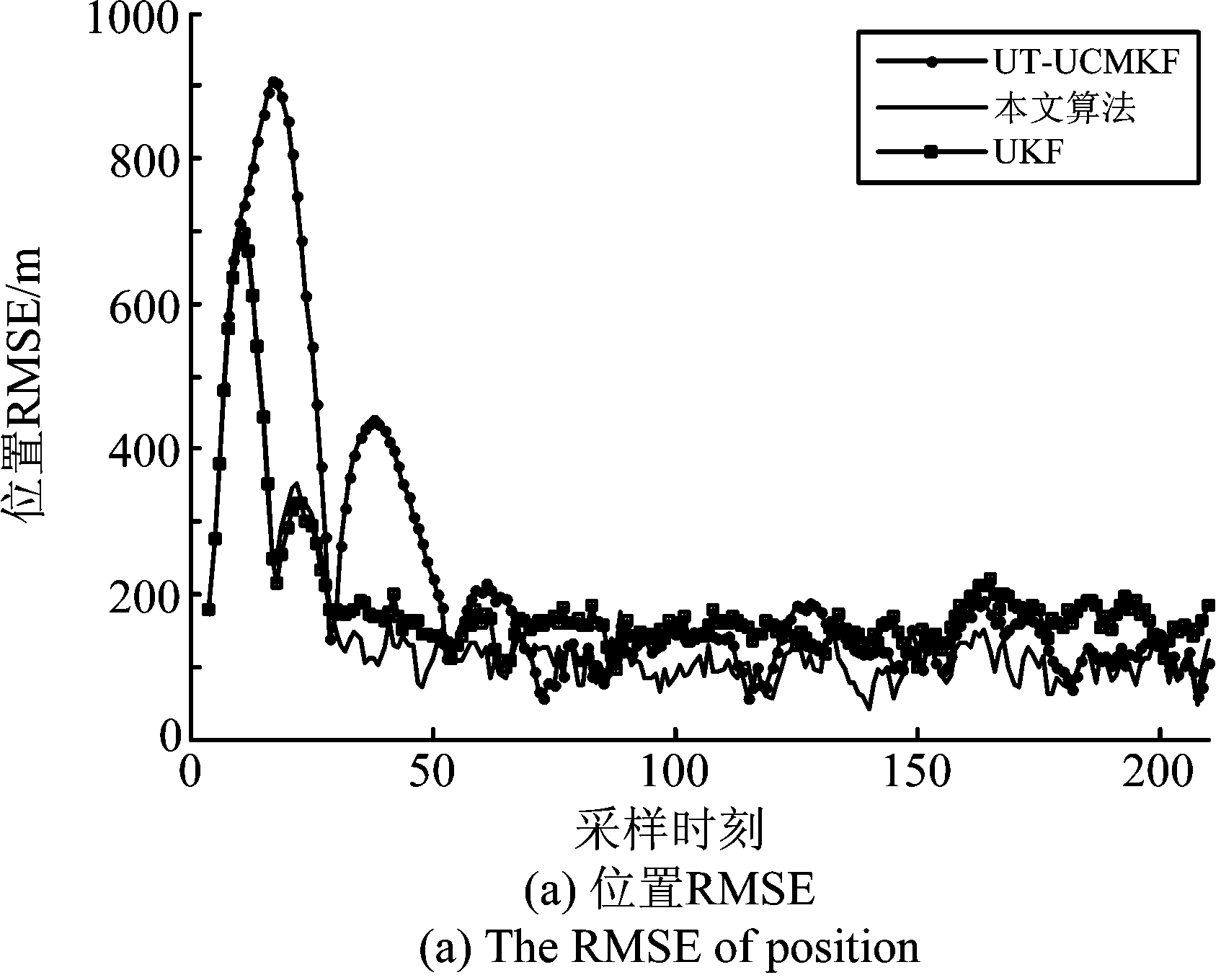
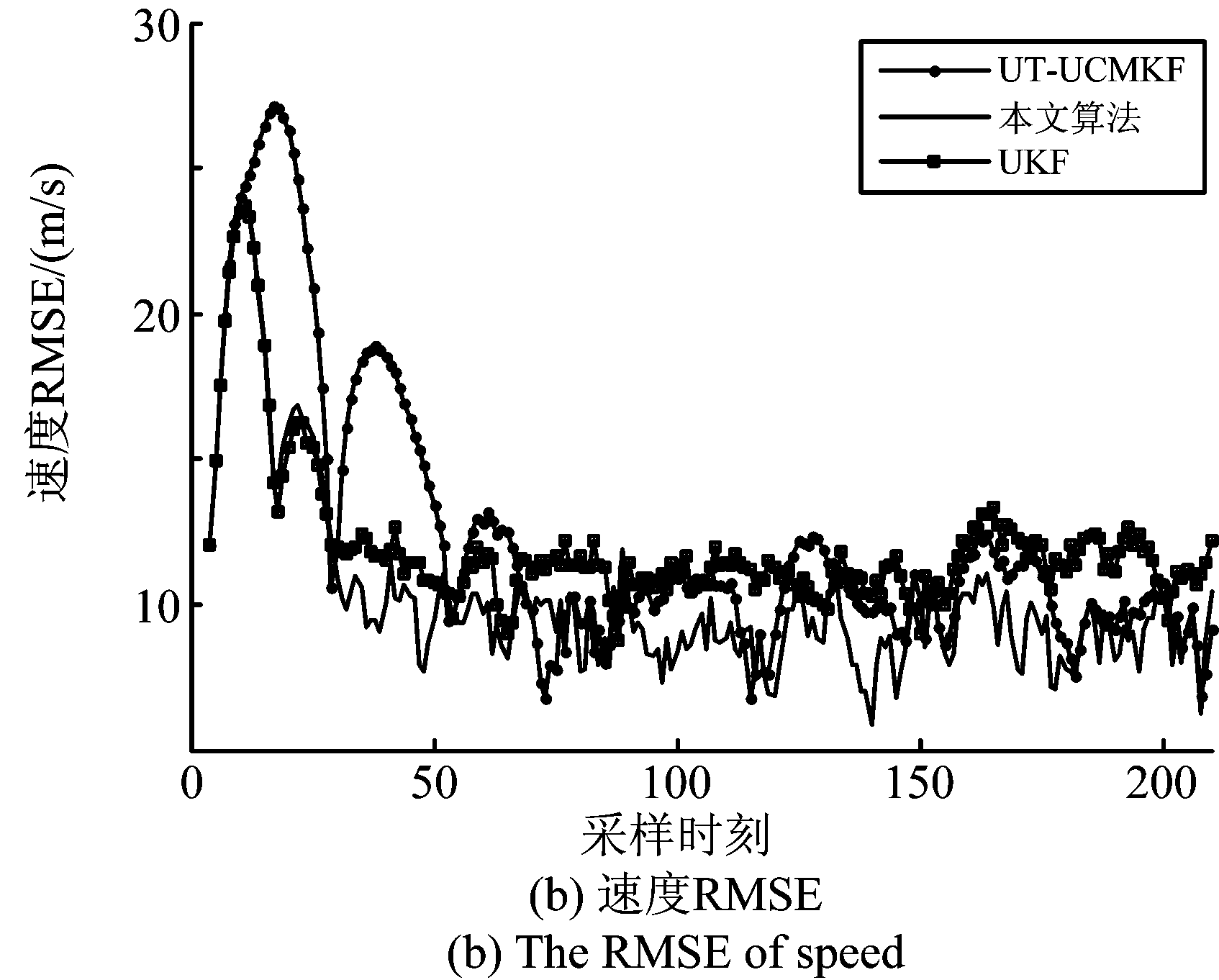
图4 未加入噪声调整系数(场景1)
Fig.4 Before importing the adjustment coefficient of the noise covariance (scene one)
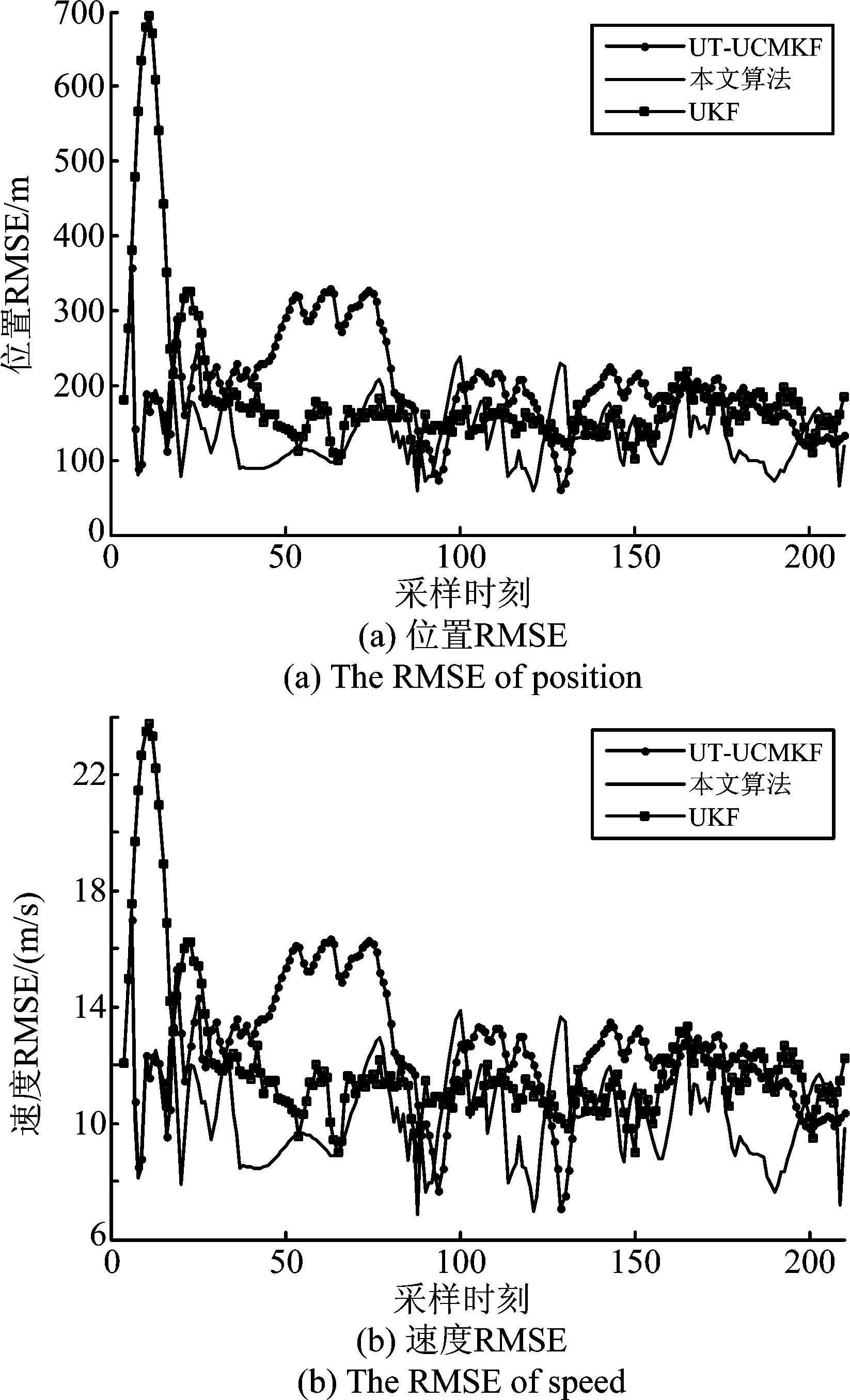
图5 加入噪声调整系数(场景1)
Fig.5 After importing the adjustment coefficient of the noise covariance (scene one)
场景2 强机动条件下算法性能
本文设定的俯冲机动的主要运动方式为急转弯机动和俯冲加速机动。目标在地心固连直角坐标系下的初始状态：
(1433.51 km,-150 m/s,0 m/s2,5349.92 km,0 m/s,0 m/s2,3176.37 km,0 m/s,0 m/s2)
在0～50 s,目标做匀速直线运动；在50～60 s,目标做急转弯机动,转弯角速度ω1=0.12 rad/s；在60～90 s,目标做加速运动,加速度矢量为(-10 m/s2,0 m/s2,-10 m/s2)；在90～94 s,目标做强转弯机动,转弯角速度ω2=-0.4 rad/s,在94～120 s,目标做减速运动,加速度矢量为(-3.33 m/s2,0 m/s2,-10 m/s2),仿真结果如图6、图8所示。
从仿真结果可知,在目标的机动性较强的情况下,本文所提算法的性能提升虽然没有弱机动情况下明显,但是总体依旧优于UT-UCMKF和UKF滤波算法。在匀速运动和加速运动阶段,本文算法的性能与非线性UKF算法的性能接近,优于传统的UT-UCMKF算法；在目标的机动性变强的阶段,例如采样时刻100～120的急转弯阶段、以及采样时刻180～188的强转弯阶段,本文所提算法的性能不及非线性UKF算法,但是依旧优于UT-UCMKF算法。
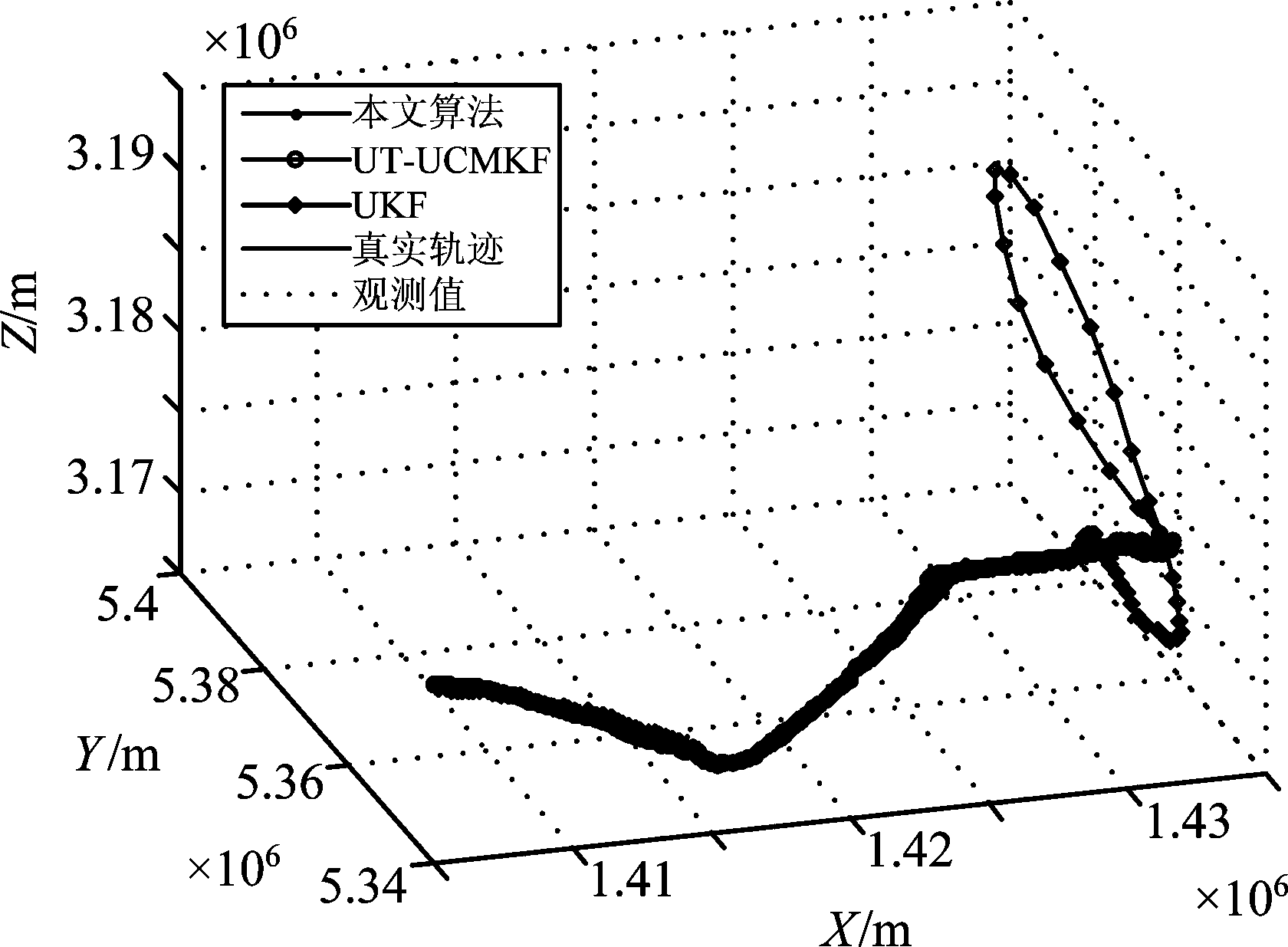
图6 场景2跟踪滤波轨迹
Fig.6 The filtering trace of scene two
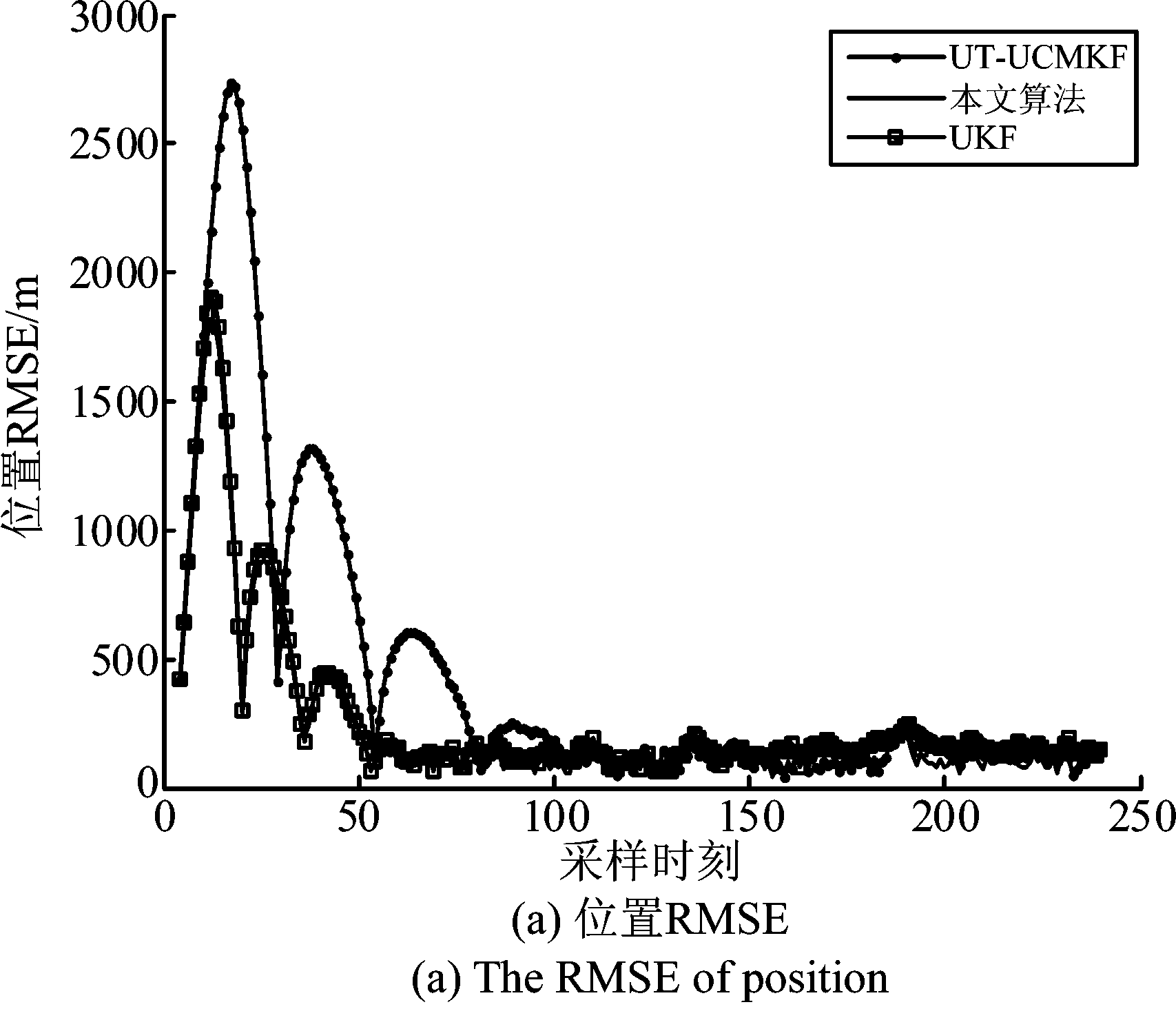
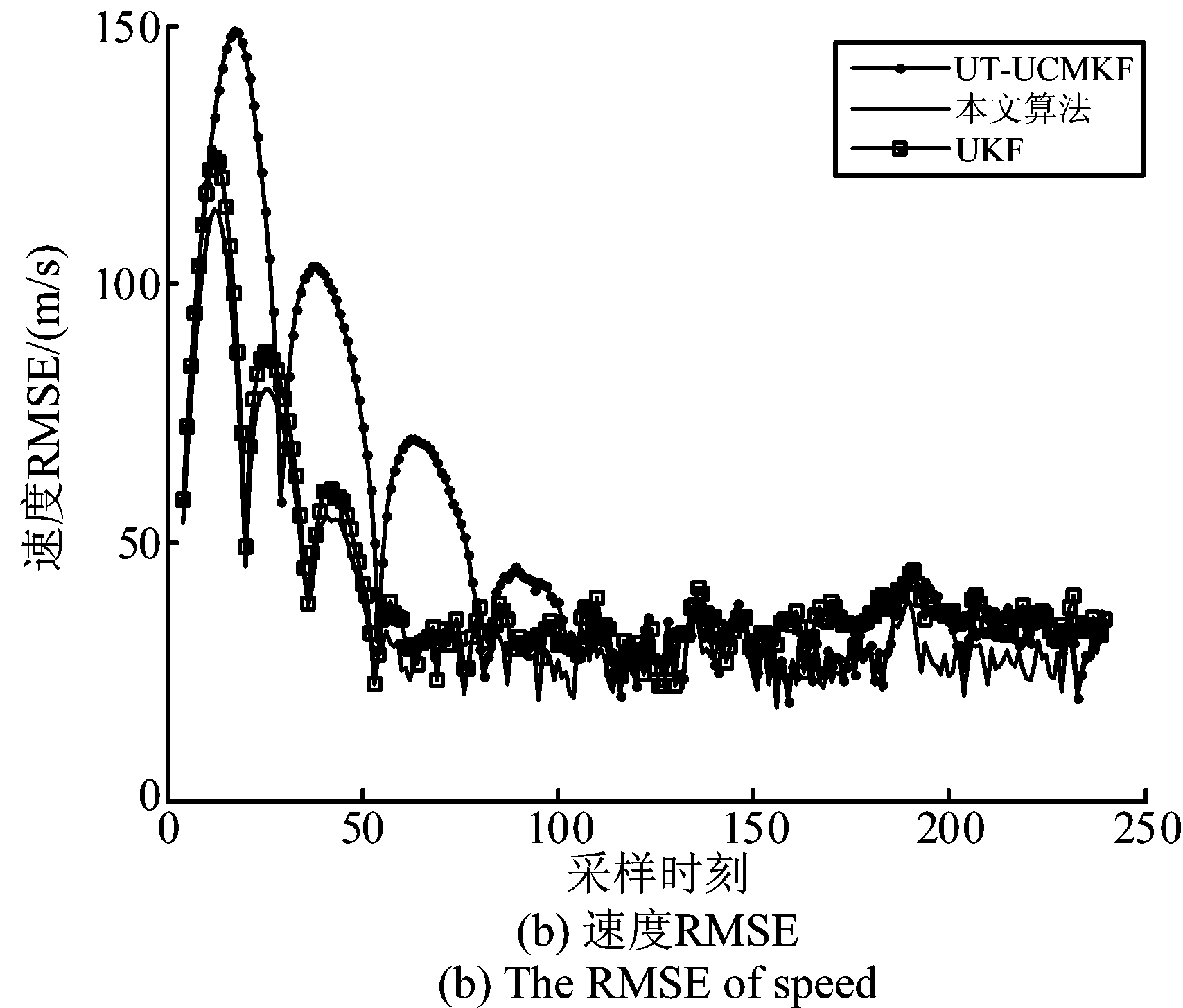
图7 未加入噪声调整系数(场景2)
Fig.7 Before importing the adjustment coefficient of the noise covariance (scene two)
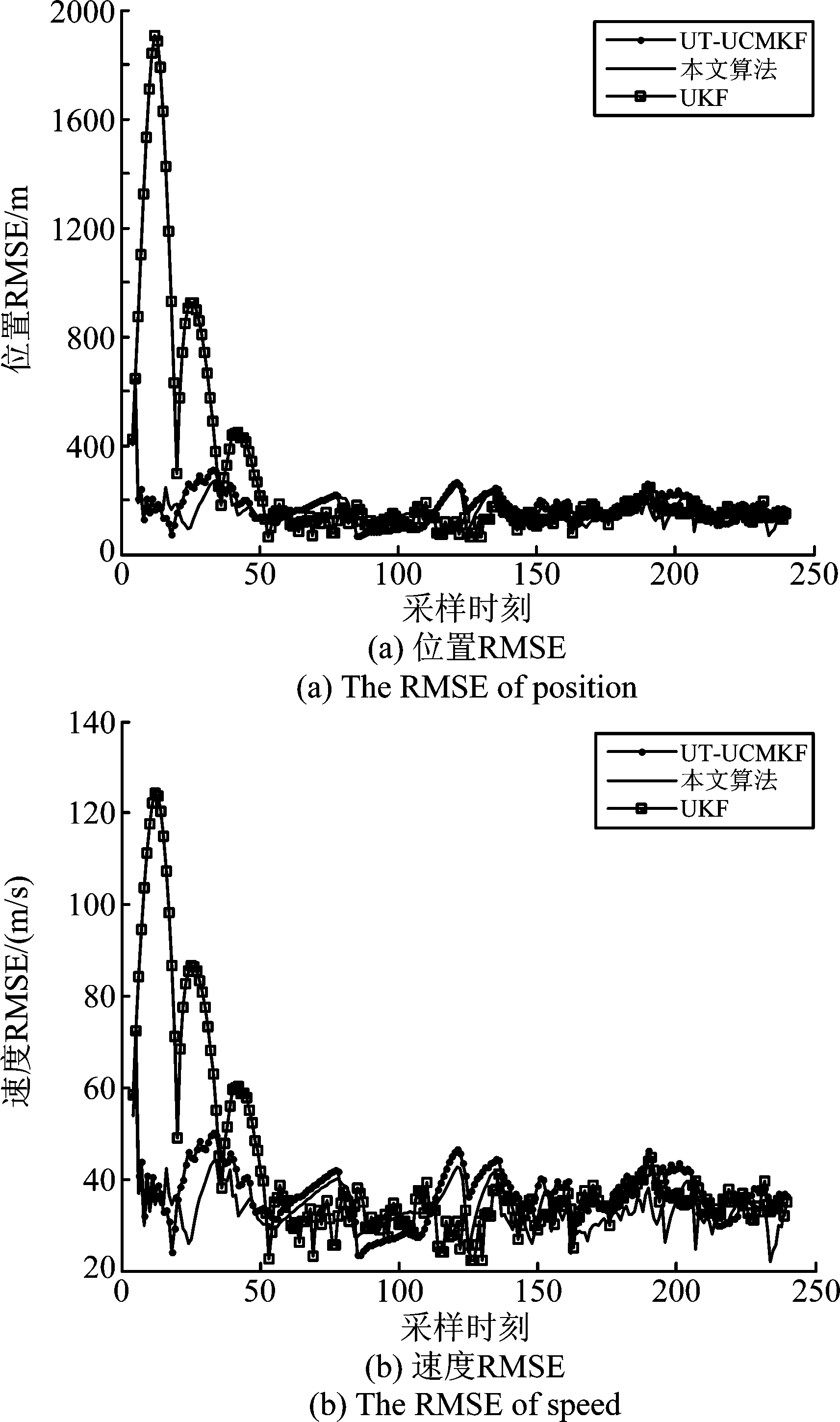
图8 加入噪声调整系数(场景2)
Fig. 8 After importing the adjustment coefficient of the noise covariance (scene two)
场景3 算法的性能对比
为了定量比较三种算法的综合性能,在场景1和场景2的基础上,引入均方根误差的均值和平均耗时指标,在相同的初始化条件下,比较三种算法的性能。仿真所用电脑的CPU为3.6 GHz,内存大小为4 GB,软件为Matlab R2008b,仿真结果如表1、表2所示,分析可知：
1)算法的误差更小。由表1、表2可知,本文算法的位置RMSE均值比传统的转换测量算法UT-UCMKF减少了31.7%,相比于非线性UKF算法减少了40.3%；本文算法的速度RMSE均值比传统的转换测量算法UT-UCMKF减少了17.3%,相比于非线性UKF算法减少了13.9%。
2)算法的运行耗时更少。由于求容积法的采样点相比于传统的UT变换更少,计算方式简单,算法运行耗时也更短,由表1、表2可知,本文算法运行的平均耗时比传统的转换测量UT-UCMKF算法减少了7.4%,相比于非线性UKF算法减少了42.1%。
表1 仿真结果性能对比(场景1)
Tab.1 The performance comparison of simulation results (scene one)
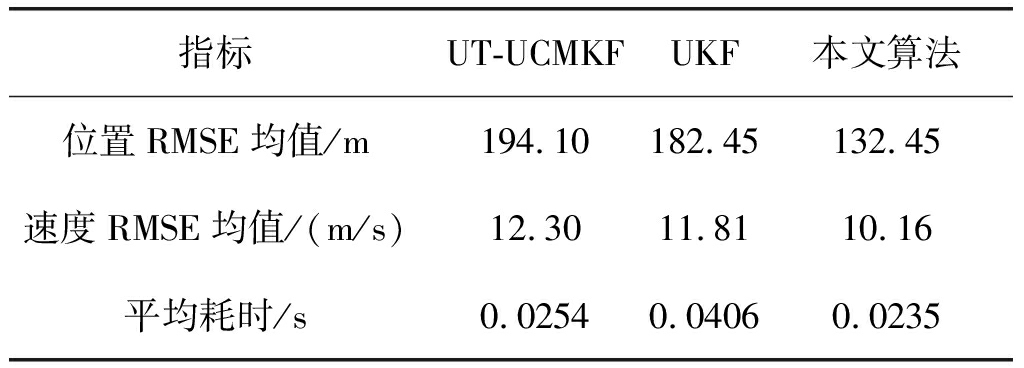
指标UT-UCMKFUKF本文算法位置RMSE均值/m194.10182.45132.45速度RMSE均值/(m/s)12.3011.8110.16平均耗时/s0.02540.04060.0235
表2 仿真结果性能对比(场景2)
Tab. 2 The performance comparison of simulation results (scene two)
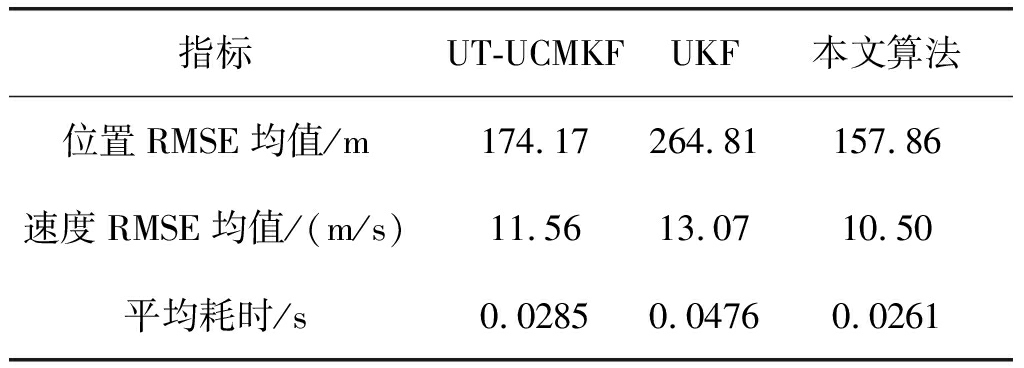
指标UT-UCMKFUKF本文算法位置RMSE均值/m174.17264.81157.86速度RMSE均值/(m/s)11.5613.0710.50平均耗时/s0.02850.04760.0261
5 结论
本文从天基预警雷达的特殊背景出发,建立了天基预警雷达的跟踪模型,提出了一种改进的去偏转换滤波算法,一方面,引入了求容积法的思想,提高了算法的滤波精度和运算速度,另一方面,引入噪声协方差调整系数,改善了滤波发散的情况,并通过蒙特卡罗仿真实验,检验了算法在弱机动和强机动两种条件下的性能,验证了所提算法的有效性。
参考文献
[1] 贲德,王海涛. 天基监视雷达新技术[M]. 北京:电子工业出版社,2014:2-3.
Ben D, Wang H T. The New technology of Space-based monitoring Radar[M]. Beijing: Publishing House of Electronics Industry, 2014:2-3.(in Chinese)
[2] 李骏,安玮,周一宇. 混合坐标系下空间目标天基光学跟踪方法研究[J]. 信号处理,2009,25(10):1624-1628.
Li J, An W, Zhou Y Y. Study on Space Object Tracking using Space-based Optical Sensor in Hybrid Coordinates[J]. Signal Processing, 2009,25(10):1624-1628. (in Chinese)
[3] Wu Weihua, Jiang Jing, Feng Xun, et al. A Sequential Converted Measurement Kalman Filter with Doppler Measurements in ECEF Coordinate System[J]. Chinese Journal of Electronics, 2016, 25(1):139-145.
[4] 盛琥,王金根,王立明,等. 量测转换卡尔曼滤波在塔康导航中的应用[J].信号处理,2015,31(1):34-38.
Sheng H,Wang J G,Wang L M, et al. Application of converted measurements Kalman filter for TACAN Navigation[J]. Journal of Signal Processing, 2015,31(1):34-38.(in Chinese)
[5] 杨春玲,倪晋麟,刘国岁,等.转换坐标卡尔曼滤波器的雷达目标跟踪[J].电子学报, 1999,27(3):121-123.
Yang C L, Ni J L, Liu G S, et al. Converted Measurement KF For Radar Target Tracking[J]. Acta Electronica Sinica,1999,27(3):121-123. (in Chinese)
[6] 李为,李一平,封锡盛. 基于卡尔曼滤波预测的无偏量测转换方法[J]. 控制与决策, 2015, 30(2): 229-234.
Li W, Li Y P, Feng X S. Tracking with prediction conditioned unbiased converted measurements[J]. Control and Decision, 2015,30(2):229-234. (in Chinese)
[7] 李莉,朱珺.无偏转换卡尔曼滤波在雷达目标跟踪中的应用[J].电子测量技术,2011,34(4):30-32.
Li L, Zhu J. Kalman filter unbiased conversion of radar target tracking[J]. Electronic Measurement Technology,2011,34(4):30-32. (in Chinese)
[8] Wen C L, Zhou D H. The multiscale state fusion estimation for nonlinear systems with multirate sensors[C]∥Barcelona: IFZC 15th World Congress,2002.
[9] 宋伟锋,杨泗智,王全忠,等.GPS在制导火箭弹中应用研究[J].沈阳理工大学学报,2013,32(5):59-63.
Song W F, Yang S Z, Wang Q Z, et al. Coordinate Transformation Analysis of GPS Applied in Guidance Rocket Missile[J]. Journal of Shenyang Ligong University, 2013,32(5):59-63. (in Chinese)
[10]Wu Weihua, Jiang Jing, Wan Yang. Tracking a maneuvering target in clutter with out-of-sequence measurements for airborne radar[J]. Journal of Systems Engineering and Electronics, 2015, 26(4):746-753.
[11]Ienkaran Arasaratnam,Simon Haying. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6):1254-1269.
[12]Liu Changyun, Shui Penglang, Li Song. Unscented extended Kalman filter for target tracking[J]. Journal of Systems Engineering and Electronics, 2011,22(2): 188-192.
[13]徐晓苏,豆嫚.基于横向地理坐标系的极区惯性导航方法研究[J].华中科技大学学报:自然科学版,2014,42(12):116-121.
Xu X S, Dou M. Inertial navigation algorithm in polar regions based on transverse geographic coordinate system[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2014,42(12):116-121.(in Chinese)
[14]Steven V Bordonaro, Peter Willett, Yaakov Bar-Shalom.Tracking with converted postion and Doppler measure ements[C]∥Signal and Data Processing of Small Target,2011.Denver: SPIE, 2011(81370D):1-14.
[15]王炜,明强,张志华.一种用于目标跟踪的UT-BLUE滤波方法[J].北京航空航天大学学报, 2007, 33(7): 798-802.
Wang W, Ming Q, Zhang Z H. UT-BLUE filter for target tracking[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(7):798-802. (in Chinese)
[16]张谦,景占荣. 一种过程噪声自适应调节的卡尔曼滤波算法[J].电子测量技术,2007,30(5):18-21.
Zhang Q, Jing Z R. Kalman filtering algorithm with process noise adjusting adaptively[J].Electronic Measurement Technology, 2007,30(5):18-21. (in Chinese)
[17]何友,修建娟,关欣. 雷达数据处理及应用[M]. 北京:电子工业出版社, 2013: 194-195.
He Y, Xiu J J, Guan X. Radar data processing with application[M]. Beijing: Publishing House of Electronics Industry, 2013: 194-195. (in Chinese)
[18]董彦非,雷洪利,周洲,等. 军用飞机隐身与高度指标综合权衡[J]. 空军工程大学学报:自然科学版, 2006, 7(4): 4-7.
Dong Y F, Lei H L, Zhou Z, et al. Synthetically analysis of military aircrafts stealth and altitude[J]. Journal of Air Force Engineer University: Natural Science Edition, 2006, 7(4): 4-7. (in Chinese)
