1 引言
图像分类,即给定一幅输入图像,通过某种分类算法来判断该图像所属的类别。图像分类的划分方式十分多样,划分依据不同,分类结果就不同。根据图像语义的不同可将图像分类为对象分类、场景分类、事件分类、情感分类。图像分类的主要流程包括图像预处理[1]、图像特征描述和提取[2]以及分类器[3]的设计。预处理包括图像滤波(例如中值滤波[4]、均值滤波[5]、高斯滤波[6]等)和尺寸的归一化等操作,其目的是为了方便目标图像后续处理;图像特征是对凸显特性或属性的描述,每一幅图像都有其本身的一些特征,特征提取,即根据图像本身的特征,按照某种既定的图像分类方式来选取合适的特征并进行有效的提取;分类器就是按照所选取的特征来对目标图像进行分类的一种算法。
传统的图像分类方法即按照上述流程分别进行处理,性能差异性主要依赖于特征提取及分类器选择两方面。传统图像分类算法所采用的特征都为人工选取,常用的图像特征有形状、纹理、颜色等底层视觉特征,还有尺度不变特征变换[7]、局部二值模式[8]、方向梯度直方图[9]等局部不变特征等,这些特征虽然具有一定的普适性,但对具体的图像及特定的划分方式针对性不强,并且对于一些复杂场景的图像,要寻找能准确描述目标图像的人工特征绝非易事。常见的传统分类器包括K最近邻[10]、支持向量机[11]等传统分类器,对于一些简单图像分类任务,这些分类器实现简单,效果良好,但对于一些类别之间差异细微、图像干扰严重等问题,其分类精度大打折扣,即传统分类器非常不适合复杂图像的分类。
随着计算机的快速发展以及计算能力的极大提高,深度学习[12-14]逐渐步入我们的视野。在图像分类的领域,深度学习中的卷积神经网络[15-17]可谓大有用武之地。相较于传统的图像分类方法,其不再需要人工的对目标图像进行特征描述和提取,而是通过神经网络自主地从训练样本中学习特征,并且这些特征与分类器关系紧密,这很好地解决了人工提取特征和分类器选择的难题。
本文第2节介绍了经典神经网络和卷积神经网络基本结构;第3节阐述了基于卷积神经网络的图像分类中常用的数据集以及所采用的主流结构模型的原理、优缺点、时间/空间复杂度、训练模型过程中可能遇到的问题和相应的解决方案以及基于深度学习的图像分类拓展模型的生成式对抗网络和胶囊网络;第4节通过仿真实验验证了在图像分类精度上,基于卷积神经网络的图像分类方法优于传统图像分类方法,综合比较了目前较为流行的卷积神经网络模型之间性能差异并简要分析其原因,并针对过拟合问题、数据集构建方法以及生成式对抗网络和胶囊网络进行实验分析说明;最后,对基于卷积神经网络的图像分类算法进行总结,并对未来该领域工作进行展望。
2 卷积神经网络
2.1 神经网络
神经网络[18]是一门重要的机器学习[19]技术,同时也是深度学习的基础。如图1(a)所示,这是一个包含三个层次的经典神经网络结构。其输入层与输出层的节点个数往往是固定的,中间层的节点个数可以自由指定;神经网络结构图中的拓扑与箭头代表着预测过程中的数据流向;结构图中的关键不是圆圈(代表神经元),而是连接线(代表神经元之间的连接),每个连接线对应一个不同权重(其值称为权值),这是需要训练得到的。神经网络其本质是由无数个神经元构成,具体的数据在神经元中的流动过程如图1(b)所示,假设图中输入1、输入2、输入3分别用x1、x2和x3表示,权值1、权值2、权值3分别用w1、w2和w3表示,偏置项为b,非线性函数用g(·)表示,输出用y表示,其过程可用如下式表示:
y=g(w1·x1+w2·x2+w3·x3+b)
(1)
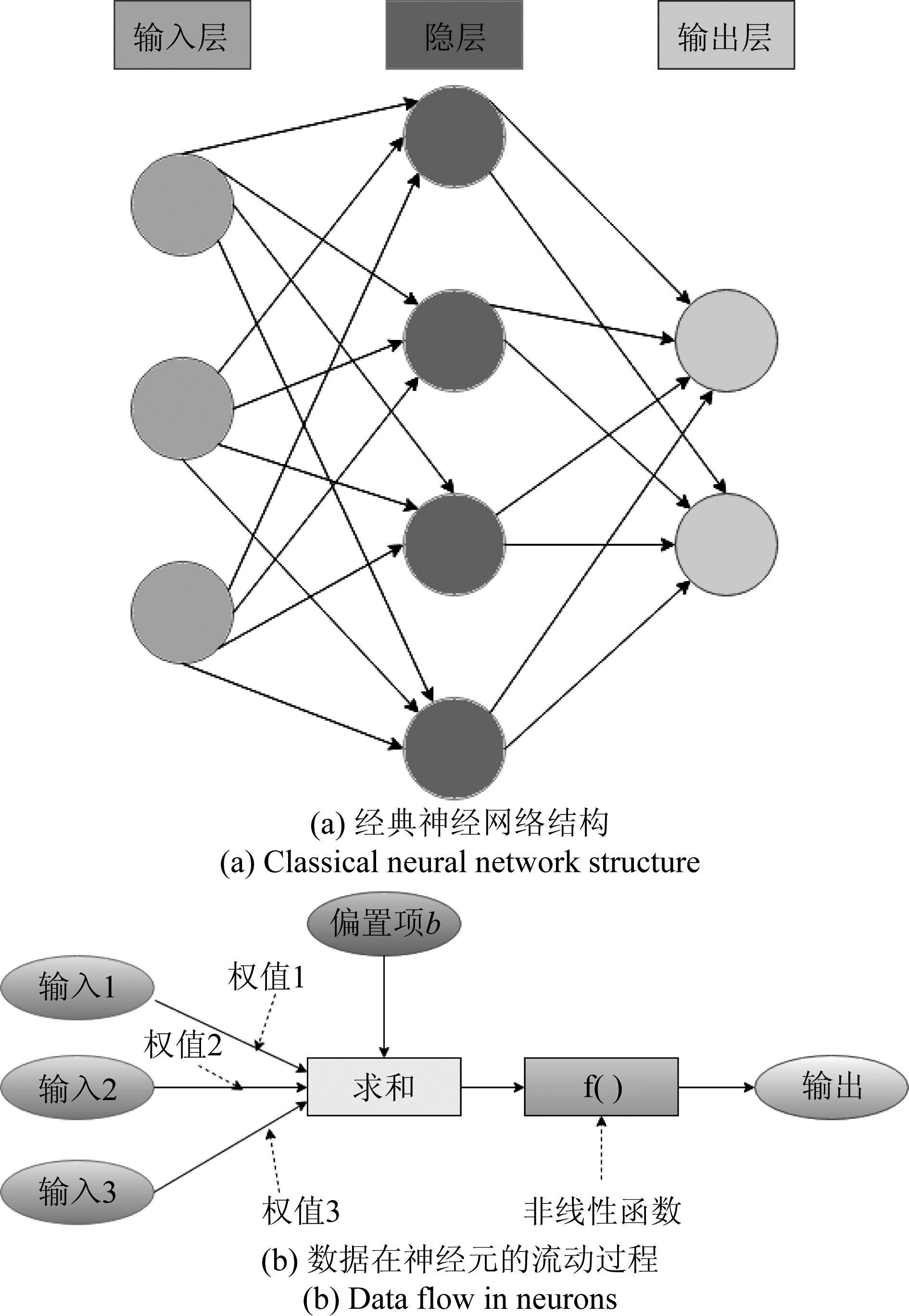
图1 神经网络结构图
Fig.1 Neural network structure
2.2 卷积神经网络
卷积神经网络(Convolutional Neural Network, CNN)[20-22]相较于一般神经网络最突出的特征是增加了卷积层(conv layer)和池化层(pooling layer),其他层级结构仍与一般神经网络一致。其数据在卷积层中的流动过程仍以图1来说明:假设一幅RGB彩色图像(5×5)输入该卷积层,括号内的数值代表分辨率。则对应的输入不再是三个值,而是该彩色图像三色通道对应的3个像素矩阵,故设其三色像素矩阵分别为x1、x2和x3,其大小都为5×5,卷积神经网络的权值也不再是一个值,一般是小于输入像素矩阵大小的一个矩阵,其在输入图像上的作用过程与图像处理中滤波器卷积过程一致,故称作卷积核,设卷积核大小分别为w1、w2和w3,w代表(2×2)权值矩阵。非线性函数用G(·)表示,偏置矩阵为b,其输出设为像素矩阵y,一般大小等于输入图像矩阵的大小。所以数据在卷积层中流动过程可用如下式表示:
y=G(w1·x1+w2·x2+w3·x3+b)
(2)
卷积层最大的特点在于运用了参数共享机制,卷积核的权重是通过训练得到的,并且在卷积的过程中卷积核的权重是不会改变的,这说明我们可以通过一个卷积核的操作提取原图的不同位置的同样特征。简单来说就是在一幅图像中的不同位置的相同目标,它们的特征是基本相同的。参数共享机制大大减少了训练参数的个数,同时也减少了过拟合的风险[23],提高了模型的泛化能力。
池化层一般连接在连续卷积层之后,对输入作降采样过程。降采样的方式多种多样,如最大池化、平均池化等。最大池化就是在图像上对应出滤波器大小的区域,在该区域内取像素点最大的值,以此得到特征数据,一般来说,该方法得到的特征数据更好地保留了图像的纹理特征;平均池化即在上述区域内,对里面所有不为0的像素取均值,以此得到特征数据,该方法更好地保留了对图像背景信息的提取,需要注意的是,平均池化中所选取的像素点中不包含0像素,如把0像素点加上,则会增加分母,从而使整体数据变低(大面积0像素,不利于特征的提取)。下面以平均池化为例,说明降采样过程,如图2所示,输入一幅4×4图像矩阵,构建一个2×2的滑动滤波器在该图像矩阵上滑动,步长为2。该滑动滤波器作用是计算其滤波范围内像素的平均值,最终将原像素矩阵降采样为2×2的像素矩阵。该层的作用也是显而易见的,一方面实现了对图像矩阵的降维(类似于主成分分析[24]),降低了模型所需的计算量;另一方面,实现了不变性,包括尺度不变性、平移不变性和旋转不变性[25]。
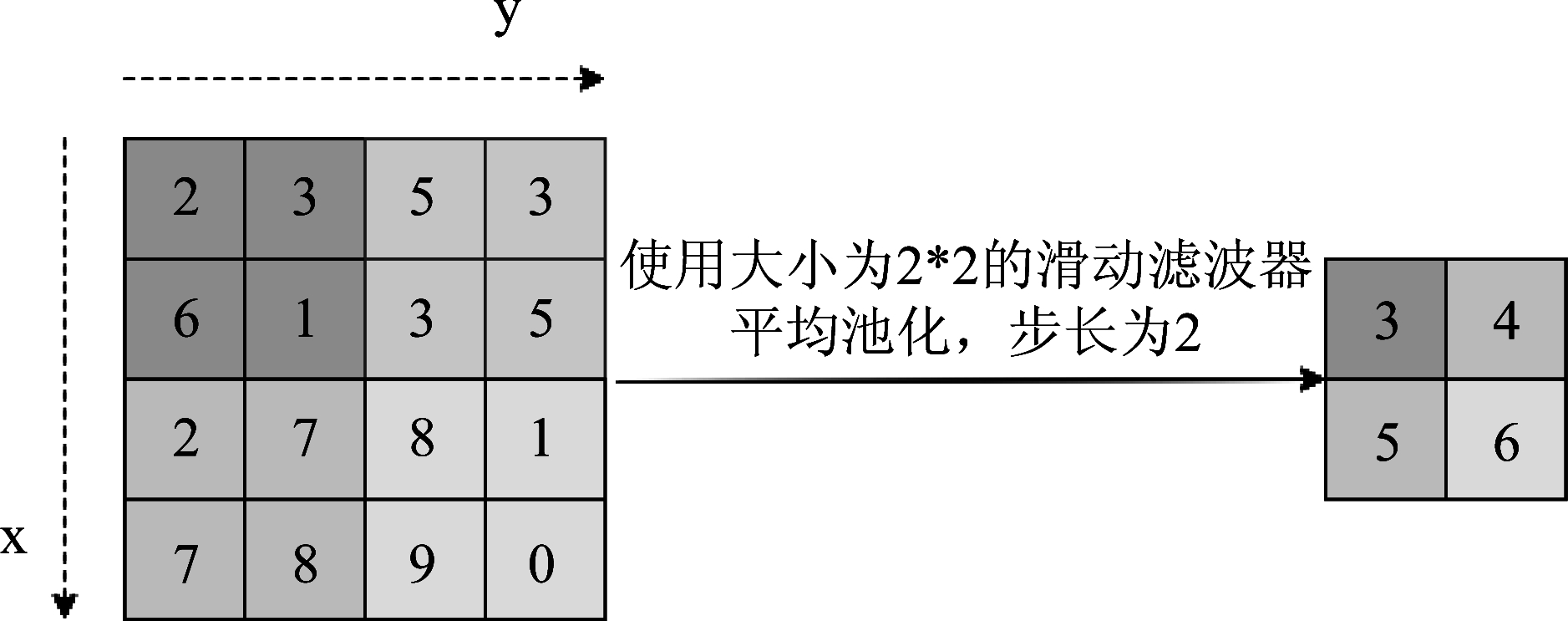
图2 降采样过程
Fig.2 Downsampling process
3 基于卷积神经网络的图像分类
通过卷积神经网络进行图像分类较之传统的图像分类方法最大的优势在于不需要针对特定的图像数据集或分类方式提取具体的人工特征,而是模拟大脑的视觉处理机制对图像层次化的抽象,自动筛选特征,从而实现对图像个性化的分类任务。这很好的解决了传统图像分类方法中人工提取特征这一难题,真正的实现了智能化。本节首先给出了基于卷积神经网络图像分类常用数据集,接着给出了图像分类中常采用的卷积神经网络模型、优缺点、时间/空间复杂度、模型训练中可能遇到的问题及相应解决方案以及在图像分类任务中模型未来发展方向及趋势的分析。
3.1 基于卷积神经网络图像分类常用数据集
以下是几种常用分类数据集,在分类难度上依次递增。
(1)MNIST[26]:训练集(training set)包含60000个样本和60000个标签,测试集(test set)包含10000个样本和10000个标签,由来自250个不同人手写数字(0-9)构成。
(2)CIFAR-10[27]:该数据集共有60000张彩色图像,这些图像的分辨率为32×32,分为10类,需要注意的是这10个类之间是相互独立的,每类6000幅图,其中50000幅图用于训练,10000幅图用于测试。
(3)CIFAR-100:该数据集同样有60000张彩色图像,图像分辨率为32×32,分为100个类,每类600幅图像,包括500幅训练图像和100幅测试图像。相较于数据集CIFAR-10,该数据集又将100个类划分为20个超类(Superclass)。
(4)ImageNet[28]:该数据集有1400多万幅图像,涵盖2万多个类别,其中有超过百万的图像有明确的类别标注和图像中物体位置的标注。图像分类、定位、检测等研究工作大都于此数据集展开。
3.2 图像分类常用经典卷积神经网络模型
常用于图像分类的经典CNN网络结构模型种类繁多,例如LeNet[29]、AleXNet[30]、GoogLeNet[31]、VGGNet[32]等多种模型。下面仅对CNN最初的模型以及历届ILSVRC大赛中获得冠亚军且较之前网络结构创新性较大的图像分类模型以及其优缺点作简要分析,然后对以上模型的时间/空间复杂度作简要说明。
(1)LeNet模型[29]: 该模型诞生于1994年,是最早的卷积神经网络之一,是深度学习领域的奠基之作。其网络共涉及60k参数。该模型的基本结构为conv1(6)->pool1->conv2(16)->pool2->fc3(120)->fc4(84)->fc5(10)->softmax,括号中的数字代表通道数。其中,卷积(conv)层用于提取空间特征,池化(pool)层进行映射到空间均值下采样(subsample),全连接层(full connection)将前层是卷积层的输出转化为卷积核为h·w的全局卷积,其中h和w分别为前层卷积结果的高和宽;全连接层将前层是全连接层的输出转化为卷积核为1×1的卷积。该层起到将“分布式特征表述”映射到样本标记空间的作用。最后,输出(output)层采用softmax[33]分类器,其输出为一个向量,元素个数等于总类别个数,元素值为测试图像在各个分类上的评分(各个分类上的元素值加起来为1),元素值最大的那一类即被认定为该测试图像所属的类别。该模型最早应用于MNIST手写识别数字的识别并且取得了不错的效果,但由于受当时计算效率低下的影响,该模型的深度浅、参数少且结构单一,并不适用于复杂的图像分类任务。
(2)AlexNet模型[30]:该网络共涉及约60M参数,ILSVRC2012冠军网络。AlexNet有着和LeNet相似的网络结构,但网络层数更深,有更多的参数。相较于LeNet,该模型使用了ReLU[34]激活函数,其梯度下降速度更快,因而训练模型所需的迭代次数大大降低。同时,该模型使用了随机失活(dropout)操作,在一定程度上避免了因训练产生的过拟合,训练模型的计算量也大大降低。但即便如此,该模型相较于LeNet模型其深度仅仅增加了3层,其对图像的特征描述及提取能力仍然十分有限。
(3)GoogLeNet模型[31]:该网络共涉及5M参数,ILSVRC2014冠军网络。该模型最大的特点在于引入了Inception模块,如图3所示,该模块共有4个分支,第一个分支对输入进行1×1卷积,它可以跨通道组织信息,提高网络的表达能力;第二个分支先使用了1×1卷积,然后连接3×3卷积,相当于进行了两次特征变换;第三个分支类似,先是1×1的卷积,然后连接5×5卷积;最后一个分支则是3×3最大池化后直接使用1×1卷积。该Inception模块的引入大大提高了参数的利用效率,其原因在于:一般来说卷积层要提升表达能力,主要依靠增加输出通道数,但副作用是计算量增大和过拟合。每一个输出通道对应一个滤波器,同一个滤波器共享参数,只能提取一类特征,因此一个输出通道只能做一种特征处理。而该模型允许在输出通道之间进行信息组合,因此效果明显。同时该模块使用1×1卷积核对输入进行降维,也大大减少了参数量。GoogLeNet相较于之前的网络模型其深度大大增加,达到了史无前例的22层,由于其参数量仅为Alexnet的1/12,模型的计算量大大减小,但对图像分类的精度又上升到了一个新的台阶。虽然GoogLeNet模型层次达到了22层,但想更进一步加深层次却是异常困难,原因在于随着模型层次的加深,梯度弥散问题愈发严重,使得网络难以训练。
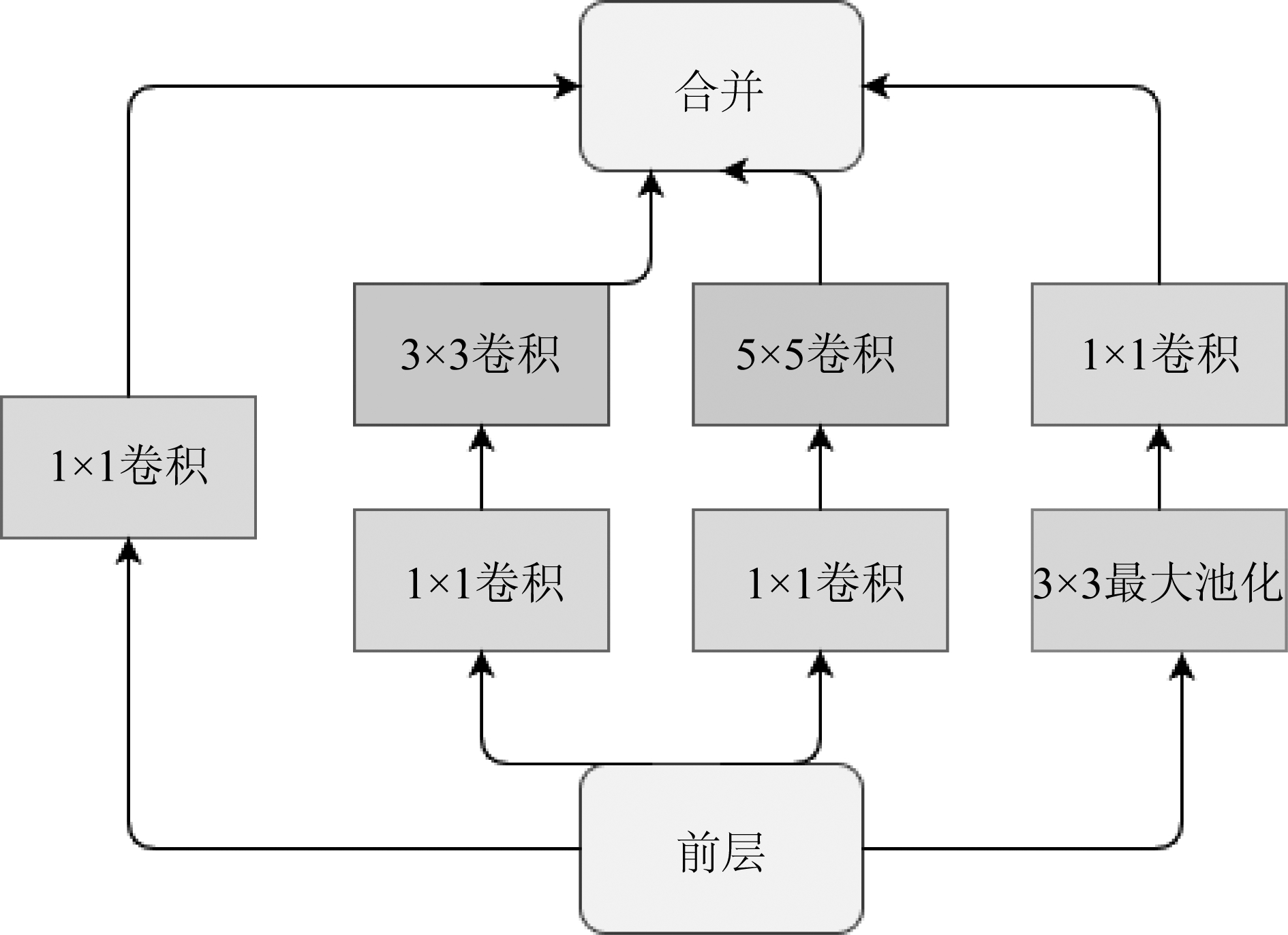
图3 Inception模块
Fig.3 Inception module
(4)VGGNet模型[32]:该模型是ILSVRC2014的亚军网络,它是从AlexNet模型发展而来,主要修改了如下两方面:(a)使用几个带有小滤波器的卷积层代替一个大滤波器的卷积层,即卷积层使用的卷积核较小,但增加了模型的深度;(b)采用多尺度(Multi-Scale)训练策略,具体来说,首先将原始图像等比例缩放,保证短边大于224,再在经过处理的图像上随机选取224×224窗口,因为物体尺度变化多样,这种训练策略可以更好地识别物体。该模型虽然在ILSVRC2014没有获得冠军,但其与冠军的成绩相差无几,原因在于上述两点改进对模型的学习能力提供了非常大的帮助。但该网络使用的参数过多,训练速度缓慢,后续研究仍可在此问题上继续优化。
(5)ResNet模型[35]:该模型是ILSVRC 2015的冠军网络。该模型旨在解决“退化”问题,即当模型的层次加深后错误率却提高了。其原因在于:当模型变复杂时,随机梯度下降(Stochastic Gradient Descent, SGD)[36]的优化变得更加困难,导致了模型达不到好的学习效果。因此文献[35]提出了Residual结构,如图4所示,即增加一个恒等映射,将原始所需要学的函数H(X)转换成F(X)+X,假设F(X)的优化会比H(X)简单的多,则这两种表达的效果相同,但是优化的难度却并不相同。该模型的出现,使得网络模型深度在很大范围内不受限制(目前可达到1000层以上),对后续卷积神经网络的发展产生了深远的意义。
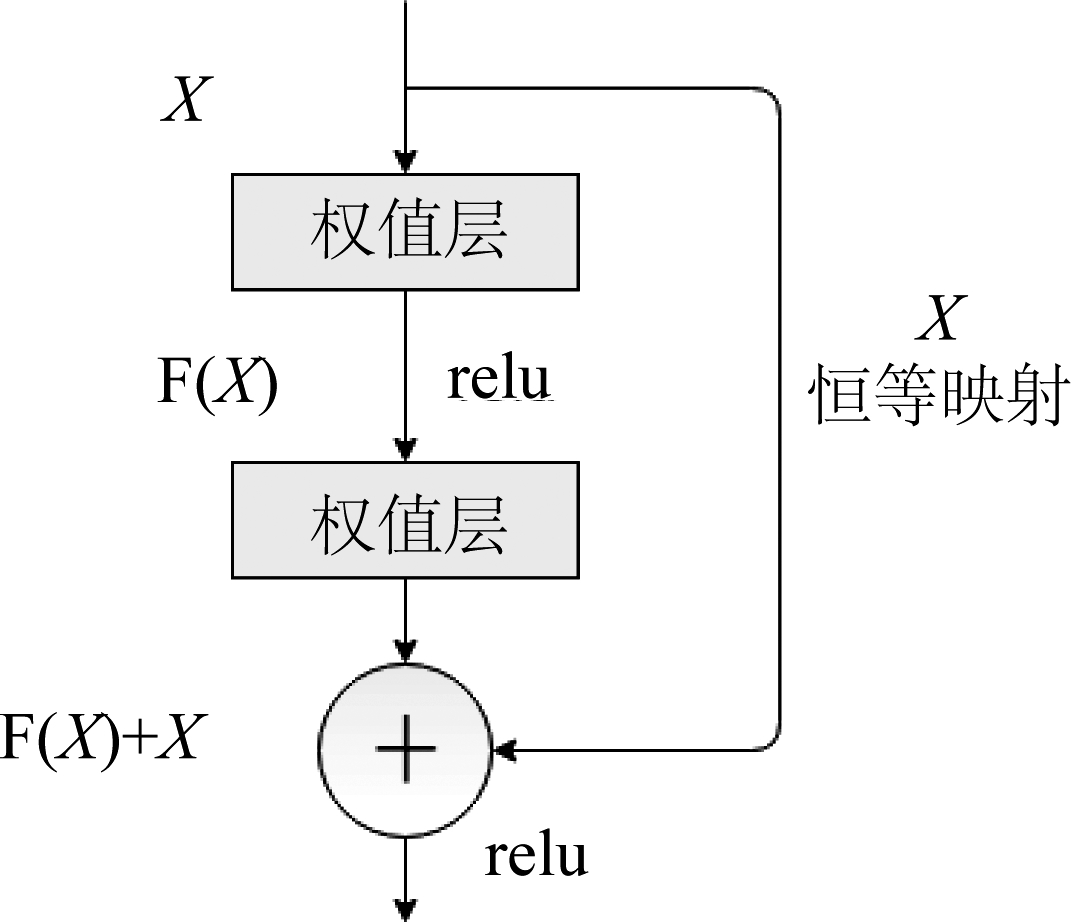
图4 Residual结构
Fig.4 Residual structure
(6)SENet模型[37]:该模型是ILSVRC 2017的冠军网络。SENet通过额外的分支(gap-fc-fc-sigm)来得到每个通道的[0,1]权重,自适应地校正原各通道激活值响应,以提升有用通道响应并抑制对当前任务用处不大的通道响应。该模型不仅在一定程度上减少了计算量,防止了模型训练的过拟合,同时更有利于对图像特征的描述。
现在,对以上在ILSVRC大赛中获得冠军的图像分类模型作错误率分析,其结果如表1所示,其中第一列CNN网络模型中“-数字”代表所训练网络的深度(即模型层数),例如ResNet-50,”-50”代表该模型有50层;Top-1错误率中的Top-1表示模型学习得到的标签(n维向量,n为数据集类别个数,向量值为各类别所对应的预测概率大小)取预测概率最大那一类作为分类结果,因而Top-1错误率代表所学习到的标签中预测概率最大的那一类不是正确类别的比率,以此类推,Top-5错误率代表所学习到的标签中预测概率最大的5个类别中不包含正确类别的比率[35,37]。表1中第二、三列为验证集上的错误率,第四列为测试集上错误率,其中所用测试集为当年ILSVRC大赛指定测试集,故参考意义较大,尤其突出的是2017年ILSVRC冠军网络SENet在测试集上Top-5错误率达到了2.25%相较于之前的网络性能上有了质的飞跃。从2012年冠军网络AlexNet到2017年冠军网络SeNet,在ImageNet数据集图像分类的错误率从15.3%下降到2.25%,可见卷积神经网络模型在近几年发展非常迅速,远没有达到瓶颈,故对卷积神经网络模型后续研究仍尤为重要。
表1 基于CNN图像分类模型在ImageNet数据集上错误率对比
Tab.1 Error rate comparison based on CNN image classification model on ImageNet dataset
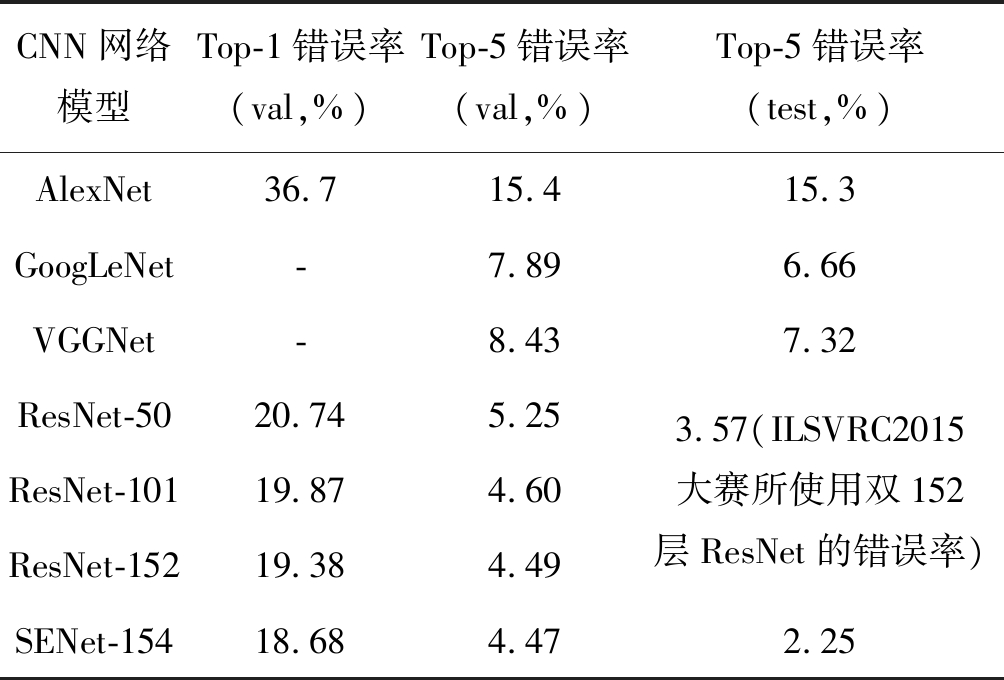
CNN网络模型Top-1错误率(val,%)Top-5错误率(val,%)Top-5错误率(test,%)AlexNet36.715.415.3GoogLeNet-7.896.66VGGNet-8.437.32ResNet-5020.745.25ResNet-10119.874.60ResNet-15219.384.493.57(ILSVRC2015大赛所使用双152层ResNet的错误率)SENet-15418.684.472.25
模型的时间复杂度和空间复杂度是衡量模型好坏的重要指标,时间复杂度决定了模型训练/预测需要运算的次数,空间复杂度决定了参数的数量。时间复杂度通常以浮点运算次数(floating-point oprations, FLOPs)来衡量,空间复杂度以模型参数数量来衡量。随着硬件水平以及计算能力的快速发展,模型的时间复杂度对训练和预测的影响总可以找到相应的方法克服(例如增大对计算成本的投入),但如若应用到一些对实时性要求高的项目中,对模型选择的取舍还需权衡时间复杂度和精度的要求。下面着重对空间复杂度进行分析,空间复杂度对模型性能优劣的重要性不言而喻,一个模型的参数数量,往往会造成维数灾难,一方面带来时间复杂度的增加;另一方面,意味着有许多参数需要被训练,因此需要训练的数据量大大增加,这无疑对数据集的样本规模提出了更高的要求。再者,空间复杂度的提升对数据分布的刻画能力也随之增强,这对于一些复杂数据集的分类任务无疑是一件好事,但对于一些简单数据集也是灾难性的,往往会造成严重的过拟合问题。表2列出了上述模型的FLOPs和参数数量,供学者针对图像分类任务要求,合理选择或改进相关网络模型。
表2 CNN图像分类模型的时间复杂度和空间复杂度
Tab.2 Time complexity and space complexity of CNN image classification model
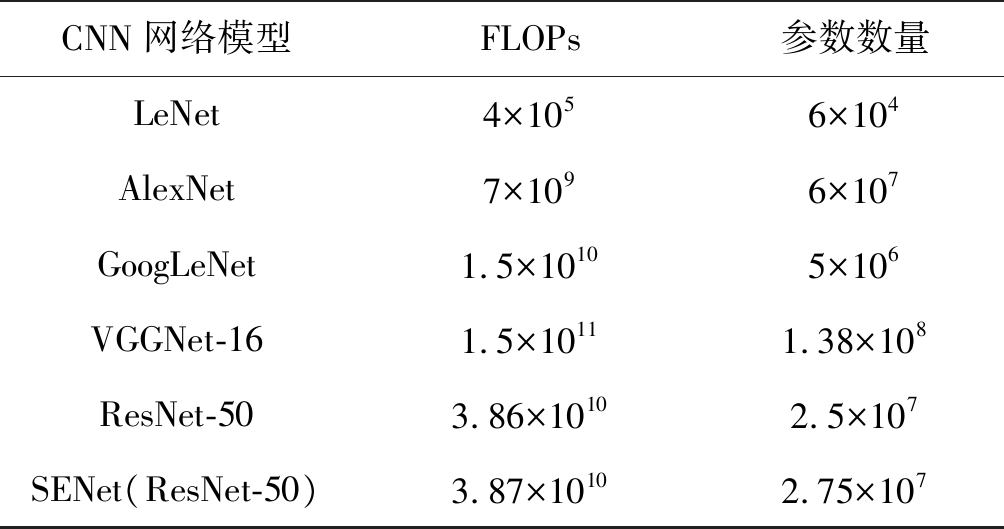
CNN网络模型FLOPs参数数量LeNet4×1056×104AlexNet7×1096×107GoogLeNet1.5×10105×106VGGNet-161.5×10111.38×108ResNet-503.86×10102.5×107SENet(ResNet-50)3.87×10102.75×107
3.3 卷积神经网络模型训练注意事项及技巧
前述网络模型除了在模型结构上有所创新之外,各模型所用训练技巧也不尽相同,下面对卷积神经网络模型训练中所遇到的常见问题及解决方法作简要分析。
(1)过拟合(overfitting):过拟合,即模型在训练集范围内能很好的拟合数据,在训练集外不能够很好的拟合数据。造成该现象的原因主要有以下3种:(a)模型的复杂度过高,包括参数过多或过训练;(b)数据图像噪声过多,例如图像数据的部分缺失、模糊等,如果模型与训练集数据完全拟合,其与真实场景偏差可能更大;(c)数据量有限,使得模型无法真正了解数据集的真实分布。因此,为了解决该问题,可从这三方面入手调优。对于模型参数过多问题,可以减少模型深度;对于过训练问题可以使用诸如对损失函数(loss function)[38]、批量损失(batch loss)[39]加正则化约束、随机失活、权值衰减等方法加以处理。对于数据图像噪声过多,可以在训练前先对数据集进行预处理,以达到降噪的目的。对于数据量过少的问题,一方面可通过扩充数据集以增加数据量,另一方面,可将原图训练集中图像进行翻转、平移、放大缩小等操作后重新加入训练集以达到扩充数据集的目的。
(2)欠拟合(underfitting):欠拟合,即模型在训练集范围内不能很好的拟合数据,该现象产生的原因主要是网络模型深度不够,不能对一些较复杂的数据集进行很好的拟合,因此,解决该问题主要考虑加深网络的层次。
(3)梯度消失(gradient vanishing)、梯度爆炸(gradient exploding):梯度消失[40]和梯度爆炸[41]本质原因归结为卷积神经网络采用反向传播方式,该方式使用链式求导,计算每层梯度的时候会涉及连乘操作,因此如果网络层次过多,连乘因子大部分小于1,最后乘积结果趋于0,也就是所谓的梯度消失;同理,如果连乘因子大部分大于1,最后乘积趋于无穷,也就是所谓的梯度爆炸。简而言之,梯度消失,即卷积神经网络后层的权值更新幅度要远大于前层权值更新幅度,当前层的权值更新幅度过小(几乎趋于停滞),后层也就失去存在的意义(相当于只训练了后层);梯度爆炸,即卷积神经网络前层的权值更新幅度远大于后层权值更新幅度,导致网络权重大幅更新,并因此使得网络不稳定,在极端情况下,前层权重的值将变得非常大直至溢出。对于梯度消失问题,常用的解决方法包括:引入ResNet模型中使用的Residual模块,改进激活函数,如AlexNet中所使用的ReLU激活函数等;对于梯度爆炸问题,解决方法除了改进激活函数之外,还可引入批量归一化(Batch normalization, BN)[42]、梯度截断(Gradient Clipping)[43]、权重正则化等优化技术。
3.4 基于深度学习的图像分类拓展模型
基于传统CNN的图像分类技术在有大量标注样本可训练的情况下已达到不错的性能,但却无法用来在没有大量标注样本的情况下训练,即无法完成半监督学习(Semi-Supervised Learning,SSL)[44]甚至无监督学习(Unsupervised Learning)[45],然而寻找大量标注的数据样本是一件十分困难的事情;此外传统CNN网络由于结构的局限性,对重叠图像分类任务性能不佳。近两年,随着生成式对抗网络(generative adversarial network, GAN)[46]以及胶囊网络(capsule network)[47]模型的兴起,在上述领域有了一定的突破,具有很大的发展潜力。下面对这两种网络进行详细介绍及分析。
(1)生成式对抗网络
GAN由生成器网络(generator network)和判别器网络(discriminator network)两部分构成。生成器网络主要从训练数据中生成伪造样本,其输出表示为x=g(z;θ(g));判别器网络用于判断输入数据为真实样本还是生成器伪造的样本,其输出表示为d(x;θ(d)),指示x是真实训练样本而不是从模型抽取的伪造样本的概率。简而言之,一个网络生成伪造样本,另一个网络判断所生成样本是真实的还是模拟的。生成伪造样本的网络要优化自己让判别网络认为所生成样本为真实样本,判别的网络也要优化自己让自己判断更加准确,二者关系行成对抗,因此称为对抗网络。该网络的全局优化函数如下所示:
(3)
其中
v(θ(g),θ(d))=Ex~pdatalog d(x)+
Ex~pmodellog(1-d(x))
(4)
从判别网络的角度来说,希望对于真实样本,其输出概率越大越好;对于伪造的生成样本来说,其输出概率越小越好,故其目标函数为:
(5)
从生成网络的角度来说,希望其生成的伪造样本由判别器判断为真实的样本的概率越高越好,即上式中第二项越小越好,上式第一项在生成网络训练过程中可看作常数,故其目标函数为:
(6)
在训练过程中,采用交替迭代策略,即先固定其中一个网络参数来优化与之形成对抗的网络。当生成器样本与实际数据不可区分,判别网络对于生成器输出样本其判别概率处处为0.5时,即达到理论上的纳什均衡,可认为模型收敛。
该网络自2016年掀起研究热潮以来,目前在网络模型算法、训练优化和应用领域拓展等方面仍处于快速发展阶段。在计算机视觉领域,自从基于GAN改进的DCGAN[48](该方法将卷积网络应用于对抗网络)问世以来,其在目标检测[49]、图像风格迁移[50]、超分辨率重构[51]等方向产生了举足轻重的影响。该网络同样可以用于图像分类[52-53],其核心思想是将生成网络的输出作为k+1类,相应地,判别网络的输出为k+1类的分类问题。该网络在图像分类方面有重要意义,它改变了传统CNN需要大量标注样本进行学习的策略,使其可以在少量标注样本及大量未标注样本上进行学习并取得了良好的效果,即所谓的半监督学习。
(2)胶囊网络
尽管目前业界最先进的传统CNN模型在图像分类上取得了不错的性能,但依然掩盖不了传统CNN网络结构对物体之间的空间关系辨识度差以及对物体大幅度旋转之后识别能力低下这两个缺陷[47]。因此,最近Hinton等人在CNN基础之上提出了胶囊网络(capsule network)[47],即一个包含多个神经元的载体,每个神经元表示了图像中出现的特定实体的各种属性。这些属性可以包括许多不同类型的实例化参数,例如姿态(位置、大小、方向)、变形、速度、色相、纹理等。胶囊里一个非常特殊的属性是图像中某个类别的实例的存在,它的输出数值大小就是实体存在的概率。
定义了胶囊这个结构,如果仍像传统CNN模型使用BP算法来训练神经元的权重,则所谓的胶囊无异于传统CNN模型中下一层节点,故Sabour等人对胶囊之间的训练提出了名为动态路由(dynamic routing)的算法[47],该算法核心内容可概括为:低级别的胶囊会将其输出发送给“同意”该输出的高级别胶囊。具体来说,即低级别的胶囊通过识别输入目标较简单的子部分来判断一个该目标可能是什么的“弱赌注”,而后,高级别的胶囊会采取这些低级别胶囊的“赌注”,假若某个较高级别的胶囊同意足够多的低级别胶囊,则这些低级别胶囊的路由即为该较高级别的胶囊。
该网络的输出层由于使用胶囊结构得到输出各个分类概率值(类似于softmax应用于多分类任务的输出形式),故其目标函数有别于传统CNN模型的目标函数,被称之为间隔损失(margin loss),如下所示:
Lk=Tkmax(0,m+-‖vk‖)2+
λ(1-Tk)max(0,‖vk‖-m-)2
(7)
其中k表示分类;Tk是分类的示性函数(k类存在为1,不存在为0):‖vk‖表示胶囊的输出概率;m+为上界,惩罚假正例(false positive),即预测k类存在实则不存在,m-为下界,惩罚假反例(false negative),即预测k类不存在实则存在;λ为比例系数,调整两者比重。
胶囊网络在MNIST数据集分类任务中取得了目前该领域内处于领先地位的成绩,仅仅一个三层的网络(一个卷积层和两个胶囊层)且并没有使用过多的训练技巧,其错误率达到了0.25%。但由于该网络对比于目前流行传统CNN模型,其只属于一个浅层网络,故其在较复杂数据集,如ImageNet上的识别准确率距离传统深度CNN网络还有一定差距,但未来通过加深网络结构、增加训练技巧、改善路由算法等,其在大型数据集分类任务中具有很大的发展潜力。
胶囊网络概念在2017年11月才由Hinton等人提出,是当前计算机视觉领域的最新技术。目前,在图像分类及图像重构领域具有开创性意义。但该网络训练速度极慢,很大程度由于内部循环的路由协议算法;此外,目前还不清楚胶囊网路是否可以增大网络深度,用于规模更大的样本数据集。
4 实验结果及分析
本节图像分类性能评估实验主要分为5部分,第1部分以图像分类精度为标准,对比了卷积神经网络与传统图像分类方法性能的优劣;第2部分,以多项性能指标综合分析近几年比较著名的卷积神经网络模型,并进一步验证各模型的优缺点。第3部分,针对3.3节所述训练模型过程中遇到的较普遍的过拟合问题展开实验,说明常见模型中所运用到的过拟合策略以及各策略对模型精度的影响。第4部分,参照3.1节公开数据集构建方法及一些构建准则,通过实验来说明数据集样本构建方法及样本规模对现有模型训练的影响。第5部分,通过实验分析生成式对抗网络及胶囊网络的优势与缺陷。
4.1 简单图像多分类任务仿真实验
下面以MNIST数据集为载体,综合比较基于卷积神经网络、基于K最近邻(k-Nearest Neighbor, KNN)[10]以及基于多层感知机(Multi Layer Perception, MLP)[54]在简单图像多分类任务中的性能。
(1)基于卷积神经网络的图像分类:利用tensorflow[55]我们设计了一个简单的CNN网络来进行图像分类,该网络结构如图5所示,该图为tensorboard[56]导出图。该CNN网络一共分为5层:输入层、两个卷积层以及两个全连接层。利用交叉熵损失函数,基于误差来进行反向传播(Back Propagation, BP)[57]训练。本次训练的模型的初始权重采用截断的随机正态分布,学习率为0.1,共迭代了6000次。
图6给出了准确率随迭代次数的变化情况,由图6可知在为训练模型过程中,随着迭代次数的增加,其在测试集上的准确率变化,准确率最终稳定维持在98.5%以上,可见CNN在MNIST数据集上的分类性能相当好。
(2)基于多层感知机的图像分类:所谓多层感知机,即指含有多个隐藏层的神经网络,其隐藏层全为全连接层。为了便于比较,同样在tensorflow上设计了一个含有两个隐层的多层感知机,所用的激活函数、损失函数及初始权重均与CNN网络相同,经过训练,发现其最终准确率在96%左右,与CNN网络还是有一定差距。
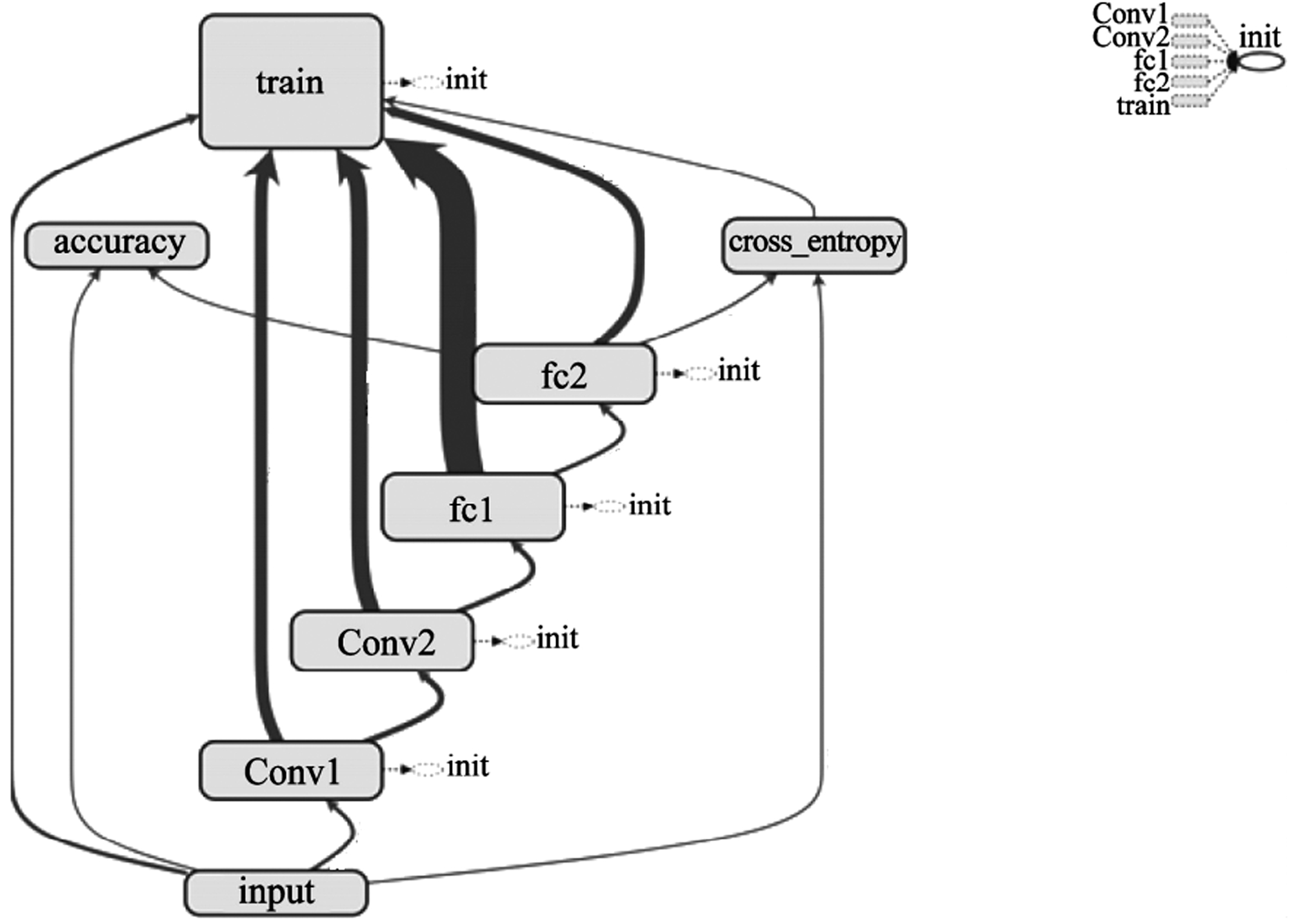
图5 CNN网络模型
Fig.5 Convolutional neural network model
(3)基于K最近邻的图像分类:用K最近邻对图像进行分类主要分为以下四个步骤:(a)计算训练样本与测试样本间的距离;(b)对样本距离升序排列;(c)选前K个距离最小的样本;(d)根据样本对数据进行投票,得到分类结果。同样使用tensorflow进行实验,共进行了200组测试,每组测试随机从测试集中选取1张图像进行预测,并与标签值进行比较,最后得到平均准确率约为89.5%。
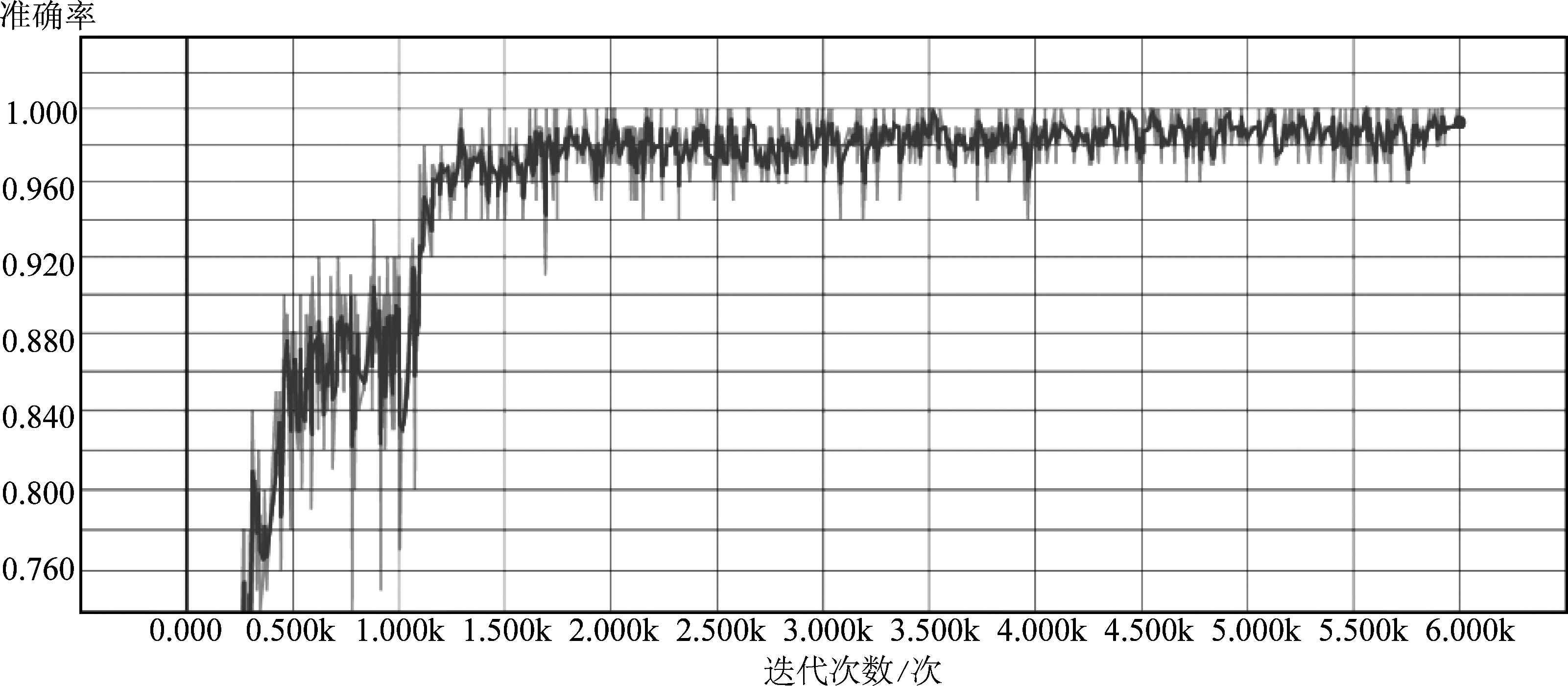
图6 准确率随迭代次数的变化
Fig.6 Accuracy changes with the number of iterations
综上所述,给出CNN、MLP、KNN算法准确率比较如表3所示。
表3 CNN、MLP、KNN算法准确率比较
Tab.3 Comparison of accuracy between CNN, MLP and KNN algorithms

算法准确率CNN98.5%MLP96%KNN89.5%
由表3可以看出,基于神经网络多层感知机算法对比传统的机器学习方法K最近邻算法在图像分类上存在较大优势,然而基于神经网络改进的卷积神经网络在图像分类上性能更是遥遥领先。
4.2 较复杂图像多分类任务仿真实验
为了更好地分析近几年卷积神经网络模型的性能及展示模型训练及评估方法,下面以CIFAR-10数据集为载体,从头训练目前较为流行的AlexNet- 8、VGGNet-16、GoogLeNet-22、ResNet-50、ResNet-101模型,“-”后为网络层数。
本次实验采用单片Tesla M40 GPU(显存12G),通过tensorflow进行训练,其训练过程仍采用tensorboard进行可视化。为了便于实验比较,本次训练的所有模型采用的优化算法均为rmsprop[58],其优化器参数及训练技巧也都相同。本次训练结果不代表各模型的最优性能,一个模型性能的好坏并不由模型结构完全决定,后期的优化(如参数调优、训练技巧的合理使用)也尤为重要。因此本次实验仅考虑模型本身带来的性能差异。
训练过程中模型损失值的变化如图7(a)所示,该5个模型使用了相同的优化算法及相应参数,相同的退化学习率(即学习率会随着迭代次数增多自适应下降),因此损失值的变化过程主要由模型结构决定。从该图可以看出除了AlexNet- 8在迭代了10万次后,损失值几乎为0,其他模型的损失值波动均在20万次~30万次之间达到稳定,可认为模型训练收敛。损失值反应了训练样本通过模型预测的准确程度,即损失值越大,模型对训练样本的刻画越不精确。因此,当模型收敛时,AlexNet- 8对训练集样本刻画最为精确,GoogLeNet较其他模型损失略大。
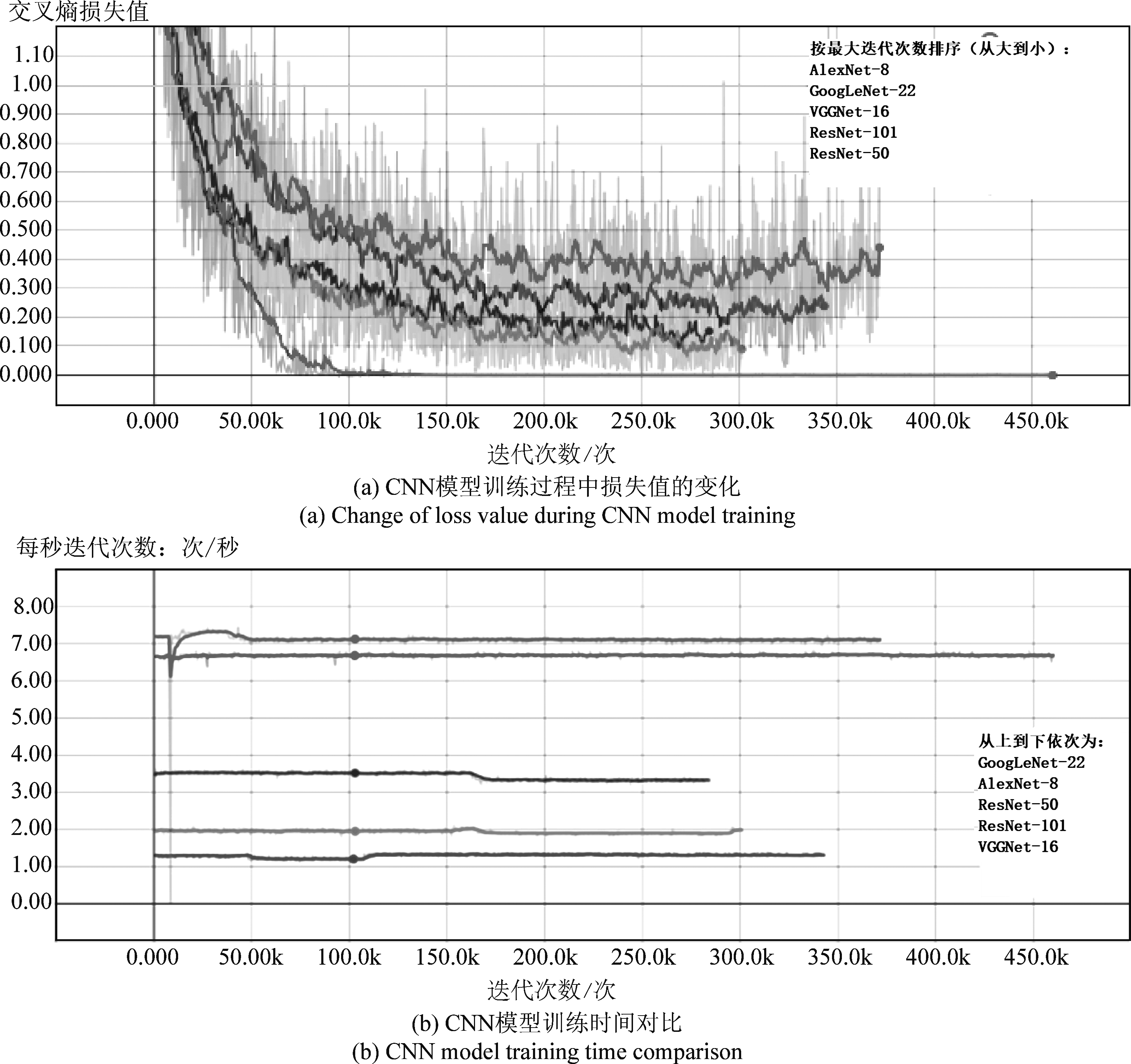
图7 CNN模型训练
Fig.7 CNN model training
图7(b)反应了CNN各模型每秒迭代次数对比,可以发现并不是模型层数越多,每秒迭代次数越少。GoogLeNet-22虽然有22层,却是所有参加对比的模型中迭代速度最快的,达到每秒迭代7次左右。这主要得益于GoogLeNet-22的模型结构,使得其参数仅为500万,为AlexNet- 8参数量的1/12。其引入的inception模块在减少参数量上厥功至伟,同时又使模型不失表达能力。对于具有相同结构的模型,仅层数加深,其训练时间跟层数呈正相关,如本次试验中ResNet-50每秒约能迭代3.5次而ResNet-101仅为2次。
以上所训练模型在CIFAR-10数据集上错误率见表4所示。
由表4可以看出其所有模型在训练集Top-1错误率远低于测试集Top-1错误率,说明在训练模型时均产生了严重的过拟合现象。表3中ResNet-50在CIFAR-10测试集上Top-1错误率表现反而略高于ResNet-101,但也不代表深度增加就毫无意义,如表1中ResNet在ImageNet测试集上Top-1错误率随着深度的增加而减小。但从上可分析得出模型的深度与数据集的复杂度存在着密切的联系。表4中各模型,除了AlexNet- 8,其他模型在测试集上Top-1错误率基本都已控制在10%以内,Top-3错误率在1.6%以内,其性能相当优秀。综合考虑训练时间和测试集准确率,在本次对比实验中,GoogleNet和ResNet网络较为优秀,其中ResNet由于Residual结构的引入使得CNN模型深度的不断增加成为可能,相信未来图像分类模型在这两个模型基础上进行改进(如引入新的模块、增加新的训练技巧、参数进一步调优等)会取得更优的性能。
4.3 过拟合实验
由于在训练基于卷积神经网络的图像分类模型中,层次较深的网络不可避免的会产生过拟合现象,为了尽量减少过拟合问题带来对模型正确率的影响,一系列策略被用于CNN模型。下面仅以ResNet模型为例,通过对比试验说明以下三种减缓过拟合策略对模型精度产生的影响。
(1)通过增加数据量来减少模型的过拟合。此策略往往效果最佳,但对于数据的收集却是一大考验,以此受到启发,产生了数据增强技术。本实验通过对比经过数据增强以及未经过数据增强训练的模型来分析该技术对模型精度的影响,其中所使用的数据增强技术主要为随机增加训练集图像的对比度、亮度、色度和饱和度,并将经过预处理后的图像一并加入训练集用于模型训练。如表5所示,在同一数据集上,使用数据增强技术与未使用此技术在模型精度上足足相差三个百分点,证明数据增强技术不失为一种解决过拟合问题好的策略。
表4 基于CNN图像分类模型在CIFAR-10数据集上错误率对比
Tab.4 Error rate comparison based on CNN image classification model on CIFAR-10 dataset
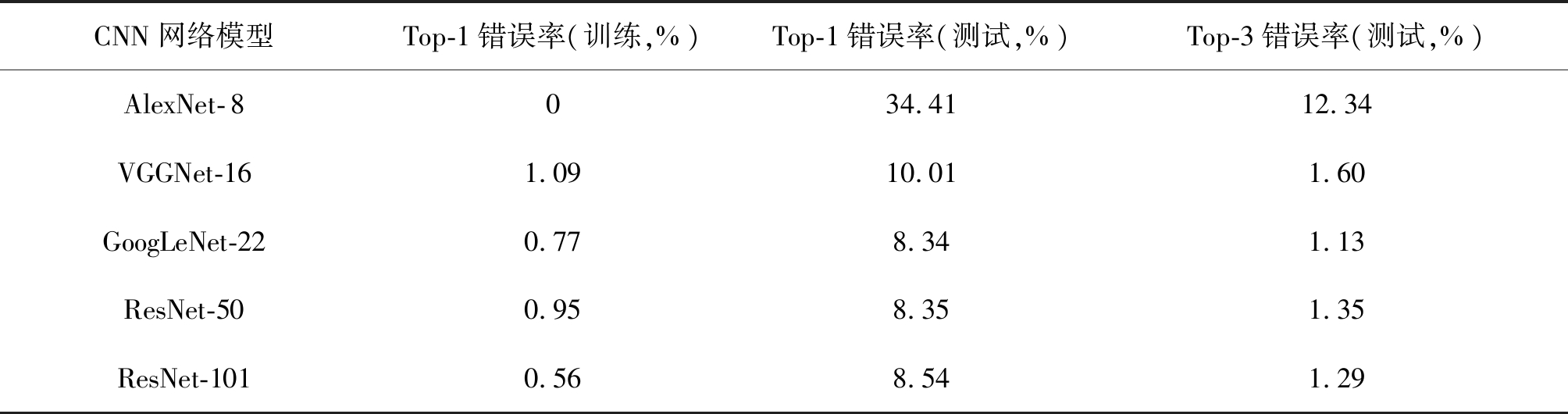
CNN网络模型Top-1错误率(训练,%)Top-1错误率(测试,%)Top-3错误率(测试,%)AlexNet-8034.4112.34VGGNet-161.0910.011.60GoogLeNet-220.778.341.13ResNet-500.958.351.35ResNet-1010.568.541.29
表5 数据增强技术对模型准确率影响
Tab.5 Influence of data enhancement technology on model accuracy

数据集是否使用数据增强技术准确率(测试,%)flowers是88.75否85.75
(2)通过使用批次归一化来减少过拟合风险。关于批次归一化技巧减少过拟合风险的有效性已在文献[59]中进行了理论证明,下面通过对比实验说明ResNet模型逐层使用批次归一化两种方式对模型精度的影响,其中方式一是在每个激活层之前使用批次归一化;方式二是在每个激活层之后使用批次归一化。为了便于训练,该实验使用flowers数据集(训练数据集大小为3320,测试数据集大小为350,分类个数为5)以及CIFAR-10上分别训练,如表6所示,可发现模型准确率在使用方式一较之方式二有明显优势,故单从批次归一化对模型精度的影响来看,建议在工程实践中采用方式一。
表6 批次归一化方式对模型准确率的影响
Tab.6 Influence of batch normalization on model accuracy

数据集批次归一化方式准确率(测试,%)flowers方式一87.75方式二85.75CIFAR-10方式一91.65方式二90.93
(3)通过减少CNN模型卷积层数来降低模型复杂度,以此缓解过拟合。该对比实验如表7所示,其实验数据来源于文献[35],该实验证明了过高的模型层数(表中模型层数为1202)反而会带来模型精度的下降,因此在训练模型时,可以根据数据集的大小及复杂度适当增加或删减卷积层数,以此减缓过拟合带来的对模型准确率的影响。
4.4 数据集构建和样本规模对训练CNN影响实验
基于图像分类任务的需要,数据集的构建往往决定着模型的训练效果,故在工程实践中,构建图像分类任务所需的数据集也是一门学问。受上文中公开数据集构建方法的启发,构建数据集可分为训练数据集(需按照图像标签类别分类存放)、测试数据集(需按照图像标签类别分类存放)以及标签文件(训练数据及测试数据图像的类别标签) 三部分,其中训练数据集及测试数据集需满足互斥关系,非严格意义的独立同分布(各类别的样本数据量尽量相同)。下面对样本规模和CNN模型之间的关系作简要说明,样本规模和CNN模型的复杂度呈正相关,模型的复杂度越高,意味着该模型能表示相对更多、更复杂的数据关系。因此,选择适合实际应用的样本规模也尤为重要。
下面通过实验说明数据集样本构建方法及样本规模对现有模型训练的影响。所选用的待测试模型为ResNet-50,数据集仍为flowers, 为了测试样本规模对现有模型的影响,重构flowers的训练集,将原本拥有3320个标注样本的训练数据集随机缩减为2500和1500进行重新训练及评估性能,而后又使用数据增强技术在原数据集上扩充数据集并进行相应实验,所使用数据增强技术的方法与4.3(a)中所述一致。其实验结果如表8所示。
表7 模型层数对模型准确率的影响
Tab.7 Influence of model layer number on model accuracy
模型层数2032561101202准确率(测试,%)91.2592.4993.0393.5792.07
表8 数据样本规模对CNN影响
Tab.8 Influence of data sample size on CNN

训练样本数收敛迭代次数/万次收敛损失值准确率(训练,%)准确率(测试,%)15002099.6779.83250070.396.9280.183320(原)100.297.4087.7513280(数据增强)5.50.399.2688.75
由表8可见,在未使用数据增强技术的情况下,训练模型迭代收敛次数与训练样本数呈负相关,模型测试准确率则与训练样本数基本呈正相关;在样本规模较小的情况下,训练模型在训练数据集上拟合效果越好,当训练样本规模为1500时,其在收敛时的损失值近乎为0,在训练集上的准确率也为实验中最高,达到了99.67%。在使用数据增强技术的情况下,由于其本质是在原始图像上随机加入噪声构成新图像,然后再加入原训练数据集进行训练,故训练集中许多样本的相似度很高,通过实验可发现,模型在达到收敛时,其迭代收敛次数仅为5.5万,远低于没通过数据增强技术扩充数据集的原训练数据集;其次,虽然该技术在收敛时损失值为0.3,但在训练集上的准确率达到了99.26%,拟合相当良好,且在测试集上的准确率达到了88.75%,为所测试实验中最高。
由以上实验分析,可得出以下结论:(a)在条件允许的情况下,对于传统深层次CNN模型,采集的样本规模越大越好。关于现有较深层次CNN模型是否能够承载庞大数据集的能力,论文[60]验证了通过扩充数据集至比ImageNet数据集大200多倍的数据集在比没扩充前的训练效果好,可见现有CNN模型具有至少200个ImageNet样本规模大小的模型承载能力。(b)在无法采集足够多的标记样本的情况下,可通过数据增强技术扩充数据集以提高模型泛化性能。
4.5 生成式对抗网络和胶囊网络实验
为了更好地分析生成式对抗网络和胶囊网络优缺点,下面通过实验进行说明:
(1)生成式对抗网络:该网络性能在有监督图像分类领域较之传统CNN网络并没有明显优势,但在半监督甚至无监督图像分类领域其性能良好,下面以Conv-CatGAN为例,说明其在图像分类半监督领域贡献。如表9所示,表中k的值表示从训练集中随即均匀选出已标注样本数据,训练集中其余样本不提供样本标注,使用Conv-CatGAN进行半监督训练,虽然其准确率没有有监督训练高,但其需要的标注样本数甚至不足原样本数的百分之一,可见此网络的潜力之大。但该网络的结构特性导致了其不容易训练,文献[52]提供了在此方面的帮助,并进一步提高了生成式对抗网络在图像分类任务的性能。
(2)胶囊网络:为了更好地分析模型性能,该实验主要考量在MNIST数据集上的分类测试准确率、训练收敛时的损失值(该损失值为胶囊网络用于图像分类的损失值),以及模型达到收敛的迭代次数来说明胶囊网络的潜力,如表10所示。该实验中,每次模型迭代中,其路由算法迭代次数为3,所训练模型基于原论文的边缘损失与重构损失之和,以此达到图像分类更好的效果。
结果显示模型达到收敛时,其迭代次数为6万次,这在不使用过多优化技巧的情况下,其收敛速度属上乘水平;模型收敛损失值达到了4.99×10-4,准确率达到了99.64%,该模型对MNIST数据集的刻画能力可媲美CNN深层模型,在文献[47]中,通过集成7个胶囊网络对CIFAR-10数据集进行训练,其在测试集上的准确率为10.6%,相比于最优CNN网络还存在一定差距。未来通过优化算法加深模型深度,其对复杂数据集的刻画能力有望超越CNN模型。
此外,该模型的另一大优势在于对重叠图像的识别,Hinton等人在MultiMNIST数据集上进行训练,该数据集基于MNIST数据集进行重构,使得每幅图像中有两个数字,且两个数字的平均重叠率为80%,在每次模型迭代中,其路由算法迭代次数设置为3,所训练模型同样基于边缘损失和重构损失[47],此时其在测试集上的准确率达到94.8%。
表9 生成式对抗网络性能分析
Tab.9 Performance analysis of generated antagonistic networks

数据集MNIST(原训练集)MNIST(k=100)CIFAR-10(原训练集)CIFAR-10(k=4000)准确率(测试集,%)98.6199.5290.6280.42
表10 胶囊网络性能分析
Tab.10 Performance analysis of capsule network

实验数据集收敛迭代次数/万次收敛损失值准确率(测试,%)MNIST64.99×10-499.64
5 结论
本文对基于卷积神经网络的图像分类进行了介绍。首先回顾了传统图像分类方法及其存在问题,以及卷积神经网络在图像分类任务上的优越性;其次,介绍了神经网络的基本结构,而后在此基础上介绍了卷积神经网络特有的池化层及卷积层的结构特点和功能作用;然后,介绍了目前较先进的基于卷积神经网络的分类方法,包括此类方法所运用的图像分类数据集和卷积神经网络模型、优缺点、时间/空间复杂度、模型训练过程中可能存在的问题及改进方案,与此同时也对基于深度学习的图像分类拓展模型的生成式对抗网络、胶囊网路进行介绍;最后,对基于卷积神经网络的分类方法和传统的机器学习图像分类方法作了个对比,以此说明卷积神经网络在图像分类任务上的优势;同时,对目前较为流行的卷积神经网络模型进行了训练及模型性能评估实验,以此比较各模型的性能及说明训练中的注意事项;再者,还对过拟合问题、数据集构建方法提出可参考性建议并通过实验验证其有效性。尽管,基于卷积神经网络的方法对于一些简单的图像分类任务取得了很好的效果,但对于一些复杂的图像分类其性能还有待提高,如图像分类的一个分支人脸识别[61],由于光照、姿态、遮挡、年龄变化、海量数据等问题,其在精度及识别速度上仍然有待提高。其次,图像分类不仅仅是一个独立的任务,更是众多图像处理任务的基础,如在目标检测的任务中,Cao等人先对图像进行分类以获得先验知识,再进行图像中目标识别的算法,对识别的精度产生了积极的影响[62]。再者,对基于半监督甚至无监督以及重叠图像分类任务的研究才刚刚起步,如何将卷积神经网络更好地运用此领域(如结合胶囊网络、生成式对抗网络等)是未来研究热点。因此,还需对基于卷积神经网络的图像分类开展更加深入的研究。
[1] Bhattacharyya S. A Brief Survey of Color Image Preprocessing and SegmentationTechniques[J]. Journal of Pattern Recognition Research, 2011, 1(1): 120-129.
[2] Vegarodriguez M A. Review: Feature Extraction and Image Processing[J]. Computer Journal, 2004, 44(2): 595-599.
[3] Zhang D, Liu B, Sun C, et al. Learning the Classifier Combination for Image Classification[J]. Journal of Computers, 2011, 6(8): 1756-1763.
[4] Perreault S, Hébert P. Median Filtering in Constant Time[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2007, 16(9): 2389-2394.
[5] Slot K, Kowalski J, Napieralski A, et al. Analogue Median/Average Image Filter Based on Cellular Neural Network Paradigm[J]. Electronics Letters, 1999, 35(19): 1619-1620.
[6] Direkoglu C, Nixon M S. Image-Based Multiscale Shape Description Using Gaussian Filter[C]∥Computer Vision, Graphics & Image Processing, 2008. ICVGIP'08. Sixth Indian Conference on. IEEE, 2009: 673- 678.
[7] Grabner M, Grabner H, Bischof H. Fast Approximated SIFT[C]∥Asian Conference on Computer Vision. Springer-Verlag, 2006: 918-927.
[8] He L, Zou C, Zhao L, et al. An Enhanced LBP Feature Based on Facial Expression Recognition[C]∥IEEE Engineering in Medicine and Biology, Conference. IEEE, 2005: 3300-3303.
[9] Déniz O, Bueno G, Salido J, et al. Face Recognition Using Histograms of Oriented Gradients[J]. Pattern Recognition Letters, 2011, 32(12): 1598-1603.
[10] Amato G, Falchi F. Local Feature Based Image Similarity Functions for kNN Classification[C]∥Icaart 2011-Proceedings of the, International Conference on Agents and Artificial Intelligence, Volume 1-Artificial Intelligence, Rome, Italy, January. DBLP, 2011: 157-166.
[11] Joachims T. Making Large-scale SVM Learining Practical[J]. Advances in Kernel Methods Support Vector Learning, 2006, 8(3): 499-526.
[12] Lecun Y, Bengio Y, Hinton G. Deep Learning[J]. Nature, 2015, 521(7553): 436- 444.
[13] Deng L, Yu D. Deep Learning: Methods and Applications[J]. Foundations & Trends in Signal Processing, 2014, 7(3): 197-387.
[14] Le Q V, Ngiam J, Coates A, et al. On Optimization Methods for Deep Learning[C]∥International Conference on Machine Learning, ICML 2011, Bellevue, Washington, Usa, June 28-July. DBLP, 2011: 265-272.
[15] Chua L O, Roska T. CNN Paradigm[J]. IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 1993, 40(3): 147-156.
[16] Matsugu M, Mori K, Mitari Y, et al. Subject Independent Facial Expression Recognition with Robust Face Detection Using a Convolutional Neural Network[J]. Neural Networks, 2003, 16(5- 6): 555-559.
[17] Moeskops P, Viergever M A, Mendrik A M, et al. Automatic Segmentation of MR Brain Images With a Convolutional Neural Network[J]. IEEE Transactions on Medical Imaging, 2016, 35(5): 1252-1261.
[18] Bhardwaj S, Tewari S, Jain S. Study on Future of Artificial Intelligence in Neural[J]. International Journal of Scientific & Engineering Research, 2013, 4(6): 597- 601.
[19] Zhou L, Pan S, Wang J, et al. Machine Learning on Big Data: Opportunities and Challenges[J]. Neurocomputing, 2017, 237: 350-361.
[20] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C]∥International Conference on Neural Information Processing Systems. Curran Associates Inc. 2012: 1097-1105.
[21] Oquab M, Bottou L, Laptev I, et al. Learning and Transferring Mid-level Image Representations Using Convolutional Neural Networks[C]∥Computer Vision and Pattern Recognition. IEEE, 2014: 1717-1724.
[22] Zagoruyko S, Komodakis N. Learning to Compare Image Patches via Convolutional Neural Networks[C]∥Computer Vision and Pattern Recognition. IEEE, 2015: 4353- 4361.
[23] Hawkins D M. The Problem of Overfitting[J]. Cheminform, 2004, 35(19): 1-3.
[24] Gottumukkal R. An Improved Face Recognition Technique Based on Modular PCA Approach[J]. Pattern Recognition Letters, 2004, 25(4): 429- 436.
[25] Tuytelaars T, Mikolajczyk K. Local Invariant Feature Detectors: A Survey[J]. Foundations & Trends in Computer Graphics & Vision, 2008, 3(3): 177-280.
[26] León M D, Moreno-B ez A, Magallanes-Quintanar R, et al. Assessment in Subsets of MNIST Handwritten Digits and their Effect in the Recognition Rate[J]. Journal of Pattern Recognition Research, 2011,2(2): 244-252.
ez A, Magallanes-Quintanar R, et al. Assessment in Subsets of MNIST Handwritten Digits and their Effect in the Recognition Rate[J]. Journal of Pattern Recognition Research, 2011,2(2): 244-252.
[27] Li H, Liu H, Ji X, et al. CIFAR 10-DVS: An Event-Stream Dataset for Object Classification[J]. Frontiers in Neuroscience, 2017, 11.(doi: 10.3389/fnins.2017.00309)
[28] Deng J, Dong W, Socher R, et al. ImageNet: A Large-scale Hierarchical Image Database[C]∥Computer Vision and Pattern Recognition. IEEE Conference on. IEEE, 2009: 248-255.
[29] He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[C]∥IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2016: 770-778.
[30] Krizhevsky A, Sutskever I, Hinton G E. ImageNet Classification with Deep Convolutional Neural Networks[C]∥International Conference on Neural Information Processing Systems. Curran Associates Inc. 2012: 1097-1105.
[31] Szegedy C, Liu W, Jia Y, et al. Going Deeper with Convolutions[C]∥IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2015: 1-9.
[32] Karen Simonyan, Andrew Zisserman. Very Deep Convolutional Networks for Large-scale Image Recongnition[C]∥International Conference of Learning Representation. arXiv: 1409.1556v6[cs.CV] 10 Apr 2015.
[33] Qi X, Wang T, Liu J. Comparison of Support Vector Machine and Softmax Classifiers in Computer Vision[C]∥International Conference on Mechanical. IEEE Computer Society, 2017: 151-155.
[34] 蒋昂波, 王维维.ReLU激活函数优化研究[J]. 传感器与微系统, 2018, 37(2): 50-52.
Jiang A B, Wang W W. Research on Optimization of ReLU Activation Function[J]. Transducer & Microsystem Technologies, 2018, 37(2): 50-52. (in Chinese)
[35] He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[C]∥IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2016: 770-778.
[36] Bordes A, Bottou L, Gallinari P. SGD-QN: Careful Quasi-Newton Stochastic Gradient Descent[J]. Journal of Machine Learning Research, 2009, 10(3): 1737-1754.
[37] Hu J, Shen L, Sun G. Squeeze-and-excitation Networks[J]. arXiv preprint arXiv: 1709.01507, 2017, 7.
[38] Lin L, Higham N J, Pan J. Covariance Structure Regularization via Entropy Loss Function[J]. Computational Statistics & Data Analysis, 2014, 72(3): 315-327.
[39] Huang Y, Cao X, Zhang B, et al. Batch Loss Regularization in Deep Learning Method for Aerial Scene Classification[C]∥Integrated Communications, Navigation and Surveillance Conference. IEEE, 2017: 1-26.
[40] Squartini S, Paolinelli S, Piazza F. Comparing Different Recurrent Neural Architectures on a Specific Task from Vanishing Gradient Effect Perspective[C]∥IEEE International Conference on Networking, Sensing and Control. IEEE, 2006: 380-385.
[41] Pascanu R, Mikolov T, Bengio Y. Understanding the Exploding Gradient Problem[J]. Arxiv Preprint Arxiv: 1211.5063. 2012.
[42] Beck O, Beck O, Purwins H. Convolutional Neural Networks with Batch Normalization for Classifying Hi-hat, Snare, and Bass Percussion Sound Samples[C]∥Audio Mostly. ACM, 2016: 111-115.
[43] Pascanu R, Mikolov T, Bengio Y. On the Difficulty of Training Recurrent Neural Networks[C]∥The 30th International Conference on Machine Learning (ICML 2013), Atlanta, GA, USA, 16-21 June 2013, 2013: 1310-1318.
[44] Hady M F A, Schwenker F. Semi-supervised Learning[J]. Journal of the Royal Statistical Society, 2006, 172(2): 530-530.
[45] Barlow H B. Unsupervised Learning[M]. Encyclopedia of Computational Chemistry. John Wiley & Sons, Ltd, 2002: 72-112.
[46] Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks[J]. Advances in Neural Information Processing Systems, 2014, 3: 2672-2680.
[47] Sabour S, Frosst N, Hinton G E. Dynamic Routing Between Capsules[C]∥Advances in Neural Information Processing Systems, 2017: 3856-3866.
[48] Radford A, Metz L, Chintala S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks[J]. arXiv preprint arXiv: 1511.06434, 2015.
[49] Wang X, Shrivastava A, Gupta A. A-fast-rcnn: Hard Positive Generation via Adversary for Object Detection[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2017.
[50] Zhu J Y, Park T, Isola P, et al. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks[C]∥IEEE International Conference on Computer Vision. IEEE Computer Society, 2017: 2242-2251.
[51] Ledig C, Theis L, Husz r F, et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network[C]∥CVPR, 2017, 2(3): 4.
r F, et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network[C]∥CVPR, 2017, 2(3): 4.
[52] Catgan: Springenberg J T. Unsupervised and Semi-supervised Learning with Categorical Generative Adversarial Networks[J]. arXiv preprint arXiv: 1511.06390, 2015.
[53] Salimans T, Goodfellow I, Zaremba W, et al. Improved Techniques for Training Gans[C]∥Advances in Neural Information Processing Systems, 2016: 2234-2242.
[54] Fiset R, Cavayas F, Mouchot M C, et al. Map-image Matching Using a Multi-layer Perceptron: the Case of the Road Network[J]. Isprs Journal of Photogrammetry & Remote Sensing, 1998, 53(2): 76- 84.
[55] Murray D G, Murray D G. A Computational Model for TensorFlow: an Introduction[C]∥ACM Sigplan International Workshop on Machine Learning and Programming Languages. ACM, 2017: 1-7.
[56] Nguyen V T, Dang T, Jin F. Predict Saturated Thickness using TensorBoard Visualization[C]∥EuroGraphics Workshop on Visualization in Environmental Sciences, 2018.
[57] Cun Y L, Boser B, Denker J S, et al. Handwritten Digit Recognition with a Back-propagation Network[J]. Advances in Neural Information Processing Systems, 1989, 2(2): 396- 404.
[58] Ruder S. An Overview of Gradient Descent Optimization Algorithms[J]. arXiv preprint arXiv: 1609.04747, 2016.
[59] Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[J]. arXiv preprint arXiv: 1502.03167, 2015.
[60] Sun C, Shrivastava A, Singh S, et al. Revisiting Unreasonable Effectiveness of Data in Deep Learning Era[C]∥Computer Vision (ICCV), 2017 IEEE International Conference on. IEEE, 2017: 843- 852.
[61] Phillips P J, Flynn P J, Scruggs T, et al. Overview of the Face Recognition Grand Challenge[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2005: 947-954.
[62] Cao Y, Lee H, Kwon H. Enhanced Object Detection via Fusion with Prior Beliefs from Image Classification[C]∥Image Processing (ICIP), 2017 IEEE International Conference on. IEEE, 2017: 920-924.



