1 引言
在现代无线通信中，正交频分复用(Orthogonal Frequency Division Multiplexing， OFDM)系统以其高频谱效率、灵活的带宽与资源分配等特点，得到了广泛的应用，如第四代移动通信、数字电视地面广播传输系统等[1]。作为一种宽带通信系统，OFDM很容易受到干扰[2]。其中，单音干扰作为一种典型的窄带干扰，可以对OFDM系统的信道误码率造成很恶劣的影响[3]。因此，如何有效抑制在OFDM系统中的单音干扰显得尤为迫切。
单音干扰抑制技术包括干扰频点幅度抑制技术和干扰重构消除技术。其中干扰幅度抑制技术包括干扰频点置零算法[4]，干扰频点限幅算法[5]等。这类技术可以降低单音干扰对系统的影响，却不能改善信道误码率，因此其干扰抑制性能有限。干扰重构消除技术的核心在于干扰参数的估计，其精度直接决定干扰消除后系统的误码性能。通过精确的干扰参数估计与重构，单音干扰可以被基本消除。因此，国内外学者对单音干扰参数估计进行了大量的研究。
单音干扰参数包括幅度、初相和频率。其中频率估计是其他参数估计的基础。单音干扰频率估计算法主要包括相位差分算法和基于离散傅里叶变换(Discrete Fourier Transform， DFT)的算法。其中相位差分算法实现简单，但其估计精度容易受噪声影响，特别是在低干噪比时[6]。基于DFT的算法一般将频率估计分为两步，首先通过DFT得到频率粗估计值，然后通过插值公式得到频率精估计值。文献[7]提出了一种三点插值公式，提高了频率估计精度。文献[8]通过对接收数据补零和一个两点插值公式，进一步提高了频谱分辨率。文献[9]在文献[8]的基础上提出了一种迭代校正算法，提高了频率估计的稳定性。文献[10]结合了加权相位平均(Weighted Phase Average，WPA)算法[11]和DFT，提出了一种DFT-WPA算法，但WPA需要较多的OFDM符号。文献[2]提出了一种DFT-MLE算法，该算法直接对所有接收数据进行DFT，然后进行三点插值，得到精确频率估计值，当OFDM符号较多时，该算法具有较高估计精度，但因其DFT变换点数过多，其计算复杂度较高。
上述频率估计算法只考虑了噪声对频率估计的影响，而没有考虑OFDM调制符号对频率估计的影响。当一次处理多个OFDM符号时，一个数据子载波将对应多个不同的调制符号，根据大数定律，该子载波对应的调制信息近似为一个零均值的噪声。而当一次处理的OFDM符号较少时，特别是只有一个OFDM符号时，大数定律将不能被满足，此时调制符号将对单音干扰参数估计造成较大偏差，从而使干扰消除基本失效，甚至引入新的干扰。为此，本文提出一种利用频域检索的单音干扰消除算法。该算法首先对补零后的接收数据进行DFT，得到干扰频点的粗估计值，然后检索干扰频点附近子载波的调制符号，消除其对单音干扰频域主瓣的影响，然后进行干扰参数估计和干扰消除，根据干扰消除后对应子载波剩余信号与其假设的调制符号组合的欧氏距离，得到最终的调制符号组合，并以此实现精确的单音干扰参数估计和消除。仿真结果表明，新算法可以有效提高单音干扰参数估计精度，实现精确的干扰重构和消除，并可以降低系统误码率。
本文内容安排如下：第2节给出系统模型；第3节介绍现有的一些单音干扰参数估计算法；第4节详细阐述了本文提出的基于频域检索的干扰消除算法；第5节进行了仿真分析；最后对全文进行了总结。
2 信号模型
OFDM信号经过加性高斯白噪声(AWGN，Additive White Gaussian Noise)信道和单音干扰后，基带接收复信号可以表示为
r[n]=s[n]+j[n]+w[n]
(1)
其中s[n]为OFDM信号, j[n]为单音干扰，w[n]为加性高斯白噪声，且w[n]～CN(0，2σ2)。 j[n]可以表示为
j[n]=Ae j (2πfTsn+φ)
(2)
其中f为干扰频率，A为幅度，φ为初相，Ts为采样间隔且Ts=1/fs, fs为采样率。
假设OFDM系统具有N个子载波，循环前缀长度为C，一次处理L个OFDM符号。为提高频谱分辨率，对去除循环前缀后的每个OFDM符号补N个0，然后分别进行2N点DFT变换，则此时第l个OFDM符号的频域信号可以表示为
Rl[k]=Sl[k]+Jl[k]+Wl[k]
(3)
其中k=0，1，…，2N-1，l=0，1，…，L-1，
(4)
(5)
(6)
其中NC=N+C，φl为第l个OFDM符号的初相。
定义f=(km+δ)Δf，其中Δf=fs/2N，km=⎣
故km∈ [0，2N-1)，δ∈ [-0.5，0.5)。因此，式(5)可以简化为
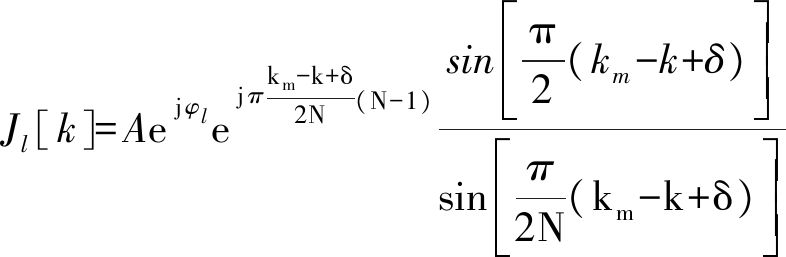
(7)
假设第l个OFDM符号的第k′个调制符号为
则s[lNC+n]可以被表示为
(8)
因此，根据式(4)和式(8)，可得
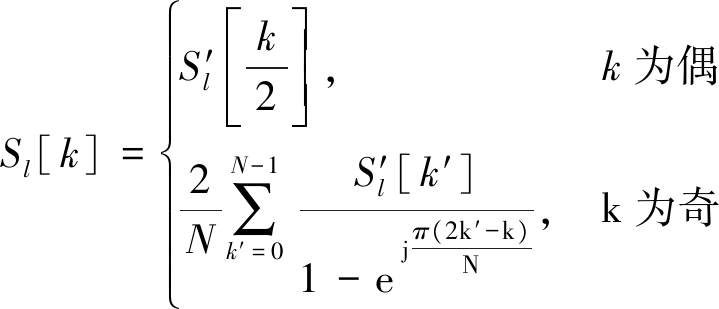
(9)
3 现有单音干扰参数估计算法
本节主要介绍现有的一些单音干扰参数估计算法，包括文献[2]中的DFT-MLE算法，文献[8]中的Fang算法以及文献[10]中的DFT-WPA算法。
3.1 DFT-MLE算法
DFT-MLE算法未对接收数据补零，直接对L个OFDM符号进行NCL点DFT，该算法将频谱R[k]中幅值最大的谱线的位置作为km的估计值
m，如式(10)所示。
(10)
当干信噪比较高时，可认为m=km。然后根据式(11)得到δ的估计值
。
(11)
其中
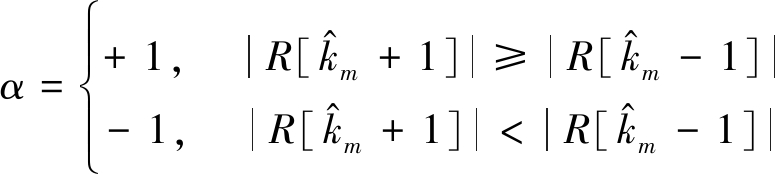
(12)
最后根据式(13)得到Ae j φ的估计值
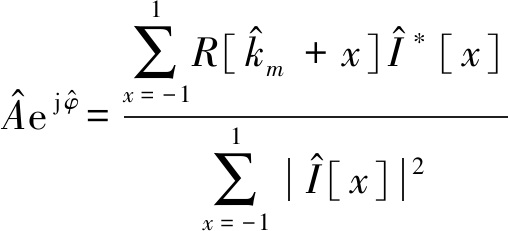
(13)
其中
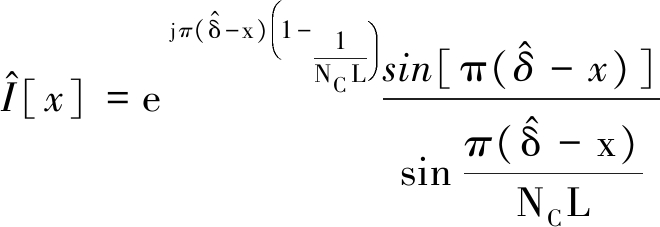
(14)
3.2 Fang算法
Fang算法仅包含频率估计算法，假设对每个OFDM符号分别进行处理。该算法对接收数据补N个0后进行DFT变换，得到2N点频谱Rl[k]，然后根据式(15)得到第l个OFDM符号对应的km估计值m，l。
(15)
当干信噪比较高时，可认为m，l=km。最后根据式(16)得到第l个OFDM符号对应的δ估计值l。
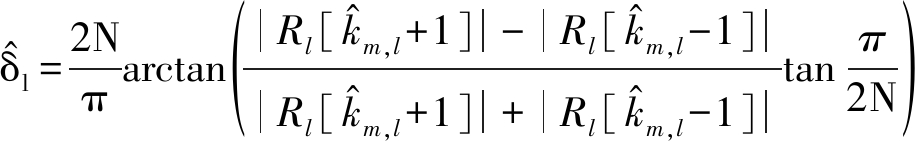
(16)
3.3 DFT-WPA算法
DFT-WPA与Fang算法类似，同样对每个OFDM符号补零后进行2N点DFT，然后根据式(15)得到2N。然后对序列
m，L-1]]进行WPA算法，得到δ的估计值。最后通过利用幅值最高谱线及其左右两根谱线，得到第l个OFDM符号对应的Ae j φl估计值
如式(17)所示。
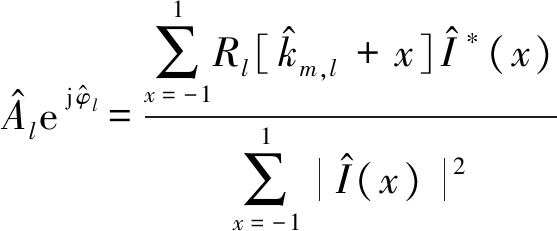
(17)
其中
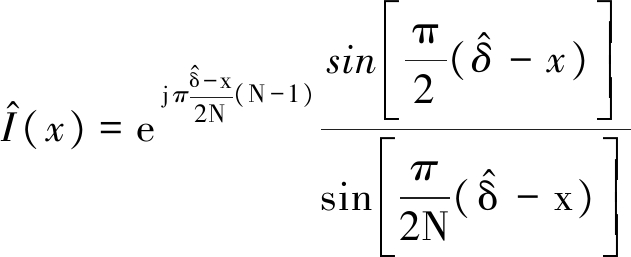
(18)
对所有OFDM符号估计完成后，根据式(19)得到Ae j φ的估计值
。
(19)
4 本文提出的单音干扰消除算法
4.1 新算法原理
现有的单音干扰参数估计算法都没有考虑OFDM系统调制符号对干扰参数估计的影响。当一次处理的OFDM符号较多时，一个子载波将对应多个不同的调制符号，因此该子载波上的调制信息近似为一个零均值的噪声。而当一次处理的OFDM符号较少时，特别是只有一个OFDM符号时，子载波对应的调制信息不能再被视为零均值的噪声，此时直接进行参数估计将会有较大偏差。为此，本文提出一种利用频域检索的单音干扰消除算法。通过充分考虑频域调制符号对干扰参数估计的影响，提高了参数估计的精度。在本节的分析中，假设干扰频点粗估计位置正确，即m，l=km。
本算法分别处理每个OFDM符号，首先利用式(15)得到m，l，再根据式(16)得到δ的初始估计值
根据式(17)得到Ae j φl的初始估计值
然后根据式(20)对干扰进行重构。
(20)
其中n=0，1，…，N-1。故此时可根据式(21)得到干扰消除后的N点频域信号。
(21)
其中k′=0，1，…，N-1。对
进行硬判决，得到初始解调符号
干扰消除后的残余干扰可近似为一个幅度较小的单音干扰。根据式(7)可知，单音干扰主瓣包含了干扰的大部分功率。因此，在忽略噪声时，解调错误仅会发生在km附近的子载波。故可对km附近的子载波的调制符号进行检索，消除调制符号对干扰主瓣的影响。
当进行2N点DFT时，OFDM子载波将位于偶数频点处。因此，当km为奇数时，干扰主瓣将主要影响km-1和km+1子载波频点。故定义检索子载波个数为p，p≤N/2且p为偶数，检索的子载波频点为
假设调制阶数为M，则总共需检索的不同调制符号组合为pM种。设第i组调制符号为
利用式(22)，对
进行更新。
(22)
根据式(9)可知，调制符号在非子载波频点km产生的信息为
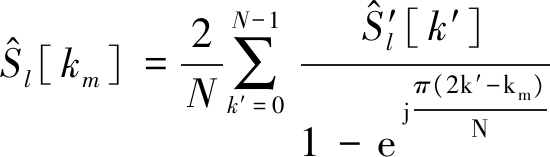
(23)
因此，可根据式(24)，消除调制符号对干扰主瓣的影响，得到去除调制符号影响的
l[km+x]，x=-1，0，1。
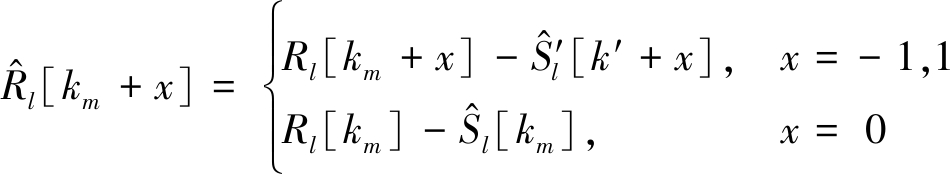
(24)
故此时将l[km+x]分别带入式(16)和式(17)，得到无调制符号影响的δ估计值
和Ae j φl估计值
然后将
带入式(18)，得到
因此，根据式(25)，可重构单音干扰在频点km+1+2d的值。
(25)
其中dm=km+1+2d。最后利用式(26)，得到第i组调制符号所对应的代价函数
。
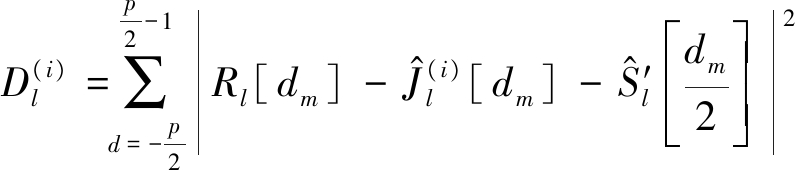
(26)
同理，当km为偶数时，干扰主瓣将主要影响km子载波频点。故定义检索子载波个数为q，q≤N/2且q为奇数，此时总共需检索的不同调制符号组合为qM种。检索的子载波频点为
假设第i组调制符号为
利用式(27)对进行更新。
(27)
然后根据式(28)，得到调制符号在非子载波频点km-1和km+1产生的信息。
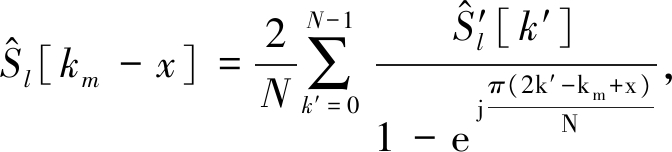
x=-1，1
(28)
因此，可根据式(29)，消除调制符号对干扰主瓣的影响，得到去除调制符号影响的
l[km+x]，x=-1，0，1。
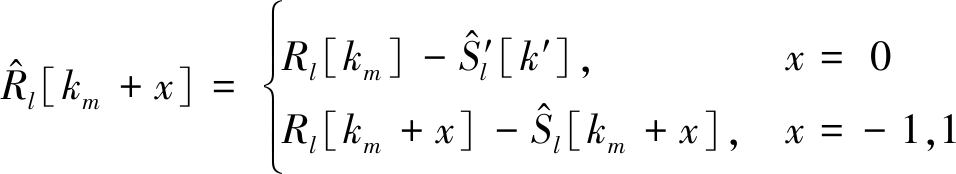
(29)
将l[km+x]分别带入式(16)和式(17)，得到无调制符号影响的δ估计值和Ae j φl估计值
然后将带入式(18)，得到
因此，根据式(30)，可重构单音干扰在频点km+2d′的值。
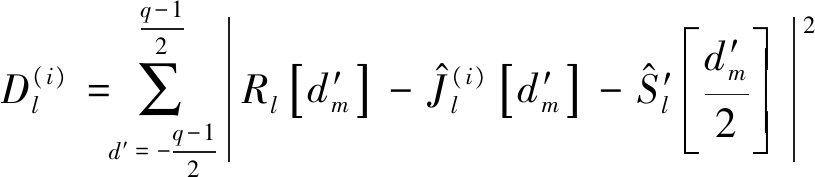
(30)
其中
最后利用式(31)，得到第i组调制符号所对应的代价函数
。
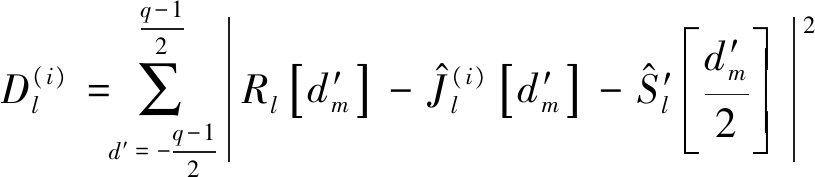
(31)
当所有调制符号组合的代价函数都得到后，根据式(32)得到最佳调制符号组合编号
l。
(32)
当所有OFDM符号的最佳调制符号组合编号l都得到后，则将
和
带入式(33)得到最终的频率估计值和。
(33)
然后根据式(34)，重构干扰信号
[n]。
(34)
其中n=0，1，…，NC-1。最后根据式(35)，得到干扰消除后的接收信号。
[n]
(35)
4.2 计算复杂度
最后，对本算法的计算复杂度进行分析。计算复杂度主要包括复数乘法次数。为简化计算量，可提前存储e j 2πγ的值，其中γ=0，1/Λ，2/Λ，…，(Λ-1)/Λ，Λ为一个较大的整数，此时利用查表法，即可得某个角度θ下e j θ的值。
对每一个OFDM符号，计算点2N点频谱需要2N2次复数乘法，由于N一般较大，可忽略式(16)和式(17)的乘法次数，根据式(20)重构干扰需N次复数乘法，根据式(21)得到N点频谱需N2次复数乘法，然后，针对每一种调制符号组合，当km为奇数时，式(23)需N次复数乘法，由于p一般远小于N，可忽略式(25)和式(26)的乘法次数，同理，当km为偶数时，式(28)需2N次复数乘法，综上所述，当km为奇数时，本算法共需约L[3N2+(1+pM)N]次复数乘法，当km为偶数时，本算法共需约L[3N2+(1+2qM)N]次复数乘法。
DFT-MLE算法对所有接收数据进行DFT，故计算频谱需(NCL)2复数乘法，重构干扰需NCL次复数乘法，再次对每个符号进行N点DFT，得到N点频谱共需LN2次复数乘法次数，故其共需约(NCL)2+NCL+LN2次复数乘法。
DFT-WPA算法需L≥2，对每个OFDM符号进行2N点DFT，共需2LN2次复数乘法，WPA算法共需约L(log2L+2)次复数乘法，重构干扰需约LN次复数乘法，再次对每个符号进行N点DFT，得到N点频谱共需LN2次复数乘法次数，故共需3LN2+L(log2L+2+N)。
表1对这三种算法的计算复杂度进行了对比。由于p或q一般较小，N较大，可认为
或
当调制方式为BPSK、QPSK等较低阶调制方式时，可认为pM<N或2qM<N，故当L≥2时，本文算法的计算复杂度小于DFT-MLE算法，略大于DFT-WPA算法。
表1 算法复杂度对比
Tab.1 Algorithm complexity comparison
算法类型复数乘法本文算法L[3N2+(1+pM)N]或L[3N2+(1+2qM)N]DFT-MLE算法(NCL)2+NCL+LN2DFT-WPA算法3LN2+L(log2L+2+N)
5 性能仿真分析
本节仿真分析了当OFDM符号数L=1和L=4时，本文所提算法与第3节所介绍算法的干扰抑制度和系统误码率。其中干扰抑制度GJ定义为
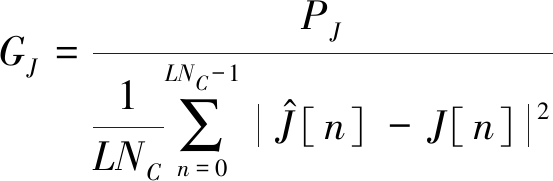
(36)
其中PJ为单音干扰时域功率。干信比定义为PJ/Ps，其中Ps为OFDM符号时域功率。
仿真参数如下：N=128，C=0, fs=2000 Hz, f～U[0, fs)，φ～U[0，2π)，调制方式为BPSK，OFDM符号时域功率Ps=1，干信比PJ/Ps=1，信道为AWGN信道。
图1为L=1时，不同单音干扰算法干扰抑制度对比。由于L=1时DFT-WPA算法无法计算频率估计值，故此处没有对比该算法。从图1可以看出，本文所提算法干扰抑制度远优于DFT-MLE算法，且随着p与q的增大，性能逐渐提升，当p≥4，q≥3时，则几乎不再有性能提升，这是因为离干扰主瓣越远，干扰的影响越小，检索离干扰主瓣越远的子载波的性能增益也越少。
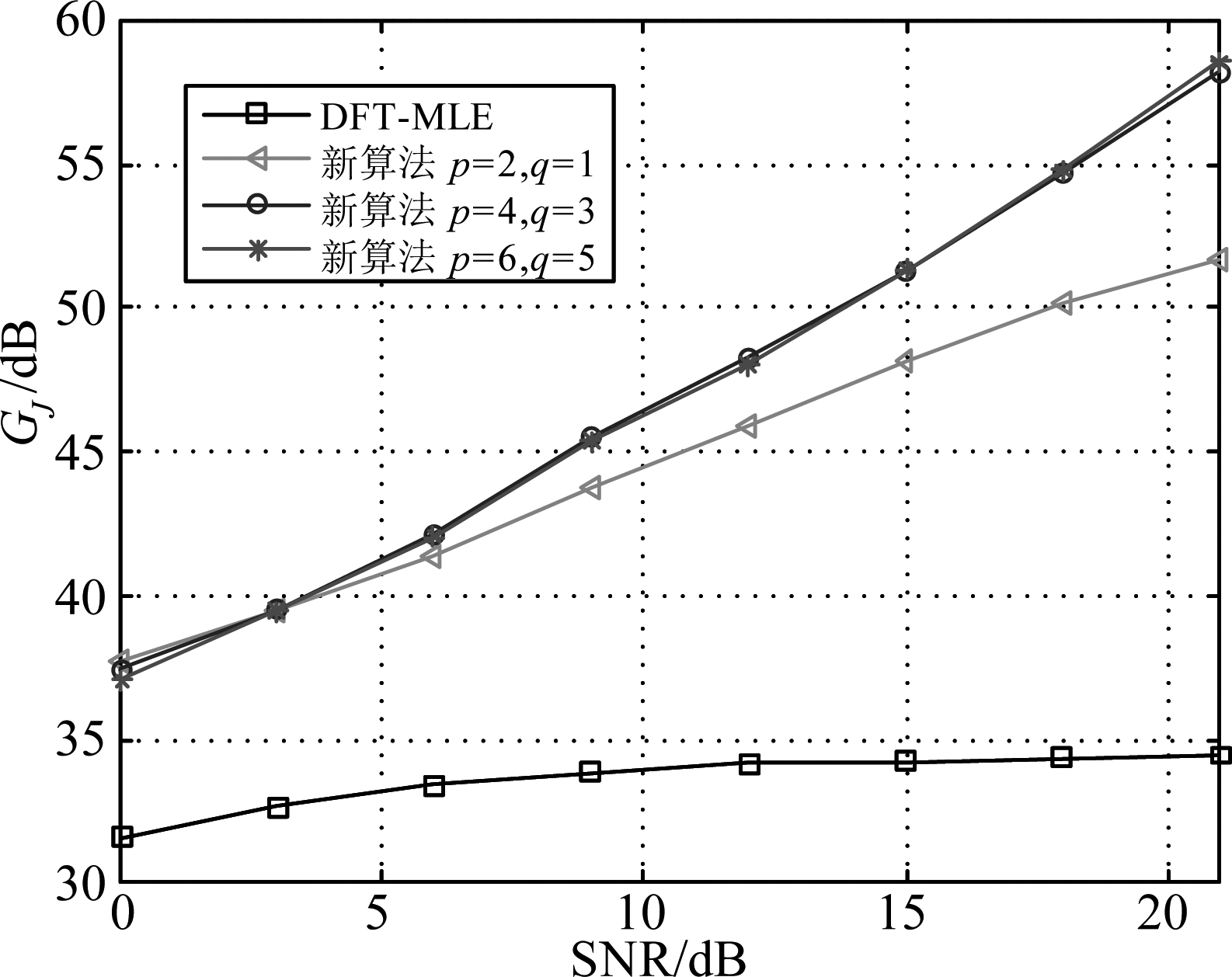
图1 L=1时，不同单音干扰消除算法干扰抑制度对比
Fig.1 Comparison of interference suppression degree of different single-tone interference cancellation algorithms when L=1
图2为L=1时，不同单音干扰算法误码率对比。从图2中可以看出，本文所提算法和DFT-MLE算法都可以降低误码率，然而DFT-MLE算法在SNR>9 dB之后即出现误码平层，这是因为OFDM符号较少时，其调制符号将对DFT-MLE算法的参数估计会产生较大偏差，且该算法不能消除这种偏差，而本文所提算法没有出现误码平层，且误码率低于DFT-MLE算法，随着p与q的增大，本文算法性能逐渐提升，当p≥4，q≥3时，则几乎不再有性能提升，这与干扰抑制度的分析一致。
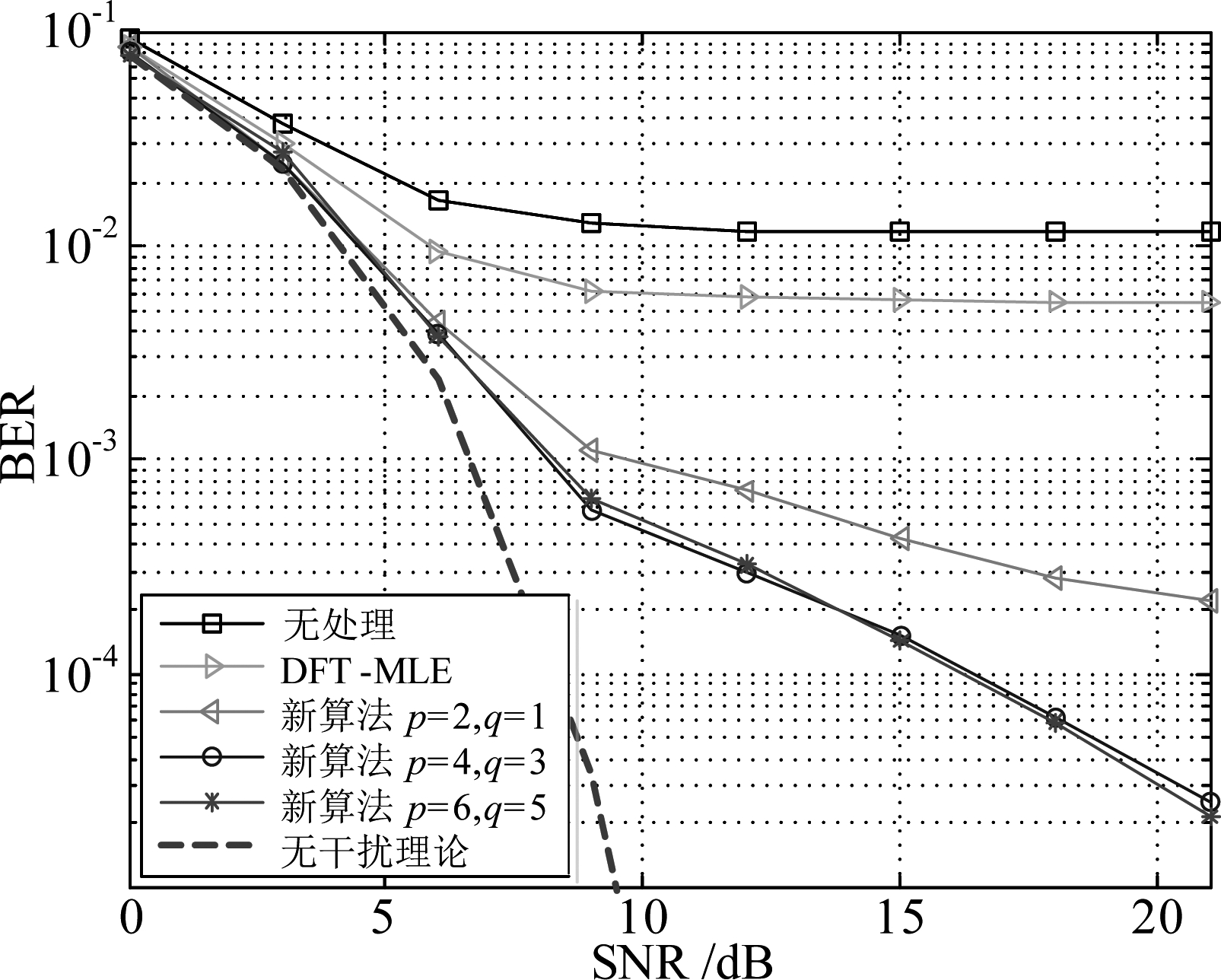
图2 L=1时，不同单音干扰消除算法误码率对比
Fig.2 Comparison of BER of different single-tone interference cancellation algorithms when L=1
图3为L=4时，不同单音干扰算法干扰抑制度对比。从图3可以看出，当SNR<3 dB时，DFT-MLE算法优于本文算法和DFT-WPA算法，这是因为随着DFT点数增多，DFT-MLE算法性能提升。当SNR>3 dB时，本文所提算法优于DFT-MLE算法和DFT-WPA算法，且随着p与q的增大，性能逐渐提升，当p≥4，q≥3时，性能提升将会变得很小。
图4为L=4时，不同单音干扰算法误码率对比。从图2中可以看出，本文所提算法、DFT-MLE和DFT-WPA算法都可以降低误码率，然而DFT-MLE和DFT-WPA算法在SNR>9 dB之后即出现误码平层，而本文所提算法没有出现误码平层，且误码率低于DFT-MLE和DFT-WPA算法，随着p与q的增大，本文算法性能逐渐提升，当p≥4，q≥3时，性能提升将会变得很小，这与干扰抑制度的分析一致。
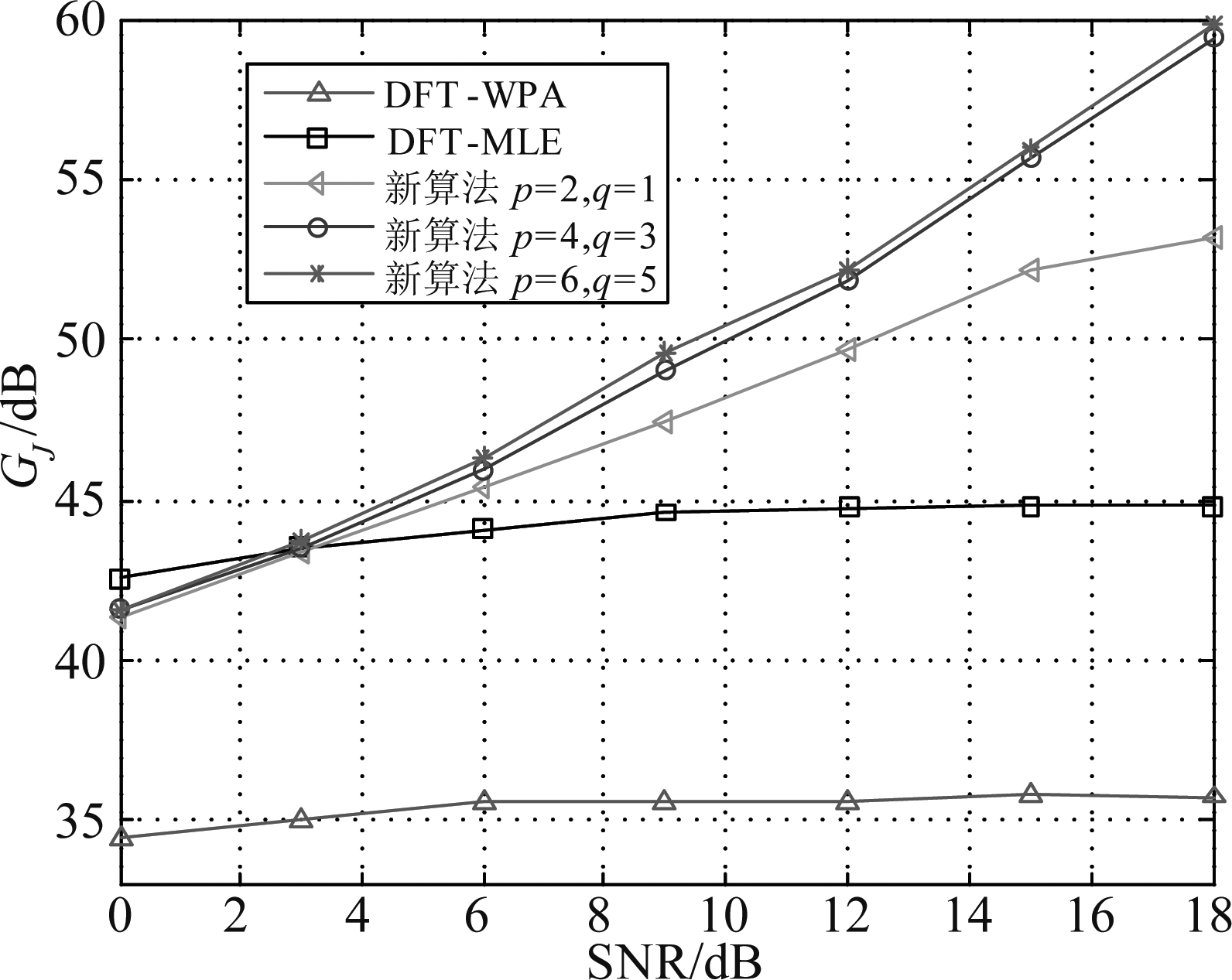
图3 L=4时，不同单音干扰消除算法干扰抑制度对比
Fig.3 Comparison of interference suppression degree of different single-tone interference cancellation algorithms when L=4
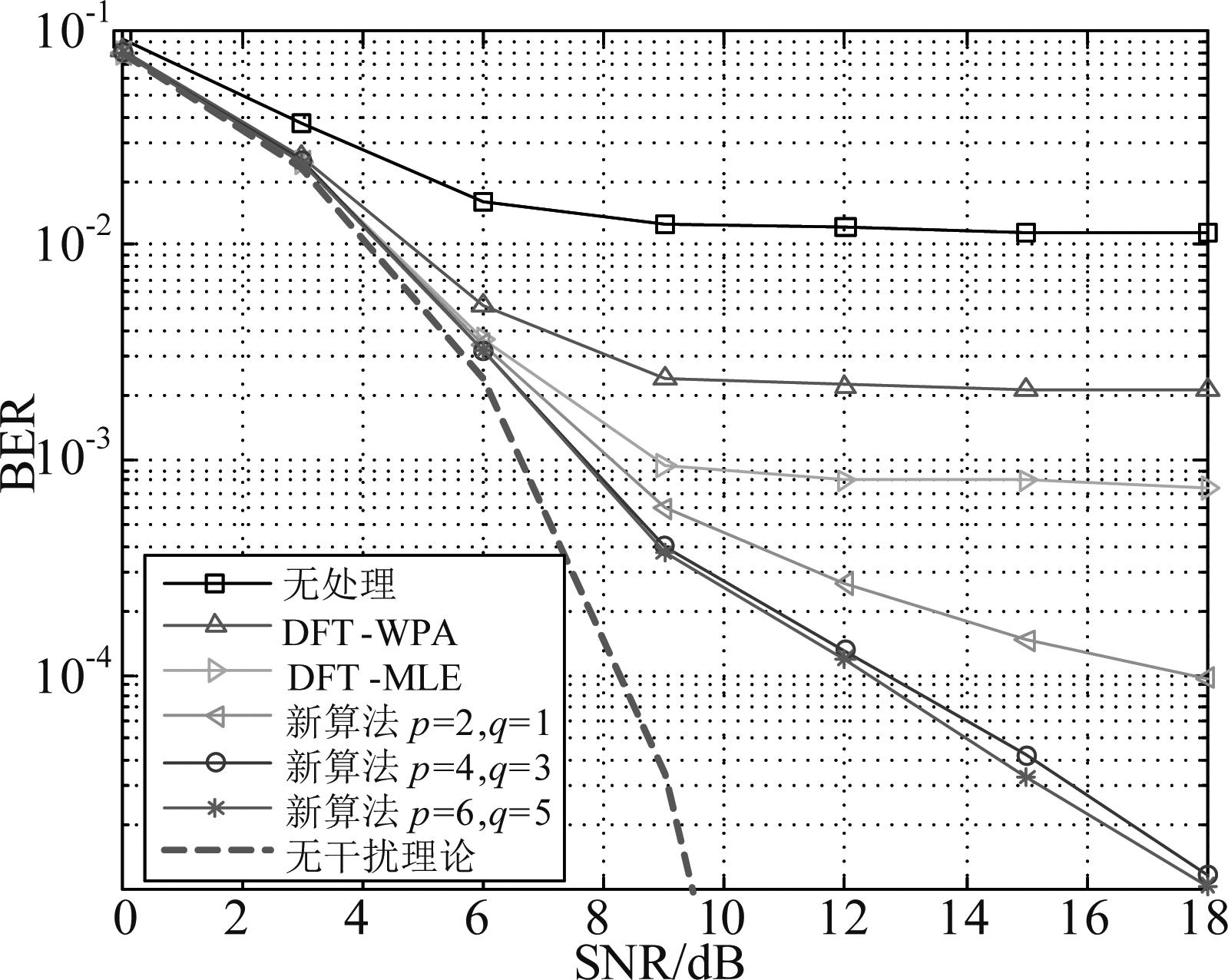
图4 L=4时，不同单音干扰消除算法误码率对比
Fig.4 Comparison of BER of different single-tone interference cancellation algorithms when L=4
6 结论
针对OFDM系统调制符号对单音干扰参数估计的影响，本文提出了一种基于频域检索的单音干扰消除算法。通过对频域中干扰主瓣附近子载波的调制符号进行检索，消除了调制符号对干扰主瓣的影响，提高了干扰参数估计的精度，实现了精确的单音干扰重构与消除，降低了OFDM系统误码率。
[1] Vahidi V, Saberinia E. OFDM high speed train communication systems in 5G cellular networks [C]∥IEEE Annual Consumer Communications & Networking Conference, Las Vegas, NV, 2018: 1- 6.
[2] 王鑫, 张晓林, 曹晏波. 一种基于迭代的多音干扰消除方案[J]. 北京航空航天大学学报, 2017, 43(3): 573-582.
Wang Xin, Zhang Xiaolin, Cao Yanbo. A multi-tone interference cancellation scheme based on iteration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 573-582. (in Chinese)
[3] 熊李娜, 李涛, 梅林, 等. OFDM系统的抗窄带干扰性能分析[J]. 通信技术, 2011, 44(10): 25-26, 29.
Xiong Lina, Li Tao, Mei Lin, et al. Performance of OFDM System under Narrow-band Interference[J]. Communications Technology, 2011, 44(10): 25-26, 29. (in Chinese)
[4] 黄李峰, 田亚飞. OFDM系统中基于最优门限选取的窄带干扰抑制方法[J]. 信号处理, 2015, 31(3): 259-266.
Huang Lifeng, Tian Yafei. Narrowband Interference Suppression Based on Optimal Threshold Selection in OFDM Systems[J]. Journal of Signal Processing, 2015, 31(3): 259-266. (in Chinese)
[5] 孙永军, 易克初. 直接序列扩谱CDMA系统中盲窄带干扰抑制[J]. 系统仿真学报, 2007, 19(16): 3756-3760.
Sun Yongjun, Yi Kechu. Blind Suppression of Multiple Narrowband Interferences in DSS/CDMA Systems[J]. Journal of System Simulation, 2007, 19(16): 3756-3760. (in Chinese)
[6] Lang S W, Musicus B R. Frequency estimation from phase differences [C]∥International Conference on Acoustics, Speech, and Signal Processing, Glasgow, 1989: 2140-2143.
[7] Candan C. A Method For Fine Resolution Frequency Estimation From Three DFT Samples [J]. IEEE Signal Processing Letters, 2011, 18(6): 351-354.
[8] Fang L, Duan D, Yang L. A new DFT-based frequency estimator for single-tone complex sinusoidal signals[C]∥IEEE Military Communications Conference, Orlando, FL, 2012: 1- 6.
[9] 柏果, 程郁凡, 唐万斌, 等. 利用DFT和迭代校正的正弦信号频率估计算法[J]. 信号处理, 2017, 33(12): 1536-1541.
Bai Guo, Cheng Yufan, Tang Wanbin, et al. A Frequency Estimation Algorithm of Sinusoidal Signal Capable of DFT and Iterative Correction[J]. Journal of Signal Processing, 2017, 33(12): 1536-1541. (in Chinese)
[10] 王桁瑶, 张晓瀛, 王杉. 单音干扰下OFDM系统中频域迭代干扰消除算法[J]. 信号处理, 2016, 32(10): 1169-1177.
Wang Hengyao, Zhang Xiaoying, Wang Shan. A Frequency-Domain Iterative Cancellation Algorithm for Single-Tone Interference in OFDM Systems[J]. Journal of Signal Processing, 2016, 32(10): 1169-1177. (in Chinese)
[11] Kay S. A fast and accurate single frequency estimator[J]. IEEE Transactions on Acoustics, 1989, 37(12): 1987-1990.
