1 引言
作为数字盲信号处理的关键技术之一，信号载频与符号率估计是通信信号调制识别、盲源分离以及盲解调等技术的基础，也是非协作通信中对未知先验信息的信号分析处理的首要步骤之一。非协作通信是指第三方在未经授权的条件下接入通信系统，并在保持通信双方正常通信的前提下，处理并分析侦察信号，广泛的应用于军事通信信号侦察领域[1]。传统的信号盲参数估计算法大多基于高斯模型，对于非协作通信，非协作端侦察信号的环境一般较差，尤其是在战场无线网中，信号受到复杂电磁环境、多用户干扰等人为因素以及大气噪声、海杂波噪声等环境因素影响，噪声模型不再符合正态分布，反而表现出不规矩的脉冲特性与厚拖尾特性[2]。针对这类噪声，高斯模型下的盲参数估计算法性能普遍较差，甚至完全失效。学者们研究发现，Alpha稳定分布模型通过调节特征参数可以有效的模拟自然界中不同脉冲噪声环境，且满足广义中心极限定理，在盲信号处理领域得到了广泛的应用[3]。
信号载波估计与符号率估计算法的研究由来已久，常见的算法有最大似然法、最小二乘法、平方包络法、小波变换法等[4]。对于循环平稳信号，研究较多的主要是根据循环特性估计信号参数，包括循环自相关、循环谱密度以及循环相干系数等。文献[5]分析了升余弦脉冲成型滤波对信号循环谱密度的影响，提出了一种符号率估计算法。文献[6]系统的分析了几种循环平稳信号(ASK,PSK,FSK等)在高斯噪声下的循环谱密度函数，实现了各种信号的载频与符号率估计。但上述算法均基于二阶循环矩推导，并不适用于脉冲噪声。结合分数低阶理论，文献[7]提出了一种适用于MPSK联合参数估计算法，根据循环谱密度函数的不同切面估计MPSK信号的码速率与载波频率，但是该算法并不适用于MQAM信号。文献[8]针对MQAM信号，通过广义化二阶矩，提出了一种基于广义平方包络谱的符号率估计算法。在不改变信号相位特性的前提下抑制信号的幅度，类似于循环谱估计，但是在计算量相当的条件下，无法同时对信号载频进行估计。
上述研究中基带信号大多为矩形脉冲成型，但由于带宽的限制，实际通信系统中一般采用升余弦脉冲成形滤波器[5]。同时，作为数字通信系统中的主要调制方式之一，迄今为止，针对脉冲噪声下的MQAM信号的基于分数低阶谱的参数估计研究鲜有报道，因此在升余弦脉冲成型的前提下研究 MQAM信号的参数估计更具有现实意义。
2 脉冲噪声下分数低阶循环谱
2.1 脉冲噪声模型
Alpha稳定分布在盲信号处理中的应用最早来源于C.L.Nikias等人[3]，经过学者们数十年的研究，被认为是模拟脉冲噪声的最佳模型。本文采用标准α稳定分布模型(symmetric α-stable,SαS)来模拟脉冲噪声，其特征函数可表示为：
φ(t)=exp(jδt-γ|t|α)
(1)
其中α∈[0,2)为特征指数，用于度量SαS分布的脉冲突刺程度与拖尾厚度，其值越小，脉冲突刺程度越强，拖尾越薄；δ∈(-
，)为位置参数，对应于高斯分布的均值，当0<α<1时，δ为中值；当1<α<2时，δ为均值；分散系数γ∈(0，+)，对应于高斯分布的方差，主要用于描述SαS分布偏离均值的程度。除了高斯分布(α=2)和柯西分布(α=1)等几种特殊情况外，SαS分布不具有封闭的概率密度函数，但是可以通过幂级数展开式来表示标准平稳密度函数[3]：
(2)
其中Γ(x)=
tx-1e-tdt为Gamma函数。如图1和2所示，分别表示不同α取值条件下的SαS分布的时域波形与概率密度函数。
2.2 共变与低阶循环谱定义
由于SαS分布不具有有限的二阶及二阶以上矩，因此在研究此类信号时常采用分数低阶矩，其定义为：
E[|X|p]=C(p,α)γp/α, 0<p<α
(3)
其中C(p,α)为与分数阶p和特征参数α相关的常数。在此基础上，研究循环平稳信号的低阶循环平稳特性需要引入共变的概念，假设周期为T的循环平稳信号为x(t)，定义其p阶共变为[10]：
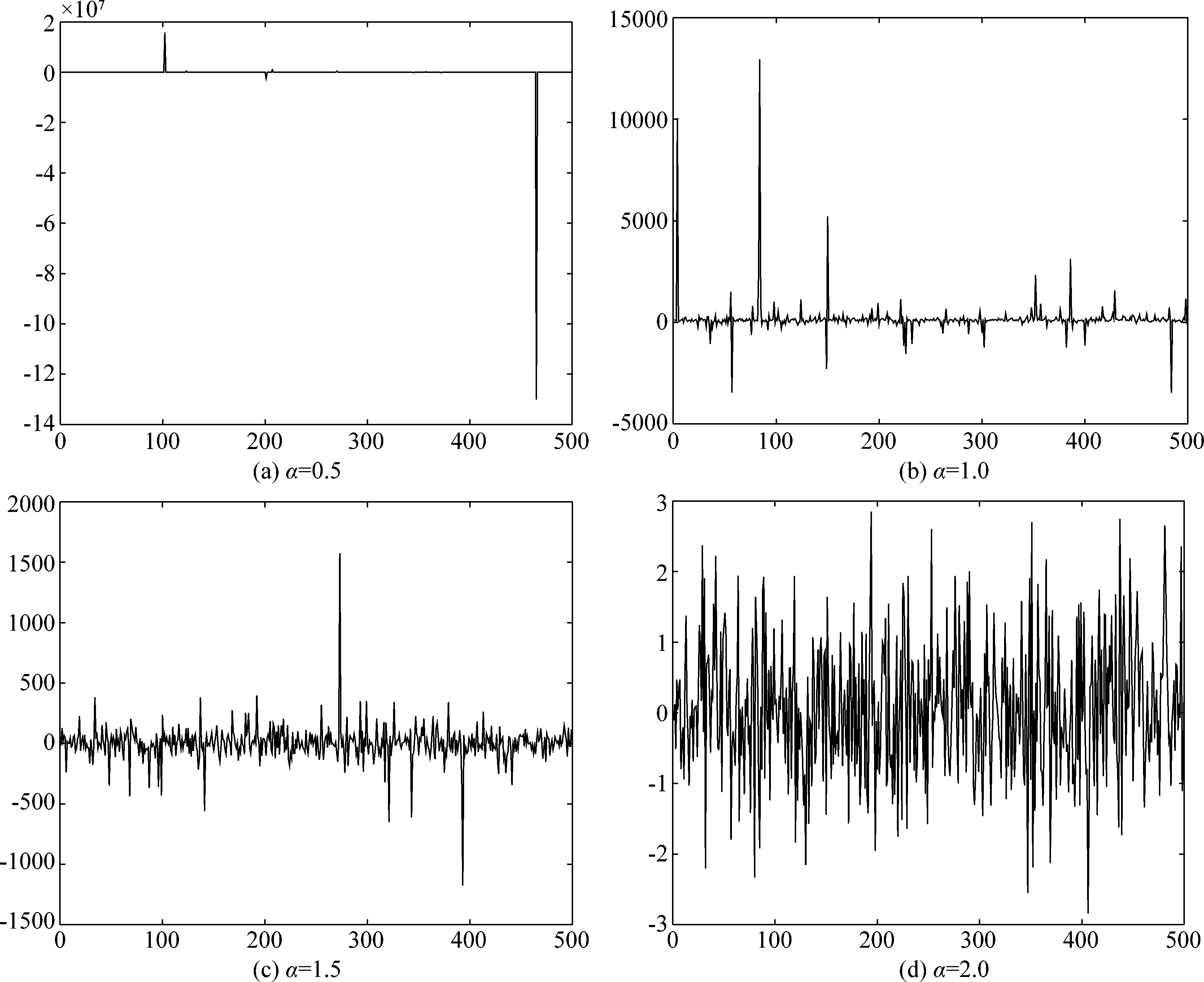
图1 不同α值时的时域波形
Fig.1 Time domain waveform at different α values
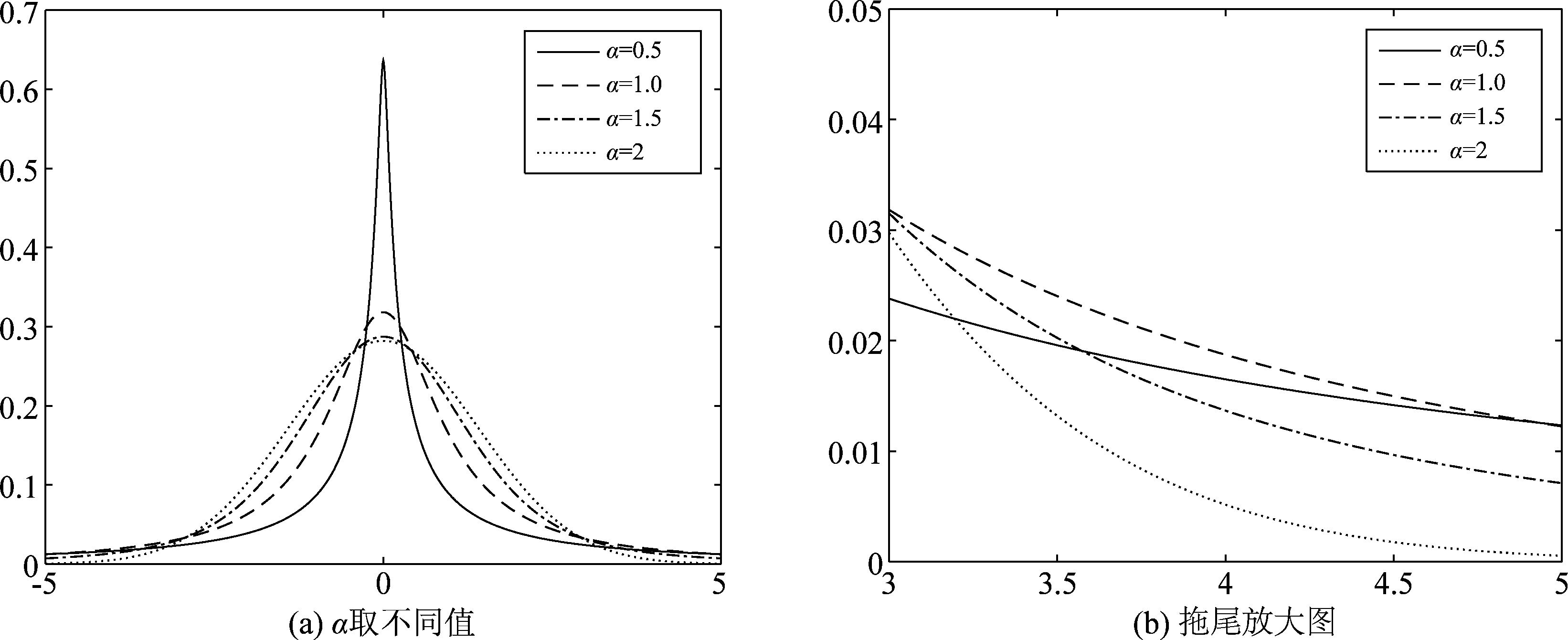
图2 不同α值的SαS概率密度曲线
Fig.2 The probability density curve of SαS different α values
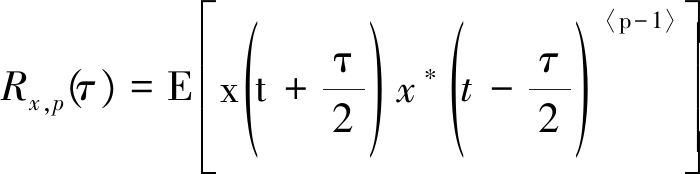
(4)
其中阶数p∈[1,α)，且对于复信号有x(t)〈p〉=|x(t)|p-1x*(t)，将式(4)按照傅里叶级数展开，其系数即为分数低阶循环自相关函数：
dt
(5)
其中ε为循环频率，功率谱为自相关函数的傅里叶变换，因此信号x(t)的分数低阶循环谱密度函数为：
(6)
3 MQAM信号分数低阶谱推导
设经过升余弦脉冲成型的MQAM信号模型为：
=νI(t)cos(2πfct)-νQ(t)sin(2πfct)
(7)
其中，νn=νI,n+jνQ,n为独立同分布的MQAM星座点，Tb为信号符号率，fc为信号载波频率。qrc(t)=g(t)⊗hr(t)表示成型脉冲，g(t)表示宽度为Tb的窗函数，hr(t)为升余弦脉冲成形滤波器。其冲激响应为：
(8)
且
为信号同相分量，
为正交分量。由共变系数的性质[10]，以同相分量为例，可以近似推导得到：
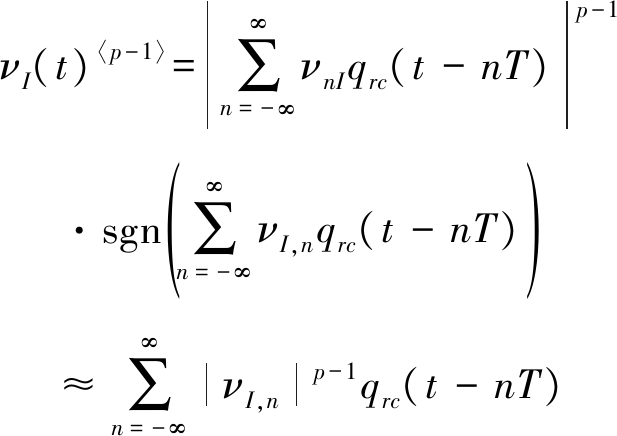
(9)
由于νI,n与νQ,n是独立同分布的，且取值均为实数，则有
E(νI,m+n|νI,n|〈p-1〉)=E(νI,m+n|νI,n|〈p-1〉)
(10)
为方便表示，令
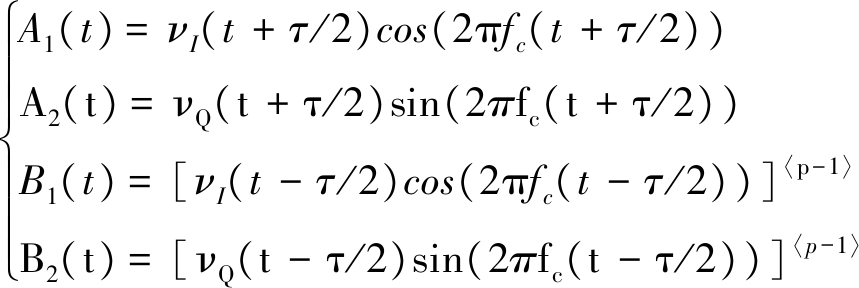
(11)
根据式(9)、(10)、(11)，MQAM信号的p阶共变可表示为：
Rx,p(τ)=E{[A1(t)-A2(t)][B1(t)-B2(t)]*}
=KpRν,p(m)cos(2πfcτ)Rq(t,τ)
(12)
上式中Kp=|cos(2πfc(t-τ/2))|p-2=|sin(2πfc(t
-τ/2))|p-2，且令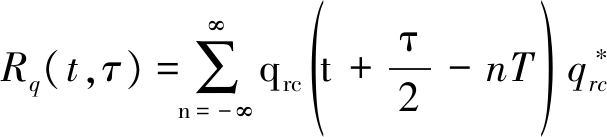
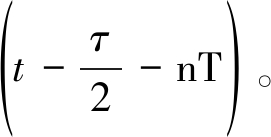因此MQAM信号的循环自相关函数为[11]：
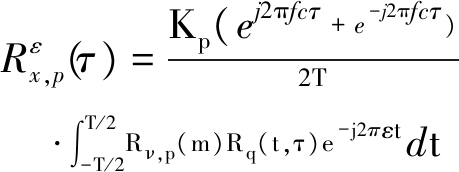
(13)
对式(13)进行傅里叶变换，则推导出MQAM的分数低阶循环谱密度函数为：
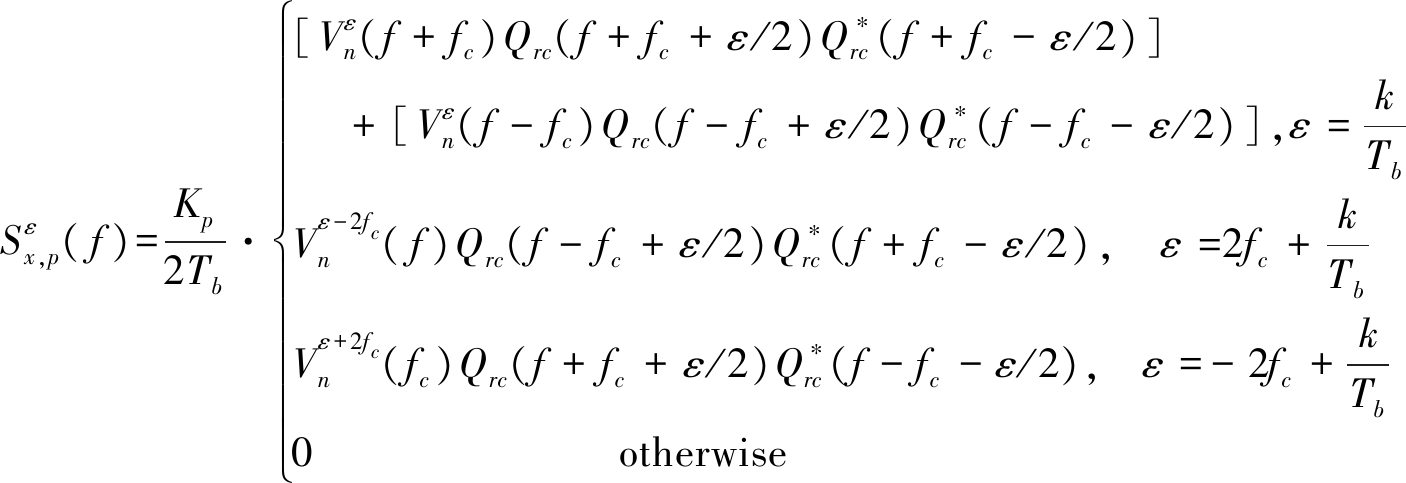
(14)
上式中
为νn的循环谱密度，成型滤波qrc(t)的傅里叶变换为[6]：
(15)
循环谱密度函数具有对称性，即：
因此，由分析可知，升余弦脉冲成型对信号起到了带限作用，不考虑噪声时，在f=0的循环谱切面上，MQAM信号仅在ε=±2fc处取得非零值；在f=±fc循环谱切面上，仅在ε=0，±1/Tb处取得非零值，且Alpha稳定噪声不具有循环平稳特性，可以以此为依据来估计MQAM信号的载波频率与符号率。
4 载频与符号率联合估计
谱估计算法作为研究循环平稳信号特性的重点，主要可以分为时域平滑与频域平滑两类算法。在实际频谱检测中，用作参数估计的接收信号样本为有限长数据，时域平滑类算法无法有效获取高分辨率的谱切面，为了实现依据信号的循环谱切面进行参数估计，一般采用数字频域平滑方法(DFSM)[12]。文献[13]提出了一种基于数据加窗的改进平均频域平滑算法(MAFSM)，利用数据重用的方法，根据较少数据量实现较高分辨率的谱估计，但是该算法引入了很大的运算量，并不适合实际应用。本文根据结合共变理论与分数低阶矩对SαS分布噪声下的DFSM算法表达式进行了推导，假设离散化的MQAM信号{x(n)}，且数据长度为N，其DFSM谱估计表达式为：
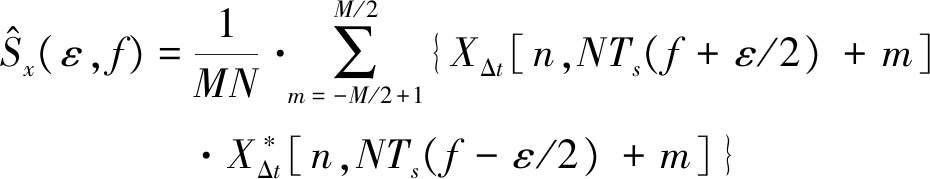
(16)
其中
，M为频域平滑窗长度，Ts为采样周期，wN(m)为长度为N的窗函数。但是上述表达式是针对高斯模型，当MQAM信号中存在特征参数为α的SαS分布噪声时，离散MQAM信号{x(n)}的分数阶短时复频谱运算可以表示为[14]：
(17)
将式(17)带入(16)，结合共变理论与分数低阶循环谱，则可以推导出基于分数低阶矩的DFSM算法：
·x*
(18)
其中WN(i,l)=wN(iTS)·wN(lTS)。算法的循环频率分辨率为Fn=1/NTs=1/Δt，谱频率f的取值间隔为Δf=MFn。因此可知ΔtΔf=M≫1。根据文献[5]中的分析，离散频域平滑法在计算谱估计时，设离散频域平滑法的两个平滑窗中心位置分别为f1=f0+ε0/2与f2=f0-ε0/2，则由于平滑窗中心移位时产生的循环频率差ε0的取值间隔为2Fn，对于有限长数据的离散循环谱估计分辨率不够高时，依据不同循环谱切面的信息来估计符号率与载频，会出现误判，从而影响估计精度，因此本文通过相邻谱切面累加取平均的方法来避免因为离散算法分辨率不足带来的误差。针对MQAM信号而言，以载频为例，分别在f=0、 f=±MFn切面上提取载频信息，计算平均值作为估计载频。类似的根据估计的MQAM信号载频
取
与
切面提取信号符号率信息。因此，本文所提出的载频与符号率估计算法步骤如表1所示。
表1 本文算法实现步骤
Tab.1 The algorithm implementation steps in this paper
Step1 计算离散MQAM信号{x(n)}的p-1(0
5 仿真实验与分析
为验证本文算法的性能，采用不同条件的SαS稳定分布模拟脉冲噪声。假设MQAM信号符号率为fb=40 kB，即符号周期为Tb=2.5×10-4的基带信号，经过采样率为400 kHz，滚降因子为0.8的升余弦脉冲成型滤波器后，并加入频率为fc=100 kHz的载波。
实验1
比较相同脉冲噪声下，本文提出的基于分数低阶循环谱估计算法与传统二阶DFSM循环谱估计算法对脉冲噪声的抑制性能。实验采用16QAM信号通过α=1.5的SαS噪声，广义信噪比为GSNR=5 dB，分数低阶矩为p=0.01，频域平滑点数M=64，循环谱检测的采样点数为N=4096，考虑到盲参数估计时，信号接收端的未知发射端脉冲成型滤波时的采样率，因此接收端对信号采样时，假设采样率为待估参数的非整数倍，即fs=450 kHz。
比较图3、图4可以看出，本文提出的分数低阶循环估计算法在α=1.5的SαS噪声条件下，较好的抑制脉冲噪声的影响，如图3(b)、(c)所示，在f=0切面与切面均可以提取有效的信号参数信息，同时这也印证了第2节中关于MQAM信号的分数低阶循环谱切面的分析。而图4中所示的基于二阶自相关的DFSM循环谱估计算法无法抑制噪声中的脉冲特性，循环谱噪底明显要高于文本算法。在f=0切面上仍可以估计出载波频率，但是误差较大，在f=fc切面，MQAM信号的符号率信息完全被噪声淹没，无法进行有效的估计。
实验2
在不同α值的SαS噪声下，分别比较本文算法、基于二阶循环谱估计算法与文献[15]算法估计载波频率的精度；比较本文算法、基于二阶循环谱估计算法与Haar小波变换法的符号率估计精度。其中文献[15]中提出的基于广义四阶循环累积量的混叠信号载波估计算法，通过非线性变换抑制脉冲噪声，然后根据高阶统计量中的参数信息估计信号载波，本文考虑在单信号的条件下比较算法的性能；Haar小波变换法首先对信号进行多尺度Haar小波变换，根据其模值的边界暂态特性估计信号符号率。本实验采用16QAM信号，且参数与实验1相同，GSNR=0 dB，进行100次蒙特卡罗实验。采用归一化均方根误差(RMSE)来评价算法的估计性能，其定义为：
(19)
其中
表示估计值，X表示待估参数的期望值。由于自然界中不并存在α<1的脉冲噪声，因此本实验采用α取值分别为1.0、1.25、1.50、1.75、2.0的SαS噪声条件，表2、表3分别是各算法的载波估计结果与符号率估计结果。
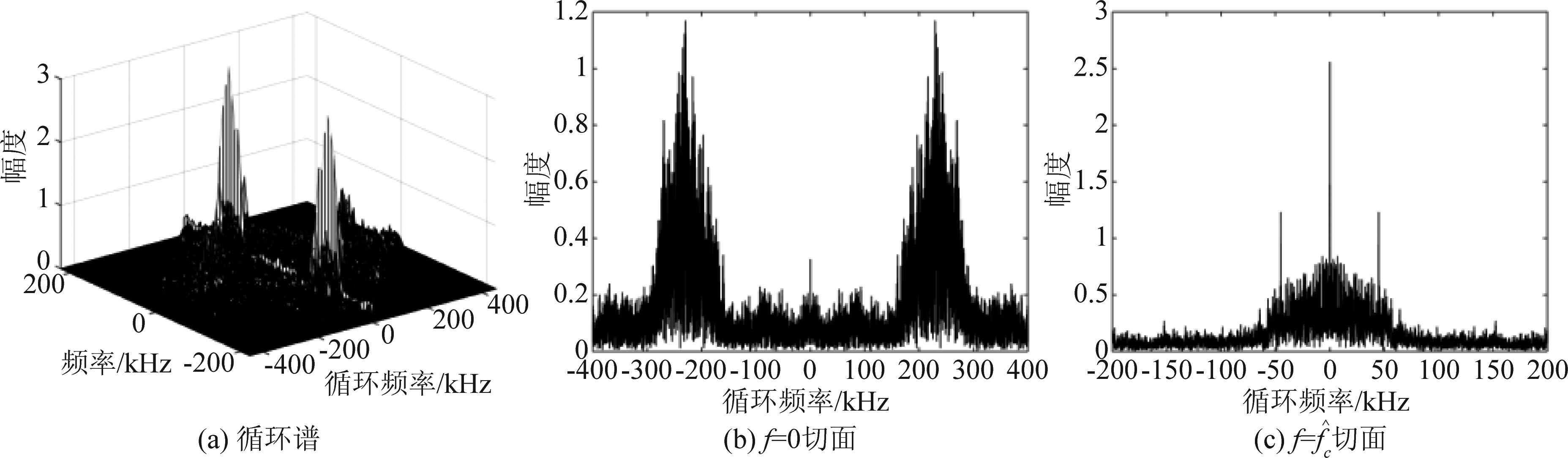
图3 本文算法的循环谱及切面
Fig.3 The circular spectrum and the surface of the algorithm in this paper
图4 二阶DFSM循环谱及其切面
Fig.4 The circular spectrum and the surface of the second-order DFSM
表2 SαS噪声下载频估计的RMSE
Tab.2 The RMSE of carrier frequency under SαS noise
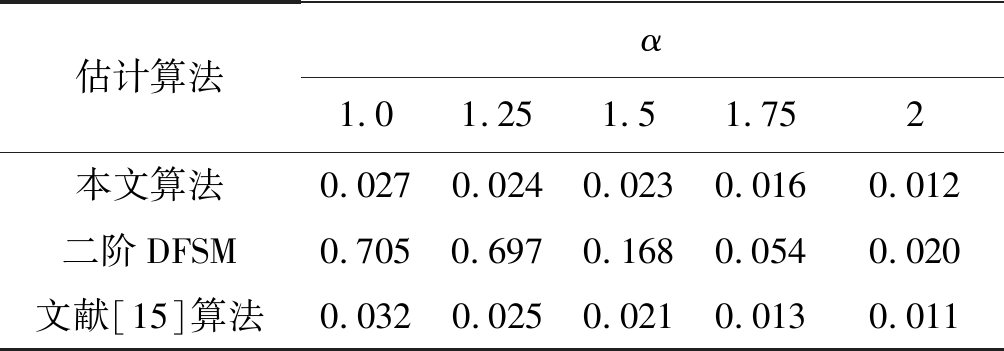
估计算法α1.01.251.51.752本文算法0.0270.0240.0230.0160.012二阶DFSM0.7050.6970.1680.0540.020文献[15]算法0.0320.0250.0210.0130.011
表3 SαS噪声下符号率估计的RMSE
Tab.3 The RMSE of symbol rate under SαS noise
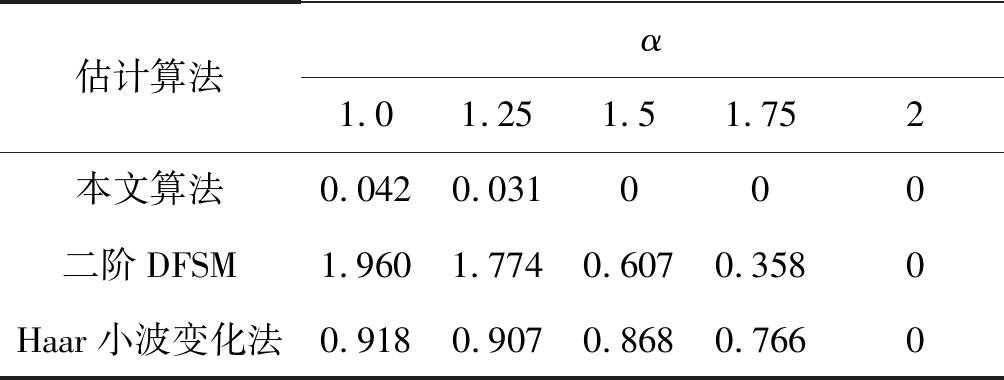
估计算法α1.01.251.51.752本文算法0.0420.031000二阶DFSM1.9601.7740.6070.3580Haar小波变化法0.9180.9070.8680.7660
SαS分布模拟脉冲噪声时，α值越大，脉冲冲激程度越小，当α=2时，SαS分布转化为高斯噪声模型。从表2、表3中可以看出，受到脉冲噪声冲激特性的影响，二阶DFSM循环谱估计算法在α<2时，载频与符号率估计的RMSE均较大，而本文算法在不同冲激程度的脉冲噪声下参数估计性能相对较为稳定，载频与符号率估计的RMSE随着α值增大而减小。Haar小波变换法在脉冲噪声下的符号率估计性能较差，无法实现有效估计。文献[15]算法对信号进行非线性变换时仅改变了幅度信息，能够在抑制脉冲噪声的条件下有效的估计信号的载波频率，由表2可知，该算法的载波估计性能与本文算法相近，但是本文能同时精确的估计信号符号率。
一般而言，算法中乘法运算主要决定了计算复杂度。根据文献[15]的分析，计算N点数据时，基于广义四阶循环累积量的算法需要7N+Nlog2N复数乘法运算；运用传统二阶DFSM算法的循环谱估计时需要进行
次复数乘法[16]，而本文通过将分数低阶统计量引入循环谱估计，需要首先计算信号的p阶矩，实际上相当于非线性变换，即仅额外增加了N次复数乘法运算，但是算法对于载频与符号率的估计精度显著提升。
实验3
比较不同数据量对本文算法估计准确率的影响，实验分别采用采样点数为N=2048、4096、8192时的16QAM信号进行仿真分析，由于平滑窗长度M=64，则算法的循环谱的循环频率和频率的切片数分别为32、64、128。其余参数设置与实验1相同，进行100次蒙特卡罗实验，假设参数估计的RMSE小于0.05，则视为准确估计。采用估计准确率来评价算法的估计性能，其定义为：
(20)
由图5可知，当N=2048时，数据量较少，本文算法的估计信号载频和符号率的性能较差，在GSNR<0时，准确率均较低。当用于估计的采样点数量增加时，明显可以看出，算法估计准确率变高。而相比于N=4096，当数据量增加到8192时，估计准确率仅仅有少许增加，但是数据量的增加，会明显加大计算复杂度。
实验4
在相同SαS噪声环境中，比较不同的广义信噪比下本文算法与二阶DFSM循环谱估计算法的载频及符号率估计性能，分别采用4QAM、16QAM、64QAM信号进行实验。本实验中α=1.5，信号的其他调制参数及算法的估计参数均与实验1中相同。
图5(a)、(b)分别为不同信噪比下算法的载频估计与符号率估计的准确率。如图5(a)所示，对于相同的调制阶数的MQAM信号而言，本文算法的载频估计准确率远高于传统二阶DFSM算法，在GSNR≥-2 dB时，估计准确率均达到了85%以上。 根据图6，以16QAM信号为例，GSNR≥-6 dB时，在相同的脉冲噪声条件下，本文算法的符号率估计准确率明显高于二阶DFSM算法，且在GSNR≤0 dB时，二阶DFSM算法无法抑制噪声中的脉冲特性，估计准确率均低于30%，而从GSNR=-2 dB本文算法的估计准确率就达到了90%以上。
当MQAM信号的调制阶数增大，算法的性能均有所下降，这是因为随着调制阶数的增加，MQAM符号点间的欧式距离减小，脉冲噪声下各个符号点互相干扰的概率变大，导致本文算法的参数估计准确率下降，但相比于4QAM与16QAM调制信号，本文算法对于64QAM调制信号在GSNR=-2 dB时仍具有较高的载频与符号率估计准确率。因此，结合上述分析，本文提出的基于分数低阶矩的MQAM载频与符号率估计算法，对脉冲噪声的抑制效果较好，即使在信噪比较低的情况下仍能够有效的估计出MQAM信号的参数信息。
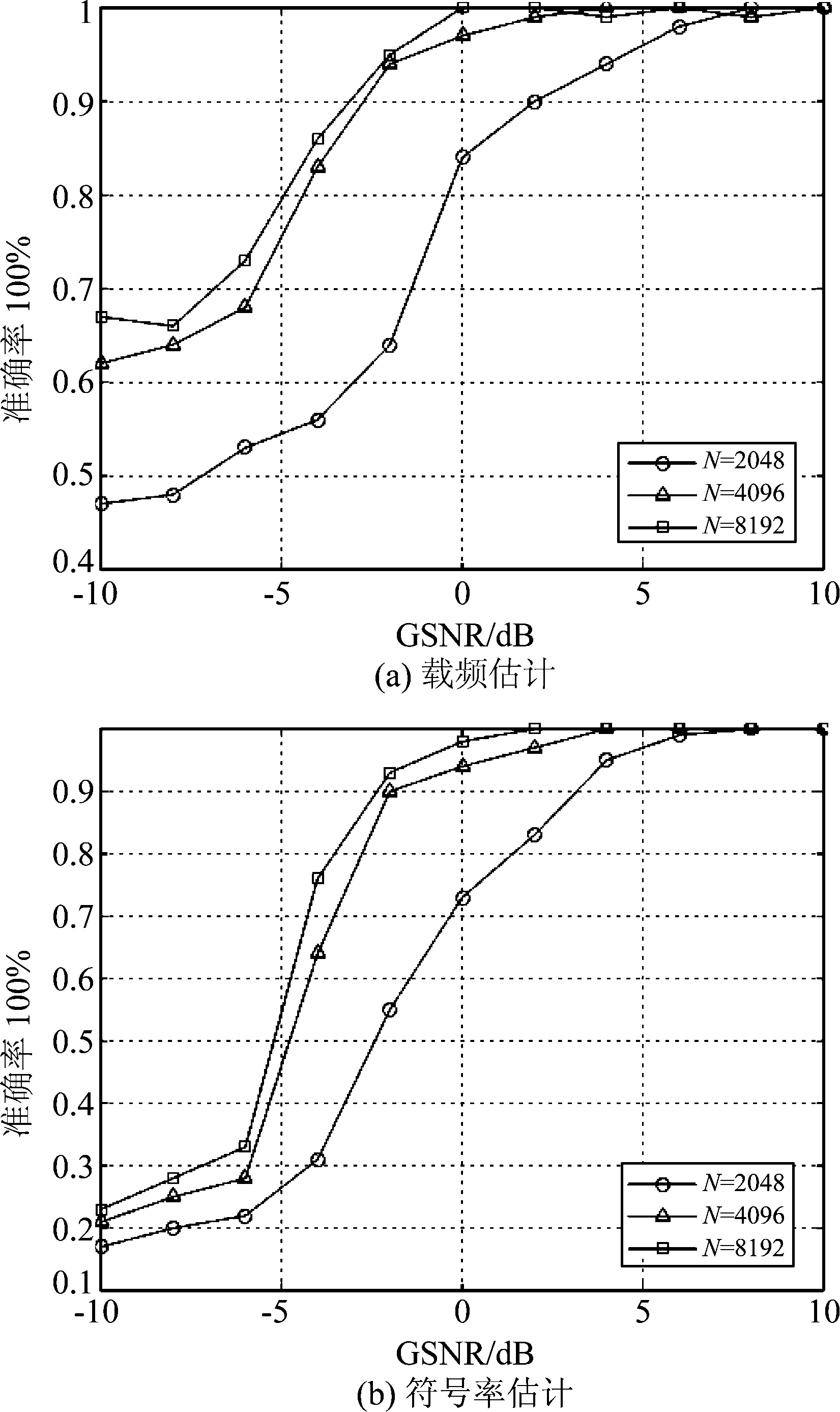
图5 不同数据量下的算法估计准确率
Fig.5 The estimation accuracy under different data volumes
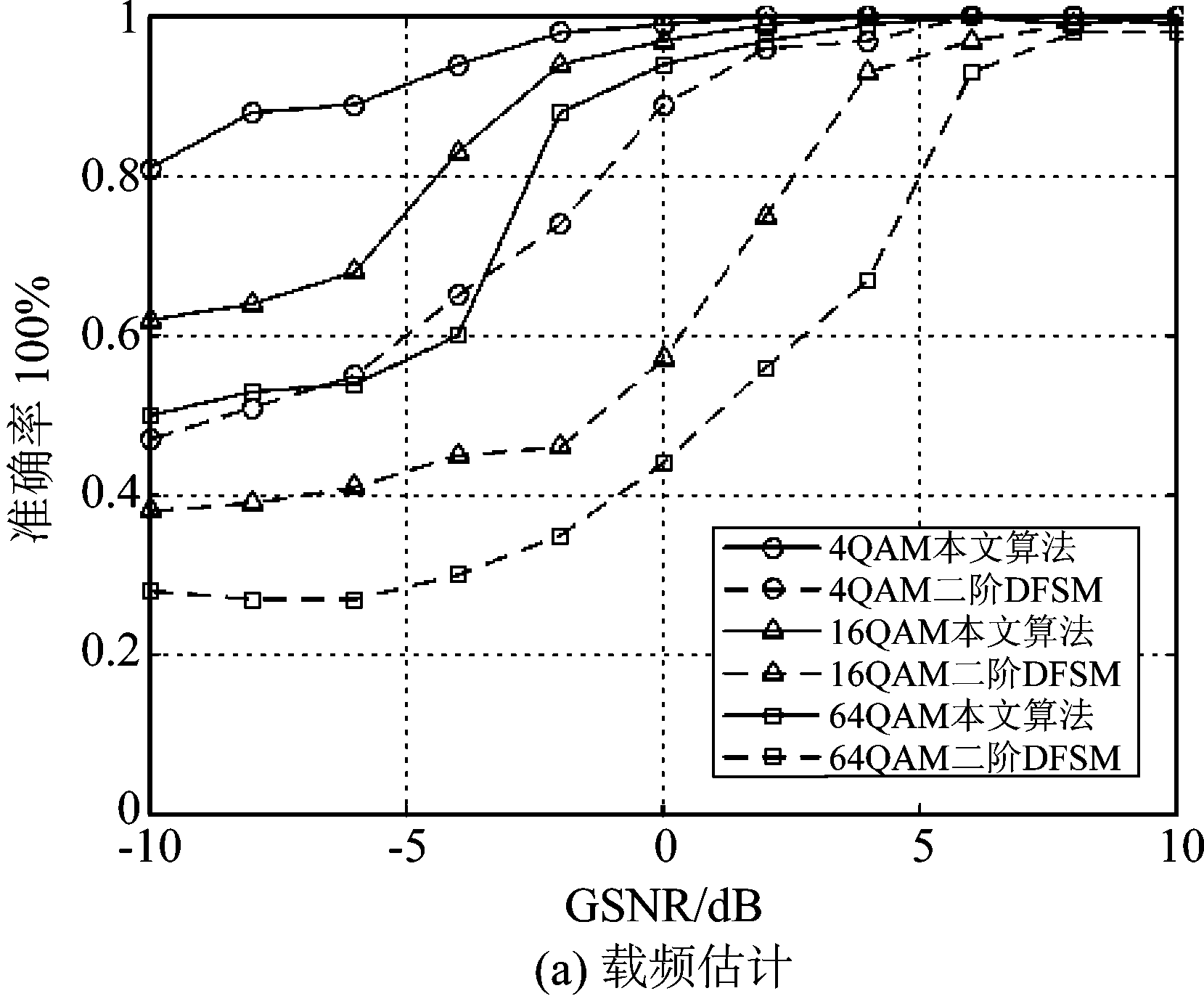
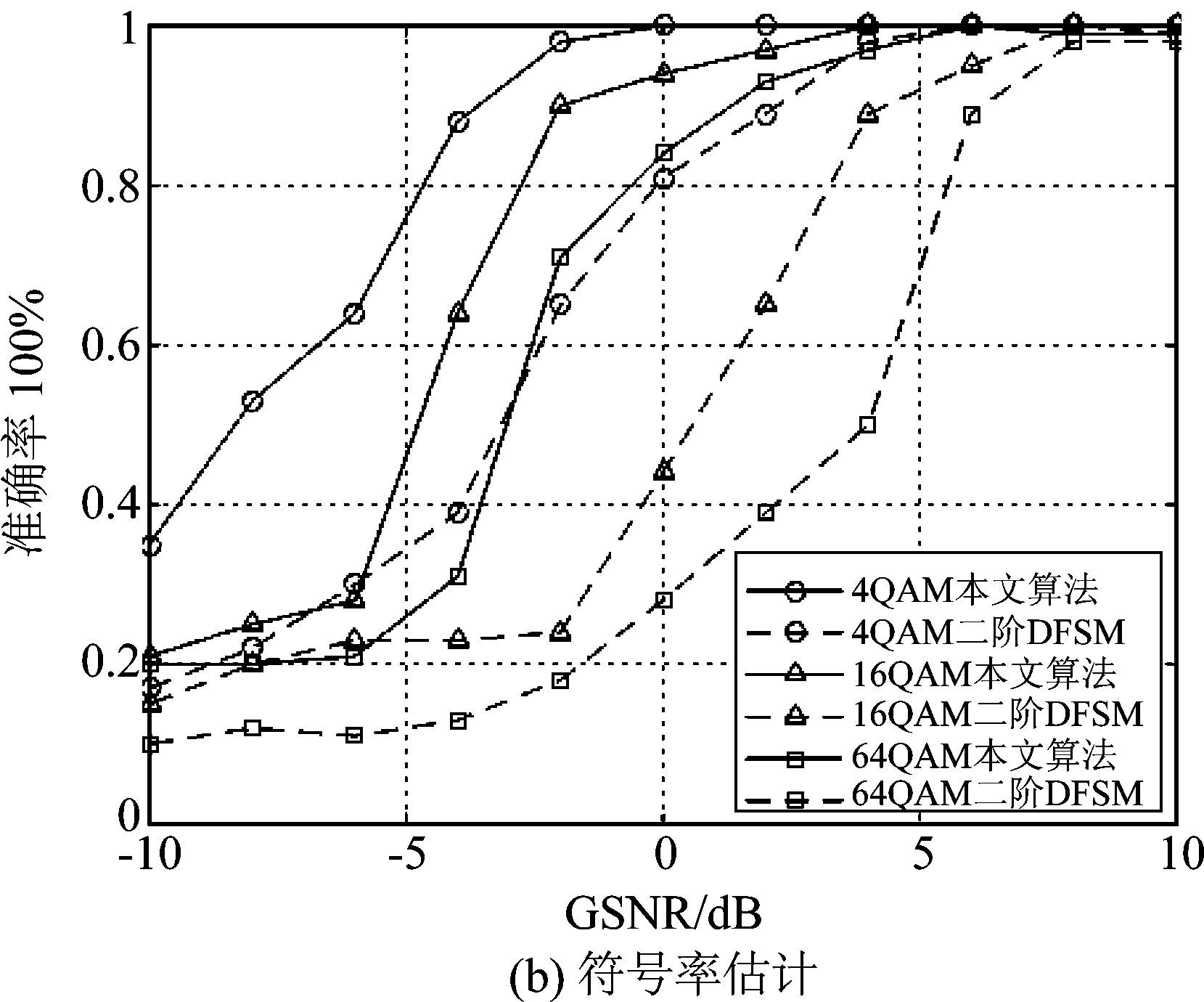
图6 MQAM信号参数估计准确率
Fig.6 The parameters estimation accuracy of MQAM signal
6 结论
本文针对传统MQAM信号载频与符号率估计算法在脉冲噪声环境下估计性能不佳的问题，结合分数低阶矩与共变理论首先推导了MQAM信号的分数低阶循环谱，在考虑升余弦脉冲成型的前提下，确定了MQAM分数低阶循环谱中不同切面间的载频与符号率信息，然后将分数低阶矩引入DFSM算法，给出了分数低阶DFSM循环谱估计表达式，提出了一种脉冲噪声环境下，基于分数低阶矩的MQAM信号载频与符号率估计算法。实验验证表明，该方法能够有效的抑制噪声中的脉冲成分，即使在α值较小，广义信噪比较低的脉冲噪声中本文算法仍具有较高的估计精度与准确率，为脉冲噪声环境下MQAM信号进一步处理提供了一定的基础。
[1] 刘明骞, 陈钱, 吴芸, 等. 非合作通信中MQAM的定时载波联合同步[J]. 西安电子科技大学学报, 2018, 45(1): 17-22.
Liu Mingqian, Chen Qian, Wu Yun, et al. Joint carrier synchronization and symbol timing for MQAM in non-cooperation communication systems[J]. Journal of Xidian University, 2018, 45(1): 17-22.(in Chinese)
[2] 廖锡畅, 雷迎科, 罗路为, 等. Alpha稳定分布下基于RHMy滤波的MQAM信号码元速率估计方法[J]. 信号处理, 2018, 34(5): 592- 601.
Liao Xichang, Lei Yingke, Luo Luwei, et al. Symbol Rate Estimation of MQAM Signal Based on RHMy Filtering under Alpha Stable Noise[J]. Journal of Signal Processing, 2018, 34(5): 592- 601. (in Chinese)
[3] Chrysostomos L. Signal processing with alpha-stable distributions and applications[M]. John Wiley & Sons, Inc, 1995.
[4] Kumar S, Bohara V A, Darak S J. Blind symbol rate estimation by exploiting cyclostationary features in wavelet domain[C]∥International Conference on Advances in Computing, Communications and Informatics. IEEE, 2016: 1757-1763.
[5] 谢然, 张效义, 田鹏武. 一种基于循环谱的MPSK信号符号速率估计方法[J]. 计算机应用研究, 2011, 28(6): 2294-2296.
Xie Ran, Zhang Xiaoyi, Tian Pengwu. Symbol rate estimation method of MPSK signals based on cyclic spectrum[J]. Application Research of Computers, 2011, 28(6): 2294-2296. (in Chinese)
[6] Wang H. Spectral correlation function of basic analog and digital modulated signals[C]∥2013 IEEE International Conference of IEEE Region 10 (TENCON 2013). IEEE, 2013(31194): 1-5.
[7] 赵春晖, 杨伟超, 成宝芝. Alpha稳定分布噪声背景下MPSK信号参数估计[J]. 沈阳工业大学学报, 2013, 35(2): 194-199.
Zhao Chunhui, Yang Weichao, Cheng Baozhi. Parameter estimation of MPSK signals in Alpha stable distribution noise environment[J]. Journal of Shenyang University of Technology, 2013, 35(2): 194-199. (in Chinese)
[8] Yang W, Yang X. Research on symbol rate estimation based on the generalized square envelope spectrum[C]∥IEEE International Conference on Communication Problem-Solving. IEEE, 2015: 391-394.
[9] 刘高辉, 张娟娟. α稳定分布噪声下数字频移键控信号的分数低阶循环谱分析[J]. 电波科学学报, 2017, 32(1): 65-72.
Liu Gaohui, Zhang Juanjuan. Fractional lower order cyclic spectrum analysis of digital frequency shift keying signals under the alpha stable distribution noise[J]. Chinese Journal of Radio Science, 2017, 32(1): 65-72.(in Chinese)
[10] 裴承全. 基于循环平稳的调制识别研究[D]. 兰州: 兰州理工大学, 2013.
Pei Chengquan. Research on Modulation Recognition Based On Cyclostationarity[D]. Lanzhou: Lanzhou University of Technology, 2013. (in Chinese)
[11] Gardner W A. Spectral Correlation of Modulated Signals: Part I--Analog Modulation[J]. Communications IEEE Transactions on Communications, 1987, 35(6): 584-594.
[12] Napolitano A, Perna I. Cyclic spectral analysis of the GPS signal[J]. Digital Signal Processing, 2014, 33(6): 13-33.
[13] 张洋, 彭华. 比特谱相关改进循环谱的单通道混合信号参数估计快速算法[J]. 信号处理, 2016, 32(4): 404-416.
Zhang Yang, Peng Hua. Parameter Estimation of Mixed Signals in Single-Channel on Modification Fast Cyclic Spectral Estimation Algorithm with One-Bit Spectral-Correlation[J]. Journal of Signal Processing, 2016, 32(4): 404-416.(in Chinese)
[14] 何继爱, 裴承全, 郑玉峰. 稳定分布下基于FAM的低阶循环谱算法研究[J]. 电子学报, 2013, 41(7): 1297-1304.
He Jiai, Pei Chengquan, Zheng Yufeng. The Realization of Low Order FAM Method Under α Stable Distribution[J]. Acta Electronica Sinica, 2013, 41(7): 1297-1304. (in Chinese)
[15] 李兵兵, 马洪帅, 刘明骞. Alpha稳定分布噪声下时频重叠信号的载波频率估计方法[J]. 电子与信息学报, 2014, 36(4): 868- 874.
Li Bingbing, Ma Hongshuai, Liu Mingqian. Carrier Frequency Estimation Method of Time-frequency Overlapped Signals with Alpha-stable Noise[J]. Journal of Electronics & Information Technology, 2014, 36(4): 868- 874. (in Chinese)
[16] 崔伟亮, 江桦, 李剑强, 等. 改进的循环谱估计快速算法与性能分析[J]. 电子与信息学报, 2011, 33(7): 1594-1599.
Cui Weiliang, Jiang Hua, Li Jianqiang, et al. Improved Fast Cyclic Spectral Estimation Algorithm and Performance Analysis[J]. Journal of Electronics & Information Technology, 2011, 33(7): 1594-1599. (in Chinese)
