1 引言
地球表面接收到的导航信号功率很小,以GPS为例,比接收机热噪声低约21 dB。当受到人为干扰时,接收信号难以恢复。运用天线阵并且进行时延扩展,形成空时二维模式,可以大幅增加自由度从而增强抗干扰能力。设阵元数为M,时间延迟数为N,则接收数据X为MN×1维向量,其协方差矩阵RX=E{XXH},为MN×MN维矩阵,其最优处理的运算量约为O((MN)3),随着空时处理维数的增加,运算量成立方倍增长,大运算量对计算资源消耗和计算时长都不可接受。文献[1]提出一种改进侧视阵声呐的混响抑制方法,该方法利用投影矩阵法设计了时域和空域混响陷波器,分别滤除了与目标同频的旁瓣混响和与目标同方位的主瓣混响,但是仍然要用空时二维联合处理滤除剩余的混响,没有讨论空时二维处理的简化运算。文献[2]着眼于雷达运动平台在下视检测目标的过程中,干扰目标污染训练样本引起的功率非均匀问题,首先从受污染样本与干净样本的差异性度量角度入手,采用均值Hausdorff距离度量样本矩阵相似性,然后结合凸优化包计算不同样本的相似度,最后根据相似度的不同,实现对受污染样本的剔除,该方法提高了协方差矩阵估计的准确性,但缺点是需要用凸优化包,即需要用最优化理论实现,这一部分难以显式表述,难于实现,且该方法仍然包含求空时二维矩阵特征值及相应逆矩阵的计算,运算量大。文献[3]针对实际数字阵列天线阵元间距大于半波长导致大角度估计时阵元相位出现模糊问题,提出一种新的基于时空DOA矩阵的多目标高性能二维角度估计算法。该算法首先计算时空DOA矩阵并进行特征值分解,接着利用空时矩阵特征向量与来波导向矢量匹配特性,对估计得到的各导向矢量分别进行相位解模糊,进而利用导向矢量联立方程组,得到各来波角度信息的最小二乘解。主要解决的是阵列不理想情况下相位模糊问题,运用该方法同样需要求得空时矩阵的特征向量,有很大的运算量。MWF有避免大矩阵分解和降维处理两个优势[4],适用于解决空时二维抗干扰处理的问题。但是在实际中运用经典MWF,噪声子空间维数估计不准,当超过最优值时,将引起信噪比较大降幅。
基于以上分析,本文通过对MWF特性的分析,用MWF输出的各阶期望信号算得一个协方差矩阵,通过对该矩阵的分析,推导出一种滑窗定阶的方法。首先用MWF粗略估计出噪声子空间维数,然后从该阶开始取一个小方阵,用幂法算得其最大特征值,与预设的门限比较,判定是否为噪声子空间维数,沿协方差矩阵对角线向右下滑动,直至估计出噪声子空间维数。在做出估计之后,可以运用经典MWF算得最优权值并对接收信号进行滤波抑制干扰。该方法的优势在于界定噪声和白噪声子空间分界点时,相对于经典算法具有更大的区分度。
2 多级维纳滤波的基本方法
多级维纳滤波是维纳滤波器的一种多级等效形式,因此运用这一方法首先需要将抗干扰处理转化为维纳滤波的问题。通过广义旁瓣对消器[5]可以从接收信号矢量分离出期望信号,形成维纳滤波的模式,如图1所示。接收信号矢量经过上面的支路得到期望信号d0(n),d0(n)包含有用信号和干扰,阻塞矩阵B0=null(h),其中null表示求零空间,下支路通过B0阻塞期望信号,则x0(n)仅含干扰。
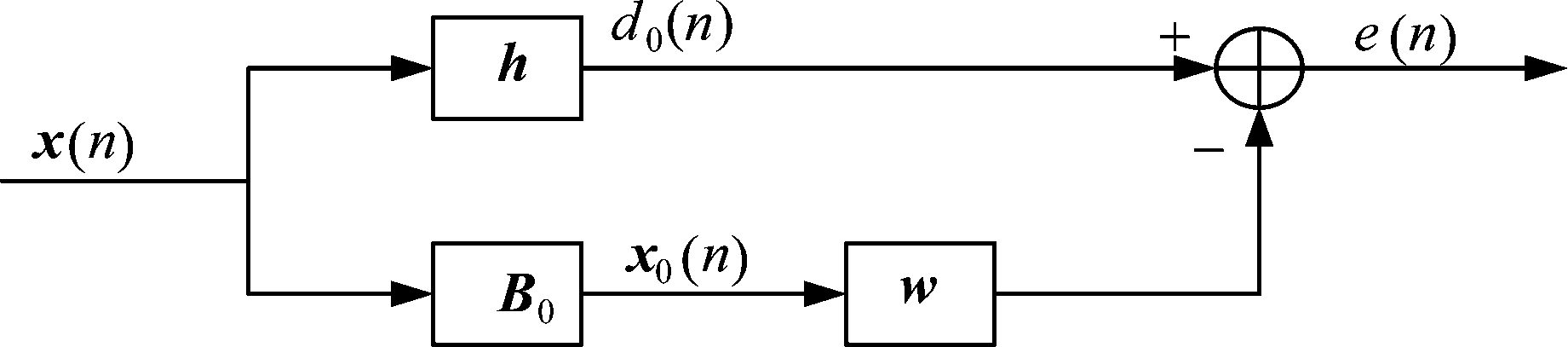
图1 广义旁瓣对消器结构图
Fig.1 Generalized sidelobe canceller
根据文献[4],经典的多级维纳滤波器结构如图2所示。按照信息论的思想,从每一步观测数据矢量xi(n)中尽量提取与di(n)相关的信息,用xi(n)与di(n)的归一化互相关矢量可以达到这个目的。xi(n)与di(n)的互相关为rxidi,其归一化矢量为hi=rxi-1di-1/‖rxi-1di-1‖。阻塞矩阵为与hi正交的[(MN-i)×(MN-i-1)]维矩阵,记为Bi,可表示为Bi=null(hi),其列矢量构成hi的零空间,即![]()
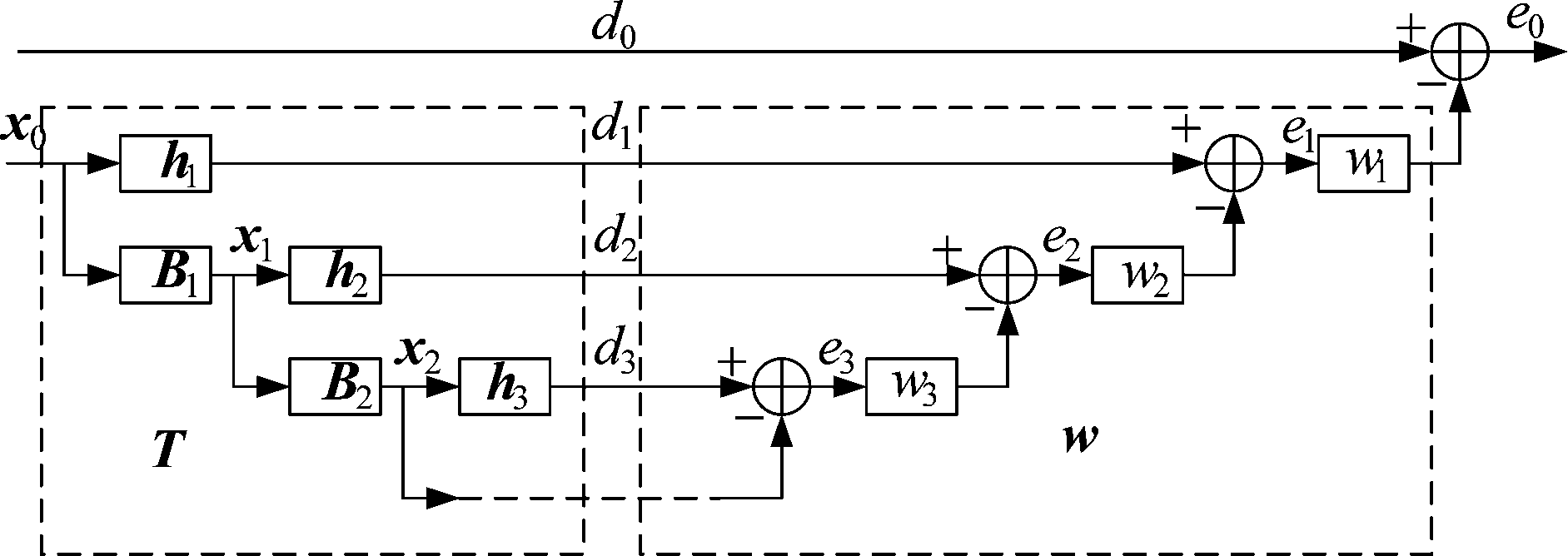
图2 多级维纳滤波器结构图
Fig.2 Multistage Weiner Filter chart
经典算法中的综合滤波器是一个反推的过程。假设预定的降维维数为P,即分解到第P级停止,由图2可知,eP(n)=dP(n),第P级实际构成了经典的维纳滤波器,根据经典维纳滤波的理论可以推出这一步标量权值![]() 其中
其中![]() 从P级往前推,第P-1级的误差为
从P级往前推,第P-1级的误差为![]() 相应的可以算得wP-1,以此类推可以算得标量形式的各阶维纳滤波器权值。此时的T为降维矩阵,由图2可知其列矢量为
相应的可以算得wP-1,以此类推可以算得标量形式的各阶维纳滤波器权值。此时的T为降维矩阵,由图2可知其列矢量为![]()
由各阶标量维纳滤波器可嵌套组成多级维纳滤波器的综合滤波器部分,求得各阶标量维纳滤波器权值之后,逐级反推可得到综合滤波器的权值
(1)
最终算得的权值为
wMWF=Tw
(2)
经典MWF算法中的迭代次数P是通过每步迭代后均方误差ξi=E{|ei(n)|2}与一个门限值(通常设为接收机热噪声方差)相比较来确定,只要ξi小于门限值,就让迭代停止,使P=i。
运用经典MWF对空时二维模式抗干扰处理降维,会使最优子空间维数难以估计准确,有两个原因:(1)噪声随环境变化,用一个固定的门限难以准确估计干扰子空间维数;(2)因为MWF的每一步按照与接收信号矢量的最大相关提取干扰分量,因此前面的迭代提取干扰分量多,后续提取少,致使后续接收信号残差方差与白噪声方差区分不明显,很难找准。
3 运用滑窗判定噪声子空间估计方法
3.1 理论推导
由经典MWF的分析可知,降维矩阵T的列矢量![]() 相互正交,可以作为子空间的基向量。降维处理的过程就是将接收信号矢量投影到由T的列矢量张成的子空间上,实现此过程包含两个关键因素:获取子空间的基矢量和子空间的维度。
相互正交,可以作为子空间的基向量。降维处理的过程就是将接收信号矢量投影到由T的列矢量张成的子空间上,实现此过程包含两个关键因素:获取子空间的基矢量和子空间的维度。
据上文,构建T的列矢量中需要计算矩阵阻塞矩阵Bi,Bi的选取不是唯一的,需要满足的条件是与MWF滤波每一级的互相关矢量hi正交。运用文献[6]提出的方法,令阻塞矩阵为![]() 可推导出
可推导出![]() 满足阻塞矩阵的要求。因为
满足阻塞矩阵的要求。因为![]() 所以有
所以有
(3)
文献[7]提出一种相关相减多级维纳滤波法,即将![]() 分为两步实现:第1步为
分为两步实现:第1步为![]() 第2步将di(n)乘上hi,得到接收信号矢量在第i维子空间的投影。减去这个投影,就完成了一次分解。
第2步将di(n)乘上hi,得到接收信号矢量在第i维子空间的投影。减去这个投影,就完成了一次分解。
根据阻塞矩阵Bi的形式可以把降维矩阵的列矢量化简。将T的列矢量记作t1,t2,…,tP,即![]() 可见如果hi之间相互正交,则有t2=h2,以此类推可以得到ti=hi。首先证明[h1,h2,…,hP]为一组标准正交向量,已知hi=rxi-1di-1/‖rxi-1di-1‖,分母为常量,在正交性分析中可以不考虑,令δi=‖rxidi‖,有
可见如果hi之间相互正交,则有t2=h2,以此类推可以得到ti=hi。首先证明[h1,h2,…,hP]为一组标准正交向量,已知hi=rxi-1di-1/‖rxi-1di-1‖,分母为常量,在正交性分析中可以不考虑,令δi=‖rxidi‖,有
(4)
因为![]() 所以有
所以有
(5)
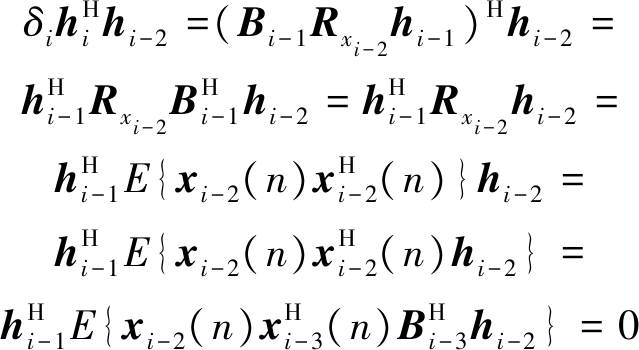
(6)
依此类推,可以得到
(7)
由此可得hi相互正交,因此t2=h2,依此类推,ti=hi,所以用![]() 替代原阻塞矩阵Bi=null(hi)后,降维矩阵也可表示为T=[h1,h2,…,hP]。
替代原阻塞矩阵Bi=null(hi)后,降维矩阵也可表示为T=[h1,h2,…,hP]。
获得子空间基矢量之后,需要确定子空间维数,下面在MWF框架下运用子空间理论进行分析。将图2所示的各阶期望信号di(n)组成矢量形式xT(n)=[d1(n),d2(n),…,dMN-1(n)]T,求取该矢量的协方差矩阵RXT,RXT为三对角矩阵[4]。理想的协方差矩阵无法获得,所采取的办法是加和求平均,设截取数据长度为L,将RXT的主对角线和副对角线元素分别简记为![]() 则有
则有
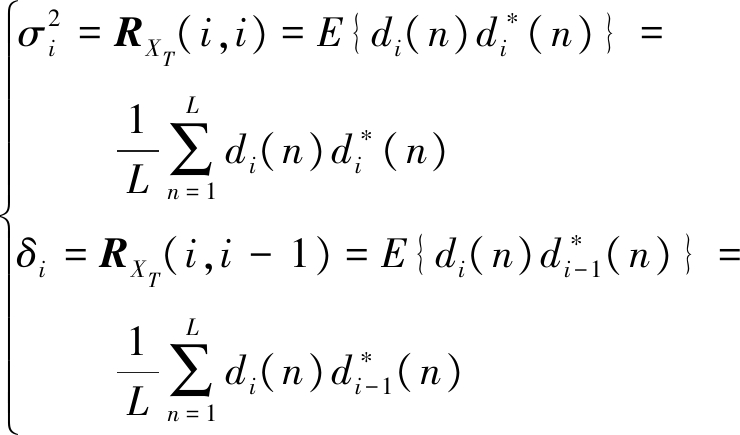
(8)
因RXT的副对角线元素是共轭对称的[4],所以只需要计算δi即可。则协方差矩阵可表示如下:
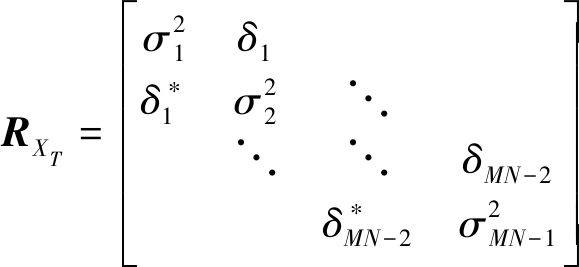
(9)
用MWF逐步提取相关干扰信息过程中,必然存在P<MN-1,经过P步投影,观测数据中不再有干扰成分。文献[8]证明:如果干扰子空间维数为P,则多级维纳滤波器做P级分解后的(MN-P-1)组观测数据矢量为白噪声矢量,且为:
(10)
式中,(·)(P)表示干扰子空间维数为P的情况,下标(·)i表示MWF的第i级,v(n)为白噪声矢量。
文献[8]在对噪声子空间进行分解过程中,通过对各阶期望信号矢量生成的协方差矩阵进行分析,类似于本文中的RXT,推导出:当阶数超过噪声子空间维数时,RXT的主对角线元素等于白噪声方差,副对角线元素接近0。本文也用到这一思路,根据式(4)对矩阵RXT进行分析。其副对角线元素可推导如下
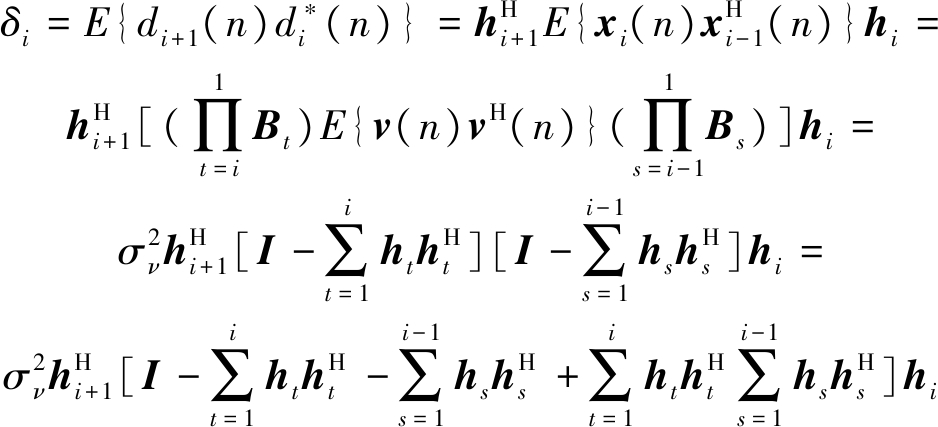
(11)
当i≥P时,因此所有含有因子hi的项均与![]() 正交,而
正交,而![]() 与hi正交,理论上可以推出δi=0。
与hi正交,理论上可以推出δi=0。
易知di(n)观测数据矢量的加权,如上文所述,P阶之后的观测数据矢量为白噪声,显然P阶之后观测数据矢量的加权di(n)也是白噪声。可知,当i>P时,主对角元素![]() 约等于白噪声方差。
约等于白噪声方差。
因此在理论上,RXT可以按照下面形式进行分块:
(12)
左上部分仍为P阶三对角矩阵,右下部分为对角矩阵,其余位置元素为零。矩阵RXT的特征值为det(RXT-λI)=0的解,有下式
det(RXT-λI)=
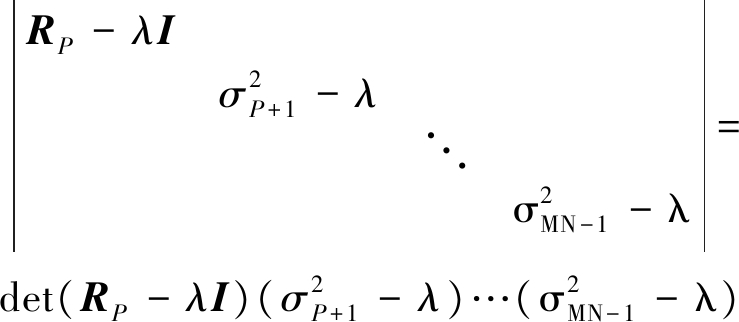
(13)
式中![]() 由此可知,高于P阶的RXT的特征值等于白噪声方差。
由此可知,高于P阶的RXT的特征值等于白噪声方差。
矩阵RXT可以分块,以噪声子空间维数P为界,左上部分为三对角矩阵,直到第P阶,右下部分为对角矩阵,对角元素约等于白噪声方差。该特性可用于估计噪声子空间维数,根据式(2),在获得子空间维数之后,需要用到降维矩阵T和综合滤波器的权值w,即可算得权值。
3.2 实现步骤
空时二维处理的主要环节是权值计算,图3为在MWF理论基础上提出的一种运用滑窗定阶的噪声子空间估计方法。运用该方法完成最优权值的计算,图1中“w”标识的部分。
运用该方法进行空时二维处理的步骤如下:
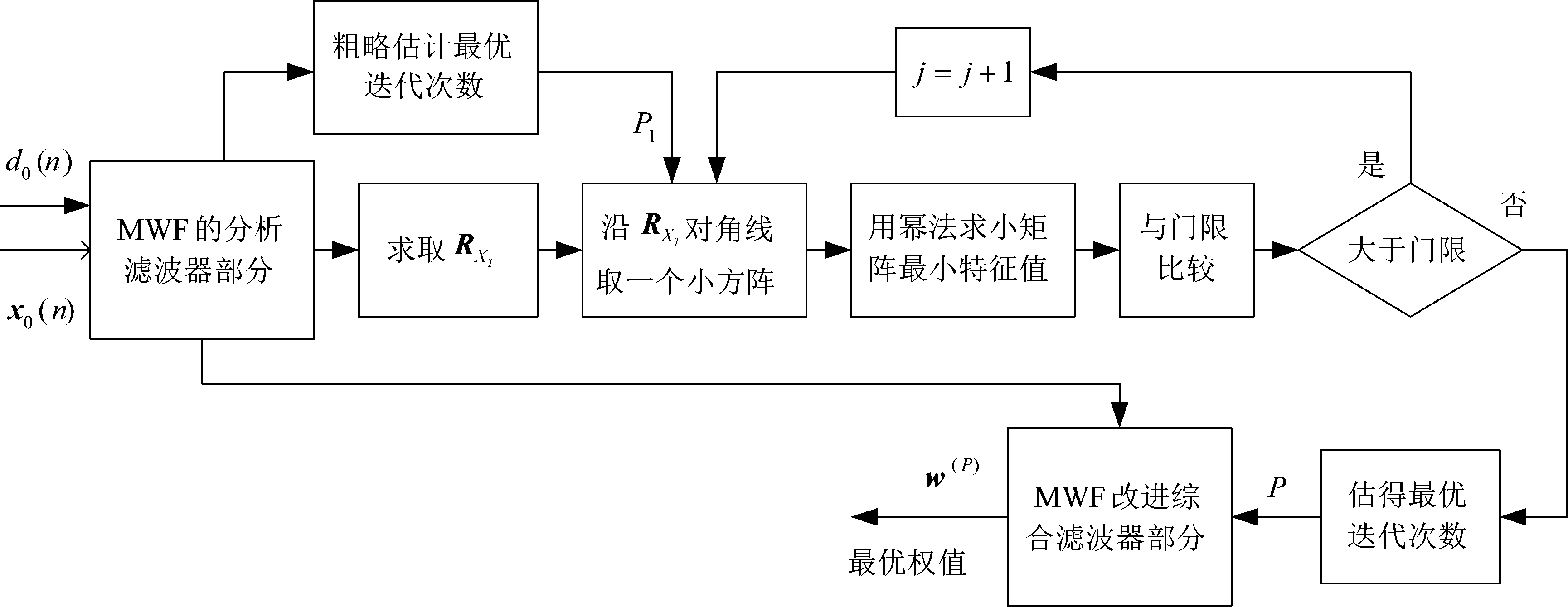
图3 运用滑窗判定的噪声子空间分解方法流程图
Fig.3 Noise space decomposition flow chart using sliding window
Step 1 将抗干扰处理问题转化为维纳滤波模式:将接收信号矢量通过广义旁瓣对消器,得到上支路的期望信号,记为d0(n),下支路x0(n)为待处理信号矢量,如图1,形成维纳滤波的模式。
Step 2 粗略估计干扰子空间维数:根据图2,按照最大相关并归一化算得h1,阻塞矩阵B1为h1的零空间矩阵,将x0(n)通过这一级滤波,得到d1(n)、x1(n),及矢量x1(n)中任意一路的方差![]() 依此类推,构建各级hi和Bi,生成
依此类推,构建各级hi和Bi,生成![]() 白噪声方差为σ2,将
白噪声方差为σ2,将![]() 与k(k一般取3~5)倍σ2进行比较,当
与k(k一般取3~5)倍σ2进行比较,当![]() 时,将此时的i作为粗略估计的噪声子空间维数,设为P1,P1几乎总是大于准确的子空间维数P。
时,将此时的i作为粗略估计的噪声子空间维数,设为P1,P1几乎总是大于准确的子空间维数P。
Step 3 准确估计干扰子空间维数:如图3所示,在MWF框架下,根据子空间理论,结合矩阵最大特征值的计算,运用滑窗逐级搜寻噪声子空间维数。这一步分解为以下四步执行:
Step 3.1 协方差矩阵计算: 将接收信号矢量经过MWF生成的各阶期望信号di(n)组成矢量形式xT(n)=[d1(n),d2(n),…,dMN-1(n)]T,求取该矢量的协方差矩阵RXT。
Step 3.2 截取小矩阵:在RXT中用一个窗口截取一个小方阵,设为Rj,不妨设方阵宽度为Dwin, j为方阵左上角元素在RXT中的阶次。首次截取的位置j=P1+1,也就是粗略估计的噪声子空间维数加1,以j=P1+1作为Rj的右下角,从P1向左上取Dwin大小的方阵,如果P1<Dwin,则矩阵取到首位。从第P1+1阶开始取矩阵的原因是:假设噪声子空间维数为P1,根据前文推导,P1的下一维对角元素才接近于白噪声方差。
Step 3.3 求取最小特征值:用反幂法求得矩阵Rj的最小特征值(Rj为三对角矩阵,且维度小,运算量小),设为λj。根据上文分析,RXT的小特征值接近于白噪声方差,因此用一个小窗口沿RXT的对角线滑动,当达到分界点时,其最小特征值必定接近于白噪声方差。
在工程计算中,可以利用反幂法按模计算Rj的最小特征值,其步骤如下:
(1)输入矩阵Rj,初始向量x,误差限ε,最大迭代次数Nmax;
(2)将迭代初始值k置为1,初始的最小特征值设为λ0=0,令矢量y=x/max(abs(x));
(3)对矩阵Rj作三角分解Rj=LU;
(4)解方程组LUx=y;
(5)令μ=max(x),λ=μ;
(6)若|λ-λ0|<ε,则输出1/λ,也就算得了最小特征值,否则执行下一步;
(7)若k<Nmax,置k←k+1,更新最小特征值为λ0=λ,再求得y=x/max(abs(x)),转到(4)。
Step 3.4 判定噪声子空间维数:将λj与1.5倍σ2比较,如果λj大于1.5σ2,则j=j+1,将窗口沿着待分析矩阵RXT的对角线向右下滑动一阶,返回到S3.2。如果不满足λj大于1.5σ2,则认为已经达到分界点,就是估计出的噪声子空间维数,即为P。
Step 4 权值计算:运用经典MWF综合滤波器反推算得最优权值,获得最佳迭代次数P之后,从第P级往前推算。由图2可知,eP(n)=dP(n),推出这一步标量权值![]() 其中
其中![]() 从P级往前推,第P-1级的误差为
从P级往前推,第P-1级的误差为![]() 相应的可以算得wP-1,以此类推可以算得标量形式的各阶维纳滤波器权值。由各阶标量维纳滤波器可嵌套组成多级维纳滤波器的综合滤波器部分,如式(1),最终算得的权值如式(2)。
相应的可以算得wP-1,以此类推可以算得标量形式的各阶维纳滤波器权值。由各阶标量维纳滤波器可嵌套组成多级维纳滤波器的综合滤波器部分,如式(1),最终算得的权值如式(2)。
得到最优权值矢量wMWF之后,用该权值对接收信号矢量进行阵列滤波,就可以达到抑制干扰的目的,获得较高的信干噪比输出。
4 运算量分析
经典MWF算法包含阻塞矩阵计算,运算量极大[4],文献[6-7]提出改进方法缩减了经典MWF算法前向迭代部分的运算量。本文方法在文献[4,6-7]的基础上增加了对噪声子空间维数的估计,该方法前向迭代部分的主要运算量分析如下:
表1 前向迭代部分主要运算量
Tab.1 The main computation of forward iteration

算法步骤乘法器数量1.求取相关矢量:rxi-1di-1=E{xi-1(n)d∗i-1(n)}4(MN-1) 2.求取归一化相关矢量:hi=rxi-1di-1/rxi-1di-12(MN-1)+8 3.求取下一阶期望信号:di(n)=hHixi-1(n)4(MN-1)4.求取RXT的第i阶对角和副对角元素:RXT(i,i)=E{di(n)d∗i(n)},RXT(i,i-1)=E{di(n)d∗i-1(n)}2+45.生成下一阶待处理信号矢量:xi(n)=xi-1(n)-hidi(n)4(MN-1)
上表中,第1步使用的乘法器数量为4(MN-1),这是一个(MN-1)阶的复矢量每一元素和一个复数相乘,因此需要4(MN-1)次乘法。第2步中,求取rxi-1di-1的模可以复用乘法器,只需要8个足够,在求取归一化相关矢量时,可以转化为一个(MN-1)维的复矢量与一个实数相乘,因此用到2(MN-1)个乘法器。第4步中,求取期望信号自相关是共轭复数相乘,只需要2个乘法器,而求取相邻两阶期望信号的互相关则需要4个乘法器,而RXT(i-1,i)即是RXT(i,i-1)的共轭,无需另外计算。第5步中,同理,归一化相关矢量与这一阶期望信号矢量相乘也是MN阶的复矢量每一元素和一个复数相乘,所以用到4(MN-1)个乘法器。
分解小维度矩阵Rj的运算量很小,主要有三个原因:(1)运算量量级为![]() 与维度成立方倍关系,由于Dwin取值小,一般取2或者3;(2)Rj具有特殊性,即三对角矩阵,相对普通矩阵而言缩减运算量;(3)文中只需要求取最小特征值,不需要求Rj的每个特征值。
与维度成立方倍关系,由于Dwin取值小,一般取2或者3;(2)Rj具有特殊性,即三对角矩阵,相对普通矩阵而言缩减运算量;(3)文中只需要求取最小特征值,不需要求Rj的每个特征值。
本文方法相对于改进的MWF增加的运算主要为表1中的第4步,以及对小维度矩阵Rj的运算,经以上分析得知,其运算量相对于大维度矢量运算而言很小,因此可以得出结论,使用本文方法增加的运算量很小。
5 仿真试验
仿真主要包括两个部分:第一、比较本文方法与传统方法在噪声子空间维数估计上的性能;第二、比较本文方法与传统方法的输出信干噪比;第三、比较本文方法与传统方法在仿真场景中的抗干扰性能,此项仿真需采用文献[9]的方法,用导航电文建立GPS卫星运动模型,以获得贴近于实际的仿真场景。
采用5元加芯圆阵,成十字型排列,半径为d=λ/2,λ为接收信号波长,时间延迟单元数N=5。无干扰时基带载噪比C/N0=Sr+Ga-10log(kT0)-NF-Ls。其中Sr为GPS信号接收功率(dBW),Ga为天线增益(dB),10log(kT0)=-205 dBW/Hz为接收机噪声密度,取常温T0=300 K,NF为接收机噪声系数,取决于天线和前置放大器噪声,一般取NF=4 dB,Ls为信号在通道内的传输及量化损耗。据IDC-GPS-200[10]规定,地球表面上Ga=0 dB增益的GPS接收机天线接收L1 频段上C/A码信号的能量为-160 dBW。接收机噪声功率密度约为-140 dBW,因此无干扰情况下的信噪比为-21 dB。
仿真试验1 按照干噪比30 dB设置两个功率相同的部分带宽干扰和两个单频干扰。进行两组仿真:(1)试验输出信干噪比(SINR)与迭代次数的关系;(2)检测本发明对于噪声子空间估计的作用。仿真中均重复多次取平均。
(1)输出信干噪比(SINR)与迭代次数的关系
运用经典MWF方法进行抗干扰滤波,逐渐增加MWF的迭代次数,观测输出SINR的变化。
如图4所示,随着迭代次数增加,SINR在达到最大值以后将大幅下降,仅仅超过最佳迭代次数一次,SINR就下降约有5 dB。
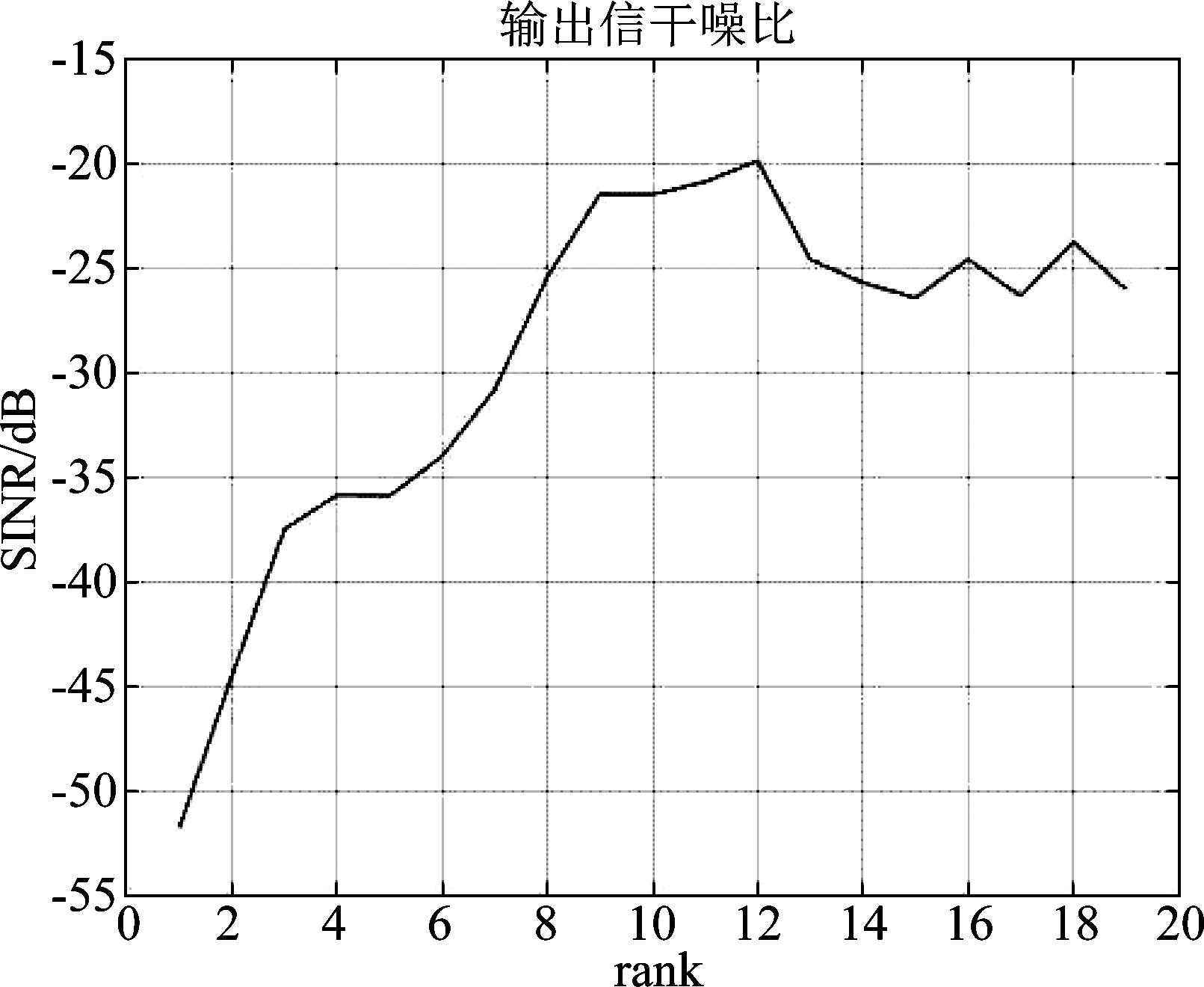
图4 输出SINR与迭代次数关系
Fig.4 Output SINR versus iteration times
(2)本文方法对于噪声子空间估计的作用
仿真中将沿RXT对角线截取的小方阵边长width定为3,即矩阵Rj的阶数设置为3。
图5的左图表示使用经典MWF,通过每步迭代运算之后均方误差确定噪声子空间维数的情况,从图5(左)可以看出,在12次迭代之后,干扰信号提取完,因为此时均方误差与白噪声方差的比值用分贝表示接近于0,即均方误差接近于白噪声方差。而在进行第13次迭代之后,均方误差与白噪声比值降了3 dB。图5的右图表示运用本文方法,在粗略判断最佳迭代次数(本场景中P1=10)之后,从P1=10阶开始,以P1=10为右下角,向左上方截取一个小矩阵,用反幂法算得该小矩阵最小特征值,求得该特征值与白噪声方差的比值,然后使窗口向右下方滑动,即以P=11为右下角,以同样的方式算得特征值与白噪声方差的比值,将所有比值记录下来,如图5(右)所示。因为场景相同,且与运用经典MWF在同一次仿真中,所以无疑最佳迭代次数为12。而在图5(右)中,第12和13阶比值的差距有7 dB。这就意味着区分度大大高于经典方法对最佳迭代次数的区分度。而且在第13阶的位置,方差接近于白噪声,与理论分析相符。因此可以得出结论,运用本方法可以使得干扰子空间分解更为准确可靠。
仿真试验2 按照一个部分带宽、一个单频干扰的顺序逐步增加干扰,干扰入射角度在入射空间内错开,干噪比30 dB。
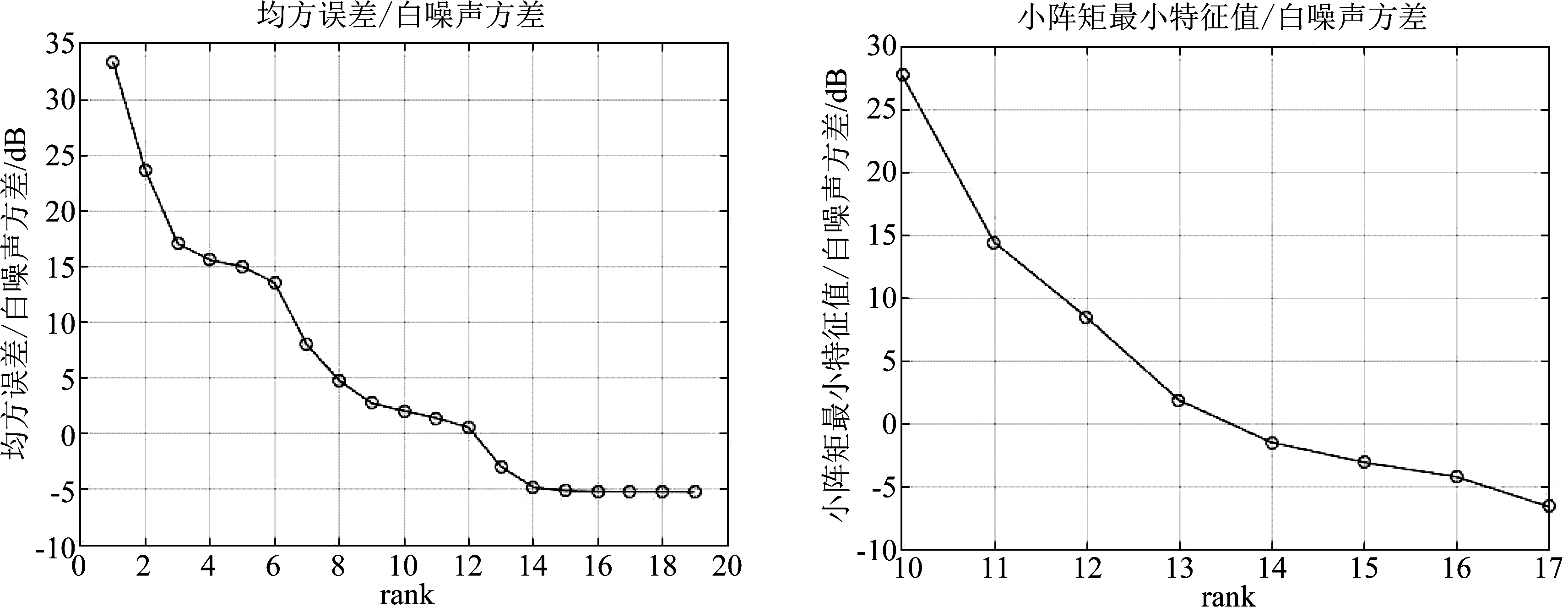
图5 经典MWF与滑窗定阶方法估计噪声子空间维数的判据
Fig.5 The criterion to estimate the noise subspace rank of classic MWF and the sliding window rank estimation method
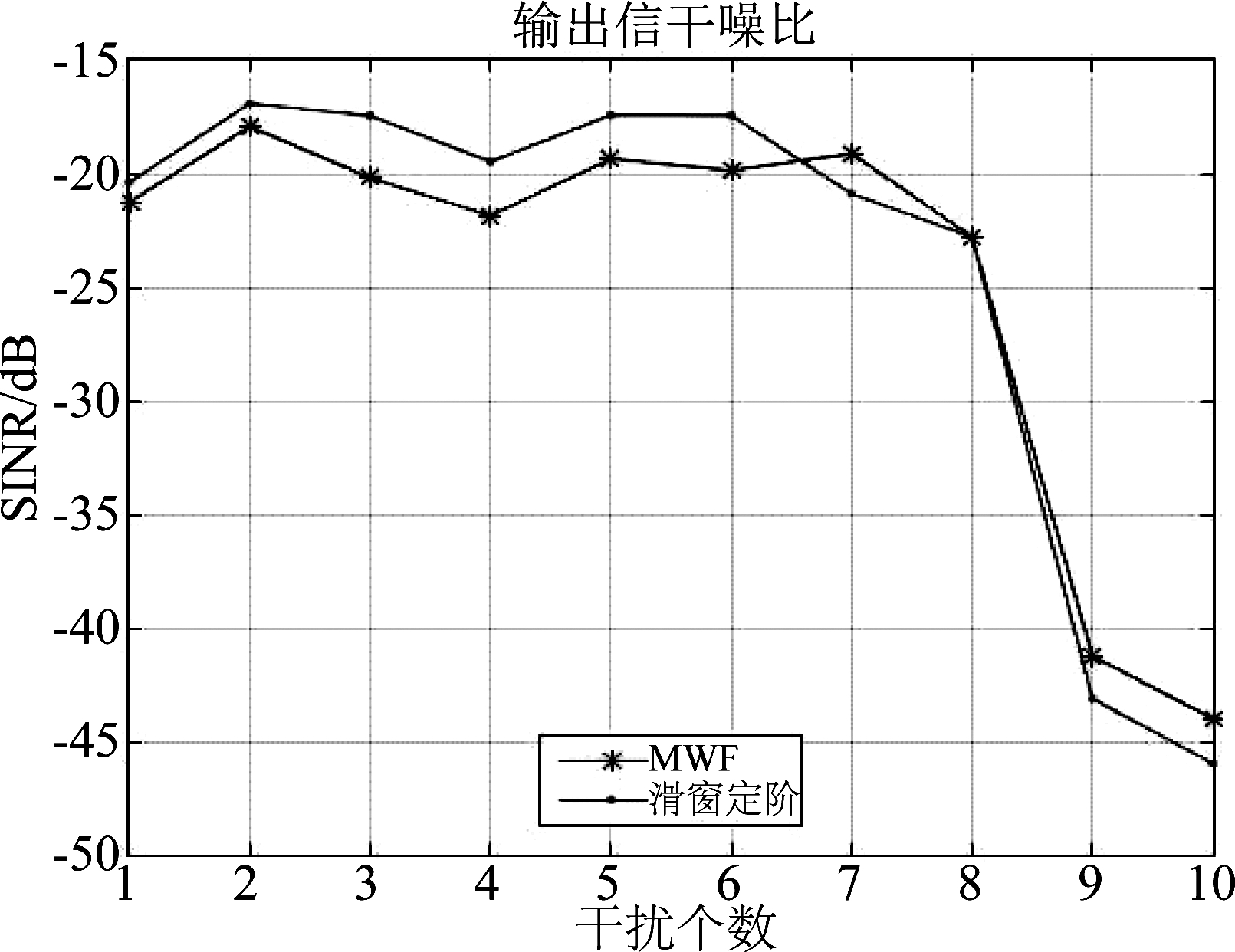
图6 经典MWF与滑窗定阶方法输出信干噪比(SINR)的对比
Fig.6 Output SINR of classic MWF and the sliding window rank estimation method
图6的表示经典MWF和本文方法在抗干扰性能上的对比。由图可以看出,干扰数为1和2时,本文的滑窗定阶法获得的输出SINR比用经典MWF高约1 dB,干扰数为3到6,滑窗定阶法获得的SINR高约2~3 dB,干扰数为7时,滑窗定阶法获得的SINR低约1 dB,干扰数为8时,两种方法获得的SINR相近。即在可抗干扰数范围内,滑窗定阶法获得的SINR大部分情况下要更高。需要指出的是:在仿真环境中,运用经典MWF时,是按照算得的白噪声方差设置门限,应为最佳门限;而在实际中,往往难以找到这样一个最佳门限,而运用滑窗定阶则大大削弱了这个问题,因为这种方法的区分度远大于经典方法。所以结论为:在实际环境中运用滑窗定阶方法相对于经典方法,可以获得更高更稳定的抗干扰性能。
仿真试验3 按照文献[9]的方法,用RINEX格式的导航电文文件adis0050.13n建立仿真场景。在一段时间内,标记出抗干扰处理之后的可用卫星。各卫星在一段时间内按规律运动,发射信号,在这一段时间内持续进行抗干扰处理,也就达到了在可视空域内对算法的抗干扰性能进行测试的目的。设接收机所在位置为东海某处上空,坐标为东经123° 00′,北纬25° 40′,即25.67°,高程为500 m。模拟产生部分带宽和单频两种干扰。部分带宽、单频干扰各2个。干扰入射方位角分别为:70°,130°,190°,250°,俯仰角分为25°,5°,15°,20°。干噪比均为30 dB。
图7、图8中,子图(a)均表示一段时间内,从接收机往上空看到的可用卫星的运动轨迹,轨迹表示可用卫星在不同时刻的空间位置;子图(b)表示同一时间可用卫星数目。可用卫星数目的多少也就反映了不同抗干扰方法的性能。图中仿真开始时间(tow)表示导航电文开始记录的时间。由仿真图可知:(1)使用经典多级维纳滤波做抗干扰处理,可用卫星比较多,能够满足定位需求;(2)使用本文方法可以抗干扰性能得到较大提升。图8(a)中卫星的轨迹较为连续,图7(a)中部分轨迹有中断的现象;由图7(b)和图8(b)可以看出,在2小时的测试时段内,图8(b)中显示的可用卫星数量明显要多于图7(b)中。由此可知,使用本文的滑窗法可以保证接收机在长时间内有更多数量的卫星可用。此外,在使用经典MWF时,通过反复比较设定了相对最优的门限,因此能获得较好性能,但是在实际环境中,往往难以进行最优设置,因此使用本文方法相对于经典MWF可以获得更好更稳定的抗干扰性能。
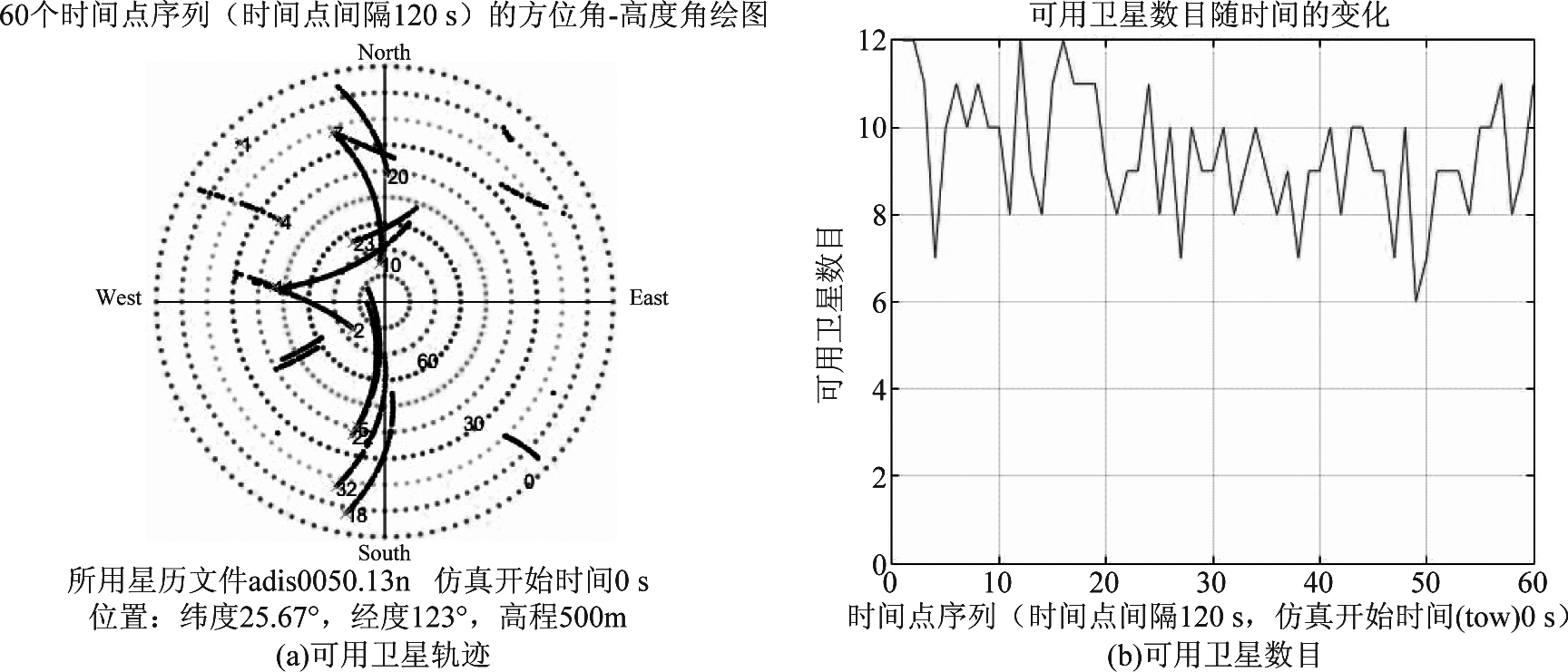
图7 用经典MWF算法抗干扰之后的可用卫星轨迹与数目
Fig.7 The usable satellite trajectory and number after using classic MWF to suppress interference
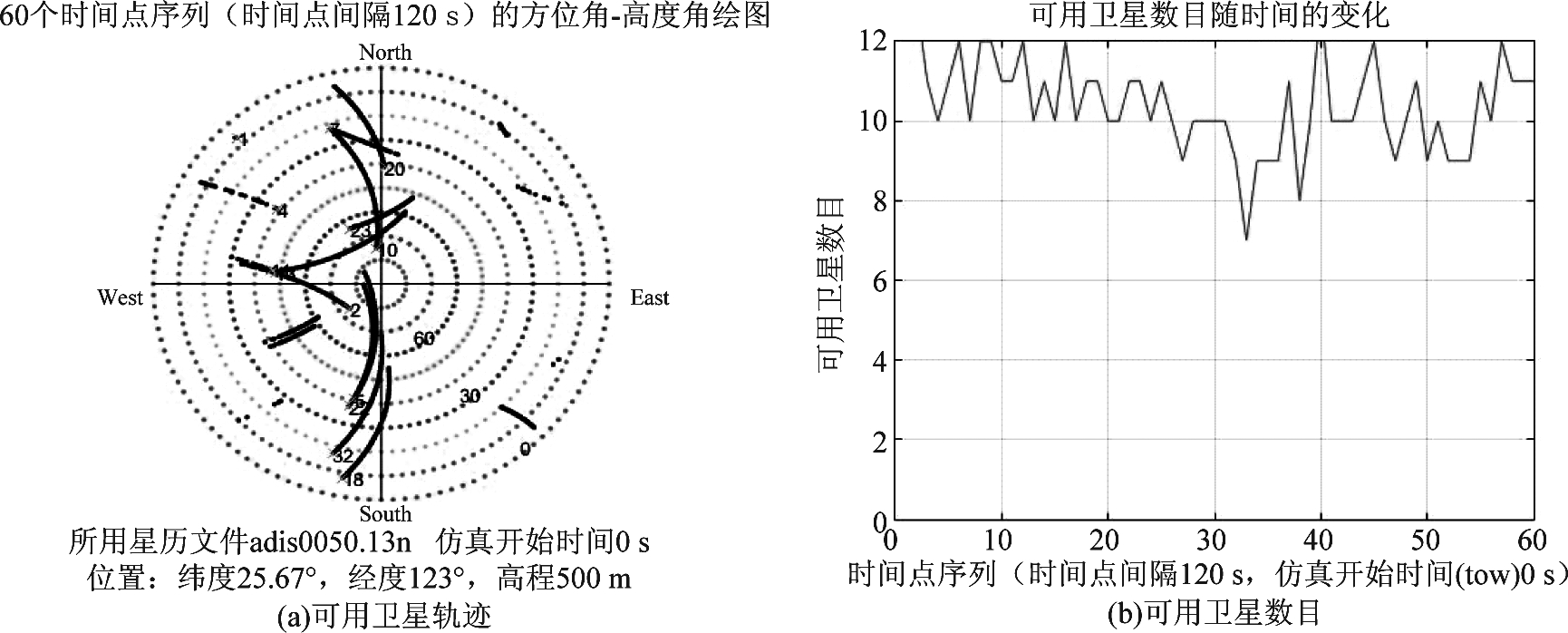
图8 用滑窗定阶方法抗干扰之后的可用卫星
Fig.8 The usable satellite trajectory and number after using sliding window rank estimation to suppress interference
6 结论
本文运用子空间理论分析多级维纳滤波过程,将接收信号矢量映射为各阶期望信号并组成矢量型式,根据此信号矢量所形成协方差矩阵的特性,推导出一种运用滑窗定阶的方法。用此方法判断噪声子空间维数,其区分度比用经典方法明显要高。仿真证明此方法在噪声子空间维数估计方面显著优于经典方法,运用此方法能获得更好的抗干扰性能。
[1] 詹昊可, 苑秉成, 朱锡. 一种基于空时联合处理的侧视阵混响抑制方法[J]. 海军工程大学学报, 2017, 29(1): 50-53.
Zhan Haoke, Yuan Bingcheng, Zhu Xi. A method of suppressing reverberation of side-looking sonar based on space-time joint processing[J]. Journal of Naval University of Engineering, 2017, 29(1): 50-53. (in Chinese)
[2] 王强, 张永顺, 刘汉伟, 等. 基于矩阵相似度的空时二维干扰检测方法[J]. 系统工程与电子技术, 2017, 39(2): 259-262.
Wang Qiang, Zhang Yongshun, Liu Hanwei, et al. Interference detecting method for space-time two-dimension based on matrix similarity[J]. Systems Engineering and Electronics, 2017, 39(2): 259-262. (in Chinese)
[3] 陈晓航, 张翔, 马晓峰, 等. 高性能空时二维角度估计改进算法[J]. 信号处理, 2016, 33(12): 1548-1554.
Chen Xiaohang, Zhang Xiang, Ma Xiaofeng, et al. Improved Algorithm for High Performance Space-time 2-Dimensional Angle Estimation[J]. Journal of Signal Processing, 2016, 33(12): 1548-1554. (in Chinese)
[4] Goldstein J S, Reed I S. A Multistage Representation of the Wiener Filter Based on Orthogonal Projection[J]. IEEE Transactions on Information Theory, 1998, 44(7): 2943-2959.
[5] Griffiths L J, Jim C W. An Alternative Approach to Linearly Constrained Adaptive Beamforming[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(1): 27-34.
[6] Ricks D C, Goldstein j S. Efficient Architectures for Implementing Adaptive Algorithms[J]. Proceedings of the 2000 Applications Symposium, 2000: 29- 41.
[7] 丁前军, 王永良, 张永顺. 一种多级维纳滤波器的快速实现算法——迭代相关相减算法[J]. 通信学报, 2005, 26(12): 1-7.
Ding Qianjun, Wang Yongliang, Zhang Yongshun. Fast Algorithm for Implementing Multistage Wiener Filter: Iterative Correlation Subtraction Algorithm[J]. Journal on Communications, 2005, 26(12): 1-7. (in Chinese)
[8] 黄磊, 吴顺君, 张林让, 等. 快速子空间分解方法及其维数的快速估计[J]. 电子学报, 2005, 33(6): 977-981.
Huang Lei, Wu Shunjun, Zhang Linrang, et al. A Fast Method for Subspace Decomposition and Its Dimension Estimation[J]. Acta Electronica Sinica, 2005, 33(6): 977-981. (in Chinese)
[9] 周柱. GPS接收机抗干扰研究[D]. 长沙: 国防科技大学, 2014.
Zhou Zhu. Research on Interference Suppression of GPS Receiver[D]. Changsha: National University of Defense Technology, 2014. (in Chinese)
[10] ARINC Research Corporation. IS-GPS-200, Navstar GPS Space Segment/Navigation User Interfaces (Revision D)[R]. Department of Defense, 2004.


