1 引言
由于无线传输的开放性特点,认知通信系统与其他无线通信系统一样,容易受到窃听和截获的安全威胁。近年来物理层安全技术利用多天线系统的信道差异性、互易性等特性和波束成形、天线选择和协作干扰等策略来增强网络的安全性受到了广泛的关注[1-2]。其中波束成形技术在提高主信道质量的同时可以削弱窃听信道的质量,是最有效地提高保密能力的方法。波束成形设计取决于系统信道状态信息的获取,CSI的准确性不仅决定了保密性能,而且还影响性能度量。文献[3]中针对发送端获取信道状态信息的完备性,研究了不同类型CSI的波束成形设计,当发送端已知系统瞬时信道状态信息时,文献[4]给出了MIMO高斯窃听信道的保密容量,当发送端已知系统的统计信道状态信息时,文献[5]和[6]分别从遍历保密容量和安全中断概率的角度对系统进行研究和分析。
近年来,有研究学者从不同角度研究了认知网络中的物理层安全传输问题[7-12]。其中,文献[7]从信息论角度对多天线认知无线电系统保密传输速率最大化和天线数的关系进行了探究。文献[8]考虑了认知无线网络中保密传输速率的输入信号方差设计问题,其中系统模型假定为一个单天线主用户和一个单天线窃听者的多输入单输出(multiple-input single-output,MISO)认知无线网络。通过在MISO认知系统中添加人工噪声(Artificial Noise,AN),文献[9]以次用户接收端的安全速率最大(Secrecy Rate Maximization,SRM)为目标利用波束成形技术来增强窃听端的噪声从而降低窃听用户对保密信息的窃取。在此基础上,文献[10]将MISO信道模型扩展到多输入多输出(Multiple-Input Multiple-Output,MIMO)信道中,作者利用连续凸估计算法(Successive Convex Approximation,SCA)将安全速率最大化问题转化为一个半正定规划问题,从而求得最终的近似解。进一步,针对发送端未知窃听者信道状态信息的情况,文献[11-12]基于最差情况约束设计了鲁棒的人工噪声安全传输算法,以保证即使信道状态信息具有较大的误差,也可以满足系统的限制条件。
不同于文献[9]和[11]假定次用户为单根接收天线,本文将人工噪声辅助安全预编码算法扩展到认知MIMOME场景。由于MIMO信道的复杂性较高,以安全速率最大化为目标,分析人工噪声协方差和次用户协方差的联合优化是一个难以求解的问题。进一步,我们将该双层迭代优化算法扩展到非理想信道信息情况,提出了一套基于最差情况的鲁棒人工噪声设计方案,最后仿真证实所提算法的有效性。
2 信号模型
考虑如图1所示的系统模型,包括一个主用户接收机(PU),一个次用户发射机(Alice),一个次用户接收机(Bob),K个窃听者(Eves),并且所有节点都配置多根天线,天线数分别为Np,Ns,Nd,Ne。这里假设窃听者的天线数相同,但本文所提算法也可以扩展到窃听者天线数不同的情况。假设Alice到Bob的信道矩阵为H0,Alice到PU的信道矩阵为G,Alice到第k个Eve的信道矩阵为Hk,k∈{1,2,…,K}。
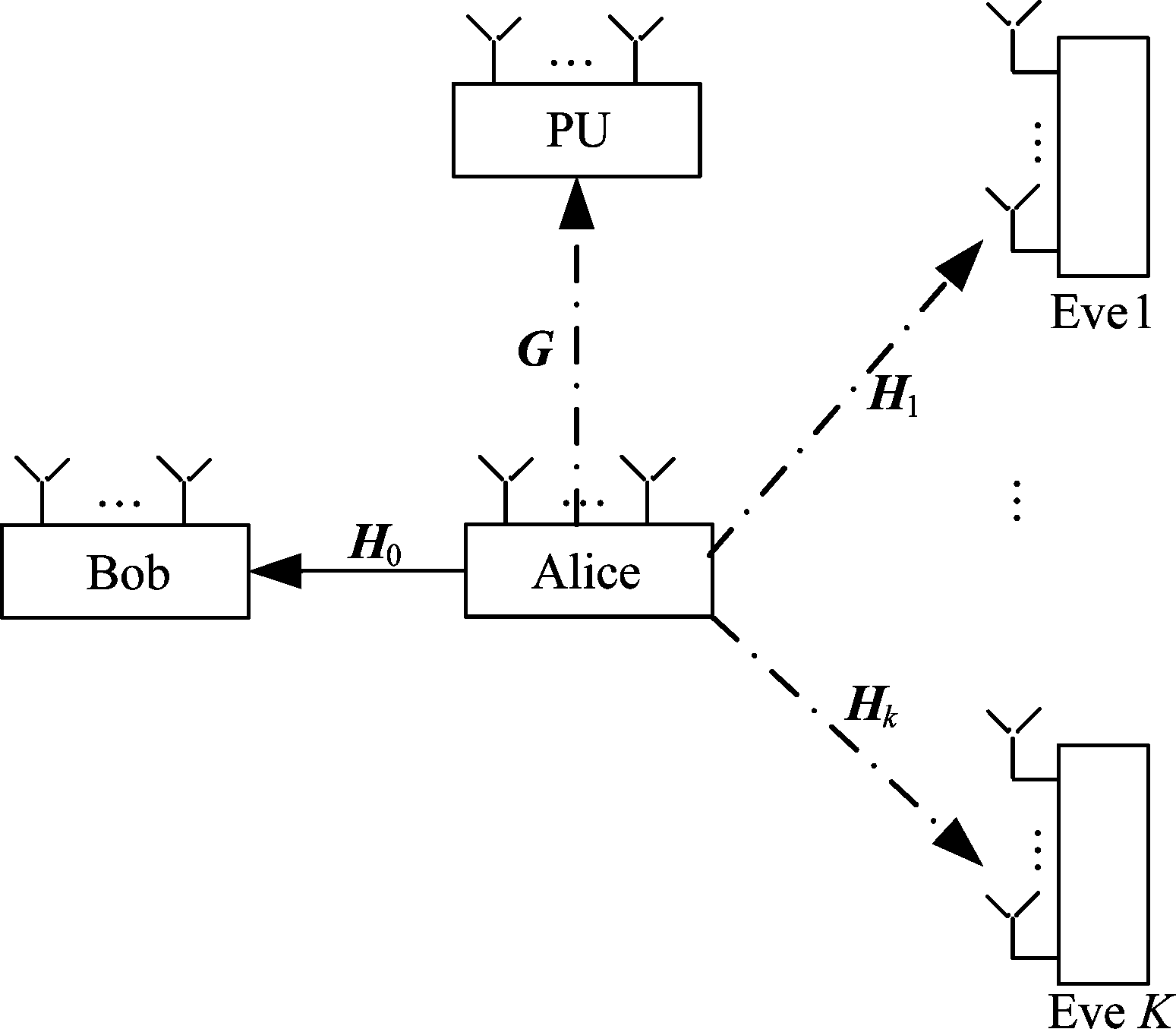
图1 认知网络MIMOME系统模型
Fig.1 Model of MIMOME system of cognitive network
系统中Bob和Eve k的接收信号分别表示为
y0=H0x+n0
yk=Hkx+ne,k,k ∈K
(1)
其中,n0,ne,k为加性高斯白噪声(其中包括了主用户对其造成的干扰),满足n0~CN(0,INd),ne,k~CN(0,INe),本文采用人工噪声辅助的物理层安全传输策略,在发送信号中加入一定功率的人工噪声后Alice的发送信号可以表示为
x=s+a
(2)
其中,s∈![]() Ns×1是传送给Bob的保密信息,a是产生的人工噪声。假设s和a是彼此独立的,此时接收端信号可以进一步表示为
Ns×1是传送给Bob的保密信息,a是产生的人工噪声。假设s和a是彼此独立的,此时接收端信号可以进一步表示为
y0=H0s+H0a+n0
yk=Hks+Hka+ne,k,k∈K
(3)
我们假设信号和噪声都服从零均值的高斯分布且s~CN(0,Q),a~CN(0,Z)。根据安全速率定义,系统的安全速率可以表示成[9]
(4)
其中,C0(Q,Z)是Alice到Bob的最大信息传输速率,表示为
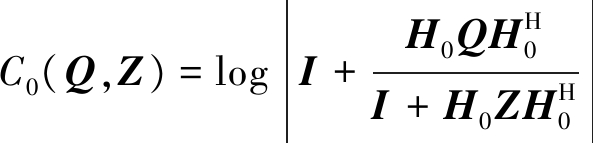
(5)
Ck(Q,Z)是Alice到第k个窃听者的最大信息传输速率,表示为
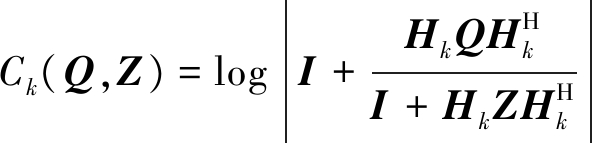
(6)
本文的主要目标在满足PU的干扰值和系统总功率约束下对系统安全速率进行最大化设计。因此优化目标函数可以表示为[13]
s.t.Tr[GQGH+GZGH]≤Γ
Tr(Q+Z)≤Pmax,Q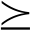 0,Z
0,Z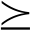 0
0
(7)
其中,Pmax表示Alice的最大传输功率,Γ表示主用户的干扰温度。
3 算法设计
我们首先假设Alice已知所有链路的信道状态信息,联合优化设计发射信号方差Q和噪声的协方差矩阵Z来最大化系统安全速率。进一步,将这一目标扩展到非理想信道状态信息情况下的鲁棒性人工噪声算法设计。
3.1 理想信道信息情况下人工噪声设计
假设发射端Alice能够获得全部的信道状态信息。优化问题的目标函数(7)是一个非凸函数,因而无法直接对其进行求解。通过一定的变换可以把优化问题转化成一个半正定规划问题,从而能够对其进行有效的求解。
首先,引入松弛变量log t代替Ck(Q,Z),需要满足条件Ck(Q,Z)≤log t且t≥1,问题可以演变为:
(8)
s.t.Tr[GQGH+GZGH]≤Γ
(9)
Tr(Q+Z)≤Pmax,Q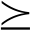 0,Z
0,Z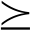 0
0
(10)
Ck(Q,Z)≤log t,∀ k∈K,t≥1
(11)
由于约束(11)非凸,并且log t在这里可以被视为窃听者最大允许互信息,为了减少计算的复杂度,在这里我们借助一个引理来对(11)进行简化[9]。
引理1
(12)
⟹![]()
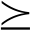 0,∀k ∈K
0,∀k ∈K
(13)
当且仅当rank(Q)≤1时,式(12)和式(13)相等,即具有相同的可行解。
注意到问题(8)中的优化变量Q,Z,t三者之间存在耦合,为了将其转化为凸函数,我们采用文献[10]所提的SCA算法对其进行处理。SCA算法的核心思想为:将优化问题中的非凸约束条件通过一阶泰勒展开近似转换成凸约束条件,然后通过递归方式求解一系列的凸优化问题。不同于文献[10]对目标函数和约束条件都采用SCA算法,本文仅对目标函数(8)进行递归求解。从而有效降低了计算复杂度。首先将C0(Q,Z)化成如下形式:
C0(Q,Z)=φ0(Q,Z)-![]() 0(Z)
0(Z)
(14)
其中![]() 相应地,
相应地,![]() 观察可知,
观察可知,![]() 0(Z)不能直接用内点法求解,依据泰勒展开式的定义首先对
0(Z)不能直接用内点法求解,依据泰勒展开式的定义首先对![]() 0(Z)进行一阶微分求导有[14]
0(Z)进行一阶微分求导有[14]
(15)
从而在给定一个初始值Zν,原始式子可以展开成
![]() 0(Z)≅
0(Z)≅![]()
(16)
因此,问题可以转换成以下形式:
s.t.Tr[GQGH+GZGH]≤Γ
Tr(Q+Z)≤Pmax
![]()
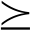 0,∀ k ∈K
0,∀ k ∈K
(17)
进一步,我们可以发现当固定变量t时,问题(17)是一个SDP问题。通过上述分析,我们可以将问题(17)转变成一个双层优化问题。其中,外层优化即是要先得到最优的t*,此时问题可以转化成一个求解单变量的优化问题,常用的搜索算法有一维搜索算法、均匀采样搜索算法和黄金搜索算法等[15]。而内层优化问题即是求解一个SDP问题。从而,为了完成线性搜索过程,需要确认变量t的取值范围,首先根据约束条件可知t≥1,t的上界确定如下:
(18)
式中,(a)是根据安全速率非负这一约束条件确定的,见目标函数(8);(b)是因![]() 并且由功率约束条件Tr(Q+Z)≤Pmax得Tr(Q)≤Pmax。因此,可以确定一维变量t满足
并且由功率约束条件Tr(Q+Z)≤Pmax得Tr(Q)≤Pmax。因此,可以确定一维变量t满足![]() 而内层优化问题能够利用标准的优化软件包如SeDuMi[16]或者CVX[17]求解得到最优解。
而内层优化问题能够利用标准的优化软件包如SeDuMi[16]或者CVX[17]求解得到最优解。
3.2 非理想信道信息情况下人工噪声设计
在实际应用中,由于估计误差、量化误差、多普勒扩展和反馈时延等因素的影响,Alice获得信道信息不可避免地存在着误差。这些非理想的信道状态信息将导致所设计的人工噪声发生噪声泄漏,降低系统的安全性能[1]。因此,需要考虑在信道信息存在误差的情况下,设计具有鲁棒性的物理层安全传输策略,来提升系统的安全性能。这里假设发送端获得的主用户信道状态信息G和窃听信道信息Hk均存在固定误差,该假设是合理的,因为主用户和窃听者通常并不是次用户网内节点。进一步,将其建模为椭球不确定集,因此主用户信道和窃听信道的矩阵分别表示为
![]() ∀ k ∈K
∀ k ∈K
(19)
其中,![]() 和
和![]() 分别是Alice到主用户和第k个窃听者的信道估计值,ΔG和ΔHe,k为相应的误差矩阵,分别建模为椭球不确定集[15],即
分别是Alice到主用户和第k个窃听者的信道估计值,ΔG和ΔHe,k为相应的误差矩阵,分别建模为椭球不确定集[15],即
G={ΔG:Tr(ΔGHCgΔG)≤1}
![]() ∀k ∈ K
∀k ∈ K
(20)
其中,Cg≻0、Ce,k≻0分别表示主用户信道和窃听信道的信道质量,它们确定了椭球误差界的形状。当Cg和Ce,k趋近于无穷大时,主用户信道和窃听信道将趋于理想情况,而当Cg和Ce,k趋近于零时,主用户和窃听信道将是最差的。
根据上述信道误差模型,基于最差情况最大化安全速率(Worst Case Secrecy Rate Maximization,WCSRM)的优化问题能够表示为:
s.t.Tr[GQGH+GZGH]≤Γ,∀ΔG∈G
Tr(Q+Z)≤Pmax,Q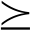 0,Z
0,Z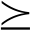 0
0
(21)
其中,![]() 为Alice的最大发送功率。从式(21)可知,基于最差情况设计的优化问题需要保证不确定集G和He,k中的每一个信道实现均满足约束条件。
为Alice的最大发送功率。从式(21)可知,基于最差情况设计的优化问题需要保证不确定集G和He,k中的每一个信道实现均满足约束条件。
通过联合设计波束成形向量Q和人工噪声协方差矩阵Z,可提髙系统的最差情况安全速率。由于对Q和Z的联合优化问题是非凸的,约束条件包含无穷多个凸集,该问题是一个NP-hard问题,通常是很难求解的。下面,通过将约束条件转变为确定的矩阵不等式,问题能够转换为一个半正定规划问题进行求解。
由于目标函数Cs(Q,Z)是非光滑函数,首先,注意到可以将C0(Q,Z)进行展开处理,![]() 通过引入松弛因子log β和log θ,对式(21)进行相应的处理,变换为
通过引入松弛因子log β和log θ,对式(21)进行相应的处理,变换为
(22)
(23)
Tr(Q+Z)≤Pmax,Q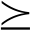 0,Z
0,Z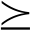 0
0
(24)
![]() ∀ k ∈K
∀ k ∈K
(25)
(26)
因为约束条件(23)、(25)及(26)是非凸的,很难得到其最优解,我们需要分别采取不同的方法对三个约束进行求解。首先,针对干扰温度约束(23)有
(27)
对(27)利用迹的转化公式和克罗内克积之间的关系:Tr(ZAZH)=vec(Z)H(I⊗A)vec(Z)、vec(ABC)=(CT⊗A)vec(B),可以将具有鲁棒性的干扰温度条件转变为
⊗![]() ⊗INp)gk}-
⊗INp)gk}-
![]() ⊗
⊗![]()
(28)
其中,![]() 因为(28)是一个半无限(Semi-infinite)约束集,我们使用S-Procedure引理来处理[12]。
因为(28)是一个半无限(Semi-infinite)约束集,我们使用S-Procedure引理来处理[12]。
引理2 令矢量函数![]() 是N维Hermitian矩阵。不等式f1(x)≥0⟹f2(x)≥0成立,当且仅当存在μ≥0,使得下列式子成立,
是N维Hermitian矩阵。不等式f1(x)≥0⟹f2(x)≥0成立,当且仅当存在μ≥0,使得下列式子成立,
⪯![]()
(29)
此时约束条件Γ(Q,Z,μ)详见式(36)。
其次,针对次用户安全速率约束(25)包含无穷多不等式,很难求出最优解的情况。类似理想信道信息下的处理方式,这里引入引理1来对(25)进行简化,log β在这里可以被视为窃听者最大允许互信息。
∀Hk∈He,k
(30)
⟹![]()
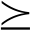 0,
0,
∀Hk∈He,k
(31)
当且仅当rank(Q)≤1时,式(30)和式(31)相等,即二者具有相同的可行解。因为式(31)是一个NP-hard问题,通常很难求解,我们引入了S-Procedure的推广[18]。
引理3 (Luo-Sturn-Zhang)
令函数满足f(X)=XHAX+XHB+BHX+C,令D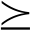 0,如果存在t≥0则下面的式子成立:
0,如果存在t≥0则下面的式子成立:
f(X)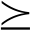 0,∀X∈ {X|Tr(DXXH)≤1}
0,∀X∈ {X|Tr(DXXH)≤1}
⟺![]()
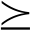 0
0
(32)
采用引理3,我们可以得到以下结果:
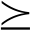 0,
0,
∀ Hk ∈He,k
(33)
⟹Tk(Q,Z, β,tk) 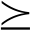 0
0
(34)
其中,Tk详见式(37)。
当且仅当rank(Q)≤1满足时,(33)和(34)是等价的,因此问题(22-26)可以表示成如下形式:
![]()
![]()
log β-log θ
s.t.Γ(Q,Z, μ)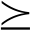 0, μ≥0
0, μ≥0
Tk(Q,Z, β,tk) 0,tk≥0,∀k ∈ K
0,tk≥0,∀k ∈ K
Tr(Q+Z)≤Pmax
(35)
通过上述分析,我们提出一个双层迭代优化算法对问题(35)求解。首先,在给定log β的值时,求解问题(35)的内部最大化问题,令其最优目标值为![]() (β),类似地通过前面的分析可知β的取值范围为
(β),类似地通过前面的分析可知β的取值范围为![]() 其次,针对外部最大化问题,对变量log θ采用一维线性搜索,同样根据安全速率非负可得θ的取值范围是
其次,针对外部最大化问题,对变量log θ采用一维线性搜索,同样根据安全速率非负可得θ的取值范围是![]() 因此问题可以采用双层迭代优化算法进行解决。
因此问题可以采用双层迭代优化算法进行解决。
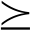 0
0
(36)
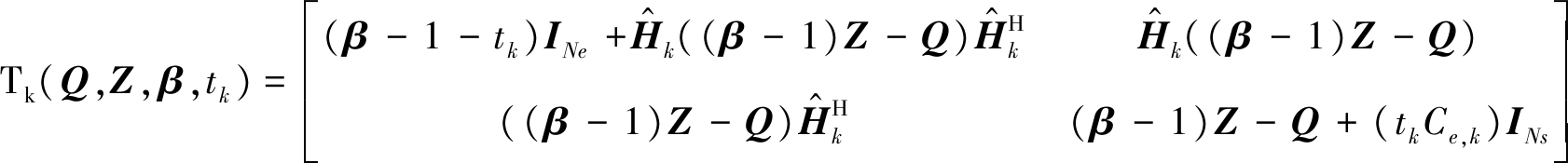
(37)
其中,∀ k ∈K。
4 仿真结果及分析
4.1 系统性能分析
下面给出仿真结果来验证所提的人工噪声辅助安全的性能。假定Bob和PU的天线数为Nd=2,Np=2,窃听者的个数为K=2。所得的最终数据是对500次独立信道实现结果的平均值。
图2给出了不同迭代次数下系统的安全速率变化情况。其中Pmax=10 dB,Alice和窃听者的天线数为Ns=4,Ne=2。从图中可以看出,随着迭代次数ν的增加,所提算法的安全速率逐渐增加,经过10次迭代以后,安全速率基本达到一个稳定的数值。由于非理想信道状态信息情况下涉及的优化变量更多,其安全速率在14次递归以后才趋于稳定。还可以看出在不同的干扰温度Γ下系统获得不同的安全速率,这是因为当Γ变大时,干扰温度约束松弛,系统能够获得更高的安全速率。
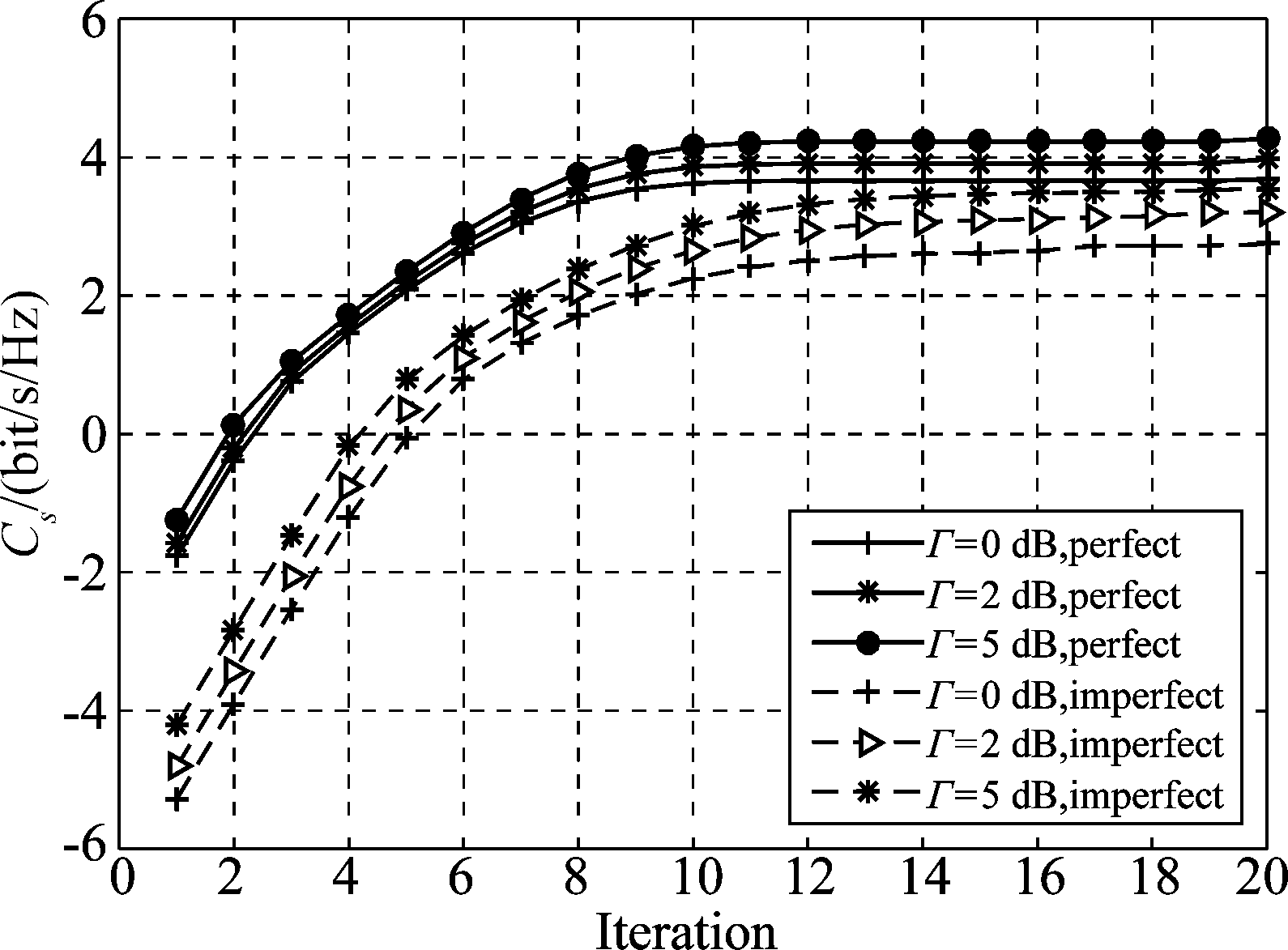
图2 不同干扰功率约束下的收敛性分析
Fig.2 Convergence analysis under different interference power constraints
图3是理想信道状态下的安全保密性能进行分析,分别在发送端Alice天线数Ns=4,Ns=6的情况下,将SCA算法[4]、没有人工噪声辅助安全时的算法和本文所提算法进行性能比较。其中干扰功率Γ=5 dB,从图3可见,随着发射功率的增加,本文所提一维线性搜索算法将获得更优的性能,尤其是当发送天线数增加时,系统将获得更高的安全速率。
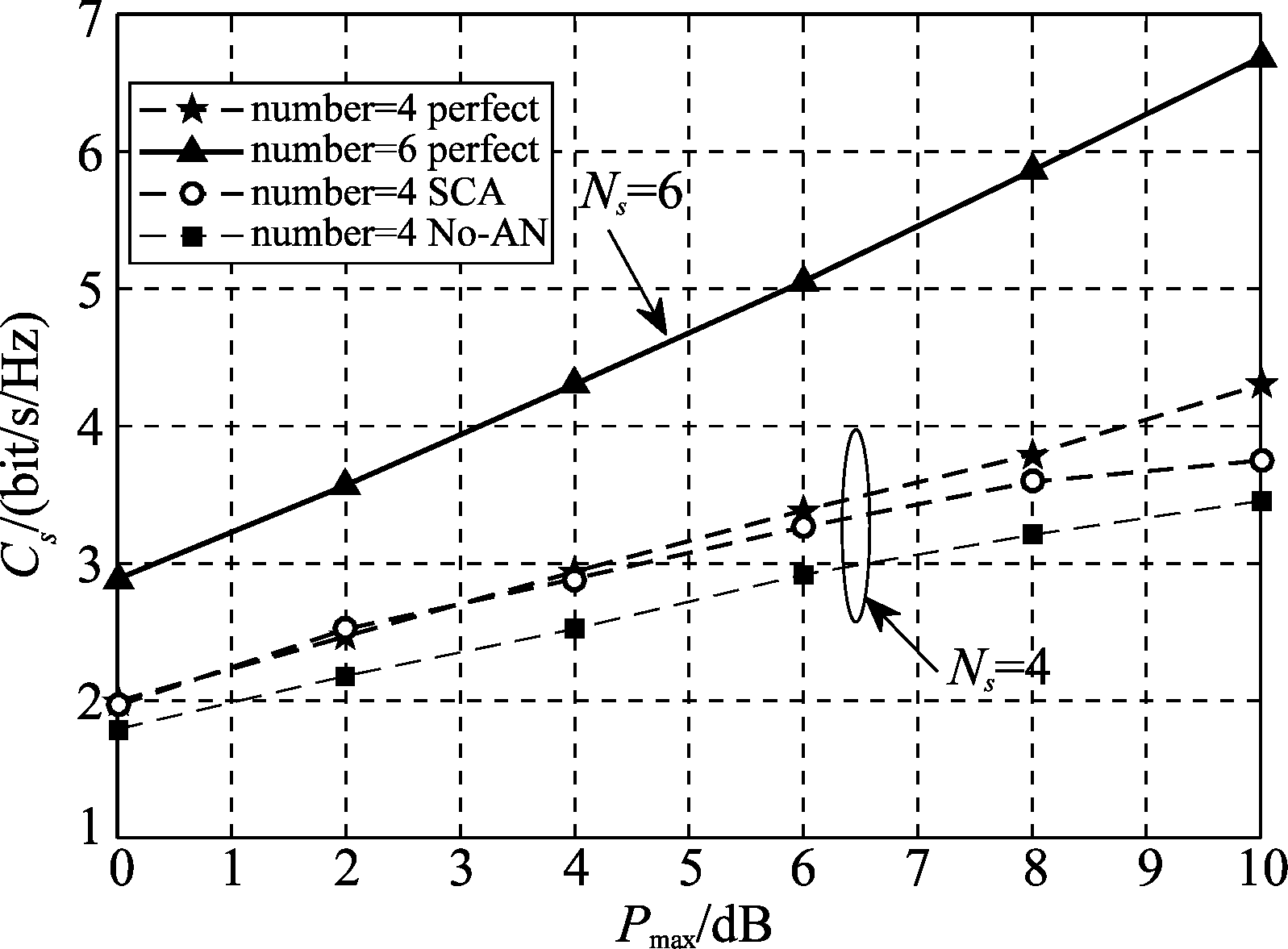
图3 安全速率与最大传输发送功率之间的关系
Fig.3 Achievable secrecy rate versus transmit power constraint of Alice
图4给出了在窃听者天线数分别是Ne=2,Ne=4时,发射功率和系统的安全速率的关系。可以看到,窃听者的天线数对整个认知系统所能达到的最大安全速率有着较大的影响,特别是当去除了主用户时,此时问题转换成传统MIMO窃听信道,随着发射功率的增加,算法将获得更高的安全速率。因为去掉干扰温度的限制条件之后,算法有了更大的自由度。虚线表示的是非理想信道状态信息在边界误差εg=εe,k=0.01的情况下的仿真结果,该结果表明,所设计的鲁棒人工噪声安全算法减弱了非理想信道信息对安全性能的影响。
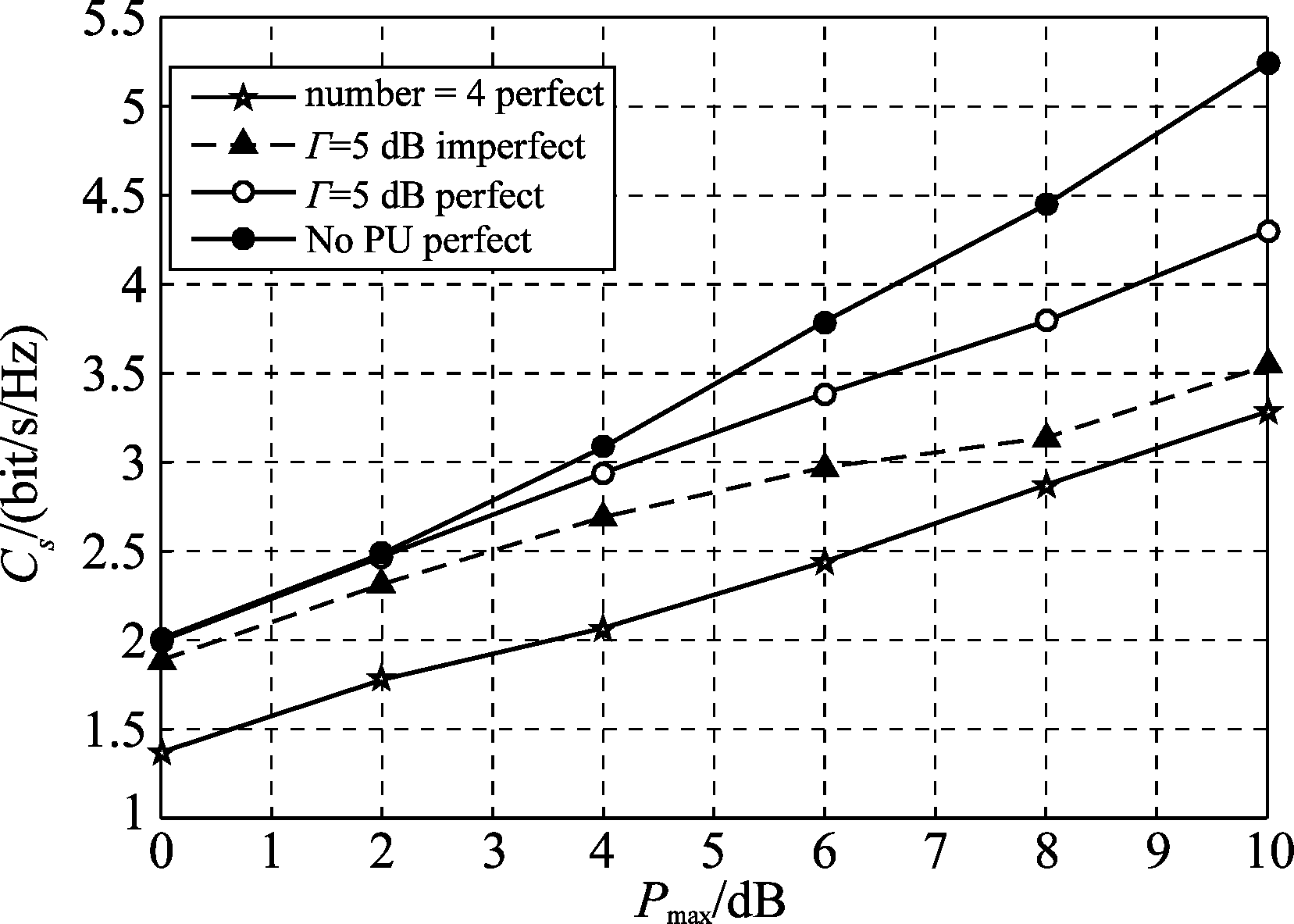
图4 安全速率与最大发送功率之间的关系
Fig.4 Achievable secrecy rate versus transmit power constraint of Alice
4.2 计算复杂度分析
目前MIMO通信网络的物理层安全研究已经有许多算法,其中比较经典的算法有SCA算法和本文采用的SDP算法,这里对两种算法的复杂度进行分析对比。可以看到所涉及到的优化问题中含有线性约束和线性矩阵不等式约束(Linear matrix inequality,LMI)。根据文献[19]可知,最差情况下的计算复杂度为![]() 其中θ为障碍参数,ε表示求解精度,L为每次计算的迭代代价。两种算法的比较详见表1。下面给出计算复杂度的具体分析过程:
其中θ为障碍参数,ε表示求解精度,L为每次计算的迭代代价。两种算法的比较详见表1。下面给出计算复杂度的具体分析过程:
1)针对问题(7),SDP算法主要包含2个维数为Ns的LMI约束,K个维数为Ne+1的LMI,以及2个线性约束。
2)SCA算法中主要包含2个维数为Ns的LMI约束,2+K个线性约束。
表1 不同算法的复杂度比较
Tab.1 Complexity comparison of different algorithms

算法复杂度顺序SDPO(nQmaxKNe+2Ns+K+2{K(Ne+1)3+2N3s+n[K(Ne+1)2+2N2s+2]+n2}),其中n=O(2N2s+1)SCAO(nDmax2Ns+K+2{2N3s+n[K+2N2s+2]+n2}),其中n=O(2N2s+1)
假设系统中窃听者和天线数分别为K=2,Ne=2,Ns=4,并且Dmax=Qmax=10,此时两者的计算复杂度结果分别为O(3.94×106),O(2.75×106)。可以看出,本文算法复杂度略高于SCA算法,但是从仿真中,我们可以发现,采用本文算法的保密速率较SCA算法的保密速率有0.6 bit/s/Hz的提升。所以算法的性能越好,其相应的计算复杂度越高。
4.3 说明备注
本文中主要考虑的是认知无线网络中次用户安全传输的保密速率优化问题,所以我们这里只考虑到次用户对于主用户的影响不能超过主用户的接收门限Γ。对于主用户传输对次用户网络的干扰在文章中归为噪声项,此时次用户端的接收噪声表示为n0=σp+σ0,其中σ0为主用户传输信号时对次用户产生的干扰,σp为传输信道中的白噪声,为了后面的方便计算,在文章中对噪声统一进行归一化处理即n0~CN(0,INd)。
5 结论
本文研究了在MIMO认知无线信道中,存在多个多天线窃听者时的安全传输问题。提出了人工噪声辅助的安全预编码算法。在发端的最大发送功率及认知用户的干扰功率受限时,联合优化发送信号矩阵和人工噪声协方差矩阵,最大化系统的安全速率。对于理想CSI和非理想CSI两种情况,采用双层优化算法,对SRM进行求解。最后仿真验证了所提安全传输方法与迫零人工噪声算法和SCA算法相比,能获得更高的安全速率。
[1] Liu Y, Chen H H, Wang L. Physical Layer Security for Next Generation Wireless Networks: Theories, Technologies, and Challenges[J]. IEEE Communications Surveys & Tutorials, 2016, PP(99): 1-1.
[2] Oggier F,Hassibi B.The secrecy capacity of the MIMO wiretap channel[C]∥IEEE International Symposium on Information Theory. IEEE,2008:524 -528.
[3] Chen X, Ng D W K, Gerstacker W H, et al. A Survey on Multiple-Antenna Techniques for Physical Layer Security[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1027-1053.
[4] Khisti A, Wornell G W. Secure Transmission With Multiple Antennas I: The MISOME Wiretap Channel[J]. IEEE Transactions on Information Theory, 2010, 56(7): 3088-3104.
[5] Li J, Petropulu A P. On Ergodic Secrecy Rate for Gaussian MISO Wiretap Channels[J]. IEEE Transactions on Wireless Communications, 2010, 10(4): 1176-1187.
[6] Li Zongmian, Mu Pengcheng, Wang Bo, et al. Practical Transmission Scheme with Fixed Communication Rate under Constraints of Transmit Power and Secrecy Outage Probability[D]. IEEE Commun. Lett, 2015.
[7] Zhang L, Zhang R, Liang Y-C, et al. On the relationship between the multi-antenna secrecy communications and cognitive radio communications[J]. IEEE Transactions on Communications, 2010, 58(6): 1877-1886.
[8] Pei Y, Liang Y-C, Zhang L, et al. Achieving cognitive and secure transmissions using multiple antennas[C]∥IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, PIMRC. Tokyo, Japan. 2009.
[9] Li Q, Ma W K. Spatially Selective Artificial-Noise Aided Transmit Optimization for MISO Multi-Eves Secrecy Rate Maximization[J].IEEE Transactions on Signal Processing, 2013, 61(10):2704 -2717.
[10] Fang B, Qian Z, Shao W, et al. Precoding and Artificial Noise Design for Cognitive MIMOME Wiretap Channels[J]. IEEE Transactions on Vehicular Technology, 2016, 65(8): 6753- 6758.
[11] Xiong J, Ma D, Wong K K, et al. Robust Masked Beamforming for MISO Cognitive Radio Networks With Unknown Eavesdroppers[J]. IEEE Transactions on Vehicular Technology, 2016, 65(2): 744-755.
[12] Luan T, Zhang X D, Gao F, et al. Robust Interference Mitigation Against Channel Uncertainty for MIMO Cognitive Radios[J]. IEEE Transactions on Vehicular Technology, 2014, 63(2): 970-975.
[13] Boyd Stephen, Vandenberghe Lieven. 凸优化[M]. 王书宁, 等, 译. 北京: 清华大学出版社, 2013: 130-136.
Boyd Stephen, Vandenberghe Lieven. Convex Optimization[M]. Wang Shuning, et al, translate. Beijing: Tsinghua University Press, 2013: 130-136. (in Chinese)
[14] 张贤达. 矩阵分析与应用[M]. 第2版. 北京: 清华大学出版社, 2013: 152-160.
Zhang Xianda. Matrix Analysis and Application[M]. The second edition. Beijing: Tsinghua University Press, 2013: 152-160. (in Chinese)
[15] 熊俊. 无线物理层安全传输关键技术研究[D]. 长沙: 国防科学技术大学, 2014.
Xiong Jun. Studies of Key Transmission Techniques in Wireless Physical Layer Security[D]. Changsha: National University of Defense Technology, 2014. (in Chinese)
[16] Sturm J F. Using SeDuMi 1.02, A Matlab toolbox for optimization over symmetric cones[J]. Optimization Methods & Software, 1999, 11(1- 4): 625- 653.
[17] Grant M. CVX: Matlab software for disciplined convex programming, version 1.21[J]. 2008:155- 210.
[18] Li B, Fei Z, Xu X, et al. Resource Allocations for Secure Cognitive Satellite-Terrestrial Networks[J]. IEEE Wireless Communications Letters, 2017, PP(99): 1-1.
[19] Wang K-Y, A M-C So, Chang T-H, et al, Outage constrained robust transmit optimization for multiuser MISO downlinks: Tractable approximations by conic optimization[J]. IEEE Trans.Signal Process., 2014, 62(21): 5690-5705.



