1 引言
分布式MIMO(Multiple-Input Multiple-Output)雷达，作为新雷达体制中的一种，自其被提出以来就引起了国内外众多学者的广泛关注[1-4]。分布式MIMO雷达的收发天线阵元在空间上分布很广，各天线接收到的信号可以认为是相互独立的，主要利用的是空间分集来获取性能增益。其对信号的处理方式分为相干和非相干两种[5-6]，相干处理要求所有收发天线阵元在时间和相位上都达到同步，但由于天线之间距离较远，对于现有器件水平而言，相位同步的要求难以满足。而非相干处理仅需满足时间上的同步，工程上易于实现。因此，本文所提的分布式MIMO雷达均采用非相干的处理的方式。
总体而言，分布式MIMO雷达大多采用时间信息或时频联合信息对目标进行定位[7-9]，而仅利用频率信息对目标定位的研究较少。然而，当发射的是窄带信号时，会导致时间信息的提取出现严重误差的问题[10]。在这样的情况下用时差(Time of Arrival, TOA)定位目标将会导致性能的大幅下降，但是，这种情况下的频率信息是足够准确的。因此，仅使用多普勒频移(Doppler Frequency Shifts, DFS)信息对目标进行定位的研究工作变得很有必要。而通常采用的定位方法分为两步进行：第1步，独立地从各接收信号中提取出测量参数(例如，时差或频差)。第2步，将这些测量参数写成与目标位置有关的公式，求解方程就可得到目标的位置估计。然而，这样的两步求解方式是次优的，因为在第1步参数提取的过程中忽略了所有测量参数必须相对于同一个目标位置的约束条件[11]。为了解决两步法中的不足，Weiss等人提出了直接定位(Direct Position Determination, DPD)的方法可以最优地估计目标位置[12]。它可以集中地处理所有接收到的数据，并利用接收数据中不同的时间延迟实现一步估计目标的位置。随后这个工作被扩展到了多个目标的定位中[13]。在窄带信号的情况下他们又提出了利用多普勒频移对多辐射源进行被动定位的方法[14]。仿真结果表明，在噪声较高的情况下，直接定位的结果优于两步定位法。上述方法解决的都是静止目标的定位问题，针对匀速运动目标，文献[15]提出了基于多普勒频率对动目标直接定位的方法。文献[16]针对接收站存在自定位误差的情况进行了直接定位算法研究并推导了此场景下的CRLB。
本文主要解决MIMO雷达系统中利用频率信息对目标进行定位的问题。我们采用直接定位的方法，使用多个移动发射和接收站对静止目标的位置进行估计。由多个发射站发射出基带正交的相同频率的窄带信号，经由目标反射，被多个接收站接收。由于接收站和目标之间存在相对运动会产生多普勒频移。将各接收站接收到的信号表示成有关目标位置的代价函数。基于极大似然(Maximum Likelihood, ML)的准则，上述代价函数的解，即为目标的位置。另外，我们还分析了该场景下的克拉美罗界(Cramer-Rao lower bound, CRLB)，并将其作为衡量算法性能的参照标准。仿真结果表明，所提DPD算法的定位性能在低信噪比(signal to noise ratio, SNR)的情况下具有显著优势。
2 定位模型
考虑分布式MIMO雷达系统中的定位场景：由M个运动站发送基带正交的窄带信号，经目标反射后被L个静止观测站接收。静止目标位置记为p=[x,y]T。 接收站对信号进行了K次观测，第k次观测时发射站的位置记为
速度记为
接收站的位置固定，标记为
其中k={1,…,K}，l={1,…,L}，m={1,…,M}。假设每次观测时长较短，发射站和接收站的状态保持不变，由于本文采用窄带信号传输，信号带宽B远小于两接收站之间传播时间的倒数(即，B≪1/τ=c/d，τ为两站之间信号的最大传播时间，d为站间距离，c为光速)。由于上述约束条件，对于各接收站来说，同一传输信号的复包络在相同的观测时刻几乎没有变化[11,14]。则经过基带变换后，第l个接收机第k次接收到的信号为：
0≤t≤T
(1)
其中T为观测时长，sm,k(t)为第k次观测中第m个发射站发出的信号包络，假设为已知。 bm,l,k为第k次观测中第m个发射信号被第l个站接收时的信号衰减系数，ωl,k(t)为接收站l在第k次接收信号时的观测噪声，假定服从均值为零的复高斯分布。fm,k为第k次观测时目标与第m个发射站之间的多普勒频移表示为：
(2)
符号c为光速，即电磁波的传播速度。载波频率记为fc，假设已知。将连续信号模型进行离散化处理，各接收站每次观测时的快拍数为N，则接收信号可表示为如下矩阵形式：
rl,k =sk⊙Akbl,k+ωl,k
(3)
其中，
bl,k = [b1,l,k,b2,l,k,...,bM,l,k]T
(4)
rl,k = [rl,k[1],rl,k[2],...,rl,k[N]]T
(5)
ωl,k = [ωl,k[1],ωl,k[2],...,ωl,k[N]]T
(6)
sk = [s1,k,s2,k,...,sN,k]T
(7)
sn,k = [s1,k[n],s2,k[n],...,sM,k[n]]T
(8)
Ak = [A1,k,...,AN,k]T
(9)
An,k = [ej2πf1,knT,ej2πf2,knT,...,ej2πfM,knTs]T
(10)
运算符号⊙表示Schur积，即矩阵的对应点相乘。注意到Ak是与目标位置有关的未知矩阵。矢量ωl,k独立同分布，协方差矩阵为
根据公式(3)，定位问题可以表述为：已知观测矢量rl,k，估计目标的位置p。对于两步定位法，通常对各接收信号做相关处理以提取定位参数[17]。提取到第k次多普勒频移测量值记为
根据ML准则，可通过最小化如下代价函数求得目标位置p：
(11)
根据公式(2)中表示的多普勒频移与目标位置的关系，可以用网格搜索的方法来求解上述问题。但测量参数提取的处理过程是独立的，其中忽略了所有测量参数必须相对于同一个目标位置的约束条件，可能会导致估计性能的下降。
通过接收信号的表达式可以看出，当目标辐射源与观测站之间存在相对运动时，目标的位置包含在多普勒频移量中。多普勒频移与目标位置的关系是一个复杂的非线性方程。针对只利用多普勒频率信息对目标状态估计的情况文献[18]进行了详细的系统可观测性分析。二维平面内，对于目标位置固定、发射频率固定的情况,若已知辐射源频率，对匀速运动的发射站通过两组以上的测量就可以实现目标定位;另外，从式(2)可以看出，
为发射站与目标的径向速度，若此项为零，则对应了系统不可观测的情况，算法失效。即
为零，或
为零(观测站运动在与目标连线的切线上)。因此，在MIMO雷达系统中，布站时要注意避免出现发射站与目标无距离变化的情况以保证算法的有效实现。
3 CRLB分析
从公式(3)中可知，接收信号服从复高斯分布r～CN(m,R)，其中接收信号矢量均值为：
ml,k = sk⊙Akbl,k
(12)
将其写成矩阵的形式为：
m
...,
H
(13)
其中，
mk = 
...,
H
(14)
由于L个接收站进行了K次观测，定义接收信号矢量和信道衰减矢量分别为：
r
...,
H
(15)
b
...,
H
(16)
其中，
rk = 
...,
H
(17)
bk = 
...,
H
(18)
定义矢量
其中
分别表示矢量b的实部和虚部。则关于信号模型(3)的未知参量可表示为
(19)
定义
为未知参数的无偏估计量，则均方误差可表示为[19]：
)
)T}≥J-1()
(20)
其中J()是关于 的Fisher信息矩阵(FIM)，可表示为如下分块矩阵的形式：
(21)
下面对每个矩阵块分开求解。其中，Jp,p是与目标位置信息相关的Fisher矩阵块，
是与目标位置和信号衰减参数相关的Fisher矩阵块，其他块的意义相似。
Fisher矩阵的每个元素可以通过下式求得[19]:
(22)
其中R{·}表示取实部运算，相应地
{·}表示取虚部运算。为求Jp,p，首先求解
和
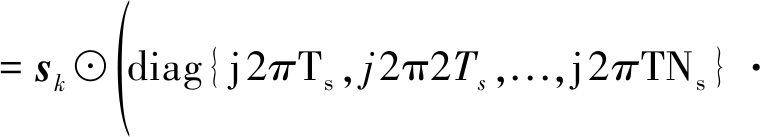
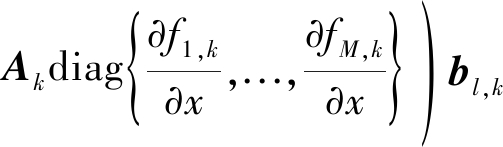
(23)
其中，
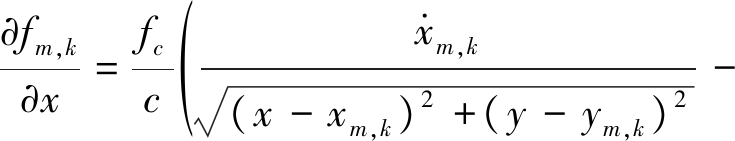
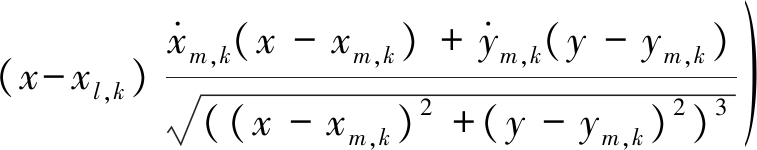
(24)
类似可以求得：
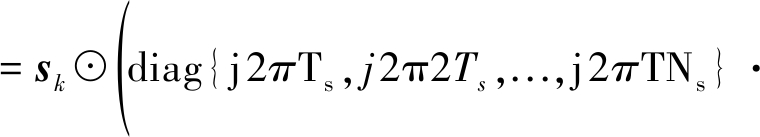
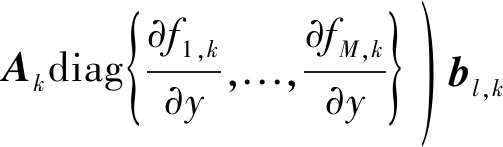
(25)
其中
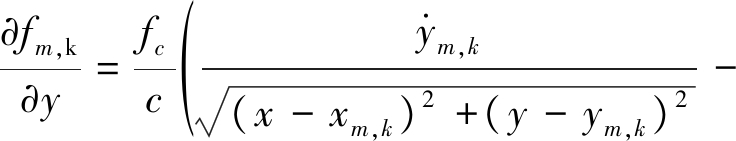
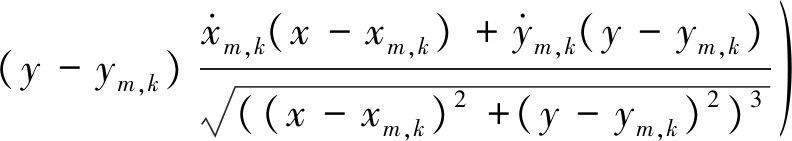
(26)
则
(27)
(28)
接下来考虑
及
的求解。首先，计算ml,k对
求导可得到：
(29)
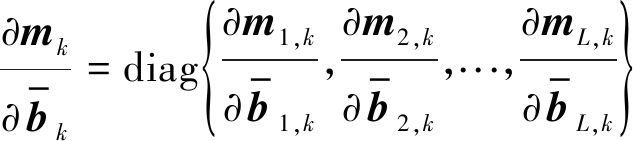
(30)
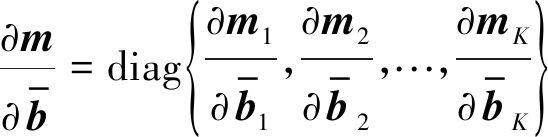
(31)
类似可以求得
由上述表达式可以得到分块矩阵中的Jp,p为：
(32)
其中，
(33)
(34)
(35)
分块矩阵中的
为：
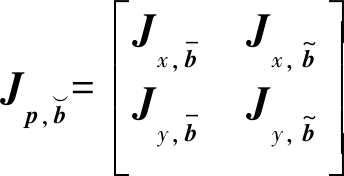
(36)
其中，
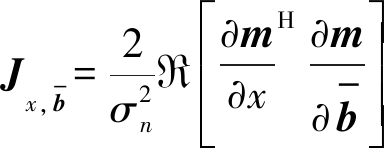
(37)
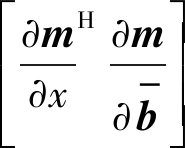
(38)
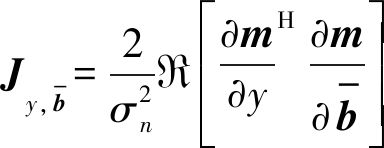
(39)
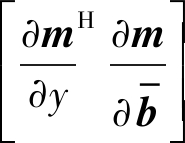
(40)
分块矩阵中的
为：
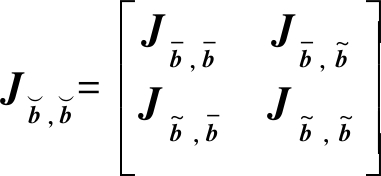
(41)
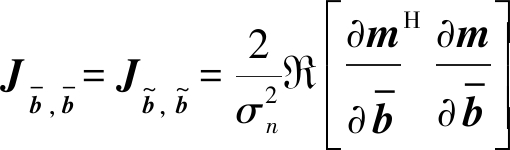
(42)
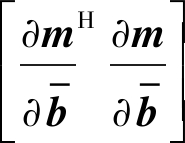
(43)
根据(21)中的Fisher信息矩阵得到关于目标位置p的CRLB为：
·
(44)
4 直接定位求解
根据公式(3)中接收信号的模型，目标位置的极大似然估计可通过求如下代价函数的最小值得到：
(45)
定义
则公式(45)可以写为：
(46)
则使得公式(46)取最小值的bl,k可表示为：
(47)
将公式(47)带入公式(46)得到：
(48)
定义，
(49)
注意Pk为投影矩阵[20]，即
因此，公式(48)可以写为：
(50)
则目标位置p的估计可以等价为求如下代价函数的最大值：
(51)
在信号包络sk已知的情况下，目标位置p只与Ak有关，可通过网格搜索的方式求上述代价函数取最大值时的p，即为目标位置的估计：
(52)
5 计算量分析
本文所提算法在波形已知的情况下，求取公式(52)的最大值点，即为目标的位置估计。其中对求得
的计算复杂度为
的计算复杂度为O(NM)，求‖Pkrl,k‖ 2的计算复杂度约为O(N2)。假设搜索网格点数为Ng，在采样点数目大于发射站数目的情况下，所提算法的主要计算复杂度可表示为O(NgKLN2M)。
对于两步定位法：假设两组信号，分别以r1[n]和r2[n]表示，数据长度为N，则此时的频差的MLE可表示为[21]：
(53)
其中r1[n]为第一个站的接收信号，r2[n]可以为已知载频的参考信号或者是另一个站接收到的信号。对
做FFT变换[22] 便可求得估计量
此过程中，针对参考波形已知的情况，其计算复杂度为O(2KMN(2+log2N))。在两步定位的第2步中，根据公式(2)及(11)估计目标位置。若搜索网格数量为Ng，则第2步中的计算复杂度为O(7NgKM)。因此，两步法的主要计算复杂度可以近似表示为 O(2KMNlog2N+7NgKM)。
通过分析可以看出，相比于两步定位法，文中所提算法的计算复杂度有所增加，但是下节的仿真实验结果会说明新算法具有更高的定位精度，因此，新算法是以提高计算量为代价来提高估计性能的。
6 仿真实验
本文采用5个发射站3个接收站的MIMO雷达模型来验证算法性能。各发射站的初始位置分别为
速度均为
共进行了3次观测，每次观测发射站位置移动1500 m，速度保持不变。接收站位置固定，分别为
我们采用蒙特卡罗实验的方法将直接定位算法性能和第2节中所提的两步定位法进行对比，并画出第3节中推导得出的CRLB界作为衡量两种算法性能的参照曲线。每个噪声功率下进行500次独立仿真实验取均值。以均方根误差表征各算法对目标位置的估计精度，其定义如下：
(54)
其中Q为蒙特卡罗次数，
为第q次蒙特卡罗实验的目标位置估计。发射为中心频率fc=1 GHz的QPSK信号，码速率为2.5 kb/s。除非另做说明，我们采取K=3次观测，每次观测的快拍数为N=100。目标位置为p=[6000,4000] m。在仿真的过程中，设置的信噪比为
假设衰减满足‖bl,k‖ 2=1，信号功率设为1，则信噪比可以表示为
其中
即为噪声的方差。
(1)仿真1
信噪比取-10 dB到10 dB时，比较两种算法的定位结果如图1所示。从图1中的仿真结果可以看出，在较低信噪比的情况下，直接定位的仿真结果要优于两步法。在较高信噪比的情况下，两种算法定位性能相当且都近似达到了CRLB。
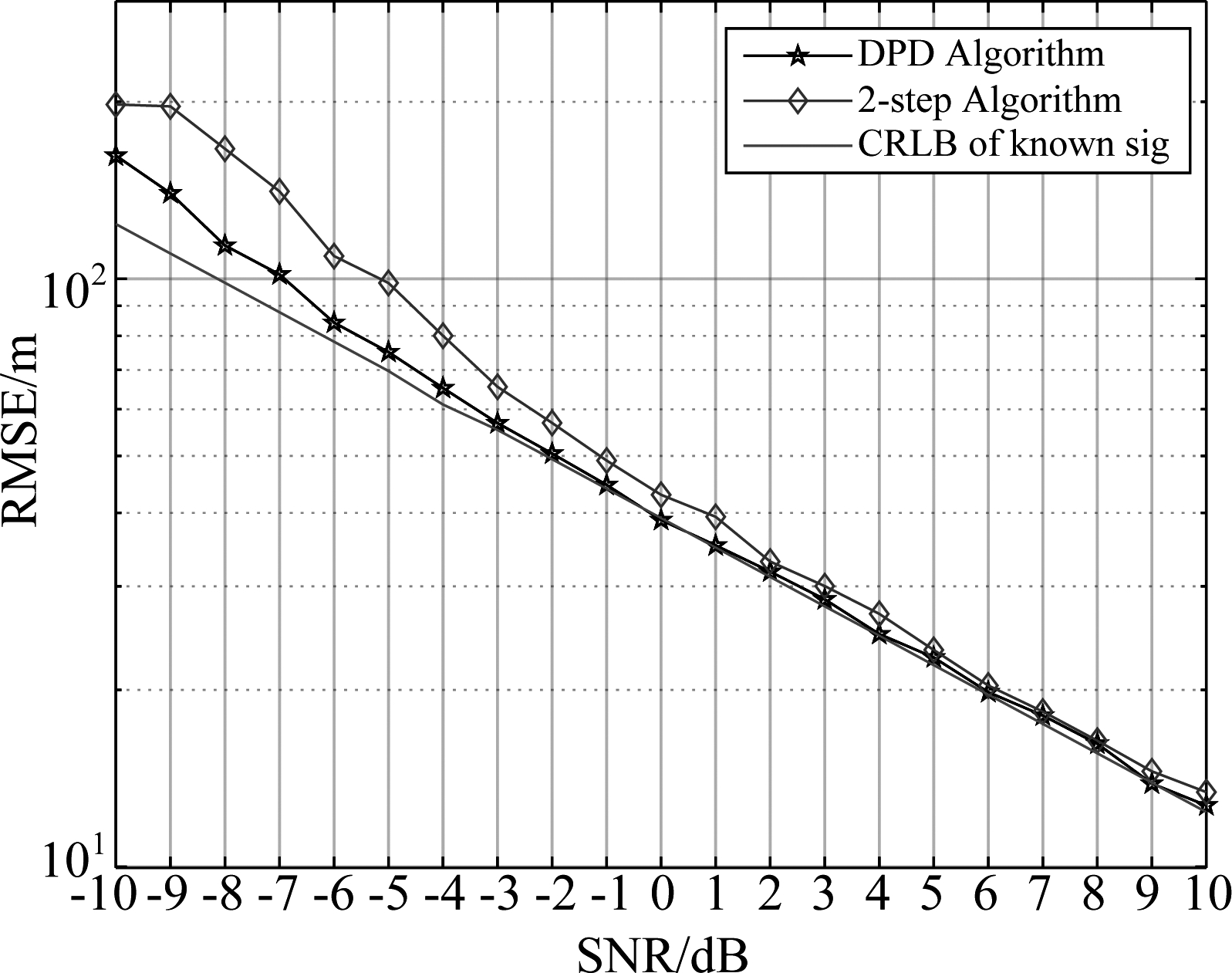
图1 不同算法的RMSE及CRLB随SNR变化曲线
Fig.1 RMSE of the different localization methods and the CRLB under the different SNR
(2)仿真2
考察定位结果随观测次数的变化情况。设置信噪比为固定值-5 dB，其余仿真参数不变。观测次数从1次增加到10次。从图2中的仿真结果可以看出，随着观测次数的增加，定位性能得到提高，且直接定位的估计精度高于两步法。
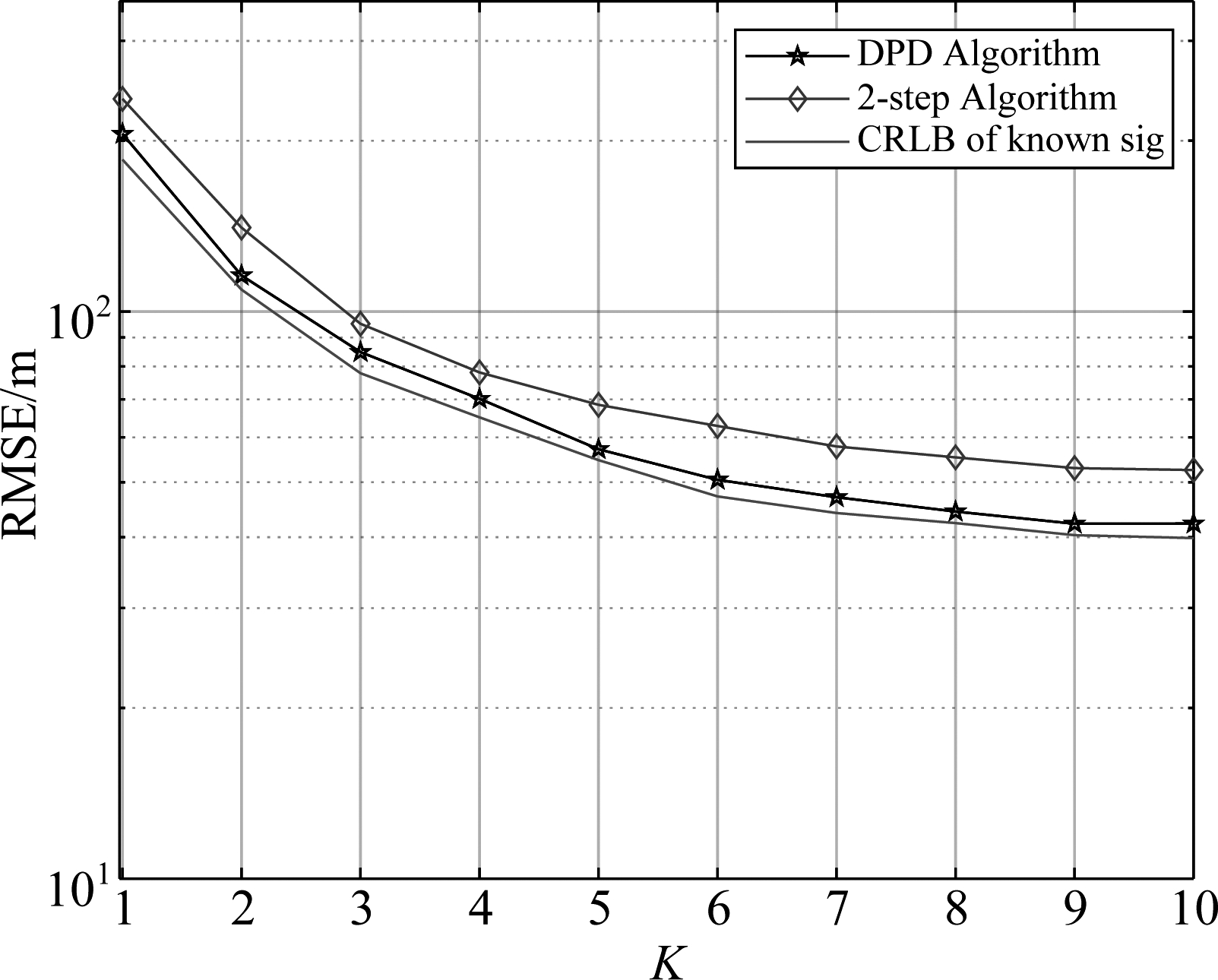
图2 不同观测次数时两种算法的RMSE
Fig.2 RMSE of the two localization methods under the different interception intervals
(3)仿真3
图3仿真了不同接收站数目下两种算法的定位结果。此时信噪比固定为-5 dB，其余仿真参数不变。从图3中可以看到随着接收站数目的增加，定位精度增加，且所提算法性能优于两步定位法，更加贴近CRLB。
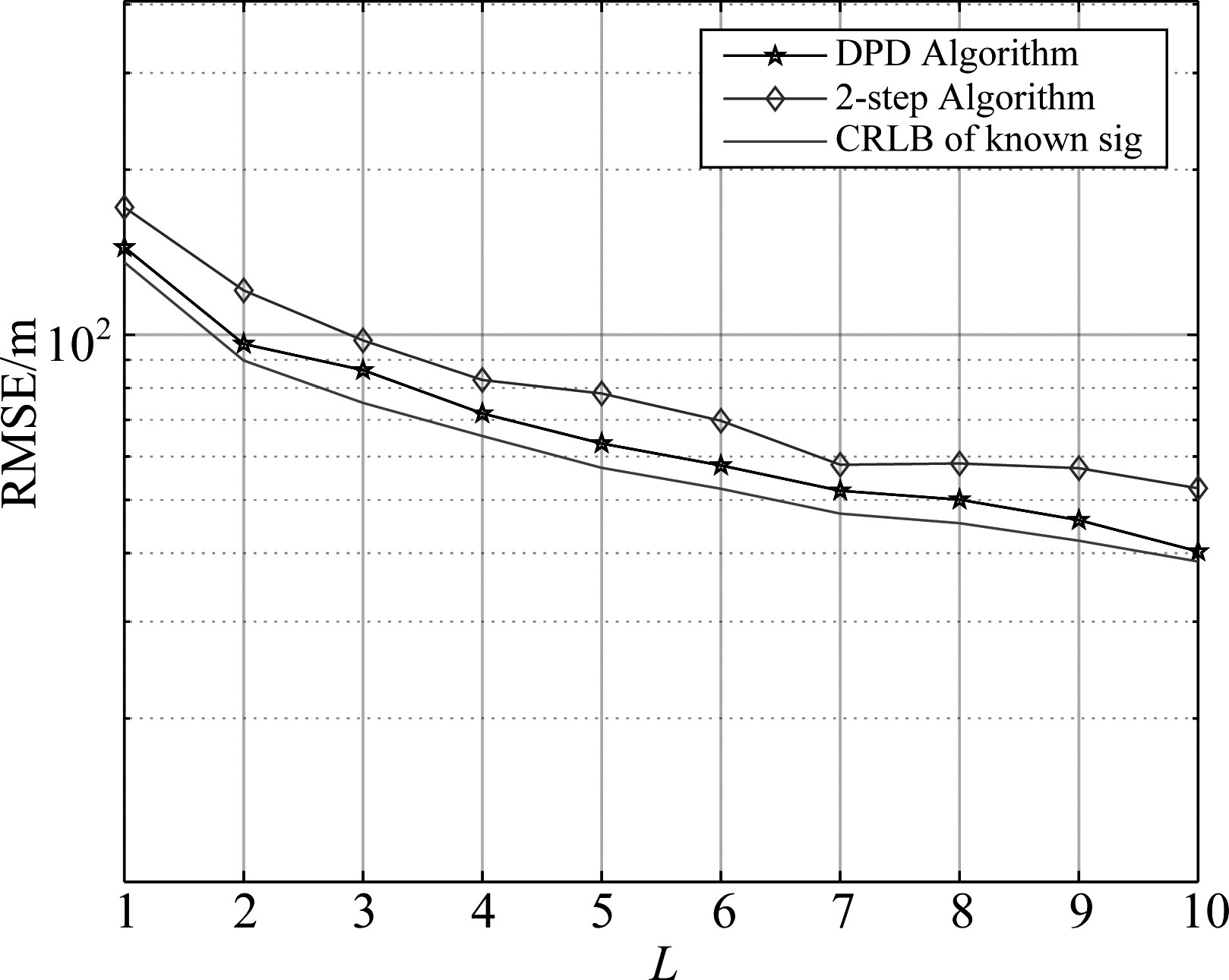
图3 不同接收站数量时两种算法的RMSE
Fig.3 RMSE of the two localization methods under the different receiver number
(4)仿真4
仿真快拍数从100到300之间变化，信噪比固定为-5 dB，其余仿真参数不变。对比两种算法的定位性能，通过图4可以看出，随着快拍数的增加，定位性得到提高，且相同快拍数目下，所提算法的定位性能优于两步定位法。
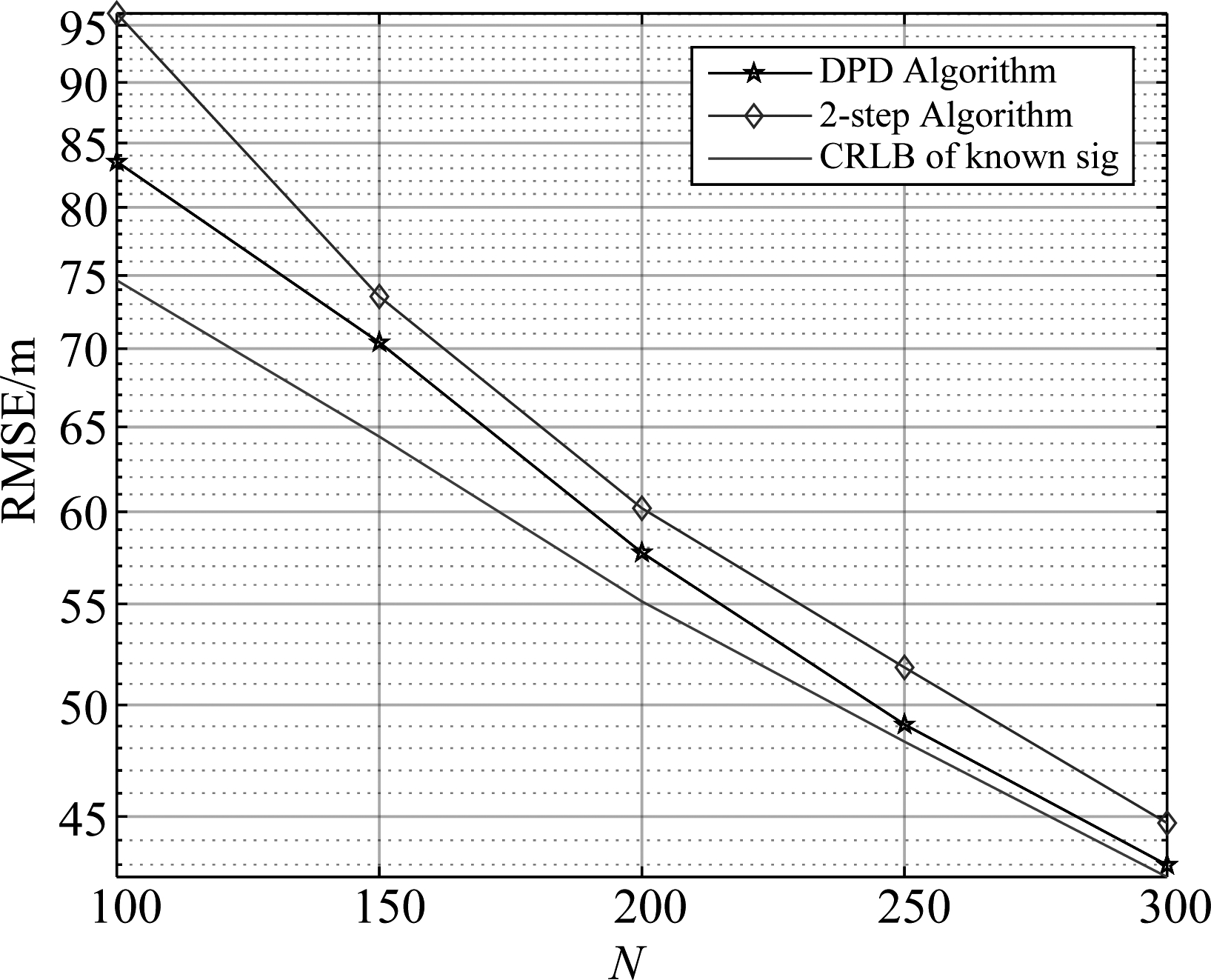
图4 不同快拍数时两种算法的RMSE
Fig.4 RMSE of the two localization methods under the different snapshots
相比于两步定位法，直接定位法具有更高的定位精度，可用于MIMO雷达系统中的高精度目标定位。本文所提的直接定位算法利用到了信号的波形信息对目标位置进行解算，但在波形未知情况下直接定位算法仍显示了高于两步法的定位精度[11,14]，可见波形信息并非算法性能提升的主要因素。因此作者下一步的研究内容，将针对MIMO场景下发射波形未知的目标定位问题进行研究和分析。
7 结论
本文主要研究了MIMO雷达系统中，在已知信号发射波形的前提下，仅使用多普勒频移信息对目标进行定位的方法。该方法不需要进行定位参数的提取，基于发射站和目标之间的相对运动产生的多普勒频移，在极大似然的准则下，直接利用所有接收到的数据实现对目标位置的一步估计。此外，本文还对此场景下的CRLB界进行了推导和仿真。仿真结果表明，所提算法的定位性能在较低信噪比下优于两步定位法，且在较高信噪比下与两步法定位精度相当，都近似地贴近CRLB界。
[1] Bar-Shalom O, Weiss A J. Direct positioning of stationary targets using MIMO radar[J]. Signal Processing, 2011, 91(10): 2345-2358.
[2] 薛永华, 李秀友, 孙艳丽, 等. 分布式MIMO天波超视距雷达阵地配置[J]. 信号处理, 2016, 32(4): 379-387.
Xue Yonghua, Li Xiuyou, Sun Yanli, et al. Sites Placement of Distributed MIMO Sky-wave Over the Horizon Radar[J]. Journal of Signal Processing, 2016, 32(4): 379-387. (in Chinese)
[3] 赵勇胜, 赵拥军, 赵闯, 等. 一种新的分布式 MIMO 雷达系统运动目标定位代数解算法[J]. 电子与信息学报, 2017, 40(3): 548-556.
Zhao Yongsheng, Zhao Yongjun, Zhao Chuang, et al. New Algebraic Algorithm for Moving Target Localization in Distributed MIMO Radar Systems[J]. Journal of Electronics & Information Technology, 2017, 40(3): 548-556. (in Chinese)
[4] 李梦婉, 景小荣, 莫林琳. 多小区大规模MIMO系统中基于部分导频交替复用的导频污染减轻方法[J]. 信号处理, 2017, 33(8): 1104-1114.
Li Mengwan, Jing Xiaorong, Mo Linlin. Pilot Contamination Reduction Method with Alternately Fractional Pilot Reuse for Multi-cell Massive MIMO Systems[J]. Journal of Signal Processing, 2017, 33(8): 1104-1114. (in Chinese)
[5] Du Y, Wei P. An Explicit Solution for Target Localization in Noncoherent Distributed MIMO Radar Systems[J]. IEEE Signal Processing Letters, 2014, 21(9): 1093-1097.
[6] He Q, Blum R S. Noncoherent versus coherent MIMO radar: Performance and simplicity analysis[J]. Signal Processing, 2012, 92(10): 2454-2463.
[7] Zou Y, Wan Q, Cao J. Target localization in noncoherent distributed MIMO radar system using squared range-sum measurements[C]∥IEEE, International Conference on Signal Processing. IEEE, 2017.
[8] Zou Y, Want Q. Moving target localization in noncoherent distributed MIMO radar systems using range and range rate measurements[C]∥Signal and Information Processing Association Summit and Conference. IEEE, 2017: 1- 6.
[9] Yang H, Chun J. An Improved Algebraic Solution for Moving Target Localization in Noncoherent MIMO Radar Systems[J]. IEEE Transactions on Signal Processing, 2015, 64(1): 258-270.
[10] Kalkan Y, Baykal B. Target localization and velocity estimation methods for frequency-only MIMO Radars[C]∥Radar Conference. IEEE, 2010: 458- 463.
[11] Amar A, Weiss A J. Localization of Narrowband Radio Emitters Based on Doppler Frequency Shifts[J]. IEEE Transactions on Signal Processing, 2004, 56(11): 5500-5508.
[12] Weiss A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513-516.
[13] Tzafri L, Weiss A J. High-Resolution Direct Position Determination Using MVDR[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6449- 6461.
[14] Tirer T, Weiss A J. High resolution localization of narrowband radio emitters based on Doppler frequency shifts[J]. IEEE Transactions on Signal Processing, 2017, 141: 288-298.
[15] 王鼎, 张刚. 一种基于窄带信号多普勒频率测量的运动目标直接定位方法[J]. 电子学报, 2017, 45(3): 591-598.
Wang Ding, Zhang Gang. A Direct Localization Method for Moving Narrowband Source Based on Doppler Frequency Shifts[J]. Acta Electronica Sinica, 2017, 45(3): 591-598. (in Chinese)
[16] Wang D, Yin J, Liu R, et al. Performance analysis and improvement of direct position determination based on Doppler frequency shifts in presence of model errors: case of known waveforms[J]. Multidimensional Systems and Signal Processing, 2018: 1- 42.
[17] Stein S. Differential delay/Doppler ML estimation with unknown signals[J]. Signal Processing IEEE Transactions on, 1993, 41(8): 2717-2719.
[18] Xiao Y C, Wei P, Yuan T. Observability and Performance Analysis of Bi/Multi-Static Doppler-Only Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1654-1667.
[19] Van-Trees H L. Detection, Estimation and Modulation Theory Part IV: Optimum Array Processing [M]. Wiley-Interscience, New York, 2002.
[20] Meyer C D. Matrix analysis and applied linear algebra [M]. Siam, 2000.
[21] Weinstein E. Measurement of the differential Doppler shift[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1982, 30(1): 112-117.
[22] Stein S. Algorithms for ambiguity function processing[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 2003, 29(3): 588-599.
