1 引言
间歇采样转发干扰可基于数字射频存储器(DRFM)产生。该干扰具有雷达信号的特征,可获得雷达的脉冲压缩增益,同时具有欺骗和压制的干扰特性,显著降低了雷达的工作性能。目前,针对间歇采样转发干扰抑制的研究取得了一定的进展。首先,空域干扰抑制利用目标、干扰来向差异实现抗干扰,但目前仍无法在被动模式下获得纯干扰协方差[1];在波形设计方面,可通过设计特殊波形,破坏干扰信号多普勒频率的输出连续性来实现抗干扰[2];此外,随着人们对目标极化散射机理理解的加深,极化鉴别技术也成为抑制间歇采样转发干扰的一个重要方法[3]。
当干扰信号从雷达天线主瓣注入接收机时,传统的抗干扰方法难以奏效。目前针对主瓣抗干扰的研究主要在空域、时频域以及极化域展开。空域抗主瓣干扰主要包括阻塞矩阵预处理、投影特征矩阵预处理、和差波束抗干扰以及大口径分布式阵列抗干扰[4]。这些方法在特定情况下均能取得一定的成效,同时也值得进一步改进;时频域主瓣抗干扰主要采用变换域方法以及失配滤波,但要求干扰不能覆盖回波频段[5];极化域主瓣抗干扰主要采用极化滤波的方法,该方法不能应用于未极化信号或变极化信号[6]。
本文针对主瓣间歇采样转发干扰,将基于时频特性分析的干扰辨识方法与基于大口径分布式雷达的空域抗干扰方法相结合。首先,通过分布式雷达阵列将单部雷达面临的主瓣干扰转换为分布式雷达的旁瓣干扰;随后,通过对回波信号进行时频特性分析在一维距离像上辨识干扰,估计纯干扰训练样本;最后,将训练样本应用于MVDR波束形成器完成干扰抑制。
本文第1部分首先介绍了主瓣干扰、间歇采样转发式干扰的背景与研究现状,介绍本文的大致思路以及安排;第2部分介绍线性分布式雷达系统,建立雷达信号、间歇采样转发干扰信号的数学模型,并描述传统的空域抗干扰MVDR波束形成器的缺陷;第3部分介绍了干扰辨识、波束形成的算法原理;第4部分通过仿真验证本文方法的有效性,并分析其抗干扰性能;第5部分对全文进行总结。
2 信号模型与问题描述
2.1 系统描述
一维分布式雷达系统由一个主雷达和N个辅助雷达组成,如图1所示。记相位中心位于原点的雷达M0为主雷达,M1～MN为辅助雷达。辅助雷达中M1～Mm位于主雷达左侧,Mm+1～MN位于主雷达右侧(1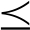
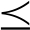mN-1)。考虑由主雷达M0发射信号照射目标,目标反射信号以及干扰机采样转发信号共同辐射各雷达。单部雷达M0工作时,波束宽度较宽,干扰机位于主瓣内,形成主瓣干扰;通过添加辅助雷达M1～Mm组成分布式阵列,其合成方向图主瓣变窄,如图1虚线所示,此时干扰机位于分布式阵列合成方向图主瓣之外,形成旁瓣干扰。
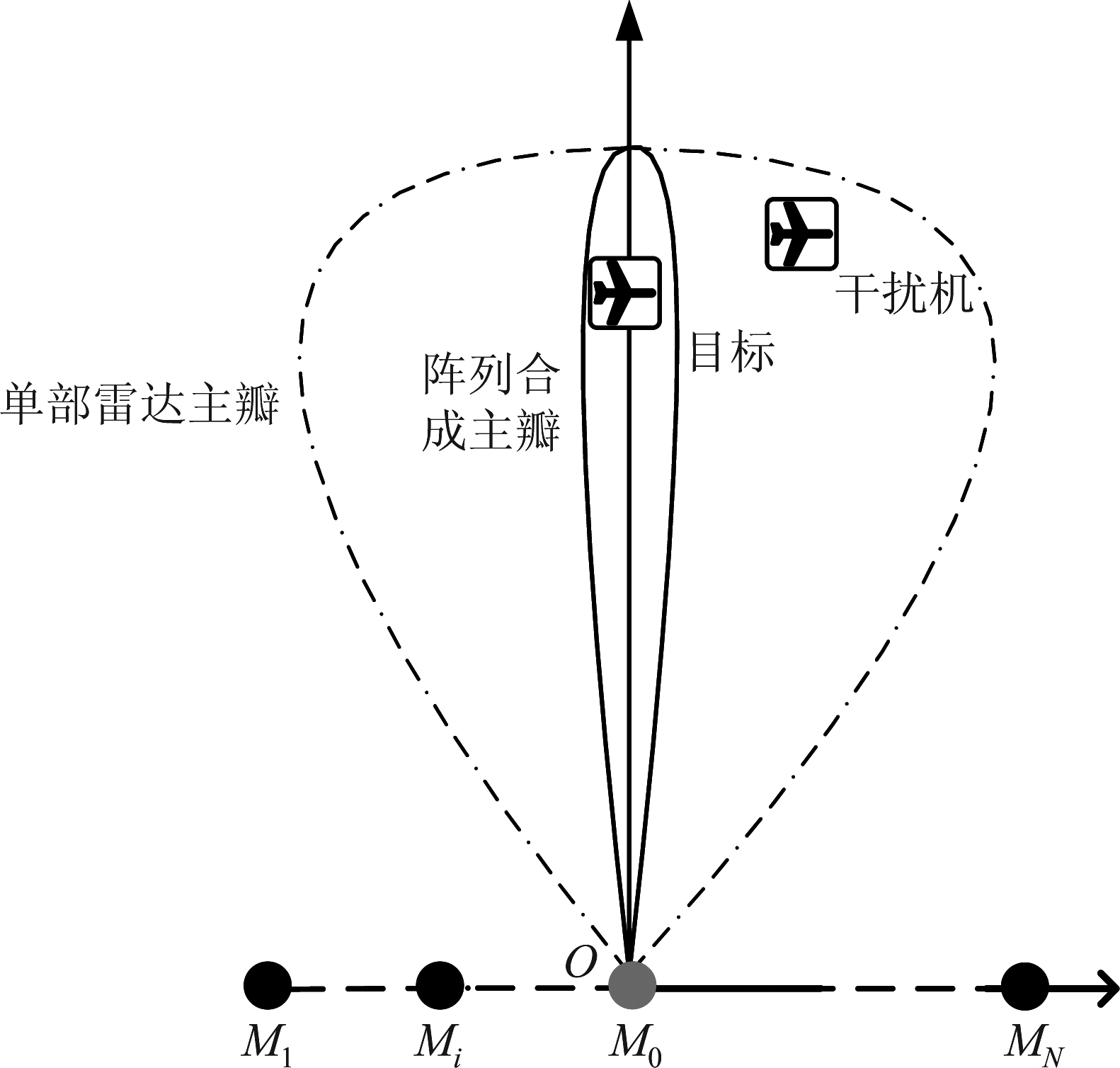
图1 分布式雷达系统示意图
Fig.1 Distributed radar system
2.2 信号建模
假设雷达发射信号为:
s(t)=p(t)exp(j 2πf0t)
(1)
其中,t为时间变量,p(t)为发射信号包络, f0为信号载频。由于各雷达与目标之间的距离存在差异,因而各雷达接收的回波信号存在不同的时延。考虑主雷达发射瞬时窄带信号时,时延的作用仅体现在相移上,信号包络时延差可忽略。雷达Mi接收目标回波信号,做下变频处理得到基带信号可表示为:
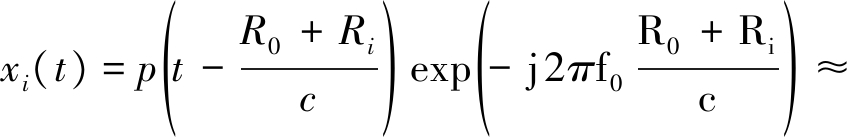
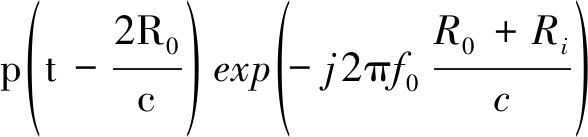
(2)
其中c为光速,Ri为雷达Mi与目标间距离(i=0,1,...,N)。
此外,DRFM干扰机会及交替采集和转发一段雷达信号,常用的采样转发方式包括直接转发、重复转发,忽略采样与转发之间的时间间隔,其示意图如下图所示:
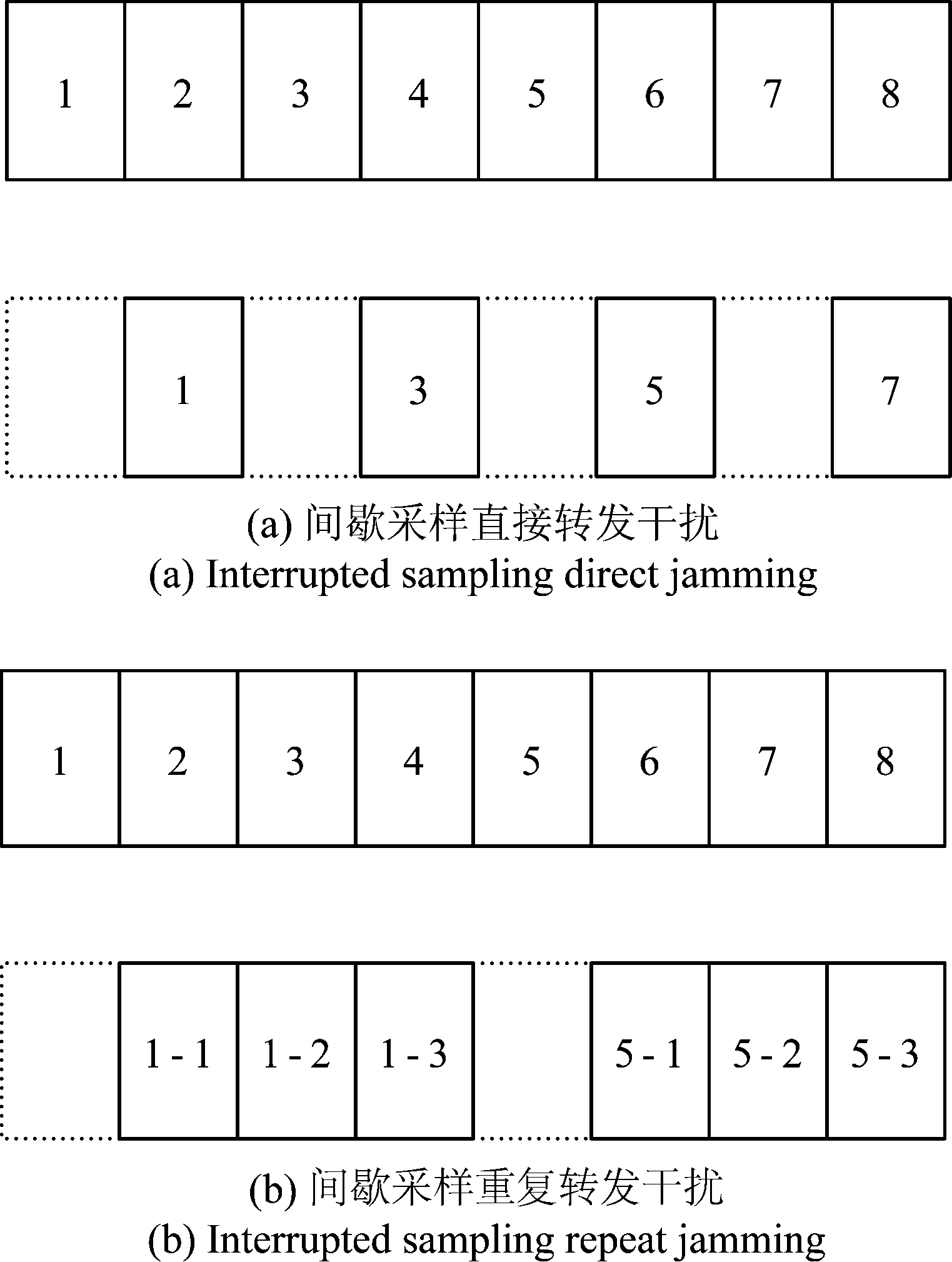
图2 间歇采样转发干扰工作原理示意
Fig.2 The principle of interrupted sampling repeater jamming
如图2所示,直接转发干扰信号可表示为:
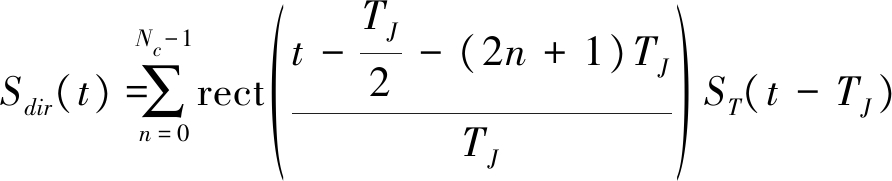
(3)
其中,TJ为切片宽度,Nc为切片个数,ST(t)为干扰机截获的雷达信号的包络。同理,重复转发干扰信号可表示为:
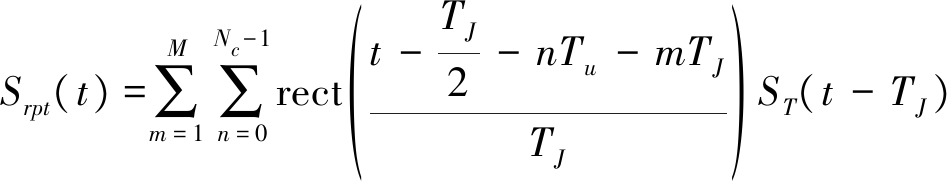
(4)
其中,M为每个切片转发的个数,Tu=(m+1)TJ为采样间隔[7]。以重复转发干扰为例,雷达Mi接收到的干扰信号可表示为:
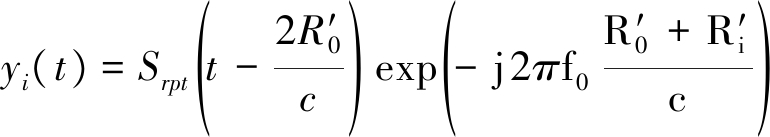
(5)
其中,
为雷达Mi与干扰机间距离(i=0,1,...,N)。
2.3 问题描述
间歇采样转发干扰由DRFM式干扰机产生。干扰机首先截获雷达发射信号,采样一个片段进行转发,再进行下一次采样,转发,依次类推,直至雷达脉冲结束。间歇采样转发干扰信号具有雷达信号的特征,可获得雷达的脉冲压缩增益。使得目标信号被淹没在密集的假目标群中。传统的空域抗干扰方法利用目标、干扰机的空间聚散性,保证目标方向信号得到增益,干扰方向信号被抑制。
DRFM干扰机在雷达停止工作后,也停止采样,因而雷达无法通过被动模式获到纯干扰信号,即抗干扰处理的训练数据中包含目标信息。空域自适应信号处理中,当目标的角度确定时,无论训练数据是否包含目标信号,均能够抑制干扰信号、保留目标信号。而在实际应用中,目标的角度并不能准确得到。在目标角度存在偏差的情况下,当训练数据不包含目标信号,通过抗干扰处理可以抑制干扰信号,同时目标信号损失较小;当训练数据包含目标信号时,通过抗干扰处理可以抑制干扰信号,但是目标信号损失较大,且目标信号强度越大,目标信号损失也越大[8]。因此,针对间歇采样转发干扰,在目标角度存在偏差的情况下,采用传统的空域自适应抗干扰方法会出现严重的信号相消问题。
3 基于干扰辨识的主瓣间歇采样转发干扰抑制方法
3.1 基于一维距离像时频分析的干扰辨识
假设干扰机产生直接转发式干扰,则分布式雷达系统中雷达Mi接收到的信号可表示为:
si(t)=Axxi+Ayyi+n0(t)=
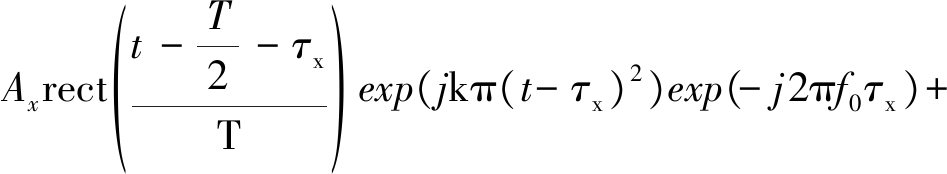
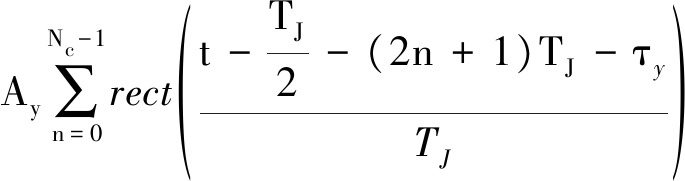
exp(jkπ(t-TJ-τy)2)
exp[-j 2πf0(TJ+τy)]+n0(t)
(6)
其中,Axxi为雷达接收到的目标分量,Ayyi为雷达接收到的干扰分量,n0(t)为雷达接收机噪声;T为雷达发射线性调频信号脉宽,Ax、Ay分别为目标、干扰脉压前的幅度,τx、τy分别为目标、干扰机与雷达Mi间的双程延时。对接收信号进行脉压得到一维距离像可表示为:
(7)
其中,φ=2πkTJ(t-TJ-τy),Ax、Ay分别为目标、干扰脉压后的幅度,第一项为目标回波脉压结果,第二项为干扰信号脉压结果,n1(t)为噪声项脉压结果。其中干扰脉压结果的幅度响应为:
(8)
由上式可推断干扰在一维距离像上为一个主假目标和多个对称分布的次假目标,整体服从sin c包络,根据包络项sin c[kTJ(t-TJ-τy)]推断主瓣宽度为2/kTJ。考虑每个切片转发M次,则相邻假目标的间隔为Δt=1/(M+1)TJ,则干扰脉压主瓣内干扰峰值个数为:
(9)
对脉压后的一维距离像做时频分析:
(10)
上式得到距离-频率二维分布图,距离维上,目标、干扰位于不同的距离门;频率维上,由于目标信号脉压后的包络为标准的sin c函数,该sin c函数主瓣宽度为带宽的倒数,该主瓣经FFT处理后频谱范围对应线性调频信号的带宽,经时频分析在频率维上表现为一条直线,且直线长度为信号带宽;而干扰信号脉压结果是由多个切片叠加组成,切片宽度较窄,表现在时频分析上频率维宽度明显小于目标,且由于截获位置差异引入不同的初始相位,故干扰的时频分析结果在频域上对应不同的频点。根据这一特征差异,可以对目标、干扰加以辨识,区分目标、干扰所在的时域距离门[9]。
3.2 主瓣间歇采样转发干扰抑制
当分布式雷达系统口径达到一定量级时,各雷达接收的回波信号已经不能近似等效为平面波。此时,需要用菲涅尔模型取代平面波模型,来计算分布式雷达系统的导向矢量。根据分布式雷达系统描述,构建菲涅尔模型下的目标的导向矢量为:
a0 =[β1,...,βm,β0,βm+1,...,βN]
(11)
其中有
...,N)[10]。
根据干扰辨识以及距离门区分结果,提取一维距离像中干扰主瓣内的2M+1个距离门对应的数据,构成训练数据X。该训练数据是纯干扰信号的估计,不包含目标信号,采用该训练数据理论上可避免传统自适应滤波中的信号相消问题。基于训练数据,估计协方差矩阵:
RX = (XXH)/L
(12)
其中L为训练样本的样本数。MVDR波束形成器在保证目标方位增益恒定,同时总输出功率最小为准则,其最优权矢量可表示为:
(13)
其中
为最优权矢量对应的最小输出功率。利用式(13)的权矢量作用于接收信号,实现干扰抑制[8]。
4 仿真验证
仿真条件:分布式雷达系统为一维线阵,一发五收有向天线,各雷达均匀排布,间隔50 m,波束指向为主雷达法线方向。目标与干扰夹角为3°。信号参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
参数参数值中心频率/MHz400信号带宽/MHz10采样率/MHz80脉宽/μs40
4.1 本文方法抗干扰方法验证
由于信号为瞬时窄带信号,可认为分布式系统对同步的要求较低;同时,各个单元雷达接收机幅相条件一致,有如下几组仿真。
仿真1:目标位于法线方向,干扰方向与目标方向夹角为3°,估计的期望信号方向与真实方向偏差0.5°;间歇采样转发干扰类型为直接转发式,切片宽度为5 μs,各切片转发1次;SNR=-5 dB、10 dB,INR=40 dB。
仿真2:目标位于法线方向,干扰方向与目标方向夹角为3°,估计的期望信号方向与真实方向偏差0.5°;间歇采样转发干扰类型为重复转发式,切片宽度为5 μs,各切片转发3次;SNR=-5 dB、10 dB,INR=40 dB。
图3(a)表示直接转发式加目标脉压的一位距离像,对其作时频分析如图3(b)所示,其中目标信号脉压后主瓣宽度为带宽倒数,结果FFT处理在频域范围对应LMF信号带宽;由于干扰切片宽度较窄,故干扰信号脉压后的时频分布表现为点阵,且带宽宽度比目标信号窄。根据干扰、目标的时频特性差异可以对其加以辨识。图4(a)、(b)分别表示SNR=-5 dB情况下传统方法和本文方法抗干扰后一维距离像对比,如图所示,传统方法在期望信号估计出现偏差情况下,在抑制干扰的同时,目标信号存在一定的损失;本文的抗干扰算法则可以抑制直接转发式干扰并保留目标信号。
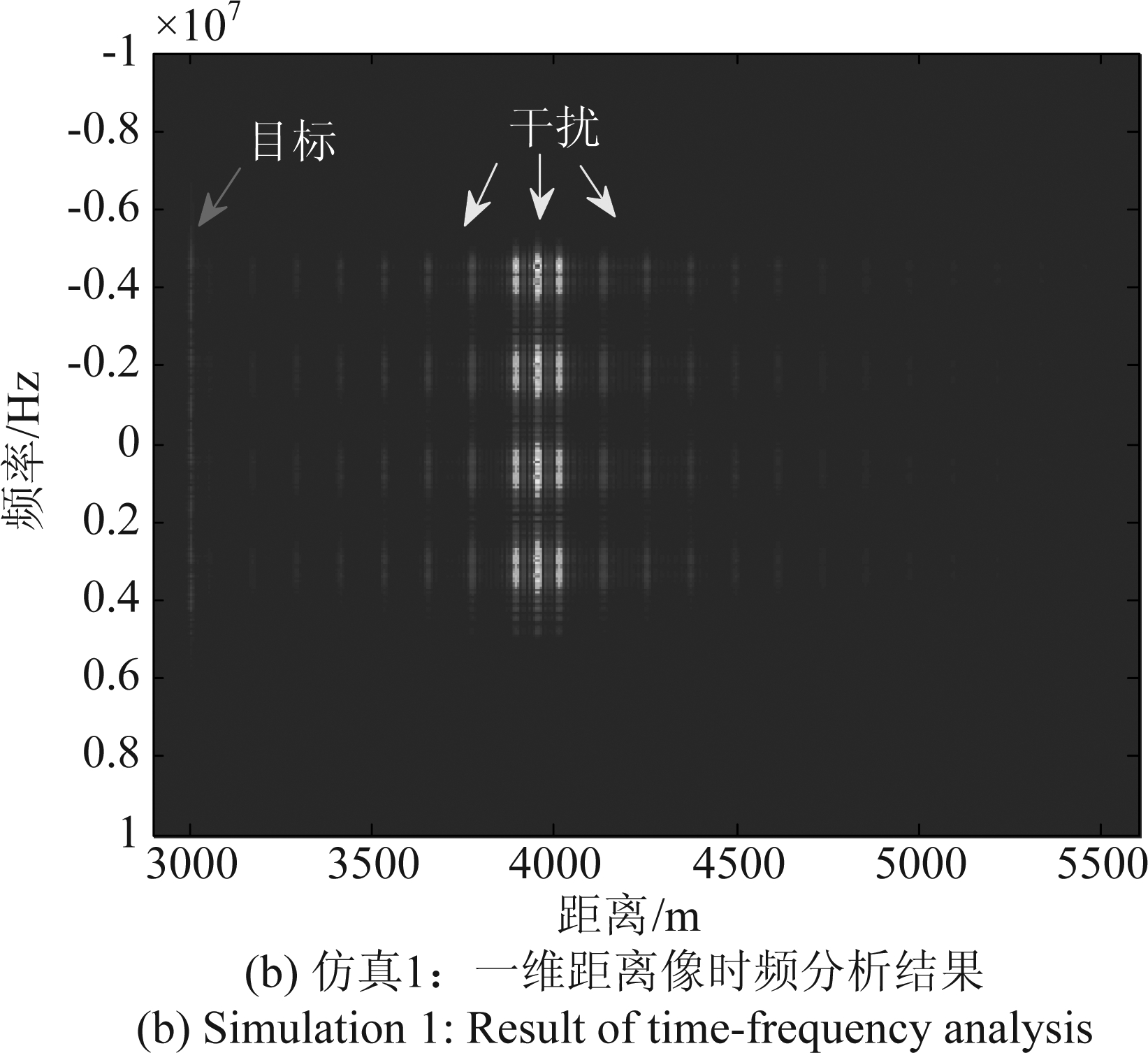
图3 直接转发式干扰的一维距离像及其时频分析结果(SNR=-5 dB)
Fig.3 One-dimensional range profile and time-frequency analysis of ISDJ (SNR=-5 dB)
图4 抗干扰后脉压结果图(SNR=-5 dB)
Fig.4 Pulse compression result of suppressing jamming (SNR=-5 dB)
图5(a)、(b)分别表示SNR=10 dB情况下传统方法和本文方法抗干扰后一维距离像对比,如图所示,在SNR较高的情况下,传统方法在期望信号估计出现偏差情况下,在抑制干扰的同时,目标信号损失更为严重;本文的抗干扰算法则可以抑制直接转发式干扰并保留目标信号。
同理,图6(a)为重复转发式干扰加目标脉压一维距离像,图6(b)为其时频分析结果。由图7(a)、(b)所示,SNR=-5 dB情况下传统抗干扰方法目标信号损失存在一定的损失,本文抗干扰方法可抑制重复转发式干扰并保留目标信号。由图8(a)、(b)所示,SNR=10 dB情况下传统抗干扰方法目标信号损失更为严重,本文抗干扰方法可抑制重复转发式干扰并保留目标信号。
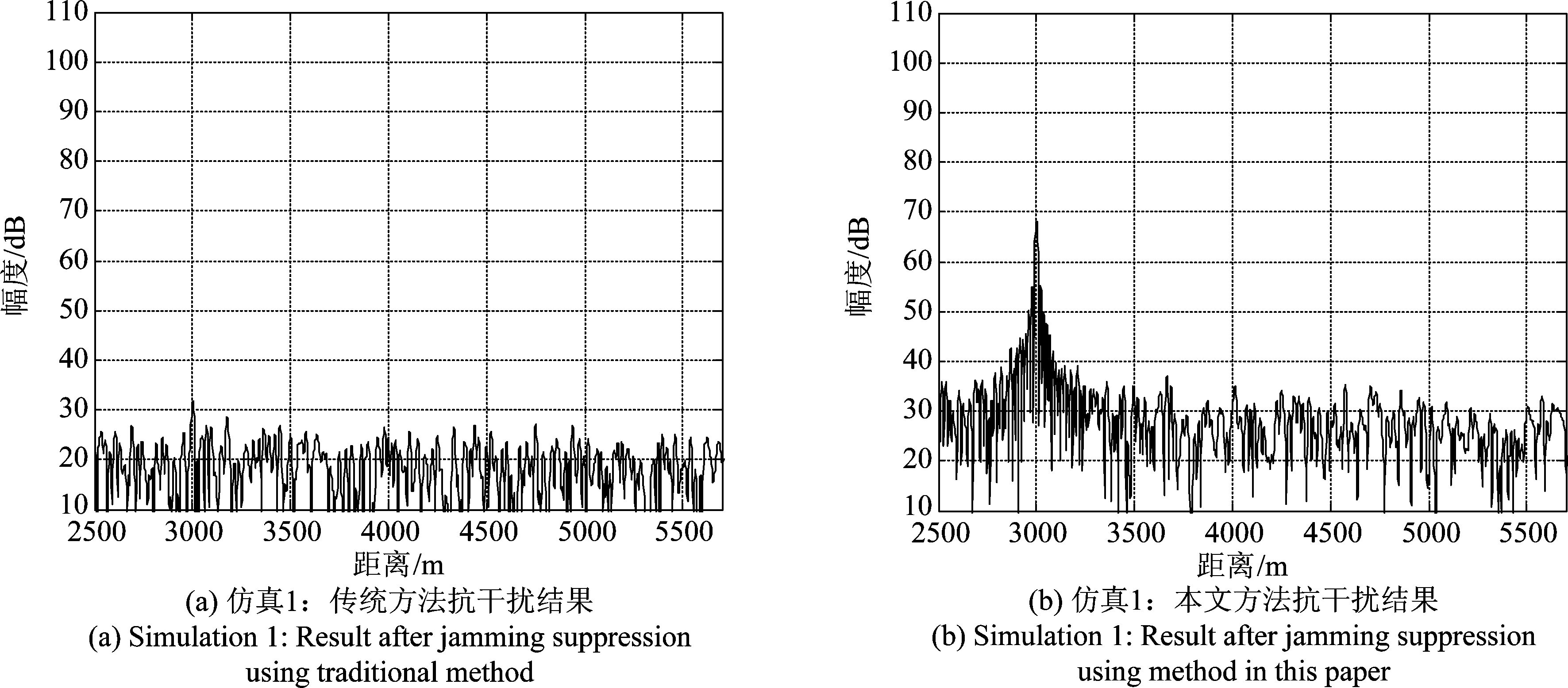
图5 抗干扰后脉压结果图(SNR=10 dB)
Fig.5 Pulse compression result of suppressing jamming (SNR=10 dB)
图6 直接转发式干扰的一维距离像及其时频分析结果(SNR=-5 dB)
Fig.6 One-dimensional range profile and time-frequency analysis of ISRJ (SNR=-5 dB)
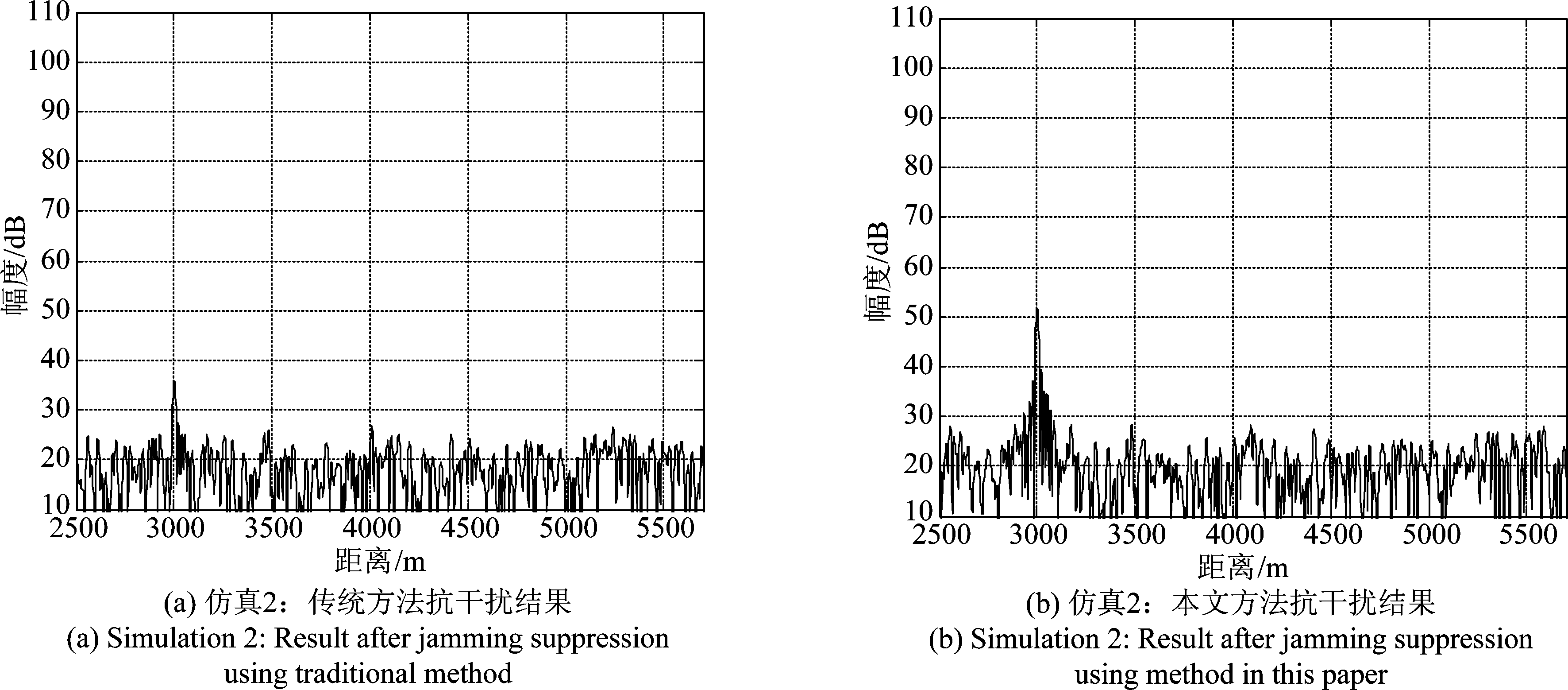
图7 抗干扰后脉压结果图(SNR=-5 dB)
Fig.7 Pulse compression result of suppressing jamming (SNR=-5 dB)
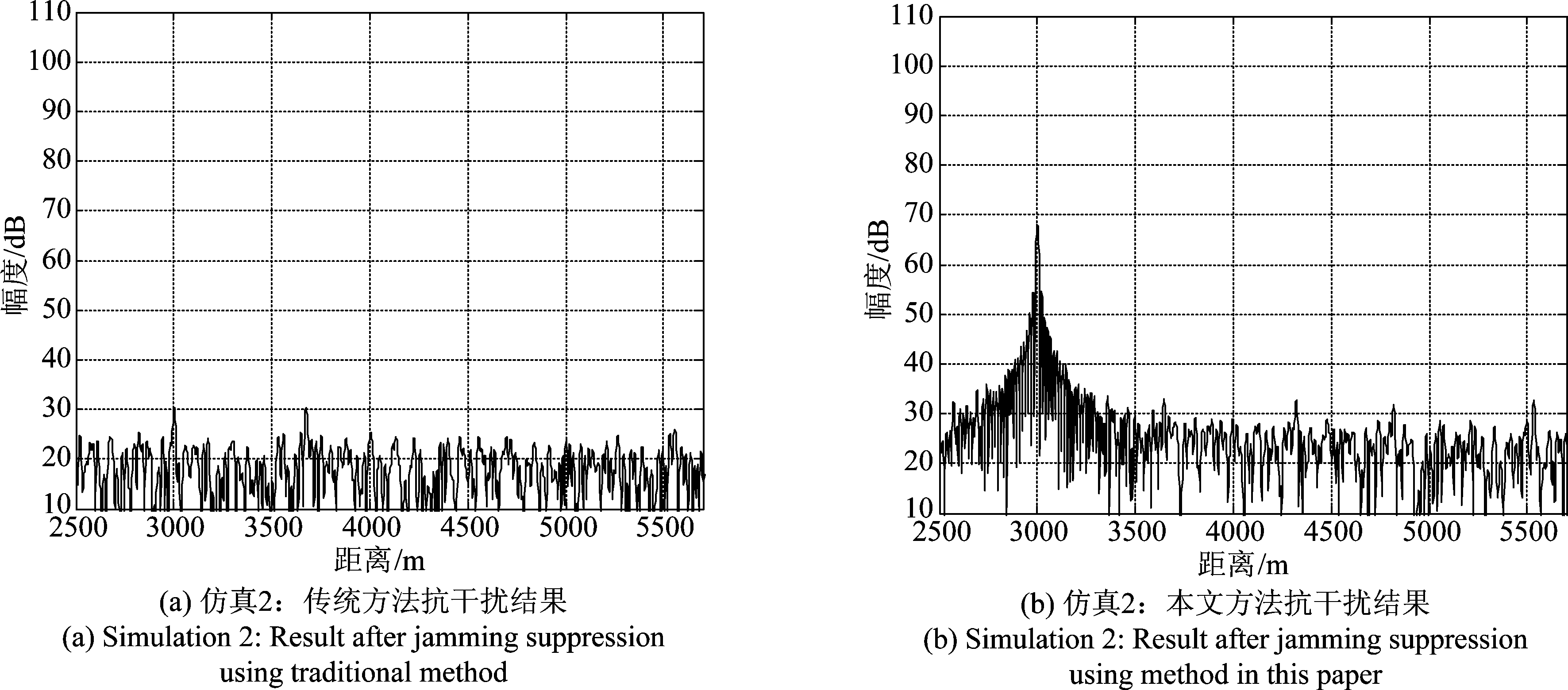
图8 抗干扰后脉压结果图(SNR=10 dB)
Fig.8 Pulse compression result of suppressing jamming (SNR=10 dB)
4.2 本文方法性能分析
仿真3:目标位于法线方向,干扰方向与目标方向夹角为3°;干扰样式及参数与仿真1相同; INR=40 dB。估计的期望信号方向与真实的目标方向夹角为0.1°;定量分析本文方法与传统方法SNR损失随雷达信号SNR的变化。
仿真4:目标位于法线方向,干扰方向与目标方向夹角为3°;干扰样式及参数与仿真1相同; SNR=10 dB。估计的期望信号方向与真实的目标方向夹角为0.1°;定量分析本文方法与传统方法SNR损失随干扰信号INR的变化。
如图9(a)所示,目标角度偏离一定的情况下,传统的抗干扰方法因训练样本包含目标信息,所以会出现较大的SNR损失,且随着雷达信号SNR的增大,SNR损失也随之增大;本文的方法训练样本不包含目标信息,所以SNR损失较小。故本文方法在SNR较高情况下效果更为明显;如图9(b)所示,在SNR以及期望信号方向估计偏差固定的情况下,随着INR的变化,传统方法抗干扰后SNR损失较大,而本文方法抗干扰后SNR损失较小。
仿真5:目标位于法线方向,干扰方向与目标方向夹角为3°;干扰机产生直接转发式干扰,干扰样式及参数与仿真1相同;SNR=10 dB,INR=40 dB。假定估计的期望信号方向与目标真实方向角度偏差从-1°到1°变化;通过仿真定量分析本文方法与传统方法的SNR损失以及SINR改善随目标角度偏离的变化。
图9 对比本文方法与传统方法的抗干扰性能
Fig.9 Anti-jamming comparison of method in this paper with traditional method
其中,SNR损失即抗干扰后回波SNR相对于抗干扰前回波SNR的损失值,同理,SINR改善即抗干扰后SINR相对于抗干扰前SINR提升值。且
分别表示目标、干扰、噪声的功率。
如图10(a)所示,当目标角度估计无偏离时,传统方法与本文方法的SNR损失均接近于0 dB;随着目标估计角度偏离越来越大,传统的方法除在某些特定偏离角度上SNR损失较小外,大部分偏离角度上都存在较大的SNR损失;而本文方法在目标角度存在不同的偏离情况下,保持较小的SNR损失。同理,如图10(b)所示,目标角度存在偏离时,传统抗干扰方法的SINR改善也较小,而本文抗干扰方法能够保证一定的SINR改善。
图10 对比本文方法与传统方法的抗干扰性能
Fig.10 Anti-jamming comparison of method in this paper with traditional method
仿真6:目标位于法线方向,干扰方向与目标方向夹角为3°;干扰样式及参数与仿真1相同; SNR=10 dB,INR=40 dB。估计的期望信号方向与真实的目标方向夹角为0.8°定量分析本文方法与传统方法SNR损失随干扰信号INR的变化。
大口径分布式雷达的方向图存在大量栅瓣,当干扰位于栅瓣位置时,自适应抗干扰处理会出现栅零点,使目标能量受损,根据阵列参数计算得到栅瓣角度为:0.86°、1.72°、2.58°…。如图11所示,当干扰位于非栅瓣角度时,本文的抗干扰方法的SNR损失相对于传统抗干扰方法有明显的改善,然而当干扰位于栅瓣角度时,本文的抗干扰方法与传统抗干扰方法一样面临较大的SNR损失。
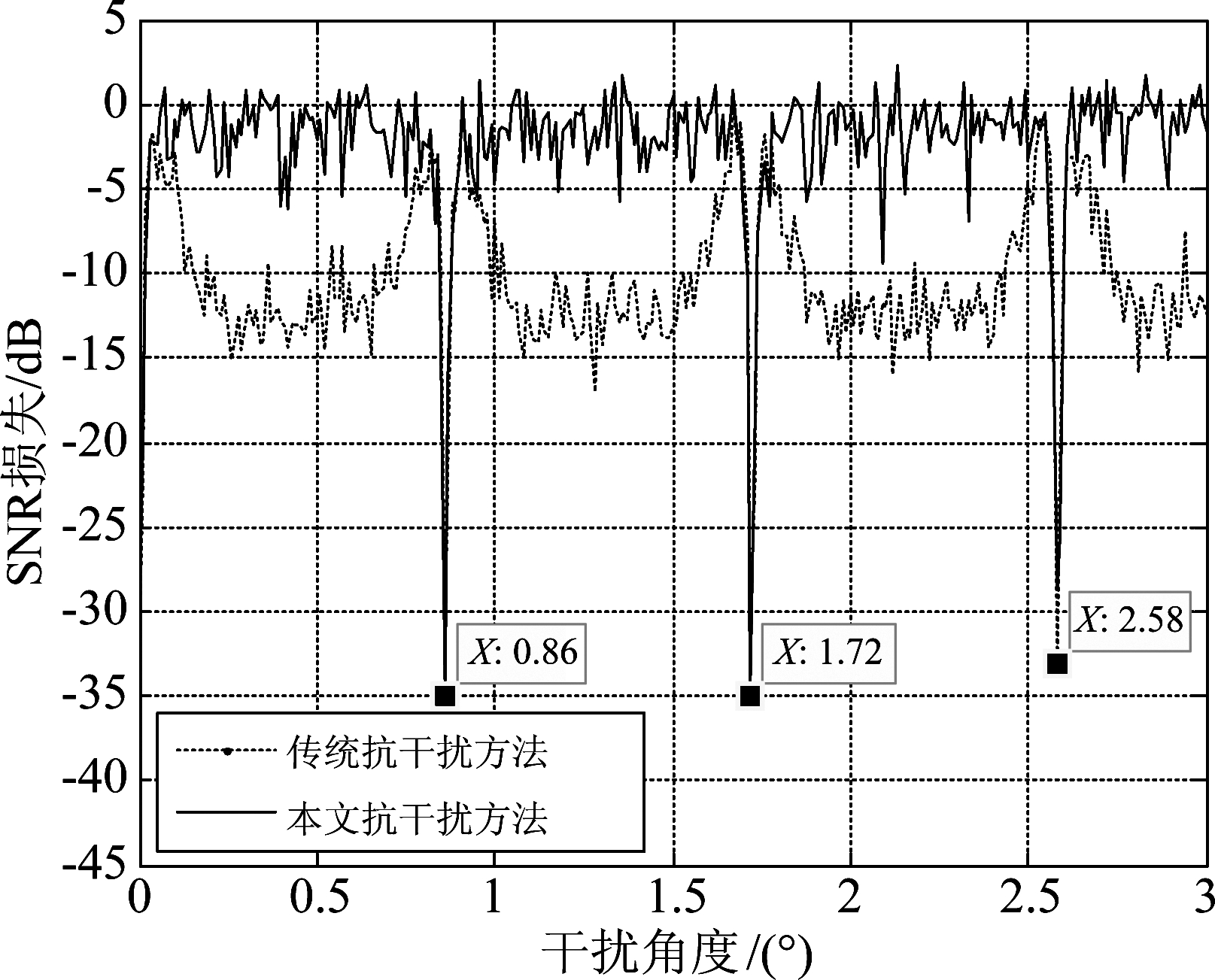
图11 SNR损失与干扰角度的关系
Fig.11 Relation between loss of SNR and angle of jamming
5 结论
目前,主瓣干扰以及间歇采样转发干扰均已成为单基地雷达正常工作的潜在威胁。构造大口径分布式雷达系统,采用空域自适应抗干扰的方法虽然能够抑制主瓣间歇采样转发干扰,却因目标角度估计存在偏差,不可避免地出现信号相消的问题。本文将基于一维距离像时频分析的干扰辨识与分布式空域抗干扰方法相结合,通过在一维距离像上辨识干扰假目标,估计出纯干扰信号协方差,用于自适应抗干扰处理,在有效抑制干扰的同时,可将信号损失控制在一定范围内。仿真结果验证了该方法对直接转发式、重复转发式的间歇采样转发干扰均匀较好的抑制效果,且在目标角度估计存在偏差情况下,抗干扰后有较小的SNR损失和较大的SINR改善。
[1] Butt F A, Jalal M. An Overview of Electronic Warfare in Radar Systems[C]∥International Conference on TAEECH, 2013: 213-217.
[2] 周畅, 汤子跃, 朱振波, 等.抗间歇采样转发干扰的波形设计方法[J].电子与信息学报, 2018, 44(9): 1- 8.
Zhou Chang, Tang Ziyue, Zhu Zhenbo, et al. Anti-interrupted Sampling Repeater Jamming Waveform Design Method[J]. Journal of Electronics & Information Technology, 2018, 44(9): 1- 8. (in Chinese)
[3] Song L Z, Qiao X L, Meng X D, et al. Study on the Method of Polarization Suppression of Cheating Jamming in Pulse Doppler Radar[J]. Journal of Systems Engineering and Electronics, 2005, 16(2): 310-315.
[4] 宁立跃, 杨小鹏.多基地极化雷达主瓣干扰抑制算法[J].信号处理, 2017, 33(12): 1571-1577.
Ning Liyue, Yang Xiaopeng. Multi-base Polarization Radar Main-lobe Interference Suppression Algorithm[J]. Journal of Signal Processing, 2017, 33(12): 1571-1577. (in Chinese)
[5] Ma Jiazhi, Shi Longfei, Li Yongzhen, et al．Angle Estimation of Extended Targets in Main-Lobe Interference With Polarization Filtering[J]．IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 169-189.
[6] Wu D, Xu Z, Zhang L, et al. Performance Analysis of Polarization-Space-Time Three-Domain Joint Processing for Clutter Suppression in Airborne Radar[J].Progress in Electromagnetics Research, 2012, 129(7): 579- 601.
[7] 施富强, 周超, 刘泉华.间歇采样重复转发干扰特性分析[J].信号处理, 2017, 33(12): 1616-1624.
Shi Fuqiang, Zhou Chao, Liu Quanhua. Characteristics Analysis of Interrupted-Sampling Repeater Jamming[J]. Journal of Signal Processing, 2017, 33(12): 1616-1624. (in Chinese)
[8] 王永良, 丁前军, 李荣锋.自适应阵列处理[M].北京: 清华大学出版社, 2009: 30- 43.
Wang Yongliang, Ding Qianjun, Li Rongfeng. Adaptive Array Processing[M].Beijing: Tsinghua University Press,2009: 30- 43. (in Chinese)
[9] 周超.雷达抗间歇采样转发式干扰的时/频域方法研究[D].北京: 北京理工大学, 2018.
Zhou Chao. Reserch on Radar Countermeasures for Interrupted Sampling Repeater Jamming in Time and Frequency Domain[D]. Beijing: Beijing Institute of Technology, 2018. (in Chinese)
[10] Zhang Honggang, Luo Jian, Chen Xinliang, et al. Fresnel based frequency domain adaptive beamforming for large aperture distributed array radar[C]∥IEEE International Conference on Signal Processing, Communications and Computing, Hong Kong, 2016: 1-5.
