1 引言
对星载SAR成像在地球观测,目标监视和海洋侦察等领域发挥着重要作用。目前,轨道上的SAR成像卫星都是低轨道卫星很难满足敏感区域连续快速遥感的需求[1-2]。高轨平台可以有效地扩展观察区域,单个光束可以覆盖数百公里成像分辨率。基于协同成像系统在地球同步轨道SAR平台上可以同时解决低轨道SAR修正时间短的问题而高轨道SAR的分辨率低,有效提高系统的及时性和空间分辨率,场景提升地图,地面目标运动特征等[3- 4]。
单通道SAR中现有的定位运动目标系统主要在图像域和回波数据域中处理。前者基于一系列单一外观SAR图像。移动参数通过连续单视SAR之间的移动目标位移来估计图片。这种方法依赖于全面的测量移动目标位置和振幅。另一种方法是广义的keystone变换,但是传统的方法当非线性范围方位角时不再适用因目标的速度或加速度而产生的距离走动[5]。本文提出了一种新的星载双基地SAR运动目标成像方法不仅可以有效抑制地面静止杂波,还可以获得良好的动目标成像性能。可以总结所提出的算法如下。首先,运动目标的杂波抑制是通过子孔径对消实现。其次,应用三阶广义keystone形成距离压缩数据用于距离徙动补偿[6]。第三,移动目标的高阶相位误差折叠因子相位项可以估算和补偿距离徙动后。最后,通过应用FFT方位压缩,我们可以获得地面运动目标的距离-多普勒图像。
1985年,Ouchi在文章中第一次在处理SAR成像时使用子孔径的方案,解释了目标在不同子孔径中的成像特点,奠定了子孔径理论的基础。划分子孔径有多种不同的方法,比如可以在时域、多普勒域及图像域。我们用的最多的是时域划分,就是对原始回波数据进行划分处理,但是应用在多普勒域的子孔径划分方法也很常见,一般应用在相干斑抑制处理中；考虑到对地面上运动目标检测问题,这里提出将广义keystone变换和子孔径结合的方法。
2 空间几何模型和信号模型
通过在SAR单通道系统对静止目标的子孔径成像技术,达到静止目标对消的效果,可以有效地抑制杂波。时域子孔径成像是指通过将合成孔径划分成多个子孔径,对每一个子孔径回波数据进行处理成像。由于静止目标在不同合成孔径时间内处理成像,但是由于其多普勒参数在不同孔径图像中保持一致性的特点,故其成像位置也是不变的。而动目标的多普勒参数在不同孔径图像中是不一样的,所以成像位置也是不一样的。由于上述特点,我们可以通过对不同孔径的信号进行对消处理,很好的对消掉静止目标,使图像中只留下运动目标的信息,有效提高信杂比,检测出运动目标。
星载高低轨 SAR和运动目标的几何图像如图1所示,其中M表示任意移动目标,V表示目标速度。发射机雷达T和接收机雷达R以Vt,Vr沿着他们自己的轨道飞行。R(τ)是从双基地星载雷达到地面运动目标的距离,可以通过R(τ)=Rt(τ)+Rr(τ)得到,其中Rt(τ)是距离从发射机雷达到目标,Rr(τ)是距离从目标到接收机雷达,τ是缓慢的时间[7]。假设发射机雷达发射线性调频信号形式如下:
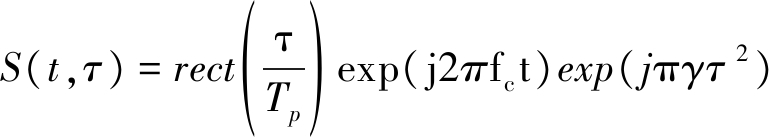
(1)
设全合成孔径划分为N个子孔径,第n个子孔径对应方位压缩后参考信号包络为Wn(s),如图2。
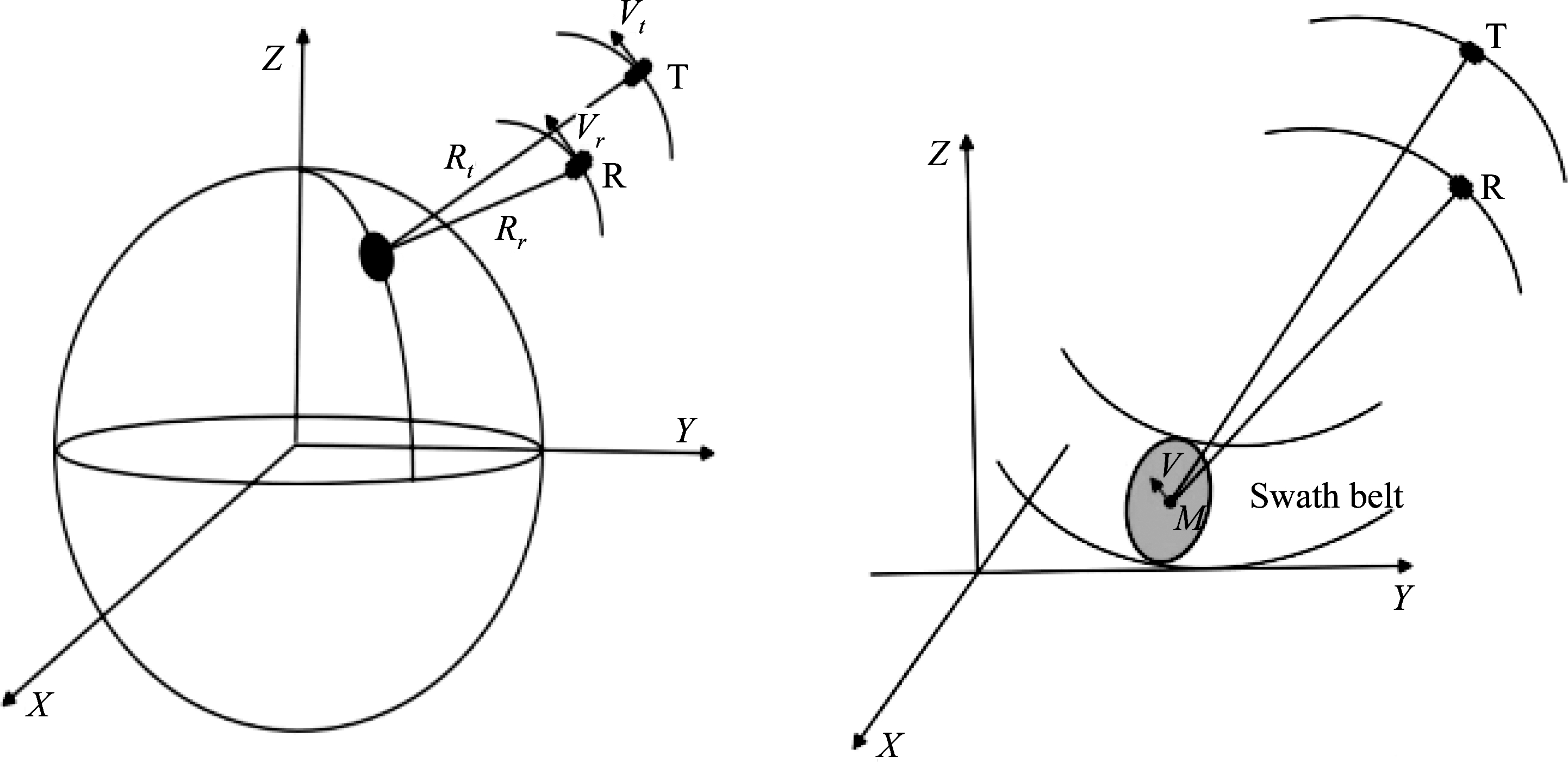
图1 星载高低轨雷达几何模型和地面运动目标几何模型
Fig.1 Geometric model of spaceborne radar and moving target
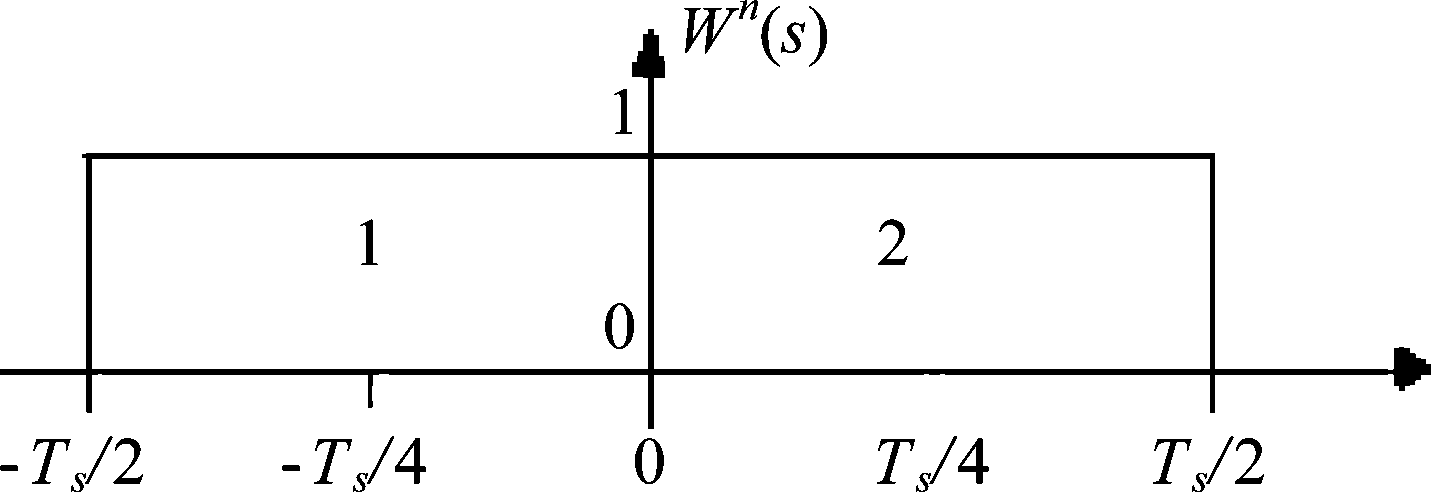
图2 两个孔径参考信号包络示意图
Fig.2 Two-view reference signal envelope
回波的方位向信号形式为
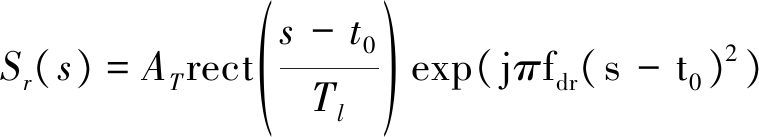
(2)
其频谱近似为
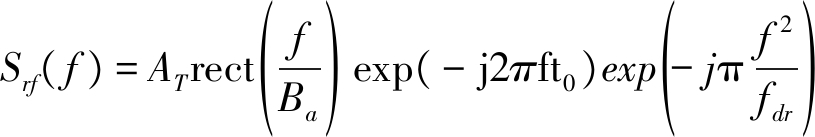
(3)
设第一个孔径匹配滤波器的脉冲响应函数为:
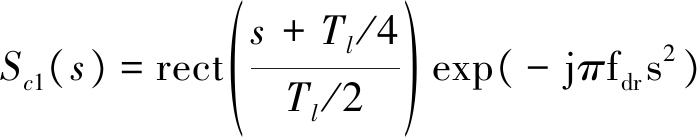
(4)
对应频谱为
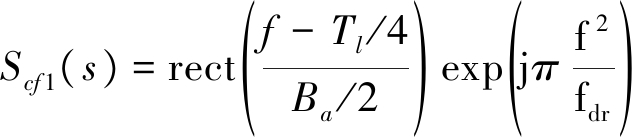
(5)
第一个孔径输出信号的频谱为:
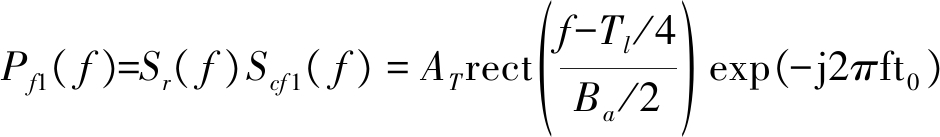
(6)
经FFT变换,得输出信号为:
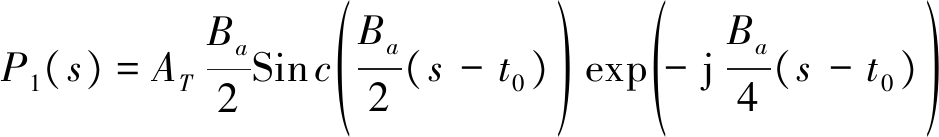
(7)
第二个孔径匹配滤波器的脉冲响应函数为:
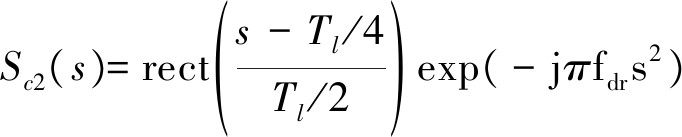
(8)
对应频谱为
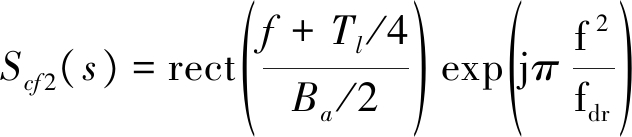
(9)
第二个孔径输出信号的频谱为:
(10)
经FFT变换,得输出信号为:
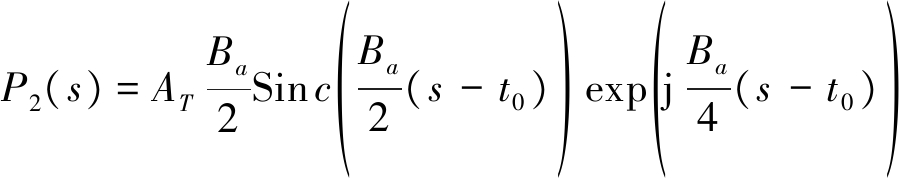
(11)
对两个孔径输出信号取模值得: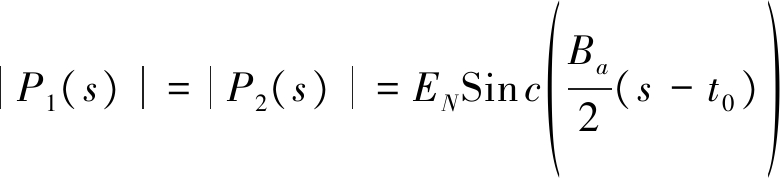
(12)
其中EN包含AT,N等不重要的常数项。从两孔径推广到多孔径可得,
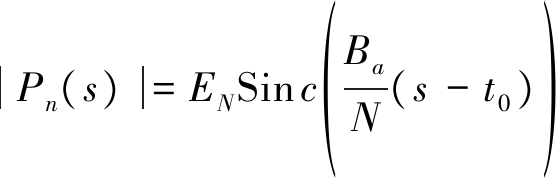
(13)
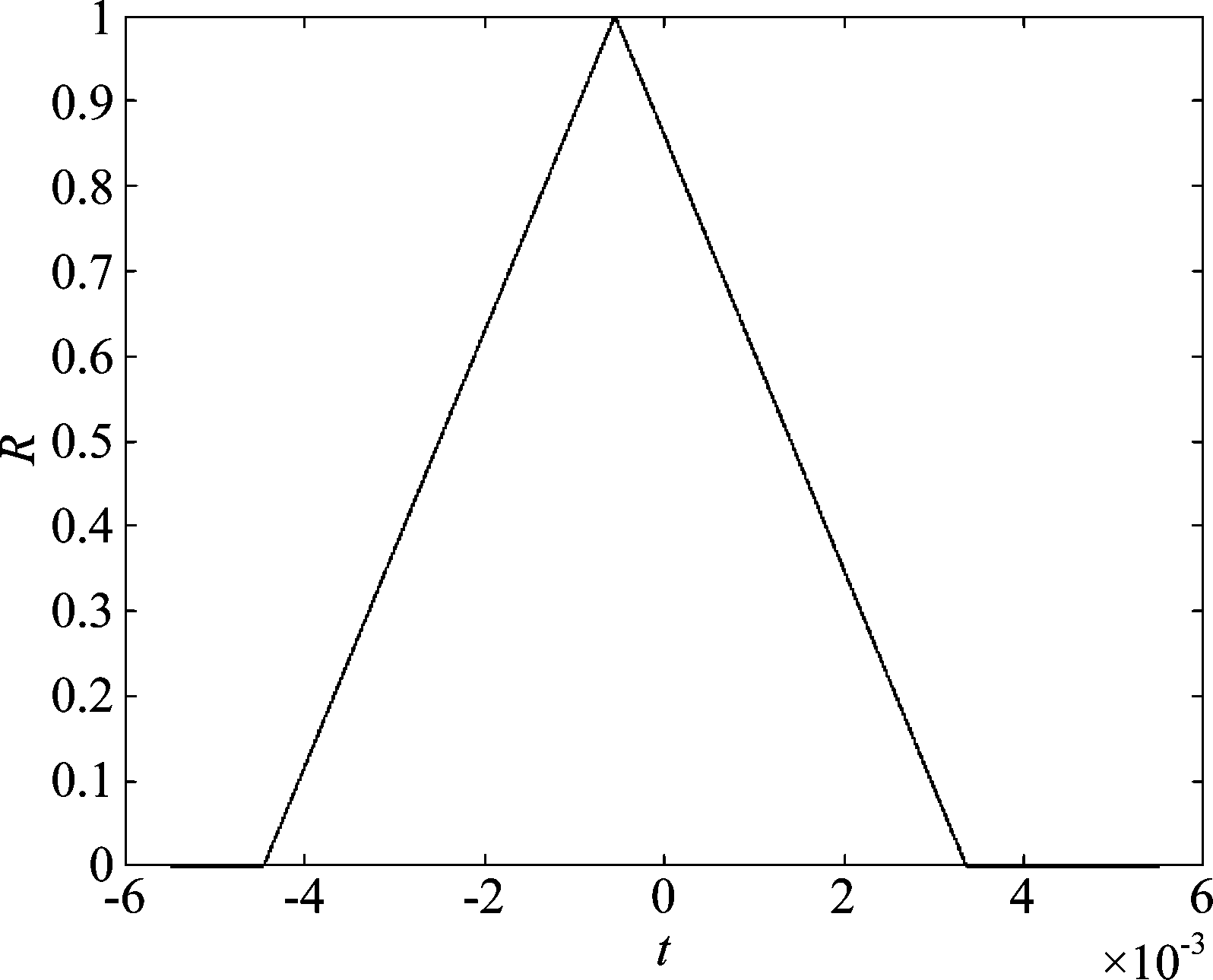
图3 静止目标回波的相关性分析
Fig.3 Correlation analysis of stationary target echoes
虽然由于雷达平台的运动使得雷达对于静止地物的瞬时锥角发生变化,一定程度上降低了这些地物回波信号之间的相关性。但是通过对相同静止目标在不同孔径的回波数据进行相关性处理,由图3可知,相同静止目标在不同孔径的回波数据相关性良好。在文献[8]中提到在天线波束对称的条件下,静止杂波回波的多普勒频谱具有对称分布的特性,由于地面运动目标本身具有径向速度,所以其回波的多普勒谱有一定的频移,这样其多普勒谱能量在不同视图像中就呈不对称分布。因此,通过两视图像非相干相减可以有效地抑制杂波,对消后会保留其运动目标的部分信息,提高输出信杂比,从而实现在低信杂比下对运动目标的检测。静止目标在各个不同子孔径图像中的成像点位置相同。而根据目标成像位置与多普勒频率的关系可推知,而在不同的子孔径图像中,动目标的成像位置是不同的[9]。且单通道的子孔径对消法相较于单通道的频域滤波法和FrFT方法,具有可抑制相干斑的优点,但在图像方位分辨率方面有所降低。
我们对接收到的回波数据分成两个子孔径分别成像。在对动目标进行成像的过程中,由于动目标的特性,为了解决非线性和线性范围的迁移同时,消除了之间的低阶耦合方位角,需要非线性变换。
R(τ)=R0 +ντ+a1τ2 +a2τ2
(14)
通过三次keystone变换,即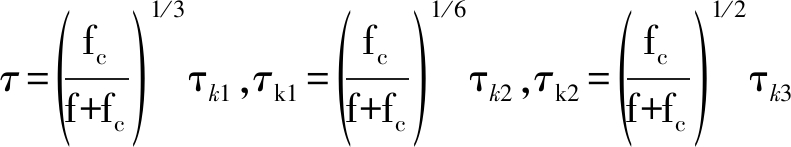
和对变换后的信号进行相应的相位补偿,我们可以得到
(15)
此时快时间频率已经和慢时间没有关系了,假设模糊数补偿函数为
(16)
令ν=Γkνb+ν0,Γ′=Γk,可得
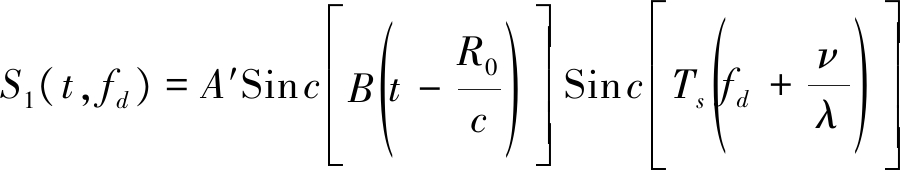
(17)
其中A′是相干累加后的幅度值,Ts表示相干累加时间, fd表示多普勒频率,易知,所有脉冲能量聚集在
处。如果目标信号峰值大于阈值,运动目标可以检测到。
由于采样、噪声等影响,在对消之前还要进行图像配准和相干斑抑制,然后将两个子孔径图像进行对消处理,消去静止目标,提高信杂比。最后通过恒虚警检测分离出运动目标[10-11]。流程图如图4所示。
仿真参数:高轨卫星高度36000 km, 低轨卫星高度570 km, 信号带宽5 MHz, 脉冲宽度10 μs,卫星速度7208 m/s,发射信号波长0.02 m,采样频率30 MHz, 合成孔径长度150 m,脉冲重复频率1000 Hz, 一个静止目标和一个运动目标初始位置均位于场景中心,其中动目标速度νr=200 m/s。
结果分析:在高低轨协同观测模式下,使用单通道子孔径对消与广义keystone变换相结合的方法,有效抑制静止杂波。根据雷达方程,我们可以计算出在输入信噪比为-10 dB时,输出信噪比可以高达29.9 dB,远超高低轨协同观测系统对输出信噪比的要求。通过对场景中三个静止目标和一个运动目标进行仿真成像处理,我们可以看到图5(a),图5(b)分别是前半孔径和后半孔径对场景中目标的成像结果,动目标的信号淹没在场景杂波中,无法有效检测出来。图5(c)展示了孔径对消后的成像结果,我们可以看到,此时,运动目标可以有效检测出来。根据信杂比的公式,我们可以计算得出,对消前,图像信杂比为1.7 dB, 对消后,图像信杂比为27.1 dB, 对消前后,信杂比提升了25.4 dB,并成功检测出运动目标。图6(a)中展示了场景中三个静止目标和一个运动目标在DPCA对消前距离压缩的结果,图6(b)展示了DPCA对消后距离压缩的结果,从图中可以看出DPCA对消后静止目标已经有效抑制,图6(c)展示了动目标最后的成像结果。通过信杂比公式我们可以计算得出DPCA对消前信杂比为3.5 dB, DPCA对消后信杂比为34 dB,对消前后,信杂比提升了30.5 dB。故在杂波对消效果来看,多通道DPCA的抑制杂波效果要优于单通道子孔径对消方法,但是在同时考虑到系统硬件复杂度和对消效果的情况下,单通道子孔径对消方法具有更好的效果。
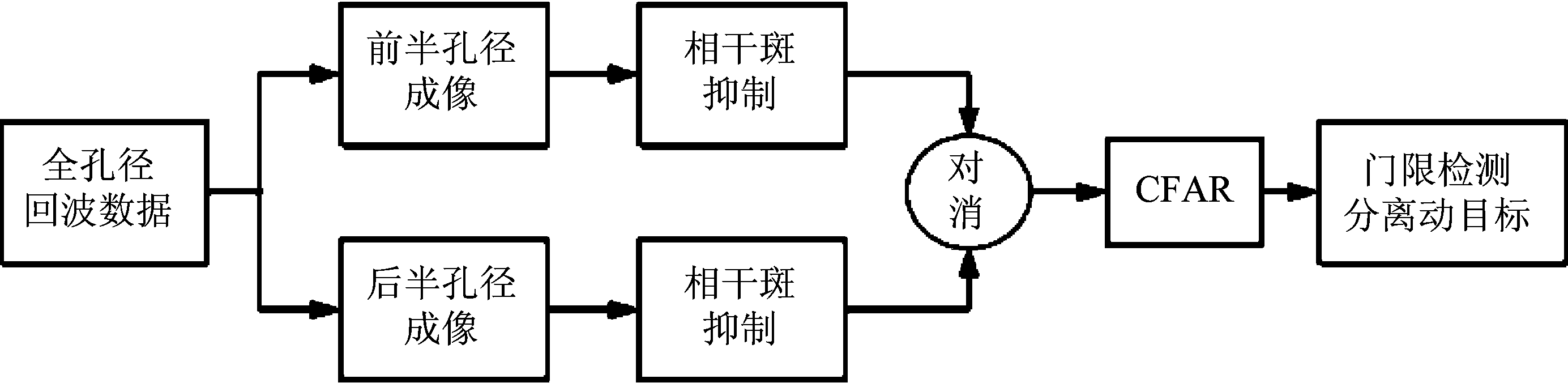
图4 子孔径对消法的实现流程
Fig.4 Implementation process of subaperture cancellation method
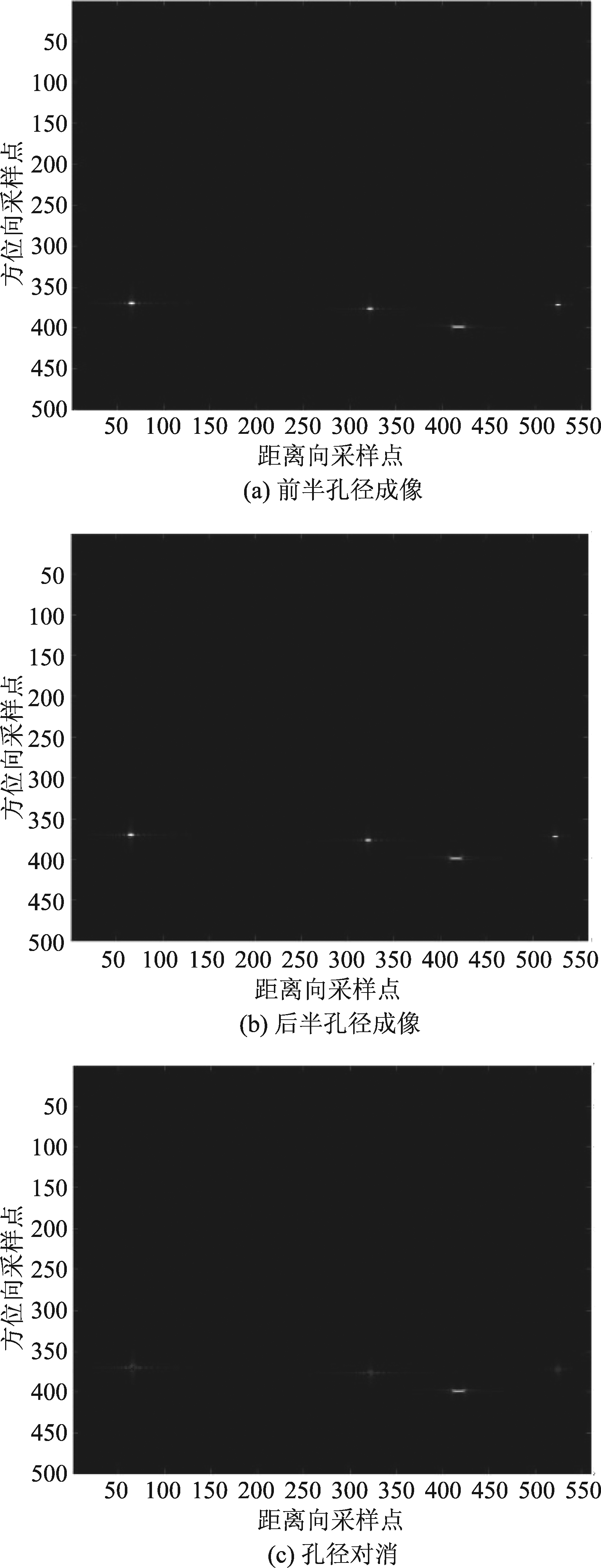
图5 单通道子孔径对消后的动目标检测结果
Fig.5 Moving target detection result after single channel subaperture cancellation
图6 多通道DPCA对消后的动目标检测结果
Fig.6 Moving target detection result after multi-channel DPCA cancellation
3 结论
本文研究了在星载高低轨平台模式下对地面运动目标的检测技术,利用单通道子孔径对消和广义keystone变换处理,有效地抑制了地物杂波,提高动目标的检测性能,仿真结果验证了方法的有效性,后期将会着重分析如何有效估计运动目标的运动参数,以及对空中目标和太空飞行器的检测。
[1] Perry R P, Dipietro R C, Fante R L. SAR imaging of moving targets[J]. IEEE Trans. Aerosp. Electron. Syst., 1999, 45(3): 188-200.
[2] Lv G, Li Y, Wang G, et al. Ground Moving Target Indication in SAR Images With Symmetric Doppler Views[J]. IEEE Trans. Geosci. Remote Sens., 2016, 54(1): 533-543.
[3] Delphine C M, Jens K, Andreas R B, et al. Wide-area traffic monitoring with the SAR/GMTI system PAMIR[J]. IEEE Trans. Geosci. Remote Sens., 2008, 46(10): 3019-3030.
[4] Wong S K. High range resolution profiles as motion invariant features for moving ground targets identification in SAR-based automatic target recognition[J]. IEEE Trans. Aerosp. Electron. Syst., 2009, 45(3): 1017-1039.
[5] Zhou F, Wu R, Xing M, et al. Approach for single channel SAR ground moving target imaging and motion parameter estimation[J]. IET Radar Sonar Navig, 2007, 1(1): 59- 66.
[6] Tian J, Cui W, Wu S. A novel method for parameter estimation of space moving targets[J]. IEEE Geosci.Remote Sens. Lett., 2014, 11(2): 389-393.
[7] Kong L J, Li X L, Cui G L, et al. Coherent integrationalgorithm for a maneuvering target with high-order range migration[J]. IEEE Trans. Signal Process., 2015, 63(17): 4474- 4486.
[8] 周峰, 李亚超, 邢孟道, 等．一种单通道SAR地面运动目标成像和运动参数估计方法[J]．电子学报, 2007, 35(3): 543-548.
Zhou Feng, Li Yachao, Xing Mengdao, et al. An effective approach to ground moving target imaging and motion parameter estimation for single channel SAR system [J]. Acta Electronica Sinica, 2007, 35(3): 543-548. (in Chinese)
[9] Kazuo Ouchil. On the Multilook Images of Moving Targets by Synthetic Aperture Radars[J]. IEEE Transactions on Antennas and Propagation, 1985, 33(8): 823- 827.
[10] Huang P H, Liao G S, Yang Z W, et al. A fast SAR imaging method for ground moving target using a second order WVD transform[J]. IEEE Trans. Geosci. Remote Sens., 2016, 54(4): 1940-1956.
[11] Gao Y C, Li H B, Himed B. Knowledge-aided range-spread target detection for distributed MIMO radar in non-homogeneous environments[J]. IEEE Trans. Signal Process., 2017, 65(3): 617- 627.
