1 引言
逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)具有全天候、全天时和远距离作用的优势,能够实现对运动目标的两维高分辨成像,是一种重要的微波遥感探测手段,在军事和民用领域得到了广泛的应用[1- 4]。在ISAR成像中,距离高分辨依靠雷达发射宽带信号并利用脉冲压缩技术实现,而方位向的高分辨依赖于雷达和目标视角变化对应的多普勒调制信息。对于不同方位位置的散射点,其多普勒信息存在差异,为方位成像提供了依据。雷达和目标视角变化越大,相邻方位位置的散射点多普勒差异越大,越容易被分辨,对应的方位分辨率越高。为了获得大的视角观测,一般长时间相干积累(coherent processing interval, CPI)是非常必要的。此时,观测目标往往表现出较强的机动特性[5-9]。同时,对于强机动目标而言,在短时间内也极有可能表现出机动特性。在观测时间内,目标的机动特性往往表现为转动速度随时间变化。相应的,目标各个散射点的多普勒响应具有时变性,表现出非平稳特性。如果直接采用传统距离-多普勒成像方法,在方位向进行傅里叶变换后,其方位向不可避免的出现“散焦”。此外,传统成像算法仅能获得目标在距离-多普勒的图像,并不能得到定标后的图像(距离和方位向尺度均为米)[5-9]。以上这些因素都不利于后续的ISAR图像目标识别和分类等。因此,有必要针对机动目标的非平稳转动进行补偿并期望获得定标后的图像。
近些年来,针对机动目标成像,研究了许多可行性的方法,取得了不错的成像结果。现有的方法通常可以划分为时频类方法[5]、CLEAN类方法[6]和转动参数估计类方法[8,10]等。时频类方法利用时频变换技术,估计目标散射点的瞬时多普勒,从而实现距离-瞬时多普勒成像。CLEAN类方法通过利用反卷积或者匹配滤波方法逐个进行强散射点的提取,相比于时频类方法,CLEAN类方法由于能够利用全孔径数据进行散射点估计,往往具有更高的分辨能力。而转动参数估计类方法直接进行目标转动参数估计,利用估计的参数进行转动误差补偿,实现良好的聚焦成像。前两类方法仅能获得目标在距离多普勒域的图像,而第三类方法由于能够估计目标转动参数,一般可以获得定标后的ISAR图像。其中,文献[8]提出通过提取和追踪两个特显点,可以实现对机动目标转动速度和加速度的估计。因此该方法依赖于特显点样本质量。在实际成像中,很难保证成功获取两个质量足够高的特显点,从而影响目标转动参数估计结果。因此,文献[8]的方法在实际中某些情况并不一定适用。此外,一种基于图像整体信息的优化类方法,例如最小熵或者最大对比度,被用来进行目标转动参数估计[11-13]。由于利用图像整体信息,能够获得更好的参数估计性能。然而,现有的方法大多数针对非机动目标,并未考虑目标的机动特性,如转动加速度甚至加加速度的存在。因此,针对机动目标,研究稳健的参数估计算法就目前而言是一个亟待解决的问题。
针对ISAR机动目标成像,本文提出了一种基于最小熵的联合高分辨成像和目标转动参数估计算法。首先,建立ISAR成像机动目标的信号模型,考虑目标加加速度存在。然后,基于最小熵准则建立目标成像和参数估计的代价函数。其次,利用坐标梯度下降法进行成像和参数估计求解。再次,利用估计的转动参数对重构的ISAR图像进行方法定标处理以获取目标二维几何。本文的方法属于目标转动参数类方法,相比于时频类和CLEAN类方法具有优势。同时,相比于文献[8]的方法,由于本文最小熵方法能够利用图像整体信息,在低信噪比下仍然能够取得较好的成像结果。最后,通过实验分析验证了本文算法的有效性。
2 信号模型
ISAR成像几何如图1所示,目标的转动可以分解为两个正交的分量:沿雷达视线Y轴方向和垂直视线的Z轴方向。在ISAR成像中,沿Y轴转动不产生多普勒调制,对成像没有贡献,一般可以忽略。对于二维转动目标,其成像平面固定,对应图1的X-O-Y平面。通常目标的运动可以分解为转动分量和平动分量,仅有转动分量对成像有意义,本文假设目标平动已被补偿。在只考虑目标转动的情况下,散射点P(xp,yp)与雷达在tm时刻的距离可以表示为
Rp(tm)=R0+cos θz(tm)·yp+sin θz(tm)·xp
(1)
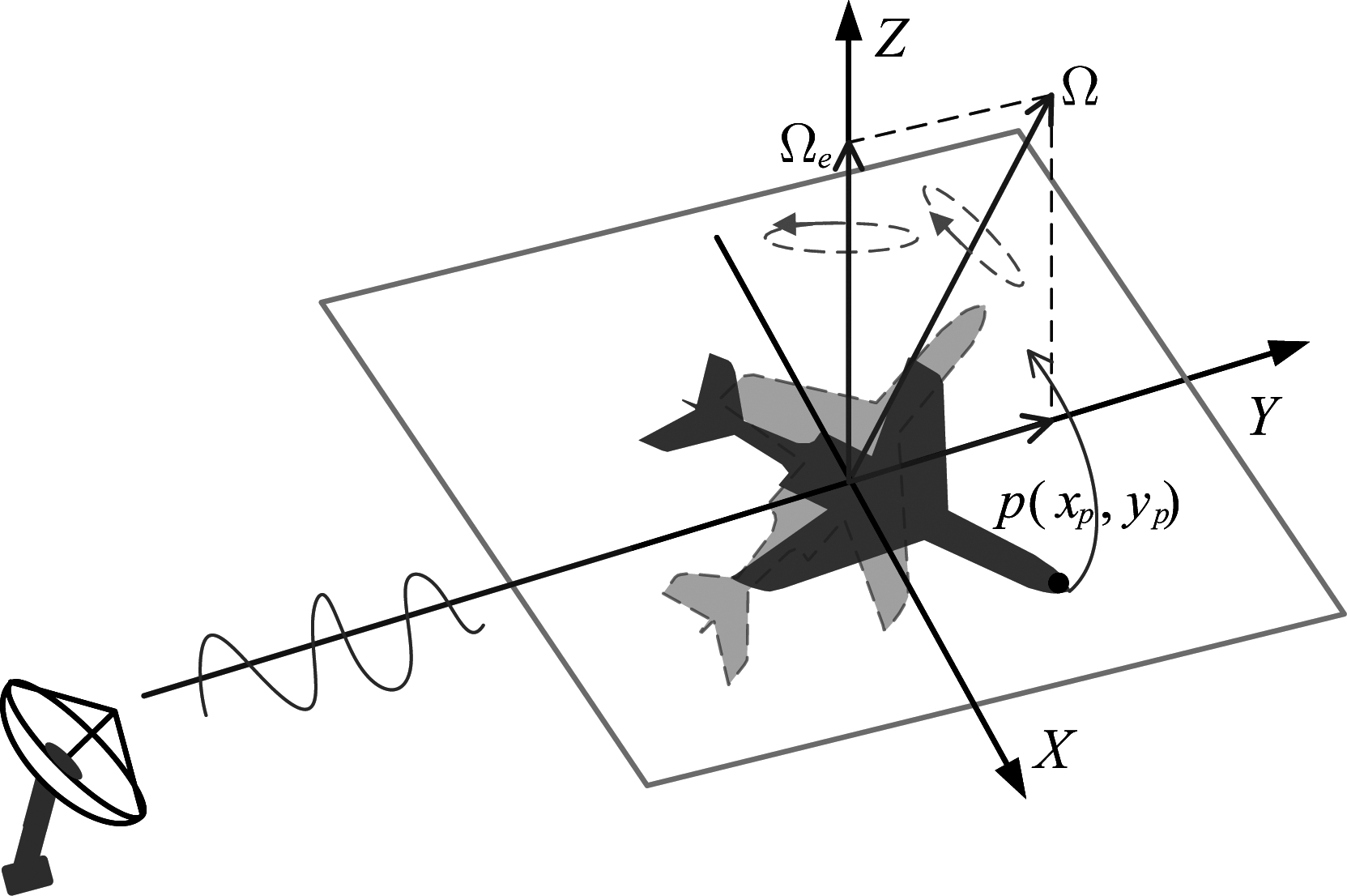
图1 ISAR成像几何示意图
Fig.1 ISAR imaging geometry
其中,R0为雷达与目标转动中心的距离,θz(tm)为目标沿Z轴的瞬时转动角度。对于机动目标,其转动速度在相干处理时间内并不恒定,具有时变性。本文考虑机动目标的转动加速度存在,即
其中
和
分别是目标转动的速度、加速度和加加速度。此时,式(1)利用泰勒级数展开可以近似为[6]
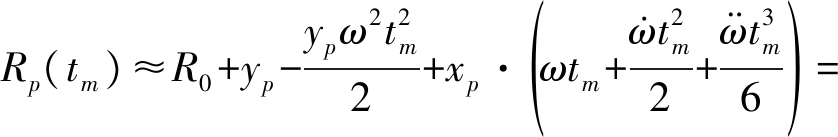
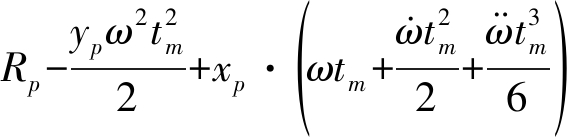
(2)
其中,Rp=R0+yp为散射点P的初始距离。
假设雷达发射线性调频信号,对回波进行距离向脉冲压缩处理,得到距离成像结果
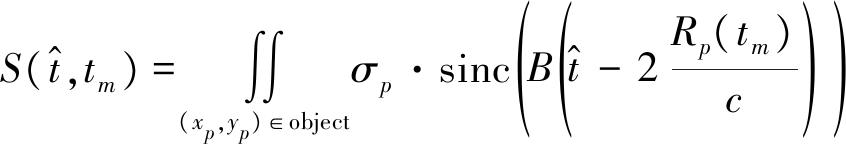
(3)
其中,σp是散射点P的散射系数,
表示距离向时间,B和fc分别为发射信号带宽和中心频率,c则表示电磁波的传播速度。将式(2)带入式(3),可得到回波信号具体形式。当Rp(tm)变化量超出1/2距离单元时,会引入距离徙动问题,是机动目标成像解决的问题。假如距离徙动可以采用一阶或者二阶Keystone方法进行校正[14],那么距离徙动校正后的回波信号表示为
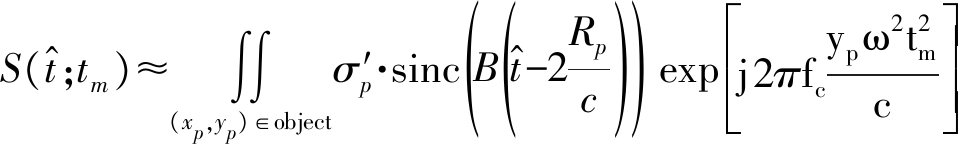
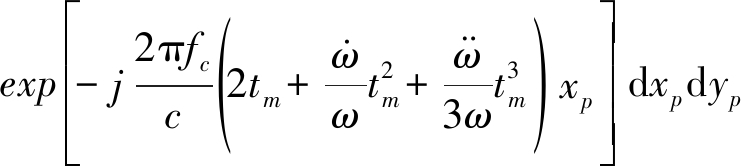
(4)
其中,
第一个相位项为宽视角下的二次相位调制项,第二个相位项为目标转动速度时变引入的高阶相位调制项。二阶及其以上高阶相位是由目标机动引入的,对应高阶的多普勒调制,需要校正。下面将式(4)进行离散化处理。通过近似假设
则式(4)可以写成
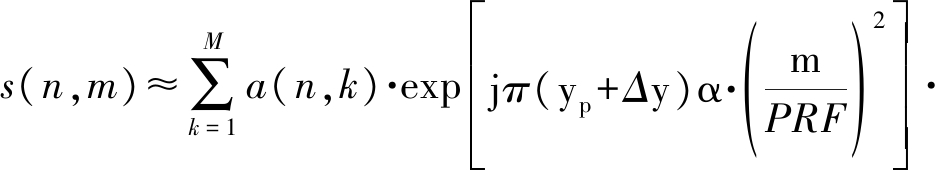
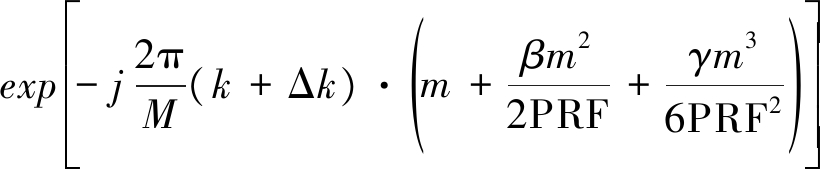
(5)
其中,M为方位向离散点数,PRF为脉冲重复频率,
对应目标未知的旋转中心,
为ISAR图像的第(n,k)个元素。由式(5)可知,对于高机动目标,s(n,m)可以表示为目标散射场景的三阶Chirp傅里叶变换,并存在两个主要问题:
1)由于目标非合作特性,目标转动参数和(α, β和γ)未知;2)在实际中,目标的转动中心未知,即(Δy,Δk),这也与平动补偿等处理有关。
如果直接对(5)进行方位傅里叶变换,ISAR图像方位向会出现“散焦”。因此,需要进行高阶相位校正以实现良好聚焦成像。
3 所提方法
为了解决成像中的目标机动特性,本节提出一种基于最小熵的联合成像和目标转动参数估计算法。在雷达成像中,图像的熵值可以作为成像质量的一个重要评价标准。简言之,当图像聚焦质量越好,图像熵值越小。针对机动目标成像而言,当高阶相位得以正确校正时,图像聚焦质量最好,熵值也最小。为了方便后续推导,定义变量
=[α β γ Δy Δk]以表示式(5)中的多个未知参数。假设
是对参数的估计值,进行校正后的ISAR图像可以表示为
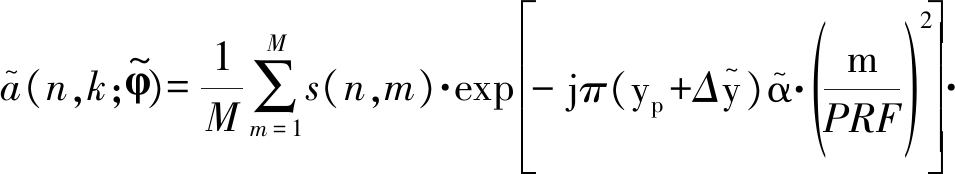
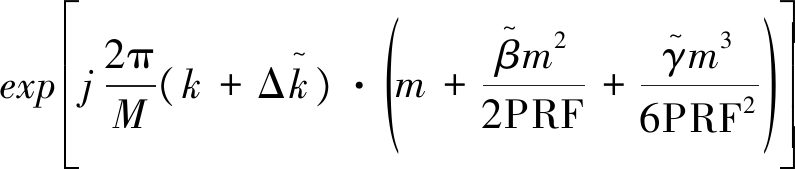
(6)
其中,
是利用参数
校正后的ISAR图像。需要指出的是,此处需要目标转动中心的估计。相应的,建立参数估计的最小熵[12]代价函数为
(7)
其中,
根据Parseval定理,相位误差并不影响信号的总能量,并且是恒定的,此处用常量Ia表示。由于式(7)不存在闭合解,因此,需要利用优化迭代的方法进行求解。为了保证算法的收敛速度和收敛性,本文采用基于拟牛顿的坐标梯度下降法[12]进行求解。在坐标梯度下降法中,通过固定其他参数,依次循环求解中的每一个参数,从而保证算法的单调收敛性。假设
为第i次迭代中已经估计的前q-1个参数,利用拟牛顿方法对第q个参数的估计可以表示为
(8)
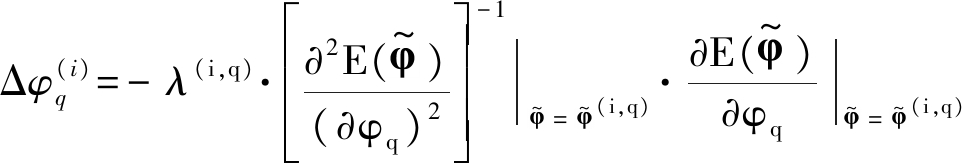
(9)
其中,
和
分别是第i-1次和第i次迭代对
的估计值,
和
分别是
关于φq的梯度向量和Hessian矩阵,λ(i,q)为拟牛顿方法的搜索步长,可以利用Armijo准则[15]估计得到。式(9)中,
具体形式为
(10)
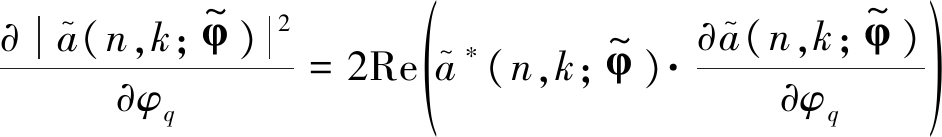
(11)
同时,
具体形式为
)|
2)·
(12)
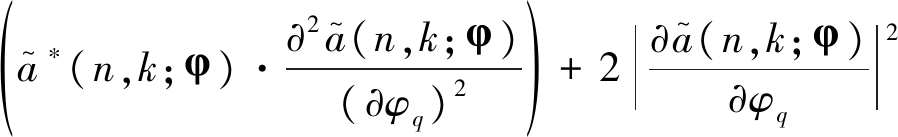
(13)
需要指出的是,式(12)中的
操作可能会出现除零的现象,从而导致牛顿迭代方法失效。为了避免此问题,可以利用
近似
其中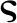
是一个很小的正数。利用式(8)和(9),可以依次估计中的每一个参数。当坐标梯度下降法达到收敛后,可以获得最终的参数估计和成像结果。最终,利用估计参数
和
对获取的ISAR图像进行方法定标处理,得到定标后的图像。
为了评估本文算法的实效性,有必要对其运算量进行分析。通过分析可知,本文算法的运算量主要表现为每次迭代中式(8)～(13)的梯度向量
和Hessian矩阵
求解。其中,求解
主要在于求解
求解向量
主要在于求解
和
通过观察式(7)可知,求解
和均对应固定chirp值的chirp-Fourier变换操作,其复杂度为Ο(N·M2)。那么,每次迭代的运算复杂度为Ο(10N·M2)(中有五个未知参数,每个参数需要分别求解和
假设本文方法的迭代次数为Niten,那么本文算法运算复杂度为Ο(10Niten·N·M2)。通过后面实验可知,本文方法一般经过20～30次迭代可实现收敛。
4 实验分析
下面通过实验分析以验证本文算法的有效性,并通过与传统成像方法比较,揭示本文算法的优势。下面的实验均在一台主频3.50GHz电脑(CPU E5-1650、内存256GB)平台以MATLAB R2010a软件实现,需要说明是本节实验所用的算法并未进行特定的代码优化。
仿真数据实验:仿真目标设置为Yak- 42飞机模型,如图2(a)所示,其尺寸大小为33.5 m×36.5 m。为了表示机动性,目标的转动速度、加速度和加加速度分别设为0.03 rad/s、0.003 rad/s2和0.001 rad/s3。为了测试算法的“鲁棒性”,对回波数据添加高斯白噪声,回波信噪比设置为5 dB。在距离成像和距离徙动校正后,进行方位成像处理。图2(b)为距离-多普勒成像结果,方位向直接进行傅里叶变换,可见,方位向存在“散焦”,一个散射点的能量会散布到相邻多个多普勒单元,这是由目标的机动性导致的。因此,有必要进行机动性的校正处理。此处利用时频类方法进行成像处理,选择具有平滑去噪能力的Wigner-Ville变换[16],图2(c)为脉冲中心时刻对应的距离-瞬时多普勒图像。由图2(c)可知,时频类方法能够克服目标的机动性,然而成像分辨率较低。然后,我们利用本文所提最小熵方法进行成像处理,迭代20次,其成像结果如图2(d)所示,转动速度、加速度和加加速度分别为0.0298 rad/s、0.0028 rad/s2和0.0096 rad/s3,非常接近真实值。由图2(d)可见,相比于时频类方法,本文的方法具有较高的成像分辨能力,同时保证良好的聚焦效果。更为重要的是,本文的方法由于能够估计目标转动参数,可以获得定标后的图像。
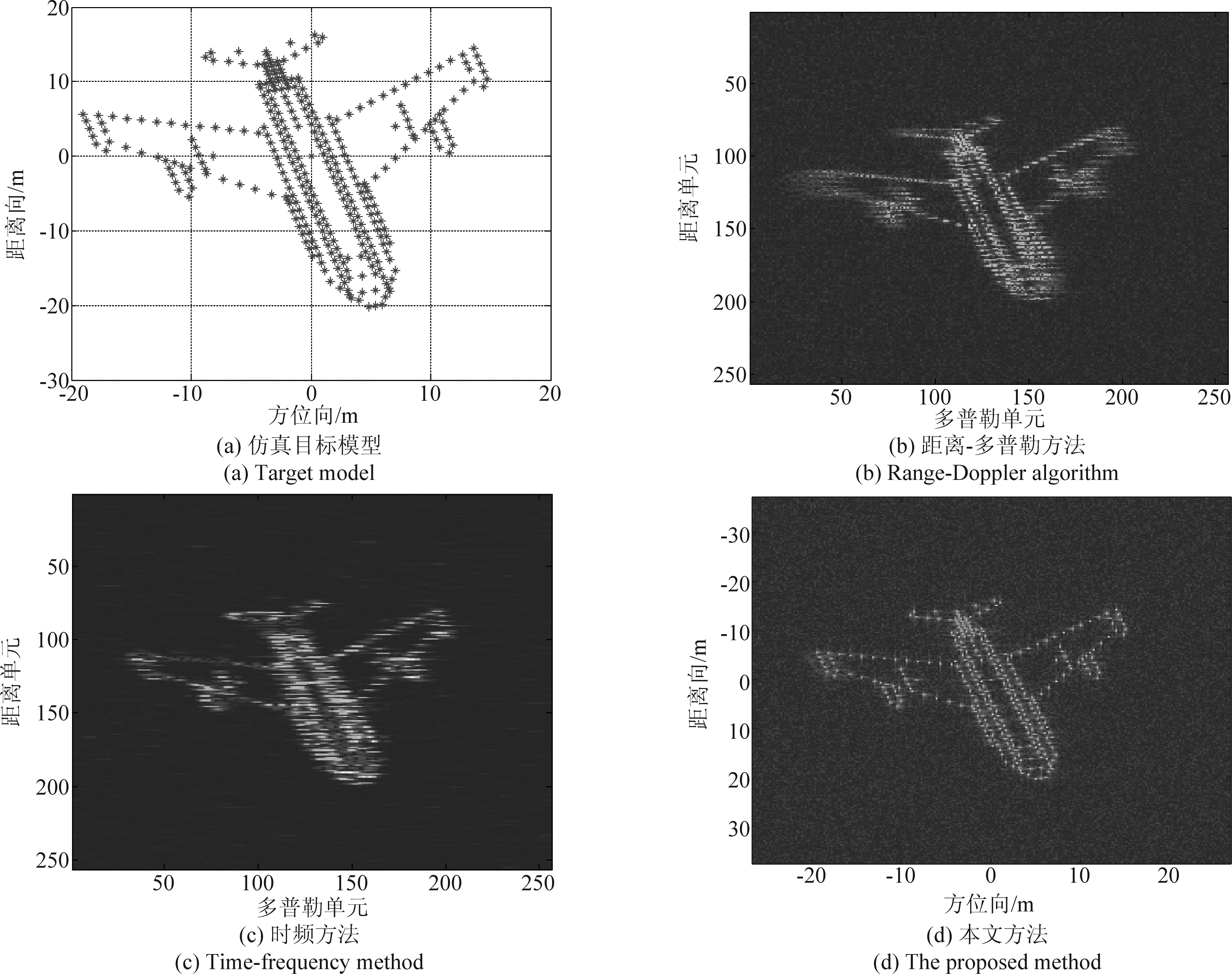
图2 仿真数据及成像结果
Fig.2 Simulated data and the imaging results
实测数据实验:此处利用实际成像雷达测量的Yak- 42飞机目标数据进行实验。图3(a)为传统距离-多普勒成像结果,可见多普勒域存在明显的“散焦”。图3(b)为Wigner-Ville时频方法结果,图3(c)为CLEAN成像结果[8]。通过比较图3(b)和(c)可知,相比于时频类方法,CLEAN方法的成像分辨率明显提高,这是因为CLEAN方法能够利用全孔径数据进行相干化处理。需要指出的是,CLEAN类方法具有噪声抑制能力,这是一般其他类方法不可比拟的。然而,由于噪声的干扰,CLEAN难以提取弱散射目标存在,造成部分散射点的“丢失”。图3(d)为本文方法的成像结果(迭代20次),通过估计目标参数,可以实现目标机动特性补偿,从而提高目标的聚焦质量,并保证全孔径成像分辨能力。相比于CLEAN类方法,不会存在散射点的“丢失”。此外,我们分别测试了时频、CLEAN和本文方法的运行时间,分别为26.5 s、4.2 s和6.6 s。本文方法运算量和CLEAN方法比较接近,这是因为CLEAN类方法同样需要利用chirp-Fourier变换实现散射点参数估计和提取。通过以上实验分析,验证了本文方法的有效性。
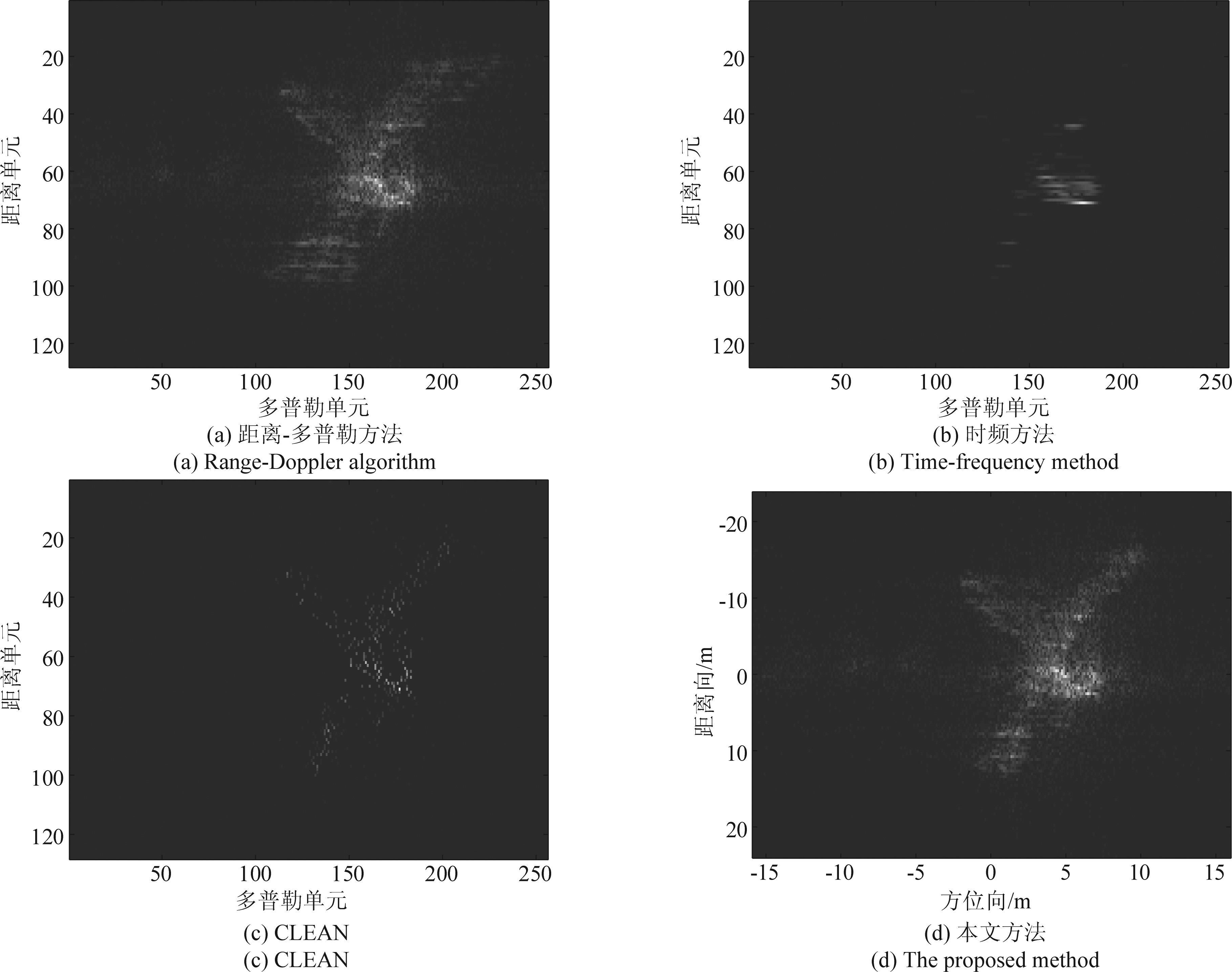
图3 实测数据成像结果
Fig.3 Imaging results of measured data
5 结论
本文针对ISAR机动目标成像,提出了一种基于最小熵的高分辨成像和参数估计算法。通过建立机动目标信号模型,利用最小熵准则构建成像和参数估计代价函数,通过求解目标函数获得聚焦良好的ISAR图像和目标转动参数。同时,利用估计的转动参数实现对图像的方位定标处理,以获得目标的二维几何尺寸。相比于传统算法,本文算法在低信噪比下仍然可以获得聚焦良好的高分辨成像结果。最后,通过仿真数据实验分析对本文算法的有效性进行了验证。需要指出的是,本文的算法限制于目标二维转动情况,而不适用于三维转动目标。
[1] 王志会, 王壮, 蒋李兵. 基于线特征差分投影的空间目标姿态估计方法[J]. 信号处理, 2017, 33(10): 1377-1384.
Wang Z H, Wang Z, Jiang L B. Pose estimation method for space targets based on the linear features differencing projection[J]. Journal of Signal Processing, 2017, 33(10): 1377-1384. (in Chinese)
[2] 吴敏, 张磊, 刘松杨, 等. OFDM-ISAR的稀疏优化成像与运动补偿[J]. 雷达学报, 2016, 5(1): 72- 81.
Wu M, Zhang L, Liu S Y, et al. OFDM-ISAR sparse optimizaitoin imaging and motion compensation[J]. Journal of Radars, 2016, 5(1): 72- 81. (in Chinese)
[3] 陈文峰, 李少东, 杨军, 等. 基于线性Bregman迭代类的多量测向量ISAR成像算法研究[J]. 雷达学报, 2016, 5(4): 389- 401.
Chen W F, Li S D, Yang J, et al. Multiple measurement vectors ISAR imaging algorithm based on a class of linearized bregman iteration[J]. Journal of Radars, 2016, 5(4): 389- 401. (in Chinese)
[4] Tian J, Cui W, Xia X G, et al. Parameter estimation of ground moving targets based on SKT-DLVT processing[J]. IEEE Trans. Comput. Imag., 2016, 2(1): 13-26.
[5] Lv X L, Xing M D, Wan C R, et al. ISAR imaging of maneuvering targets based on the range centroid Doppler technique[J]. IEEE Trans. Image Process., 2010, 19(1): 1-13.
[6] Chen V C, Miceli W J. Time-varying spectral analysis for radar imaging of maneuvering targets[J]. IEE Proc. -Radar Sonar Navig., 1998, 145: 262-268.
[7] Xu G, Yang L, Bi G A, et al. Maneuvering target imaging and scaling by using spare inverse synthetic aperture[J]. Signal Process., 2017, 149(11): 149-159.
[8] Martorella M, Acito N, Berizzi F. Statistical CLEAN Technique for ISAR Imaging[J]. IEEE Trans. Geosci. Remote Sens., 2007, 45(11): 3552-3560.
[9] Wang G Y, Xia X G. An adaptive filtering approach to chirp estimation and ISAR imaging of maneuvering targets[C]∥IEEE Int. Radar Conf., 2000: 481- 486.
[10] Munoz-Ferreras J M, Perez-Martinez F. Non-uniform rotation rate estimation for ISAR in case of slant range migration induced by angular motion[J]. IET Radar, Sonar & Navigation, 2007, 1(4): 251-260.
[11] Xu G, Xing M D, Xia X G, et al. Enhanced ISAR imaging and motion estimation with parametric and dynamic sparse Bayesian learning[J]. IEEE Trans. Comput. Imag, 2017, 3(4): 940-952.
[12] Morrison R L, Do M N, Munson D C. SAR image autofocus by sharpness optimization: A theoretical study[J]. IEEE Trans. Image Process., 2007, 16(9): 2309-2321.
[13] Thomas K J, Alaa K A. Monotonic iterative algorithm for minimum-entropy autofocus[C]∥IEEE International Conference on Image Processing, Atlanta. 2006, 5: 645- 648.
[14] Xing M D, Wu R B, Lan J Q, et al. Migration through resolution cell compensation in ISAR imaging[J]. IEEE Geosci. Remote Sens. Lett., 2004, 1(2): 141-144.
[15] Oppenheim A. Willsky A, Signal and Systems[M]. 2nd ed. Prentice Hall, Upper Saddle River, NJ, 1997.
[16] Bao Z, Wang G, Luo L. Inverse synthetic aperture radar imaging of maneuvering targets[J]. Opt. Eng., 1998, 37(5): 1582-1588.
