1 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天时、全天候工作的优势,在地球监测领域如洪水监测、海冰监测、土壤湿度调查、森林资源清查、地质调查等方面起到非常重要的作用。双基地合成孔径雷达(Bistatic Synthetic Aperture Radar, BiSAR)系统通常指收发天线平台分置的SAR系统。相比单基地SAR系统,双基地优势明显,例如可以获取多角度散射信息,利于目标数据融合；接收机与发射机分置,配置灵活,抗干扰能力强。相比脉冲体制的雷达,调频连续波(Frequency Modulated Continuous Wave,FMCW)体制的BiSAR雷达不仅具有体积小、重量轻和抗干扰能力强等特点,还具有BiSAR的高分辨率和配置灵活等特点,非常适合在制导武器和无人机等小平台应用,也是SAR小型化发展的重要方向。
在调频连续波体制的BiSAR成像仿真研究中,需要建立目标的回波模型。传统的回波模型基于点目标假设,对于连续分布的目标,例如线段目标或面目标,一种常规的做法是将连续分布目标视为大量离散的散射点,将目标回波近似地表示为有限的点目标回波的叠加。这种方法得到的回波模型精度受到目标的离散点采样间隔的影响,为了保证回波模型的准确性需要采用小于1/10信号波长的采样间隔,这将导致计算量巨大。最严重的是,目标的离散方式会影响产生的回波模型,对同一目标采用不同采样方式,对应的SAR成像结果可能具有很大差异,该现象大大降低了这一近似方法的可信度。
本文提出了一种连续目标的SAR回波建模方法,推导具有明确几何结构的连续目标的回波频谱解析表示式,直接根据目标的尺寸参数和方位参数计算回波,克服了基于离散采样的点目标建模方法的上述缺陷。将连续目标的回波建模方法与双基地调频连续波雷达结合,有助于进行双基地调频连续波雷达的分析和研究,对于理解其工作原理、观测几何和回波特性具有重要意义。
2 问题的提出
2.1 点目标回波模型
双基地雷达[1]观测俯视场景如下图,慢时间k时刻的接收雷达和发射雷达到坐标系原点的斜距向量分别为Rt(k)和Rr(k),发射雷达和接收雷达的观测角度分别为θt和θr,点目标到场景中心的距离向量为r。
FMCWSAR一般发射具有大时宽带宽积的线性调频信号[2],每个信号周期内发射的信号一般可以表示如下:
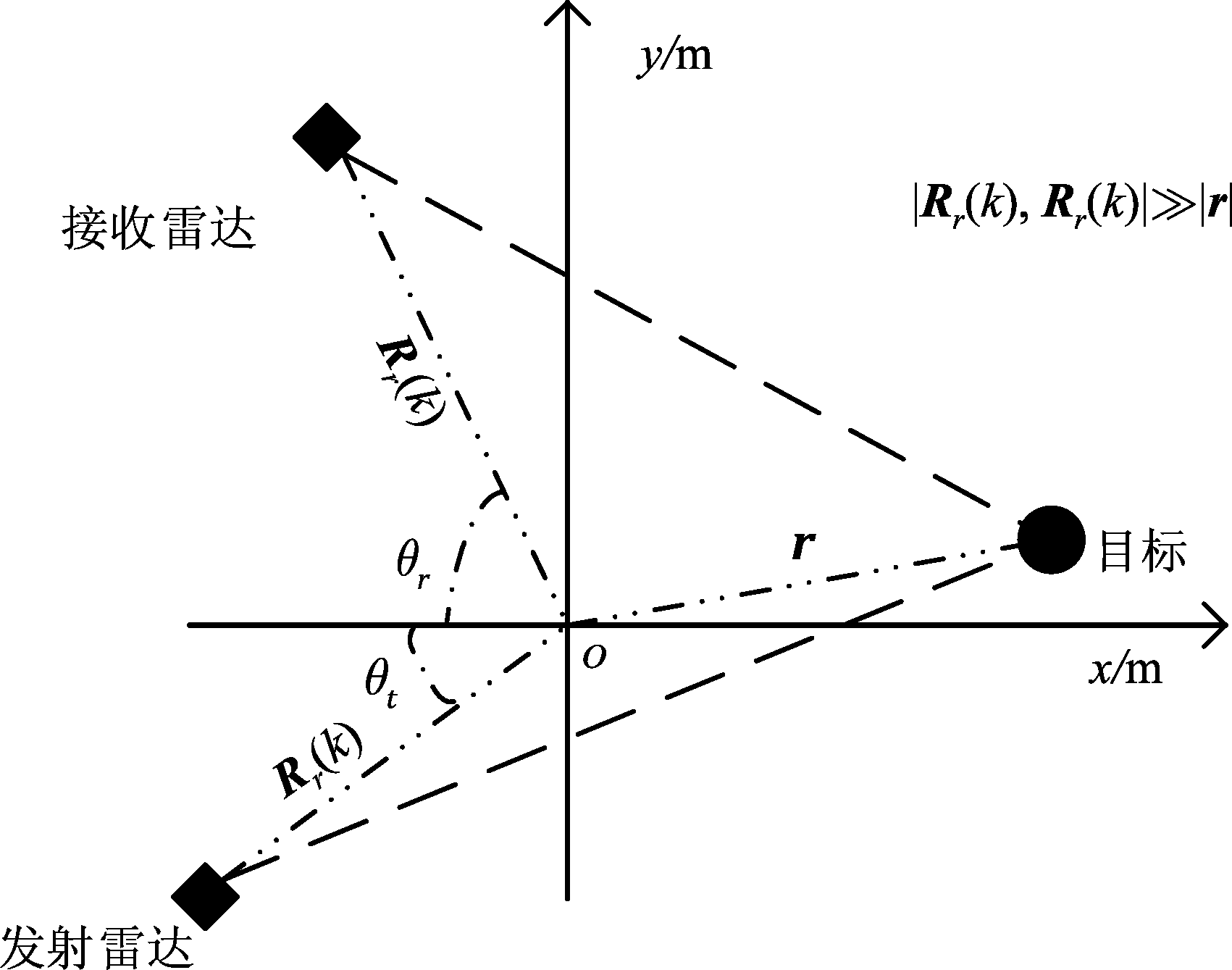
图1 双基地雷达观测场景
Fig.1 Bistatic radar observation scene
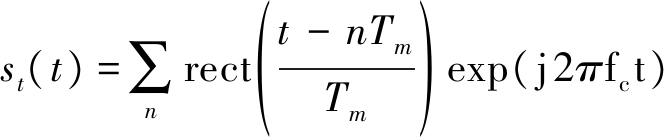
exp(j πKr(t-nTm)2)
(1)
在式(1)中,Tm为锯齿波周期,Kr为调频率, fc为雷达载频,
是(0,Tm)范围的窗函数。
对于双基地雷达模型,在慢时间k时刻点目标模型与发射雷达和接收雷达的斜距分别为Rr和Rt,时延τ(k)=(Rt(k)+Rr(k))/c,c 为光速,第n个周期内的回波信号如下:
sp(t,k)=st(t -τ)=
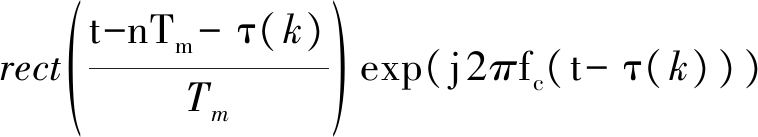
exp(j πKr(t -nTm -τ)τ(k)2)
(2)
第n个周期内回波信号为例进行成像处理[3]:先与发射信号混频,进行去斜处理如下:
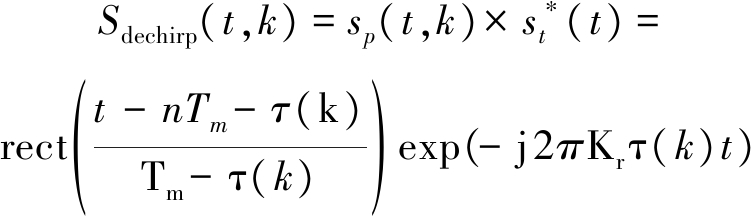
exp( -j 2πfcτ(k))exp(j π(nBτ(k) + Krτ(k)2))
(3)
对去斜处理后信号进行傅里叶变换后得到:
Sf(f,k)=F(Sdechirp(t,k))=
(Tm -τ)sin c((Tm -τ(k))(f+Krτ(k)))
exp( -j 2πfcτ(k))exp( -j 2π(nTm+τ(k)/2)f)
(4)
将频率轴变为时延时间轴,即f=-Krt 得到距离压缩后信号:
Sf(f,k)= (Tm -τ(k))sin c((B-Krτ(k))(t-τ(k)))
exp( -j 2πfcτ(k))exp(j 2π(nTm+τ(k)/2)Krt)
(5)
观察可知,距离压缩后信号与脉压体制信号差别在于增加最后一项RVP相位,由于τ未知,用t近似进行相位补偿,相当于将主瓣峰值点相位补偿为理想相位,补偿量为:
φRVP =-π(2nTm +t)Krt
(6)
再进行脉冲体制雷达成像即可得到成像区域图像。
以上是调频连续波体制下的单点目标成像过程,雷达回波如上式(2)所示,若对二维场景中具有连续结构的目标如线目标或面元目标进行仿真,则需要构建连续结构目标的回波模型。
2.2 基于散射点集的回波模型
为简化分析,本文在二维场景中进行成像仿真。SAR的基于散射点集的回波模型是将场景区域按分辨率划分成二维网格,用网格格点上的散射系数值来近似表示场景散射系数图,表示如下:
(7)
其中,ri表示第i个网格点的位置,在二维平面上可以表示为ri=(xi,yi),σi 表示第i个网格点处的散射系数,δ(·)为狄拉克冲激函数。
双基地雷达观测俯视场景如图1,发射信号的频谱为St( f ),则单点目标回波频谱表示如下:
Sp( f )=F(sp(t))=F(st(t-τ))=St( f )exp( -j 2πfτ)
(8)
慢时间k时刻的发射雷达和接收雷达到坐标系原点的斜距向量分别为Rt(k)和Rr(k),则τ(k,r)=(|Rt(k)-r|+|Rr(k)-r|)/c为k时刻位置r散射点的回波时延,接收信号是点目标回波的叠加可表示为如下[4- 6]:
(9)
式(9)中,发射信号为线性调频连续波,信号频谱如下所示[7]:
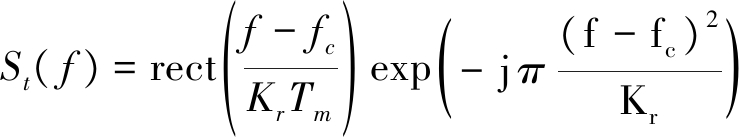
exp( -j 2π(f-fc)nTm)
(10)
将回波信号沿快时间域进行逆傅里叶变换,得到时域回波如下:
(11)
2.3 基于散射点集的回波模型问题分析
基于散射点集的回波模型原理是将连续目标体离散为大量的点模型,回波模型是点回波模型的叠加。误差的主要影响因素有两个:目标体的离散密度和离散方式,以下展开分析。
目标体的离散密度影响:为了保证回波模型的可靠性和稳定性,理论上要求离散采样间隔小于等于回波载频的半个波长,对于电大尺寸的目标,离散采样间隔大会导致模型误差大,离散采样间隔小会导致离散点过多,仿真计算量巨大。
目标体离散方式影响:在基于离散模型的仿真中,常采用固定的离散密度,离散方式有直角坐标等间距离散和极坐标等间距离散方法,如图2所示。对于同一目标,不同的离散采样方式的模型误差分布不同,会出现成像结果不一致的问题,降低了这一近似方法的可信度,对研究造成干扰。例如对同一圆盘目标进行SAR成像仿真,分别采用图2两种离散采样方式,成像结果如图3所示。
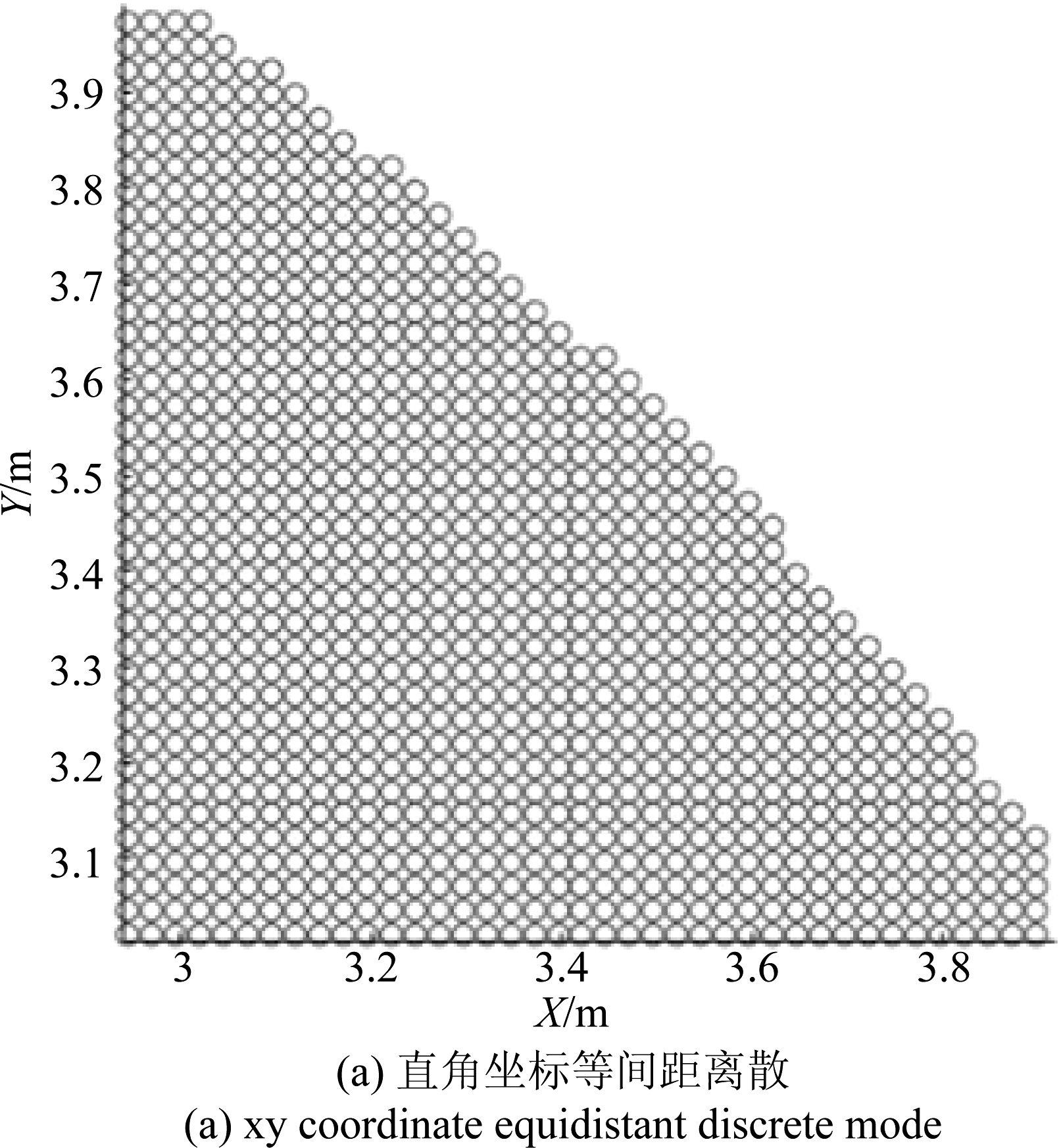
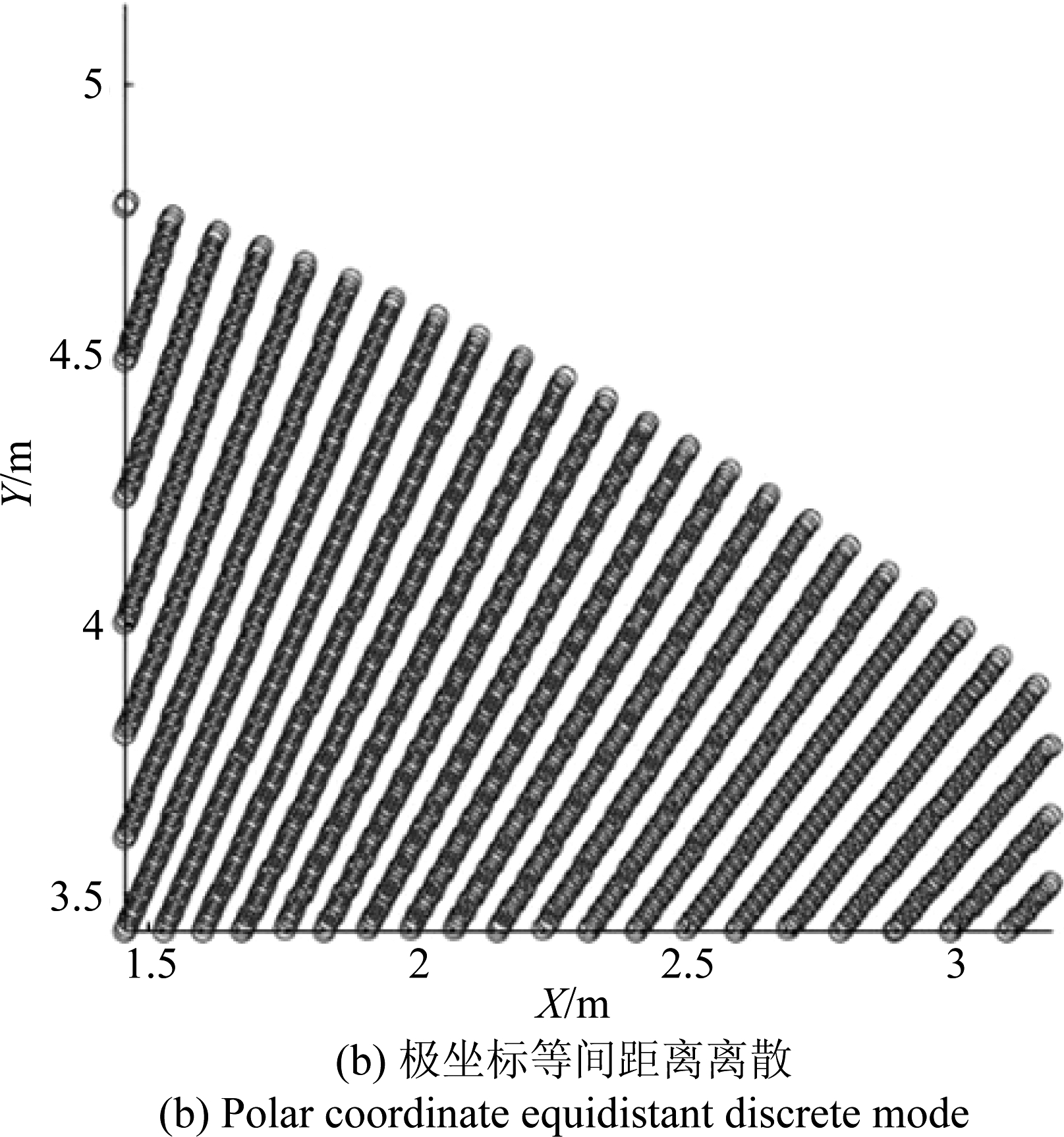
图2 离散模型离散方式
Fig.2 Discrete methods of the discrete echo model
比较图3(a)和图3(b),对于同一圆盘目标的圆迹SAR成像结果,采用直角坐标等间距离散模型成像结果为点图像,极坐标等间距离散模型成像结果为圆环图像。比较图3(c)和图3(d),对于同一圆盘目标的条带SAR成像结果,采用直角坐标等间距离散模型成像结果为两侧端点图像,极坐标等间距离散模型成像结果为一系类等间隔离散点图像。成像结果差异显著,基于散射点集的回波模型受到离散方式的影响大,需要改进,避免离散带来的干扰。
3 连续目标回波模型
本文提出了连续目标回波建模方法,直接生成固定几何结构目标的雷达回波模型的解析表达式,且回波模型仅由目标的尺寸参数和方位参数以及雷达参数决定,不受目标离散方式的影响。
图3 圆盘成像结果
Fig.3 Circle plate target sampling strategies
3.1 连续目标回波模型的生成方法
设成像目标为连续分布的二维散射体, 其分布区域用尺寸参数和方位参数集合Θ来表示,则目标区域为S(Θ)。若慢时间k时刻的回波时延为τ(k,r)=(|Rt(k)-r|+|Rr(k)-r|)/c,雷达接收到的目标区域内的点目标回波如下:
Sp(f,k)=σ(r)St( f )exp( -j 2πfτ(k,r))
(12)
在式(12)中,点目标的斜距为r,反射系数为σ(r),慢时间k时刻的发射雷达和接收雷达位置向量为Rt(k)和Rr(k)。
为避免离散带来的干扰,SAR回波模型是离散间隔趋于无穷小的散射点回波的叠加,则求和转化为积分,表示为:
(13)
对于几何结构明确的目标,可以通过参数集Θ表示目标区域,积分得到的回波模型表示为以参数Θ为变量的解析式。一是避免了离散密度不足带来的回波误差；二是解决不同离散方式可能对应不同的成像结果的问题；三是通过解析式直接计算目标回波可以大大降低计算量。
以下将以二维平面的线段目标和圆盘目标为例,生成连续目标回波模型。
3.2 线段目标回波模型生成
线段目标的表示参数为Θ={x0,y0,φ,L},其中(x0,y0)是线段中心点位置坐标,φ是直线倾角,L是直线长度,假设线段目标反射系数为固定常数σ(r)=1。以直线周围任意一点O为场景中心点构建场景坐标系,如下图4所示。
图4 线目标场景
Fig.4 Line target scene
设慢时间k时刻发射雷达和接收雷达的观测角度分别为θt和θr,雷达到坐标系原点的斜距向量分别为Rt(k)和Rr(k),由于雷达斜距远大于目标尺寸,即Rt,Rr≫x,y,直线上任意一点(x,y)到发射雷达和接收雷达距离近似为
|Rt(k) -r| =
Rt(k) -xcos θt -ysin θt
(14)
|Rr(k) -r| =
Rr(k) -xcos θr -ysin θr
(15)
设置发射雷达与接收雷达的观测角度的夹角固定,即β=(θt-θr)/2为定值,令ω=(θt+θr)/2,慢时间k时刻雷达接收回波的时延为
(16)
线目标参数设为:(x0,y0)是线段中心点位置坐标,φ是直线倾角,L是直线长度,线目标的两端点坐标为(x1,y1)和(x2,y2)。线目标的成像区域可以通过参数解析表示为:S(Θ):y=xtanφ+b,且b=-x0tanφ+y0,区域范围:x2-x1=Lcos φ。
将目标区域关系S(Θ)和时延τ(k,x,y)带入到连续模型的计算式(13)中,由于Rt,Rr≫x,y,满足远场条件,波束近似平行[8],得到线段目标回波模型的解析表达式如下:
Sr(f,k)=
St( f )exp(j 2πfτ(k,x))dx/cos φ=
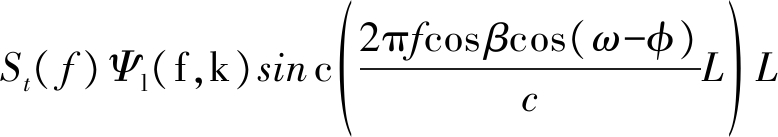
(17)
其中固定相位为:
Ψl(f,k)=
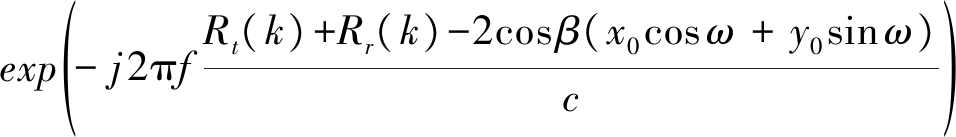
(18)
其中调频连续波发射信号频谱为:
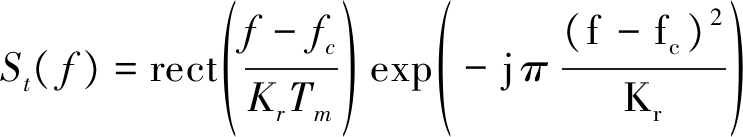
exp( -j π(f-fc)Tm)
(19)
将发射信号频谱式(19)和固定相位式(18)带入到式(17)中,得到线段目标回波频谱模型的解析表达式。对信号频谱模型进行傅里叶逆变换即可得到时域回波模型,再进行成像仿真。
3.3 圆盘目标回波模型生成
圆盘目标参数Θ={x0,y0,R},其中(x0,y0)为圆盘中心点坐标,R为圆盘半径,圆盘目标成像区域表示为:S(Θ):(x-x0)2+(y-y0)2=R2,场景如下图5所示。
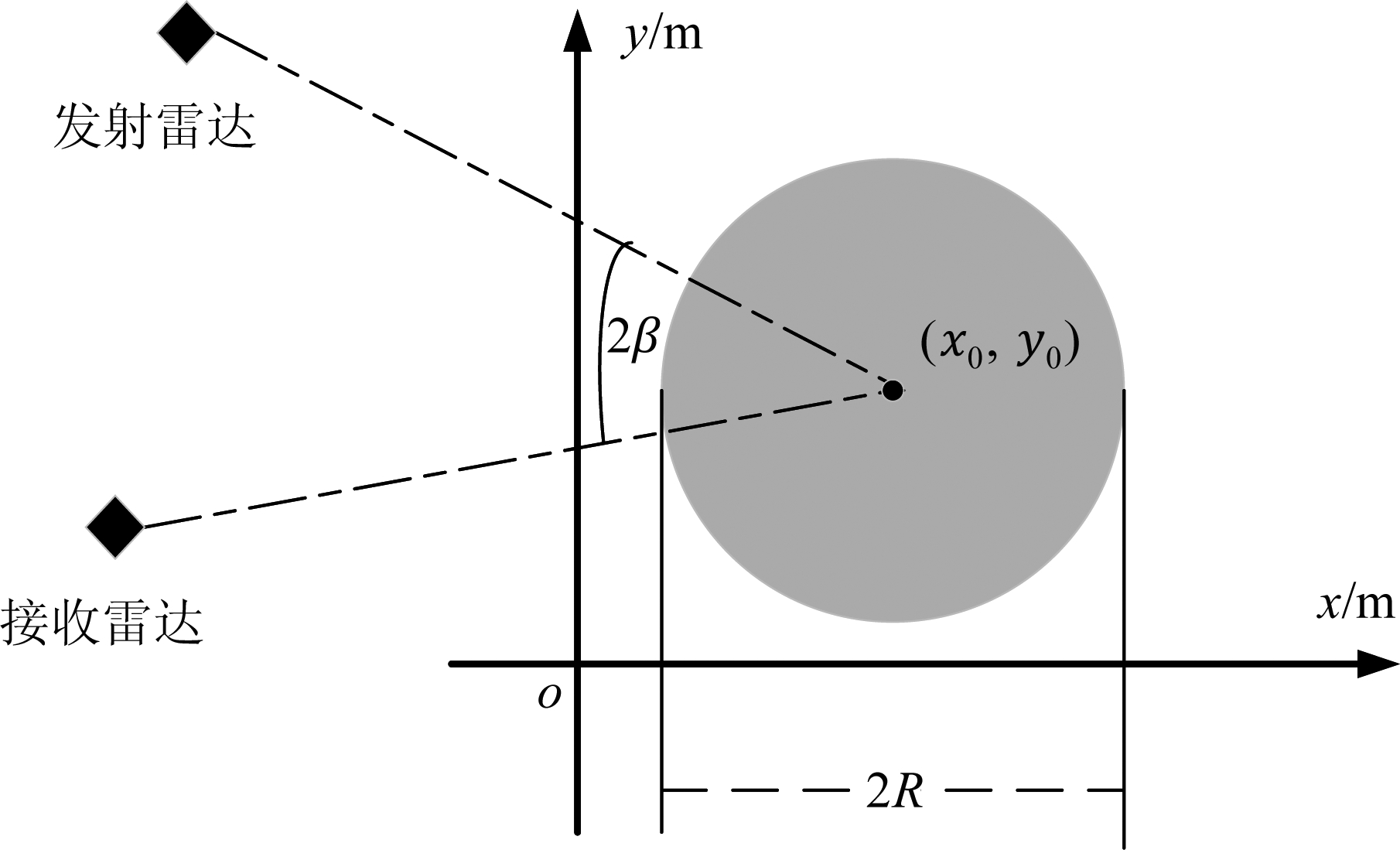
图5 圆盘目标场景
Fig.5 Circle plate target scene
圆盘目标上割线对应的回波相位相同,即xcos(ω)+ysin(ω)=C(x,y),割线回波相位为式(20)。若以发射雷达与接收雷达的角平分线为x轴位置,建立坐标系,则ω=0,C(x,y)=x。
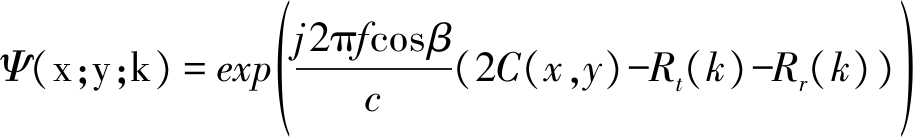
(20)
圆盘回波表示为[9]
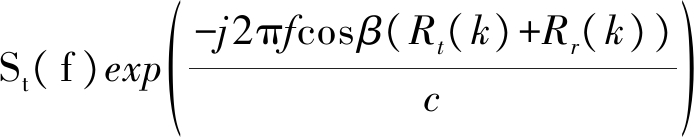
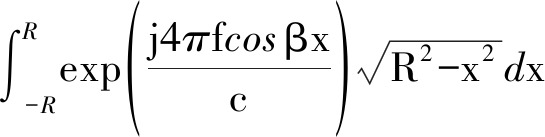
(21)
积分项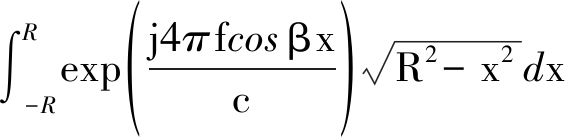
无法计算解析表达式,有两种方法进行处理。一是将积分项
进行泰勒展开,根据允许的误差设置展开阶数,在将展开值带入公式进行积分,得到解析表达式。注意展开式阶数与圆盘半径大小有关,在改变参数时要实时变更表达式,保证合理性,例如在半径R=1 m的圆盘,设置泰勒展开式值与真值偏差在1×10-4 条件下,展开式阶数为14。二是可以通过快速逆傅里叶变换实现,令z=2xcos β/c,则积分项变为:
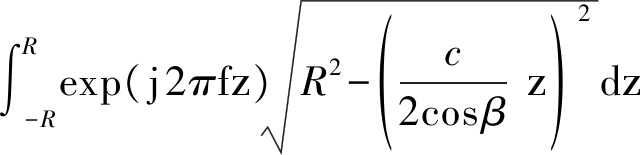
(22)
积分结果等效为对函数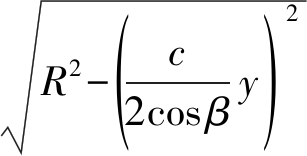
的逆傅里叶变换,虽然仍对目标的x轴向进行了离散操作,但与基于散射点集回波模型中对目标场景进行离散不同,一是此处的离散只是为了进行快速计算,在设计了圆盘目标的参数后,直接将x表示为[-R/2,R/2]间的离散值即可,在离散间隔足够小的条件下,离散方式不影响计算结果,消除了离散方式对成像结果的影响；二是可以通过快速傅里叶变化直接得到圆盘目标回波,节省大量计算资源,传统对目标场景进行离散后叠加离散点回波的方法要依次叠加大量数据,浪费大量计算资源。
除线目标和圆盘目标外,最常见的三角面元目标也可得到回波的解析表达式。三角面元参数设置为,三顶点坐标(x1,y1),(x2,y2),(x3,y3),长度分别为L1,L2,L3,三边的倾斜角度角分别为α1,α2,α3。则在倾角中无90°角时,回波表示为:
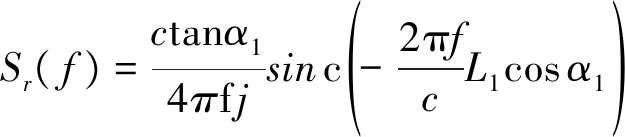
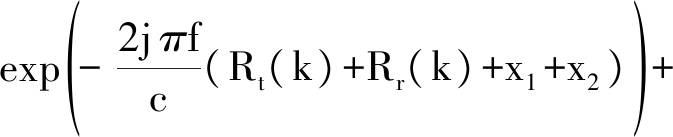
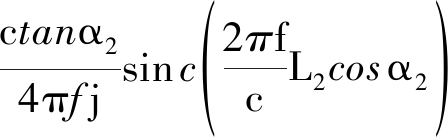
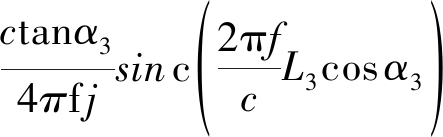
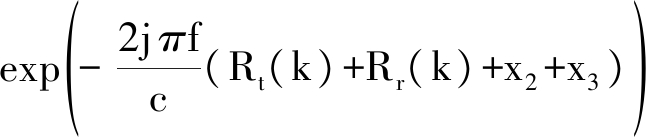
(23)
若其中一边倾角为90°,如α2=90°,则回波表示为:
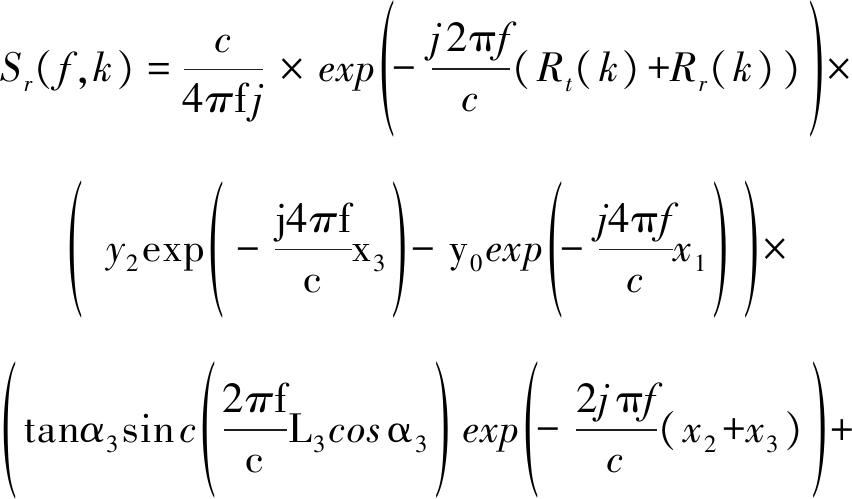
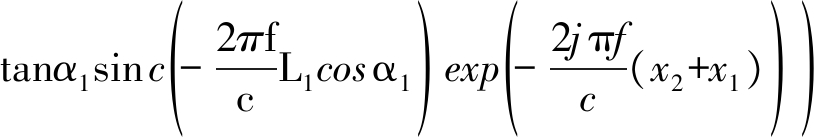
(24)
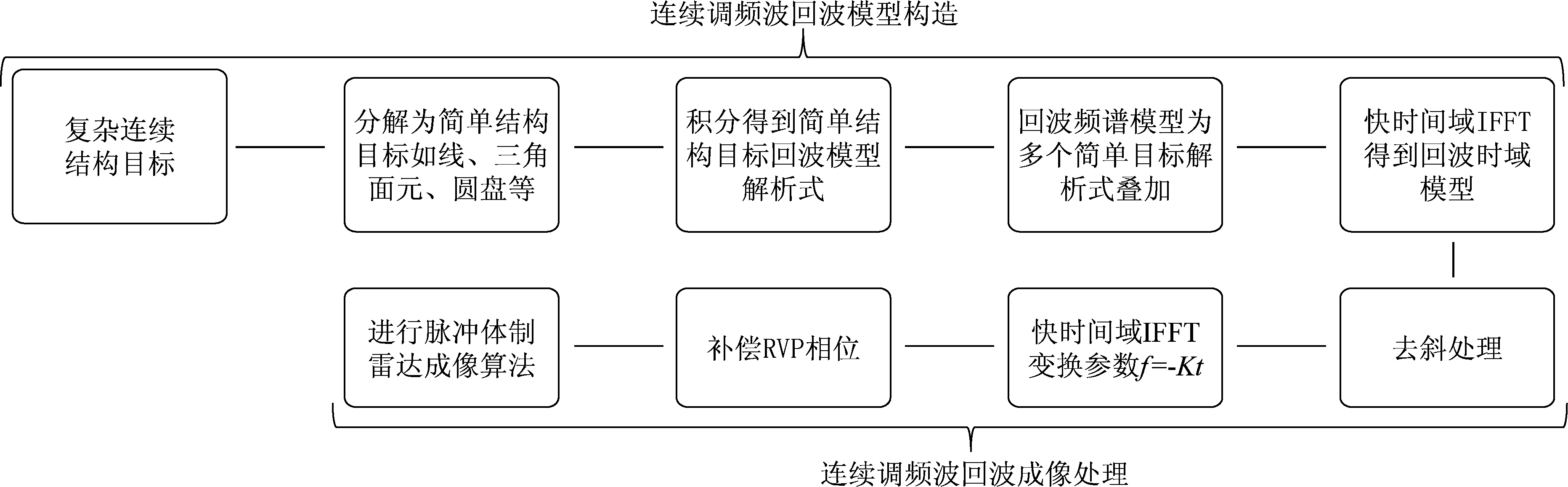
可以通过三角面元参数直接构建三角面元的回波模型。具有复杂结构的目标通常可以分解为线目标、三角面元目标和圆盘目标的集合,可以将复杂场景回波模型表示为多个简单几何目标回波模型的叠加的形式,便于通过回波直接对场景频谱特性进行分析,消除离散方式对成像结果的影响,同时降低计算量。
综上,得到对连续结构目标的回波构造和成像处理过程框图:
3.4 矩形平板的连续目标回波模型与属性散射中心模型对比
矩形平板目标参数Θ={a,b},其中a和b为平板的长和宽,平板的长与x轴平行,且平板中心与场景中心重合为(0,0),雷达与目标在同一水平面,发射雷达和接收雷达观测角的角平分线角度θ,此时雷达距坐标原点距离R0(θ),令雷达信号波长为
则基于上述连续目标的成像方法构造矩形平板目标的回波模型为:
exp( -jk(Rr(θ) + Rt(θ)))
(25)
假设雷达在与目标在同一水平面仍可接收到目标回波,在如上目标参数下的矩形平板的属性散射模型公式为:
(26)
比较上式(25)和式(26)可知,由于计算矩形平板目标的连续目标回波模型时假设矩形平板的各部分散射强度均为1,导致与属性散射中心模型的幅度项和相位项不同,但两种模型的波形形式相同,连续目标回波模型具有合理性。
4 仿真结果与分析
进行双基地调频连续波成像算法[10]仿真,设线段目标参数为:线段中心点坐标(x0,y0)=(1,1),倾斜角度φ=30°,线段长度L=4。基于散射点集的回波模型采用直角坐标等间距离散方式,固定离散间隔为(Δx,Δy)=(5×10-3,8.66×10-3)。基于散射点集的回波模型与连续目标回波模型成像仿真结果分别如下图6(a)和(b)。两种模型成像结果一致,都能反映目标的几何结构。
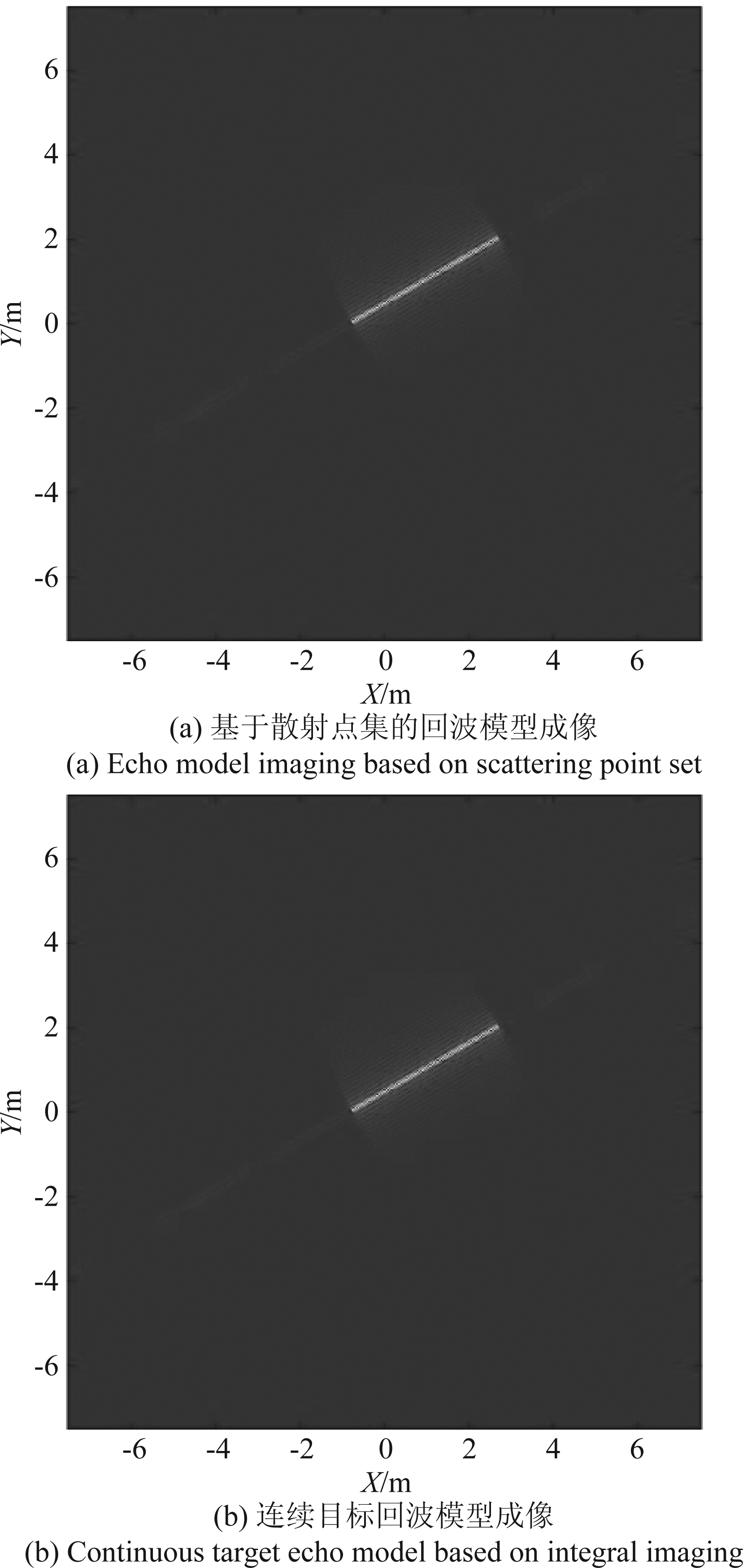
图6 线段目标成像结果比较
Fig.6 Comparison of line segment target imaging results
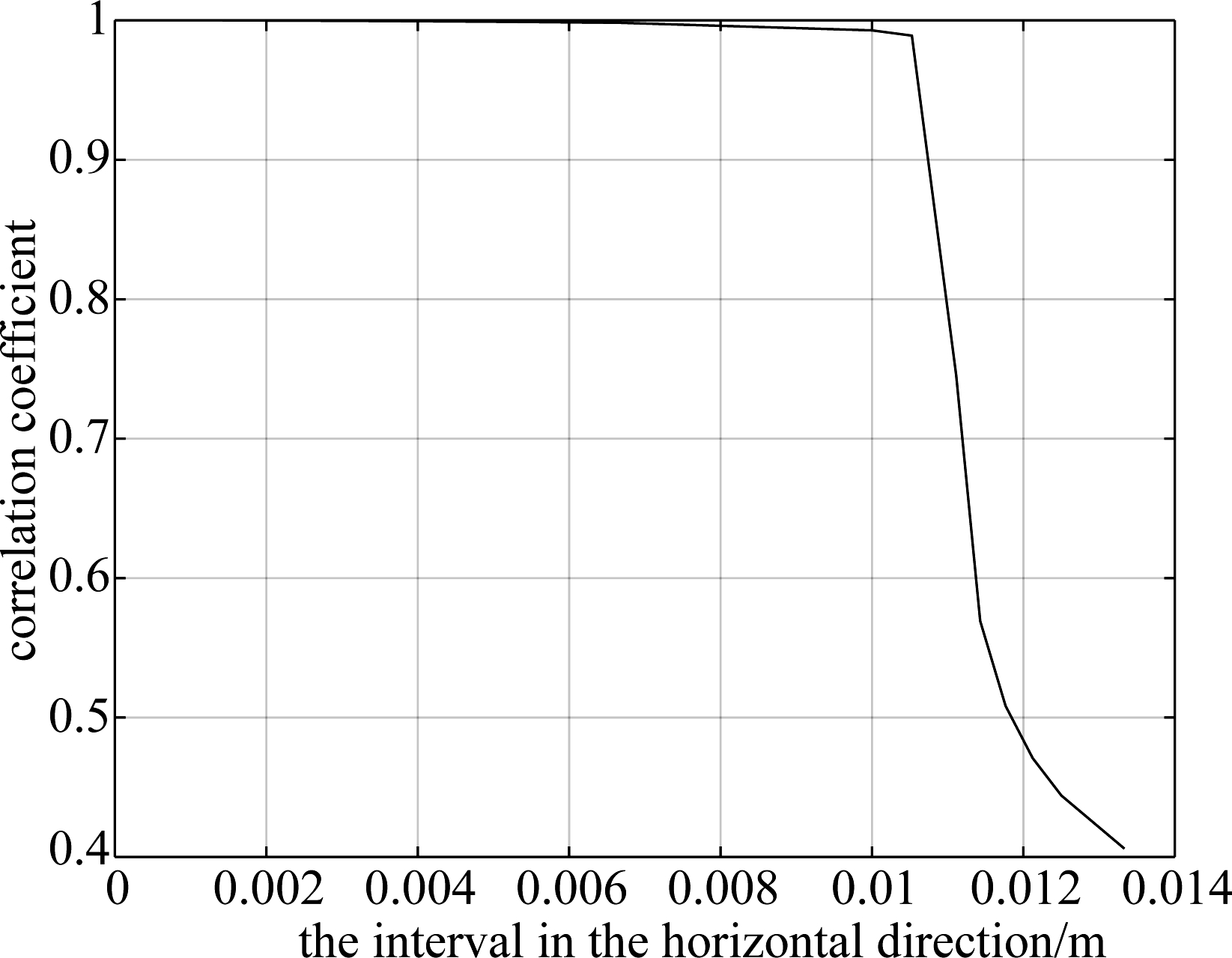
图7 模型间的协方差系数与离散间隔关系图
Fig.7 Relationship between the covariance coefficient and the discrete interval
比较两种模型的等价性:线段目标的基于散射点集的回波模型与连续目标回波模型的协方差随基于散射点集的回波模型的离散采样间隔的减小而减小,如图7,当离散间隔减小到Δx=1.25×10-3时,两种模型间协方差趋近于1,两种模型近似一致。
对圆盘目标进行成像仿真,目标参数为圆心坐标参数为(x0,y0)=(0,0),半径为R=1 m,采用泰勒展开的方式得到回波解析式,展开式阶数为14。连续目标回波模型的圆迹SAR成像结果与极坐标等间距离散方式的点集回波模型成像结果一致,连续目标回波模型的条带SAR成像结果与直角坐标等间距离散方式的点集回波模型成像结果一致如下图8。
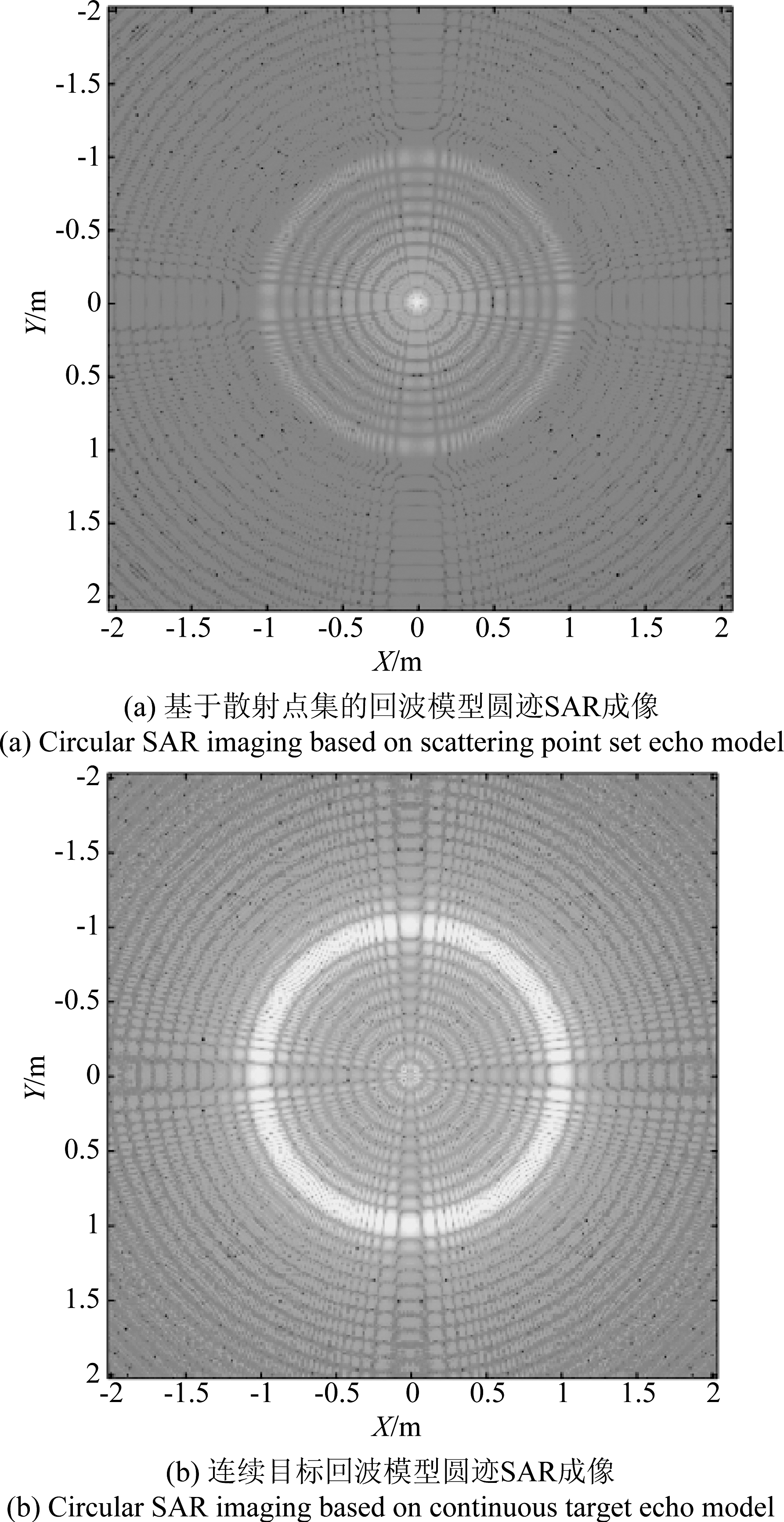
图8 圆盘目标成像结果比较
Fig.8 Comparison of circle plate target imaging results
一是连续目标回波模型由于消除了离散过程,避免了不同离散方式对应的成像结果不一致的问题。二是连续目标回波模型直接通过解析式计算回波值,大大降低了计算量,基于散射点集回波模型为保证圆盘模型与真实目标的近似性,需要离散点间隔小于波长的1/10,对于半径为1 m的圆盘,需要1.8×105 个离散点,则回波模型为1.8×105个离散点的回波叠加,计算量巨大。
5 结论
本文提出了基于双基地调频连续波雷达的连续目标回波模型,在误差允许范围内,该模型与传统的由点模型集合构成的基于散射点集的回波模型一致。连续目标回波模型解决了基于散射点集的回波模型中离散方式影响成像结果的问题,并且大大降低了计算量,便于应用于双基地调频连续波雷达成像仿真和目标回波特性分析。
[1] 曾涛. 双基地合成孔径雷达发展现状与趋势分析[J]. 雷达学报, 2012, 1(4): 329-341.
Zeng T. Bistatic SAR: State of the Art and Development Trend[J]. Journal of Radars, 2012, 1(4): 329-341. (in Chinese)
[2] 张军, 毛二可. 线性调频连续波SAR成像处理研究[J]. 现代雷达, 2005, 27(4): 42- 45.
Zhang J, Mao E K. A Study on LFMCW Signal Processing[J]. Modern Radar, 2005, 27(4): 42- 45. (in Chinese)
[3] 汪玲, 岳怡然, 熊倩. 利用多普勒分辨率的FMCW SAR成像算法[J]. 信号处理, 2017, 33(7): 961-969.
Wang L, Yue Y R, Xiong Q. A FMCW SAR Imaging Algorithm Capable of Exploiting Doppler Resolution [J]. Journal of Signal Processing, 2017, 33(7): 961-969. (in Chinese)
[4] Yang L, Yu W, Zheng S, et al. Ef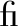
cient Bistatic SAR Raw Signal Simulator of Extended Scenes[J]. International Journal of Antennas & Propagation, 2015, 2014(3): 1-9.
[5] Anghel A, Vasile G, Cacoveanu R. Scattering Centers Monitoring in SAR Images[M]. Infrastructure Monitoring with Spaceborne SAR Sensors. Springer Singapore, 2017.
[6] Deng Y, Liu Y, Wang R, et al. FMCW SAR raw signal simulator for extended scenes[C]∥European Conference on Synthetic Aperture Radar. VDE, 2012: 462- 465.
[7] 刘勇, 张国毅, 张旭洲. 线性调频连续波雷达信号的参数估计[J]. 信号处理, 2014, 30(7): 848- 855.
Liu Y, Zhang G Y, Zhang X Z. Parameter Estimation of LFMCW Radar Signal[J]. Journal of Signal Processing, 2014, 30(7): 848- 855. (in Chinese)
[8] Brown G S. Scattering from randomly rough surfaces and the far field approximation[J]. Radio Science, 2016, 18(1): 71- 81.
[9] Zhai W, Zhang Y, Zhang X. SAR Imaging Simulation for Subsurface Target Detection[C]∥International Symposium on Antennas, Propagation & Em Theory. IEEE, 2006: 1-5.
[10] Wang S, Fan C, Huang X, et al. Bistatic ISAR imaging based on BP algorithm[C]∥Progress in Electromagnetic Research Symposium. IEEE, 2016: 2858-2862.
