1 引言
利用多个发射机和多个接收机同时进行目标观测的分布式无源雷达成像系统,相比于传统收发一体的单站雷达能够获取更多的目标信息,具有更好的成像性能,因而成为雷达成像的一个热门研究领域。在分布式无源雷达成像系统中,由于接收到的是空间频率非均匀分布的空间信号,致使基于传统的SAR/ISAR算法并不能取得良好的成像效果[1]。研究表明,可以利用目标回波空间频谱和目标散射点之间的傅里叶变换关系实现分布式无源雷达成像[2]。
在实际的成像系统中,成本的制约使得难以构造数量众多的发射机和接收机来满足目标网格空间划分,考虑到接收信号空间谱和目标散射点的稀疏特性,基于压缩感知的成像技术会具有更好的性能。文献[3]中指出接收信号的空间频率对成像结果有重要的影响,它们与信号频谱,发射机和接收机的位置直接相关,同时将互相关系数作为优化目标函数对固定发射机位置情况下的接收机布局进行优化,因此在本文第2部分讨论了采用成像分辨率作为优化目标函数,基于遗传算法配置接收机的位置以实现最佳成像问题。
通过对分布式无源雷达系统接收机的布局优化能够在一定程度上提高其稀疏成像性能,但是在信噪比较低的情况下,基于OMP的稀疏重构算法需要引入大量其他信号分量来降低对前面信号的错误估计造成的影响[4],而稀疏贝叶斯学习的方法假设信号的每一个分量独立和具有不同的先验概率分布,进而获得信号的稀疏表示,如果将其应用于信号重构,能有效改善低信噪比情况下的成像性能[5]。因此在本文第3部分讨论了一种基于 SBL和协方差稀疏表示的分布式无源雷达成像算法来提高成像精度。在接下来的第4部分通过仿真实验对前面讨论的算法进行验证,最后总结全文。
2 分布式无源雷达接收机配置优化
2.1 分布式无源雷达稀疏成像模型
图1表示一个包含m个发射机和n个接收机的分布式无源雷达成像系统,假设发射机m发射的信号为:
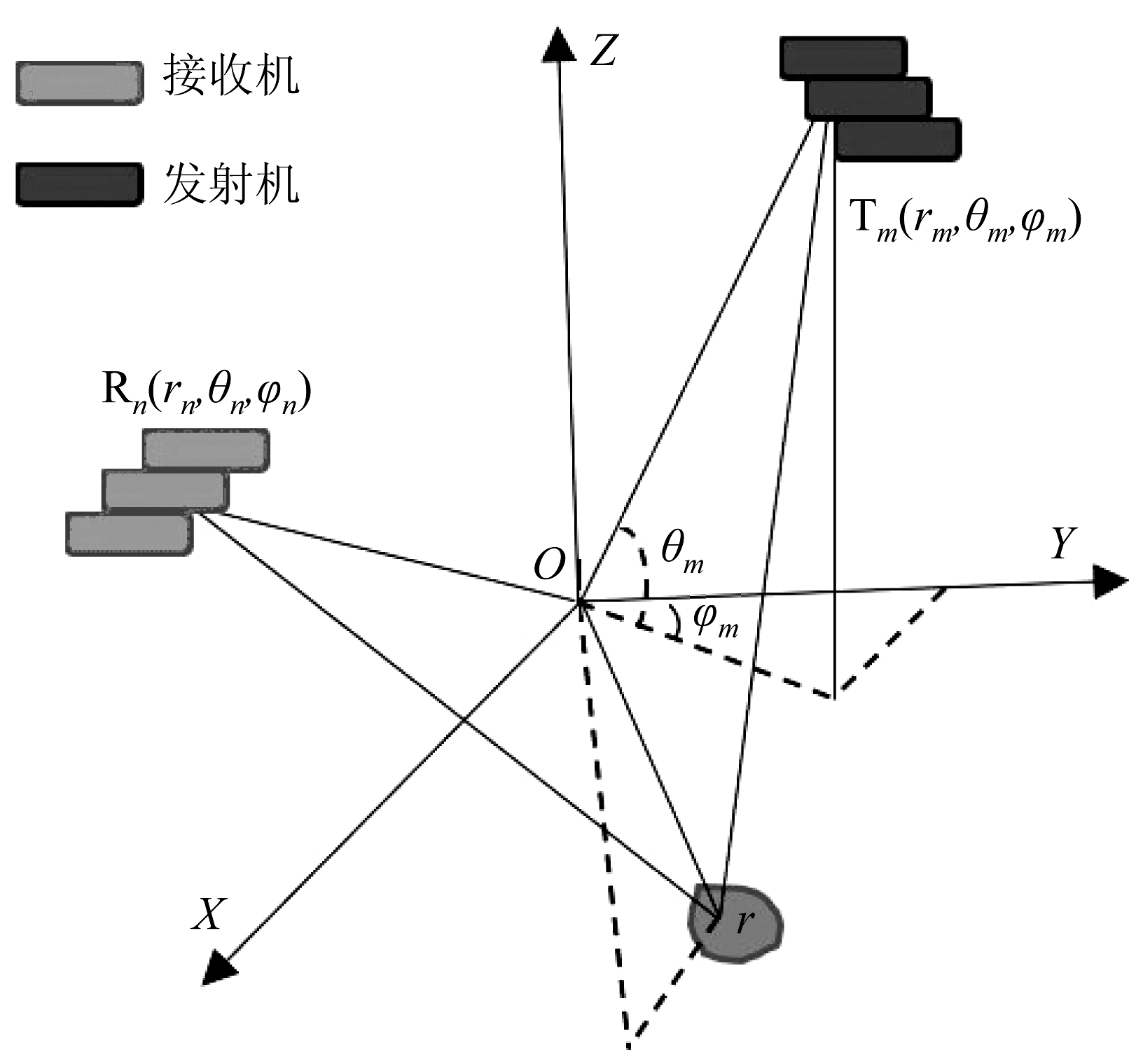
图1 分布式雷达成像构型示意图
Fig.1 Schematic diagram of distributed radar imaging configuration
sm(t)=um(t)exp(j2πfmt)
(1)
式中um(t)和fm分别为信号的包络和载频,则在成像空间Ω中接收机n接收到经过目标反射的发射信号为:
τmn(r)]exp(j2πfm(t-τmn(r))]dr+nn(t)
(2)
式中A(r)为传播路径衰减,α(r)为目标散射系数,nn(t)为接收噪声,τmn(r)为传输时延。
对式(1)(2)做相关处理并在滤波后信号的峰值进行采样后得到:
(3)
其中kmnx、kmny和kmnz为空间谱域离散点所对应的点,将成像空间划分为G=KLQ离散空间网格,K、L和Q是X、Y和Z方向的网格点数,推导出矩阵表示的形式可得:
ymn =
mnσ+emn
(4)
式中σ为在离散网格上取值所构成的向量,mn为DFT矢量,可表示为:
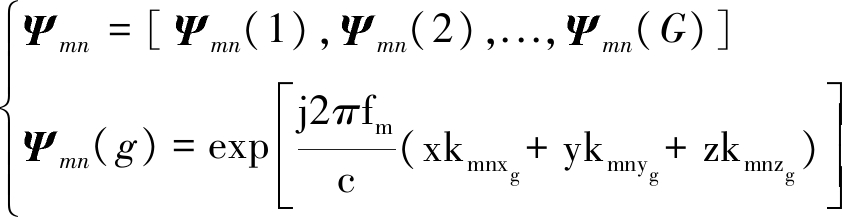
(5)
根据压缩感知理论[6],如果矢量σ是稀疏矢量,则可以使用OMP算法来求解。
2.2 基于遗传算法的布局优化
分布式雷达的空间谱与其几何构型有关,当按照距离向和方位向对空间谱范围进行划分时,可推导出当前构型的理想成像分辨率为:
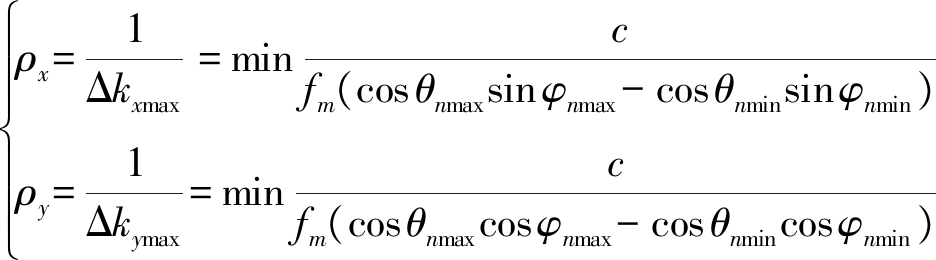
(6)
x和y分别是x和y方向的极限分辨率,kxmax和kymax分别表示x和y方向上空间采样点分布的最大范围。由于ρx和ρy为θ和φ的非线性函数,则可以将成像分辨率最高作为优化目标函数,通过最优化算法就可以求出使得距离向分辨率和方位向分辨率最高的接收机分布。
由于发射机、接收机分布参数空间较大,采用暴力搜索等一般优化算法具有较高的时间复杂度,因此采用智能优化算法中的遗传算法来求取次优解[7],其算法流程图如图2所示。将θ和φ编码到[-45°,45°]范围内,然后将种群个体解码成解空间向量带入(5)所示的重构矩阵,将OMP算法求得的成像结果
带入(6)计算分辨率,根据每次迭代种群淘汰概率保留最优种群,接下来采用交叉变异操作产生新的种群,并不断迭代,直到满足遗传算法终止条件,文章第4部分将对仿真结果进行分析。
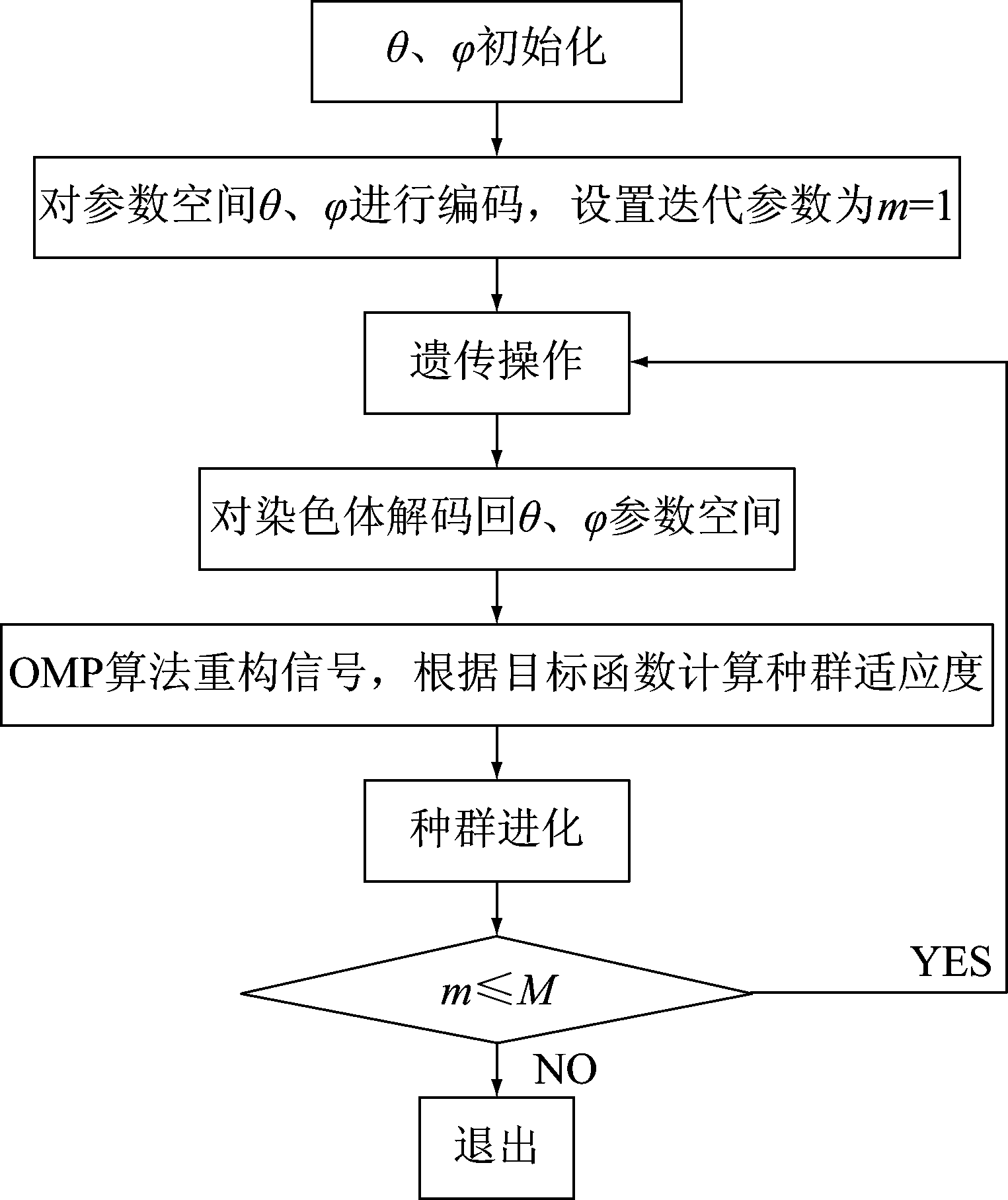
图2 基于遗传算法的布局优化流程图
Fig.2 Flow chart of layout optimization based on genetic algorithm
3 分布式无源雷达成像技术
3.1 协方差稀疏表示模型
在对空中静止或运动目标一次快拍下成像时,基于压缩感知的稀疏成像算法是以目标信号的线性组合与噪声之和的数据模型为基础,因此,不同的模型会由于参数估计的误差得到不同的结果[8],针对这个问题,提出一种以观测数据协方差稀疏表示为基础的分布式无源雷达成像算法。
当在稀疏度为K的空间成像时,由于发射信号受到高斯白噪声的影响,则可以表示为:
Yt=
αt+nt,t∈{1,...,L}
(7)
其中, =[ψ11;...;ψMN]为重构矩阵,αt =[αt(1),...,αt(G)]T为入射信号,nt=[nt(1),...,nt(MN)]T为高斯白噪声,L为快拍数。接收信号数据的协方差为:
Rα H+σ2IMN
(8)
其中发射信号的协方差为
为单位矩阵,σ2为噪声方差。引入H=[h1,h2,...,hMN]为每一列都具有相同的稀疏结构,以及h°=[h°1,h°2,...,h°MN]T,其中h°是H中第i行的二范数,则信号恢复就转化为求解一个联合最稀疏解的过程[9],并可以使用如下模型求解:
(9)
3.2 基于协方差稀疏表示和稀疏贝叶斯学习的成像算法
根据贝叶斯理论,观测信号的高斯似然函数为[10]:
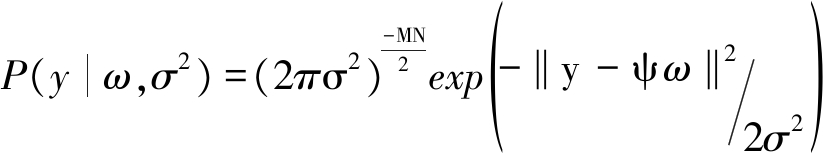
(10)
其中σ2为等效噪声转换为白噪声后的协方差,我们通过加入目标成像空间稀疏化先验约束来避免数据的过学习,假定参数σ2和γ是已知的,则其稀疏系数ω的高斯后验概论分布为:
P(ω|y,γ,σ-2)=
(11)
其中μ为均值,∑为协方差,可以通过EM算法估计参数σ2和γ,从而求得稀疏系数ω的高斯后验概率分布。通过稀疏贝叶斯求得的ω=[ω1,...,ωG]相当于式(9)中H,可利用BP算法求解式(9),也就可以得出目标在稀疏向量的位置。又根据(8)可知,H=Rα H,则H的非零位置与Rα的非零位置是一致的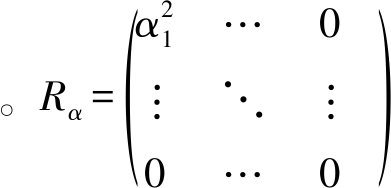
的对角线上有K个非零值,该非零值为对应信号的功率,因此通过H的非零位置在Rα中的对应位置可求出信号的幅度,进行目标成像。具体算法流程如图3所示,仿真结果将在第4部分进行分析。
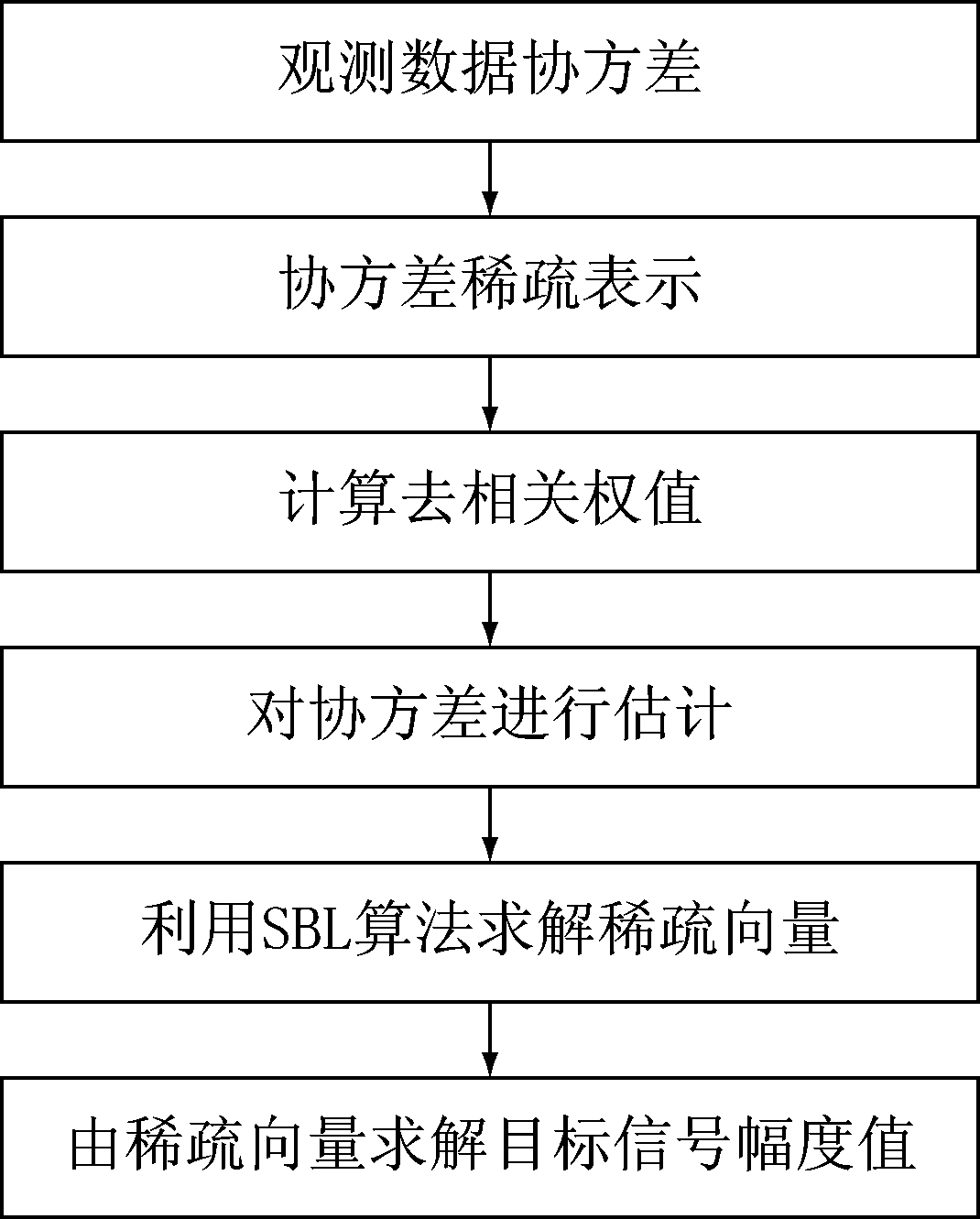
图3 基于协方差稀疏表示的SBL算法
Fig.3 SBL algorithm based on covariance sparse representation
4 仿真结果分析
4.1 分布式无源雷达接收机配置优化
为了验证第2部分接收机布局优化对于成像分辨率的改进,本小节设发射机分布固定,以理论分辨率表达式(6)为优化目标函数,用遗传算法优化对接收机分布进行优化设计。优化前接收机在
内等间隔均匀分布,优化后接收机位置分布如图4所示,优化前后理论分辨率分别为0.02001 m和0.0109 m,结果有所改善。根据式(6),优化后θmax和θmin都约等于
使得表达式取得最小值,而分辨率达到最大,说明该方法具有有效性。同时,图4中可见,接收机分布呈现随机性,能够减小重构矩阵各列的相关系数,从而提高OMP算法的重构性能。
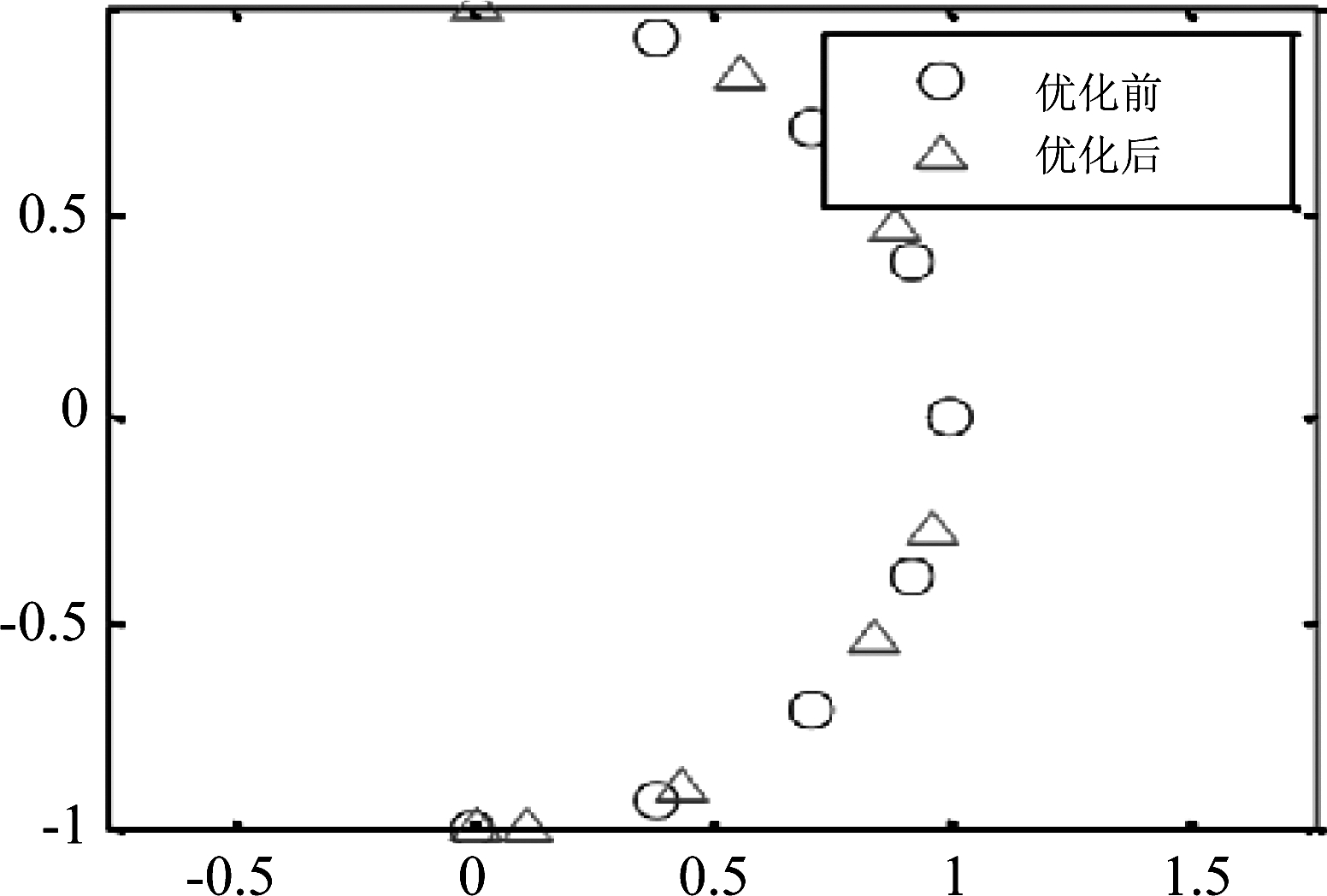
图4 遗传算法优化前后接收机配置示意图
Fig.4 Schematic diagram of receiver configuration before and after genetic algorithm optimization
4.2 分布式无源雷达成像技术
为了验证基于协方差稀疏表示的SBL成像算法的有效性,首先对比该算法对于静止点目标二维场景的重构能力,仿真参数如表1所示,由图5所知,协方差域成像恢复结果与仿真场景一致,原始数据域已经无法成像。
表1 分布式无源雷达成像仿真参数
Tab.1 Distributed passive radar imaging simulation parameters
发射机数量10接收机数量8空间网格数量1024散射点数量9载频12.5 GHz网格间距1 m信噪比-15 dB快拍数200蒙特卡洛次数200SBL迭代次数50
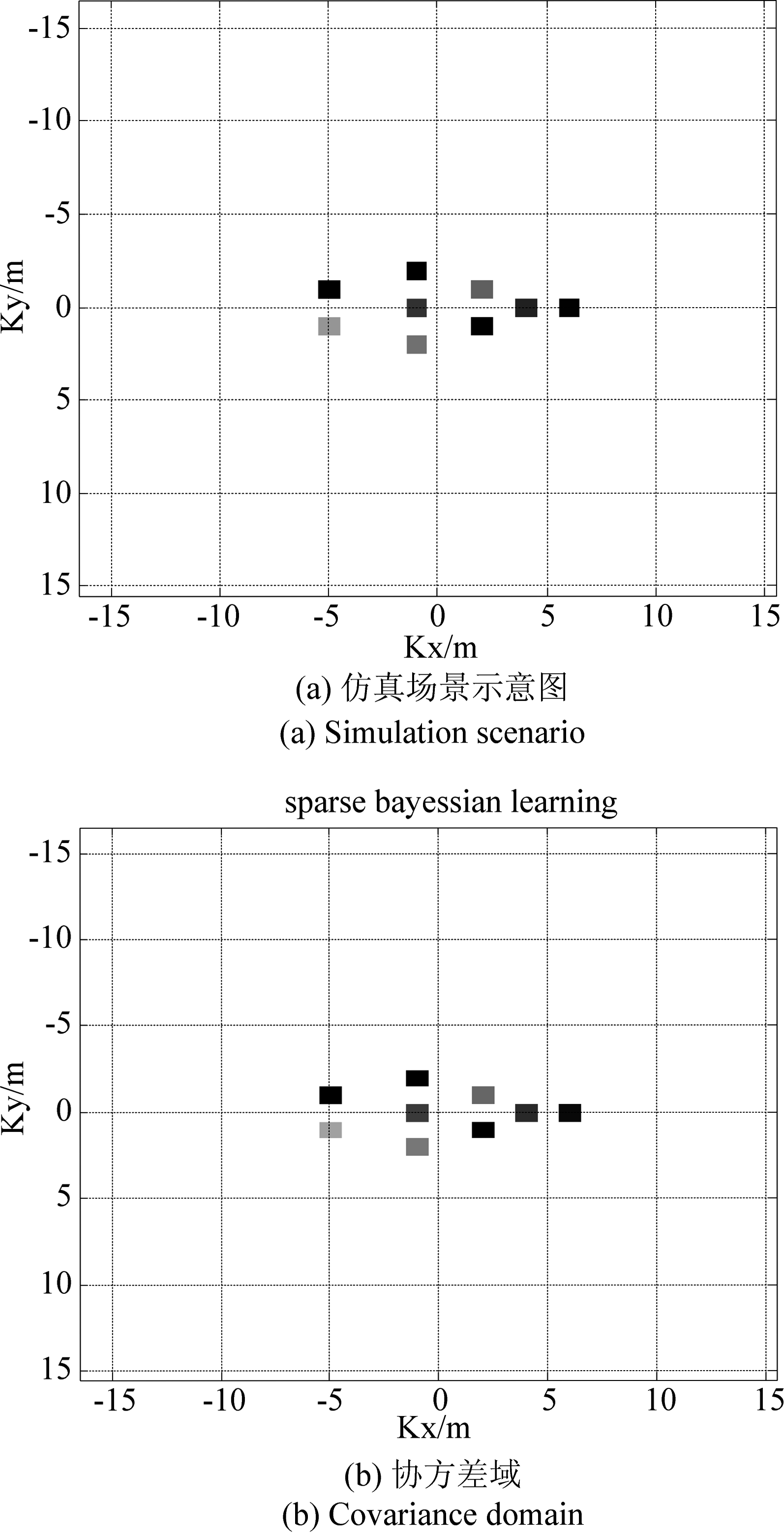
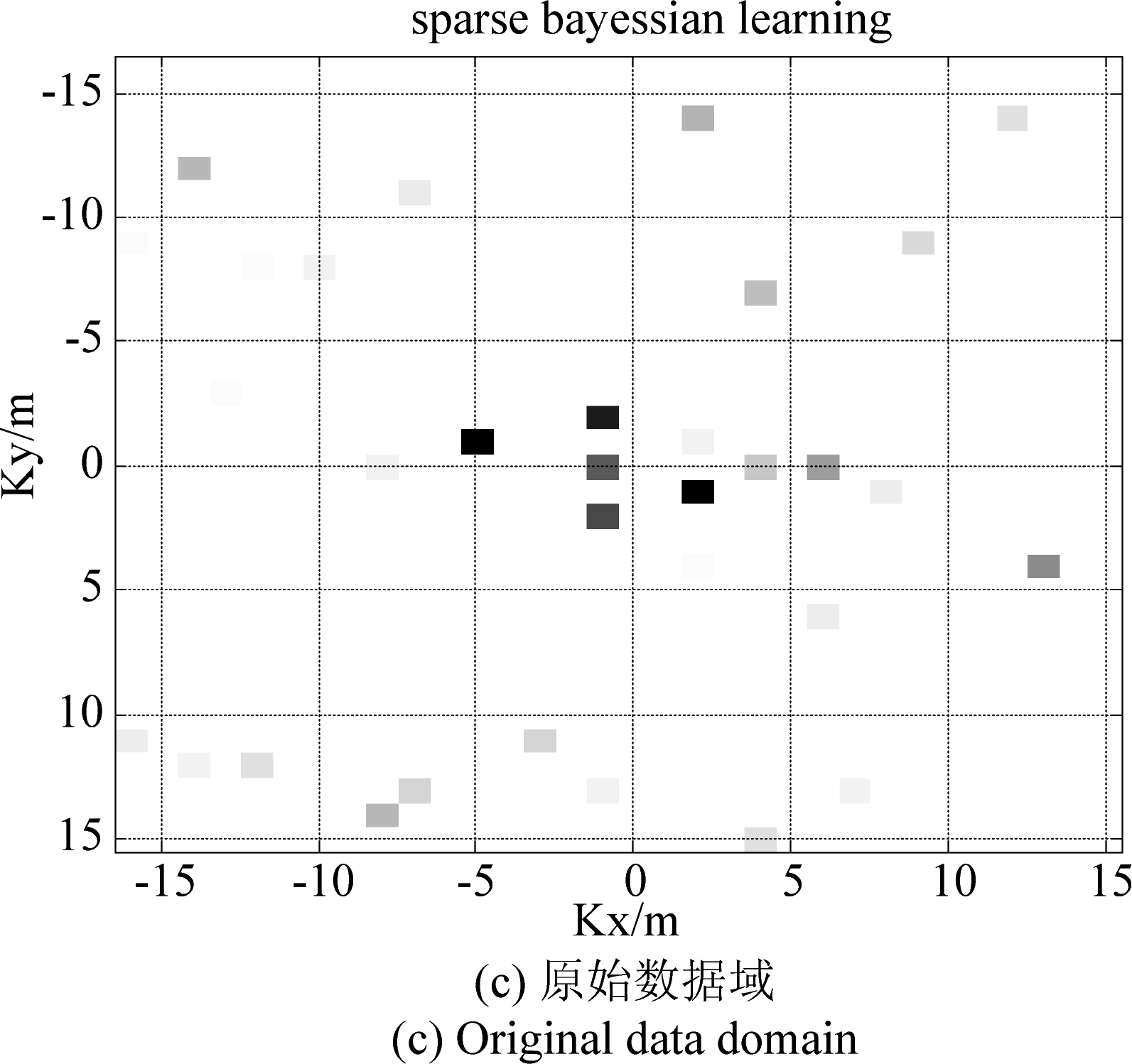
图5 基于协方差稀疏表示的SBL算法成像仿真结果对比
Fig.5 Comparison of imaging simulation results of SBL algorithm based on covariance sparse representation
其次对比基于协方差稀疏表示的SBL算法和基于数据域表示的算法在恢复性能上的差异,设计不同信噪比下协方差域与数据域SBL算法归一化重构信号误差RMSE蒙特卡洛仿真如图6所示。
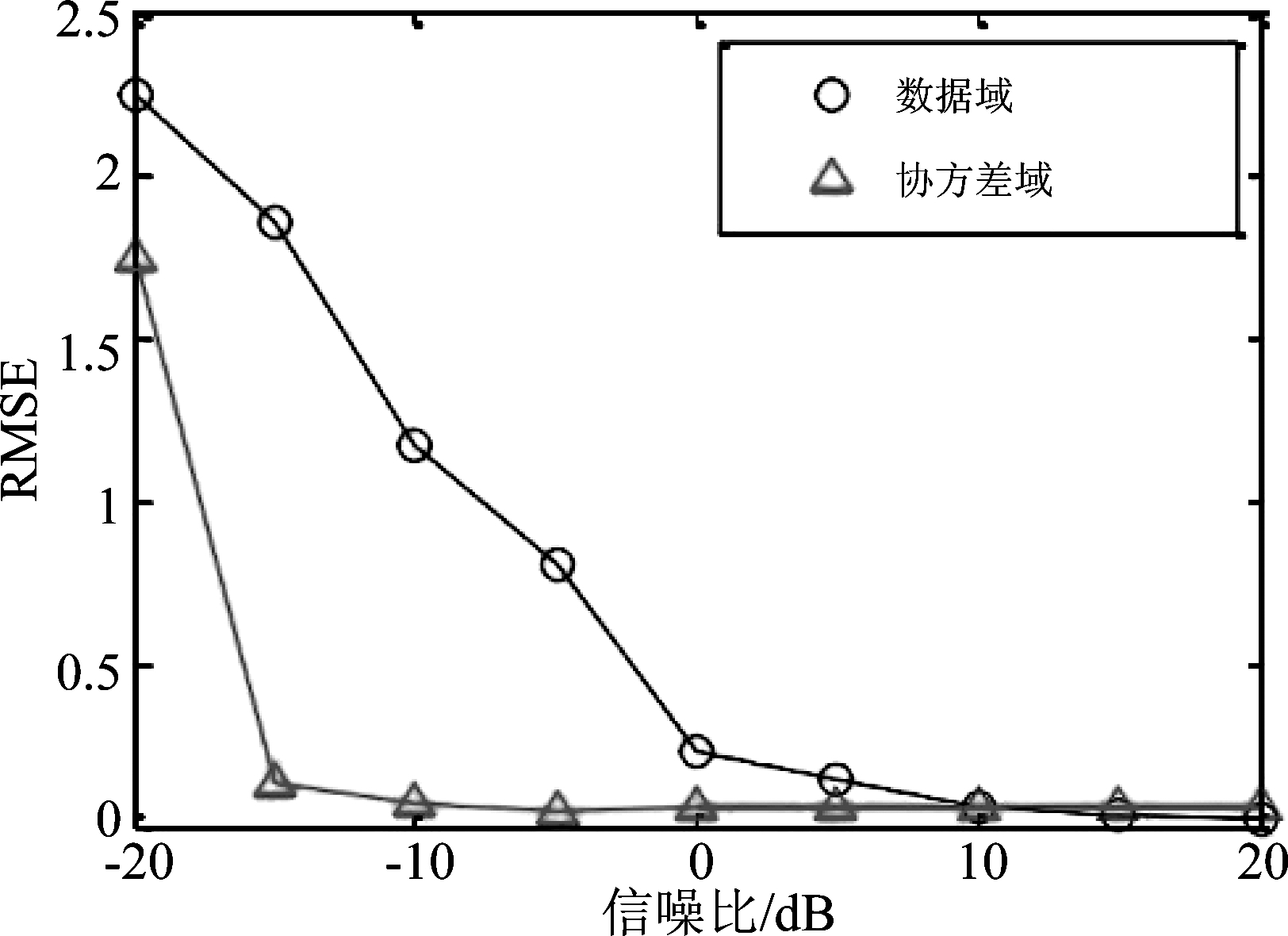
图6 数据域与协方差域重构误差对比
Fig.6 Comparison of data domain and based on covariance domain reconstruction error
图6所示,当信噪比大于5 dB时,二者相差不大,都能实现重构;当信噪比在-10 dB ～ 0 dB的时候,数据域性能极具下降,但是协方差域重构误差变化不大,仍然能够得到较好的图像。仿真结果说明,在低信噪比的情况下,基于协方差域的成像算法重构性能要好于基于数据域的成像算法。
5 结论
本文针对分布式无源雷达稀疏成像问题,提出以成像分辨率为优化目标函数,基于遗传算法的接收机配置优化方法,并通过仿真结果表明优化后对成像性能有明显的提升。同时针对OMP算法在低信噪比情况下成像精度较差的问题,提出基于协方差稀疏表示的分布式无源雷达成像算法,并将稀疏贝叶斯学习(SBL)方法应用于目标场景重构,并通过仿真验证在低分辨率下算法的良好恢复性能。
[1] Liu C C, Chen W D. Sparse frequency diverse MIMO radar imaging[C]∥46th Asilomar Conference on Signals, System and Computer. Pacific Grove, USA: IEEE Press, 2012: 853- 857.
[2] Engl H W, Ramlau R. Regularization of Inverse Problems[M]. Kluwer Academic, 1996.
[3] 王硕. 分布式无源雷达成像方法研究[D]. 中国科学技术大学, 2014.
Wang Shuo. Research on Distributed Passive Radar Imaging Method[D]. University of Science and Technology of China, 2014. (in Chinese)
[4] Yin J, Chen T. Direction-of-Arrival Estimation Using a Sparse Representation of Array Convariance Vectors[J]. Signal Processing IEEE Transactions on 2011, 2011, 59(9): 4489- 4493.
[5] Alam M, Jamil K. Maximum likelihood (ML) based localization algorithm for multi-static passive radar using range-only measurements[C]∥IEEE Radar Conference. IEEE, 2015: 180-184.
[6] 王天云. 分布式雷达稀疏成像技术研究[D]. 中国科学技术大学, 2015.
Wang Tianyun. Research on Distributed Radar Sparse Imaging Technology[D]. University of Science and Technology of China, 2015. (in Chinese)
[7] Hu X, Zhang S, Lu Z, et al. Receiver disposition optimization in disposition optimization in distributed passive radar imaging[C]∥IGARSS 2016-2016 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2016: 1018-1021.
[8] Ottersten B, Stoica P, Roy R. Covanriance Matching Estimation Techniques for Array Signal Processing Applications[J]. Digital Signal Processing, 1998, 8(3): 185-210.
[9] Scherzer O. The use of Morozov’s discrepancy principle for Tikhonov regularization for solving nonlinear ill-posed problems[J]. Computing, 1993, 51(1): 45- 60.
[10] Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244.
