1 引言
近年来,随着动平台分布式雷达系统如无人机(Unmanned Aerial Vehicle, UAV),在区域监视、目标跟踪、定位、物流、搜索和紧急救援等方面的广泛应用,研究动平台分布式雷达系统协同探测已经引起了广泛关注[1]。动平台分布式雷达系统在执行任务时可以利用空间分集从不同角度对目标进行观测,并在某种准则(检测概率、定位精度等)来自适应地调整动平台的位置,以提高系统对目标的探测、跟踪和识别的能力[2]。
在进行探测任务时,如何利用动平台分布式雷达实现对目标的快速实时高精度探测成为了一个亟待解决的重要问题。新世纪以来,大量的研究机构一直致力于解决动平台分布式雷达的路径优化问题[3-15]。总的来说,动平台分布式雷达路径优化通常被建模为数学优化问题[4-5],决策过程一般通过最小化代价函数(最短路径、均方误差等)或者最大化与量测相关的费歇尔信息矩阵(Fisher Information Matrix, FIM)也即克拉美罗下界的逆(Cramer-Rao Lower Bound, CRLB)来控制系统的输入[6-7]。针对地面目标的跟踪,一种基于信息理论的方法在[8]中被提出来优化动平台的路径。文献[9]以后验克拉美罗下界(posterior Cramer-Rao lower bound, PCRLB)为目标函数, 针对测向传感器模型, 建立了动平台分布式雷达最优协同观测模型,并提出了一种金字塔式搜索方法。文献[10]以目标位置协方差矩阵行列式为目标函数,采用梯度下降法对基于测向测距组合传感器的多平台观测航迹进行设计。文献[11]研究了基于目标状态方差的动平台分布式雷达路径优化问题,并且分析了目标和跟踪无人机的定位误差的上界和下界。在文献[13]中,针对静止目标研究了基于波达方向和到达时间差量测模型的动平台路径优化算法,目标函数是FIM(克拉美罗界CRLB的逆),并提出了一种贪婪算法从而提高定位性能。最近,文献[15]研究协同跟踪问题时,利用滚动时域控制的方法用来预测FIM,采用分布式求解框架优化动平台的路径。国内对于动平台分布式雷达系统协同路径优化研究的较少,文献[17]基于角度量测研究了无人机编队的队形对多机协同定位影响,但没有研究无人机的路径规划方法。文献[18]研究了在两个动平台的路径确定的条件下,用于运动多平台无源跟踪的滤波方法。需要指出的是上述算法的代价函数大都无法用于多个动平台对目标的快速实时高精度跟踪,而且对有约束的多动平台分布式雷达路径优化问题研究的很少。此外,以上很多算法基本都是基于遍历的方法实现的,因而均具有较高的计算复杂度,从而大大限制了动平台分布式雷达的实际应用。因此,研究一种实时高效的用于目标跟踪的动平台分布式雷达路径优化方法具有重要的实际应用价值。
本文着眼于动平台分布式雷达协同跟踪静止或移动目标的路径优化问题,基于角度量测导出了闭合形式的费歇尔信息矩阵,以D最优准则建立了包含目标和动平台位置信息的代价函数,提出了一种基于最速下降法的动平台分布式雷达路径优化算法,从而实现动平台分布式雷达快速高效的跟踪目标。此外,本文还研究了动平台在威胁区域和动平台固有的物理限制下有约束的动平台分布式雷达路径优化问题,利用惩罚函数来修正代价函数来规避障碍,并应用物理约束来限制动平台的转弯角。最后通过仿真实验验证了所提方法的有效性。
2 动平台分布式雷达系统协同跟踪目标模型
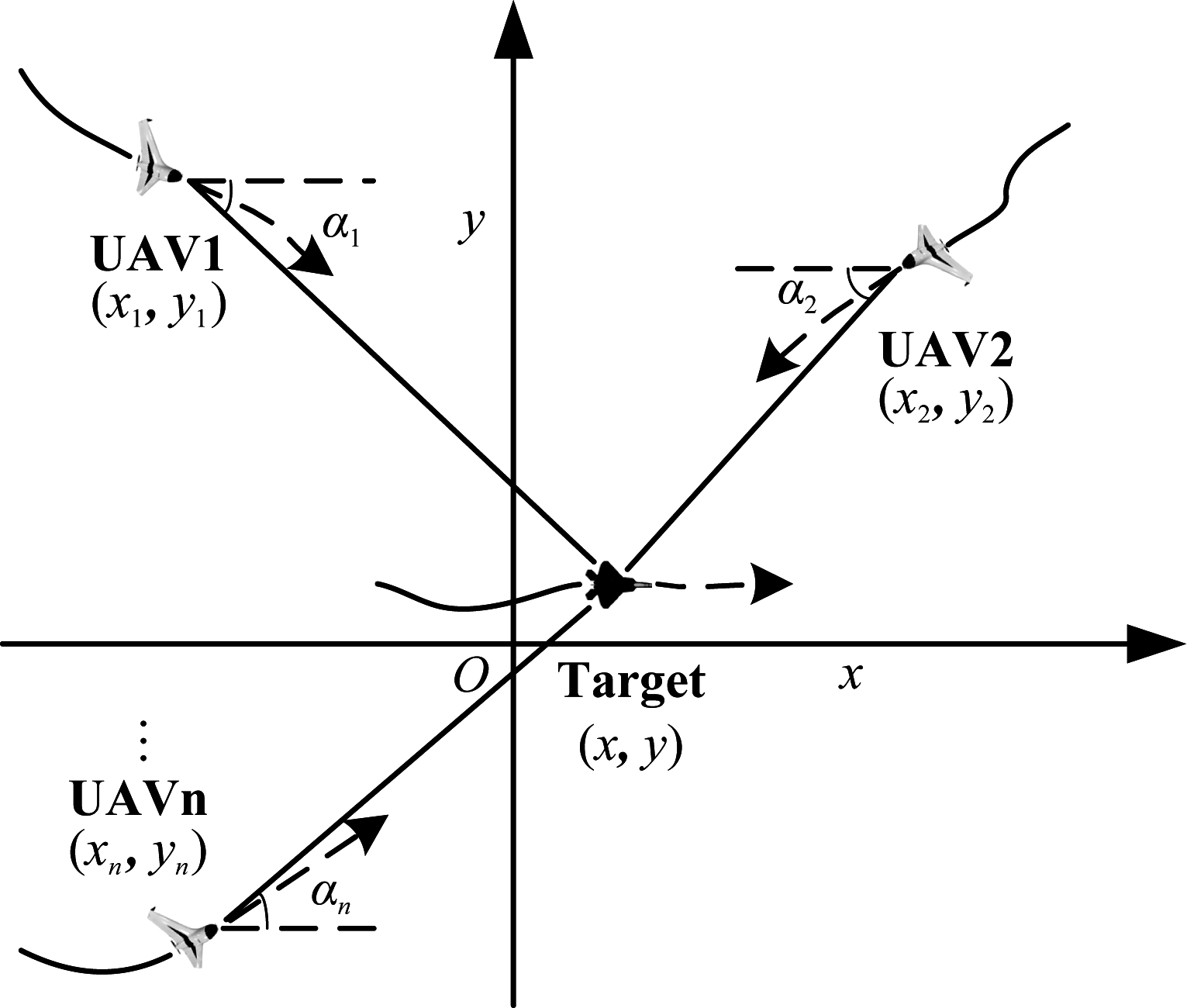
图1 动平台分布式雷达系统协同跟踪目标示意图
Fig.1 Distributed radar system with moving platform for cooperative target tracking
如图1所示,本文研究在二维空间中的n≥1个动平台分布式雷达系统(以无人机为动平台载体)采用角度量测协同跟踪运动目标的场景,动平台在k,k=1,2….时刻的位置表示为![]() 其中
其中![]() 是二维笛卡尔坐标系下的x轴坐标和y轴坐标,T表示矩阵转置。假设目标以近似匀速直线运动模型运动,即
是二维笛卡尔坐标系下的x轴坐标和y轴坐标,T表示矩阵转置。假设目标以近似匀速直线运动模型运动,即
xk+1=Fxk+Γvk
(1)
其中,![]() 是目标在k时刻的状态向量,状态向量由目标位置[xk,yk]T和目标速度
是目标在k时刻的状态向量,状态向量由目标位置[xk,yk]T和目标速度![]() 组成,系统状态转移矩阵为
组成,系统状态转移矩阵为
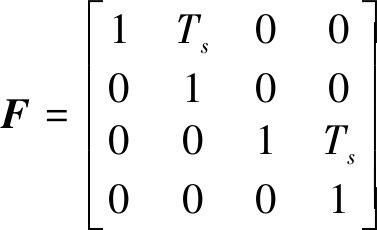
(2)
Ts表示采样周期,系统过程噪声输入矩阵为
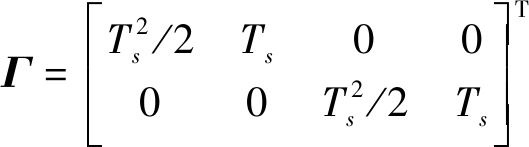
(3)
系统噪声vk假设是零均值的高斯白噪声,即vk~N(0, Qk),Qk是过程噪声vk的协方差矩阵。
对于纯角度跟踪,动平台分布式雷达系统对目标的量测方程为
Zk=h(xk)+wk
(4)
其中,Zk代表n个动平台分布式雷达在k时刻的角度量测,上式中的量测函数可表示为
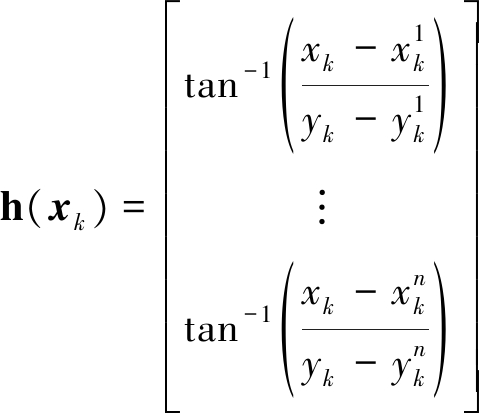
(5)
wk是零均值的高斯白噪声,即wk~N(0, Rk),且Rk满足
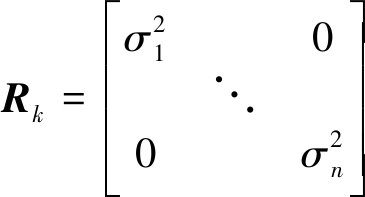
(6)
σi是第i架动平台分布式雷达的角度量测噪声的标准差,假设不同动平台分布式雷达的量测噪声相互独立。
3 代价函数的推导
3.1 费歇尔信息矩阵的推导
在一定条件下,任何估计量都存在一个方差的下限,估计量的方差只能大于等于此下限,此下限称之为克拉美-罗下界。通常,推导费歇尔信息矩阵并不是特别困难,对于纯角度量测,量测模型与目标的速度相互独立,因而本文在费歇尔信息矩阵推导中仅考虑目标位置分量,于是,从新定义xk=[xk,yk]T用于本文以下的推导。如果![]() 是xk在k时刻的基于量测的无偏估计,则,
是xk在k时刻的基于量测的无偏估计,则,
(7)
估计量方差的CRLB定义为费歇尔信息矩阵G(xk)(FIM)的逆,即
(8)
上式中的不等式意味着CRLB(xk)-G-1(xk)是半正定矩阵。对于量测的似然函数,费歇尔信息矩阵[20]G(xk)表达式为
G(xk)  Ε[(
Ε[(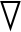 ln p(α|x))(
ln p(α|x))(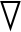 ln p(α|x))T]x=xk
ln p(α|x))T]x=xk
(9)
上式中的α表示角度参数估计值,假设参数的概率密度函数p(α|x)服从高斯分布,FIM的计算可以很容易得到
(10)
其中,Rk是量测噪声的协方差矩阵,J是雅克比矩阵,即
(11)
假设各动平台分布式雷达以相同的飞行高度飞行,那么在二维笛卡尔坐标系中,上式可进一步表示为
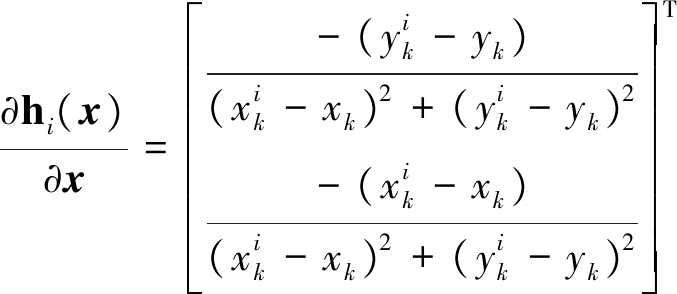
(12)
由式(10~12),可得G(xk)是2×2的矩阵,即
(13)
其中
(14)
(15)
(16)
一个恰当的代价函数以及优化准则对于路径优化至关重要,为了构建一个恰当且便于计算的代价函数,本文利用FIM的行列式作为代价函数。在优化理论中,这种优化准则被称为D最优准则(D-optimality Criterion)。参数的D优化准则的数学含义是使由CRLB产生的不确定性椭圆体的体积最小化[11]。D最优准则被广泛应用于路径优化问题[20],并且它相较于E最优更具优势,因为它将FIM的每一个元素都考虑进去,而E最优仅考虑了FIM的主对角线的元素[2]。本文采用D最优准则得到的代价函数如下式所示:
(17)
其中![]() 费歇尔信息矩阵Gk的行列式定义为Ψ(xk),是目标状态,噪声分布和传感器位置的函数。FIM的计算需要已知目标位置xk,实际上通过滤波估计目标的位置
费歇尔信息矩阵Gk的行列式定义为Ψ(xk),是目标状态,噪声分布和传感器位置的函数。FIM的计算需要已知目标位置xk,实际上通过滤波估计目标的位置![]() 代替。本文利用扩展的Kalman滤波算法(extended Kalman filter,EKF)来估计局部目标状态,然后采用分布式融合的方法得到全局目标状态估计
代替。本文利用扩展的Kalman滤波算法(extended Kalman filter,EKF)来估计局部目标状态,然后采用分布式融合的方法得到全局目标状态估计![]()
xk|k-1=Fxk-1|k-1
(18)
Pk|k-1=FPk-1|k-1FT+Γk|k-1QkΓTk|k-1
(19)
(20)
xk|k=xk|k-1+Kk(Zk-h(xk|k-1))
(21)
Pk|k=(I-KkHk)Pk|k-1
(22)
其中, xk|k-1是滤波器在k时刻的一步状态预测, Pk|k-1是滤波器在k时刻的一步预测误差的协方差矩阵, xk|k是在k时刻的卡尔曼滤波状态估计, Pk|k是在k时刻的卡尔曼滤波状态估计误差协方差矩阵, Kk是卡尔曼增益, Hk是非线性量测h(xk)的雅克比矩阵。
分布式融合是每个传感器对目标状态估计及其协方差的进行交换和组合,以产生最终的全局估计。使用以下简单但通用的融合关系来组合量测[19]:
(23)
(24)
其中,![]() 是融合后的全局状态估计误差协方差矩阵,
是融合后的全局状态估计误差协方差矩阵,![]() 是k时刻第i个动平台分布式雷达系统经局部滤波器得到的目标局部状态估计误差协方差矩阵
是k时刻第i个动平台分布式雷达系统经局部滤波器得到的目标局部状态估计误差协方差矩阵![]() 是融合后的目标全局状态估计,
是融合后的目标全局状态估计,![]() 是k时刻第i个动平台分布式雷达经局部滤波器得到的目标局部状态估计。
是k时刻第i个动平台分布式雷达经局部滤波器得到的目标局部状态估计。
3.2 有约束的代价函数
在任务优化时,由于先验知识,可能已经确定了附近的某些威胁,威胁位置的先验信息可用于约束代价函数。增加约束的目的是为了是使动平台远离已识别的威胁。本文通过修正代价函数使动平台避免威胁,修正的代价函数为:
ΨZ(xk)=Ψ(xk![]() ∏ni=1∏mj=1
∏ni=1∏mj=1
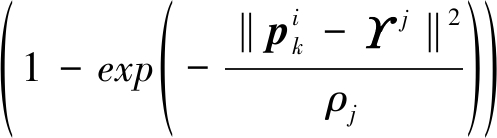
(25)
其中,![]() j表示在战场已知m个威胁中的第j个威胁的位置。ρj表示第j个威胁的威胁强度,威胁强度通常由已知的炮火密集程度或者敌方雷达的照射面积确定。ρj越大,表示威胁
j表示在战场已知m个威胁中的第j个威胁的位置。ρj表示第j个威胁的威胁强度,威胁强度通常由已知的炮火密集程度或者敌方雷达的照射面积确定。ρj越大,表示威胁![]() j对动平台的飞行路径影响越大。观察修正的代价函数可以发现,当动平台距离威胁很近时,则ΨZ≈0,进而对动平台的飞行路径有较大影响;当动平台距离威胁越远时,ΨZ会越大,基本不会对动平台的飞行路径有影响。
j对动平台的飞行路径影响越大。观察修正的代价函数可以发现,当动平台距离威胁很近时,则ΨZ≈0,进而对动平台的飞行路径有较大影响;当动平台距离威胁越远时,ΨZ会越大,基本不会对动平台的飞行路径有影响。
由于动平台具有固有的物理限制,如速度、加速度和偏转角等,因此动平台在移动过程中不能突然改变方向,动平台只能以小于或等于预定最大转向角φmax的角度移动。由于动平台固有的物理约束且优先于其他约束,因此最后解决动平台的偏转方向问题。动平台的偏转角约束可以表示为
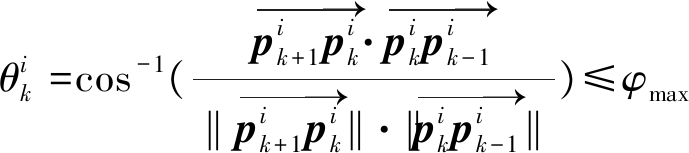
(26)
当动平台移动方向![]() 时,动平台只能以最大转向角φmax飞行,此时
时,动平台只能以最大转向角φmax飞行,此时![]()
在实际电子战环境中,由于先验知识,动平台分布式雷达需要避免一些威胁,且动平台具有固有的物理限制,因此,需要解决带有威胁和动平台物理约束的优化问题。路径优化的目标是确定移动传感器的轨迹以最大化跟踪性能。本文提出的代价函数是采用D最优下的费歇尔信息矩阵,于是最终建立的带有约束的路径优化问题的数学模型为
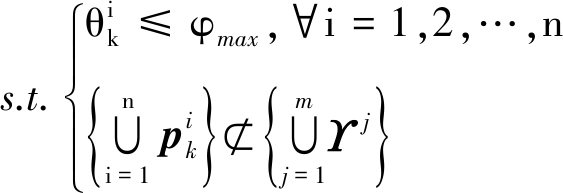
(27)
费歇尔信息矩阵可以较好的评估动平台分布式雷达对目标的跟踪性能,D最优准则又能较好的利用费歇尔信息矩阵的全部信息,因此本文提出的D最优准则下基于费歇尔信息矩阵的代价函数可以很好的用于动平台分布式雷达路径优化。修正的代价函数可以用于动平台分布式雷达对已知威胁的规避,动平台偏转角的约束可以让动平台的飞行路径光滑,利于动平台的实际飞行。最终建立的带有约束的数学优化问题可以很好的反应动平台分布式雷达协同跟踪目标的实际场景。由于本文在上节推导出了费歇尔信息矩阵的闭式形式,因此即使是修正后的代价函数也不是特别复杂,于是提出利用梯度下降法求解该优化问题。
4 算法描述
在本节中,为了解决动平台分布式雷达系统路径优化问题,提出了一种基于最速下降的高效动平台分布式雷达路径优化方法。图2是基于最速下降[17]的动平台分布式雷达路径优化算法框架。梯度控制是该算法框架的核心,它包含代价函数的梯度计算。
如果当前时刻动平台分布式雷达的位置由向量![]() 表示,则下一个时刻的位置为
表示,则下一个时刻的位置为
ξk+1=ξk+uk
(28)
其中,uk是包含动平台移动步长和移动方向的控制输入。随着动平台的数目增加,代价函数的计算将复杂,如何快速的得到各个动平台分布式雷达的控制输入将变得的至关重要。为了解决这一难点,本文提出利用最速下降法来求解最优的控制输入。实际上,动平台以梯度的方向移动是使费歇尔信息矩阵的行列式ΨZ增长最快的方向,也就是最大化代价函数的方向,于是更多的信息被利用,从而提高协同跟踪精度。动平台分布式雷达下一时刻位置的更新公式如下:
ξk+1=ξk+εk 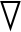 ΨZ(ξk)
ΨZ(ξk)
(29)
其中εk是动平台分布式雷达的移动步长。动平台分布式雷达下一时刻的移动方向为
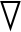
![]()
(30)
其中,![]() 是第i个动平台分布式雷达在k时刻的移动方向。为了便于计算,本文假设动平台以恒定的速度ν运动,那么动平台一个时间周期的移动距离为sk=νTs。于是,动平台的移动步长可以写为
是第i个动平台分布式雷达在k时刻的移动方向。为了便于计算,本文假设动平台以恒定的速度ν运动,那么动平台一个时间周期的移动距离为sk=νTs。于是,动平台的移动步长可以写为
(31)
利用公式(28~31),式(28)可改写为
(32)
在本文所提的方法中,动平台分布式雷达首先将获得的量测进行局部滤波得到目标的局部状态估计,然后分布式融合中心将动平台分布式雷达的目标状态估计融合得到更加准确的全局目标状态估计。之后计算代价函数,然后采用梯度法计算动平台的最优移动方向和移动步长。最后,动平台移动至下一点以获取新的量测,如此循环迭代更新得到动平台的路径。
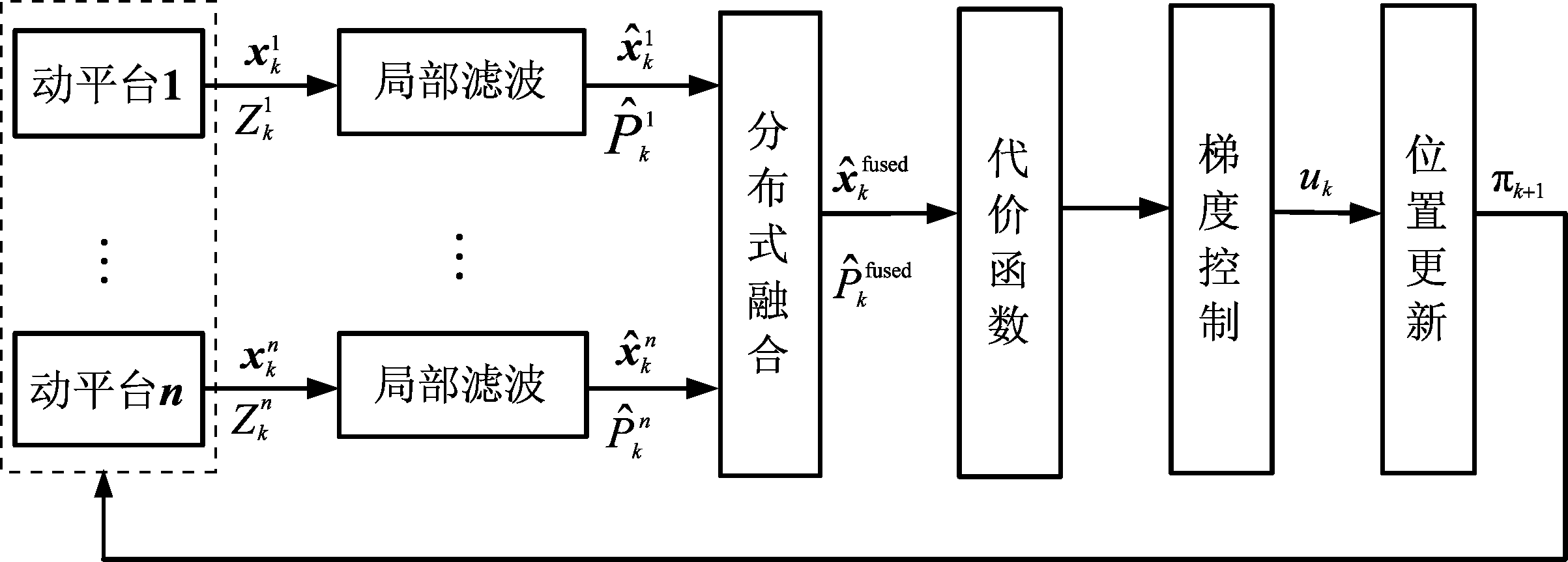
图2 基于最速下降的动平台分布式雷达路径优化算法框架
Fig.2 Flow chart of efficient path planning algorithm based on steepest descent for cooperative target tracking
5 仿真实验
首先,针对三个动平台分布式雷达协同跟踪静止目标的场景进行了仿真实验。本仿真实验的动平台均以无人机为载体。假设静止目标的位置为x0=[3500 m,2300 m]T,连续量测之间的时间间隔为Ts=1 s。三个动平台的初始位置为![]() m,1700
m,1700 ![]() [750 m,1600 m]T和
[750 m,1600 m]T和![]() [600 m,1650 m]T。量测协方差矩阵为R0=
[600 m,1650 m]T。量测协方差矩阵为R0=![]() diag[1,1,1,1],也就是角度量测的标准差为10,过程噪声的协方差矩阵为Q0=1e-4*diag[1,1],动平台的速度均为ν=40 m/s。滤波初值和滤波误差协方差矩阵的初值分别为
diag[1,1,1,1],也就是角度量测的标准差为10,过程噪声的协方差矩阵为Q0=1e-4*diag[1,1],动平台的速度均为ν=40 m/s。滤波初值和滤波误差协方差矩阵的初值分别为![]() [3500 m,0 m/s,2300 m,0 m/s]T,P0=5I。图3是所提方法在偏转角约束和栅格搜索法[20](grid based search method)没有偏转角约束下跟踪静止目标得到的动平台分布式雷达移动路径。从图中可以看出,所提方法和栅格搜索法得到的动平台路径都能很好的跟踪静止目标,动平台从初始位置彼此分开,然后逐渐靠近目标,这是因为动平台分布式雷达利用空间多样性从多个方向探测目标获取更多信息的结果。此外,对比图3(a)和(b)中动平台的飞行路径,可以发现所提方法得到的动平台移动路径几乎与栅格搜索法相同,而且相比于栅格搜索法所提方法得到的动平台移动路径更加平滑,表明动平台偏转角约束的有效性,有利于动平台的实际移动。
[3500 m,0 m/s,2300 m,0 m/s]T,P0=5I。图3是所提方法在偏转角约束和栅格搜索法[20](grid based search method)没有偏转角约束下跟踪静止目标得到的动平台分布式雷达移动路径。从图中可以看出,所提方法和栅格搜索法得到的动平台路径都能很好的跟踪静止目标,动平台从初始位置彼此分开,然后逐渐靠近目标,这是因为动平台分布式雷达利用空间多样性从多个方向探测目标获取更多信息的结果。此外,对比图3(a)和(b)中动平台的飞行路径,可以发现所提方法得到的动平台移动路径几乎与栅格搜索法相同,而且相比于栅格搜索法所提方法得到的动平台移动路径更加平滑,表明动平台偏转角约束的有效性,有利于动平台的实际移动。
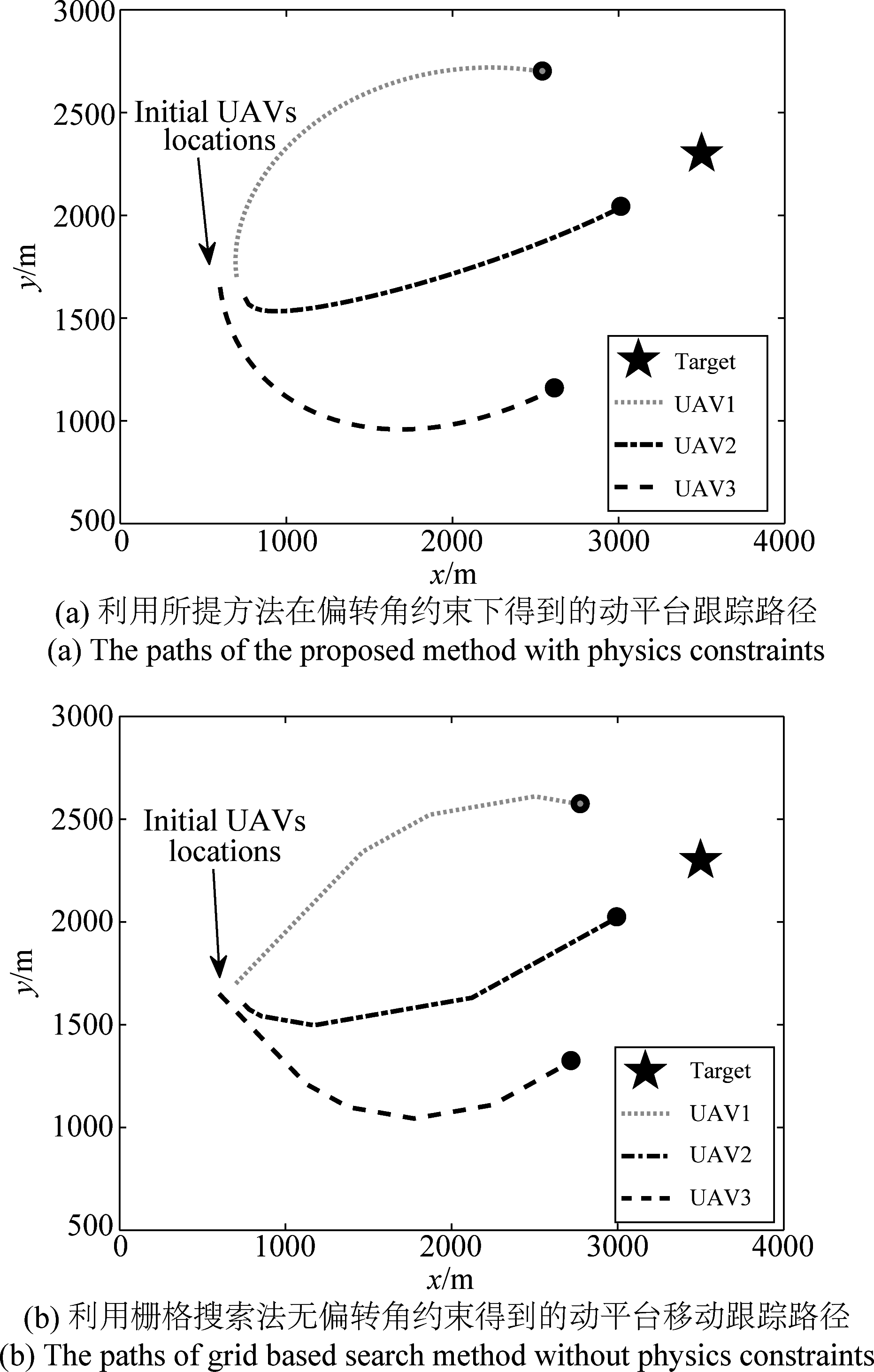
图3 两种方法跟踪静止目标得到的动平台移动路径(五角星代表静止的目标位置,圆代表动平台最终位置)
Fig.3 The paths of distributed radar system with moving platform for tracking a fixed target obtained by the proposed method and grid based search method (The target location and final sensors locations are marked with pink star, green circle, red circle and blue circle, respectively)
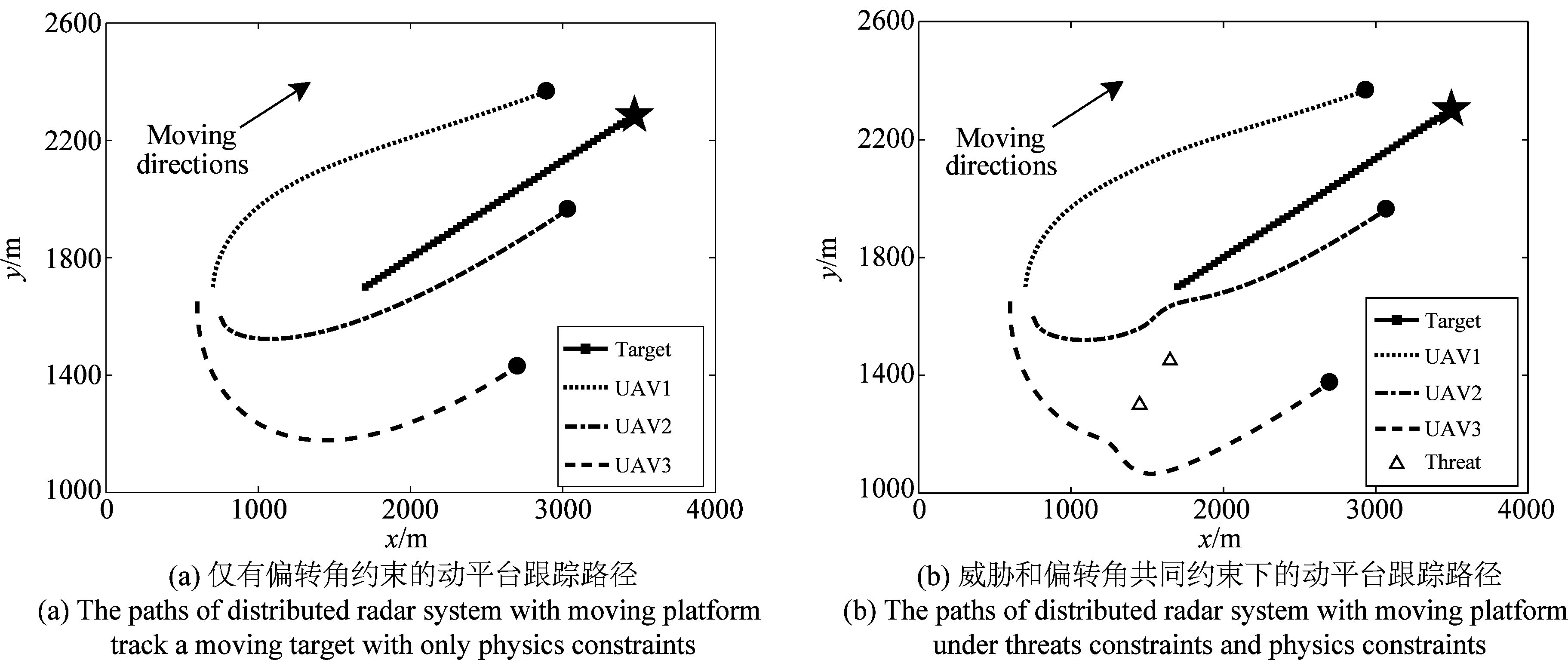
图4 所提方法得到的动平台跟踪移动目标路径
Fig.4 The paths of distributed radar system with moving platform track a moving target obtained by the proposed method
图4是三个动平台跟踪移动目标的仿真实验。假设移动目标的初始状态为x0=[1700 m,30 m/s,1700 m,10 m/s]T,动平台的速度相等且恒定均为ν=40 m/s,动平台的初始位置为ξ0=[700 m,1700 m,750 m,1600 m,600 m,1650 m]T。滤波初值和滤波误差协方差矩阵的初值分别为![]() [1725 m,30 m/s,1680 m,10 m/s]T,P0=5I。从图4中可以得到与动平台跟踪静止目标时相似的结论,利用所提方法得到的动平台路径能很好的跟踪移动目标且路径平滑,利于动平台的实际移动。比图4(a)和图4(b),可以发现,所提方法得到的动平台移动路径可以很好的避开威胁区域且移动路径较为平滑。这验证了所引入的惩罚函数的有效性,当动平台接近威胁时,代价函数会受到惩罚,迫使动平台远离威胁。
[1725 m,30 m/s,1680 m,10 m/s]T,P0=5I。从图4中可以得到与动平台跟踪静止目标时相似的结论,利用所提方法得到的动平台路径能很好的跟踪移动目标且路径平滑,利于动平台的实际移动。比图4(a)和图4(b),可以发现,所提方法得到的动平台移动路径可以很好的避开威胁区域且移动路径较为平滑。这验证了所引入的惩罚函数的有效性,当动平台接近威胁时,代价函数会受到惩罚,迫使动平台远离威胁。
图5是所提出的方法与栅格搜索法在代价函数值、均方误差和运行时间方面的性能比较。图5(a)表明所提方法可以达到与栅格搜索法基本相当的代价函数值,说明了本文所推导的代价函数的精确性和有效性。代价函数随着时间逐渐上升,表示动平台分布式雷达所搜集的信息逐渐增加,跟踪性能也越好。图5(b)描述了所提出的算法求解每帧的优化问题需要大约0.45 ms,而栅格搜索法则需要55 ms。对比图5(b)和图5(c)可以发现所提方法得到与栅格搜索法几乎没有差异的均方误差,但栅格搜索法所用时间却是所提算法的几十倍。仿真结果表明所推导的代价函数的有效性,此外,所提出的动平台路径优化方法可以快速实时的以较为平滑的路径跟踪静止和移动目标,相比于栅格搜索法,所提方法在计算复杂度上具有明显优势。
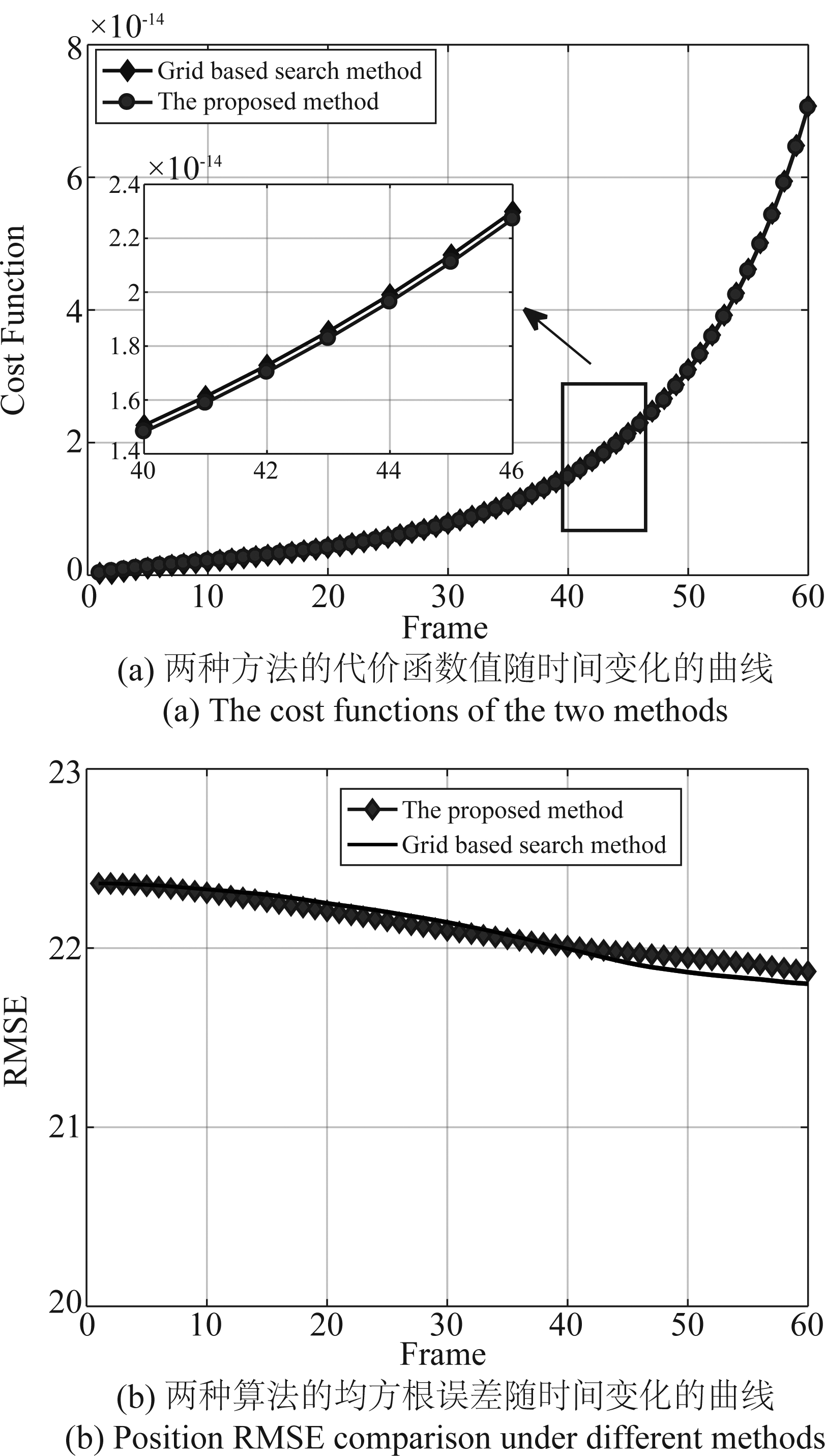
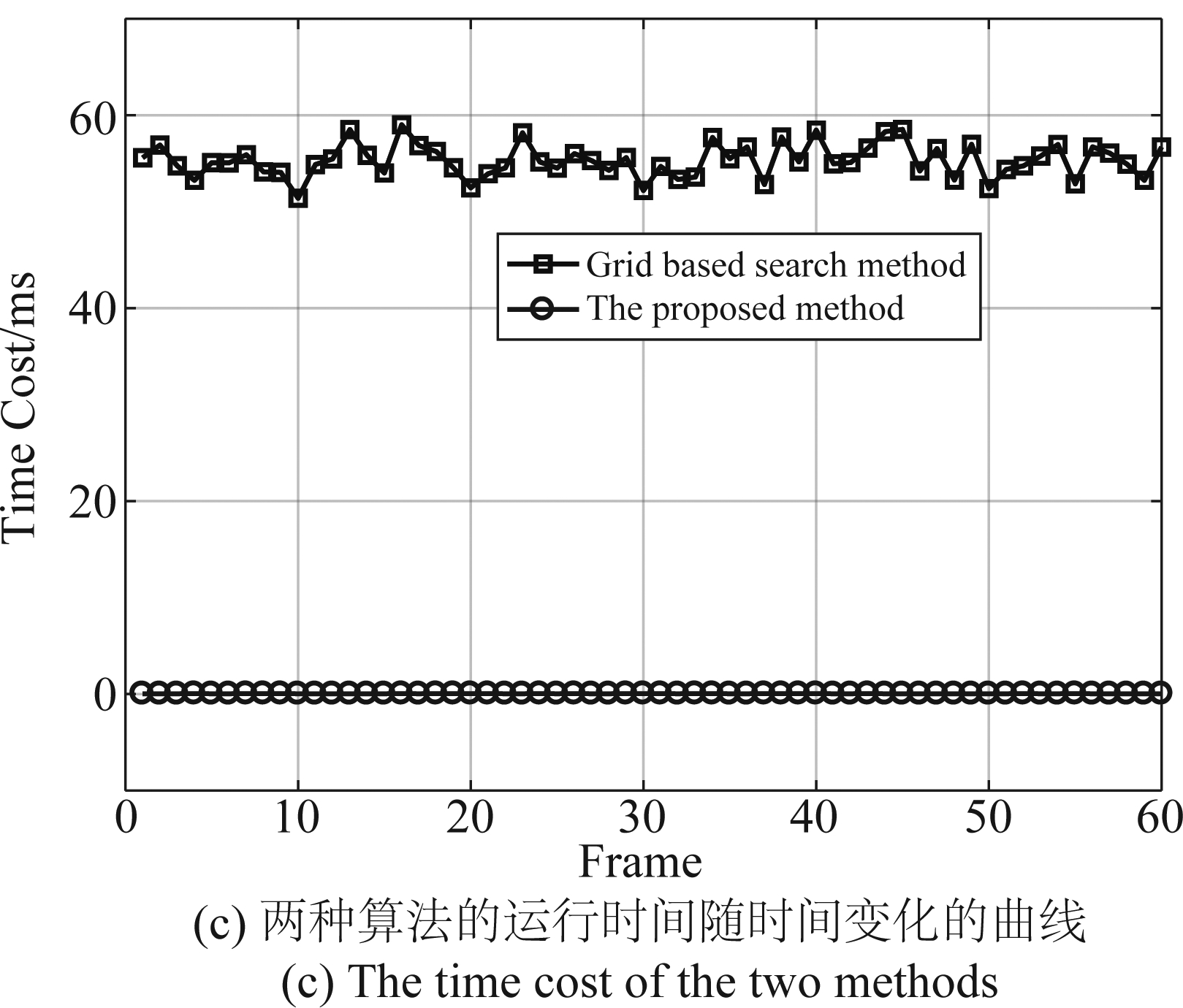
图5 两种方法的性能分析
Fig.5 The performance comparison of the two methods versus time
6 结论
本文讨论了动平台分布式雷达协同跟踪目标的路径优化问题,提出了一种快速实时的高精度跟踪目标的动平台路径优化算法。首先,本文导出了闭合形式的费歇尔信息矩阵,之后利用D最优准则建立包含目标和动平台位置信息的代价函数,然后提出了一种基于最速下降的方法来解决该优化问题。另外,本文还研究了有约束的动平台路径优化问题,利用惩罚函数来修正代价函数来规避障碍,并应用物理约束来限制动平台的转弯角。最后,通过仿真实验证明了本文所提算法的优越性。数值仿真结果验证了所推导的闭式代价函数的精确性和有效性,且所提出的动平台分布式雷达路径优化方法可以快速实时的以较为平滑的路径跟踪静止和移动目标;此外,相比于栅格搜索法,所提方法在计算复杂度上具有明显优势。
[1] Win M Z, Conti A, Mazuelas S, et al. Network localization and navigation via cooperation[J]. IEEE Communication Magazine, 2011, 49(5): 56- 62.
[2] Passerieux J M, Cappel D Van. Optimal observer maneuver for bearings-only tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(3): 777-788.
[3] Oshman Y, Davidson P. Optimization of observer trajectories for bearings-only target localization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 892-902.
[4] Krishnamurthy V. Algorithms for optimal scheduling and management of hidden Markov model UAV[J]. IEEE Transactions on Signal Processing, 2002, 50(6): 1382-1397.
[5] Ragi S, Chong E K P. UAV path planning in a dynamic environment via partially observable markov decision process[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2397-2412.
[6] Fawcett J A. Effect of course maneuvers on bearings-only range estimation[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1988, 36(8): 1193-1199.
[7] Le Cadre J P, Jauffret C. Discrete time observability and estimability analysis for bearings-only target motion analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 178-201.
[8] Sinha A, Kirubarajan T, Bar-Shalom Y. Autonomous ground target tracking by multiple cooperative UAVs[C]∥IEEE Aerospace Conference, 2005: 892-902.
[9] Hernandez M L. Optimal UAV trajectories in bearings-only tracking[C]∥International Conference on Information Fusion, 2004: 893-900.
[10] Chung T H, Burdick J W, Murray R M. A decentralized motion coordination method for dynamic target tracking[C]∥IEEE International Conference on Robotics and Automation, 2006: 2416-2422.
[11] Morbidi F, Mariottini G L. Active target tracking and cooperative localization for teams of aerial vehicles[J]. IEEE Transactions on Control Systems Technology, 2013, 21(5): 1694-1707.
[12] Pitre R R, Li Xiaorong, Delbalzo R. UAV route planning for joint search and track missions-An information-value approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2551-2565.
[13] Dogancay K. UAV path planning for passive emitter localization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1150-1166.
[14] Hoffmann G M, Tomlin C J. Mobile UAV network control using mutual information methods and particle filters[J]. IEEE Transactions on Automatic Control, 2009, 55(1): 32- 47.
[15] Koohifar F, Kumbhar A, Guvenc I. Receding horizon Multi-UAV cooperative tracking of moving RF Source[J]. IEEE Communications Letters, 2016, 21(6): 1150-1166.
[16] 陈新, 彭科举, 周东翔, 等. 基于优选数据准则的空基多平台协同定位方法[J]. 信号处理, 2010, 26(10): 1466-1472.
Chen Xin, Peng Keju, Zhou Dongxiang, et al. Bearing only method based on optimal data in Multi-UAV co-location[J]. Signal Processing, 2010, 26(10): 1466-1472. (in Chinese)
[17] 骆卉子, 曲长文, 冯奇. 运动多平台无源跟踪截尾不敏卡尔曼滤波算法[J]. 信号处理, 2016, 32(12): 1434-1439.
Luo Huizi, Qu Changwen, Feng Qi. Truncated unscented Kalman filtering algorithm for target tracking using moving multi-platform[J]. Journal of Signal Processing, 2016, 32(12): 1434-1439. (in Chinese)
[18] Meng Wei, Li Hua, Xiao Wendong. Communication aware optimal UAV motion coordination for source localization[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(11): 2505-2514.
[19] Bar Shalom Y, Fortman T E. Tracking and Data Association[M]. San Diego, CA: Academic Press, 1988.
[20] Wang Xuezhi, Ristic B, Himed B, et al. Joint passive UAV scheduling for target tracking[C]∥International Conference on Information Fusion, 2017: 1-7.


