1 引言
星载合成孔径雷达(SAR)是一种全天时、全天候的微波遥感成像工具,在灾害监测、地表测绘、生态评估等方面具有不可替代的重要作用[1-5]。顺飞双站条带模式是星载SAR的一种重要的数据获取方式,相对于单站SAR,顺飞双站条带星载SAR在实时干涉、动目标检测、隐身目标探测[6]等方面具有显著优势,典型的系统是TerraSAR-X、TanDEM-X双星系统[7-8]。目前,双站星载SAR造价高昂,其实际应用受成本限制较大。因此,用低成本小卫星代替高成本大卫星的方法吸引了很多人的关注。然而,虽然小卫星具有一定的成本优势,但在系统设计方面却面临着一些大卫星不具有的限制。以平台稳定性为例,小卫星平台的稳定性通常劣于大卫星,采用传统的侧向天线将大大增加姿态控制的难度。为确保整星具有较好稳定性,通常将较重的相控阵天线以指向星下点的方式安装,再通过电扫描的方式将波束调整到所需方向。这样的天线安装方式对SAR系统设计具有直接且重要的影响,其中之一就是星载SAR系统的多普勒导引方式。
多普勒导引是指星载条带SAR通过调整波束指向来抵消地球自传对回波信号多普勒中心调制的方法[9-11]。偏航控制是实现多普勒导引的一种重要手段[12-13]。对于顺飞双站星载条带SAR,传统的多普勒导引方法是分别对主、辅星进行基于偏航控制的独立导引(如TerraSAR-X和TanDEM-X系统)[14-15]。然而,对于具有星下点天线指向的高频段小卫星,该多普勒导引方法不再有效,理由如下。第一,当卫星天线斜向安装时,波束指向会随偏航角变化;但当卫星天线具有星下点指向时,改变偏航角不再改变天线的波束指向,即不再影响回波信号的多普勒中心频率。第二,当星载SAR工作于较高频段时(如Ka波段),雷达波束较窄,主、辅星3 dB波束在地表的重合面积缩小,导致回波信号增益损失增加。当双星基线较长时,该增益损失将尤为明显,表现为星载SAR系统的等效噪声系数(NE 
0)指标显著恶化,有效成像区域明显减少。
为解决上述问题,本文提出了一种面向顺飞双站小卫星条带SAR的电扫多普勒中心导引方法。针对基于偏航控制的多普勒中心导引方法不适用于具有星下点天线指向的小卫星SAR的问题,该方法以解析形式给出了以波束电扫描多普勒中心导引代替传统的基于偏航控制的多普勒中心导引的方法,显著提升了多普勒导引的适用范围与灵活性;针对高频段双星独立偏航导引导致回波增益显著降低的问题,该方法以解析形式给出了双星联合电扫描多普勒导引方法,显著降低了双星多普勒导引方法对雷达波段、基线长度的依赖性。本文所提方法已经计算机仿真实验充分验证,真实且有效。
本文结构如下,第2节简介了传统的基于偏航控制的多普勒导引方法,并指出了该方法在顺飞双站星载条带SAR模式中的限制。第3节详细介绍了基于电扫描的顺飞双站星载条带SAR多普勒导引方法。第4节通过计算机仿真实验对本文所提方法进行了仿真,验证了方法的正确性与有效性。第5节对本文研究进行了总结。
2 基于偏航控制的多普勒导引方法
对于顺飞双站星载条带SAR,传统的多普勒导引方法是分别对主、辅星进行基于偏航控制的独立导引。下面首先以单星为例,介绍传统基于偏航控制的多普勒中心导引原理。随后将在顺飞双站模式下分析独立导引的原理及其带来的波束重叠面积减小的问题。文中假设地球为理想球体,卫星运行轨道为标准圆轨道,卫星视为质点且其运动仅受地球引力影响。
为说明传统一维偏航导引的工作原理,首先建立如图1所示的坐标系。设卫星位于Z轴上,位置为S,其速度方向在YOZ平面内,且平行于Y轴。在天线斜向安装的情况下,卫星波束应位于XOZ平面内,且照射点为M。传统一维偏航控制过程中,波束将随卫星绕Z轴旋转,照射点在圆弧MN上移动。设一维偏航控制后照射点为T,则∠MOT为偏航角,∠OST为下视角。
根据定义,主、辅卫星雷达天线相位中心与目标散射体之间的多普勒频率均可以表示为:
(1)
其中,r=xs-xt表示斜距矢量,R为其大小。xs表示卫星位置矢量,xt表示照射点位置矢量,
表示r在时间上的一阶微分,即
因此,雷达与目标之间的相对速度可以看作是由两部分组成的:由卫星运动引起的运动矢量vs,以及由地球自转引起的运动矢量vt。
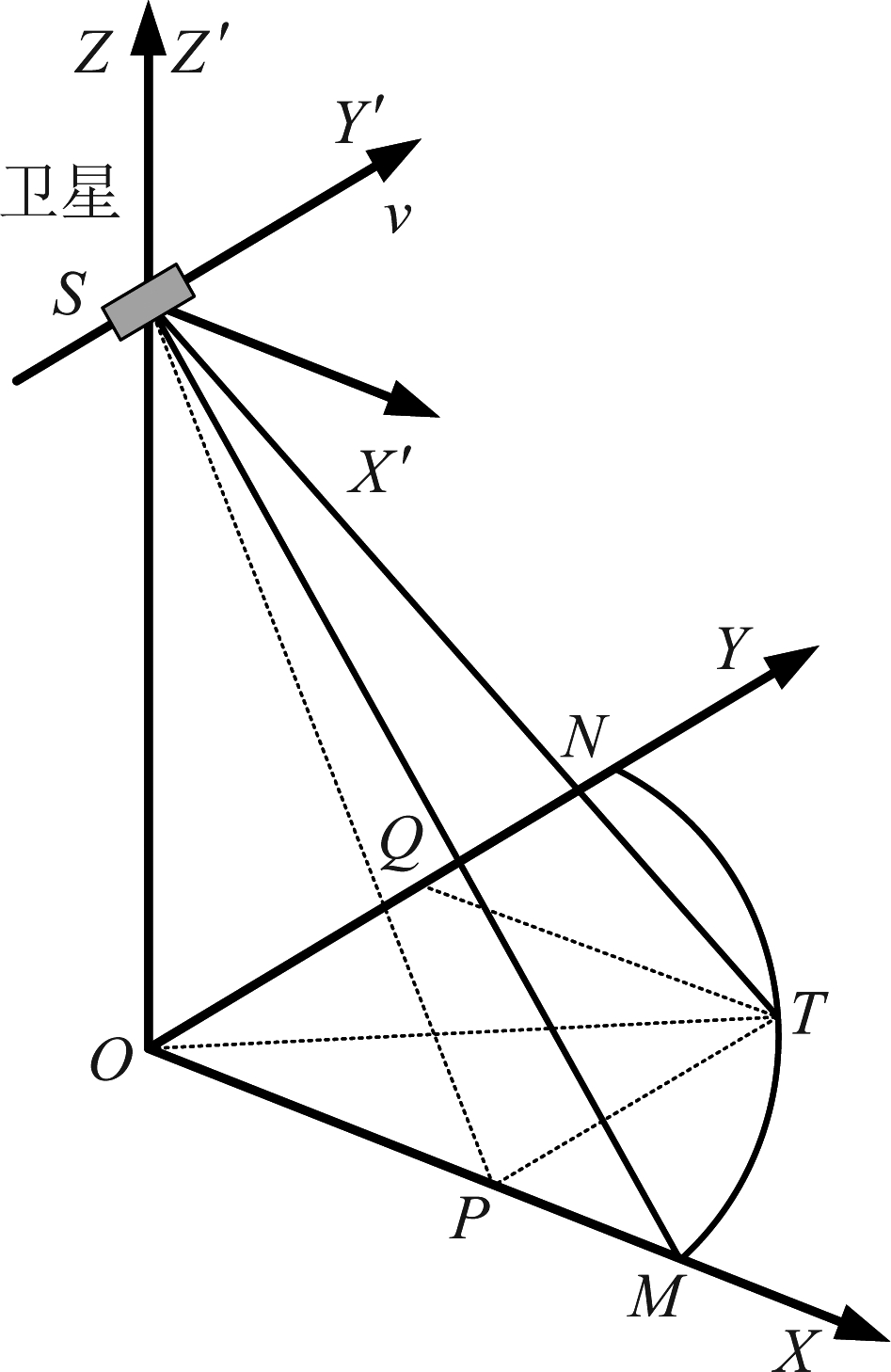
图1 传统偏航导引几何模型
Fig.1 Geometric model of traditional yaw-steering
在圆轨道情况下,由于vs·xs=0,且vt·xt=0,可将式(1)展开为:
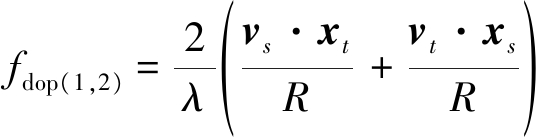
(2)
根据星载SAR的几何关系,可将式(2)继续展开[12]:
fdop(1,2)=(2νs/λ)sin γcos θ1·
(1-(ωe/ω)(cos βsin φtanθ1-cos φ))
(3)
其中,νs表示卫星速度大小,λ表示雷达波长,ωe表示地球自转角速度,ω表示卫星角速度,β为纬度幅角,φ为轨道倾角,θ1为偏航角,γ1为下视角。在式(3)中令fdop(1,2)=0,即可得出多普勒导引所需的偏航角:
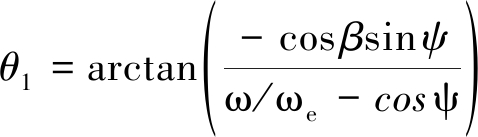
(4)
对于发射机和接收机位于不同卫星上的双站系统来说,多普勒中心会同时受到发射卫星和接收卫星的影响,此时信号的多普勒中心频率如式(5)所示:
(5)
其中,λ是工作波长,r1是发射卫星到目标的斜距矢量,r2为接收卫星到目标的斜距矢量,R1和R2分别为两斜距矢量的大小。
为了控制多普勒中心的偏移,传统的方法是收发卫星分别进行基于偏航控制的多普勒导引,使式(5)中的两项各自为零,但这种方法严重依赖于系统的天线指向、基线长度和工作频段。高频段小卫星条带SAR天线指向星下点,进行偏航转动并不能影响波束指向,如图2所示;且对于窄波束来说,对主、辅星分别进行多普勒导引会引入较大的增益损失,这一损失在基线较长的情况下更为严重,会使有效成像面积大幅减少,如图3所示。因此,传统双站多普勒导引方法仅适用于短基线、宽波束的情况,对于长基线、窄波束的高频段顺飞双站小卫星,需要重新设计多普勒导引方法。
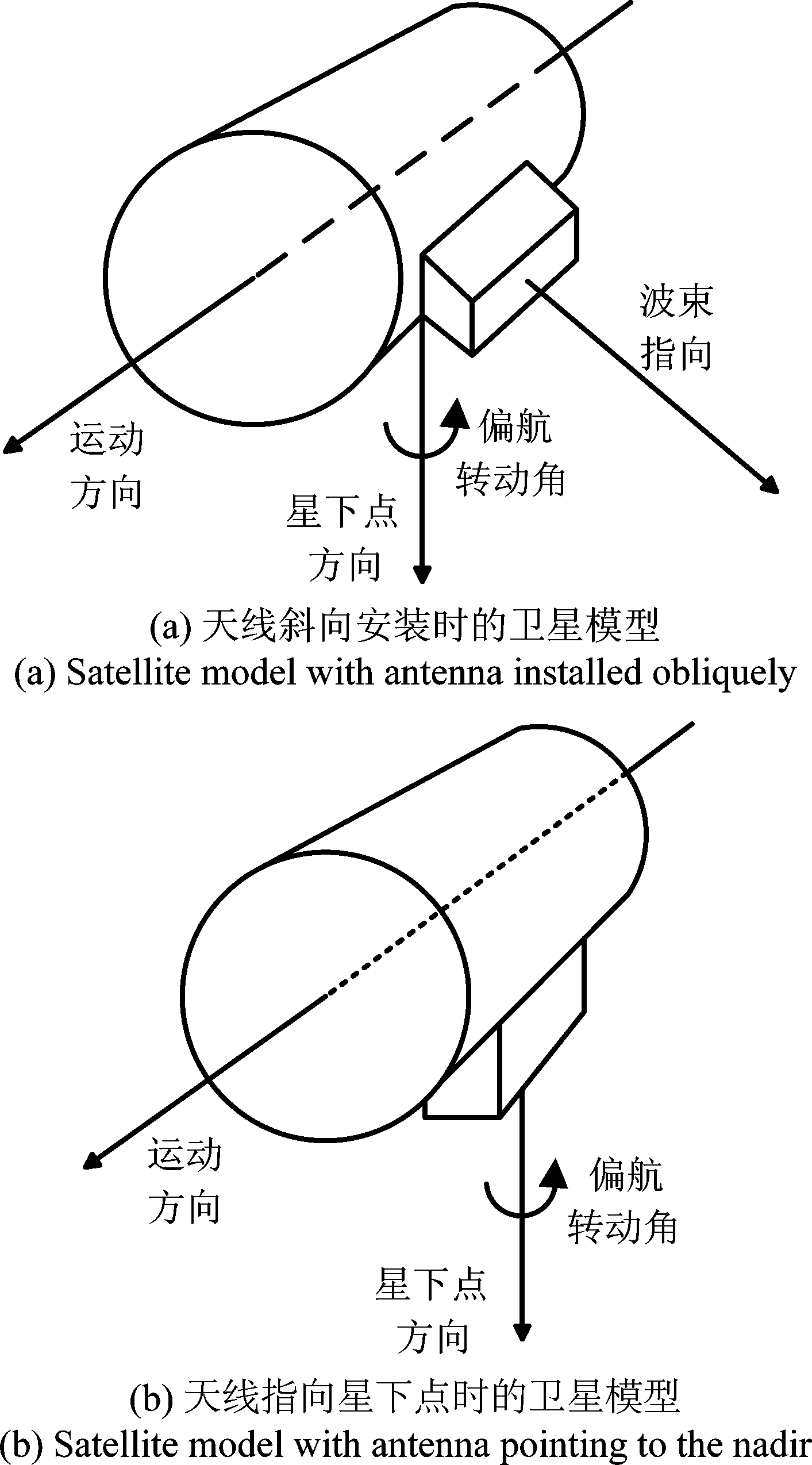
图2 天线指向对偏航导引方法的限制
Fig.2 Limitation of antenna installation on yaw-steering method
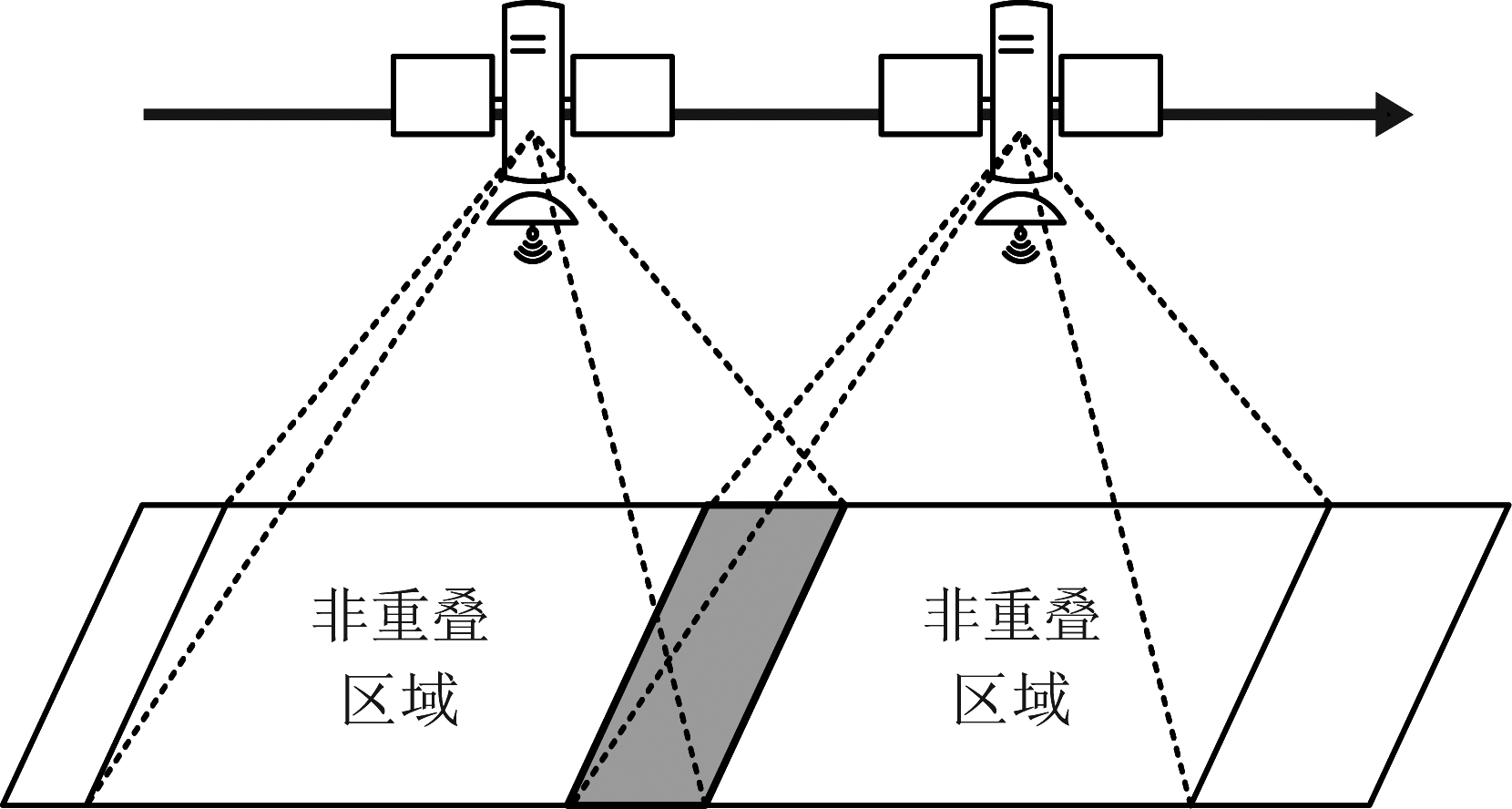
图3 传统偏航导引导致的重叠面积减小
Fig.3 Reduction of overlapping area caused by yaw-steering
3 基于电扫描的多普勒导引方法
为摆脱多普勒导引方法对天线指向、雷达波段与基线长度的限制,本文提出了一种面向顺飞双站小卫星条带SAR的电扫多普勒中心导引方法。下面将首先对电扫描多普勒导引原理进行介绍,给出电扫描角度的解析表达式,从而解决天线指向的问题;随后将提出双星联合导引的方法,在不减小波束重叠面积的情况下实现对多普勒中心的抑制。
3.1 基于电扫描的单站多普勒导引方法
在顺飞双站小卫星SAR的多普勒中心导引方法中,首先要解决的是由天线指向带来的波束调整方式问题,传统偏航导引方法有效的前提是卫星天线斜向安装,但对于小卫星而言,受限于控制性、稳定性的需求,其天线一般选择指向星下点安装,此时单纯采用偏航控制不能改变波束指向,需要采用电扫描的方式对波束指向进行调整,这里首先以单站为例说明电扫描的原理。
一维偏航导引的几何模型如图1所示,图中卫星位置为S,速度方向平行于Y轴,但由于卫星天线指向星下点,此时的初始照射点变为O点。以卫星位置S为坐标原点建立如图所示的卫星坐标系X′Y′Z′,对于天线指向星下点的小卫星来说,Z′轴是波束照射方向的反向,波束指向的调整可以看作对Z′轴指向的调整。
在图1所示的几何模型下,若要达到与传统偏航导引相同的效果,需要通过横滚向、俯仰向两个方向的电扫描互相配合来将照射点调整到T点。其中,横滚向电扫描可以看作卫星绕Y′轴旋转,在这一过程中,波束会随Z′轴在X′OZ′平面内旋转,在XOY平面内表现为照射点沿X轴或者与X轴平行的直线上移动;而俯仰电扫描过程即波束绕X′轴旋转的过程,此时,Z′轴在Y′OZ′平面内旋转,在XOY平面内表现为沿Y轴或平行于Y轴的直线移动。将向量
分解到上述两个方向上,可从几何关系上得出扫描角度的公式。
需要注意的是,进行横滚向与俯仰向电扫描的顺序决定了扫描角度的大小。在先横滚向后俯仰向的顺序下,∠OSP即为多普勒导引所需的横滚向扫描角度,∠PST即为多普勒导引所需的俯仰向扫描角度。在图1中,
代表了卫星到目标的斜距矢量,即|ST|=R,|OS|和|OT|结合下视角得出,|OP|和|PT|可以结合传统偏航控制中偏航角得出。根据上述结果即可得到横滚向与俯仰向的扫描角度。
(6)
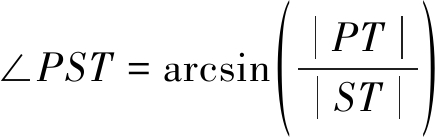
(7)
其中,
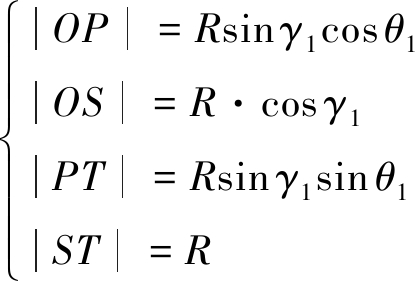
(8)
同理,在先俯仰向后横滚向扫描的顺序下,根据几何关系,可以得到另外一组扫描角度:
(9)
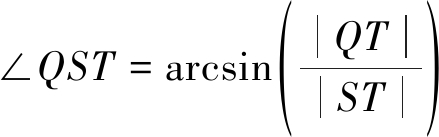
(10)
其中,
(11)
上述两组扫描角度在效果上是完全相同的,但只有与正确的顺序对应才能发挥作用。
3.2 基于电扫描的双站多普勒导引方法
在双站情况下,接收信号的多普勒中心如式(5)所示。根据2.2节的分析结果,收发卫星分别进行偏航导引会使二者的照射区域不能完全重合。因此,需要根据收发卫星多普勒中心互相抵消的思路进行联合多普勒导引方法的设计。
顺飞双站小卫星SAR联合多普勒导引的几何模型如图4所示,其中B为基线长度,α为基线倾角,两卫星轨道平面相同,但高度不同,主星发射信号,从星接收回波。为方便分析,首先不考虑电扫描过程,将多普勒导引视为由主辅卫星的偏航控制完成,角θ1和θ2称为等效偏航角。根据式(3),若要使收发卫星多普勒中心之和为零,二者的轨道参数需要满足如下关系:
fdop1+fdop2=0
(12)
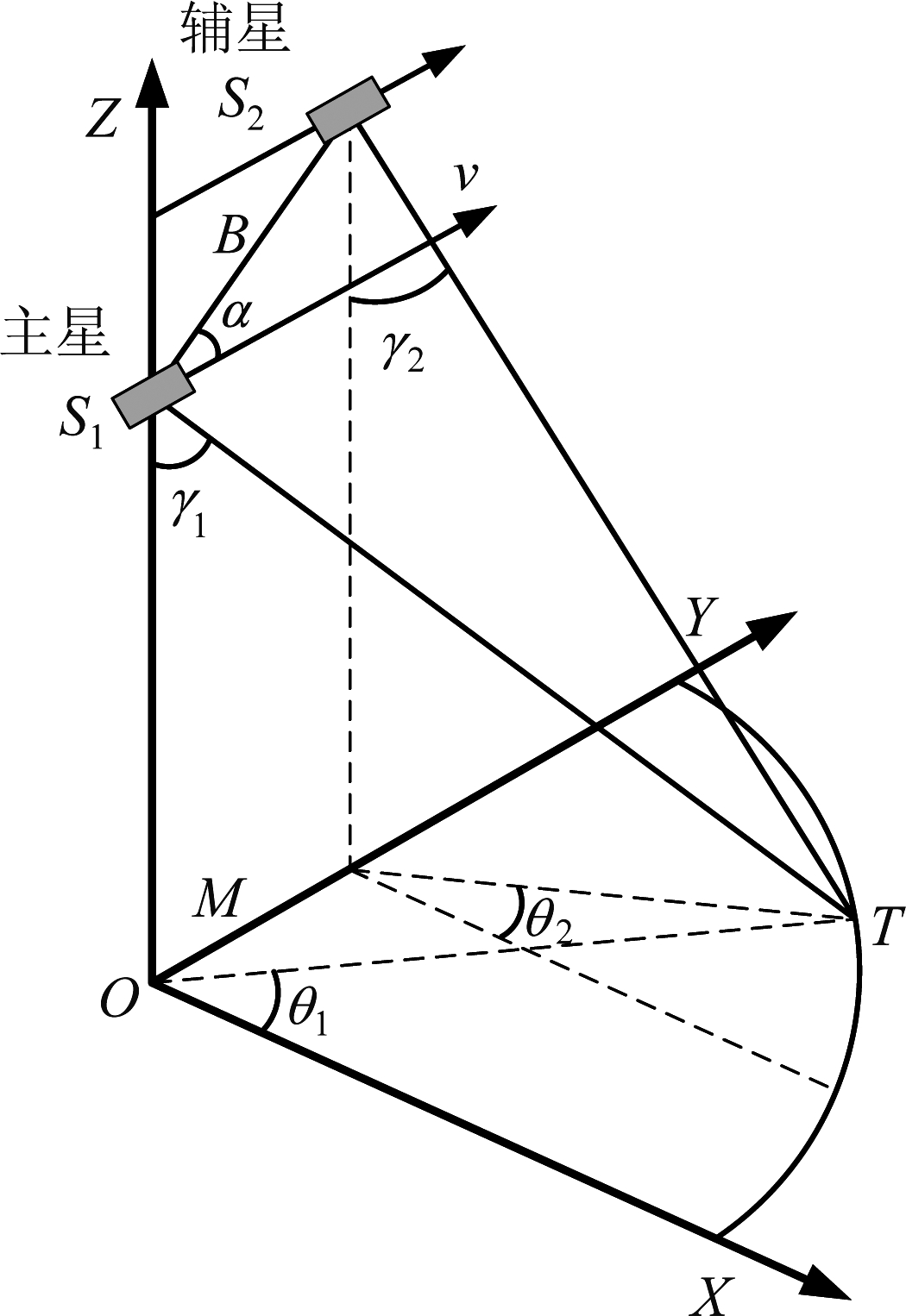
图4 顺飞双站条带SAR几何模型
Fig.4 Geometric model of pursuit bistatic strip-map SAR
其中,
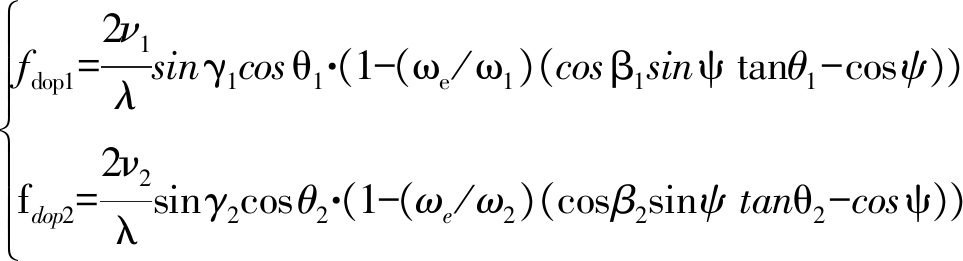
(13)
其中,ν1和ν2,ω1和ω2分别表示主辅卫星的线速度和角速度。γ1和γ2,θ1和θ2分别为两卫星的下视角和等效偏航角。ψ为两卫星的轨道倾角。β1和β2分别为两卫星的纬度幅角。
图4中,S1和S2分别为两卫星的位置,M为S2在XOY平面上的投影,T为多普勒导引后收发卫星的照射点。在XOY平面内,M点坐标可以根据S2的位置得到,T点坐标可以根据斜距和下视角得到:
(14)
根据M点和T点的坐标,可计算出矢量
在XOY平面内的大小和斜率
的斜率即为接收卫星的等效偏航角。
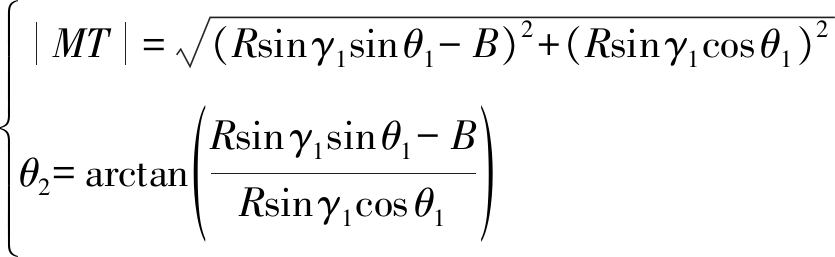
(15)
根据|S2M|和|MT|可进一步得到γ2的大小:
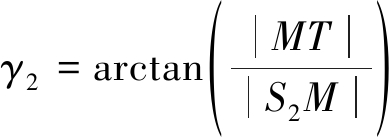
(16)
其中,
|S2M|=Rcos γ1+Bsin α
(17)
将(15)与(16)代入(13),则在已知两卫星轨道半径,轨道倾角,纬度幅角的情况下,方程(13)被化简为二元方程,其未知量仅有γ1和θ1,因此可得到θ1关于γ1的一组解,在地面上表现为一条曲线。在发射卫星下视角确定的情况下,能够找到满足零多普勒中心的唯一一点。将解出的γ1和γ2,θ1和θ2代入(6)与(7)或(9)与(10)中即可得到对应的扫描角。
4 仿真实验
首先采用表1所示的主星轨道参数对单星多普勒导引方法进行仿真。在天线斜向安装情况下,无偏航导引时多普勒中心的变化以及采用传统偏航导引时多普勒中心的变化如图5(a)所示。从图中可以看到,无偏航导引时多普勒中心最大达到60 kHz,而进行基于偏航控制的多普勒导引后,多普勒中心被减小到10-10 Hz,基于偏航控制的多普勒导引在天线斜向安装时的有效性得到了验证。
表1 仿真参数
Tab.1 Simulation parameters
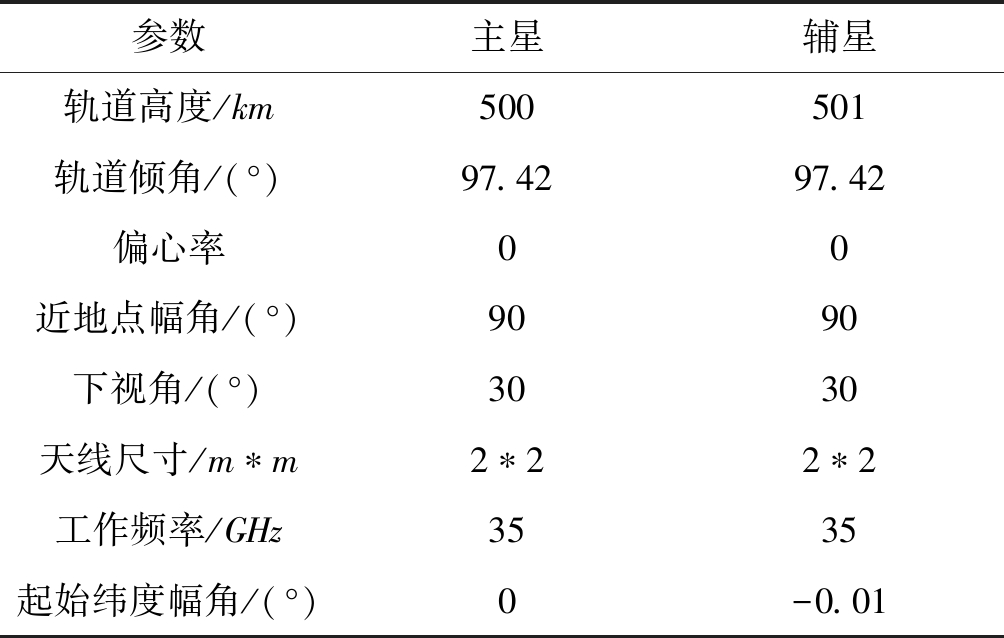
参数主星辅星轨道高度/km500501轨道倾角/(°)97.4297.42偏心率00近地点幅角/(°)9090下视角/(°)3030天线尺寸/m∗m2∗22∗2工作频率/GHz3535起始纬度幅角/(°)0-0.01
在天线指向星下点安装的情况下,无偏航导引时的多普勒中心变化、采用基于偏航控制的多普勒导引时多普勒中心变化以及采用电扫描多普勒导引时多普勒中心变化如图5(b)所示。可见由于天线指向星下点,基于偏航控制的多普勒导引方法已经不能起到抑制多普勒中心的作用,而电扫描多普勒导引能够摆脱天线指向的约束,将多普勒中心减小到10-9 Hz,从而验证了电扫描多普勒导引在天线指向星下点安装时的有效性。
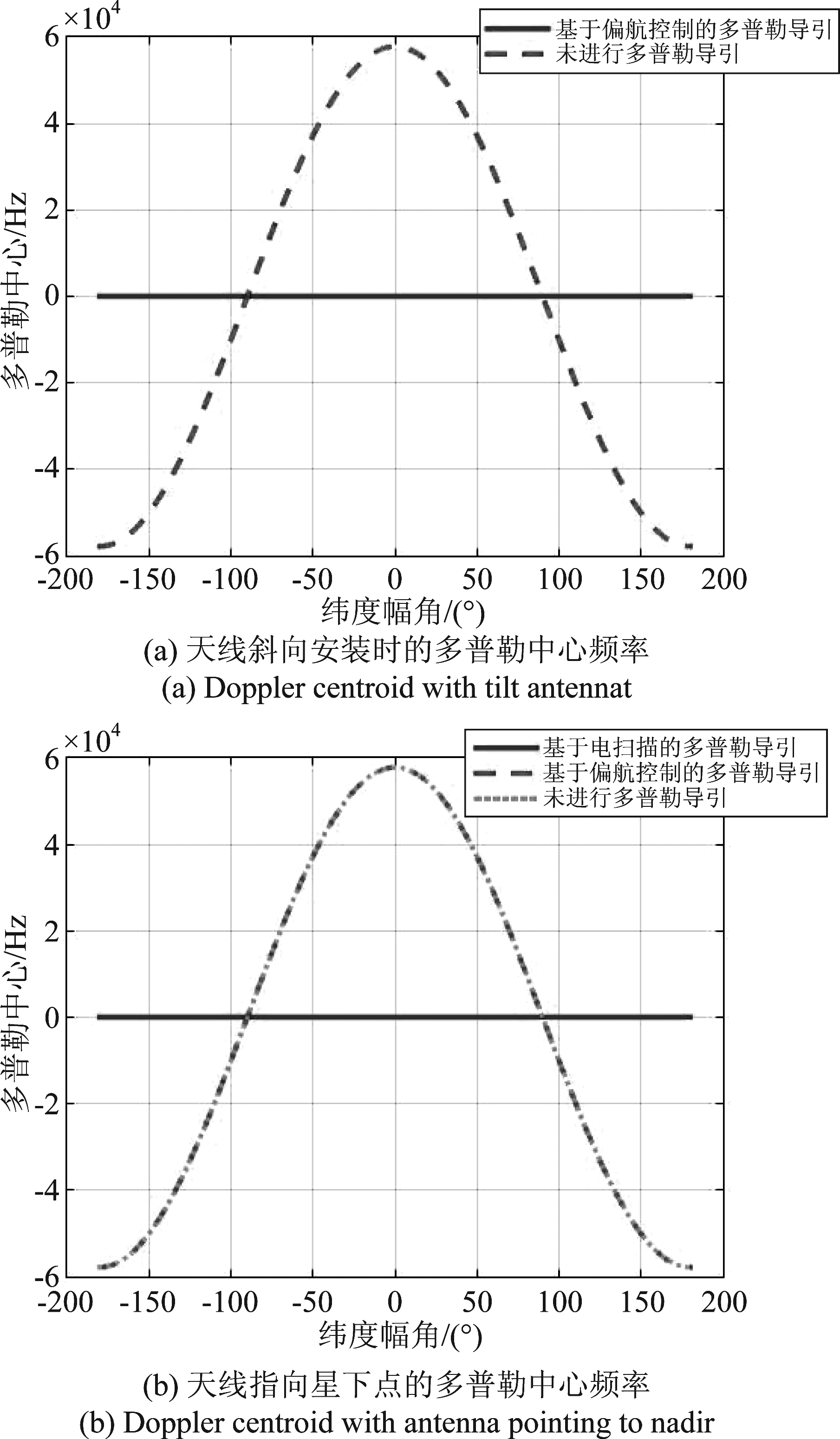
图5 单站偏航导引仿真
Fig.5 Simulation of monostatic yaw-steering
随后,在主、辅卫星分别进行偏航导引的情况下,对不同频率、不同基线下有效成像面积占波束照射面积的百分比进行仿真,得到的结果如图6所示。在顺飞双站SAR系统中,波束照射面积随着工作频段的升高而减小,波束中心随基线增大而相互远离,因此,基线越大、频率越高,对应的有效成像面积占波束照射面积的比例会越来越低。以Ka波段30 GHz频率为例,仿真结果表明,当基线为1000 m时,主、辅卫星有效成像面积缩小到照射面积的65%;当基线为2000 m时,这一比例仅为30%;当基线为3000 m时,该系统有效成像面积几乎为零。这一结果说明了主辅卫星分别进行偏航导引的局限性,只有引入联合多普勒导引方法,才能摆脱有效成像面积对工作频率和基线长度的依赖。
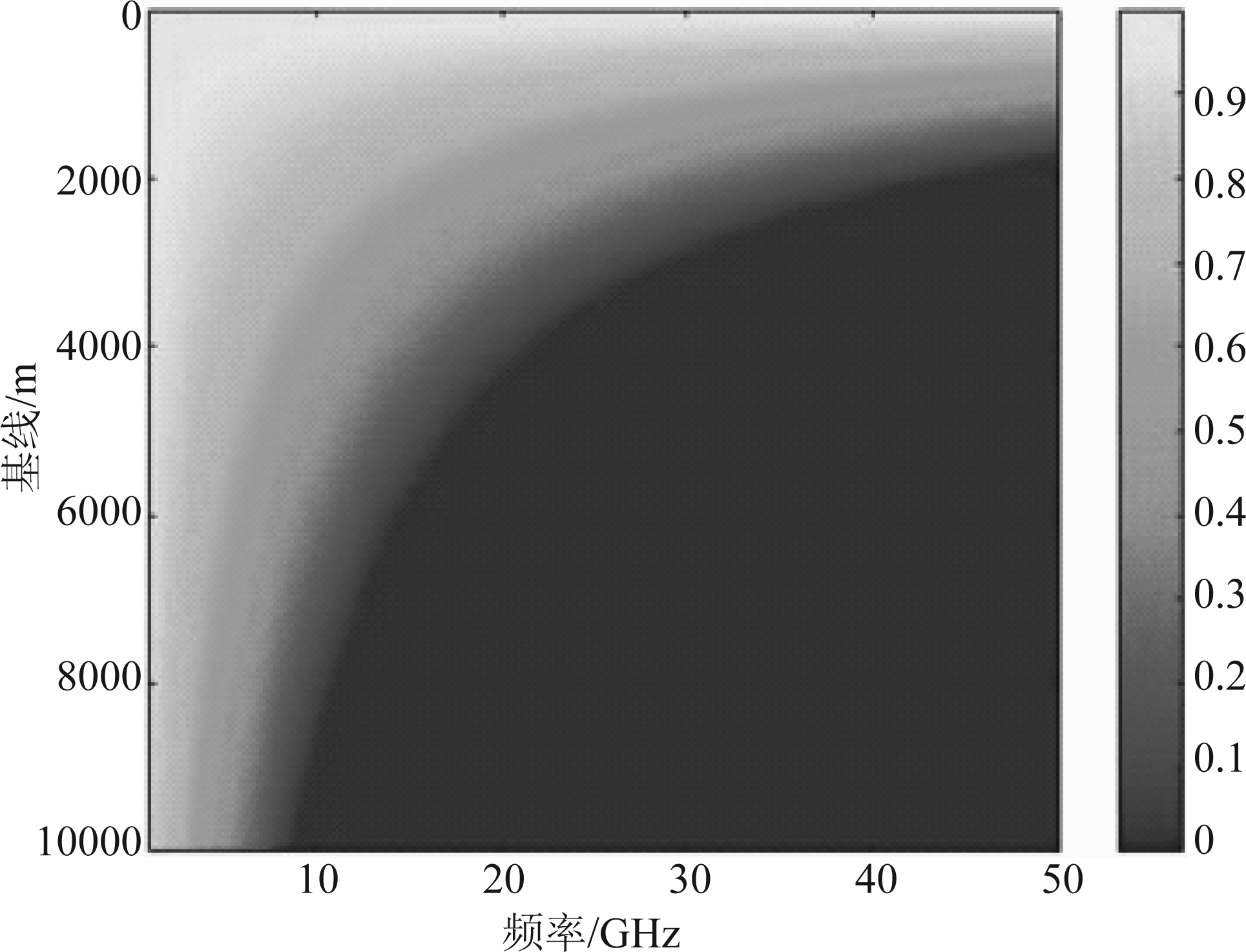
图6 主辅卫星有效成像区域
Fig.6 Effective imaging area of master and slave satellites
考虑本文提出的方法,根据前面的结论可知,在轨道周期的任一时刻均可根据式(12)得到θ1关于γ1的一组解,而这一组解构成的解集就是该时刻联合多普勒导引的可行域。为验证这一结论的正确性,首先用表1中的参数对不同下视角下的扫描角度进行仿真,由此可以得到电扫描角度与下视角的关系,当主星纬度幅角为零时,这一关系如图7所示。在实际双站系统中,主辅星之间的距离一般不大于1000 m,因此主辅卫星扫描角度的差别在1°以下,该差异在图中表现得并不明显,但足以让主辅卫星的波束保持重合。选取30°下视角以及40°下视角两种情况进行整周期的多普勒导引仿真,得到的联合多普勒导引结果如图8所示。可见,在联合多普勒导引方法下,接收卫星和发射卫星各自的多普勒中心频率均不为零,但二者能够互相抵消,因此总的多普勒中心在整个周期内均能保持在10-9 Hz水平,从而验证了电扫描多普勒导引在双站情况下的有效性。
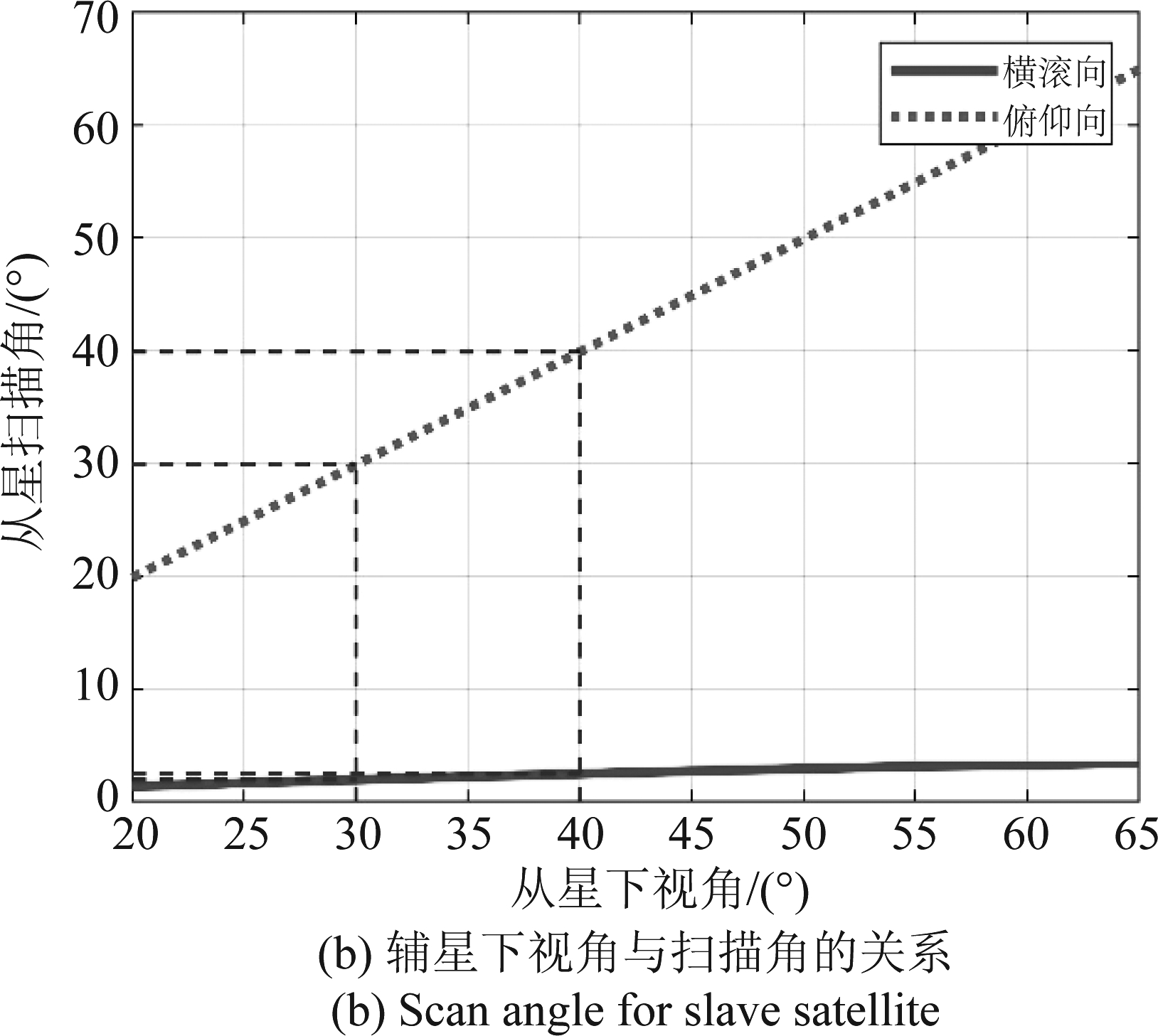
图7 双站多普勒导引的可行域
Fig.7 Feasible region of bistatic Doppler-steering
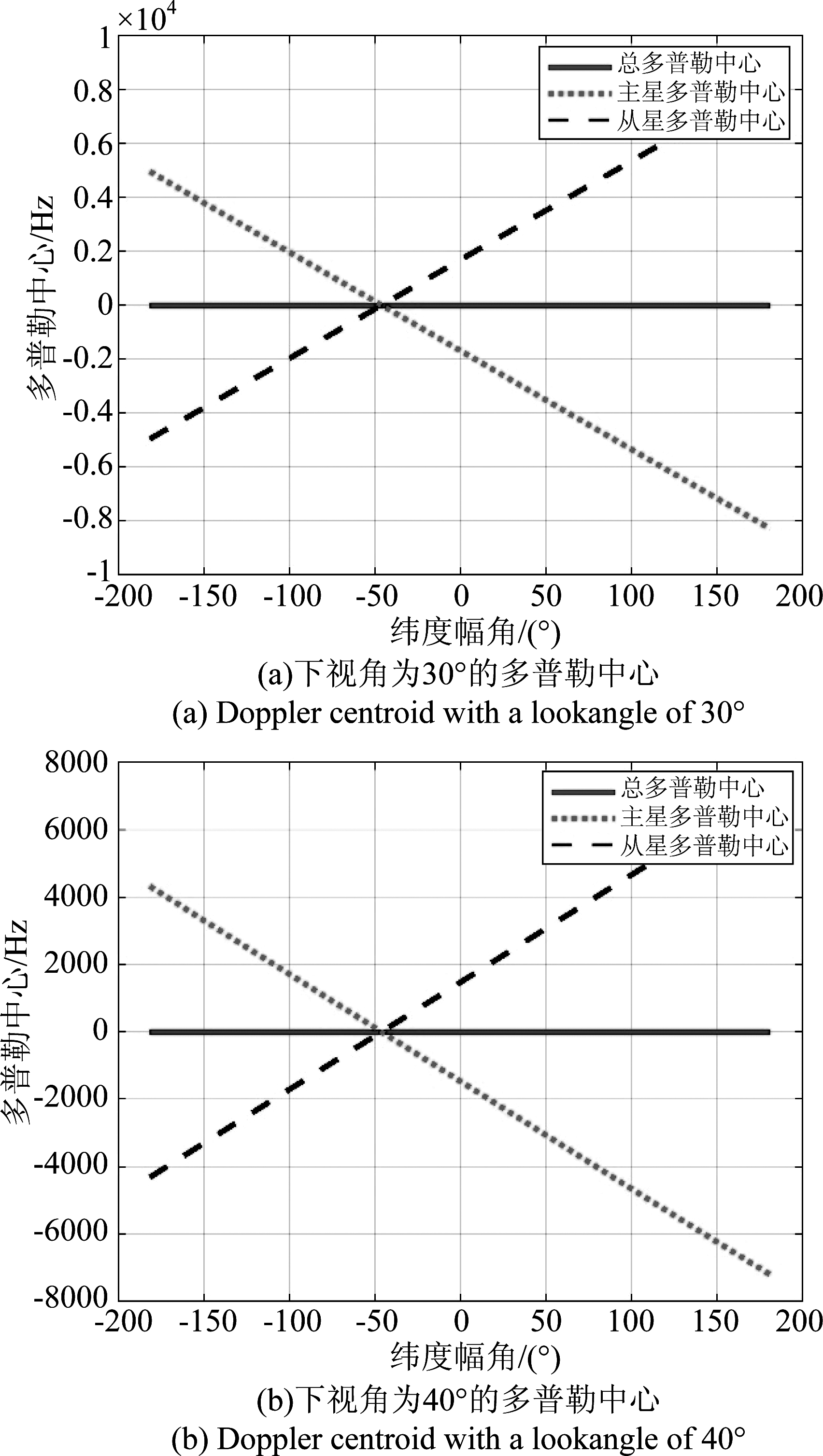
图8 进行联合多普勒导引后的多普勒中心频率
Fig.8 Doppler centroid after joint Doppler-steering
5 结论
本文研究了传统体制卫星和顺飞双站小卫星在多普勒中心导引方面的区别,分析了基于偏航控制的多普勒导引方法在天线指向、基线长度和工作频率方面受到的限制,说明了在顺飞双站小卫星构型下进行电扫描多普勒导引的必要性。随后并在保证有效成像区域的前提下,依据收发卫星多普勒中心频率互相抵消的思路,提出了基于二维电扫描的主辅卫星联合多普勒导引方法。从仿真结果来看,采用本文的方法实现多普勒中心频率的有效抑制,从而验证了该方法在高频段顺飞双站小卫星SAR中的有效性。
[1] Cumming I G, Wong H C. Digital processing of synthetic aperture radar data: algorithms and implementation[C]∥International Radar Conference, 1980: 168-175.
[2] 袁孝康. 星载合成孔径雷达导论[M]. 北京: 国防工业出版社, 2003: 1- 6.
Yuan X K. Introduction to spaceborne synthetic aperture radar[M]. Beijing: National Defense Industry Press, 2003: 1- 6. (in Chinese)
[3] Franceschetti G, Lanari R. Synthetic Aperture Radar Processing, Second Edition[M]. CRC Press, Inc. 2016.
[4] 张昊男. 多基星载SAR构型分析及应用[D]. 哈尔滨: 哈尔滨工业大学, 2017.
Zhang H N. Analysis and application in structure of multi-baseline spaceborne SAR[D]. Harbin: Harbin Institute of Technology, 2017. (in Chinese)
[5] 李春升, 王伟杰, 王鹏波, 等. 星载SAR技术的现状与发展趋势[J]. 电子与信息学报, 2016, 38(1): 229-240.
Li C S, Wang W J, Wang P B, et al. Current situation and development trends of spaceborne SAR technology[J]. Journal of Electronics & Information Technology, 2016, 38(1): 229-240. (in Chinese)
[6] 毛二可, 曾涛, 胡程, 等. 基于地球同步轨道合成孔径雷达的双基地探测系统: 概念及潜力[J]. 信号处理, 2013, 29(3): 285-292.
Mao E K, Zeng T, Hu C, et al. Bistatic detection based on geosynchronous SAR concept and potentiality[J]. Journal of Signal Processing, 2013, 29(3): 285-292. (in Chinese)
[7] Werninghaus R, Buckreuss S. The TerraSAR-X Mission and System Design[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 48(2): 606- 614.
[8] Wessel B, Breunig M, Bachmann M, et al. Concept and First Example of TanDEM-X High-resolution DEM[C]∥Eusar 2016: European Conference on Synthetic Aperture Radar, Proceedings of. VDE, 2016.
[9] 陈溅来, 杨军, 孙光才, 等. 高轨SAR多普勒中心补偿的二维姿态控制方法[J]. 电子与信息学报, 2014, 36(8): 1972-1977.
Chen J L, Yang J, Sun G C, et al. A two-dimensional attitude steering method to compensate Doppler centroid GEO SAR[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1972-1977. (in Chinese)
[10] 张永俊, 黄海风, 张永胜, 等. 椭圆轨道全零多普勒导引律研究[J]. 电子与信息学报, 2010, 32(4): 937-940.
Zhang Y J, Huang H F, Zhang Y S, et al. Research on elliptic orbit total zero Doppler steering[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1972-1977. (in Chinese)
[11] Long T, Dong X, Hu C, et al. A New Method of Zero-Doppler Centroid Control in GEO SAR[J]. IEEE Geoscience & Remote Sensing Letters, 2011, 8(3): 512-516.
[12] Raney R K. Doppler properties of radars in circular orbits[J]. International Journal of Remote Sensing, 1986, 7(9): 1153-1162.
[13] Fiedler H, Boerner E, Mittermayer J, et al. Total zero Doppler steering—a new method for minimizing the Doppler centroid[J]. IEEE Geoscience & Remote Sensing Letters, 2005, 2(2): 141-145.
[14] Krieger G, Fiedler H, Zink M, et al. TanDEM-X: A satellite formation for high-resolution SAR interferometry[C]∥IET International Conference on Radar Systems. IET, 2009: 3317-3341.
[15] Krieger G, Moreira A, Fiedler H, et al. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry[J]. IEEE Transactions on Geoscience & Remote Sensing, 2007, 45(11): 3317-3341.
