1 引言
现代电子对抗技术的发展严重压缩了传统单基地雷达的生存空间。组网雷达是一种能够有效应对各种复杂环境的雷达体制。相比于单基地雷达,组网雷达不仅拥有更强的生存能力,同时借助多节点观测充分利用了目标的空间频率等分集特性,进而实现系统探测性能的提升。电子干扰是复杂电磁环境的重要组成部分,组网雷达能够有效应对欺骗干扰[1,8],而对于压制式干扰,尤其当干扰源和目标位于同一波瓣时,使用传统单节点处理方法的组网雷达会同时抑制干扰信号和目标回波,无法实现有效探测[9]。
本文针对工作在单点辐射源环境中的大基线组网雷达,设计了一种相参、非相参处理相结合的自适应对消方法。并通过信号级仿真,初步验证了算法对单点辐射源的抑制效果。
2 单点辐射源环境下的组网雷达信号模型
假设雷达网由M个雷达节点组成,其中包含1个收发节点以及M-1个接收节点(不失一般性,取节点1为发射节点),各个节点位于Rk,k=1,...,M。观测场景中存在一由N个点散射体组成复杂目标,其位置分别为Xn,n=1,...,N。假设雷达网采用同步扫描方式,则各节点处单个点散射体回波形如下式:
(1)
其中![]() 表示发射节点、接收节点以及位于Xn的点散射体之间的传播延时
表示发射节点、接收节点以及位于Xn的点散射体之间的传播延时![]() 即点散射体与节点k之间的单程传播延时), fc表示载波频率。将节点k接收到的所有点散射体的回波信号相加,可以得到下式:
即点散射体与节点k之间的单程传播延时), fc表示载波频率。将节点k接收到的所有点散射体的回波信号相加,可以得到下式:
(2)
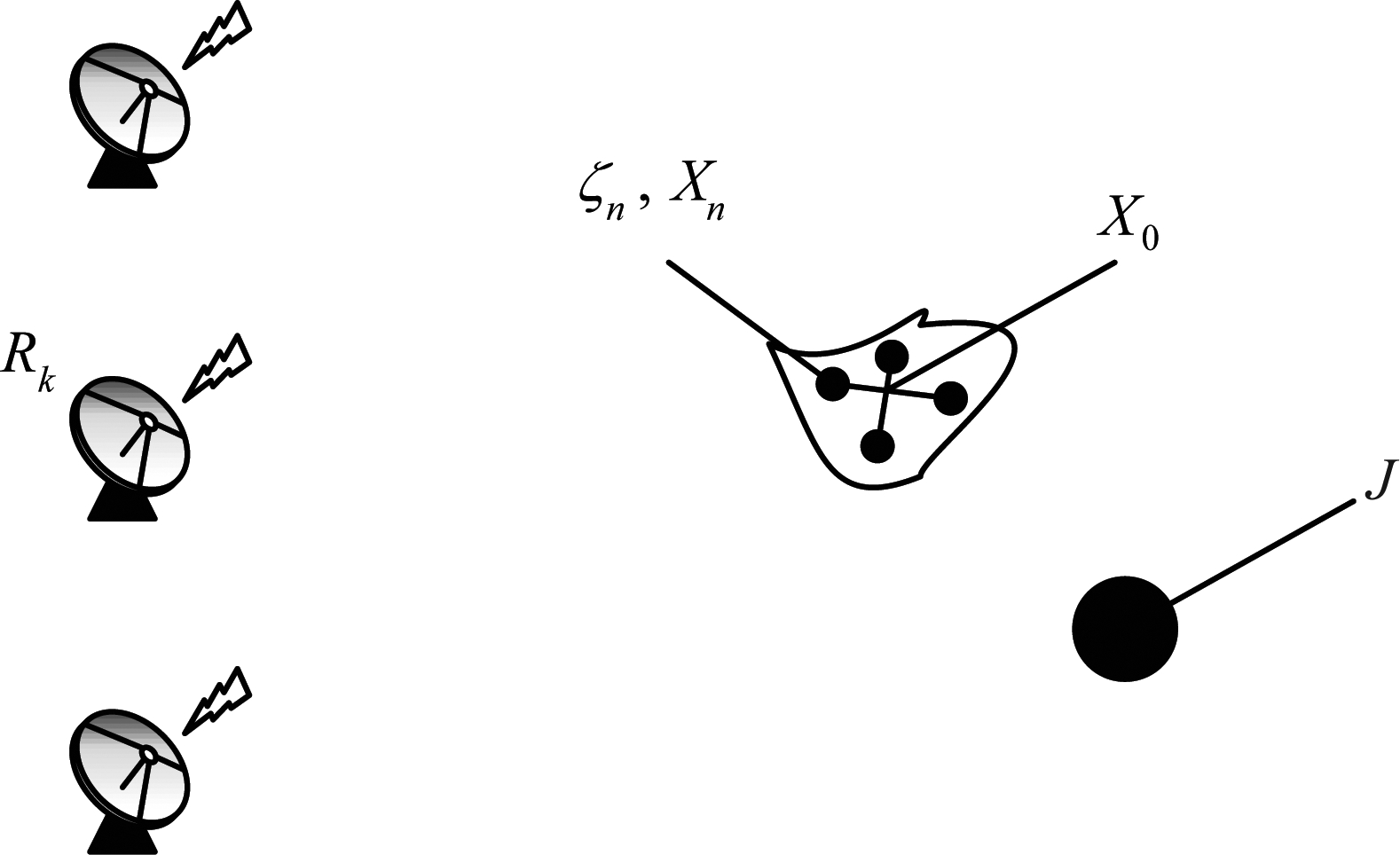
图1 典型单点辐射源环境示意图
Fig.1 Typical single point radiation source environment
假设发射信号的带宽不足以分辨各个点散射体,且各散射点的RCS质心位于坐标X0,上式可近似为:
(3)
其中
(4)
类似的,各节点接收到的干扰信号有如下形式:
(5)
上式中J为干扰源位置坐标,可得到各节点接收信号:
Zk(t) =Sk(t) +Gk(t) +wgn(t)=![]()
+
(6)
式中wgnk(t)为节点k内的高斯白接收机噪声。
当组成目标的散射体的个数N足够大,且各散射体具有相近的散射特性时(即目标的起伏特性符合Swerling-I模型),可以证明σk服从0均值的循环对称的复高斯分布[2],即
σk ~ CN(0,σ)
(7)
其中为σ为目标RCS均值。
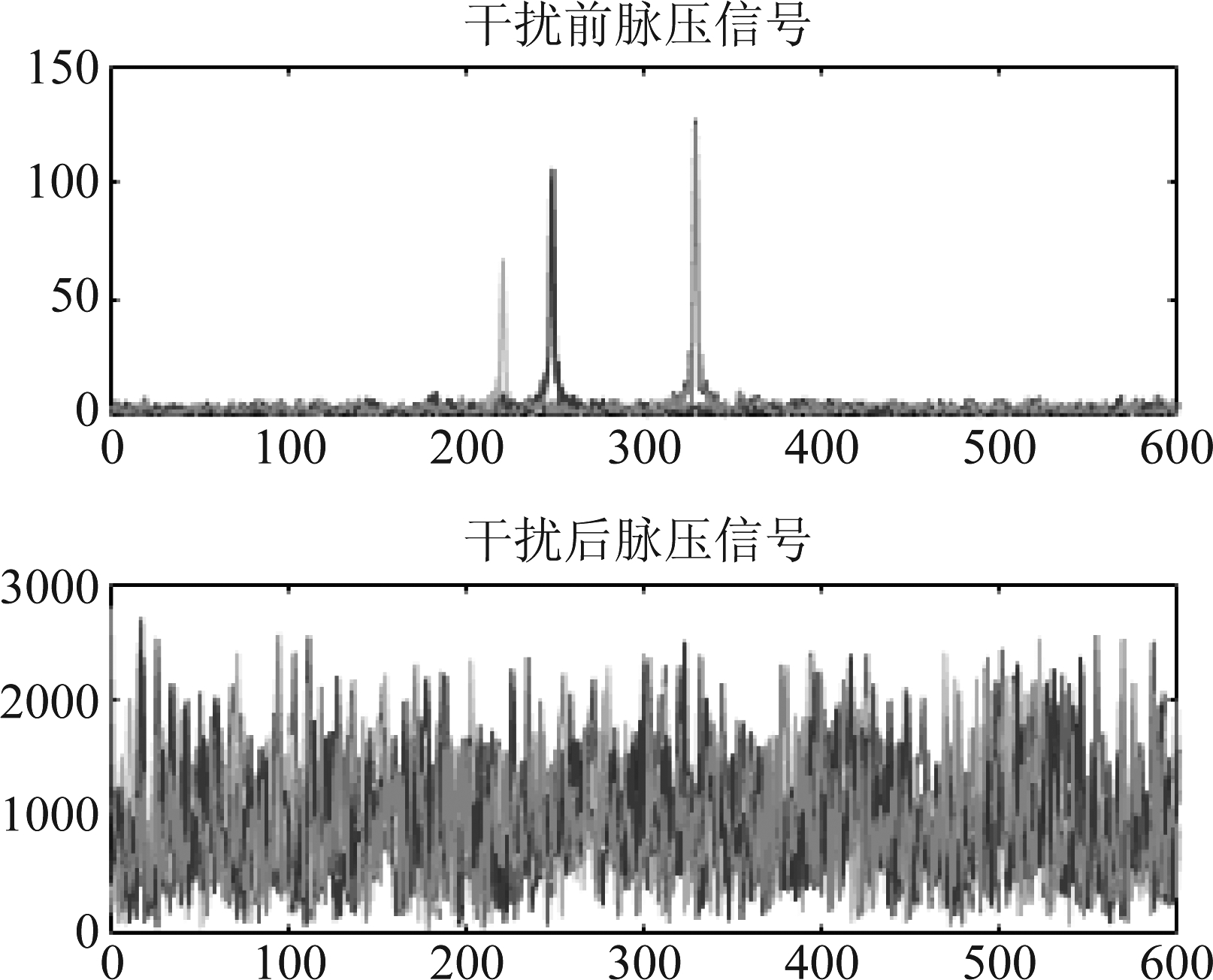
图2 干扰前后脉压信号对比
Fig.2 Comparison of pulse-compressed signals with or without interference
上图为干扰源开机前后脉压接收信号对比,可以看出由于INR远远高于SNR(超过30 dB),干扰信号完全压制目标回波。
3 大基线组网雷达自适应处理算法
当干扰源位于天线旁瓣区域时,传统自适应波束形成算法能够对其进行有效的抑制,极大地提高输出信号的信干噪比。但当干扰源进入天线的主瓣区域时,传统的自适应波束形成算法会导致旁瓣抬高、波束畸变以及波峰偏移问题[3,5- 6,10]。在干扰源和目标位于各个节点相同波瓣,且随目标移动的情况下,组网雷达各节点均无法独立完成自适应对消。
针对这种情况,本文提出一种先进行双节点对消然后融合不同对消输出的自适应处理算法,处理流程图如图4所示。
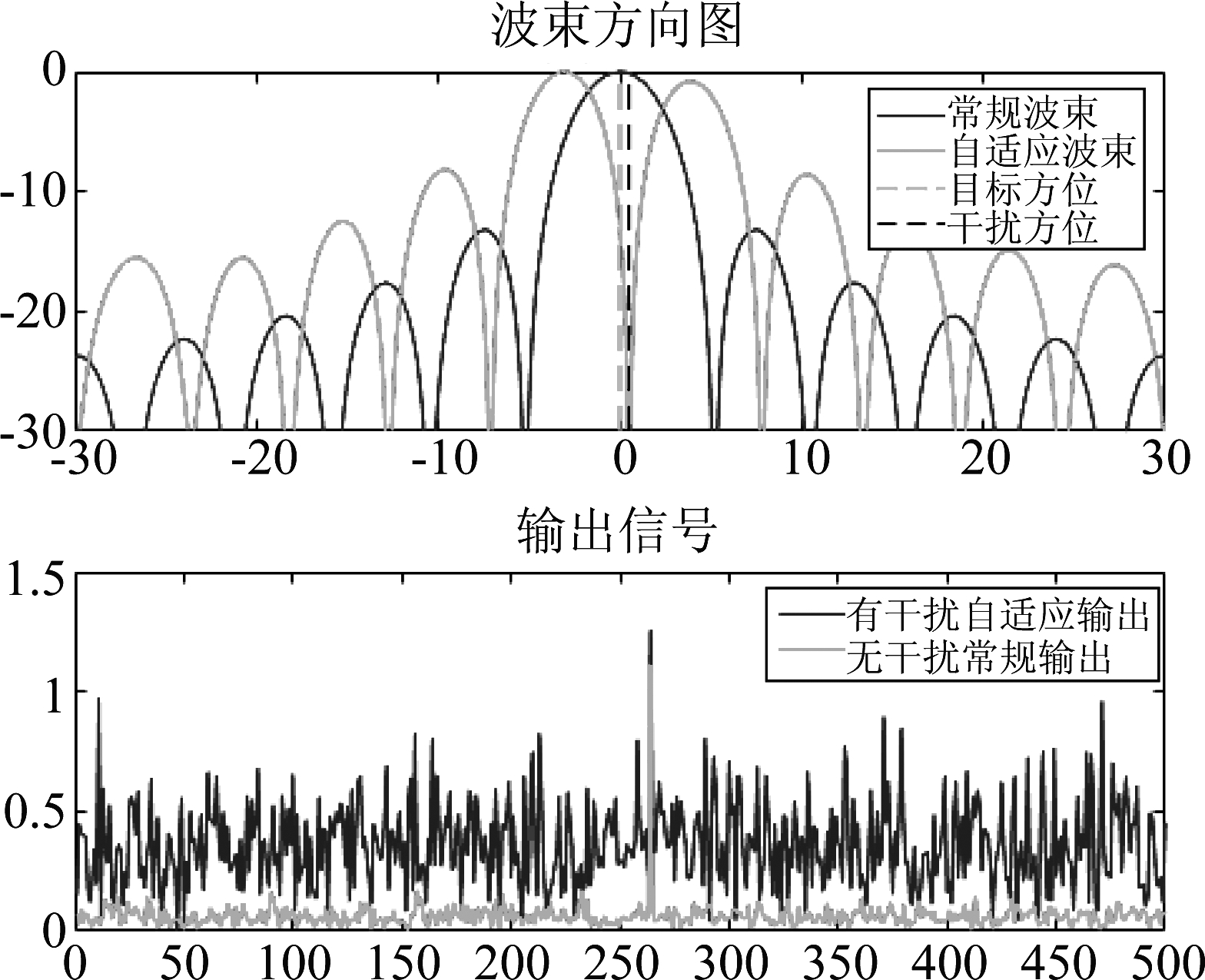
图3 传统自适应波束形成抗主瓣干扰效果示意图
Fig.3 The output of traditional adaptive beamforming against main lobe interference
![]()
图4 算法处理流程
Fig.4 The flowchart of the algorithm
3.1 包络对齐
为了实现双节点自适应对消,首先需要对接收信号的包络进行对齐。通过对接收信号进行上采样及互相关处理可对干扰源和各接收节点之间的传播延时之差进行估计,进而通过线性相位矫正实现接收信号中干扰分量的包络对齐。
以节点1的回波作为参考,对齐后信号有如下表达式:
Δτk(X0))exp( -j2πfc[τk(X0)])+
(8)
可以发现,由于目标和干扰源的空间位置并不相同,无法保证目标包络被完全对齐。式中,Δτk(X0)=![]() 即目标包络的对齐误差。
即目标包络的对齐误差。
当J与X0之间距离较小时,Δτk(X0)之间的差异可以忽略,上式可近似为:
(9)
该近似成立需要满足|Δτk(X0)|≤1/5B。
可以发现,由于目标和干扰源的空间位置并不相同,无法保证目标包络被完全对齐。式中,Δτk(X0)=![]() 即目标包络的对齐误差。
即目标包络的对齐误差。
当J与X0之间距离较小时,Δτk(X0)之间的差异可以忽略,上式可近似为:
(10)
该近似成立需要满足|Δτk(X0)|≤1/5B。
图5为基线长度200 km的5节点均匀直线型雷达网络(雷达节点坐标(-100,-300) km、(-50,-300) km、(0,-300) km、(50,-300) km、(100,-300) km)观测不同位置目标时的对齐差异可忽略区域,图中白点为目标位置,当干扰源位于对应的菱形区域时,目标包络的对齐误差可以忽略。
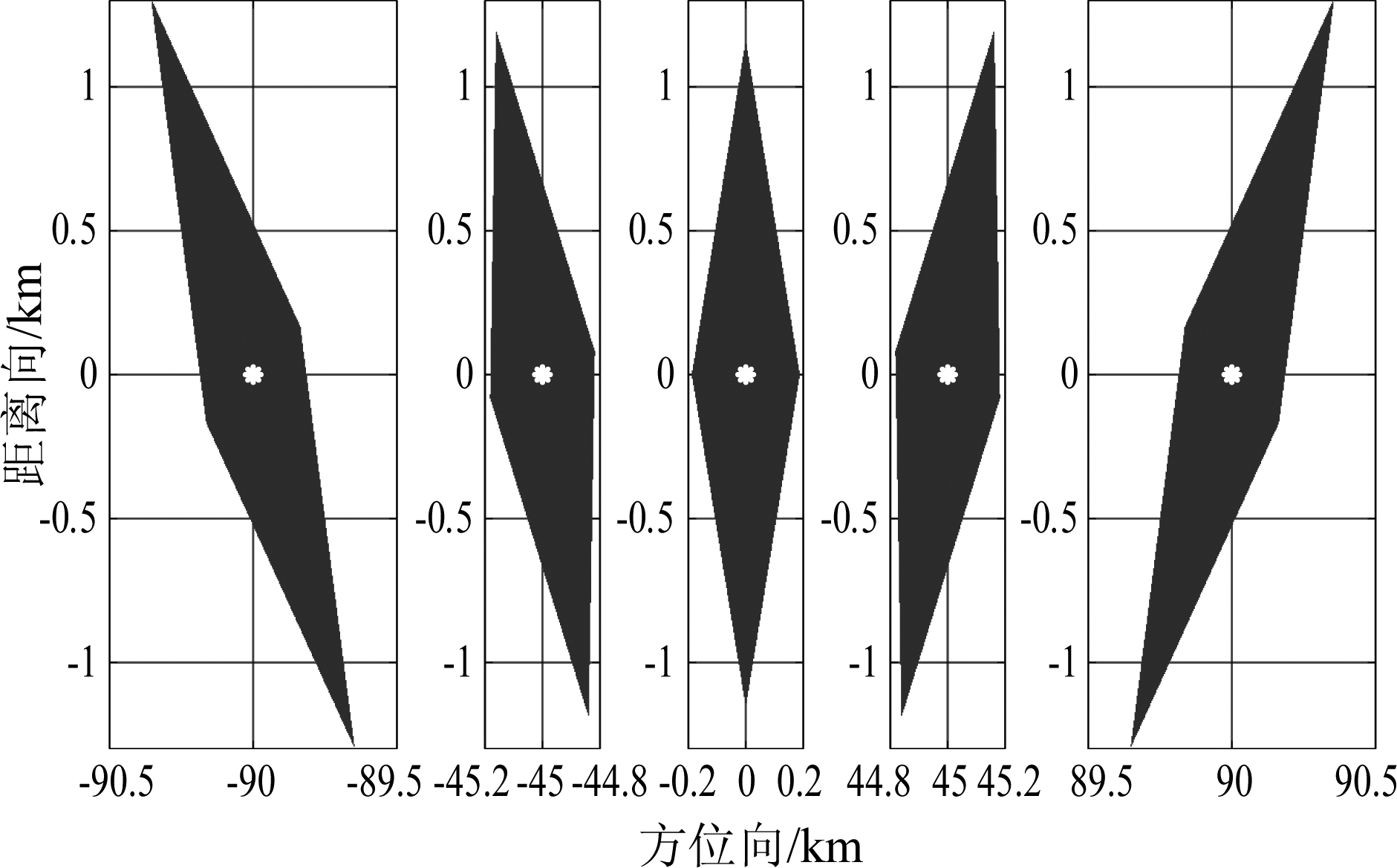
图5 包络对齐差异可忽略区域
Fig.5 Area with negligible alignment error in target’s envelop
本文假设干扰位于该包络对齐可忽略区域内。否则,由于目标包络没有对齐,后续处理中会出现目标包络的分裂甚至产生虚假目标。
3.2 双节点自适应对消
式(10)与传统阵列雷达信号模型类似,依据LCMV准则可以得到使用全部节点进行自适应对消的最优波束形成系数,即:
(11)
其中R为理想协方差矩阵,在实际信号处理中需要替换为采样协方差矩阵,对应的波束形成系数为[4,7,9]:
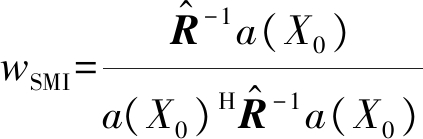
(12)
处理后的信号为:
(13)
对于单个阵列雷达,σk的幅相变化可以忽略。但在大基线组网雷达系统中,σk的相位和幅度均非常数,直接累加会导致严重的能量损失。
为了尽可能避免这种损失,本文将参与对消的节点数目减少,仅在双节点内进行自适应对消。由式(13)可以得到各个双节点对消的输出信号,其表达式为:
(14)
式(14)中的σkl=σk+σl,可以视作该节点对组成的组网雷达观测到的目标散射系数,由式(7)以及σk、σl之间的独立性可知:
σkl~CN(0,2σ)
(15)
值得注意的是,式(14)中的σkl和wgn′(t)仅在没有公共节点的双节点组合之间保持独立。
3.3 数据筛选融合
数据融合是组网雷达实现性能提升的关键步骤,本文通过能量累积实现双节点对消输出的数据融合。
为了保证数据融合的效果,将输出信号中的噪声功率统一,将自适应波束形成因子修正为:
(16)
由于包络对齐存在误差,输出信号中存在对消残余,这会严重影响融合后的信号质量。为解决该问题,本文借助无回波快拍对输出信号的INR进行评估,仅允许INR较小的双节点对消输出参与融合。
4 算法仿真及结果分析
取M=5个雷达节点组成总基线长度为200 km的均匀直线型雷达网络。场景中心位于距离雷达基线300 km处,其中目标(包含N=6个各向同性点散射体)位于中央节点正前方,干扰源和目标之间存在200 m 的方位向偏移,由图5可知,该干扰源位于对齐差异可忽略区域。
各雷达节点的参数以及目标点散射体的参数如表 1、表 2所示。
表1 雷达参数
Tab.1 Parameters of radar nodes

参数参数值载频440 MHz天线尺寸10 m信号带宽1 MHz采样频率2 MHz平均信噪比13 dB平均信干比-30 dB
表2 点散射体参数
Tab.2 Parameters of scattering center

编号n位置Xn散射系数ζn1(-1.25 m,0 m)12(-4 m,1.16 m)13(-4 m,-1.16 m)14(-6.25 m,1.5 m)15(1 m,-4 m)16(1 m,4 m)1
4.1 包络对齐仿真结果
图6为对齐效果的示意图,从图中可以看出包络对齐的效果非常明显。由于各节点接收回波的INR达到了43 dB,借助上采样以及各节点接收信号之间的互相关处理可以得到很高精度的相对传播延时估计。
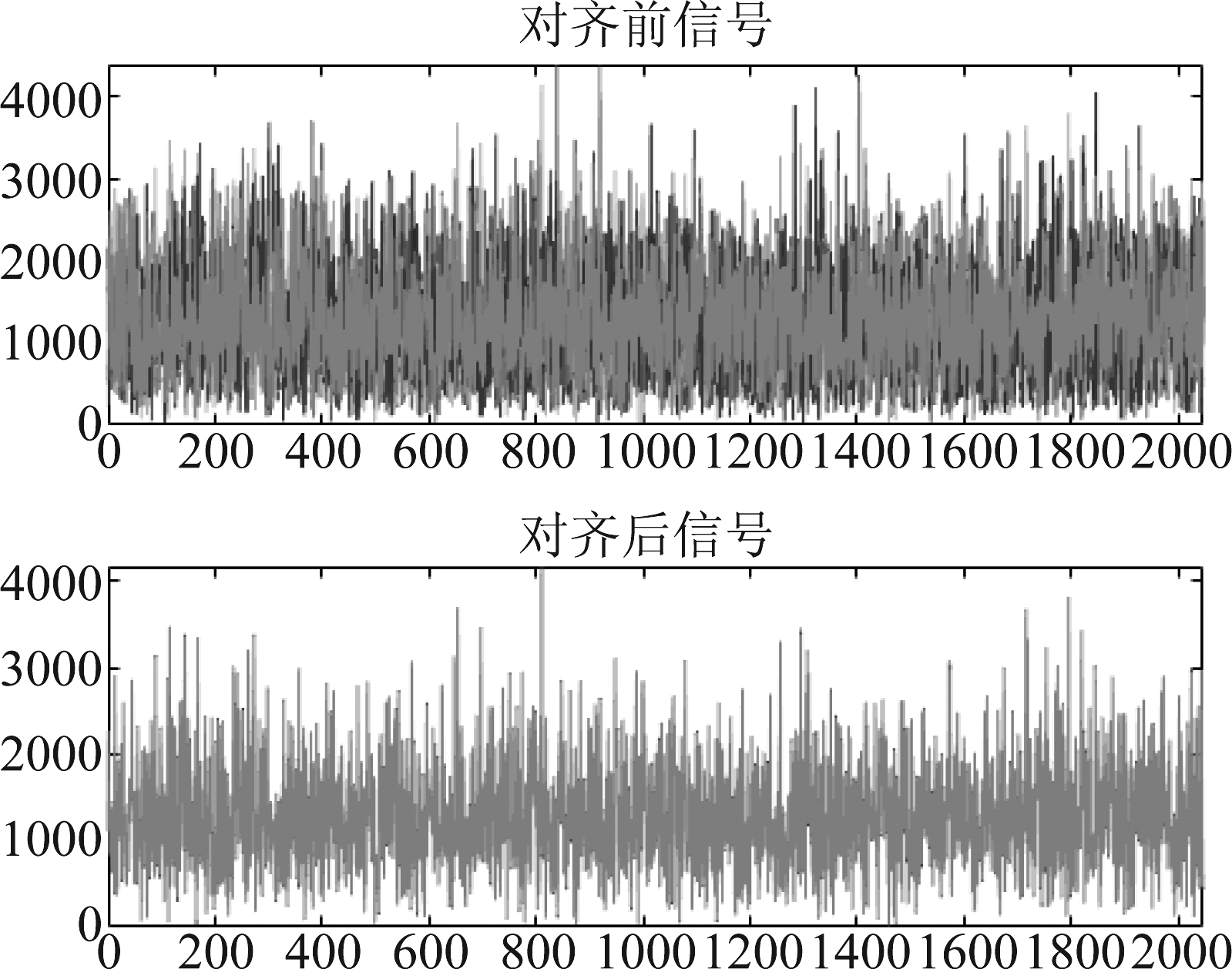
图6 包络对齐示意图
Fig.6 Time delay alignment
4.2 双节点自适应对消仿真结果
图7为双节点自适应对消效果示意图,图中蓝线表示常规波束形成的输出信号,红线表示自适应波束形成的输出信号,可以看出对消的效果非常明显,但是也存在部分双节对的对消残余较大(节点对(1,4)、(1,5)以及(2,5)),其整体平均功率明显高于其余双节点组合。
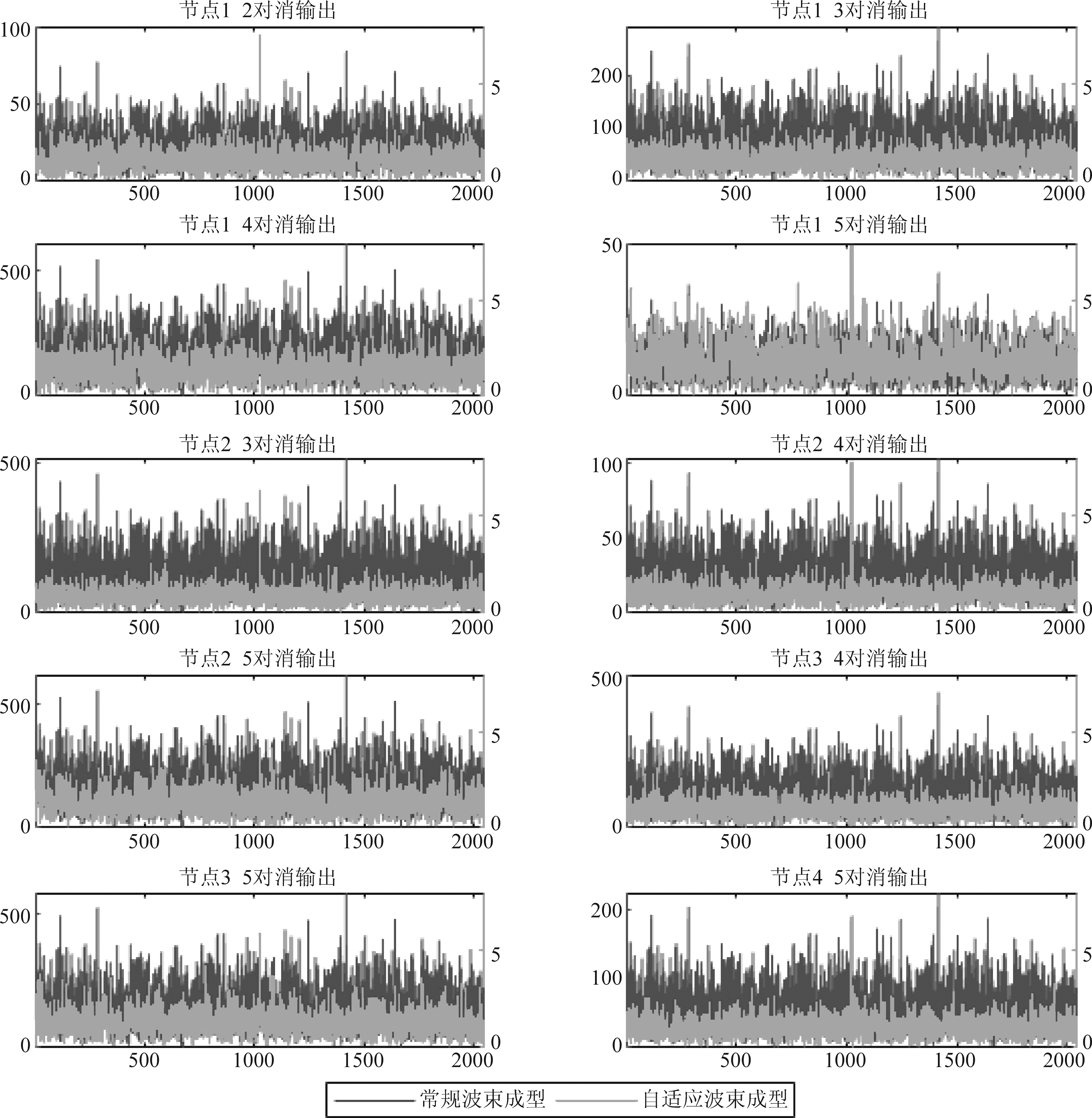
图7 双节点自适应对消效果示意图
Fig.7 The output of dual-node cancellation
从图7中同样可以发现不同双节点对消输出的目标回波能量有非常明显的差异。除去式(14)中σkl之间的幅度差异,式(16)中归一化后的自适应波束形成系数导致的目标能量损失也是不可忽略的因素。
4.3 筛选融合仿真结果
图8为筛选前后数据融合效果的对比图,可以发现通过对输出信号的INR进行评估可以有效的避免对消残余较高的数据对融合结果的影响,有效地提高输出信噪比。
在实际的信号处理中需要根据实际参与融合的对消输出数目调整目标检测的门限。
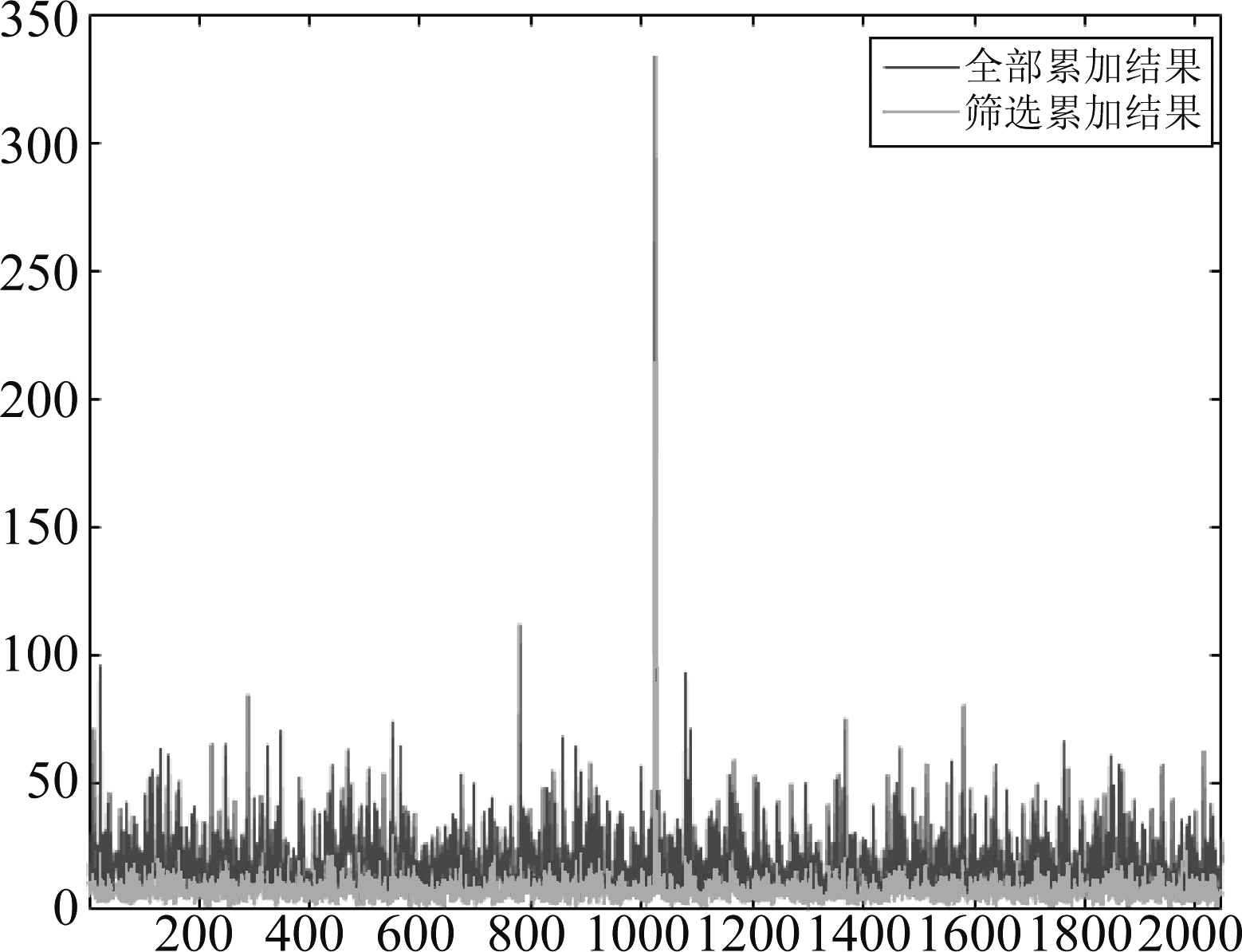
图8 筛选前后融合结果对比图
Fig.8 Comparison of fusion results with or without channel-selection
5 结论
本文提出了一种先进行双节点自适应对消,再对对消输出进行能量累积的信号处理算法。从信号级仿真的结果可以看出,该算法能够在有效去除回波中的干扰分量的同时,保留组网雷达利用目标RCS空间分集的特性,进而实现对目标的有效观测。 该算法同样存在一些问题,主要包括无法应对多个辐射源、无法应对位于对齐差异可忽略区域外的单辐射源以及无法处理宽带信号的问题。这些需要在后续的研究中进一步优化。
[1] 刘洁怡, 张林让, 赵珊珊, 等.欺骗式干扰下组网雷达优化布站方法分析与仿真[J].电子科技大学学报, 2017, 46(4): 513-519.
Liu Jieyi, Zhang Linrang, Zhao Shanshan, et al. Analysis and simulation of optimized station method for networked radar under deceptive interference[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(4): 513-519. (in Chinese)
[2] Haimovich A M, Blum R S, Cimini L J.MIMO Radar with Widely Separated Antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116-129.
[3] 张宗傲.阵列雷达自适应主瓣干扰抑制算法研究[D]. 北京: 北京理工大学, 2015.
Zhang Zongao. Array radar adaptive main lobe interference suppression algorithm[D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese)
[4] Horowitz L J, Blatt H, et al. Controlling adaptive antenna arrays with the sample matrix inversion algorithm[J]. IEEE Tram Aerosp Lecton Syst, 1978, 10(5):840- 847.
[5] Lorenz R G, Boyd S P. Robust minimum variance beamforming[J]. IEEE Trans. Signal Process, 2005, 53(5): 1684-1696.
[6] Hassanien A, Vorobyov S A, Wong K M. Robust adaptive beamforming using sequential quadratic programming: An iterative solution to the mismatch problem[J]. IEEE Signal Process, 2008, 15: 733-736.
[7] Mallipeddi R, Lie J P, Razul S G, et al. Robust adaptive beamforming based on covariance matrix reconstruction for
look direction mismatch[J]. Progress In Electromagnetics Research, 2011, 25: 37- 46.
[8] Deligiannis A, Rossetti G, Panoui A, et al. Power allocation game between a radar network and multiple jammers[C]∥Radar Conference (RadarConf), 2016 IEEE. IEEE, 2016: 1-5.
[9] Vendik O G, Kozlov D S. Phased antenna array with a sidelobe cancellation for suppression of jamming[J]. IEEE Antennas and Wireless Propagation Letters, 2012, 11: 648- 650.
[10] 李荣锋, 王永良, 万山虎.一种在主瓣干扰条件下稳健的自适应波束形成方法[J].系统工程与电子技术, 2002, 24(7): 61- 64.
Li Rongfeng, Wang Yongliang, Wan Shanhu. Robust adaptive beam forming under main lobe interference conditions[J]. Systems Engineering and Electronics, 2002, 24(7): 61- 64. (in Chinese)



