1 引言
MIMO(Multiple-Input Multiple-Output,多输入多输出)雷达是近些年来发展起来的一种新体制雷达,其发射端和接收端均采用多天线结构,各个发射天线同时辐射相互正交的信号波形,接收端的每个天线接收所有发射信号并在后端进行信号分选,从而得到远多于实际收发阵元个数的观测通道和自由度[1]。若收发阵列均为集中式阵列,根据收发阵列相对于目标的位置可以将MIMO雷达分为单基地MIMO雷达和双基地MIMO雷达[2]。其中,单基地MIMO雷达的收发阵列相对于目标而言位于同一观测角度,而双基地MIMO雷达的收发阵列相对于目标而言位于不同观测角度。
近年来随着MIMO技术的发展,地基MIMO成像雷达系统大有替代传统地基SAR系统的趋势。相比于传统的地基SAR(Synthetic Aperture Radar,合成孔径雷达)系统,地基MIMO成像雷达由于采用虚拟孔径技术[3],无需滑轨即可实现方位向高分辨,避免了运动补偿的问题且便携性更好。同时,MIMO成像雷达能大大提高图像帧频,将采集一幅图像的时间由传统地基SAR系统的分钟级[4]缩短到亚秒级,为基于图像的二维振动测量提供了可能。因此吸引了大量的研究者的关注,并且在边坡稳定性监测[5- 6]、安全检查[7- 8]等领域取得了良好的效果。
与此同时,文献[9]指出通过多部MIMO雷达从多个角度对同一场景进行联合观测可以对观测区域内的三维形变进行反演,从而有效地对地质灾害进行预警。在这种多部雷达协同观测的情况下,不同雷达的收、发阵列协同工作组成双基地MIMO构型进行观测,能够对传统的自发自收模式的单基地构型观测进行有效的补充,从而显著提高系统的自由度,获取观测区域更丰富的散射特性[10]。
由于收发阵列分置,双基地MIMO雷达系统的成像性能与传统单基地MIMO成像雷达系统存在较大差异,单基地MIMO雷达系统中常用的等效阵列理论失效,同时传统的方向图理论已经不能对其各方向分辨特性进行分析[11]。针对这一问题,本文结合系统的几何构型对系统回波信号进行建模,通过推导系统的广义模糊函数给出了双基地MIMO成像雷达系统的分辨特性分析,最后通过Maltab仿真验证了分析结论的正确性。
2 双基地MIMO雷达及其广义模糊函数定义
按照目标相对于收发阵列的位置分类,MIMO雷达可以分成两种工作模式:单基地模式和双基地模式[2]。单基地模式可视作相控阵雷达的扩展形式,其发射和接收两端仍然采用传统的共址阵列构型,目标位于收发阵列的同一观测角度;双基地MIMO雷达可视作双/多基地雷达的扩展形式,其发射-接收天线采用大间距分布形式,目标位于收发阵列的不同观测角度[12]。二者的结构如图1和图2所示。
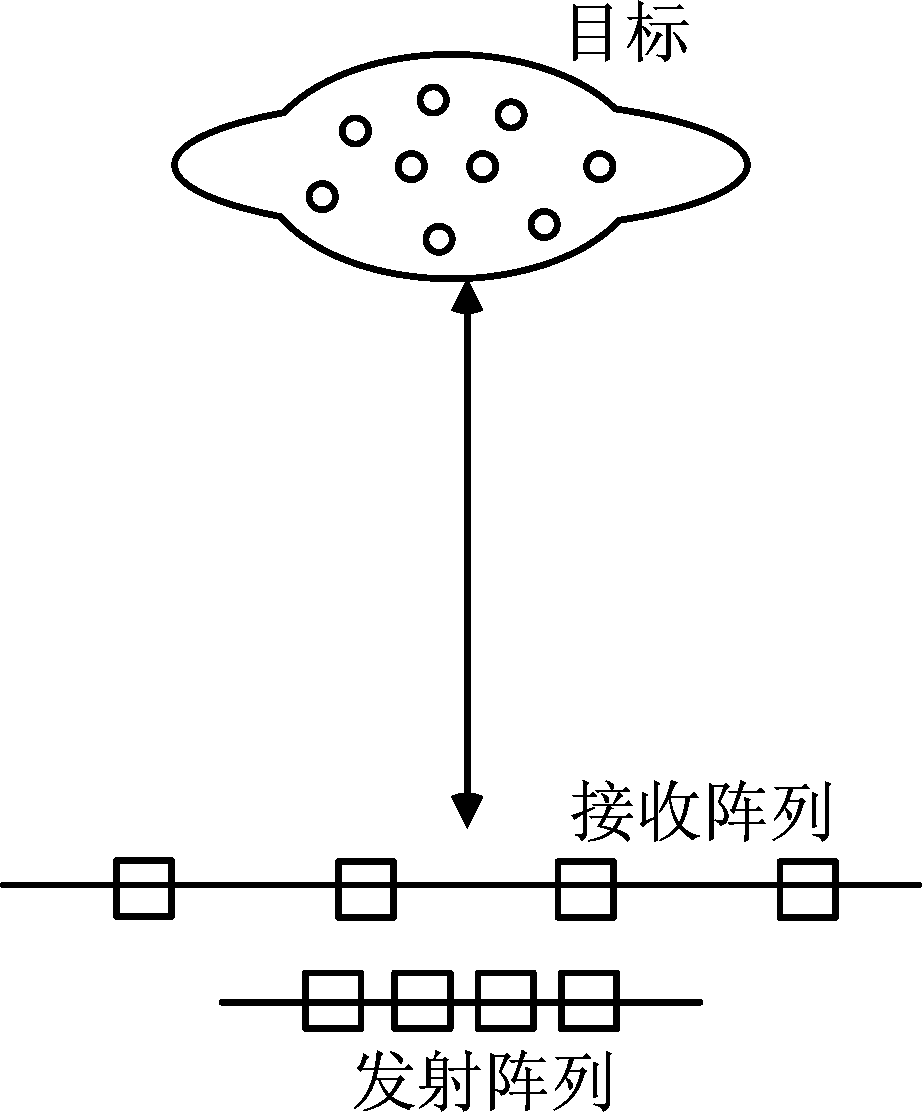
图1 单基地MIMO阵列
Fig.1 Monostatic MIMO array
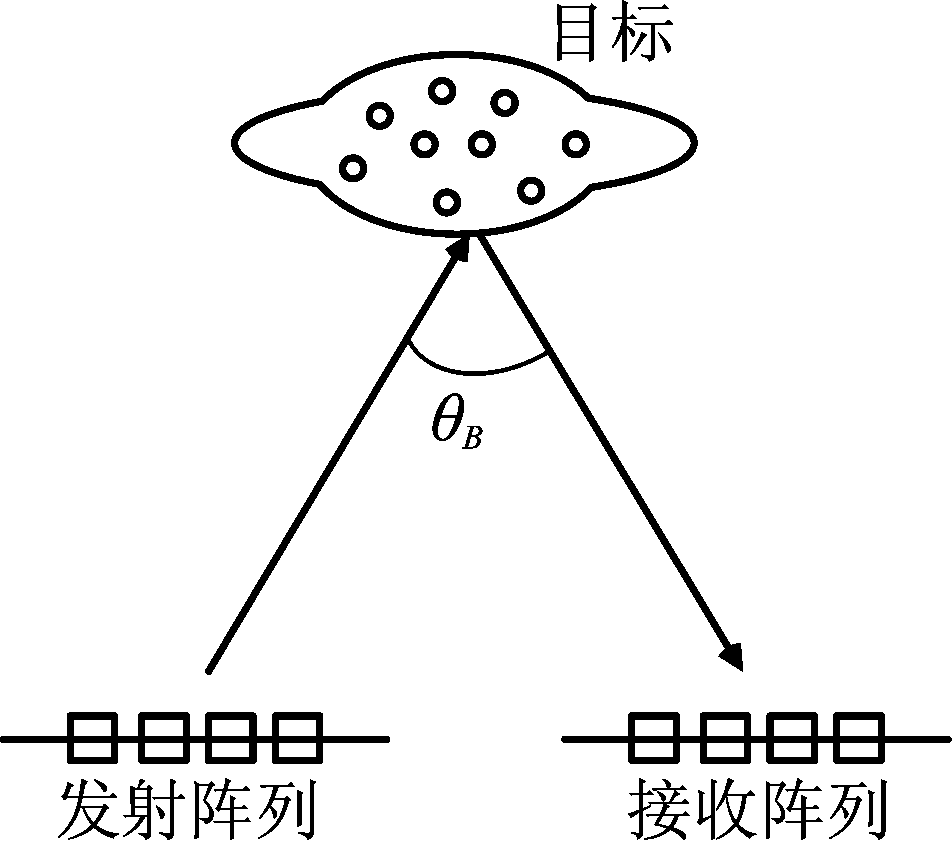
图2 双基地MIMO阵列
Fig.2 Bistatic MIMO array
考虑一种典型的双基地MIMO雷达,其收发阵列均为线阵且共面。记发射阵列和接收阵列的阵元个数分别为M个和N个。假设所有收发阵元和目标均位于同一平面,以接收阵列中心作为原点建立直角坐标系,令所有接收阵元均位于y轴上,目标位于y轴右侧。记所有接收阵元的位置为{(0,yR,n)|n=1,2,...,N},而发射阵元的位置为{(xT,m,yT,m)|m=1,2,...,M},如图3所示。
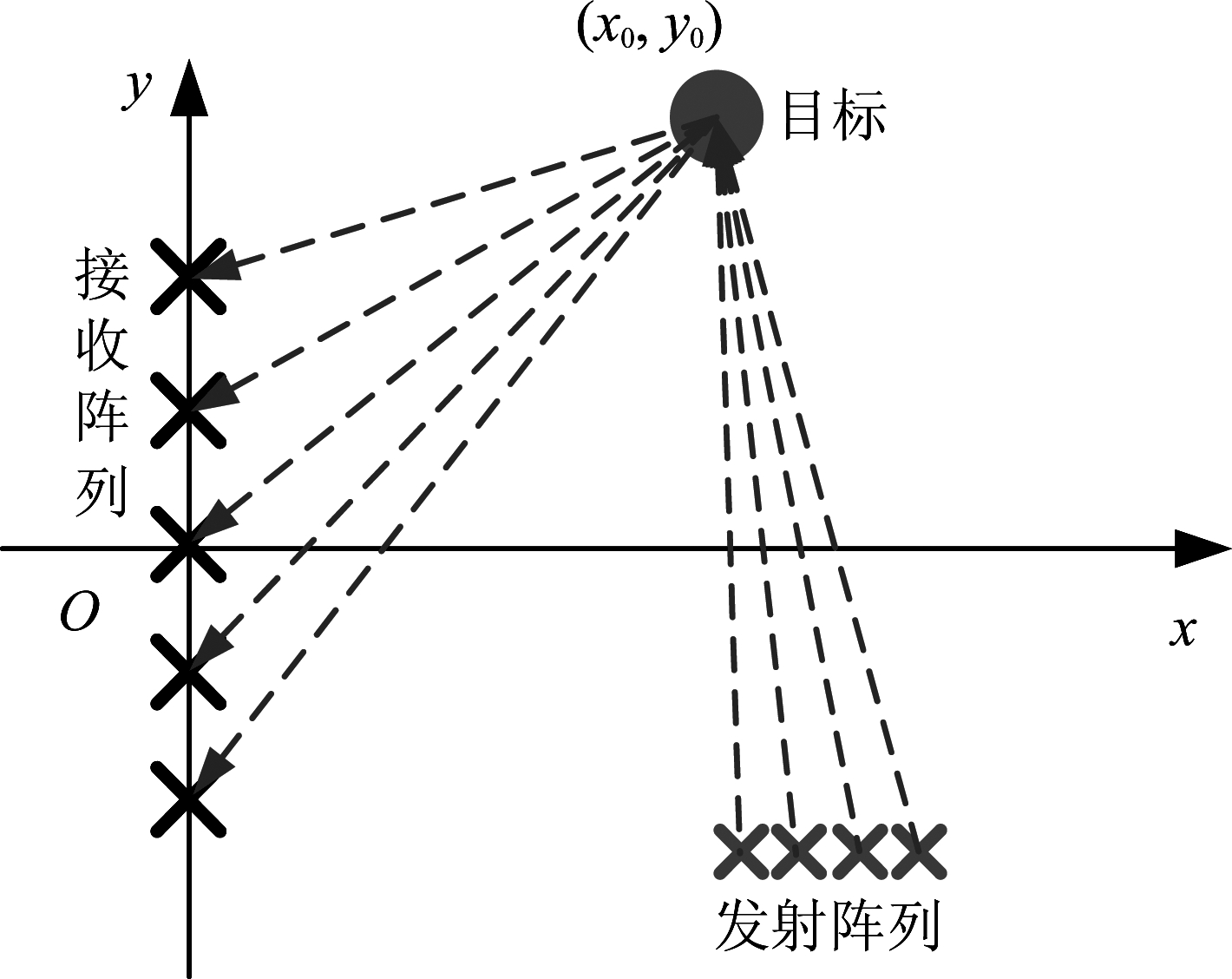
图3 一般情况下的双基地MIMO阵列构型
Fig.3 Geometric configuration of general bistatic MIMO array
对于一个位于(x0,y0)处的目标而言,第m个发射阵元和第n个接收阵元到目标的距离分别为
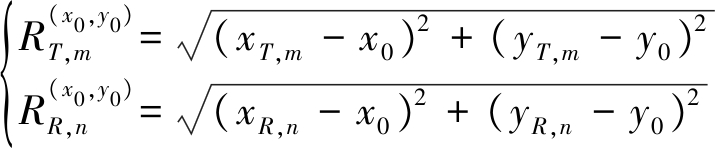
(1)
考虑发射信号为s(t),则第m个发射阵元和第n个接收阵元对应的通道接收到的回波信号为
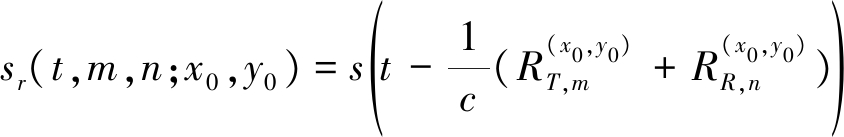
(2)
其中,c为光速。根据定义,广义模糊函数为相邻的两个目标回波的内积[13],因此可以写出其表达式
(3)
将式(2)代入式(3),结合Parseval’s定理可以得到:
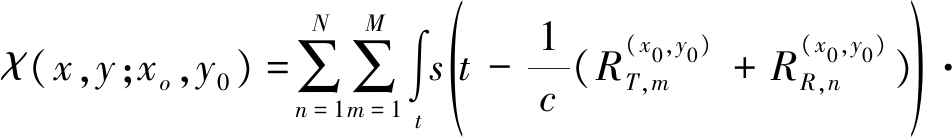
(4)
其中,P( f )为发射信号的功率谱。认为发射信号是载频为fc、带宽为B线性调频信号,那么其功率谱可以写成
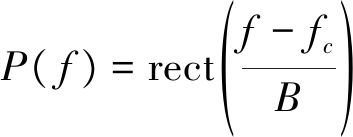
(5)
另外,定义发射和接收阵列的单频方向图分别为:
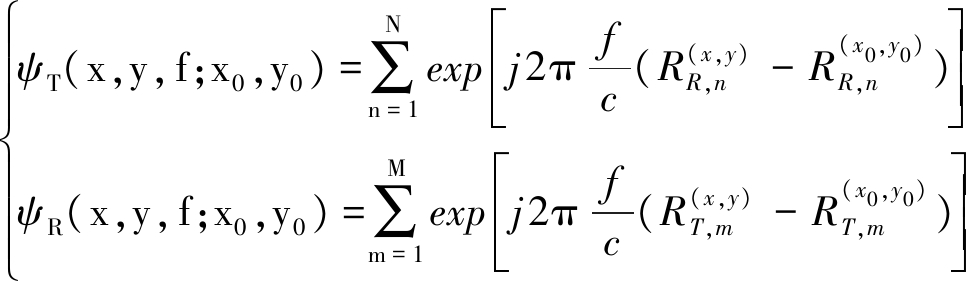
(6)
此时,可以将式(4)简化为
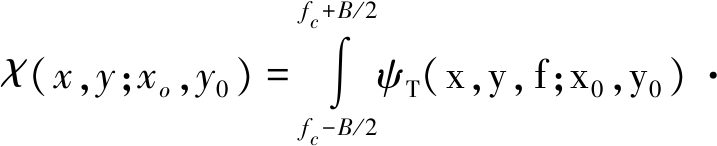
ψR(x,y, f;x0,y0)df
(7)
至此,双基地MIMO雷达的广义模糊函数可分解成收发单频方向图乘积在观测频谱上的频域积分,其表现形式与单基地MIMO雷达的情况[14]类似。
3 远场等效下的双基地MIMO雷达广义模糊函数特性分析
众所周知,传统单基地MIMO成像雷达的设计及性能评估可以由其等效阵列的性能等价进行[13]。但是等效阵列理论基于远场假设条件,即目标处于阵列的远场区。根据文献[14]的分析可知,MIMO阵列的临界远场距离为:
(8)
由于双基地MIMO雷达的收发阵列位于目标的不同视角,因此双基地阵列的总长度(收发阵元间的最大距离)与目标的距离为同一量级,显然无法满足MIMO阵列意义下的远场条件。但是,由于发射阵列和接收阵列均为共址阵,目标到收发阵列的距离远大于收发阵列各自的长度,因此,目标对于收发阵列各自而言均位于远场区。不加强调地,下面讨论的双基地MIMO雷达均指这种双基地MIMO雷达,双基地MIMO雷达的远场均指这种相对于收发阵列的远场。综上,对于这种阵列而言,目标相对于发射阵列和接收阵列均位于远场区,但是目标相对于两个阵列的观测角度不同,如图4所示。
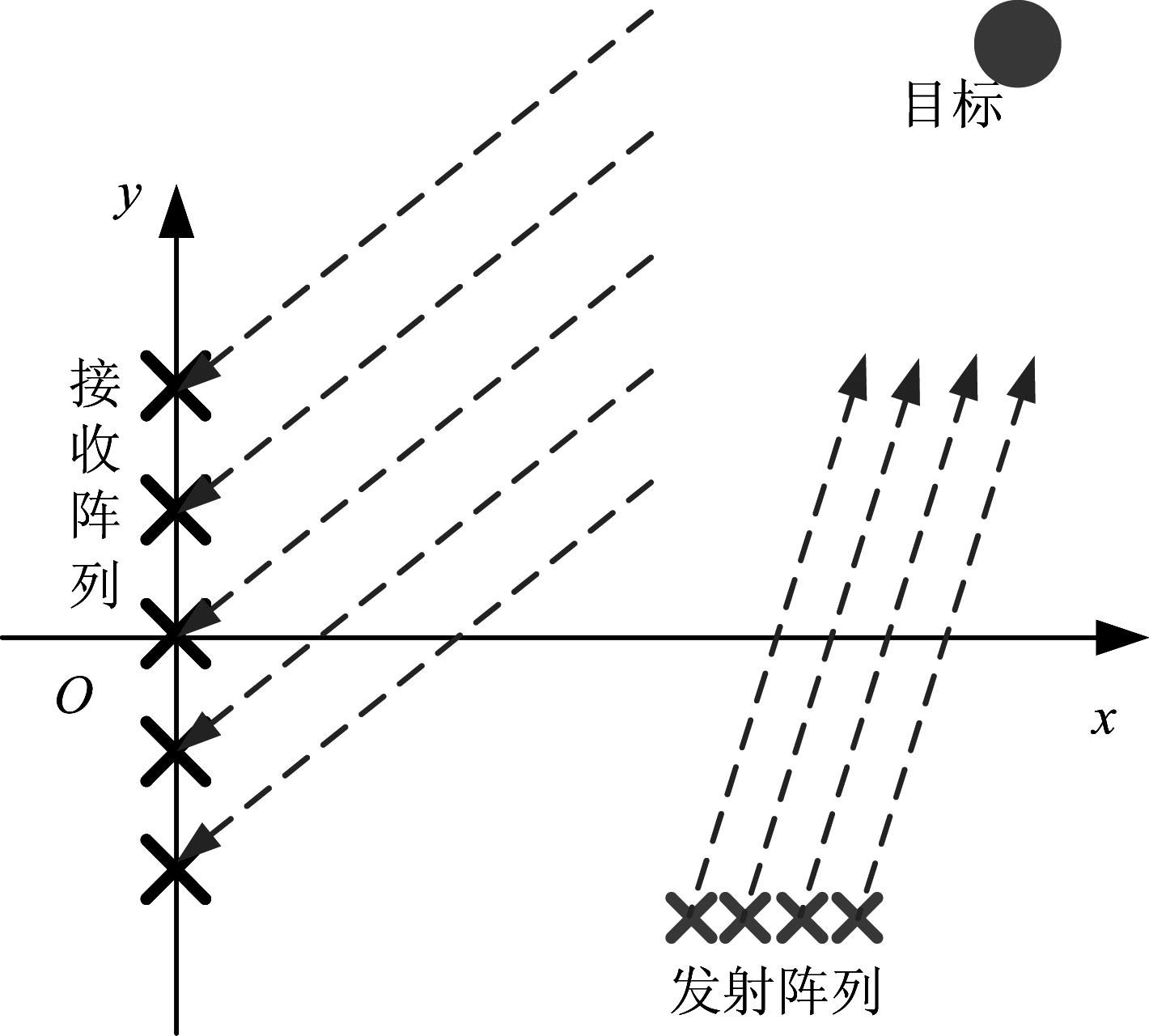
图4 远场假设下的双基地MIMO阵列构型
Fig.4 Geometric configuration of bistatic MIMO array under far-field assumption
在收发阵列均满足远场假设的情况下,对于接收阵列而言,其斜距可以近似写为[14]
(9)
其中,(ρ,θ)为点(x,y)对应的极坐标表示。于是远场接收方向图可以写成
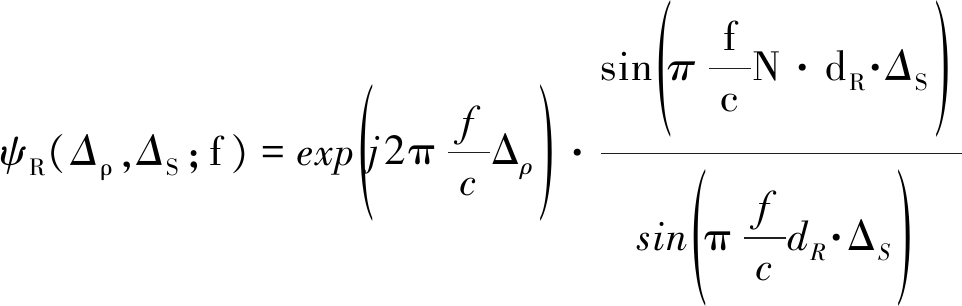
(10)
其中,
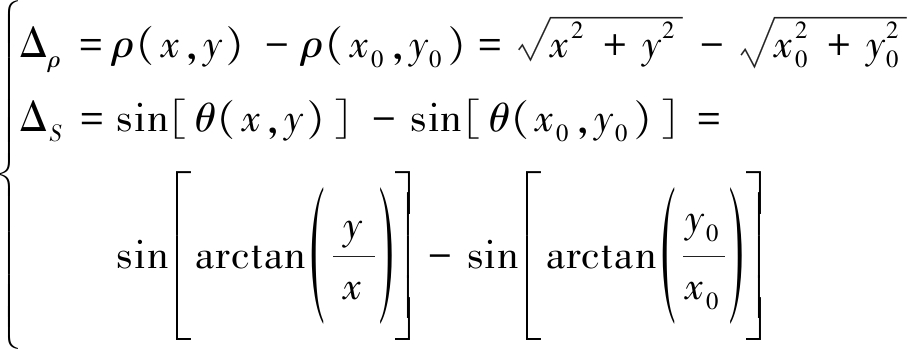
(11)
类似的,可以得到在发射阵列坐标系的发射阵列方向图
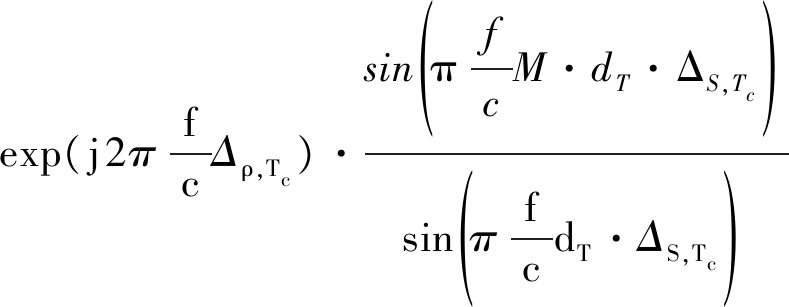
(12)
其中,
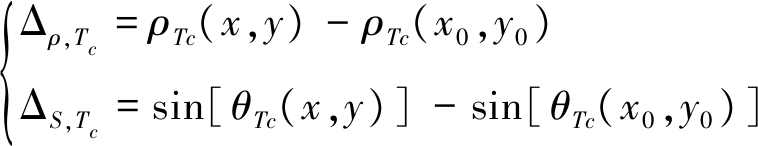
(13)
其中的ρTc(x,y)和θTc(x,y)分别为目标(x,y)相对于发射阵列中心(xTc,yTc)的距离和方位角。定义发射阵列的方向向量
目标(x,y)相对于发射阵列中心的位置向量为
则这一距离和方位角可以写为:
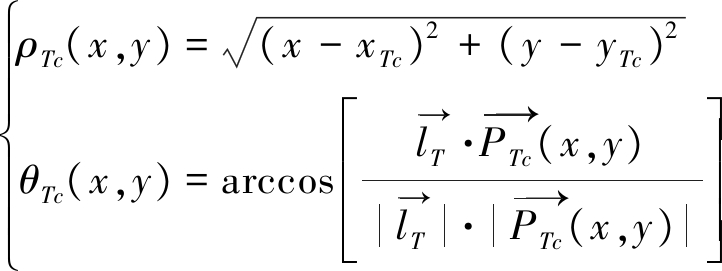
(14)
因此,双基地MIMO阵列的点扩展函数形式如下:
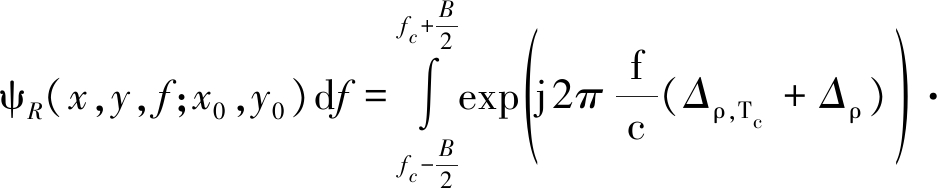
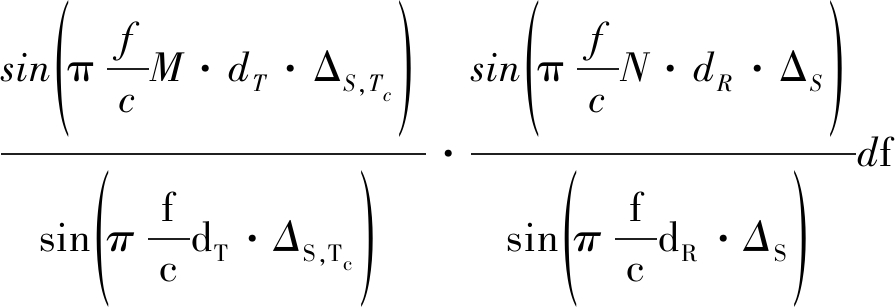
(15)
在这种远场条件下的系统广义模糊函数的表现形式为相对不同原点的两个角度域周期sinc函数的乘积在频域进行积分。
4 远场等效下的双基地MIMO雷达等效阵列特性分析
一般而言,单基地MIMO雷达的性能可以很好地利用等效阵列理论进行评估。但是正如上面讨论的,本文讨论的双基地MIMO阵列并不存在传统意义上的等效阵列。为了更加直观的从阵列角度解释双基地MIMO雷达的特点,下面结合传统等效阵列的等效思想分析双基地MIMO雷达的等效阵列。对于图3所示的双基地MIMO阵列而言,第m个发射阵元发射、第n个接收阵元接收的信号,其回波斜距为
sin θTc(x,y)-yR,n·sin θ(x,y)
(16)
其中,ΔT,m为第m个发射阵元相对于发射阵列中心的有向距离。考虑收发阵列均为均匀阵列,且收发阵元之间的间距分别为dT,dR,那么上式可以改写为
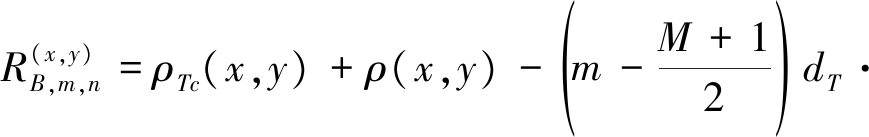
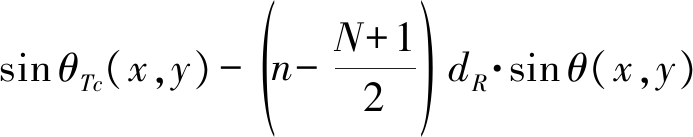
(17)
对于成像雷达系统而言,一般会保证收发阵列阵元间距之间存在倍数关系,不妨考虑发射阵列为密集阵列,接收阵列为稀疏阵列,dR=M·dT,将其代入上式可得:
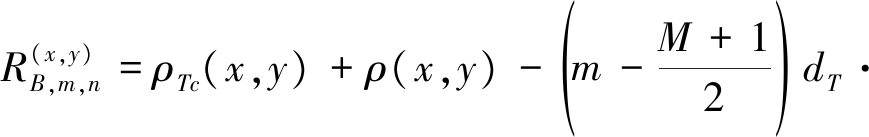
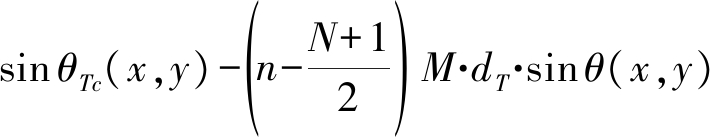
(18)
记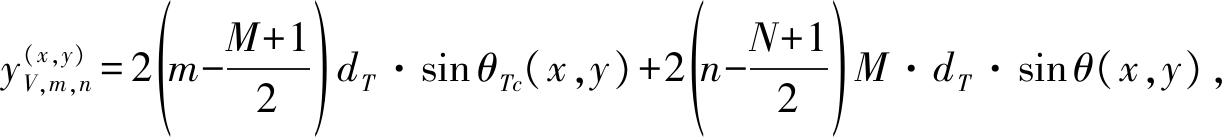
此时双基地距离和可以等效为
(19)
在这种等效中,我们认为第(m,n)通道的回波等效为发射阵列中心处的发射阵元进行发射,位于
处的等效阵元进行接收的信号,同时目标相对于等效阵列的方位角度固定为30°。根据空间卷积原理[2],上面的等效阵列的空间采样函数可以分解成发射阵列空间采样函数和接收阵列空间采样函数的卷积的形式,即
TopV(y)=TopT(y)⊗TopR(y)
(20)
其中,
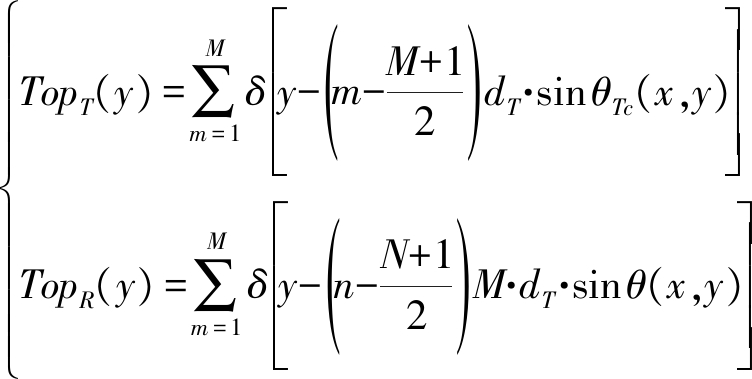
(21)
其中,δ(·)为单位冲激函数。一般而言,依据单基地最佳成像准则设计的MIMO阵列其收发阵列的空间卷积应该恰好形成均匀满阵,然而,在双基地构型下,由于sin θTc≠sin θ,上式中的两个空间采样函数生成的等效阵列为周期非均匀采样。记γ(x,y)=sin θTc(x,y)/sin θ(x,y)为压缩系数,则上式可以进一步化简为
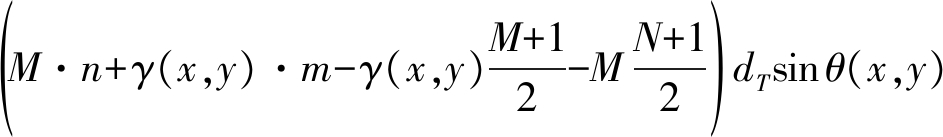
(22)
不考虑常数项的影响,可以看出此时的双基地距离和无法保证均匀采样,即此时的等效阵列无法保证均匀采样,此时相对于接收阵列中心的等效阵列形式如下图所示。
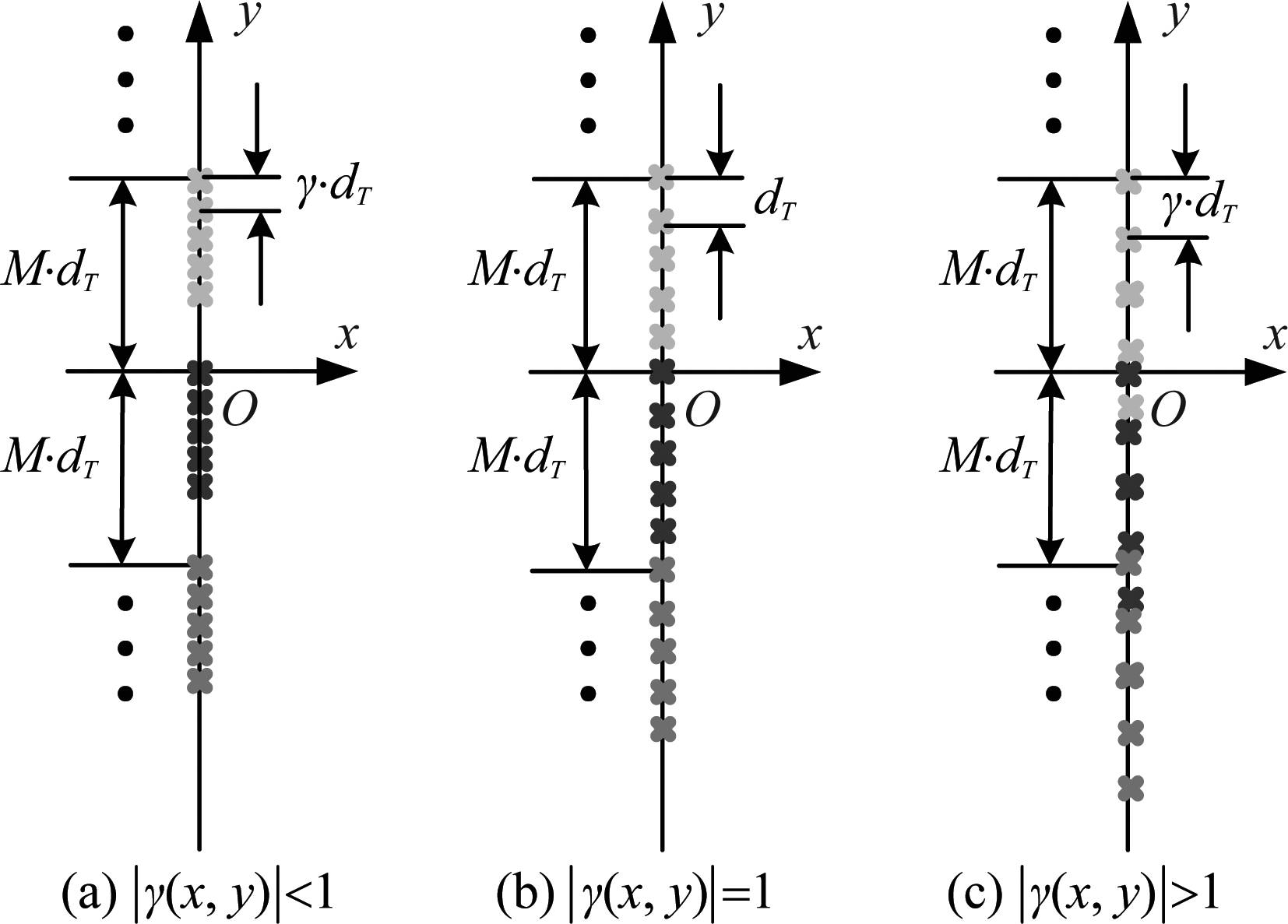
图5 不同压缩系数γ(x,y)情况下的等效阵列
Fig.5 Equivalent arrays with different γ(x,y)
上面结合等效阵列的思想对双基地MIMO阵列的等效阵列进行了定性的分析,从上面的结果不难看出,由于压缩系数γ(x,y)随目标位置具有二维空变性,并且只有极少数的目标点能使得等效阵列为均匀阵列,因此,等效阵列理论并不能用于分析双基地MIMO雷达的分辨性能。值得注意的是,由于等效阵列一般为非均匀阵列,因此双基地MIMO系统里一般会有方位向栅瓣出现。
5 双基地MIMO雷达系统的旁瓣走向及分辨特性分析
5.1 系统旁瓣走向分析
公式(15)给出了一般构型下点目标的点扩展函数表达式。下面结合上述结论对双基地MIMO雷达系统的旁瓣走向问题进行分析。从公式(15)不难看出,其中的两个周期sinc函数即为信号的合成单频方向图,主要决定方位向的成像性能;而前面的相位项主要决定距离向的成像结果。不考虑超宽带雷达系统,一般雷达系统的载频均远大于发射信号带宽,在此假设下,后面的两项周期sinc项中的频率f都可以由中心频率fc近似代替,那么上式可以近似写为
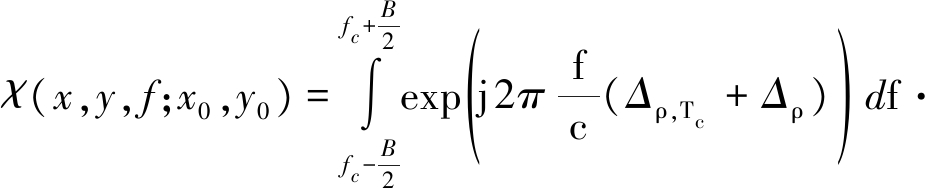
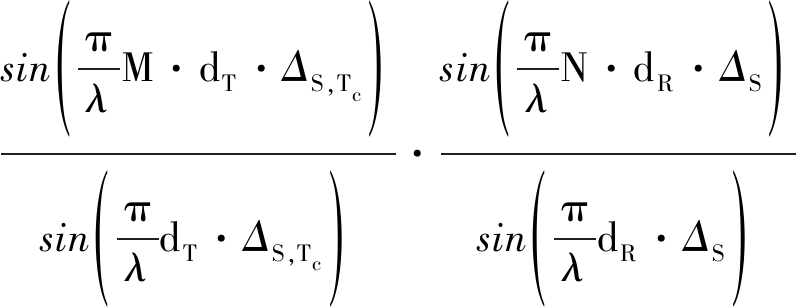
(23)
在距离向主瓣近端,上面的表达式能够较好地反应系统的成像性能,此时上面的积分项可以写为
(24)
考虑到接收机的解调,后面的相位项也可以去除,因此在主瓣近端的距离向成像结果为
(25)
根据上式可以得知,目标的距离向成像结果的近端旁瓣走向在上述sinc函数的峰值位置处
ρTc(x,y)+ρ(x,y)=ρTc(x0,y0)+ρ(x0,y0)
(26)
即广义模糊函数的方位向旁瓣沿等双基地距离和线(椭圆)上延展。
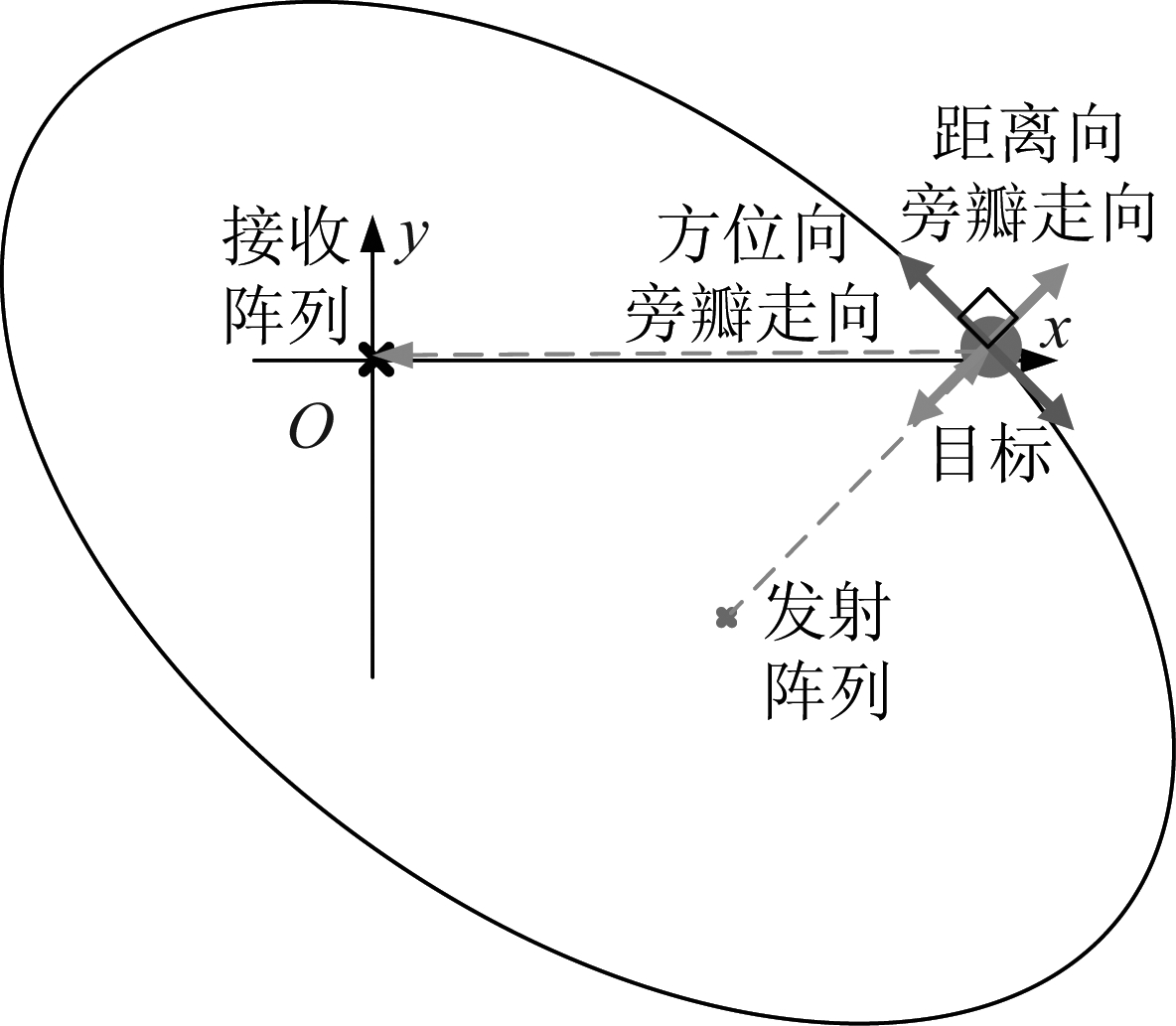
图6 双基地MIMO雷达系统方位向旁瓣走向示意图
Fig.6 Schematic diagram of azimuth side-lobe’s direction of bistatic MIMO radar system
5.2 二维分辨特性分析
下面利用空间梯度法[15-16]对双基地MIMO成像雷达的二维空间分辨率进行分析,对上式中的双基地距离和曲线在(x,y)处求梯度,得到:
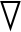
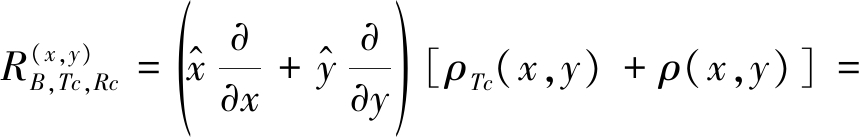
(27)
式中:
(28)
因此,该梯度的绝对值为
|
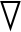
(29)
可以求得距离向(等双基地距离和曲线的法线方向)的地距分辨率为
(30)
上面给出了距离向的分辨率,而方位向的分辨率(等双基地距离和曲线的切线方向)主要由收发阵列方向图的乘积给出。对于双基地MIMO雷达系统,由于其等效阵列并非均匀线阵,此时不能直接利用等效阵列的长度进行精确求解。考虑到一般地基MIMO雷达阵列的收发阵列长度相差很大[14],因此考虑接收阵列长度远大于发射阵列长度的情况。此时较短的阵列其方位向分辨率较差可以忽略,因此较长阵列的方位分辨率是分析的重点,此时可以得知接收阵列的波束宽度为
(31)
该方位向分辨率梯度方向与其距离梯度方向垂直,即为
(32)
与此同时,等双基地距离和曲线的切线方向与该点处双基地距离和的梯度方向垂直,即
(33)
容易求得分辨率梯度方向与等双基地距离和切线方向(即方位向旁瓣走向)的夹角为
(34)
从而可以得出,方位向分辨率应为
(35)
5.3 方位向栅瓣位置分析
根据公式(10)和(12)可以知道,对于稀疏的接收阵列和密集的发射阵列而言,接收栅瓣位于:
...
(36)
即
...
(37)
同时,栅瓣位置应满足双基地距离和式,即
ρTc(xGL,yGL)+ρ(xGL,yGL)=ρTc(x0,y0)+ρ(x0,y0)
(38)
即
(39)
联立式(37)和(39)即可求得栅瓣的具体位置。
6 仿真验证
6.1 单点目标仿真
上面给出了地基双基地MIMO成像雷达的旁瓣走向及二维分辨率分析,下面通过仿真验证上述结论的正确性。假设阵列构型为收发共线阵列,收发阵元中心间距为200 m,其几何构型如图7所示,系统的参数如表1所示。
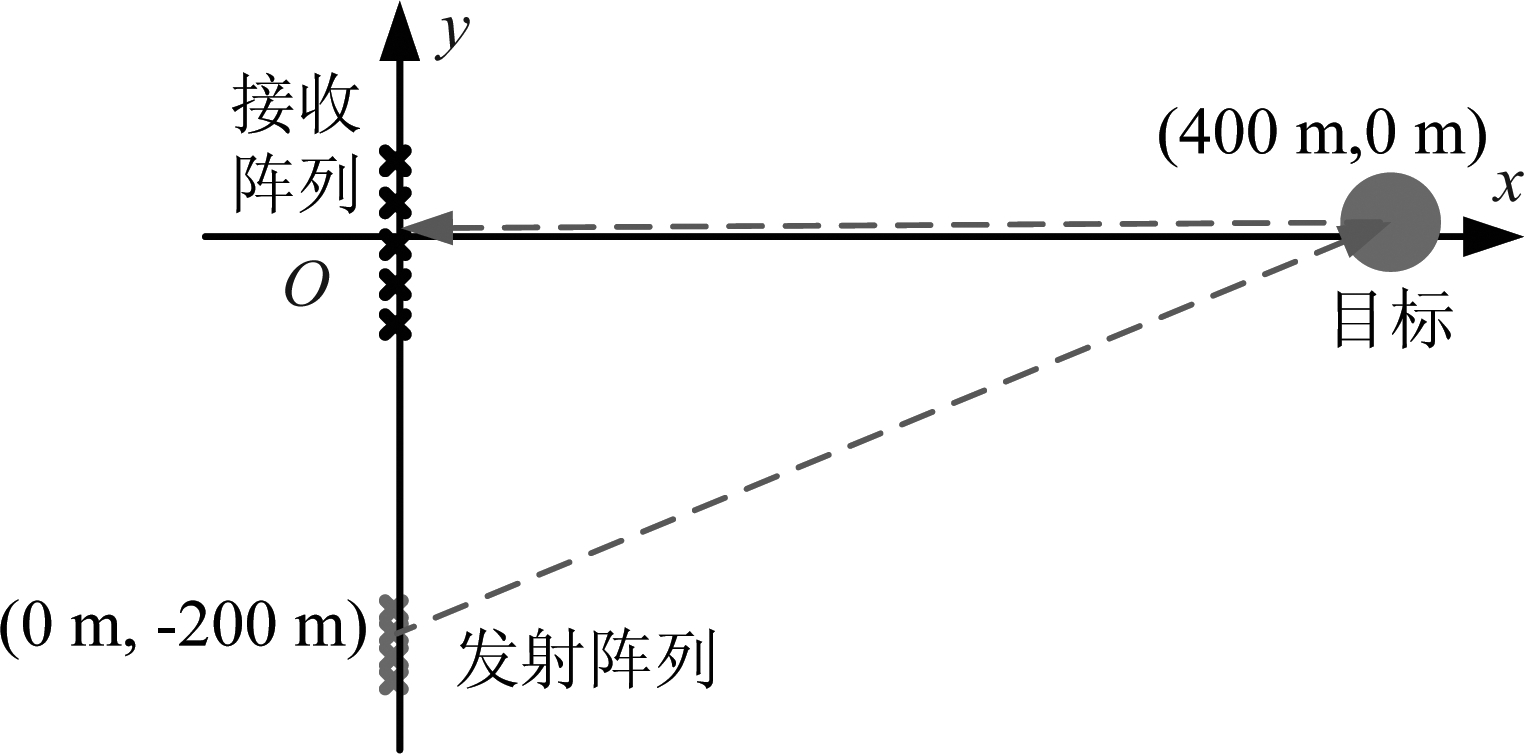
图7 仿真系统MIMO阵列构型
Fig.7 MIMO array configuration of the system for simulation
表1 仿真系统参数
Tab.1 System parameters for simulation
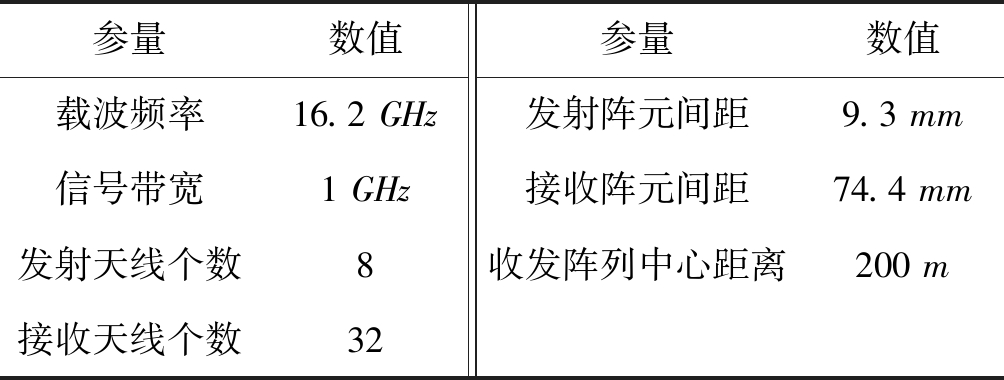
参量数值参量数值载波频率16.2 GHz发射阵元间距9.3 mm信号带宽1 GHz接收阵元间距74.4 mm发射天线个数8收发阵列中心距离200 m接收天线个数32
对上述目标点进行成像处理,可以得到其在二维空间中的成像结果如图8所示,从中能够明显看出方位向栅瓣。为了验证方位向的旁瓣走向,我们将等双基地距离和曲线上点的横纵坐标对应关系绘制如图9所示。通过图8和图9的对比可以清晰地看出,整条方位向旁瓣都是沿着椭球的边沿分布的。
图8 目标点成像结果
Fig.8 Imaging result of the point target
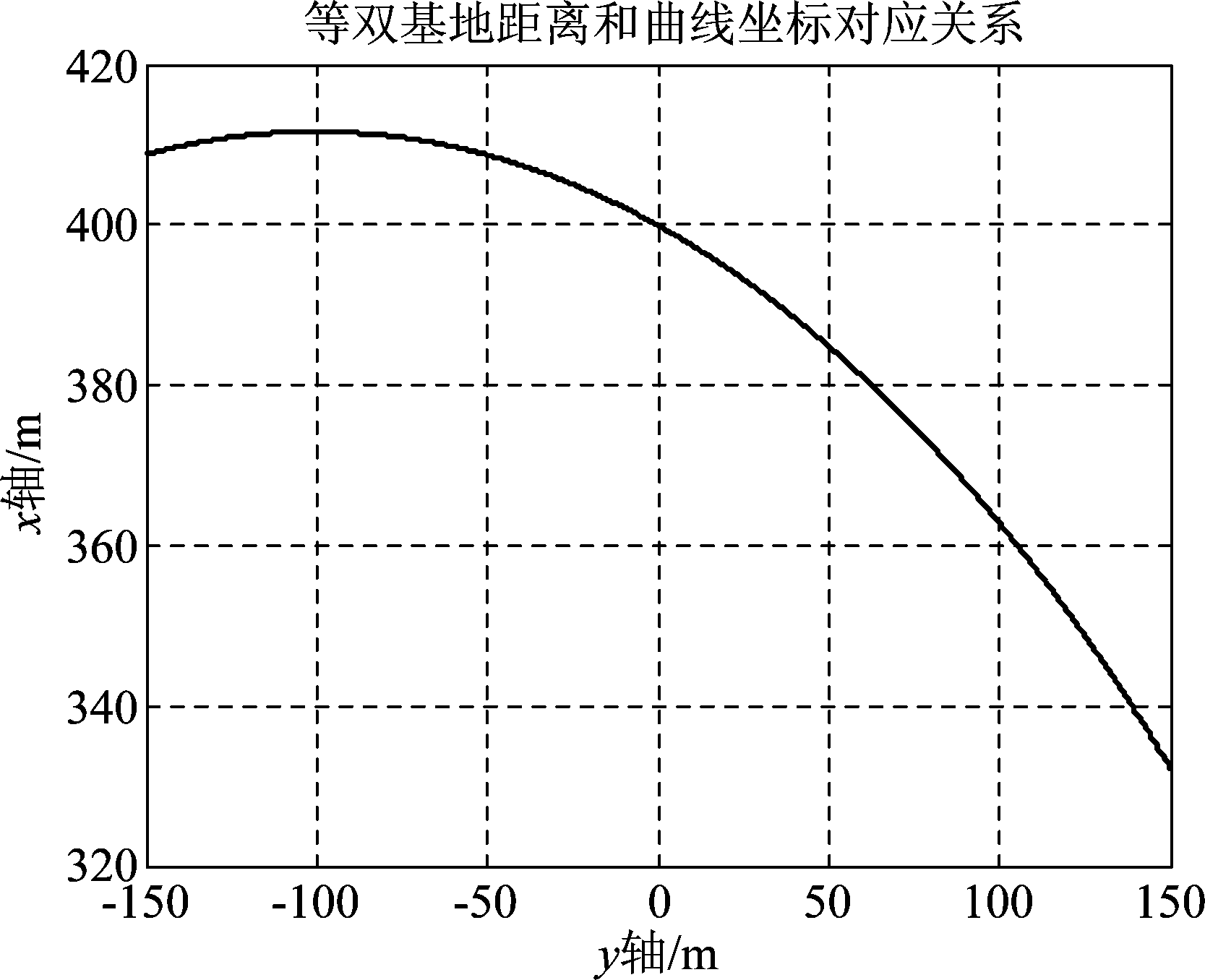
图9 等双基地距离和曲线横纵坐标对应关系
Fig.9 Correspondence between horizontal and vertical coordinates along the equi-bistatic-distant curve
虽然图8中远端距离向旁瓣的走向与公式(25)不一致,但是公式(25)能够很好地表征系统的近端距离向旁瓣走向,如图10所示。
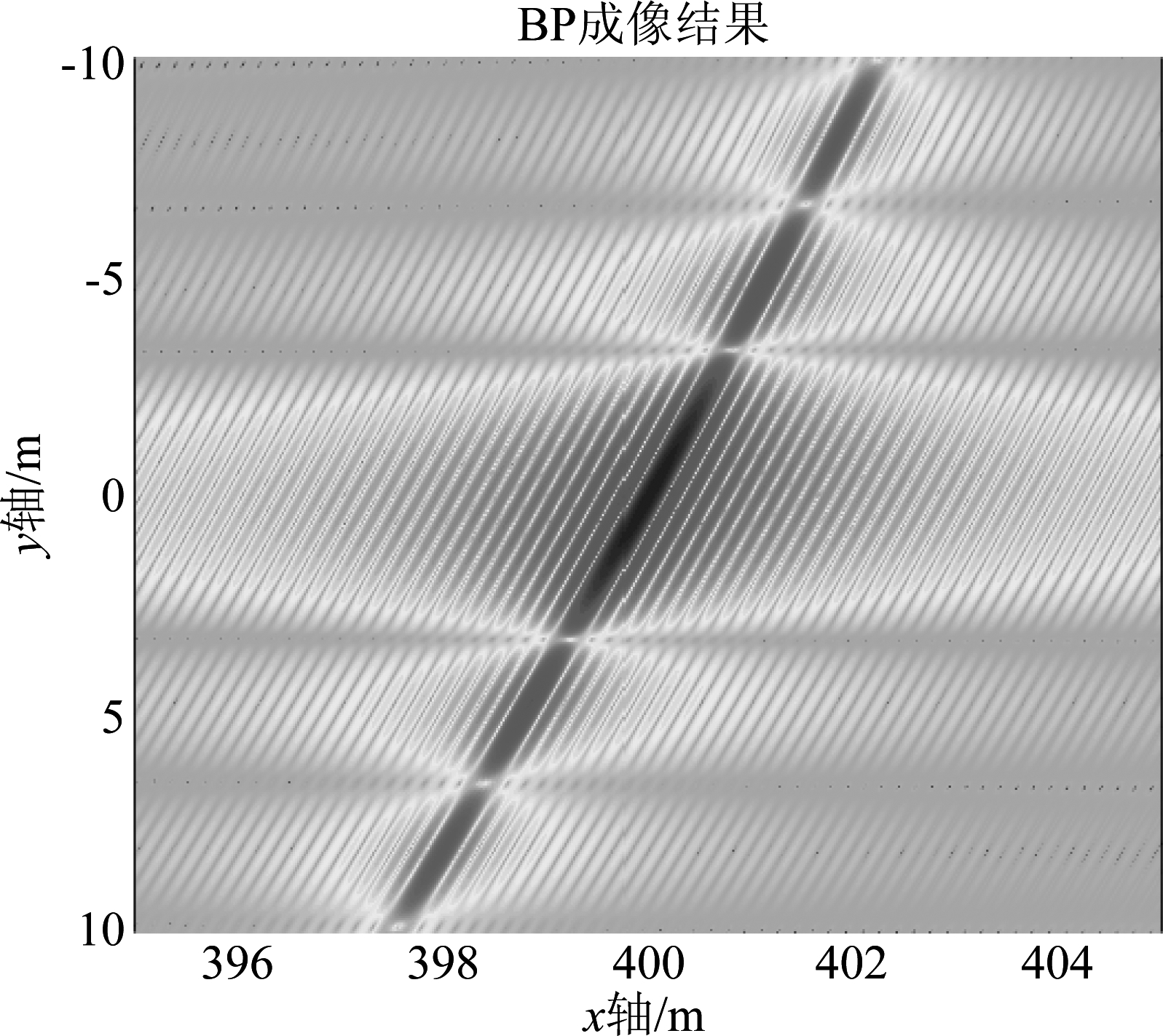
图10 目标点成像结果(局部放大图)
Fig.10 Imaging result of the point target (partial enlargement)
将图10中两个方向上的一维成像结果画出,得到图11和图12。通过数值仿真求取该目标在距离向和方位向的空间分辨率与公式(30)和公式(35)进行对比,可以得出表2所示的结果。
表2 仿真二维分辨率、栅瓣位置与理论值对比
Tab.2 Simulation two-dimensionalresolutions vs. theoretical ones
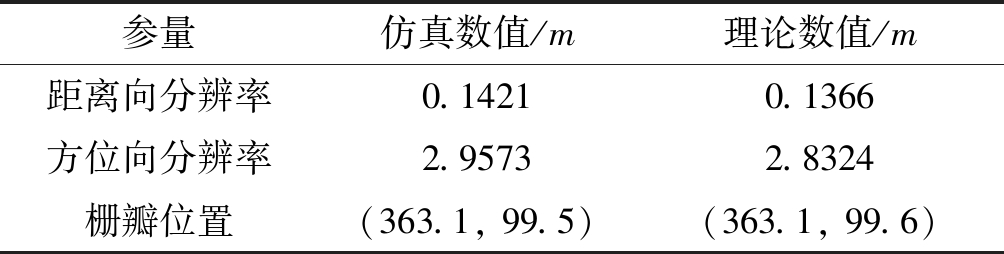
参量仿真数值/m理论数值/m距离向分辨率0.14210.1366方位向分辨率2.95732.8324栅瓣位置(363.1, 99.5)(363.1, 99.6)
如表2所示,仿真得出的二维分辨率及栅瓣位置与本文给出的结果基本一致,充分证明了本文给出的分辨率计算方法的正确性。
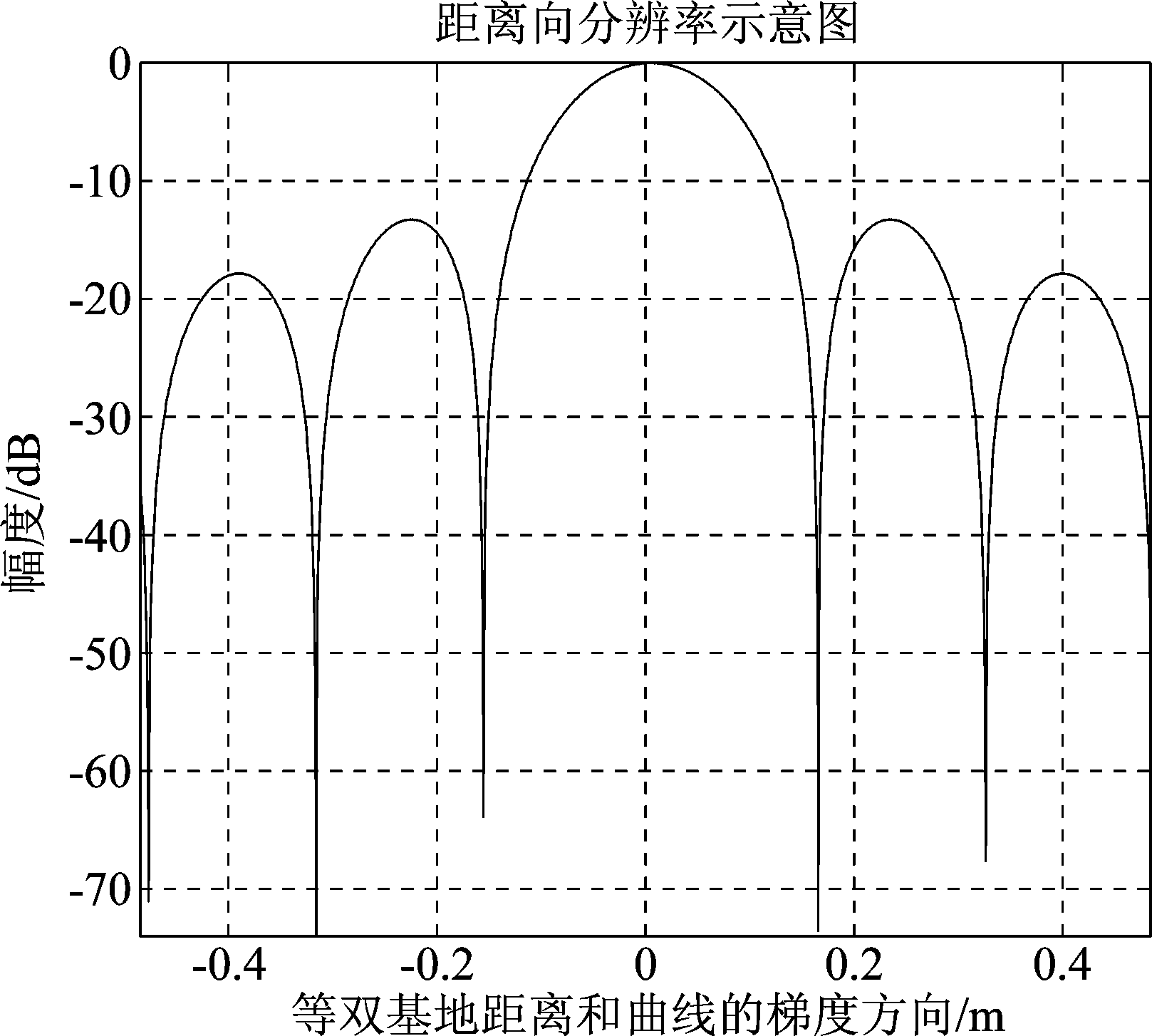
图11 距离向成像结果
Fig.11 Image in the range dimension
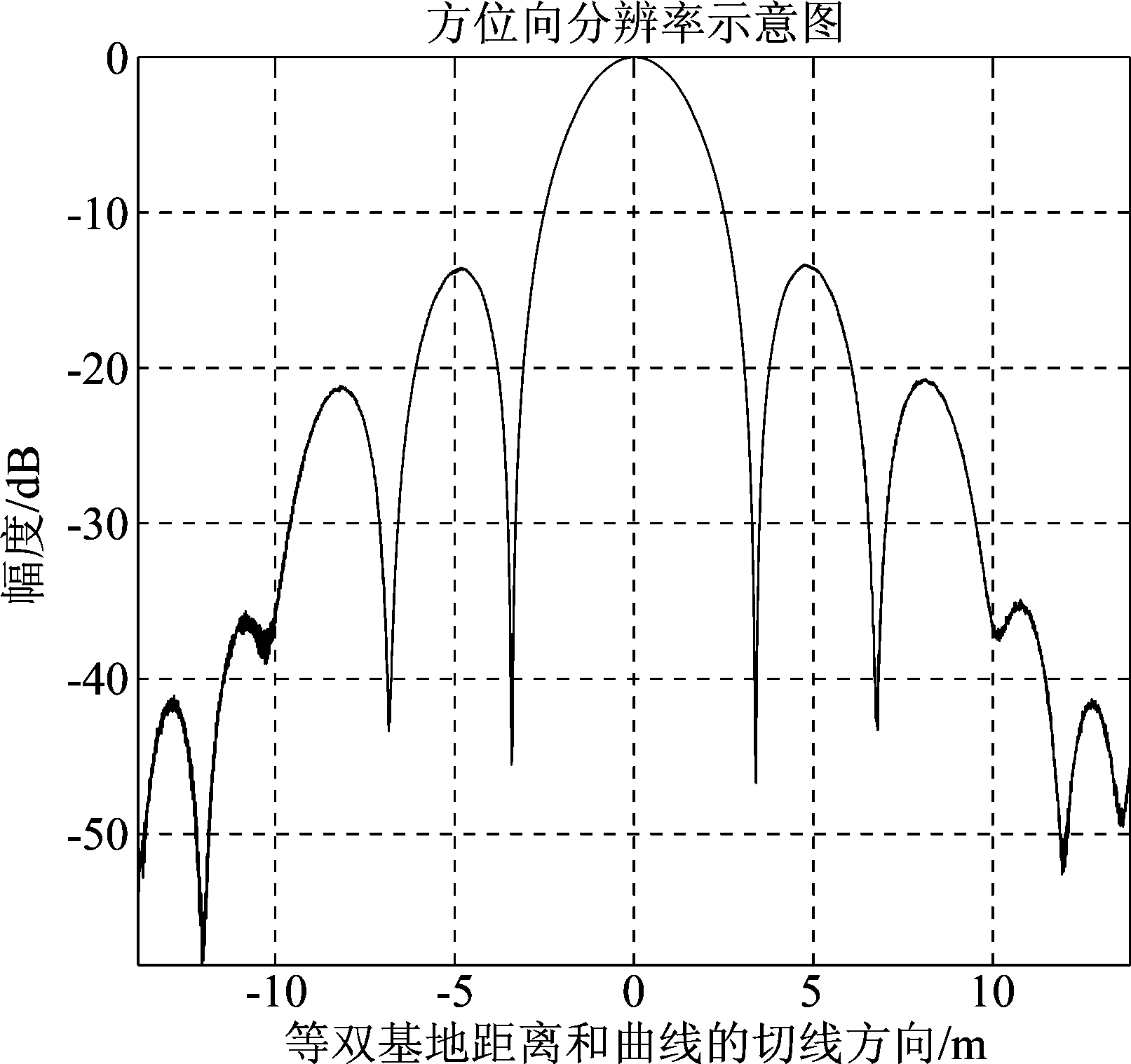
图12 方位向成像结果
Fig.12 Image in the azimuth dimension
6.2 两点目标仿真
为了验证双基地MIMO成像雷达的成像性能,下面设置两个目标点验证系统的分辨能力。考虑到当两个目标的距离刚好为分辨率时,目标的成像质量对相对距离误差十分敏感,因此将两个目标的相对距离设置为分辨率的1.1倍。首先分析方位向的分辨能力,两个目标的位置如表3所示。
表3 方位向两目标仿真参数
Tab.3 Simulation parameters of two targetssimulation in azimuth direction
目标点距离位置/m方位位置/m目标一4000目标二399.243.2192
从图13和图14可以看出,两个目标的距离为方位分辨率的1.1倍的时候即可实现目标分辨,充分证明了分析结果的正确性。图14中目标二的幅度较小是因为方位向分辨率较差,等双基地距离和曲线的切线方向无法完全取到目标二的主瓣。下面利用两点目标仿真验证距离向分辨率的分析结论,两个目标的的位置如表4所示。
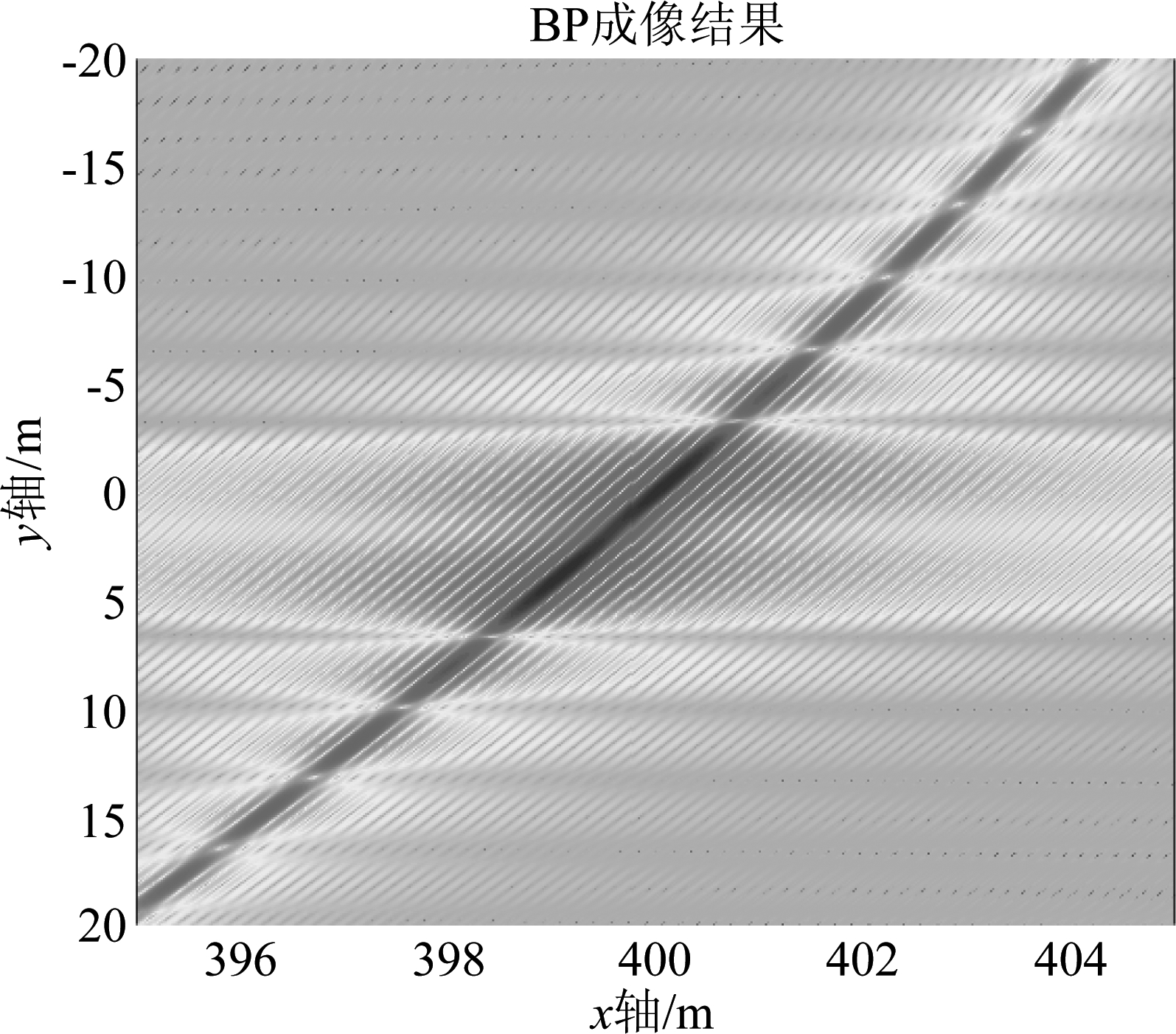
图13 方位向两目标成像结果(二维)
Fig.13 Image of two targets in azimuth direction (2D)
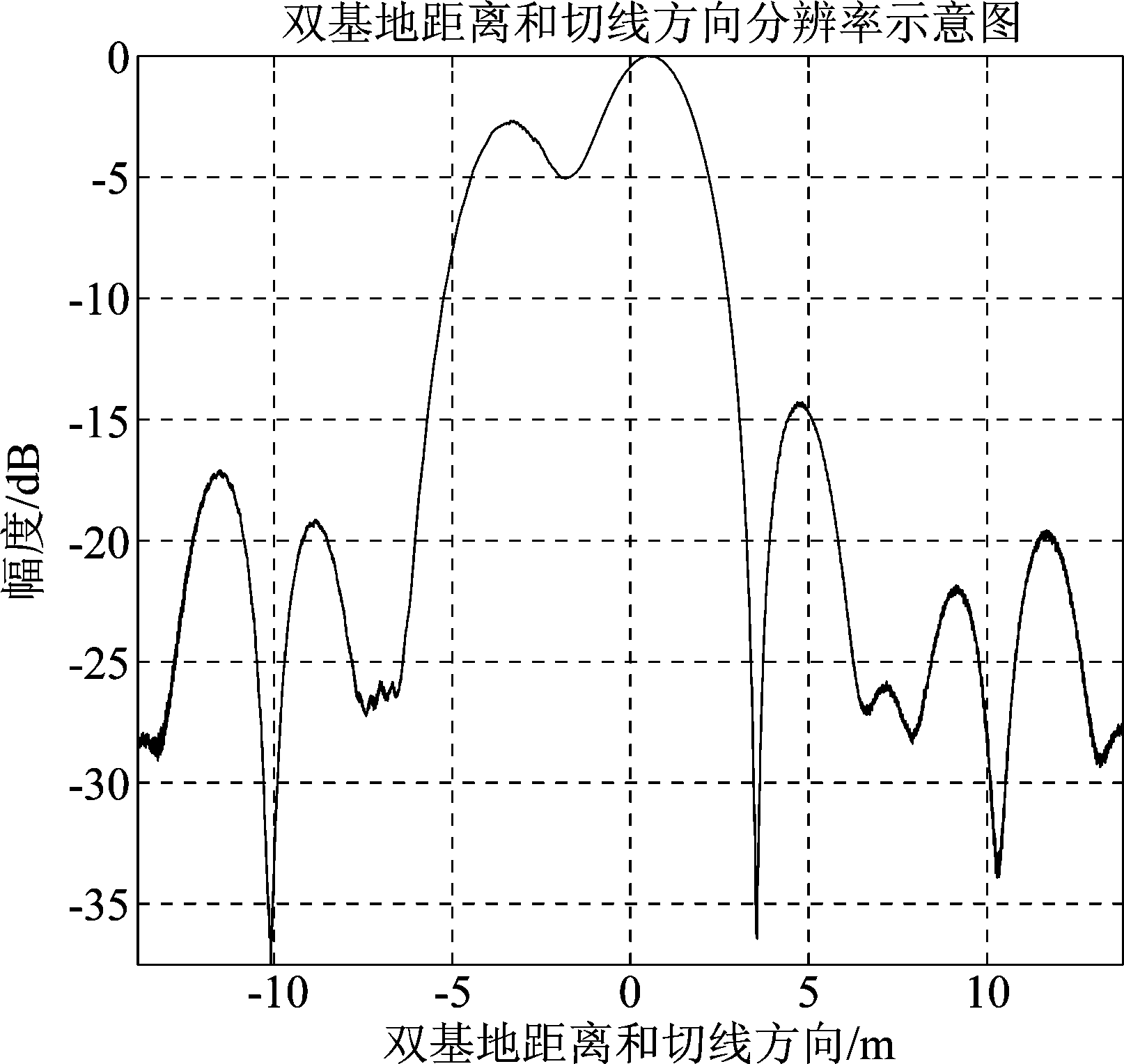
图14 方位向两目标成像结果(一维)
Fig.14 Image of two targets in azimuth direction (1D)
表4 距离向两目标仿真参数
Tab.4 Simulation parameters of two targetssimulation in range direction
目标点距离位置/m方位位置/m目标一4000目标二400.15210.0359
从图15和图16可以看出,两个目标的距离为距离分辨率的1.1倍的时候即可实现分辨。与方位向两目标的情况相比,由于分辨率较高,两个目标的强度没有明显的起伏。综上,本文分析的二维分辨率与仿真结果基本一致,充分地证明了本文结论的正确性。
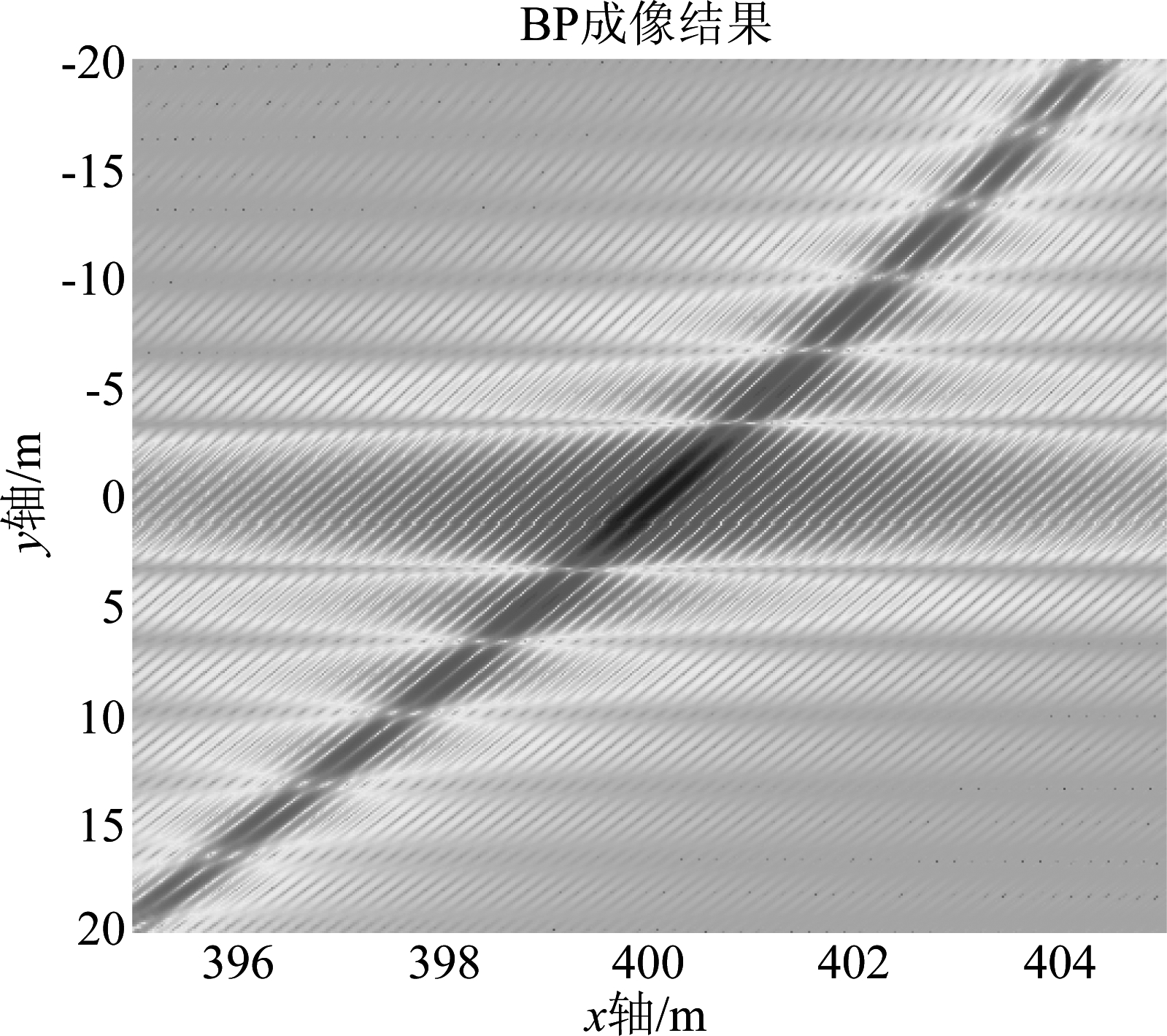
图15 距离向两目标成像结果(二维)
Fig.15 Image of two targets in range direction (2D)
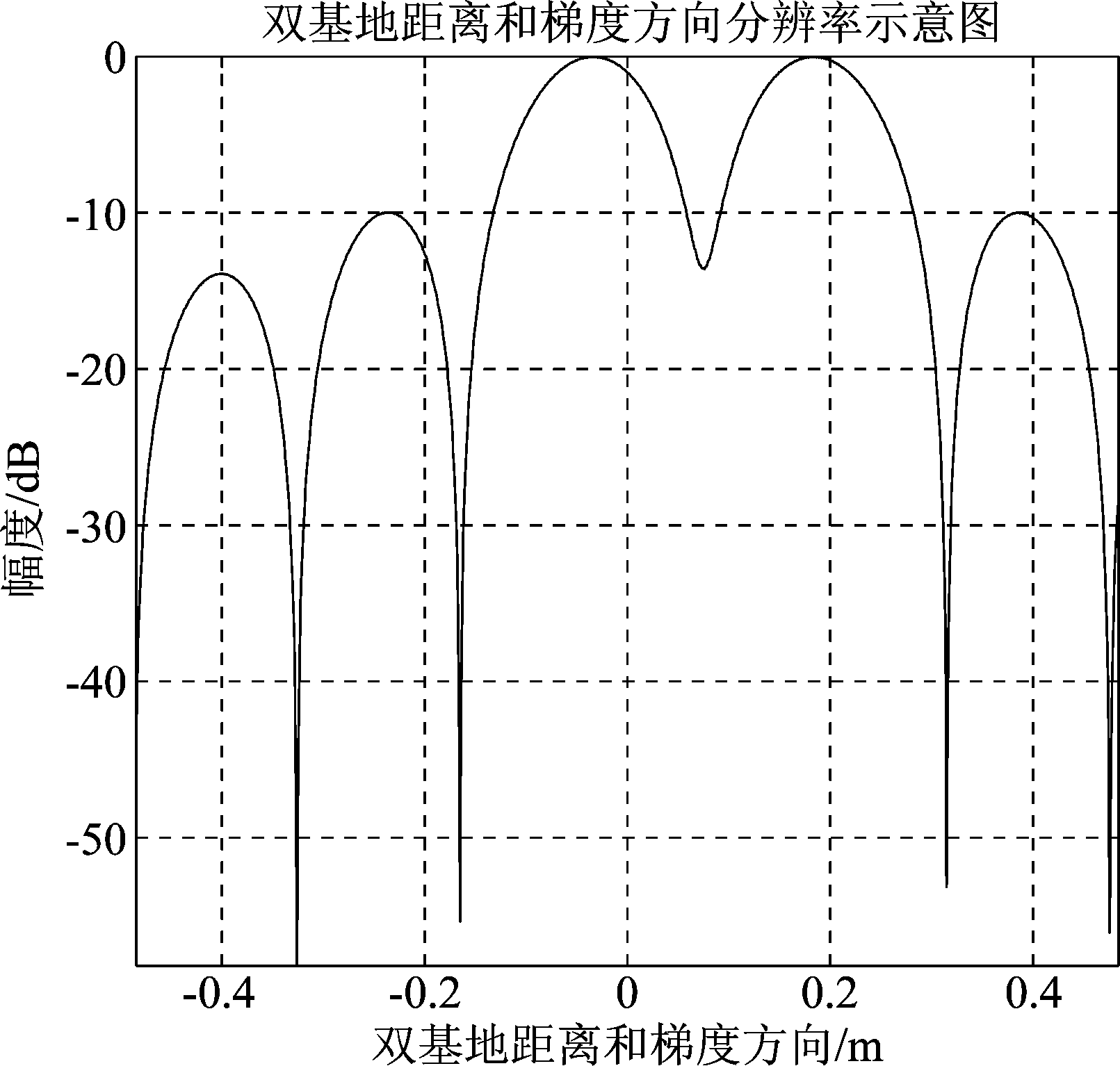
图16 距离向两目标成像结果(一维)
Fig.16 Image of two targets in range direction (1D)
7 结论
本文针对地基双基地MIMO成像雷达系统成像性能目前尚无有效分析手段的问题开展了研究,分析了地基双基地MIMO成像雷达的广义模糊函数、等效阵列特性及二维空间分辨特性。首先,结合雷达系统几何构型建立了地基双基地MIMO成像雷达的回波信号模型,并推导了该系统的广义模糊函数在二维空间域的表达式;然后,结合双基地距离和特性定性分析了双基地MIMO雷达的等效阵列,并解释了方位向栅瓣产生的原因;之后,通过对广义模糊函数进行化简分析了系统在二维空间域的旁瓣走向问题,并利用梯度法给出了距离向和方位向空间分辨率的计算方法。最后,利用Matlab仿真验证了旁瓣走向分析、栅瓣位置及二维分辨率计算方法的正确性。
[1] Fletcher A S, Robey F C. Performance bounds for adaptive coherence of sparse array radar[J]. Proceeding of the Adaptive Sensor Array Processing Workshop, 2003.
[2] 王怀军. MIMO雷达成像算法研究[D]. 长沙: 国防科学技术大学, 2010.
Wang Huaijun. MIMO radar imaging algorithms[D]. Changsha: National University of Defense Technology, 2010. (in Chinese)
[3] Gumbmann F, Schmidt L. Millimeter-Wave Imaging With Optimized Sparse Periodic Array for Short-Range Applications[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(10): 3629-3638.
[4] Hu C, Zhu M, Zeng T, et al. High-precision deformation monitoring algorithm for GBSAR system: rail determination phase error compensation[J]. Science China Information Sciences, 2016, 59(8): 082307.
[5] 王昊飞. 地基 MIMO 形变监测雷达成像与干涉测量技术研究[D]. 北京: 北京理工大学, 2016.
Wang Haofei. Research on Ground-Based MIMO Deformation Monitoring Radar Imaging and Interferometry Techniques[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese)
[6] 毛聪. 地基边坡雷达系统分析及信号处理算法研究[D]. 北京: 北京理工大学, 2016.
Mao Cong. Research on Ground Based Slope Stability Radar System and Signal Processing Algorithm[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese)
[7] Zhuge X, Yarovoy A G. A Sparse Aperture MIMO-SAR-Based UWB Imaging System for Concealed Weapon Detection[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 49(1): 509-518.
[8] Zhuge X, Yarovoy A G. Study on Two-Dimensional Sparse MIMO UWB Arrays for High Resolution Near-Field Imaging[J]. IEEE Transactions on Antennas & Propagation, 2012, 60(9): 4173- 4182.
[9] Zeng T, Mao C, Hu C, et al. Multi-static MIMO-SAR three-dimensional deformation measurement system[C]∥IEEE Asia-Pacific Conference on Synthetic Aperture Radar, 2015: 297-301.
[10] 范学祯, 刘飞峰, 张天, 等. 基于北斗导航卫星的BiSAR大场景成像[J]. 信号处理, 2017, 33(4): 546-550.
Fan Xuezhen, Liu Feifeng, Zhang Tian, et al. Large Scene Imaging of BiSAR Using BeiDou Navigation Satellite System[J]. Journal of Signal Processing, 2017, 33(4): 546-550. (in Chinese)
[11] Wei Z, Chen H, Liu Y, et al. Resolution analysis of MIMO SAR based on generalized ambiguity function[J]. Journal of National University of Defense Technology, 2013, 35(6): 77- 81.
[12] 段翔, 刘周, 刘红明, 等. 双基地MIMO雷达搜索处理方法研究[J]. 信号处理, 2013, 29(3): 319-325.
Duan Xiang, Liu Zhou, Liu Hongming, et al. Research on bistatic MIMO radar search processing method[J]. Journal of Signal Processing, 2013, 29(3): 319-325. (in Chinese)
[13] Hu C, Wang J, Tian W, et al. Generalized Ambiguity Function Properties of Ground-based Wideband MIMO Imaging Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018. (Preprint)
[14] Hu C, Wang J, Tian W, et al. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) with Non-Collinear Arrays[J]. Sensors, 2017, 17(3): 598.
[15] 黄钰林, 杨建宇, 武俊杰, 等. 机载双站SAR分辨率特性分析[J]. 电波科学学报, 2008, 23(1): 174-178.
Huang Yulin, Yang Jianyu, Wu Junjie, et al. Resolution characteristic analysis for bistatic airborne SAR[J]. Journal of Radio Science, 2008, 23(1): 174-178. (in Chinese)
[16] 蔡复青, 何友, 王捷, 等. 一种新的双基地SAR地面距离分辨率计算方法[J]. 电子与信息学报, 2008, 30(9): 2065-2068.
Cai Fuqing, He You, Wang Jie, et al. A New Approach to Bi-SAR Range Resolution in the Ground Plane[J]. Journal of Electronics & Information Technology, 2008, 30(9): 2065-2068. (in Chinese)
