1 引言
滑坡灾害是地质灾害中发生频率最高和危害最大的一种,给人类的生命和财产安全带来巨大的威胁[1]。在边坡宏观失稳之前,其表面都会先发生微小位移。因此,获取监测区域的表面形变信息,对于滑坡灾害的预测预警具有很重要的意义。近二十年来,地基SAR(Synthetic Aperture Radar,合成孔径雷达)在形变监测领域得到了广泛的应用,如对矿区边坡、陡峭山体、冰川、水电站大坝和危险建筑物等的滑坡监测[2]。作为一种高精度的形变测量仪器,地基SAR具有全天时、全天候、大范围覆盖、非接触式测量、高精度和形变测量速度快等优点。
在实际应用中,地基SAR系统的一个典型缺点是,仅能获取雷达视线方向的一维形变信息[3]。如采用地基SAR系统对矿区边坡、陡峭山体等进行形变测量时,由于不同类型的坡体会表现出不同的表面形变模式,且同一坡体的不同区域的表面形变特征也不同。仅采用一部地基SAR获取一维视线方向的形变信息,可能与监测区域的真实形变方向存在较大的偏差[4]。因此,地基SAR形变测量技术还存在较大的改进空间。如果可以获取到可能会发生滑坡区域的三维形变信息,结合相应的力学机理及地质模型,有利于进行预报预警。
在地基SAR领域,为实现三维形变信息的测量,最基本的解决方案是采用至少三部地基SAR从不同位置联合观测,并获取目标区域在不同方向上的一维形变信息,然后实现三维形变信息的解算[5]。但在地基SAR成像时,获取的是观测区域的三维地形在雷达成像平面上的投影,由于几何畸变的影响,不同观测角度下的地基SAR图像差别较大,基于常规的多项式拟合的变换方法无法实现图像配准。因此,需要提出一种新的适合多部地基SAR联合观测下的图像配准方法。
针对上述问题,本文提出了一种几何配准方案。首先获取观测场景的DEM(Digital Elevation Model,数字高程模型)信息以及各部雷达的位置信息,并将场景高程信息及各部雷达统一到同一坐标系,其次基于雷达成像的投影原理,实现各部雷达的图像中同名投影点的关联。
2 雷达图像配准
2.1 常规配准方案
在星载干涉SAR领域,由于获取两幅SAR图像的观测几何存在差异,为保证用于干涉计算的两幅图像像素对应于地面同一散射单元,需要对图像进行配准处理。一般情况下,图像配准的方案是基于某一种配准测度准则,计算两幅SAR图像在一些控制点处的匹配度量值,然后建立多项式模型来求解出其他像素点处的配准偏移量,从而实现像素级或者亚像素级的配准[6]。
(1)
式(1)为图像配准中常用的二阶多项式模型,其中,a0～a5、b0～b5为拟合参数,(x1,y1)、(x2,y2)分别为同名控制点在主辅图像中的坐标。如果可以确定多对同名控制点的坐标,则可以根据式(1)采用最小二乘法求解出拟合系数。
图1 多部雷达联合观测示意图
Fig.1 Diagram of joint measurements of multiple GB-SAR
在采用多部地基SAR联合观测进行三维形变测量时,为获取较高的三维形变测量精度,各部雷达系统的观测视角应存在较大的差异,如图1所示。但在地基SAR成像时,获取的是观测区域的三维地形在雷达成像平面上的投影[7],由于几何畸变的影响,不同观测角度下的地基SAR图像差别较大,需要分析基于常规的多项式拟合的配准方法是否依然适用。
假设有两部地基SAR系统,分别为雷达1和雷达2,在同一个参考三维直角坐标系下,雷达1的孔径中心位于坐标原点,轨道方向平行于x轴,雷达2的孔径中心的三维坐标为(xC,yC,zC),轨道方向与x-y平面内的投影分量的夹角为φ,即俯仰角,在x-y平面内的投影分量与x轴正方向的夹角为θ,即方位角。现在分别以这两部雷达为参考构建各自的雷达坐标系,坐标原点为孔径中心,x轴平行于雷达轨道方向,y轴与x轴在水平面内垂直,z轴与x轴、y轴构成右手直角坐标系。则在参考坐标系下,雷达1坐标系的坐标原点为C1(0,0,0),三个方向的单位矢量分别为
雷达2坐标系的坐标原点为C2(xC,yC,zC),单位矢量分别为
如果参考坐标系中存在一点P(xp,yp,zp),首先基于地基SAR成像的投影原理,分析该点P在这两个雷达坐标系下的投影点P1(xp1,yp1)和P2(xp2,yp2)。图2所示为地基SAR成像的几何示意图,雷达1的合成孔径方向沿x轴,孔径中心位于坐标原点,雷达1的成像平面为x-y平面。在雷达1坐标系下,投影点P1的坐标可以表示为
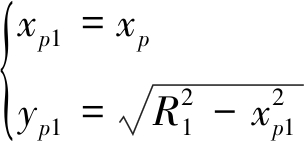
(2)
其中,xp1为投影点P1的方位向坐标,yp1为距离向坐标,
为点P到雷达1的斜距[8]。
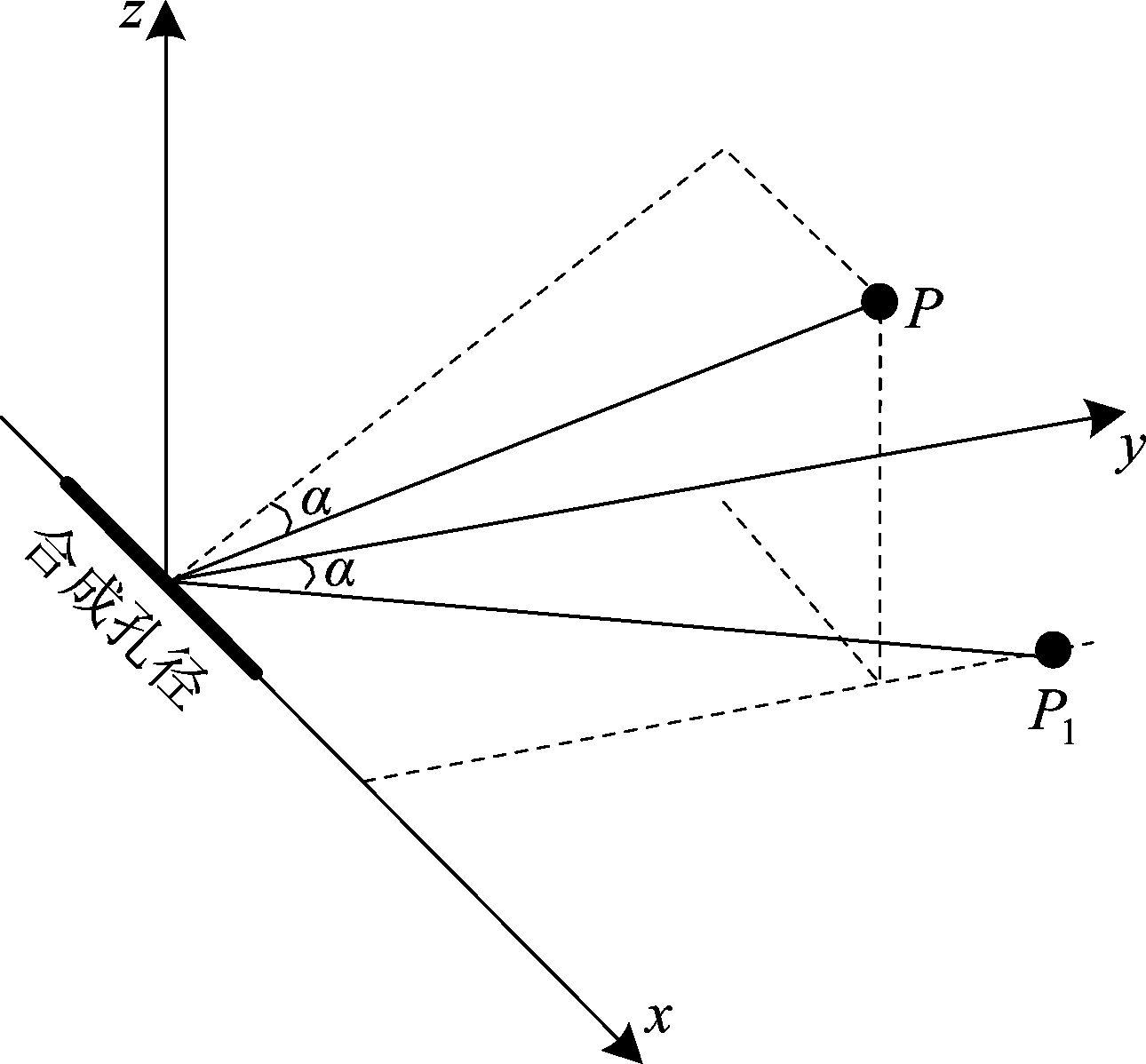
图2 地基SAR成像几何示意图
Fig.2 Diagram of GB-SAR imaging
对于点P在雷达2坐标系下的投影点P2,需要先通过坐标系变换,获取点P在雷达2坐标系下的三维坐标
然后再计算投影点P2。
两组单位矢量之间的关系可以表示为
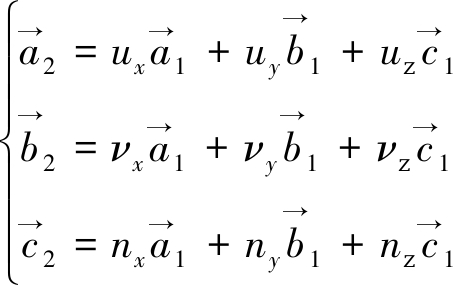
(3)
其中,ux=cos θcos φ,uy=sin θcos φ,uz=sin φ,νx=-sin θ,νy=cos θ,νz=0,nx=-cos θsin φ,ny=-sin θsin φ,nz=cos φ。
两个雷达坐标系之间的变换关系可以表示为[9]
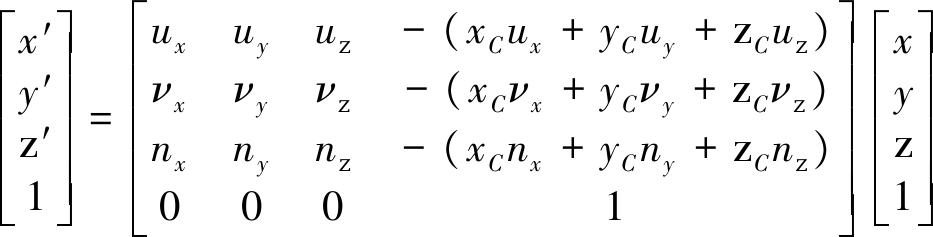
(4)
其中,(x,y,z)和(x′,y′,z′)分别为一点在两个雷达坐标系下的坐标。则点P在雷达2坐标系下的三维坐标可以表示为
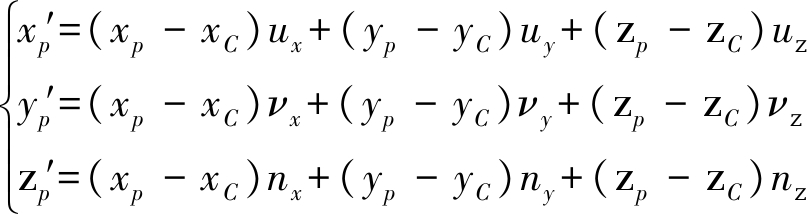
(5)
因此,在雷达2坐标系下,投影点P2的坐标可以表示为
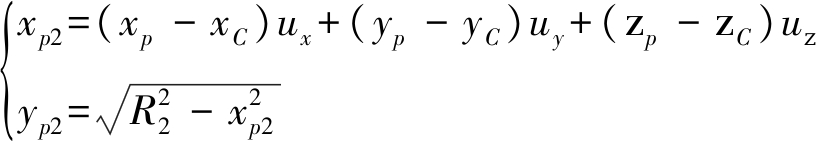
(6)
其中,xp2为投影点P2的方位向坐标,为点P到雷达2的斜距,yp2为距离向坐标。
结合式(2)和式(6),可以看出,点P在两个雷达坐标系下的投影点坐标(xp1,yp1)和(xp2,yp2)之间无法建立起式(1)所示的多项式转换关系。这也就意味着,基于常规的多项式拟合的变换方法无法实现多部地基SAR联合观测下的图像配准。
2.2 几何配准方案
为解决多部(M部)地基SAR联合观测进行三维形变测量时存在的图像配准问题,本文提出了一种几何配准的方案。关键问题包括两个:三维坐标系变换和同名像素点关联。
首先采用激光雷达获取观测场景的DEM信息,然后采用差分GPS获取各部雷达的坐标信息。由于激光雷达和差分GPS分别采用各自的坐标系,因此需要解决三维坐标系变换的问题,将场景DEM和各部雷达统一到同一坐标系下。
将场景DEM及各部雷达统一到同一坐标系后,可以基于雷达成像的投影原理,将表征DEM的每一个地形点在各部雷达的成像视角下进行投影。为实现各部雷达的图像的配准,需要研究同名像素点的关联方法。
2.2.1 三维坐标系变换
为确定两个三维直角坐标系之间的变换关系,需要已知至少三个控制点在这两个坐标系下的三维坐标[10]。在采用激光雷达获取场景DEM时,布设多个棱镜作为控制点,测量这些棱镜的三维坐标,之后采用差分GPS同样获取这些棱镜的三维坐标。
假设一个控制点在两个三维直角坐标系下的坐标分别为(xs,ys,zs)T和(xt,yt,zt)T,可以建立如下变换关系:
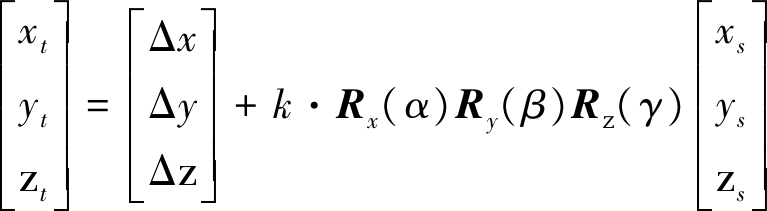
(7)
其中,(Δx,Δy,Δz)T 为两个坐标系之间的平移参数,k为尺度因子,α、β和γ为三个旋转参数,Rx(α)、Ry(β)和Rz(γ)为三个旋转矩阵,且
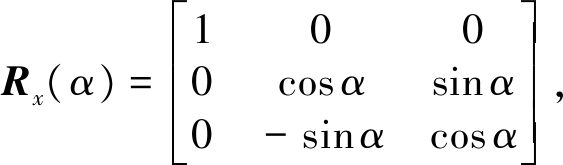
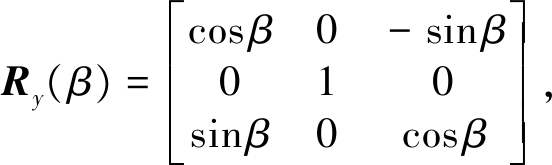
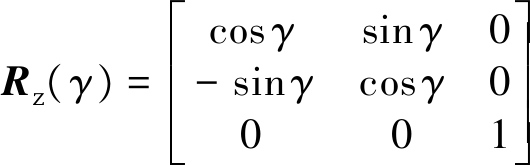
建立误差方程V=f(X)-L,其中X为需要估计的参数向量,L=(xt,yt,zt)T为观测向量, f(X)为由未知参数X组成的非线性函数。
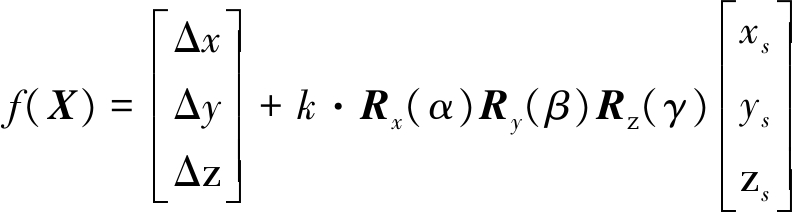
(8)
通过求解误差方程V的非线性最小二乘估计量
即可以确定两个三维直角坐标系之间的变换关系。
2.2.2 同名投影点关联
在将场景DEM及各部雷达统一到同一坐标系后,可以获取到各部雷达的孔径中心坐标(xC,yC,zC)及轨道角度信息(θ,φ),根据式(5)和式(6)可以计算出场景DEM中任一地形点P(xp,yp,zp)在各部雷达坐标系下的投影点
...,M,M表示雷达数量。
由于雷达成像结果中部分像素点对应的是非有效回波区域,可以先对雷达图像中的所有像素点进行筛选,如利用多幅雷达图像,可以基于幅度离差法选择出一些幅度高度稳定的像素点[11],定义为像素点子集Si,i=1,2,...,M。每个子集Si中的像素点表示为Kn,i,n=1,2,...,Ni,Ni为第i个子集中的像素点数量。
对于地形点P在i部雷达的成像视角下的投影点
需要判断其是否可以与子集Si中的某一个像素点Kn,i(xn,i,yn,i)关联起来。一个简单的判断准则如下,
(9)
其中,Δx和Δy分别表示各部雷达成像时的x方向和y方向的取样间隔。
如果一个地形点P在各部雷达成像几何下的投影点
均可以与各部雷达的像素点子集Si中的一个像素点Kn,i关联起来,则借助于雷达成像的几何关系,实现了各部雷达的图像中同名像素点的关联。
3 雷达图像配准
为验证本文提出的方法的有效性,基于北京理工大学自主研发的两部SAR系统,对河北省迁安市马兰庄的一处露天铁矿进行了监测。图3(a)所示为监测场景的照片,红色和绿色五角星分别代表两部雷达的摆放位置。图3(b)所示为采用激光扫描仪获取的雷达监测区域的DEM结果,方位向和距离向上采样间隔均为1 m。该矿坑具有典型的边坡结构,矿坑直径约500 m,矿坑周围存在山体,符合大场景成像的需求。
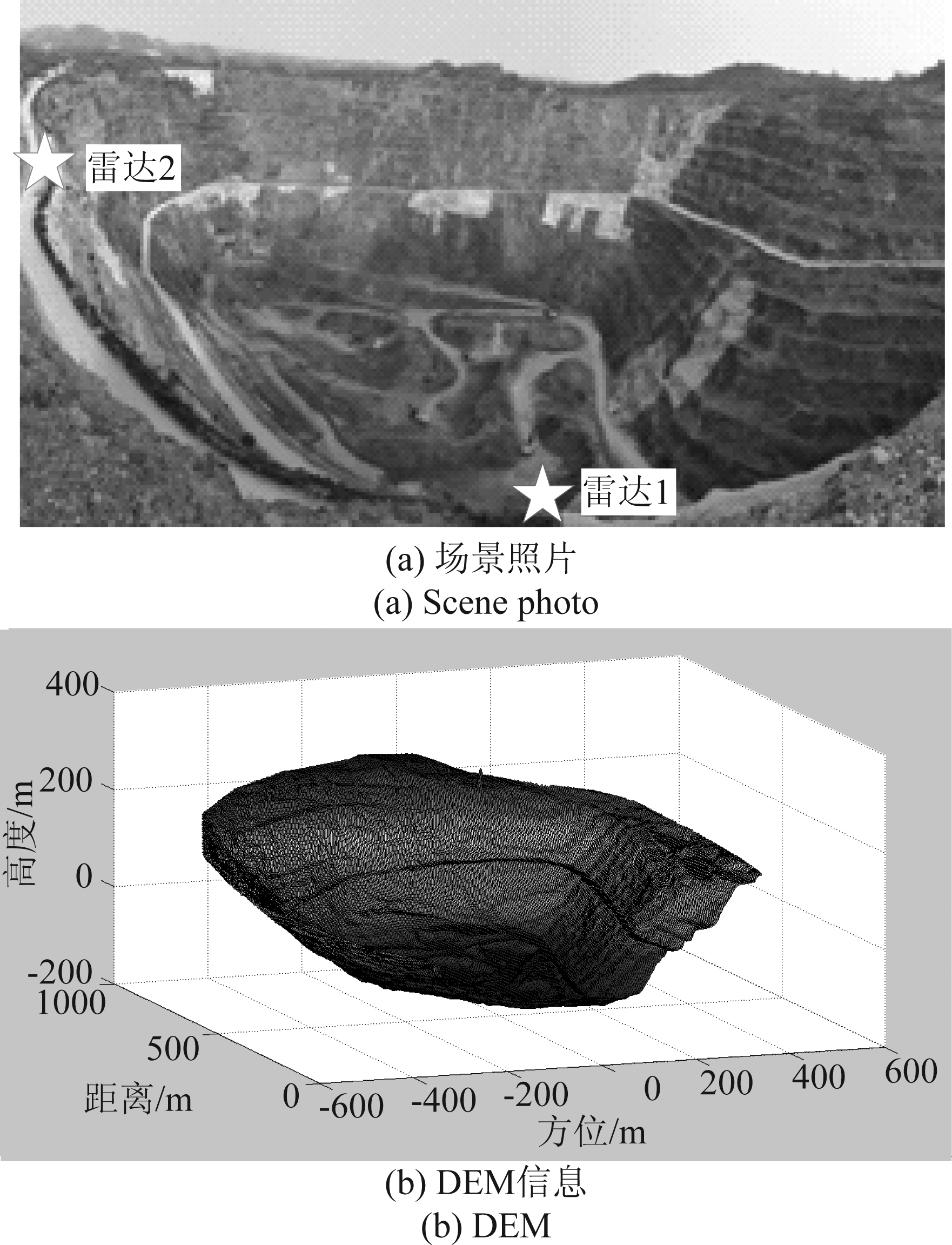
图3 露天矿坑
Fig.3 Open-pit mine
图4 雷达照片
Fig.4 Photos of the radar systems
雷达1为一部轨道SAR,基于天线沿着高精密滑轨的机械移动来形成合成孔径,如图4(a)所示[12]。雷达2为一部MIMO-SAR(Multiple-Input Multiple-Output SAR),采用多输入多输出技术,通过多个发射天线和接收天线的特殊排列来等效成一个大的合成孔径,可以视为一种特殊工作体制的地基SAR,如图4(b)所示[13]。
表1所示为两部雷达系统的参数,除了雷达1的合成孔径长度为1.2 m,雷达2的合成孔径长度为1.138 m,以及相应的方位角分辨率有所不同外,其他参数均相同。相比于轨道SAR,MIMO-SAR的优势在于不需要采用高精密滑轨来实现合成孔径,可以避免天线在滑轨上运动时,由于天线的振动所带来的轨道相位误差。
表1 雷达系统参数
Tab.1 System parameters
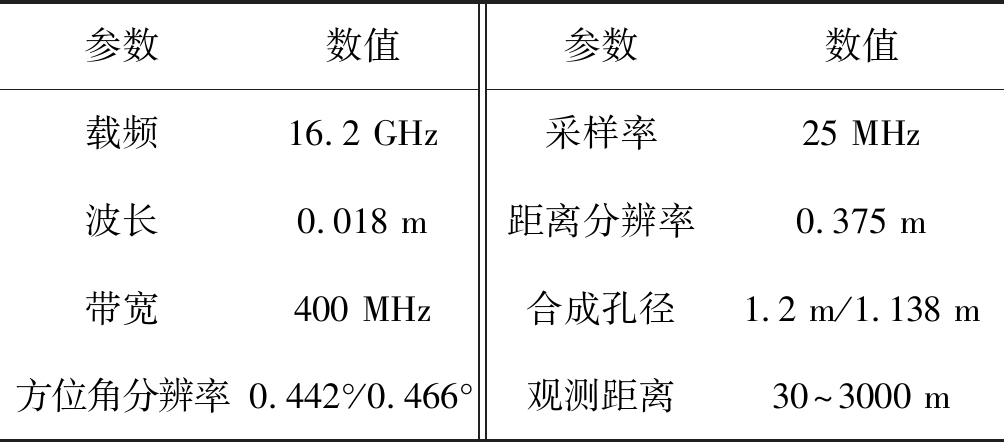
参数数值参数数值载频16.2 GHz采样率25 MHz波长0.018 m距离分辨率0.375 m带宽400 MHz合成孔径1.2 m/1.138 m方位角分辨率0.442° /0.466°观测距离30～3000 m
基于上述两部雷达系统,在2017年12月8日,对马兰庄矿坑进行了持续一小时的同步监测,分别获取了30幅雷达图像。在图像获取前,采用激光扫描仪获取观测场景的DEM信息,然后在其扫描范围内布设4个棱镜,并获取这4个棱镜在激光扫描仪坐标系下的三维坐标,之后再采用差分GPS对这4个棱镜及两部雷达进行三维坐标的测量。以这4个棱镜为控制点, 基于2.2.1小节的三维坐标变换方法,获取将差分GPS坐标系转换到激光扫描仪坐标系的转换矩阵,则可以计算出两部雷达在激光扫描仪坐标系下的位置信息和角度信息。计算可得,雷达1孔径中心三维坐标为(0.18 m,2.21 m,-0.27 m),方位角和俯仰角分别为θ1=0°和φ1=1.621°,雷达2孔径中心三维坐标为(-346.73 m,88.45 m,31.2 m),方位角和俯仰角分别为θ2=23.10°和φ2=-3.71°。
图5(a)和5(b)所示分别为这两部雷达的成像结果(dB图),由于两部雷达的观测视角差别较大,成像结果的几何特征很明显存在差别。在成像时,方位向及距离向的采样间隔均为1 m,即图像中像素点的大小为1 m×1 m。
图5 成像结果
Fig.5 SAR imaging results
由于雷达成像结果中部分像素点对应的是非有效回波区域,尤其是对幅值很弱的像素点。基于幅度离差法,对这两部雷达的30幅图像分别进行了永久散射体的选择,选择门限设置为0.25。图6(a)和图6(b)所示分别为基于雷达1和雷达2的30幅图像选择出的永久散射体,对应的即为小节2.2.2中的像素点子集S1和S2。
基于小节2.2.2中的同名投影点关联方法即可以实现对这两部雷达的图像配准,图7所示为雷达图像配准结果。图中,红色的地形点表示其在两部雷达的观测视角下均为永久散射体,蓝色的地形点仅在雷达1的观测视角下为永久散射体,黄色的地形点则仅在雷达2的观测视角下为永久散射体。
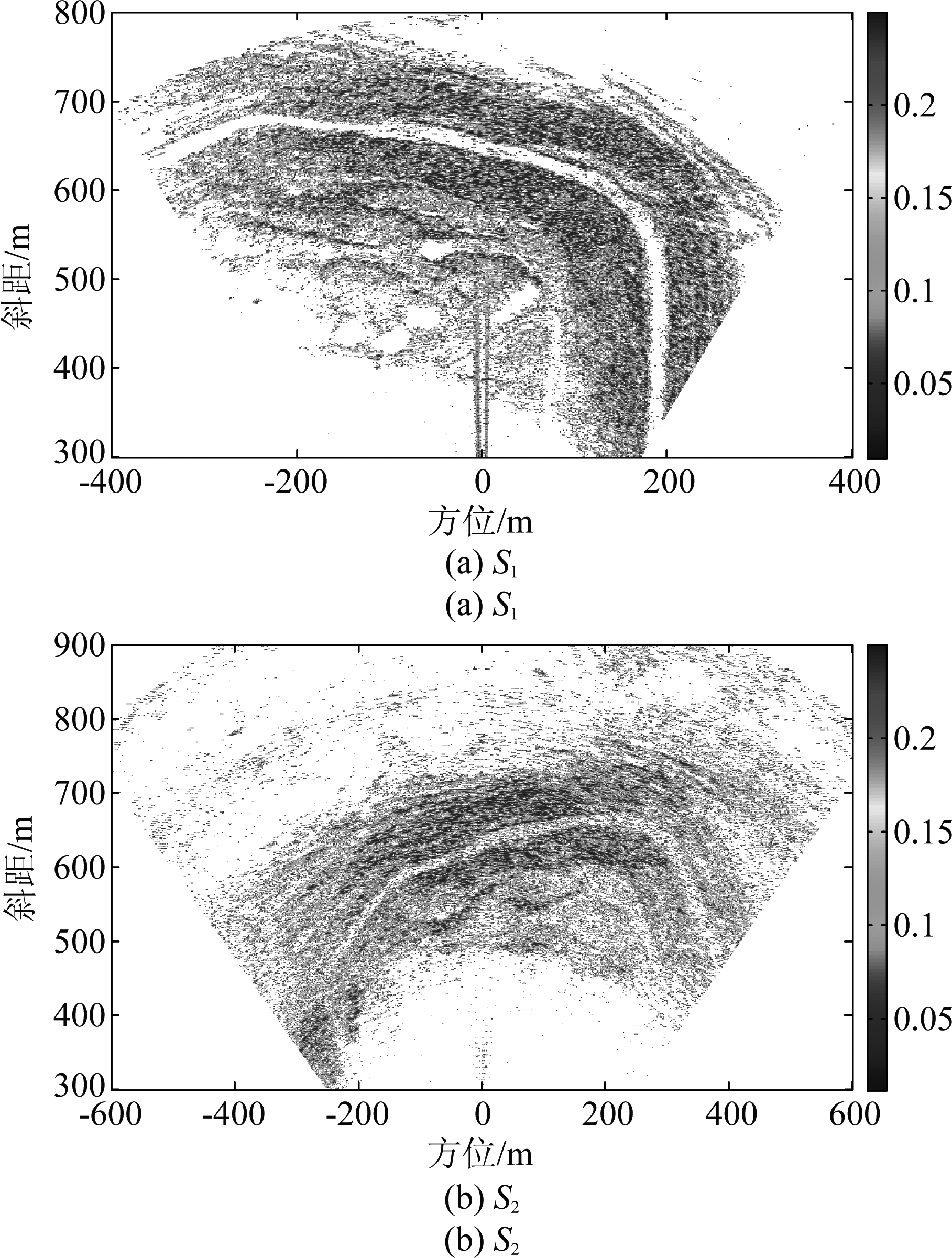
图6 像素点子集
Fig.6 Pixel subsets
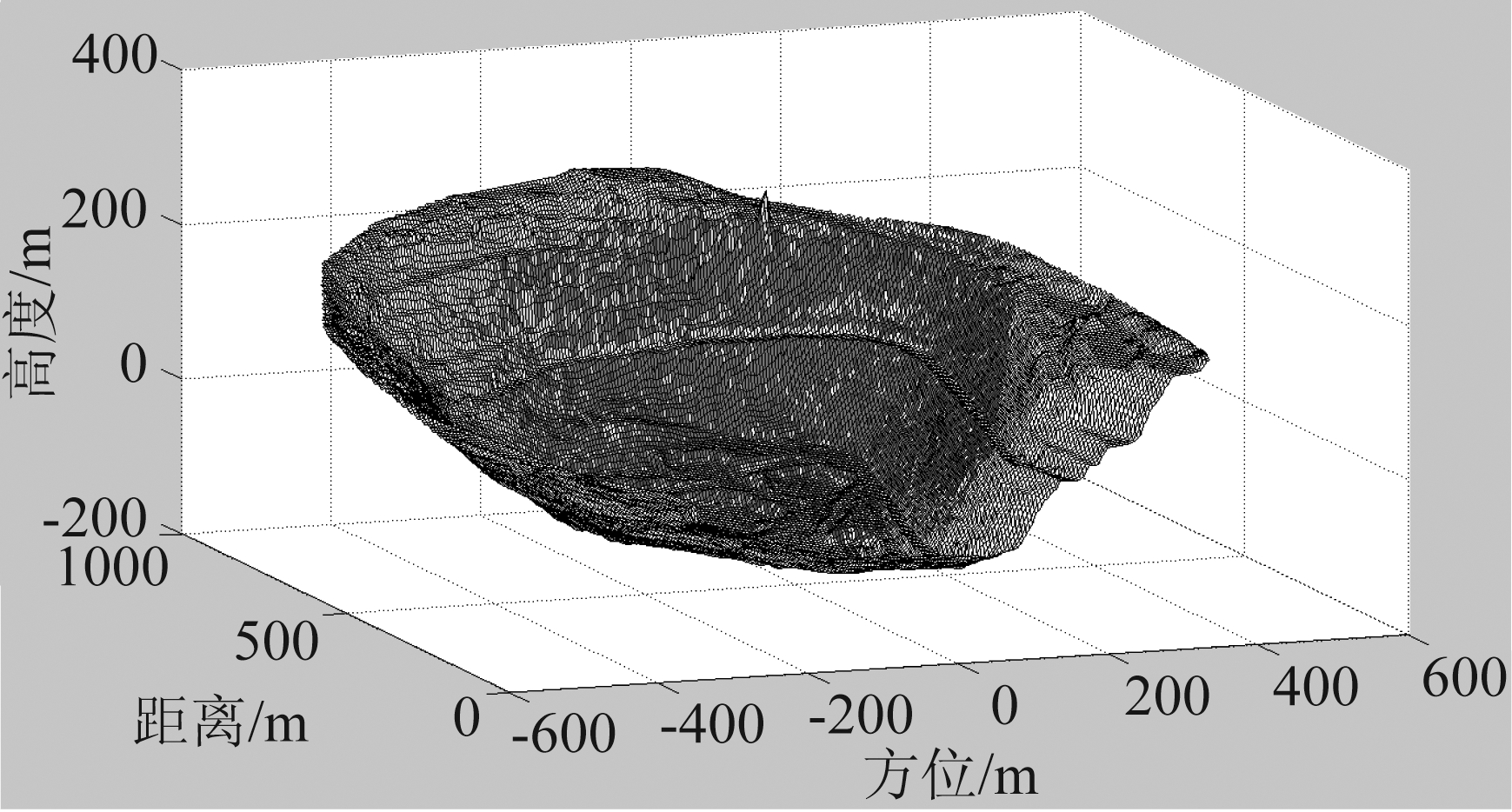
图7 雷达图像配准结果
Fig.7 Image registration result
4 结论
本文提出了一种新的适合多部地基SAR联合观测下的几何配准方案。通过一部轨道地基SAR和一部MIMO-SAR对一个露天矿坑从不同的位置进行了观测,首先基于多个棱镜实现了三维坐标系的变换,将两部雷达与场景地形信息统一到同一坐标系下,其次基于永久散射体方法分别选择出了两部雷达的图像中的像素点子集,并基于本文提出的同名投影点关联方法,实现了两部雷达的图像配准。文章基于实测数据初步验证了该方法的可行性,但还存在一些不足,如需要在观测场景中布设多个参考点验证配准精度、需要验证基于该配准方法实现多部雷达联合观测时三维形变测量的准确性等。
[1] 刘传正. 中国崩塌滑坡泥石流灾害成因类型[J]. 地质评论, 2014, 60(4): 858- 868.
Liu Chuanzheng. Genetic Types of Landslide and Debris Flow Disasters in China[J]. Geological Review, 2014, 60(4): 858-868. (in Chinese)
[2] 刘斌, 葛大庆, 李曼, 等. 地基合成孔径雷达干涉测量技术及其应用[J]. 国土资源遥感, 2017, 29(1): 1- 6.
Liu Bin, Ge Daqing, Li Man, et al. Ground-Based Synthetic Aperture Radar and Its Applications[J]. Remote Sensing for Land and Resources, 2017, 29(1): 1- 6. (in Chinese)
[3] 朱茂. 基于动态PS的地基合成孔径雷达高精度形变测量技术研究[D]. 北京: 北京理工大学, 2016.
Zhu Mao.High Precision Deformation Measurement Using Ground-Based Synthetic Aperture Radar (GBSAR) Based on Dynamic Persistent Scatter (PS) Technique[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese)
[4] 杨光华, 钟志辉, 张玉成, 等. 滑坡灾害的机制与力学特性分析[J].岩石力学与工程学报, 2016, 35(2): 4009- 4017.
Yang Guanghua, Zhong Zhihui, Zhang Yucheng, et al. Analysis of Mechanism and Mechanical Characteristics of Landslide Disaster[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(2): 4009- 4017. (in Chinese)
[5] Zeng Tao, Mao Cong, Hu Cheng, et al. Multi-static MIMO-SAR Three Dimensional Deformation Measurement System[C]∥Synthetic Aperture Radar. IEEE, 2015: 297-301.
[6] 罗小军, 刘国祥, 黄丁发, 等. 几种卫星合成孔径雷达影像配准算法的比较研究[J].测绘科学, 2006, 1: 19-21.
Luo Xiaojun, Liu Guoxiang, Huang Dingfa, et al. Comparison of algorithms for co-registration of satellite synthetic aperture radar images[J]. Science of Surveying and Mapping, 2006, 1: 19-21. (in Chinese)
[7] 毛聪, 胡程, 曾涛, 等. 地基SAR子图相干合成快速成像算法[J]. 信号处理, 2015, 31(11): 1396-1403.
Mao Cong, Hu Cheng, Zeng Tao, et al. Ground-Based SAR Fast Imaging Algorithm Based on Sub-Image Combination[J]. Journal of Signal Processing, 2015, 31(11): 1396-1403. (in Chinese)
[8] 邹进贵, 田径, 陈艳华, 等. 地基SAR与三维激光扫描数据融合方法研究[J]. 测绘地理信息, 2015, 3: 26-30.
Zou Jingui, Tian Jing, Chen Yanhua, et al. Research on Data Fusion Method of Ground-Based SAR and 3-D Laser Scanning[J]. Journal of Geomatics, 2015, 3: 26-30. (in Chinese)
[9] 吕志鹏, 伍吉仓.三维坐标变换算法的比较[J]. 大地测量与地球动力学, 2016, 36(1): 35-39.
Lv Zhipeng, Wu Jicang. Comparison of Three-Dimensional Coordinate Transformation Algorithm[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 35-39. (in Chinese)
[10] 包欢, 付子傲, 陈刚, 等.基于非线性平差模型的坐标转换公式[J]. 测绘学院学报, 2004, 3: 175-177.
Bao Huan, Fu Zi’ao, Chen Gang, et al. Formula of Coordinate System Transformation Based on Nonlinear Adjustment Method[J]. Journal of Institute of Surveying and Mapping, 2004, 3: 175-177. (in Chinese)
[11] 周伟, 黄其欢, 张顺迎. 基于PS方法的地基SAR在大坝变形监测中的应用[J]. 勘察科学技术, 2016, 1: 18-22.
Zhou Wei, Huang Qihuan, Zhang Shunying. Application of Ground-Based SAR in Dam Deformation Monitoring Based on PS Method[J]. Site Investigation Science and Technology, 2016, 1: 18-22. (in Chinese)
[12] Hu Cheng, Zhu Mao, Zeng Tao, et al. High-precision Deformation Monitoring Algorithm for GBSAR System: Rail Determination Phase Error Compensation[J]. Science China Information Sciences, 2016, 59(8): 082307.
[13] Hu Cheng, Wang Jingyang, Tian Weiming, et al. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO-SAR) with Non-Collinear Arrays[J]. Sensors, 2017, 17: 1-19.
[14] 杨俊, 乞耀龙, 谭维贤, 等. 地基SAR图像与地形数据的几何映射三维匹配方法[J]. 中国科学院大学学报, 2015, 3: 422- 427.
Yang Jun, Qi Yaolong, Tan Weixian, et al. Three-Dimensional Matching Algorithm for Geometric Mapping between GB-SAR Image and Terrain Data[J]. Journal of University of Chinese Academy of Sciences, 2015, 3: 422- 427. (in Chinese)
