1 引言
随着定位技术的飞速发展，基于位置的服务(Location Based Service，LBS)应运而生，受到人们越来越多的关注。在生活中，LBS为人们的生活提供越来越多的便捷服务，例如外出旅游时，LBS可以在当时的位置提供餐饮、娱乐等信息查询服务，在发生事故时可以更快地提供应急救援服务和人员位置跟踪，但是LBS对位置精度要求很高[1]。在室外环境中，通常采用全球定位系统(Global Positioning System，GPS)，但是当卫星信号进入室内后，由于障碍物(如墙壁和橱柜等)的阻挡，信号变弱，导致定位误差较大，不能满足室内环境对定位的需求，因此需要采用其他技术对室内环境进行定位[2]。影响室内无线定位的主要因素有两个：信号的非视距传播和多路径传播[3]，为解决这两个问题，常利用TOA、信号到达时间差(Time Difference of Arrival，TDOA)、DOA和RSS等定位参数来进行室内环境下的定位分析。在利用TOA进行定位估计时，它能在视距情况下取得一个较高的精度，但是在NLOS环境中其定位精度下降严重。为此，在[4]中首先利用基于随机特征的粗NLOS检测方案，再使用迭代最小残差的方法来减轻NLOS的影响，但其定位精度十分依赖于随机特征检测方案；在室内定位中常常利用RSS，因其具有低成本，易获取的特性，但其定位精度十分依赖于路径损耗预测模型，在[5]中，使用Bluetooth LE技术时提高RSS的计算值准确度，是一种高精度，小误差率的路径损耗模型，但其只适用于10～12英尺之间的非常短的范围；在[6]中介绍了一种基于RSS/TDOA的融合定位算法，综合了两种定位方法的优势，减少了位置指纹查找时间和计算过程，但实时性较差。在[7]中介绍了一种利用虚拟基站和凸优化算法来处理信号在NLOS情况下的传输问题，但其只适用于室外情况。在[3]中介绍了一种基于虚拟基站的TOA、DOA室内信号模型和算法，利用虚拟基站将非视距路径转化为视距路径，以此减少非视距的影响，但其定位至少需要使用两个基站，成本较高且受到基站的限制较大。在本文中，提出一种利用RSS进行协助定位，融合TOA、DOA几何传输模型的ray-tracing算法，首先通过RSS模型得到信号源可能存在的位置，随后利用ray-tracing原理并使用虚拟基站，将非视距路径定位问题转化为视距路径定位问题，TOA和DOA对直射、透射、反射和绕射情况进行分析建模，最后使用最小二乘法对可能的位置进行筛选，得到信号源的最终位置。本算法利用信号RSS测量值优化算法，实现TOA、DOA和RSS协同定位，提高室内多径及非视距环境下，无线定位的精度，降低算法复杂度，提高算法处理信号多重散射的能力，并降低了对基站的依赖性适用环境更为广泛，仿真结果表明其具有较高的定位精度。
2 基于信号强度的测距模型
当信号传播时，接收信号的强度随着距离的增加而衰减，这种衰减特性包含了距离信息。在自由空间中，信号强度与传播距离的平方成负相关性，通过计算发射功率和接收功率的差，就可以获得距离值，这个计算过程被称为路径损耗，且它因环境而异，令Pr(d)表示接收者在距离信号源距离为d的位置接收到的信号强度，它们之间的关系可以用Friis公式表示[8]：
(1)
其中，Pt为信号源的发射功率，Gt和Gr为天线在发送和接收信号时的增益，λ为电磁波的波长。在室内环境中，由于散射，反射和散射引起的多径衰落和室内遮蔽效应，信号强度随着距离线性增加呈现出非线性如图1，与线性曲线y=ax+b相比RSS值呈现出抛物线型。
对周围环境基本没变化，且反射路径较少的情况，可以利用以下反射模型来进行计算：
(2)
其中r1是发射端到障碍物的距离，r2为障碍物到接收端的距离， σ为反射因子，表示反射对象的雷达截面积的入射功率和散射功率的比值，且人的反射因子σ=1[9]。
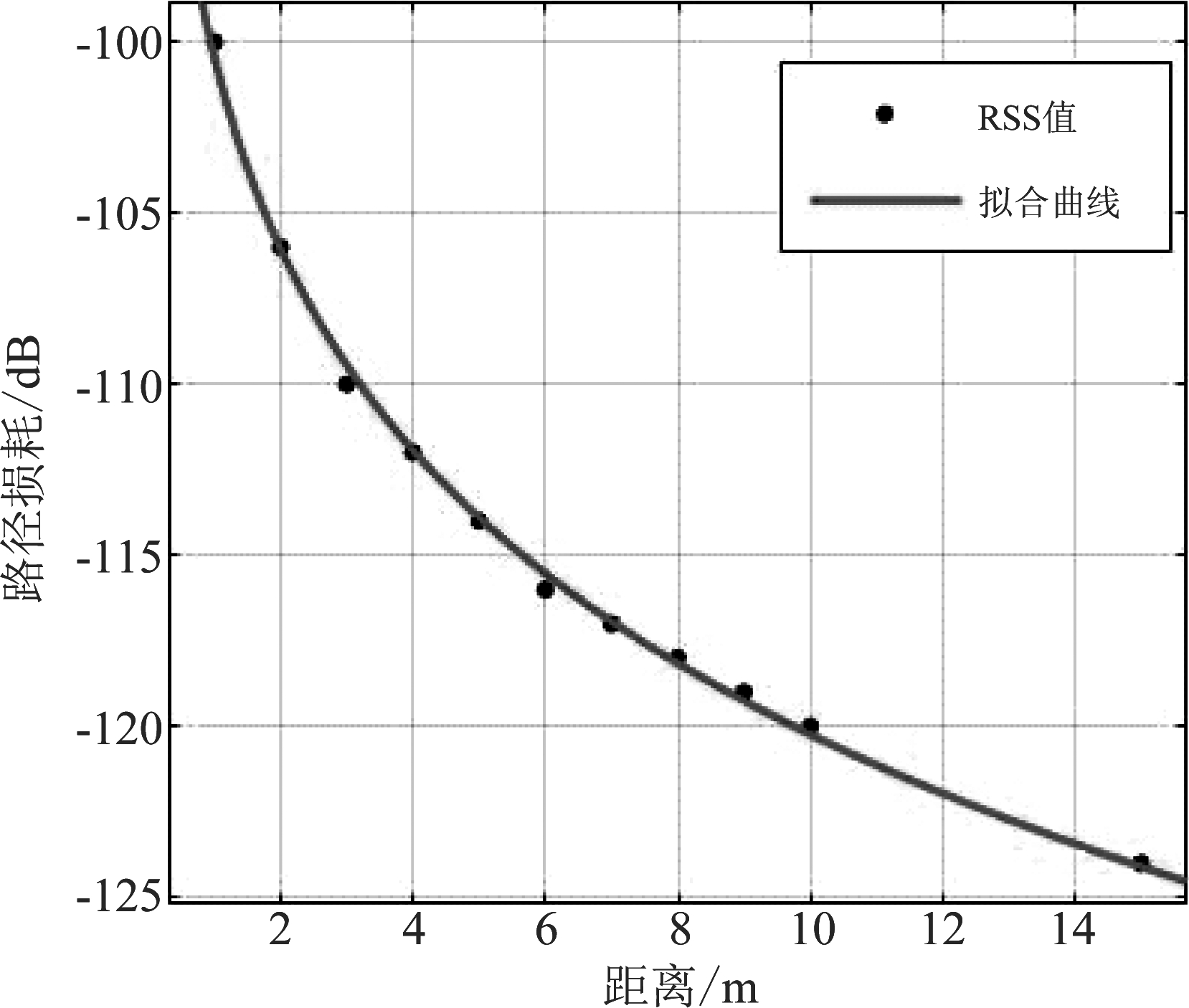
图1 RSS的非线性
Fig.1 Nonlinearity of RSS
由于传统的RSS测量的是多径信号的叠加信号，对于典型的多径传播环境，发射信号通过不同的衰减、延迟和相移的多径传播到接收端，因此多径传播是RSS测距的主要误差源，针对这种环境，可以使用更细粒度的信道模型—信道冲击响应(Channel Impulse Response, CIR)。CIR在时域上刻画了小尺度多径效应，用时域线性滤波器表示，假设时不变，CIR可以表示为：
(3)
其中，ai、θi和τi代表第i条多径分量的幅度、相位和时延，N为多径总数，δ(τ)为Dirac冲激函数。要想利用CIR的信号功率测距，可以将CIR与Friis公式相结合，同时可以解析全部多径分量[10]。假设有N条多径分量，每条多径分量的传播距离为di，其中i=1,2,…,N;并且假设每条多径分量仅发生一次反射，对应的反射系数为Γi，根据定义，Γ1=1。则波长为λk的发射信号经由第i条多径分量传播，接收到的功率P(di,Γi,λk)可以表示为:
(4)
其中，di和Γi为第i条多径分量的传播距离和反射系数，n为衰减因子。将该发射信号的N条多径传播的接收功率叠加，并进行正交分解，可得:
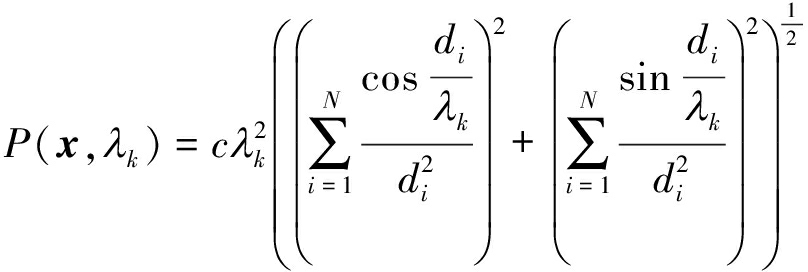
(5)
其中，x=(c,Γ2,…,ΓN,d1,…,dN)∈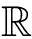
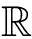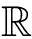2N，P(x,λk):2N→为波长为λk的单音信号经由全部N条路径传播的总接收功率。如果测量足够多个频点fk=υ/λk就可以求解出该组方程，从而可以得到LOS路径的传播距离d1，令dR=d1。基于CIR信号模型的测距精度取决于对多径分量的时间分辨率即系统带宽，所以高宽频的WLAN协议可以进一步的提高其性能。
对于一个基站，在通过RSS解算得到的距离dR后，只能确定信号源处于以基站为圆心，以解算得到的距离dR为半径的圆上，并不能得到其具体的位置。
3 虚拟基站的建立
在利用虚拟基站进行定位时，需要用到ray-tracing原理来建立几何模型，其主要是利用无线信号的传播特性与光的传播特性相似，因此可以将光的传播特性用来分析信号在特定环境的传播路径。这里分析暂时不考虑路径损耗。对于室内环境，无线信号的传播方式主要有以下几种:直射、透射、反射、绕射和混合路径。
3.1 直射路径
对于直射路径，信号从未知的信号源发出，经过直射路径到达基站，假设信号源的位置为xm=[xm,ym]T，基站的位置为xB=[xB,yB]T，基站测得的TOA值为t，DOA值为θ，其中θ∈[-π,π]，对信号源到基站的距离d有：
(6)
其中，c为传播速度，egauss为高斯噪声，bnlos为非视距误差，遵循指数分布，且有：
所以，最终信号源的位置可以表示为：
xm=xB+[dcos(θ),dsin(θ)]T
(7)
因为xB的位置已知，所以我们可以直接得到未知信号源xm的位置。对这种情况，不需要建立虚拟基站。
对于透射路径，可以直接当成直射路径来进行分析处理，因为在几何方法中，非视距引起的误差远大于一般透射引起的误差[3]。
3.2 反射路径
3.2.1 单次反射
对于反射路径，信号因被障碍物阻挡而发生反射，根据ray-tracing原理，所有反射均被认为是镜面反射，虚拟基站与基站关于反射面对称，如图2所示。
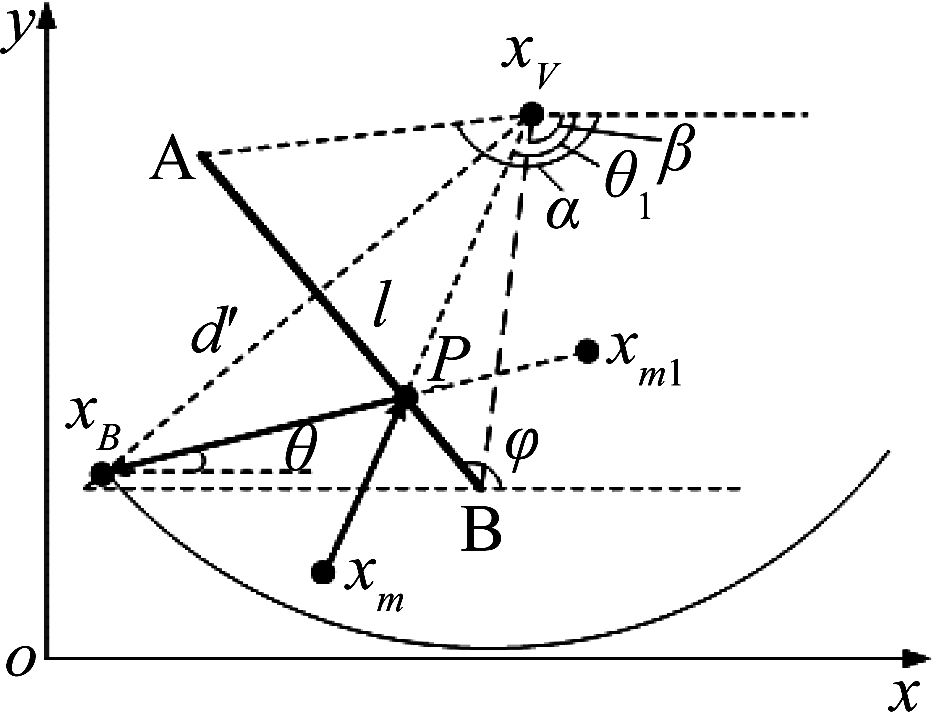
图2 单次反射
Fig.2 Single reflection
信号从信号源xm=[xm,ym]T经过反射面AB到达实体基站xB=[xB,yB]T，基站所测得的TOA值和DOA值分别为t和θ，将反射面AB用一条直线l来表示：
Ax+By+C=0
(8)
可以得到虚拟基站xV=[xV,yV]T的坐标可表示为:
xV=xB+G
(9)
其中
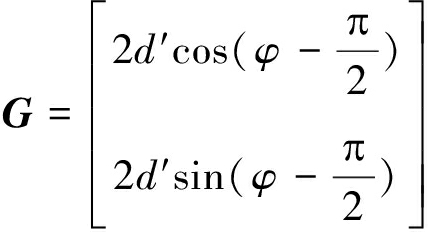
实体基站到直线l的距离为d′，反射面l与x轴正向的夹角为φ，当实体基站位于反射面AB的下方或者左侧时，d′取正值，反之取负值。P为反射点，且有xB与P点构成的直线：
y-yB=tan θ(x-xB)
因此有P点坐标可以通过下式求得：
信号从信号源到达实体基站的条件，即发生反射的条件为：
(1)估计的TOA距离大于实体基站与反射面之间的距离，即d>|d′|；
(2)反射点P需要在反射面AB上，即θ1∈(α,β)。
其中θ1为虚拟基站看信号源的DOA值，且有θ1=θ-2φ，α和β分别为直线AxV和直线BxV与x轴正向的夹角。
所以可以得到信号源的位置：
xm=xV+F
(10)
其中
F=[dcos(θ′),dsin(θ′)]T
所以，当虚拟基站设立后，可以将原信号的反射路径看作信号从信号源发出，通过直射路径到达虚拟基站，从虚拟基站所测得的TOA距离值和DOA值分别为d和θ′。
若考虑存在透射情况，即存在另一个信号源点xm1，xm1可以表示为:
xm1=xB+[dcos(θ),dsin(θ)]T
(11)
3.2.2 多次反射
在实际情况中，因为环境十分复杂，可能存在多次反射的情况，对于多次反射，需要建立多个虚拟基站，因为三次以上反射衰减就非常大，所以不考虑这种情况。对于多次反射，如图3所示。
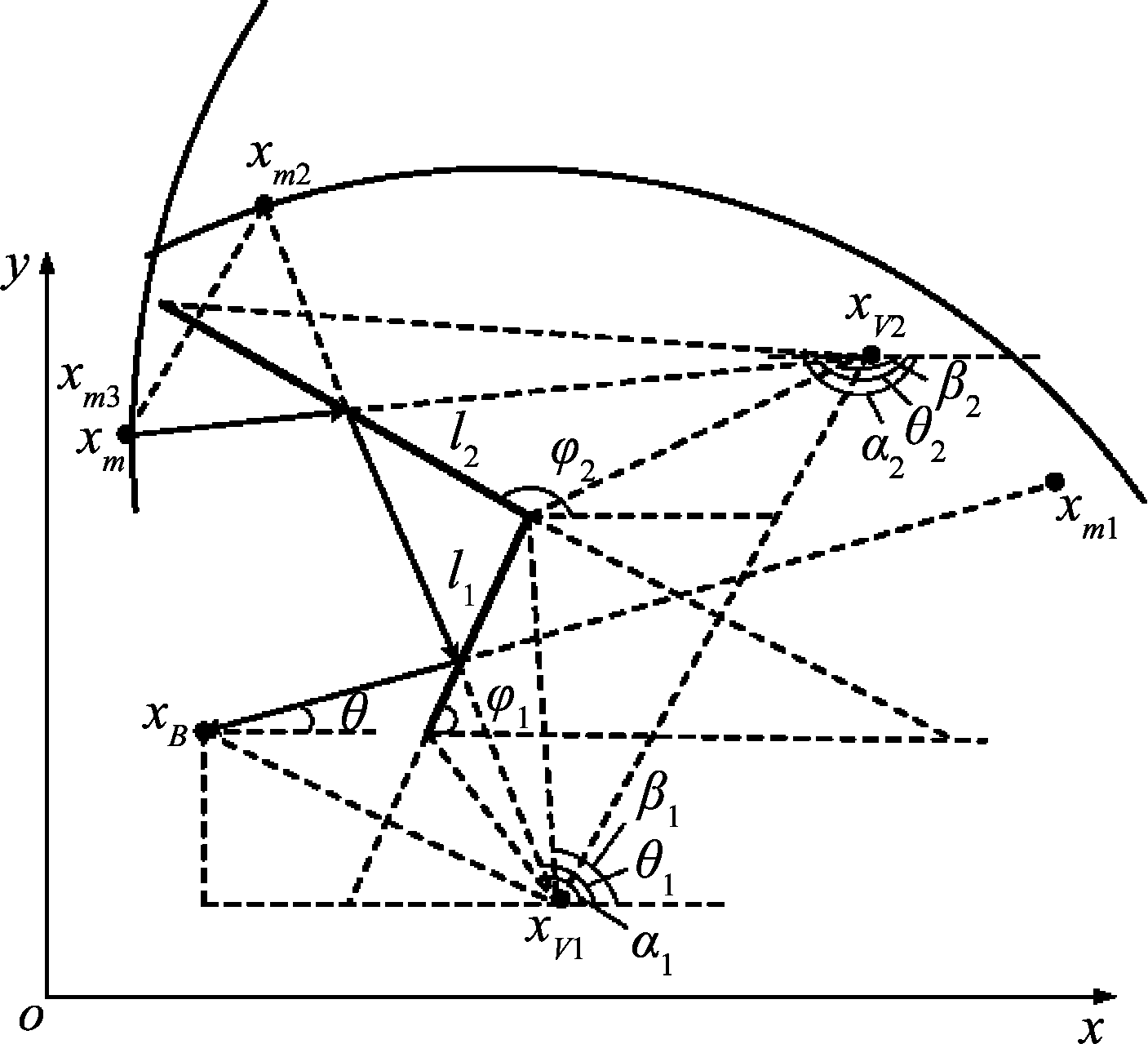
图3 多次反射
Fig.3 Multiple reflection
假设有n个反射面(为了简洁，图中只画了两个)，分别用直线li表示，即：
Aix+Biy+Ci=0 i=1,2,…,n
设估计的信号的TOA距离值和DOA值分别为d和θ，从虚拟基站看的DOA值为
由前面分析，对每个反射面，其都有可能发生透射和反射，因此必须设立一个虚拟基站来估计出两个可能的信号源的位置。
对于反射面li，虚拟基站的位置为xVi，信号源可能的位置为xmi，表示信号发生透射后，经过反射面li到达实体基站(当i=1时)或虚拟基站(当i>1时)；xm(i+1)表示另一个可能的信号源的位置，表示信号发生反射后，经过反射面li到达实体基站(当i=1时)或虚拟基站(当i>1时)，此时对虚拟基站有：
xVi=xV(i-1)+Gi
(12)
其中
xV 0=xB
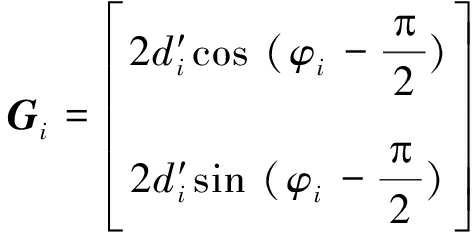
其中φi为直线li与x轴正向的夹角，当实体基站位于直线li的下方或者左侧时，d′取正值，反之取负值。αi和βi分别为直线li的反射边界，所以信号源的位置为：
xmi=xV(i-1)+Fi-1
(13)
其中：
之后，对下一次反射进行分析，即分析下一个i，直到所有反射面全部被分析完，或者反射条件已不成立，则停止分析，停止条件如下(三者满足其一则可以停止分析)：
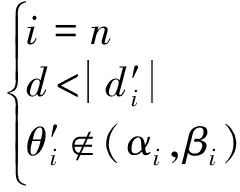
3.3 绕射
因为信号可能会在障碍物端点发射绕射，如图4所示，假设信号在A点处发生绕射，将虚拟基站xV设立在绕射点A处，信号由信号源发出，经过障碍物端点，即绕射点A到达基站。由绕射性质可知，当信号发生绕射时，信号在绕射点的所有方向上均发生绕射，即θ′∈[-π,π]，因此只能知道信号源可能的位置，其轨迹为一个圆，且圆心位于绕射点A，所以有：
(14)
其中：
dV为基站到绕射点之间的距离，可以从室内布局图中得到。
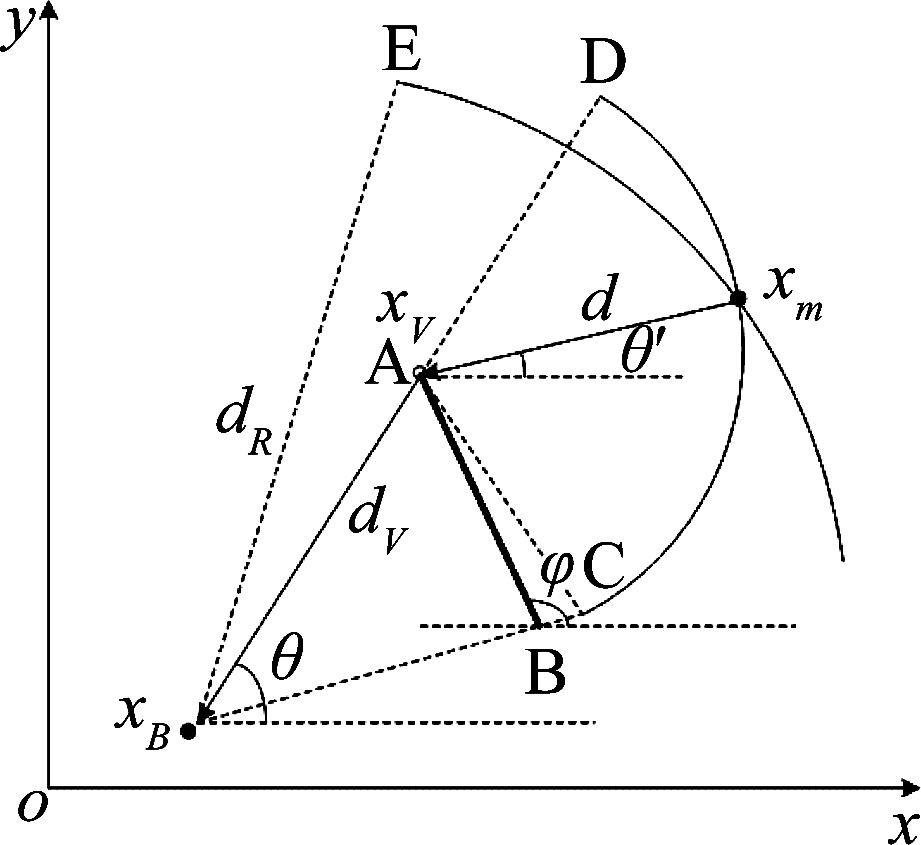
图4 绕射
Fig.4 Diffraction
因为在视距的区域中，直射信号能量要远远高于绕射信号[3]，所以信号源的位置应处于xBA与xBB的延长线所夹的轨迹圆的圆弧上，即弧
上，且有发生绕射的条件为：
4 位置筛选
由上两节可知，对一个实体基站而言，当信号发生反射时，每条路径均有一组成对的TOA距离值和DOA值，可以通过设立多个虚拟基站，从而计算出多个可能的信号源的位置，即有i+1个解算点，但在这些解算点中，只有一个是信号源的真实位置。而对于信号发生绕射的情况，只能得到信号源在一段圆弧上，通过RSS解算出的信号源位置也是一个轨迹圆，因此可以利用RSS协助TOA、DOA筛选出信号源真正所处的位置，令
为通过TOA、DOA解算出的可能的信号源的位置,其中i=1,2,…,n1，n1为可能的信号源的数量;
为通过RSS解算出的可能的信号源的位置，其中j=1,2,…,n2，n2为可能的信号源的数量。
对直射、反射和绕射路径，因为能量在传播中信号能量会衰减损耗，所以通过TOA所测量得到的距离值d是大于RSS解算出的距离值dR，即d>dR。
对于反射路径，以虚拟基站为圆心，以RSS解算出的距离值dR为半径，建立一个圆，即：
(15)
对于直射、透射和绕射则以基站为圆心，以RSS解算出的距离值dR为半径，建立一个圆：
(16)
因为对于每个虚拟基站都会计算得到两个解算点xmi和xm(i+1)，对每个虚拟基站，将两个解算点带入上式中，即：
(17)
若解算点满足上式，因其明显小于RSS解算出距离值dR，这显然是与现实不符的，故可以将该解算点排除。
对于绕射路径，因为只通过TOA和DOA估计时其轨迹是圆弧，而通过RSS估计时，得到的是一个圆(也可视为圆弧)，其必相交于一点，如图4所示，相交的这一点就为信号源的实际位置。
但是，由于误差的确存在，因此，将距离最短的一对和作为期望的
和
即：
(18)
其中：
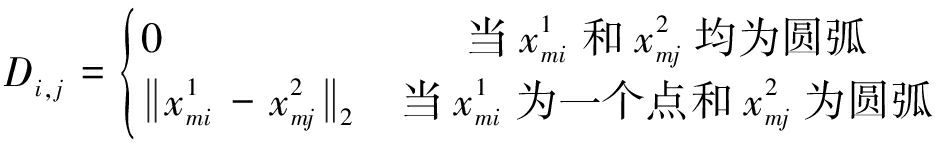
由此，便可以筛选出信号源的位置。
5 仿真实验
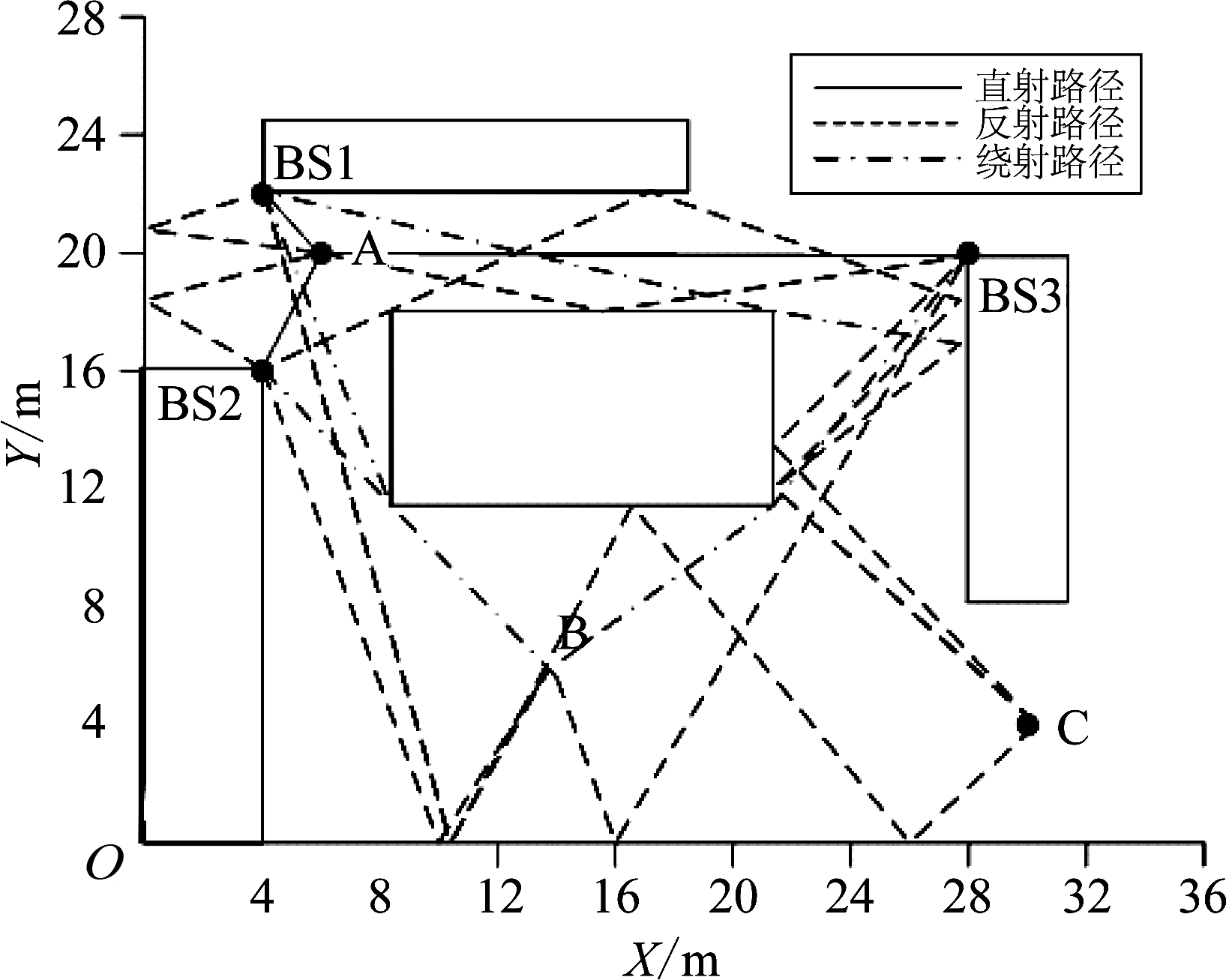
图5 仿真环境
Fig.5 Simulation environment
在如图5的室内环境中，所有障碍物(包括墙面)都被认为是光滑的反射面。在仿真中，使用三个基站，位置分别为：BS1(4,22)，BS2(4,16)，BS3(28,20)，三个信号源，位置分别为：A(6,20)，B(14,6)，C(30,4)。假设每个基站与信号源之间，提取了RSS信号值，并估计出了TOA和DOA值，信号的路径如图5中所表示。当信号源的位置位于A点时，信号源处于所有基站的视距路径下，因此所有的主路径为直射路径，次路径为一次反射路径；当信号源的位置位于B点时，所有的主次路径为一次反射路径或者一次绕射路径；当信号源的位置位于C点时，几乎所有的路径为多重反射路径或者混合路径；根据ray-tracing算法提前得出所有路径实际的TOA和DOA值，并且加上零均值高斯白噪声。将本算法与其他两种算法通过3000次蒙特·卡罗方法来进行比较分析，算法1[3]同是利用ray-tracing原理和虚拟基站的TOA和DOA参数模型算法，但是它是通过两个基站的得出两条信号路径，得到的最后的结果，在通过最小二乘法来计算出最后的位置；算法2[11]利用加权因子来减少多径的影响。
利用平均均方根定位误差(average root mean square error，ARMSE)来评估各算法的定位性能。设置仿真条件为TOA的噪声标准差为1 m，DOA的噪声标准差从1°到10°，其间隔为1 s，仿真结果如图6所示。
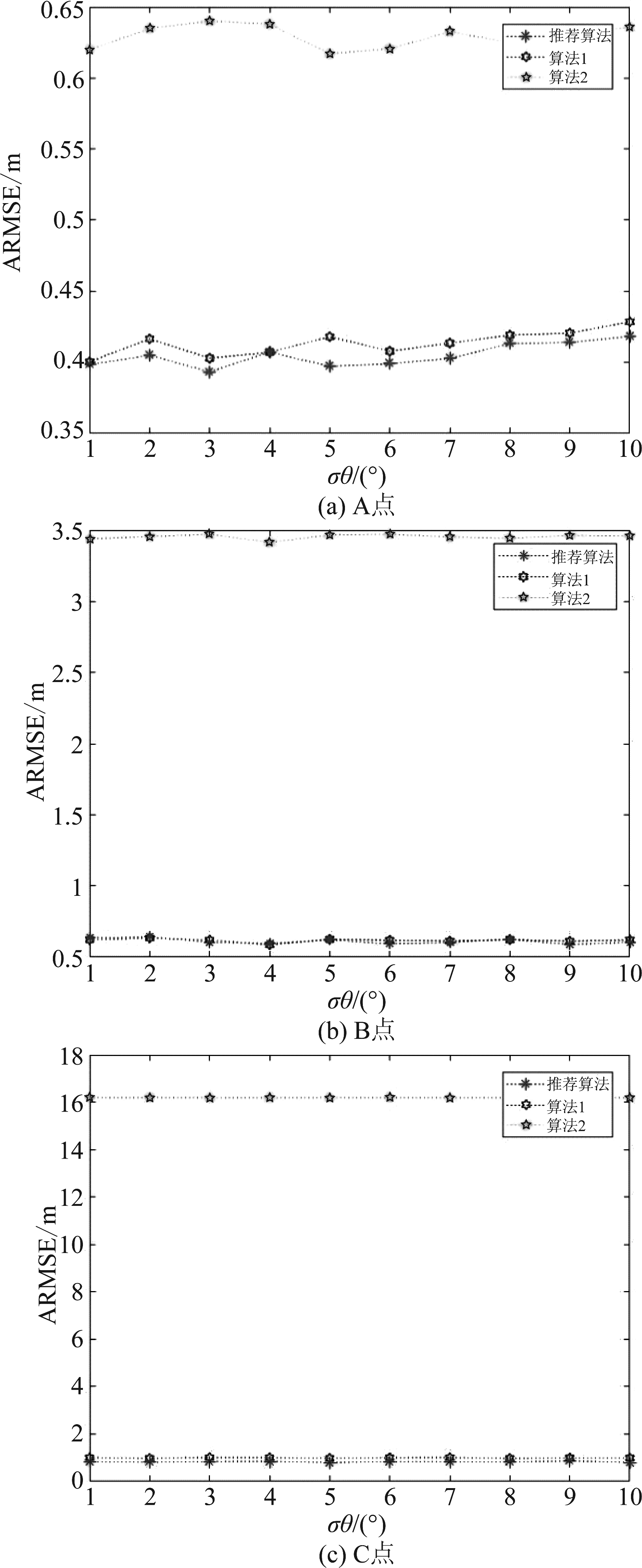
图6 ARMSE对比
Fig.6 Comparison of ARMSE
由仿真结果可以看出，当信号源处于A点时，由于基站都处于视距情况下，因此三种算法的定位误差相差不多，但总的而言，本文所推荐的算法和算法1误差更小，算法1的误差为0.39～0.43 m，所推荐的算法为0.38～0.42 m，优于算法1。当信号源处于B点时，因为处于非视距的情况，推荐的算法和算法1的误差相差不多，均在0.58～0.65 m之间，但算法2的误差达到了3.4～3.5 m，明显不足以用于室内环境。当信号源出于C点时，非视距情况十分严重，但推荐的算法的误差在0.785～0.9 m，算法1的误差为0.95～1 m。
得益于精确的CIR信道模型，所推荐的算法精度优于算法1特别是算法2。虽然视距情况下如处于A点精度对比算法1只有0.01 m的提升，因为在这种情况下，由TOA、DOA所得到的精度已经足够高，CIR所能提供的协助精度有限，因此精度相差无几，但是随着非视距程度的不断加深，特别是处于C点时，推荐的算法的优势就已经很明显了，结果也很好的表明推荐算法提高了处理信号多重散射的能力。
为了凸显CIR在少基站情况下的优势，在实验中，只使用基站BS2和BS3，对B点和C点再一次进行仿真验证并与算法1进行对比分析，结果如图7所示。对比B点在只使用两个基站的情况下，两种算法都比原先的精度0.58～0.65 m有所下降，但是推荐的算法精度为0.67～0.7 m，而算法1的精度却下降到0.95～0.97 m;在C点这种现象表现的更为明显，推荐的算法下降至0.85～0.94 m，而算法1已经下降到1.38～1.4 m，由此可以分析出算法1对基站的依赖性较大，相对而言，推荐算法受限基站的影响小。
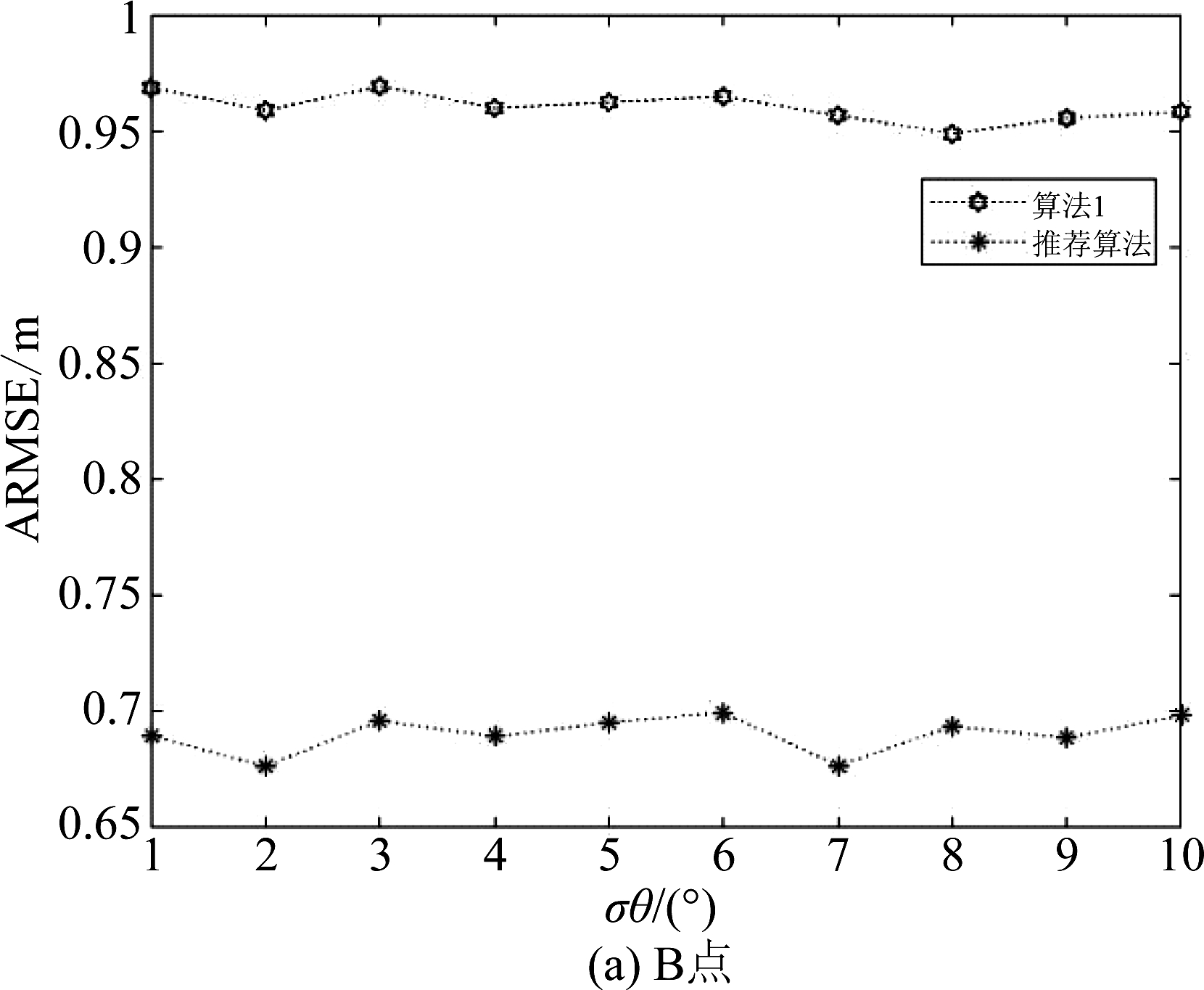
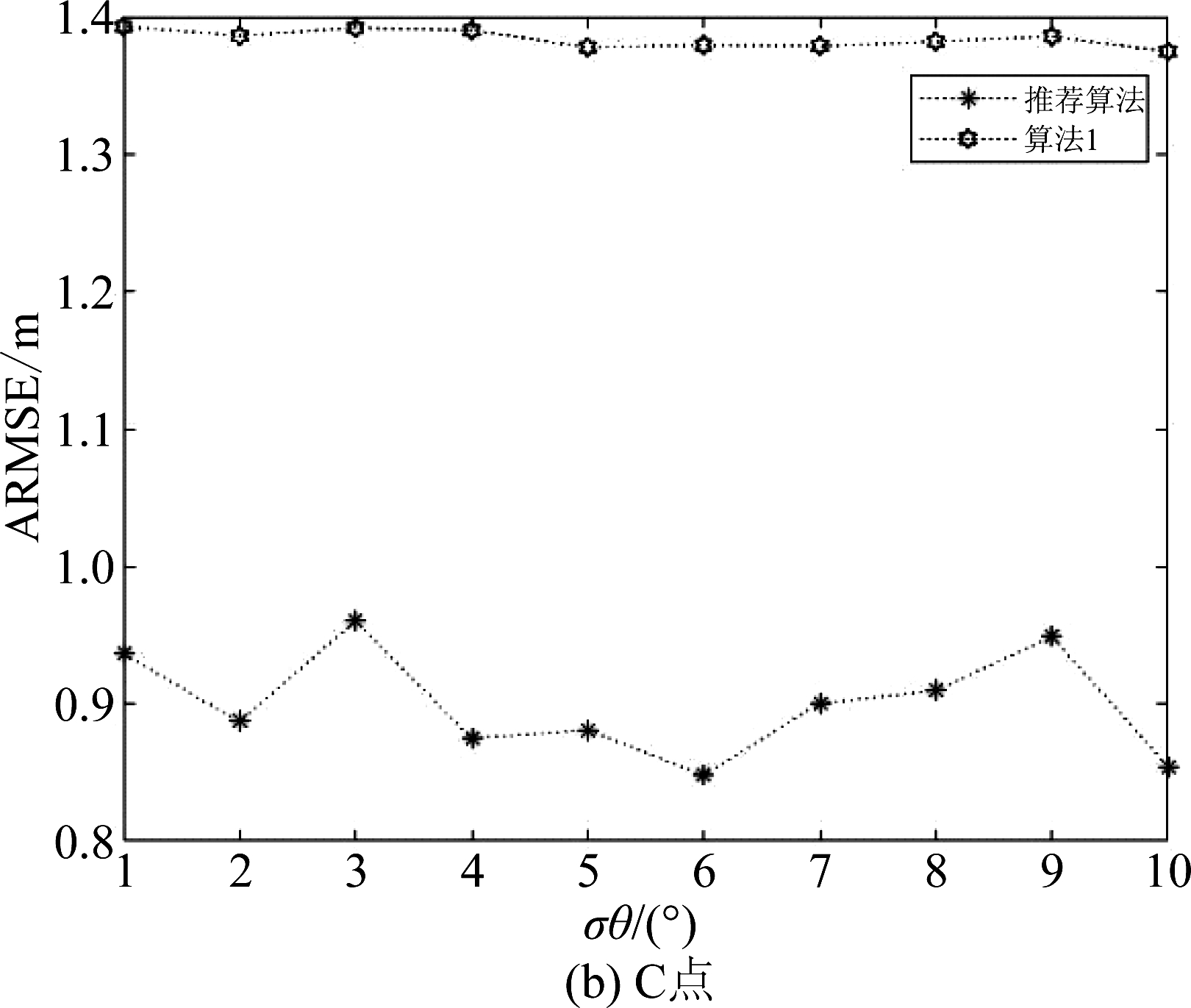
图7 双基站时ARMSE对比
Fig.7 Dual base station ARMSE comparison
从仿真结果可以得到，推荐算法提高了处理信号多重散射的能力，并降低了对基站的依赖性适用环境更为广泛，且具有较高的定位精度。
6 结论
针对室内环境因信号受到非视距和多径影响，提出一种利用RSS进行协助定位，融合TOA、DOA几何信道模型的ray-tracing算法，通过利用虚拟基站和ray-tracing原理，将非视距情况转化为视距情况来进行处理分析，建立了基于TOA和DOA在直射、透射、反射和绕射情形下的几何信道模型，使其能很好地处理复杂的非视距室内环境，并利用RSS对其定位进行的筛选和辅助估计定位，仿真结果表明，推荐算法提高了处理信号多重散射的能力，并降低了对基站的依赖性适用环境更为广泛，且具有较高的定位精度，若能有一个更为精确的信号能量衰减模型，定位精度能进一步的提高。
[1] Rajalakshmi K, Goyal M. Location-Based Services: Current State of The Art and Future Prospects[M]∥Optical and Wireless Technologies. Springer, Singapore, 2018: 625- 632.
[2] Choi M S, Jang B. An Accurate Fingerprinting based Indoor Positioning Algorithm[J]. International Journal of Applied Engineering Research, 2017, 12(1): 86-90.
[3] 刘德亮. 室内环境下无线定位关键技术研究[D]. 天津:天津大学, 2015.
Liu Deliang. Research on wireless localization in indoor environment[D]. Tianjin: Tianjin University, 2015. (in Chinese)
[4] Horiba M, Okamoto E, Shinohara T, et al. An improved NLOS detection scheme using stochastic characteristics for indoor localization[C]∥Information Networking (ICOIN), 2015 International Conference on. IEEE, 2015: 478- 482.
[5] Viswanathan S, Srinivasan S. Improved path loss prediction model for short range indoor positioning using bluetooth low energy[C]∥SENSORS, 2015 IEEE. IEEE, 2015: 1- 4.
[6] 陈艺灵. RSS及混合室内可见光定位算法研究[D]. 大连:大连海事大学, 2016.
Chen Yiling. RSS and hybrid algorithm for indoor visible light localization[D]. Dalian: Dalian Maritime University, 2016. (in Chinese)
[7] Huang L H,Shr K T, Lin M H, et al. A Noise-Robust Convex-Optimized Positioning System Based on Code-Aided RSS Estimation and Virtual Base Station Transform[J]. Journal of Signal Processing Systems, 2016, 84(3): 309-323.
[8] 杨铮, 吴陈沭, 刘云浩. 位置计算: 无线网络定位于可定位性[M]. 北京：清华大学出版社,2014.
Yang Z, Wu C M, Liu Y H. Location-based computing: localization and localizability of wireless networks[M]. Beijing：Tsinghua University Press,2014. (in Chinese)
[9] 郭晨. 基于RSSI的无线网络定位技术研究[D]. 南京:东南大学, 2015.
Guo Chen. Research on RSSI-BASED localization technology in wireless network[D]. Nanjing: Southeast University, 2015. (in Chinese)
[10] Zhang D, Liu Y, Guo X, et al. On distinguishing the multiple radio paths in rss-based ranging[C]∥INFOCOM, 2012 Proceedings IEEE. IEEE, 2012: 2201-2209.
[11] Tai C S, Tan S Y,Seow C K. Robust non-line-of-sight localisation system in indoor environment[J]. Electronics Letters, 2010, 46(8): 593-595.
