1 引言
波达方向(direction of arrival， DOA)估计是阵列信号处理的重要内容之一，受到了众多学者广泛的关注[1]。其中，二维DOA估计算法被广泛应用于各种形式的阵列，例如双平行均匀线阵[2-3]，三平行均匀线阵[4-5]，L型均匀线阵[6-13]等。L型阵列具有形式简单且能够提供较好的角度估计性能等优点。因此，学者们提出了大量基于L型阵列的二维DOA估计算法。文献[8]通过构建匹配矩阵实现了方位角和俯仰角的自动配对，但它需要类似谱峰搜索的运算。文献[11]解决了角度兼并问题，在欠定条件下可实现角度估计且能够自动配对。
上述的算法有一个共同的特点，即阵元间距小于等于半波长。扩展孔径可以有效地提高阵列的分辨率和角度估计精度，但会出现角度模糊的现象。文献[15]提出了一种获得高精度无模糊方向余弦的方法，因此有效地提高了DOA估计性能。当包含方向余弦估计信息的DOA矩阵具有相同的对角线元素时，它不能解决奇异点问题，即不能获得正确的方向余弦估计值。在此基础上，文献[16]提出的算法将扩展孔径的阵列应用到xoy平面的两个双平行阵列中，且使用传播算子算法[17]降低了计算复杂度，但仍不能解决奇异点问题。针对特征值相等时的角度配对失效现象，文献[18]提出一种基于子空间正交的新配对方法，故能够解决部分奇异点问题。
为了解决扩展孔径的二维DOA估计存在的奇异点问题，本文提出了非均匀L型阵列的联合对角化二维DOA估计算法。首先，从延时互相关矩阵中提取信号子空间。然后，通过联合对角化方法获得自动配对的两种方向余弦，即高精度模糊的方向余弦和低精度无模糊的方向余弦。值得注意的是，即使DOA估计矩阵具有相同的对角元素，也可以获得正确的方向余弦。最后，为了实现解模糊，以无模糊估计值为参考，从模糊估计值中得到高精度无模糊的估计值。因此，提出的算法解决了在扩展孔径的二维DOA估计中的奇异点问题，并且在欠定条件下具有良好的表现性能。
符号:(·)T,(·)*,(·)H和(·)+分别表示转置,共轭,共轭转置和伪逆运算。⊙和⊗分别表示 Khatri-Rao (KR)积和Kronecker积。E[·]表示统计期望，arg(·)表示相位。IM是一个维数 M×M单位矩阵。diag{·}是由列向量元素组成的对角矩阵。blkdiag{·}表示块对角化。 circshift(·,m)是沿着行向右循环移动m个单位。
2 阵列结构和数据模型
本文采用的非均匀L型阵列如图1(a)所示，将L型阵列划分为4个子阵，每个子阵均包含M个阵元。其中，子阵内部相邻阵元间距为ds (ds=hλ/2，h为正整数，λ为信号波长)，各坐标轴上的两个子阵间距为d(d=λ/2)。坐标轴上子阵结构类似，以图1(b)所示的
轴方向的阵列为例。子阵Z的第一个阵元位于原点，相邻阵元间距为ds；子阵W的第一个阵元位于与原点的间距为d，相邻阵元间距也为ds。因此，子阵内部包含扩展孔径的模糊方向余弦估计信息，两个子阵之间包含无模糊的方向余弦估计信息。
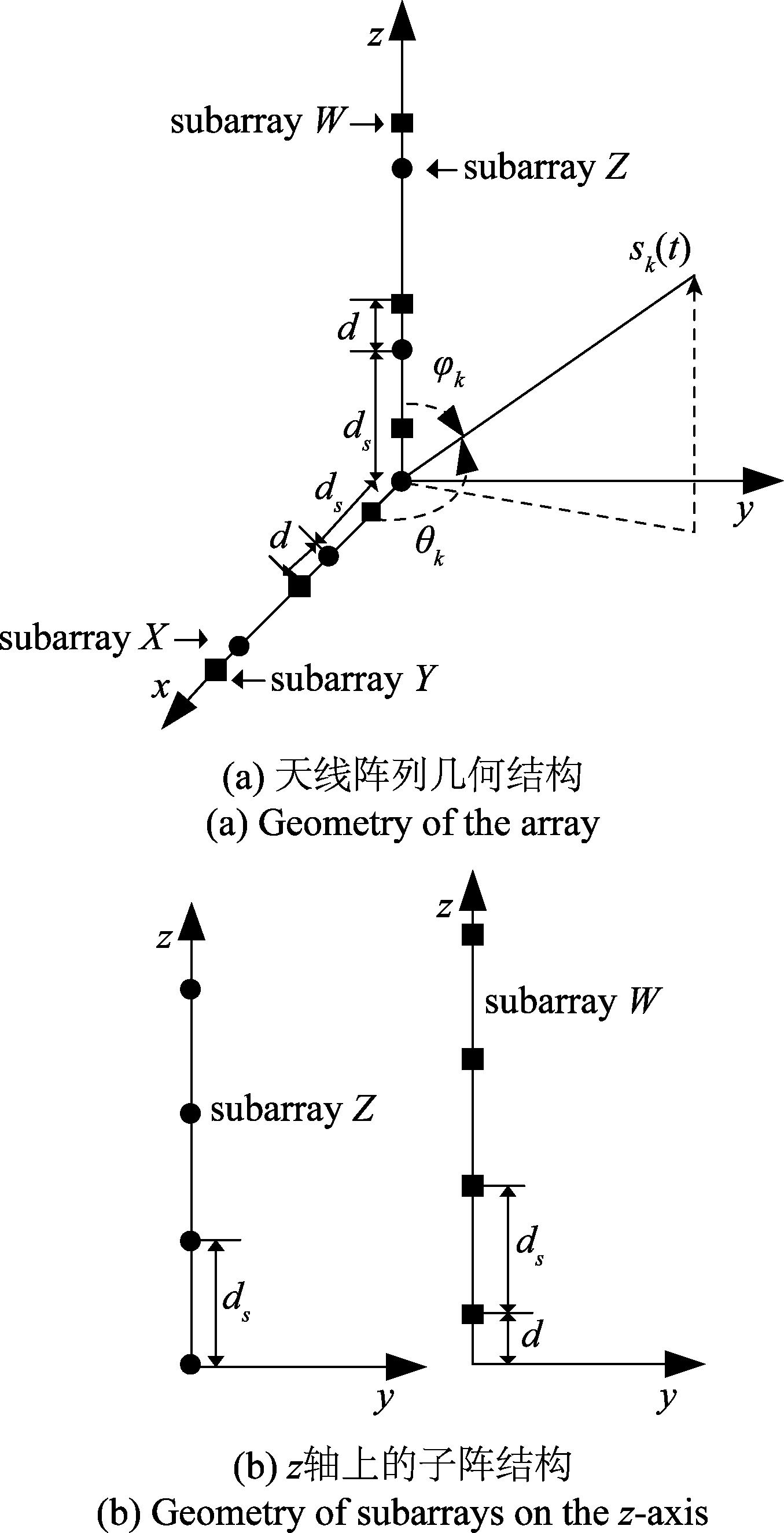
图1 阵列插图
Fig.1 Illustration of array
假设有K个窄带非相关远场信号
(t=1,2,…,N, N表示快拍数)入射到非均匀L型阵列上，其中第k个信号的方位角和俯仰角表示为(θk,φk)(k=1,2,…,K)。将位于坐标原点的阵元作为参考阵元，则t时刻的接收数据矢量ρε(t)可表示为
ρε(t)=Aεs(t)+nε(t)
(1)
式中，
是均值为0，方差为σ2的加性高斯白噪声，且与信号s(t)相互独立。Aε=[αε(φ1,θ1),…,αε(φK,θK)]表示阵列流型矩阵。
分别与子阵Z和子阵X相对应。相应的αε(φ,θ)具体形式如下式所示：
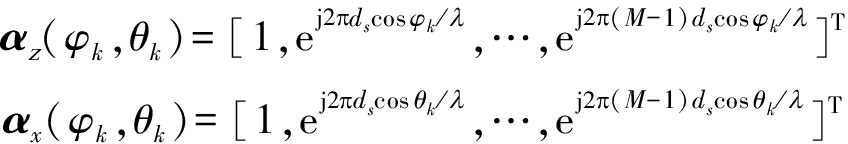
(2)
此外，其他两个子阵的阵列流型矩阵如下
(3)
式中，
(φ)=diag{ej2πdcos φ1/λ,...,ej2πdcos φK/λ}，(θ)=diag{ej2πdcos θ1/λ,...,ej2πdcos θK/λ}。
3 提出的算法
所提出的算法主要包括三个部分。首先，根据KR运算构造延时互相关矩阵。其次，在延时互相关矩阵和选择矩阵运算得到对角矩阵的基础上，通过联合对角化方法得到自动配对的两种方向余弦估计值，即高精度模糊的方向余弦估计值和低精度无模糊的方向余弦估计值。最后，通过解模糊方法得到高精度无模糊方向余弦估计值，进一步得到方位角和俯仰角。
3.1 延时互相关矩阵的构造
为了消除高斯白噪声的影响，根据接收数据矢量ρx(t)和
构造互相关矩阵
表示如下
(4)
因此，根据KR运算得到的延时互相关矩阵表示如下
(5)
式中，
rM,M(l)]T， Rs=diag{r1(l),r2(l),...,rK(l)}，rs(l)=(r1(l),r2(l),...,rK(l))T。
为了充分利用阵列接收信号的空时二维特性，对接收数据矢量ρx(t)和依据时域最大重叠原则分别划分为L帧数据，第l(l=1,2,...,L)帧数据可以表示为
(6)
因此，我们可以构造延时互相关矩阵
如下
(7)
式中，
表示延时自相关矩阵Rss的第k行第l列。
按照同样的方式分别构建延时互相关矩阵
和
在此基础上，定义一个新的矩阵表示如下
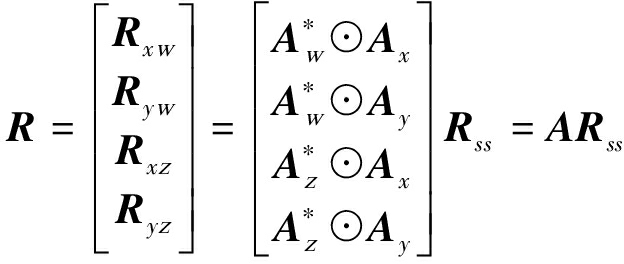
(8)
根据式(8), 对应的阵列形式如图2所示。
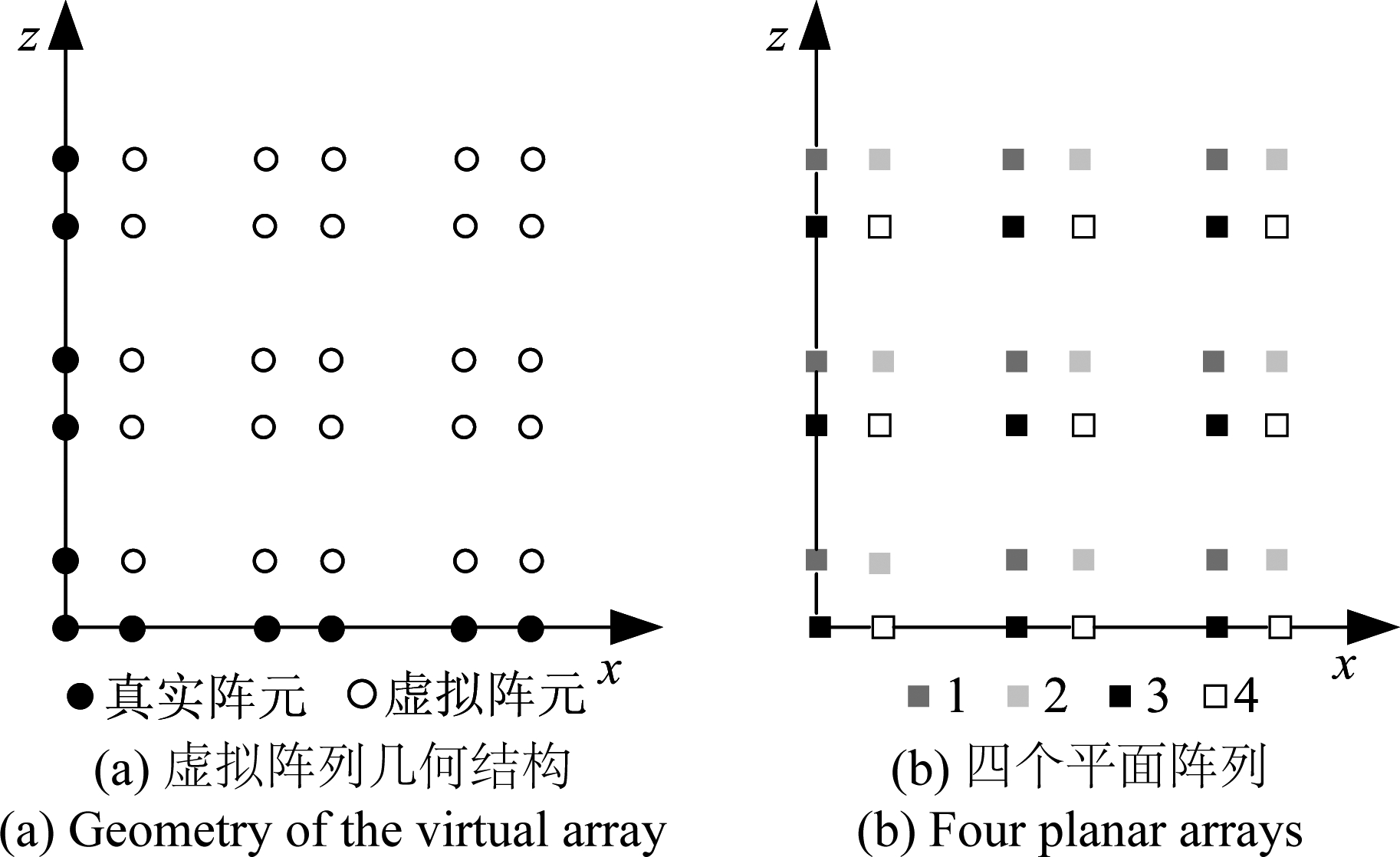
图2 阵列划分
Fig.2 Partition of array
由图2(a)可知KR运算有效地增加了阵元个数。与式(8)相对应，我们将虚拟阵列划分为四个平面阵列如图2(b)所示。其中，平面阵列1、2、3和4分别与
和
相对应。
3.2 方向余弦的估计
通过对R进行奇异值分解(Singular Value Decomposition，SVD)，可以得到信号子空间Us以及具有K个较大奇异值的对角矩阵Λs
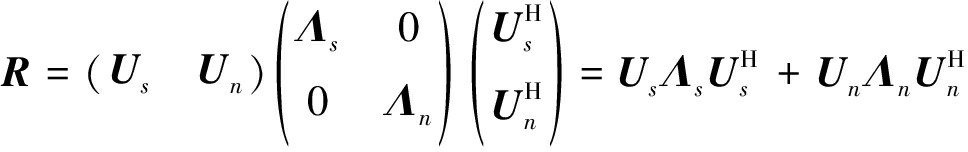
(9)
从式(8)和图2(b)易知，平面阵列1与2、1与3、3与4以及2与4之间的间距均为d，且四个平面阵列内部相邻阵元间距为ds，故Us包含高精度模糊的方向余弦信息以及低精度无模糊的方向余弦信息。
平面阵列1与2，3与4之间均包含x轴低精度无模糊的方向余弦信息。因此，构造选择矩阵G1=[G01,G00,G02,G00]，用于选取与平面阵列1、3相对应的Us中两个子块；G2=circshift(G1，M2)用于选取与平面阵列2、4相对应的Us中的两个子块。其中，G00=02M2×M2，G01=[IM2;0M2]，G02=[0M2;IM2]。因此，包含x轴低精度无模糊的方向余弦对角矩阵可表示如下
(θ)T
(10)
式中，T=A+UsΛ1/2 是一个酉矩阵。
平面阵列1与3，2与4之间均包含轴低精度无模糊的方向余弦信息。因此，构造选择矩阵G3=[G01,G02,G00,G00]，用于选取Us与平面阵列1、2相对应的两个子块；G4=circshift(G3,2M2)用于选取Us与平面阵列3、4相对应的两个子块。因此，包含轴低精度无模糊的方向余弦对应对角矩阵表示如下
(φ)T
(11)
四个平面阵列中均包含x轴高精度模糊的方向余弦信息，对应对角矩阵表示如下
(12)
式中，G5=I4M⊗[IM-1,0(M-1)×1]，G6=circshift(G5,1)，Φ(θ)=diag{ej2πdscos θ1/λ,...,ej2πdscos θK/λ}。
为了得到轴高精度模糊的方向余弦信息， 对Us的顺序进行调整，
=G7Us，G7=blkdiag{H01,H01,H01,H01}，H01=[(circshift(H00,0))T,...,circshift(H00,M-1))T]T，H00=blkdiag{[1,0,...,0]1×M,...,[1,0,...,0]1×M}，H00∈CM×M。
四个平面阵列中均包含轴高精度模糊的方向余弦信息，对应对角矩阵表示如下
(13)
式中，Φ(φ)=diag{ej2πdscos φ1/λ,...,ej2πdscos φK/λ}。
在得到四个联合对角矩阵的基础上，通过联合对角化方法[14]，可得到自动配对的
和
因为d=λ/2，则轴低精度无模糊的方向余弦估计值为
(14)
由于ds>λ/2，方向余弦
取不同的值对应一系列轴高精度模糊的方向余弦估计值
(15)
式中， 「α⎤ 表示取不小于α的最小整数, ⎣α」 表示取不大于α的最大整数。由于
与
自动配对，故得到的两种方向余弦估值仍然是配对的。
同理，通过对
进行特征值分解可以得到x轴低精度无模糊的方向余弦估计值
通过对
进行特征值分解以及扩展可以得到一系列高精度模糊的方向余弦估计值
3.3 二维DOA估计的实现
因为得到了配对的方向余弦估计值，故分别估计
和nx即可。利用文献[15]中解模糊的方法，轴高精度无模糊的方向余弦估计值为
(16)
其中，
用下式进行估计
(17)
同理，通过解模糊运算可得到x轴高精度无模糊的方向余弦估计值为
根据以上的分析，第k个信号的方位角和俯仰角估计表达式如下
(18)
因此，我们可以得到自动配对的俯仰角和方位角。所提出算法主要步骤概括如下：
(1)构造式(7)所示的延时互相关矩阵。
(2)构造选择矩阵，通过延时互相关矩阵以及选择矩阵的运算分别得到如式(10)～(13)所示的四个对角矩阵。
(3)通过式(14)和式(15)分别得到轴低精度无模糊的方向余弦估计值以及一系列高精度模糊的方向余弦估计值。
(4)同理得到x轴上对应的两种方向余弦估计值。
(5)通过解模糊方法得到高精度无模糊的方向余弦估计值
(6)根据式(18)得到俯仰角和方位角的估计值
和
3.4 算法分析
(1)角度估计
选择矩阵的维数直观地说明了所提出的算法可实现多达2M2个信源估计。因此，所提出的DOA估计算法在欠定条件下仍能实现方位角和俯仰角的估计与自动配对。同时，当俯仰角和方位角满足以下三种情况时，所提出的算法仍能获得正确的方向余弦估计:
情况 1 θk=θp，cos φk≠cos φp±oλ/ds。
情况 2 φk=φp，cos θk≠cos θp±oλ/ds。
情况 3 θk≠θp，φk≠φp,cos θk=cos θp±oλ/ds，cos φk=cos φp±oλ/ds。
其中，o为正整数表示两个来波信号在同一方向上的方向余弦估计值的差值为整数倍λ/ds。
证明如下：
由于R=ARss，故通过判断A的阶数即可得到R的阶数。
1)首先，判断A中互不相关行的个数。
由式(8)可知,阵列流型矩阵A中第k列中的不同行之间可能存在的关系分别为ej2πdcos φk/λ，ej2πdcos φk/λ，ej2πdscos θk/λ，ej2πdscos φk/λ。
当角度关系满足情况 1时，ej2πdscos θk/λ=ej2πdscos θp/λ且ej2πdcos θk/λ=ej2πdcos θp/λ，但由于cos φk≠cos φp±oλ/ds，故ej2πdscos φk/λ≠ej2πdscos φp/λ且ej2πdcos φk/λ≠ej2πdcos φp/λ，结合3.2中关于高精度模糊的方向余弦信息的选择矩阵的维数可知A中线性无关的行数至少为2M2。
当角度关系满足情况 2时，与情况1同理。
当角度关系满足情况3时，ej2πdcos θk/λ≠ej2πdcos θp/λ，ej2πdscos φk/λ≠ej2πdscos φp/λ且ej2πdscos θk/λ=ej2πdscos θp/λ，ej2πdcos φk/λ=ej2πdcos φp/λ，结合3.2中关于低精度无模糊的方向余弦信息的选择矩阵的维数可知A中线性无关的行数为至少为2M2。
2)其次，判断A中互不相关列的个数。
由式(8)可知, 阵列流型矩阵A中的各列之间并不存在线性关系，除非两个信号的方位角与俯仰角完全相同。故对于以上三种情况，A中各列始终线性无关。
综上所述，由于2M2>K，因此通过对R进行SVD分解可以得到信号子空间Us以及K个较大奇异值。
3)最后，文献[11]指出联合对角化可以有效处理角度兼并问题，因此所提出的算法在以上三种情况下仍能实现良好的角度估计。
(2)克拉美罗界
本文所提出算法的克拉美罗界(Cramer-Rao bound，CRB)[19]表达式如下
(19)
式中，1表示维数2×1矩阵且元素值均为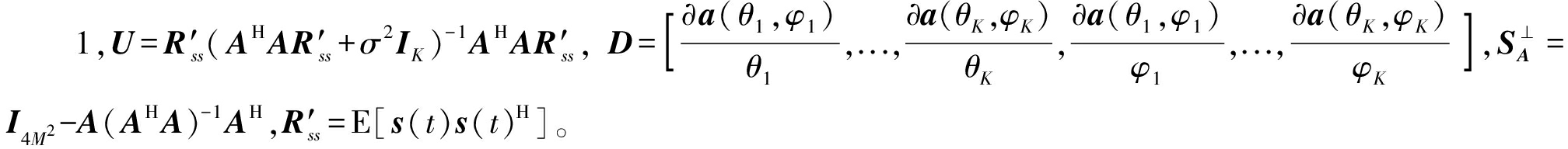
4 仿真实验
本文所提出算法的角度估计性能与文献[11]、文献[18]中的算法以及CRB[19]进行比较。所有信源的联合均方误差定义为
(20)
式中，
和
表示第ν次蒙特卡洛仿真φ和θ相应的估计值。
在所有的仿真实验中，所提出算法中子阵的阵元个数M=3，文献[11]中子阵的阵元个数为6，即L型阵列中共有11个阵元。由于文献[18]中算法应用的阵列结构不同，令其共包含13个阵元。此外，所有的仿真实验均进行1000次蒙特卡洛仿真。
仿真实验1
假设在一种欠定条件下，其中快拍数N、数据帧数L、信源个数K、信噪比SNR和扩展孔径ds分别为1000，500，18，30 dB，5λ。图3显示了欠定条件下所提出算法仍具有良好的估计性能。
如图3所示，当方位角和俯仰角满足情况1和情况2时，算法仍能够较好地实现方位角和俯仰角估计。当M=3时，本文提出的算法可实现多达18个信源估计。
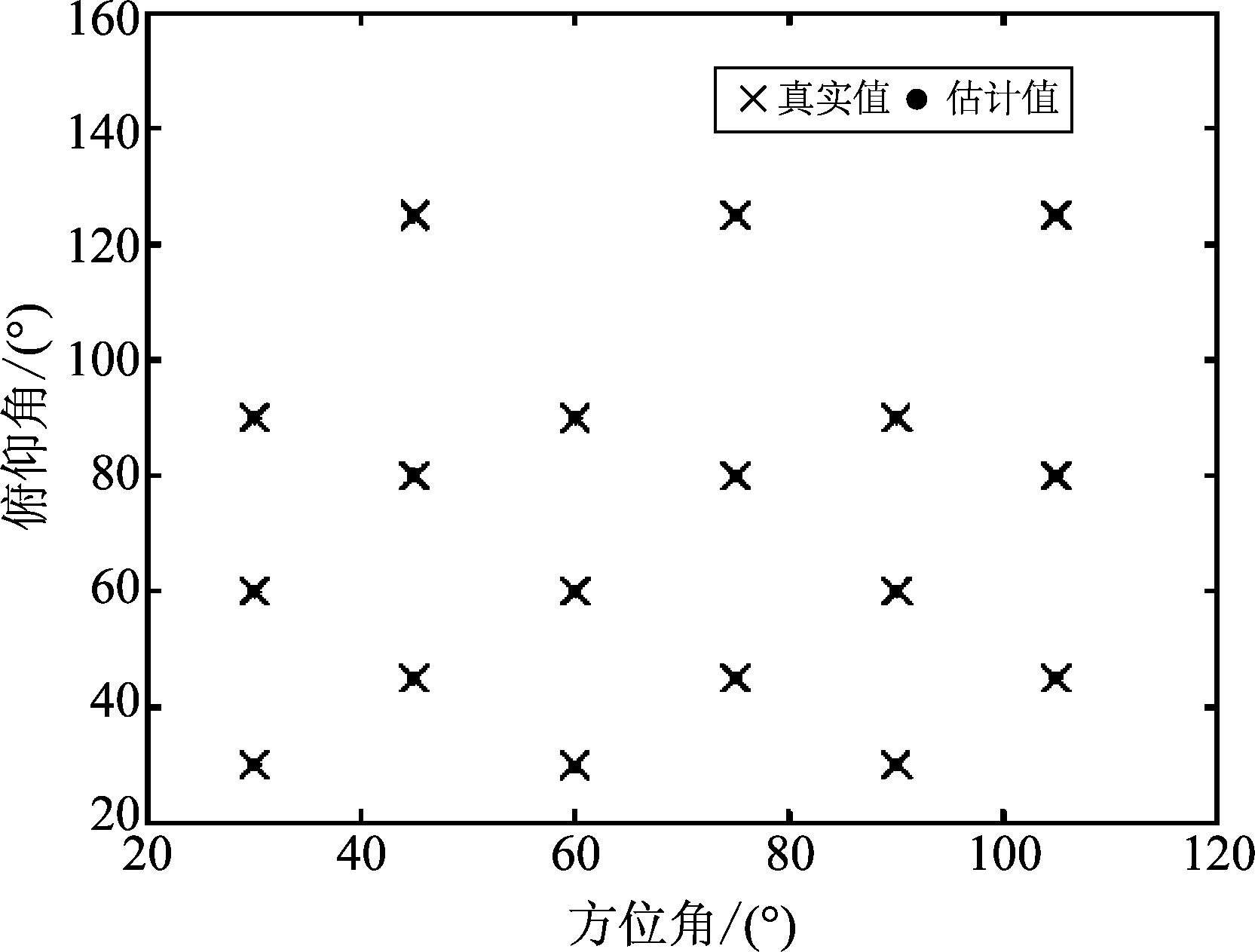
图3 欠定条件下的角度估计性能
Fig.3 Angle estimation performance in the underdetermined case
仿真实验2
当方位角和俯仰角满足情况3时，验证所提出算法的有效性。假设有K=2个信号入射到天线阵列，两个信号分别为(90°,60°)，(120°,90°)或(65°,33°)，(85°,60°)。即o1=1，ds=2λ，cos 60°=cos 90°+1/2且cos 90°=cos 120°+1/2；o2=1，ds=3λ，cos 65°=cos 85°+1/3且cos 33°=cos 60°+1/3。其他实验条件均与仿真实验1相同。图4为角度估计值分布散点图。值得注意的是文献[18]中的算法不能实现此种情况下的角度估计。
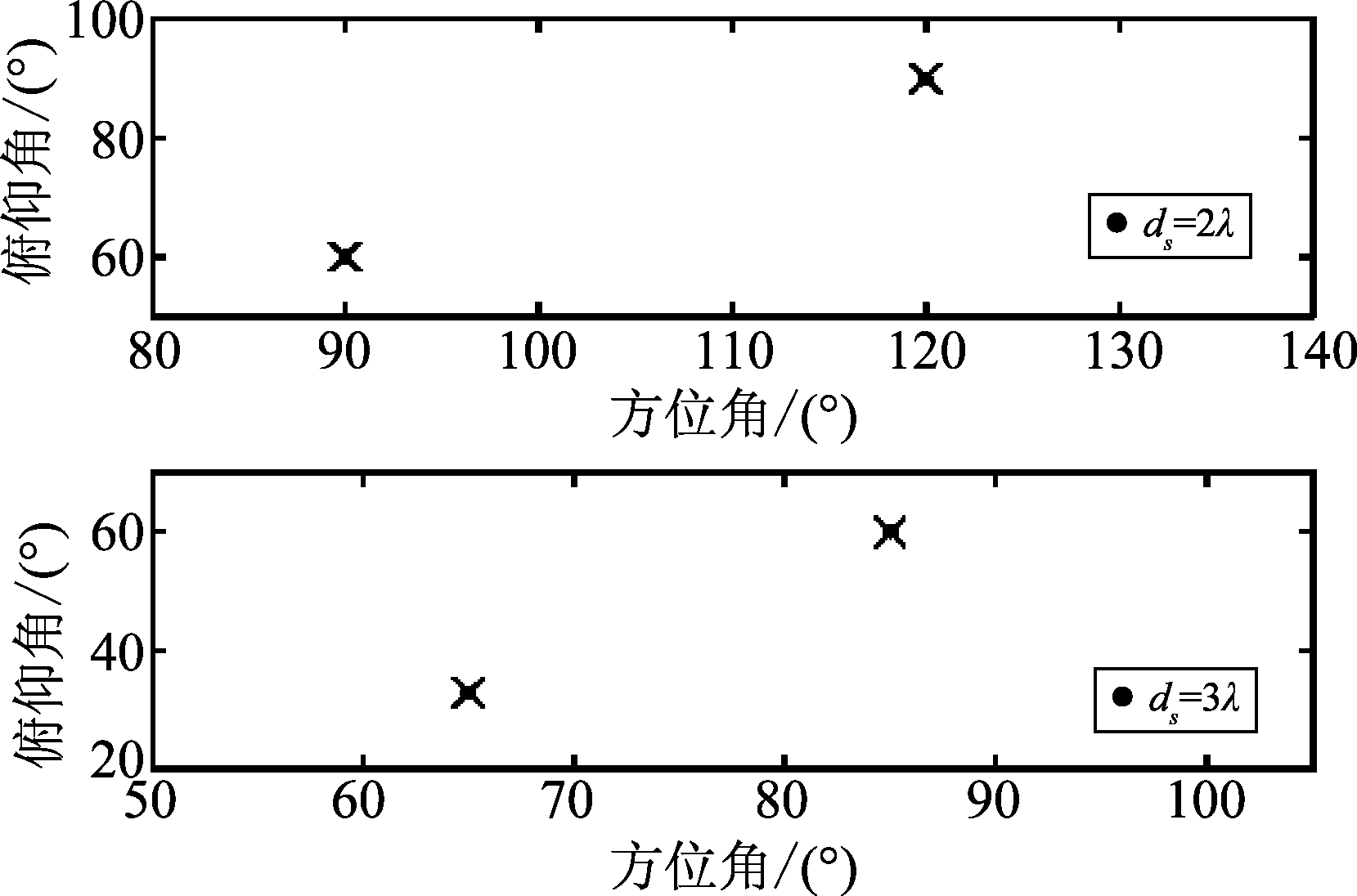
图4 情况3下的角度估计性能
Fig.4 Angle estimation performance for Case 3
从图4可以看出，当方位角和俯仰角满足情况3时，所提出的算法能够清晰地分辨这两个来波信号。根据文献[20]中的定理1可知，式(10)～(13)所示的四个对角矩阵中没有相等的对角元素时，算法才可获得正确的方向余弦估计值。在扩展孔径的二维 DOA估计算法中随着ds的增大，存在o，ds使得cos θ1(cos φ1)=cos θ2(cos φ2)+oλ/ds成立。因此，实验1和实验2证明了所提出的算法已解决了在扩展孔径的二维DOA估计算法中的奇异点问题，且角度估计性能较好。
仿真实验3
研究所提出算法的估计性能随阵元间距ds增大的变化情况。其中快拍数N、数据帧数L和信噪比SNR分别为500，10，10 dB。两个信号分别为(θ1,φ1)=(90°,60°)，(θ2,φ2)=(120°,90°)。图5分别给出了第一个信号的低精度无模糊估计值
均方根误差以及高精度无模糊的方向余弦估计
均方根误差随阵元间距ds的变化情况。(图中所描点对应的ds的取值分别为1λ、2λ、4λ、6λ、8λ、10λ、14λ、20λ、36λ、46λ、88λ)
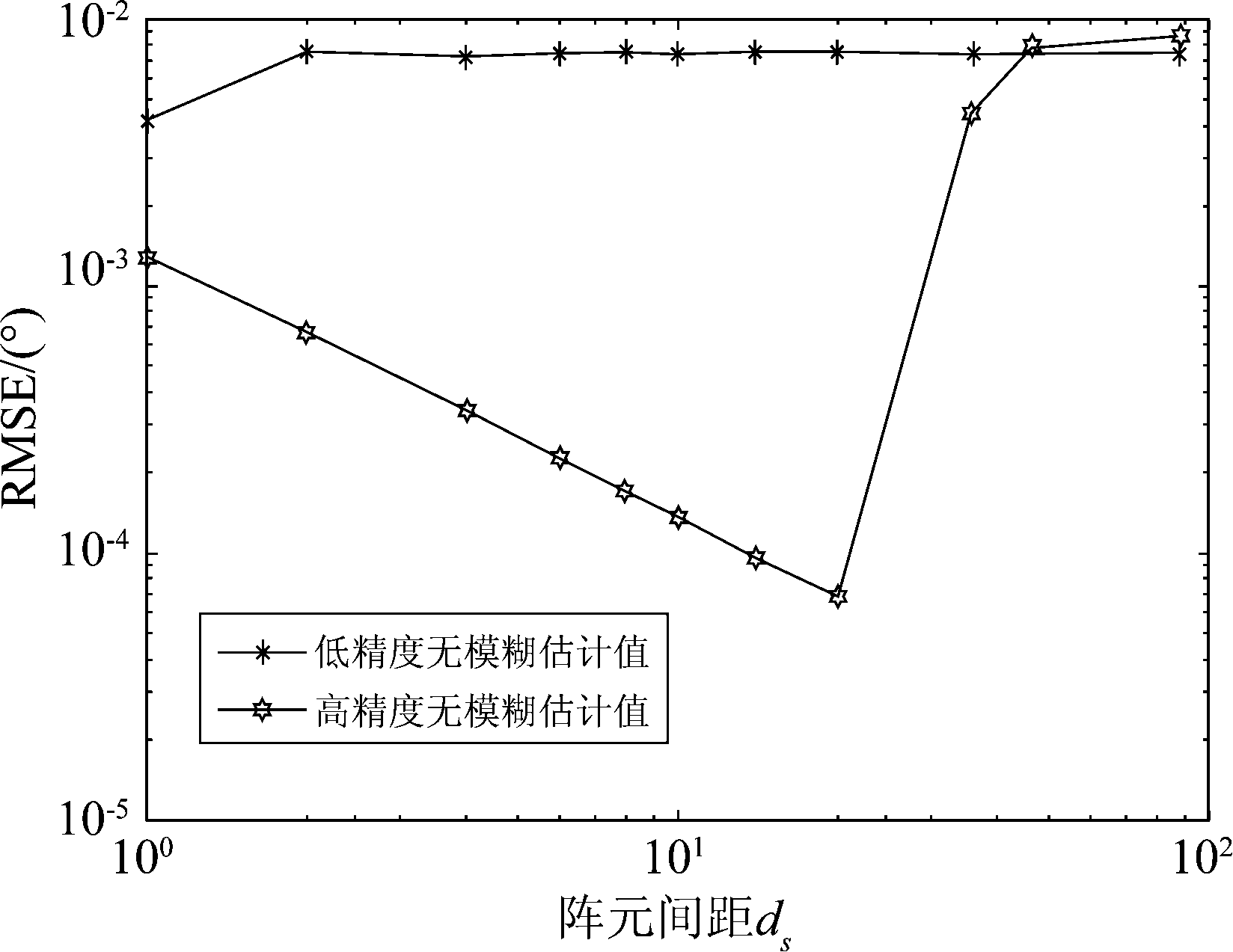
图5 RMSE随阵元间距的变化
Fig.5 RMSE versus element spacing
由图5可知，随着ds由1λ增长到14λ，角度估计的联合均方误差线性减小；扩展孔径有效地提高了角度估计性能。当ds>14λ时，误差却反向增大；当ds≥24λ时,解模糊得到的余弦估计误差越来越接近参考估计误差。由式(15)可知，一系列高精度模糊的方向余弦估计
的间隔为整数倍的λ/ds，随着ds的增大，两个相邻的模糊方向余弦估计值越来越接近，因此判别到相邻方向余弦估计概率增加。尽管没有作图，第2个信号的RMSE曲线具有相似的变化趋势，验证了以上规律。关于扩展孔径的非均匀阵列的详细研究，请参考文献[15,21]。同时，本实验ds的取值再次验证了所提出算法解决奇异点问题的有效性。
仿真实验4
本实验研究所提出算法的估计性能随信噪比的变化情况。其中，N=200， L=50，ds=8λ。假设有K=4个等功率非相关信号入射到天线阵列，信号的方位角和俯仰角分别为(60°,90°)，(60°,110°)，(80°,90°)和(80°,110°)。算法的角度估计性能随信噪比的变化情况如图6所示。
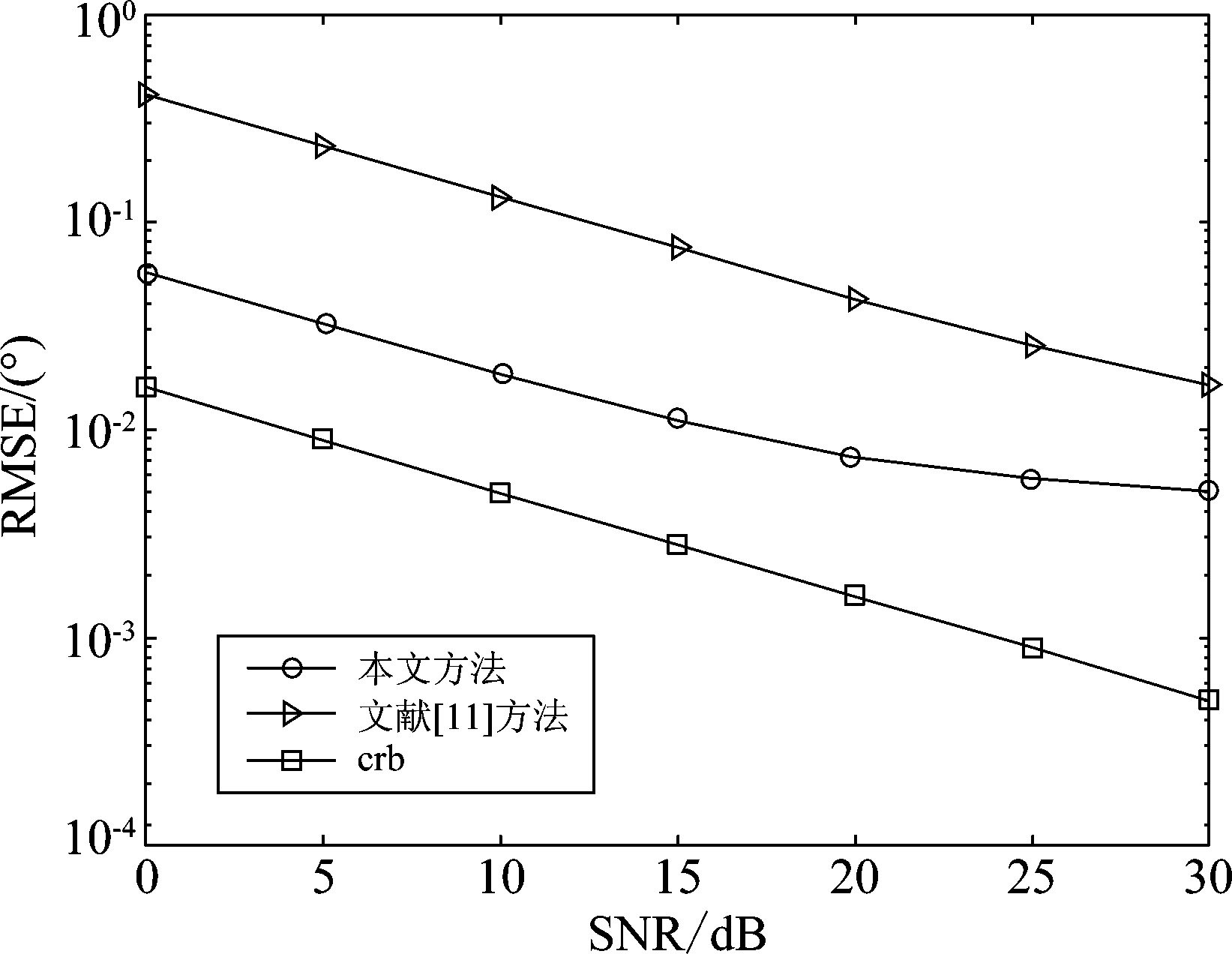
图6 RMSE随SNR的变化
Fig.6 RMSE versus SNR
仿真实验5
本实验研究所提出算法的估计性能随快拍数的变化情况。其中SNR=0 dB，其他实验条件均与仿真实验4相同。算法的角度估计性能随快拍数的变化情况如图7所示。
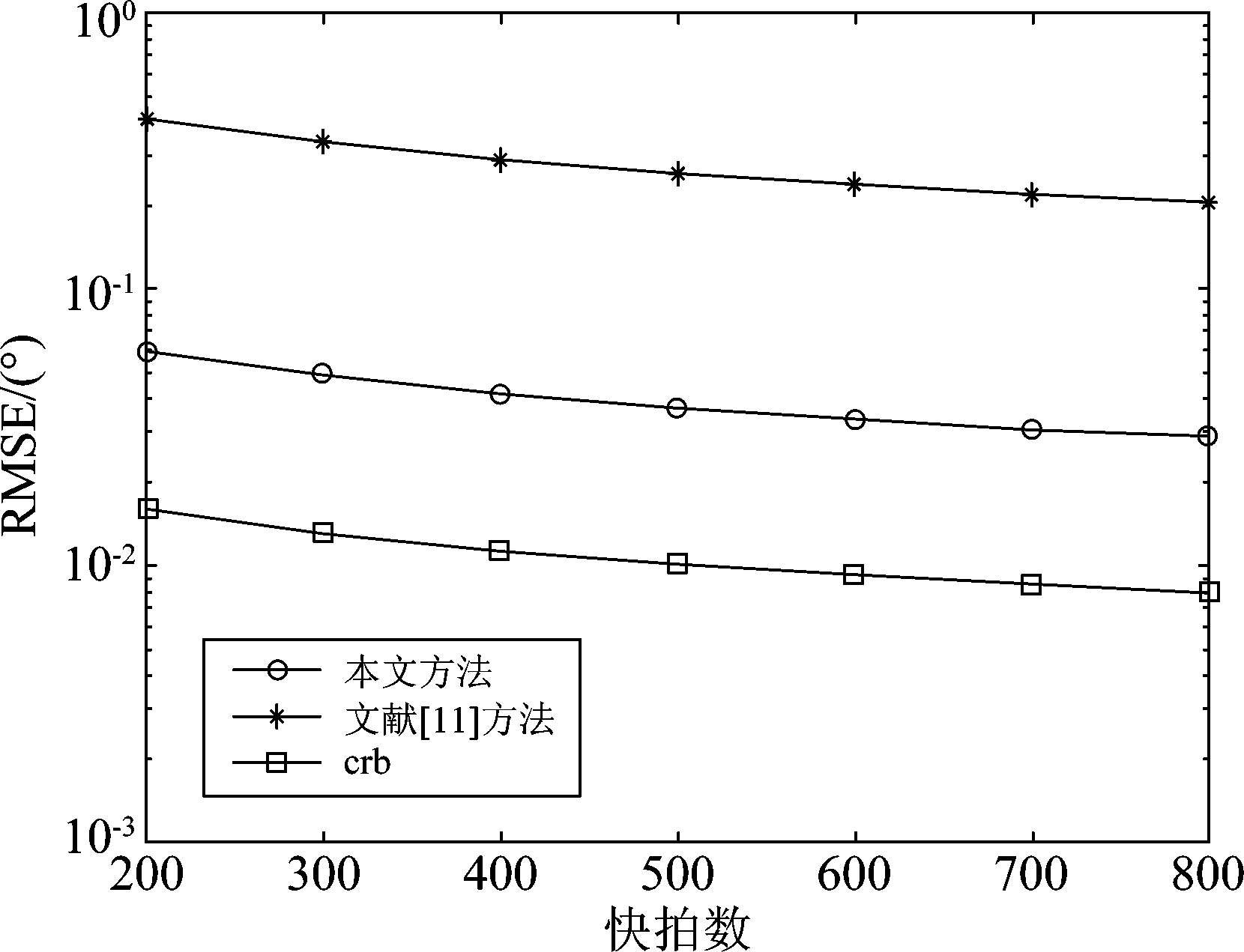
图7 RMSE随快拍数的变化
Fig.7 RMSE versus the number of snapshots
从图6和图7可以看出，随着SNR和快拍数的增加，两种算法的RMSE均减小,证明了所提出算法的有效性。值得注意的是，所提出的算法比文献[11]中的算法具有更好的角度估计性能。这是由于所提出的算法使用了扩展孔径的非均匀L型阵列，因此阵列孔径更大。
仿真实验6
本实验研究所提出算法对应不同角度的估计情况。其中快拍数N、数据帧数L、信噪比SNR和扩展孔径ds分别为200，10，15 dB，8λ。信号的方位角和俯仰角均在10°～80°之间以2°的步长变化。图8为对应不同角度的角度估计联合均方误差。
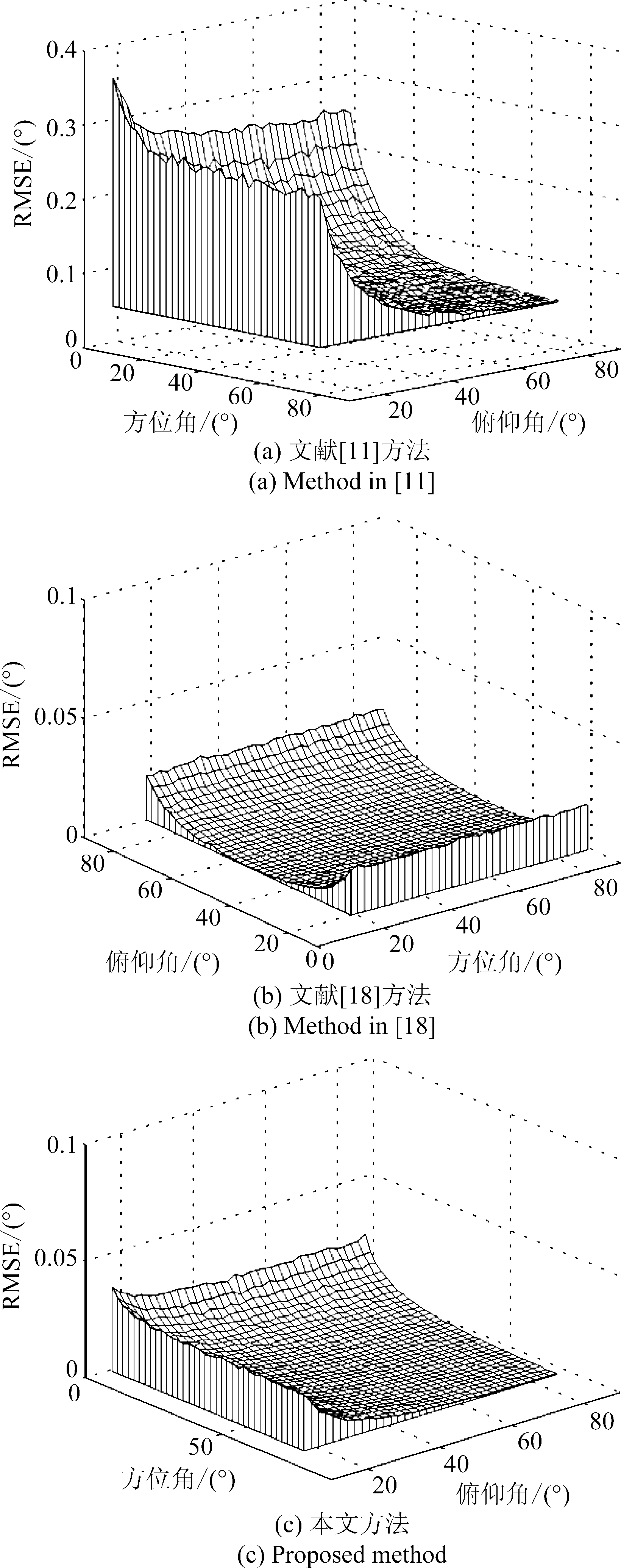
图8 不同方位角俯仰角的RMSE
Fig.8 RMSE for different azimuth-elevation angles
本文,文献[11]以及文献[18]中算法对应的平均联合误差分别为0.0154，0.1292，0.0160。与文献[11]中的算法相比，本文提出算法的角度平均估计性能较好。两种算法均应用于L型阵列，由于阵列结构本身的特点，对应俯仰角和方位角较小的角度组合，角度估计误差值相对较大。但由于本文在x轴和
轴上具有更大的阵列孔径，因此在给定角度范围内，本文方法的角度估计性能更好。与文献[18]中的算法相比，由于两种算法均使用扩展孔径因此仿真得到的平均联合误差是一个数量级。但在实际移动通信范围内(俯仰角为70°～90°)，本文算法的角度估计性能更好。
仿真实验7
由于文献[18]中的算法不能实现欠定条件下的角度估计，故研究其算法实现对两个信号源(60°,70°)，(60°,80°)的角度估计。其中，信噪比SNR=15 dB。其他实验条件均与仿真实验4相同。图9为两种算法角度估计值分布对比散点图。由图9可知，与文献[18]中的算法相比，本文所提出的算法在解决奇异点问题时的估计性能更好。
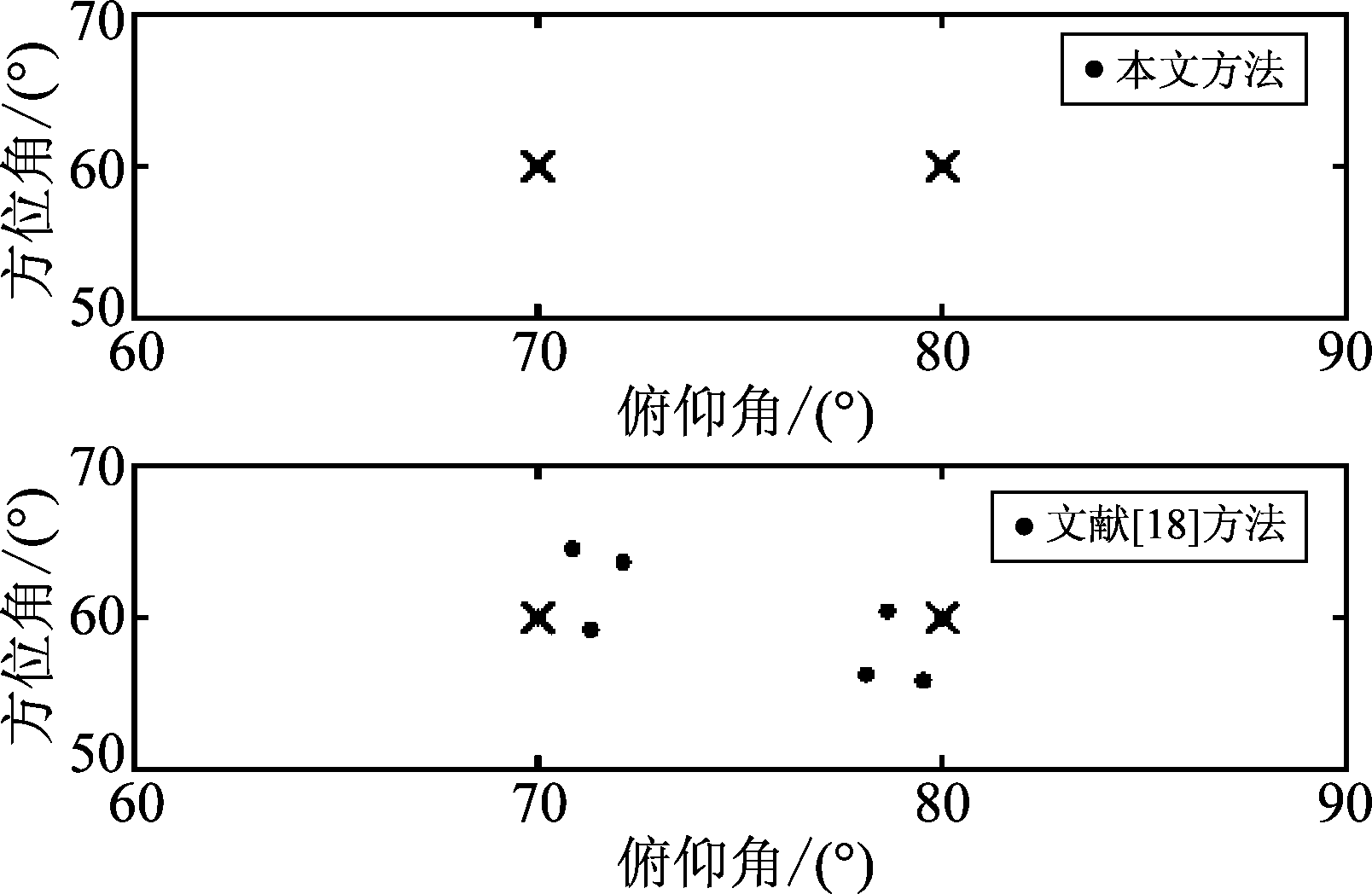
图9 情况1下的角度估计性能
Fig.9 Angle estimation performance for Case 1
5 结论
本文提出了一种扩展孔径的二维DOA估计算法。基于非均匀L型阵列，所提出的算法首先构造了四个延时互相关矩阵并对延时互相关矩阵进行奇异值分解得到了信号子空间。其次，利用选择矩阵从信号子空间中获得对角矩阵。再次通过联合对角化方法得到自动配对的精确和模糊的方向余弦估计值。最后，以低精度无模糊的方向余弦估计值为参考，从高精度模糊的方向余弦估计值中获取高精度无模糊的方向余弦估计值。所提出的算法能够实现方位角和俯仰角的自动配对。仿真结果表明所提出的算法有效地解决了扩展孔径的二维DOA估计算法中的奇异点问题。
[1] Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4):67-94.
[2] Wu Y, Liao G, So H C. A fast algorithm for 2-D direction-of-arrival estimation[J]. Signal Processing, 2003, 83(8):1827-1831.
[3] Li J, Zhang X, Chen H. Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method[J]. Signal Processing, 2012, 92(12):3032-3038.
[4] 杨晋生, 孙光涛, 陈为刚. 三平行线阵中基于改进传播算子的二维DOA估计方法[J]. 信号处理, 2016, 32(12):1446-1453.
Yang Jinsheng, Sun Guangtao, Chen Weigang. 2-D DOA estimation algorithm for three-parallel ULAs based on improved propagator method[J]. Journal of Signal Processing, 2016, 32(12):1446-1453. (in Chinese)
[5] Chen H, Hou C, Wang Q, et al. Improved azimuth/elevation angle estimation algorithm for three-parallel uniform linear arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14:329-332.
[6] Tayem N, Kwon H M. L-shape 2-dimensional arrival angle estimation with propagator method[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(5): 1622-1630.
[7] Gu J F, Wei P. Joint SVD of two cross-correlation matrices to achieve automatic pairing in 2-D angle estimation problems[J]. IEEE Antennas and Wireless Propagation Letters, 2007, 6:553-556.
[8] Tayem N, Majeed K, Hussain A A. Two-Dimensional DOA estimation using cross-correlation matrix with L-shaped array[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1077-1080.
[9] Wang G, Xin J, Zheng N, et al. Computationally efficient subspace-based method for two-dimensional direction estimation with L-shaped array[J]. IEEE Transactions on Signal Processing, 2011, 59(7):3197-3212.
[10] Xi N, Li L. A computationally efficient subspace algorithm for 2D DOA estimation with L-shaped array[J]. IEEE Signal Processing Letters, 2014, 21(8):971-974.
[11] Dong Y Y, Dong C X, Shen Z B, et al. Conjugate augmented spatial temporal technique for 2-D DOA estimation with L-shaped array[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14:1622-1625.
[12] Dong Y Y, Dong C X, Xu J, et al. Computationally efficient 2-D DOA estimation for L-shaped array with automatic pairing[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15:1669-1672.
[13] Dong Y, Dong C, Liu W, et al. 2-D DOA estimation for L-shaped array with array aperture and snapshots extension techniques[J]. IEEE Signal Processing Letters, 2017, 24(4):495- 499.
[14] Cardoso J F, Souloumiac A. Jacobi angles for simultaneous diagonalization[J]. Siam Journal on Matrix Analysis and Applications, 1996, 17(1):161-164.
[15] Zoltowski M D, Wong K T. Extended-aperture underwater acoustic multisource azimuth/elevation direction-finding using uniformly but sparsely spaced vector hydrophones[J]. IEEE Journal of Oceanic Engineering, 1997, 22(4):659- 672.
[16] He J, Liu Z. Extended aperture 2-D direction finding with a two-parallel-shape-array using propagator method[J]. IEEE Antennas and Wireless Propagation Letters, 2009, 8: 323-327.
[17] Marcos S, Marsal A, Benidir M. The propagator method for source bearing estimation. Signal Processing[J]. Signal Processing, 1995, 42(2):121-138.
[18] 顾陈, 何劲, 李洪涛,等. 基于扩展孔径ESPRIT算法的高精度无模糊二维DOA估计[J]. 兵工学报, 2012, 33(1):103-108.
Gu Chen，He Jin，Li Hongtao，et al． High accurate and unambiguous 2D direction finding estimation based on extended aperture ESPRIT algorithm[J]． Acta Armamentarii，2012， 33(1): 103-108. (in Chinese)
[19] Xia T, Zheng Y, Wan Q, et al. Decoupled estimation of 2-D angles of arrival using two parallel uniform linear arrays[J]. IEEE Transactions on Antennas and Wireless Propagation, 2007, 55(9):2627-2632.
[20] 殷勤业,邹理和,Newcomb R. 一种高分辨率二维信呈参量估计方法—波达方向矩阵法[J]. 通信学报, 1991,4:1-7.
Yin Q Y, Zhou L H, Newcomb R. A high resolution approach to 2-D signal parameter estimation—DOA matrix method[J]. Journal of China Institute of Communications, 1991, 4:1-7. (in Chinese)
[21] Zoltowski M D,Wong K T.Closed-form eigenstructure-based direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid[J]. IEEE Transactions on Signal Processing,2000,48(8):2205-2210.
