1 引言
随着各应用领域信号带宽的不断增加，目前的商用数字模拟转换设备(Analog-to-Digital Converter，ADC)已经难以达到所需的采样率要求，就算达到了采样率要求，大量的样本数据的存储和传输也将是一大难题。2006年提出的压缩感知(Compressed Sensing，CS)理论[1-2]解决了稀疏信号样本数据量大的问题，也为其采样提供了理论基础。随机解调(Random Demodulator，RD)[3-5]系统首次将CS应用于模拟域，实现了模拟信息转换[6](Analog to Information Conversion, AIC)，完成了对多音信号(multitone)的压缩采样，但是现实生活中，信号频率大多数情况下都不仅是多个单频点，这时用RD系统进行压缩采样就难以保证信号的正确重构。随后调制宽带转换器(Modulated Wideband Converter，MWC)[7- 8]实现了稀疏多带信号的欠奈奎斯特采样。由于通信、雷达和医疗等应用领域的信号都可以建模为稀疏多带信号，所以MWC结构具有很强的实用性。2016年李智[9]团队将其扩展到分布式领域，提出了分布式MWC(Distributed Modulated Wideband Converter，DMWC)。Eldar团队在2017年提出了基于均匀线性阵列(Uniform Linear Array，ULA)的MWC系统[10]。可见MWC正在逐步向分布式发展，分布式传感器网络在具有扩大探测范围、提高探测实用性等优点的同时还有一个很大的弊端就是节点分布造成的硬件资源浪费。且对于无人机探测等三围空间的分布式传感器网络，硬件质量需要严格控制到克量级才能达到无人机飞行的载重要求。所以用软件的方法找到一个可以准确恢复的最小通道数，以尽量少的硬件代价实现高概率恢复很有必要。
重构作为MWC系统的核心部分之一，一直以来都广受关注[11-16]。近年来提出的多种算法中包括正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法[7]，RMMV(Random Multiple Measurement Vectors)算法[11]，ReMBo(Reduce MMV and Boost)算法[12]，MVT(Measurement Vectors Transform)算法[13]，ISOMP(Improved Simultaneous Orthogonal Matching Pursuit)算法[14]，RPMB(Randomly Project MMV and Boost)算法[15]等。但是以上各类算法在没有噪声的情况下，实现高概率(≥99%)重构所需的最小通道数还远高于理论极限值。文献[7]提出可以通过扩展通道来降低采样通道数，但是这个方式需要增大硬件低通滤波器的截止频率、增大ADC的采样速率、增加后端数字扩展。因此，仅仅只在软件上提高重构性能、降低所需通道数，不仅能降低MWC系统的整体采样率，还可以节约硬件设备，减少硬件体积，满足无人机通信等分布式传感器网络对接收机设备小型化的要求。
本文提出了可提高低通道数下重构性能的最小相关性(Minimum Correlation，MinCor)支撑集重构算法和最大-最小相关性(Maximum and Minimum Correlation，Max-MinCor)支撑集重构算法。两种算法首先都通过特征值分解进行降维[7]，然后根据MUSIC(Multiple Signal Classification)思想[16]将测量值矩阵分为信号子空间和噪声子空间。MinCor算法根据噪声子空间与感知矩阵之间的最小相关性求取支撑集。在无噪声条件下，MinCor算法达到高恢复率(≥99%)所需的通道数接近理论极限值，但是信噪比小于10 dB时其恢复率下降。为了提高其抗噪性，Max-MinCor算法联合利用信号子空间与感知矩阵的最大相关性以及噪声子空间与感知矩阵的最小相关性分别求取支撑集。Max-MinCor算法在MinCor算法的基础上增加了抗噪性能。
2 MWC系统描述
针对稀疏多带信号，MWC的系统框图如图1所示，奈奎斯特率为fnyq的稀疏多带信号x(t)同时进入m个通道，在第i个通道内，与伪随机序列pi(t)混频得到一个带限的信号
在±1之间随机变化，变化周期为Tp。混频后的信号通过低通滤波器(Low pass filter, LPF)截断频谱，得到基带频谱，其中截止频率为fs/2， fs=1/Ts。最后以fs的采样率采得m个通道的观测样本yi(n)，其傅里叶变换可以表示为：
(1)
其中
可以将上式简写为：
(2)
其中A为感知矩阵，由cil组成，
为原始信号的各个频段X(f-lfp)表示的L(L=2L0+1)维向量。上式可看成一个CS模型，所以用观测样本yi(n)和CS恢复算法对原始信号进行恢复[7]，即可求得原始稀疏多带信号x(t)的支撑集，进而通过频谱逆搬移重建出信号
在MWC恢复过程中重构支撑集是非常重要的一步。理论上只需要m≥2N就可以重构出原始信号的支撑集[7]，N为x(t)中的频带数。然而，对于长度为L的N-稀疏信号，OMP算法需要m≥2Nln(L)，基追踪算法(Basis Pursuit, BP)需要m≥Nlog2(L)[17]。只要未知信号长度L大于4，两者均大于2N。文献[7]将OMPMMV算法应用于MWC的支撑集重构，实验表明当m>4Nlog(M/2N)时可以达到高概率重构，其中M为伪随机序列长度，但该结果与理论下限2N还有较大差距。针对该问题本文提出MinCor和Max-MinCor算法。
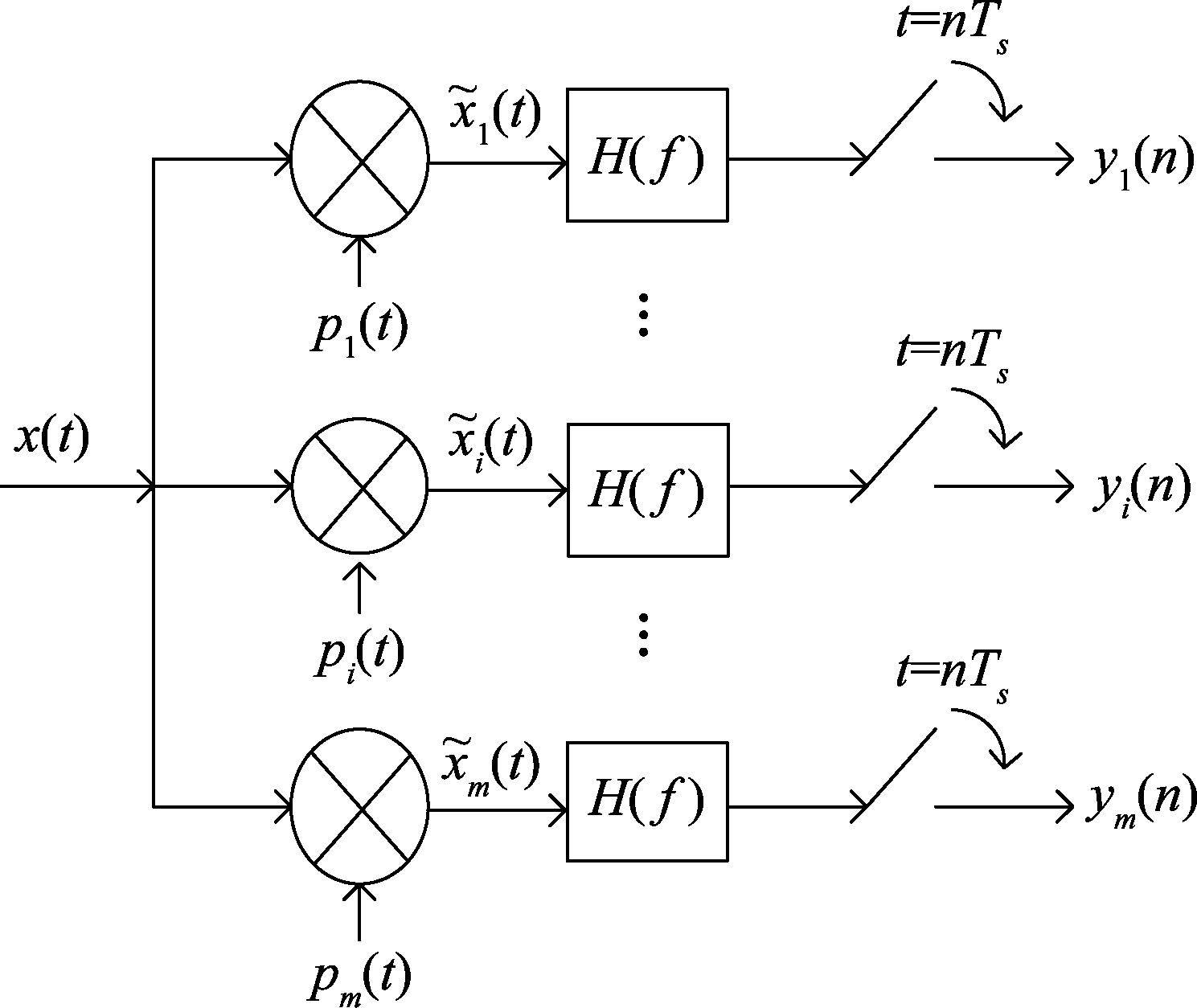
图1 MWC系统框图
Fig.1 Block diagram of modulated wideband converter
3 MinCor算法和Max-MinCor算法
3.1 MinCor算法
现有的MWC恢复算法都是通过观测样本矩阵与感知矩阵的最大相关性来求支撑集，因此与感知矩阵不具有最大相关性的那部分观测值就被舍去了，没有用于计算，然而，剩余部分观测值与感知矩阵的最小相关性中也包含有支撑集信息，用其计算支撑集的数学表达式如下：
(3)
其中W为样本矩阵Y的噪声子空间，j为感知矩阵A中的列序号，S为所求得的支撑集，由2N个满足上述条件的i组成。下面以定理形式引入，并对其进行证明。
定理1 设降维后的MMV模型为V=AU，其中U与原始信号
有相同的支撑集，矩阵A是感知矩阵，A∈Rm×L，其中m为MWC的通道数，L为伪随机序列pi(t)的长度，矩阵V为观测样本矩阵Y通过降维得到的矩阵[7]，为Y的信号子空间，V∈Rm×K，K为U的稀疏度，通常m>K。矩阵A的Kruskal秩[11]即A中最大线性无关的列数σ(A)=m≥K+1，U的支撑集S=supp(U)中有K个非零项，即|S|=K。W与V正交即WTV=0，即W为剩余观测值组成的矩阵，W∈Rm×(m-K)。则没有噪声时，当且仅当j∈S时，W在Aj上的投影为0，可以表示为<W，Aj>=0。
证明 在没有噪声时，由支撑集S的定义可知，V=ASUS，其中AS表示对应于S的A的列子集，US表示对应于S的U的行子集。因此由已知条件可得WTV=WTASUS=0。因为U的稀疏度为K，得出rank(US)=K，即U的S列线性无关，所以US可逆。于是WTAS=0，即当j∈S时，<W，Aj>=WTAj=0成立。
假设除了j∈S外，还有j0
S使<W,Aj0>=0成立，即WTA[S, j0]=0。从WTV=0可以知道，剩余观测值W的列组成的矩阵的秩为m-K。又因为WTA[S, j0]=0，根据线性方程组理论rank(WT)+rank(A[S, j0])≤m,又因为rank(A[S, j0])≥rank(AS)=K所以rank(A[S, j0])=K，说明A中最大线性无关的列数为K，与A中最大线性无关的列数为K+1相矛盾。所以当且仅当j∈S时，<W，Aj>=WTAj=0成立。
由以上定理可以推出在没有噪声时，当m≥K+1时，通过计算噪声子空间W在A的各列上的投影值，即<W，Aj>，j∈1,2,…,L可以求出支撑集。在有噪声的情况下，由于<W，Aj>，j∈S不再为零，需要通过比较<W，Aj>的数值，取较小的K项即可求出支撑集。向量W在另一个向量A上的投影可以反映向量W与向量A之间的相关性[14]。所以将以上描述的算法命名为最小相关性算法(MinCor算法)。
由以上证明可以看出，采用噪声子空间W来计算MWC支撑集需要满足以下要求：1)感知矩阵A的任意m列线性无关；2)矩阵W的秩等于m-K。因为构成MWC感知矩阵的伪随机序列pi(t)的随机性，1)得到保证[7]。如果rank(U)=K，因为AS中各个列互不相关，所以：
rank(W)=m-rank(V)=m-rank(U)=m-K
(4)
即满足2)。其算法如表1所示。
表1 MinCor算法
Tab.1 MinCor algorithm
输入:样本矩阵Y,感知矩阵A,频带数量N。 输出:支撑集S,未知矩阵的估计X^(n)。
续表1
初始化:残差R=A,S=⌀,设置迭代次数iter=1。步骤 1 对Y的相关矩阵进行特征值分解,取较小的m-2N个特征值及其所对应的特征向量为噪声子空间W。步骤 2 循环:1)i=argminj∑col〈Wcol,Rj〉∧2其中W的每一列记为Wcol,R的每一列记为Rj;2)S=S∪{i},保存相关性最小的A的列数;3)找到i的对称的频带索引值并一起加到支撑集向量S中;4)A(:,S)=-inf; R=R-A;更新残差,将已选中的A的列置为无限大;5)iter=iter+1;当iter大于最大迭代次数N时,循环结束。步骤 3 通过伪逆完成重构,返回输入信号的估计值X^(n)。
3.2 最大-最小相关性算法
针对MinCor算法在信噪比小于10 dB时，恢复性能下降的问题，本文提出最大-最小相关性算法(Max-MinCor)。该算法综合了最大相关性与最小相关性算法各自的优点，分别用最大相关性方法和最小相关性方法计算支撑集，然后将两种方法求得的支撑集求并集得到初步支撑集，在初步支撑集项数大于通道数时添加判决条件删除多余支撑集。算法步骤如表2所示。
表2 Max-MinCor算法
Tab.2 Max-MinCor algorithm
续表2
5)iter=iter+1;当iter大于最大迭代次数N时,循环结束。步骤 3 执行最小相关性算法,并将支撑集保存到S2。步骤 4 初步支撑集S=S1∪S2。步骤 5 添加判决条件:当S中支撑集项数大于通道数m时,求判决量Z=║WTA(:,Sj)║2,j=1,2,…,length(S),删除S中Z的值较大的m-length(S)个支撑集。得到最终支撑集S^。步骤 6 通过伪逆完成重构,返回输入信号的估计值X^(n)。
4 实验结果
本节设计以下三个实验对提出算法进行验证：4.1节对比了MinCor、Max-MinCor和OMP、RPMB算法的重构成功率情况，其中RPMB算法中解MMV模型用OMPMMV方法，重复尝试次数设置为10，门限值设置为0.1，投影维度为2N；4.2节比较了以上几种算法在运行时间上的差异；4.3节验证了MinCor、Max-MinCor算法在扩展通道情况下可用于进一步减少通道数。
采用文献[7]中的信号模型和采样参数，实验中的多带信号由式(5)产生：
cos(2πfi(t-τi))+n(t)
(5)
其中n(t)为高斯白噪声，MWC系统中的参数设置为：频带数N=6， fnyq=10 GHz，带宽B={50,50,50}MHz，能量系数E={10,20,30}，延迟时间τ={3.159，5.528，1.580}μs， fi∈[-fnyq/2， fnyq/2]，且fi随机产生，伪随机序列长度L=195，样本长度为405。
图2为一个加入SNR=20 dB的高斯白噪声的信号与其频谱图。设置m=30，图3和图4分别为对图2信号进行MWC采样后，用MinCor算法和Max-MinCor算法恢复的信号和频谱图。从图3和图4可以看出，此时，MinCor算法和Max-MinCor算法的恢复效果在时域和频域显示都很好。
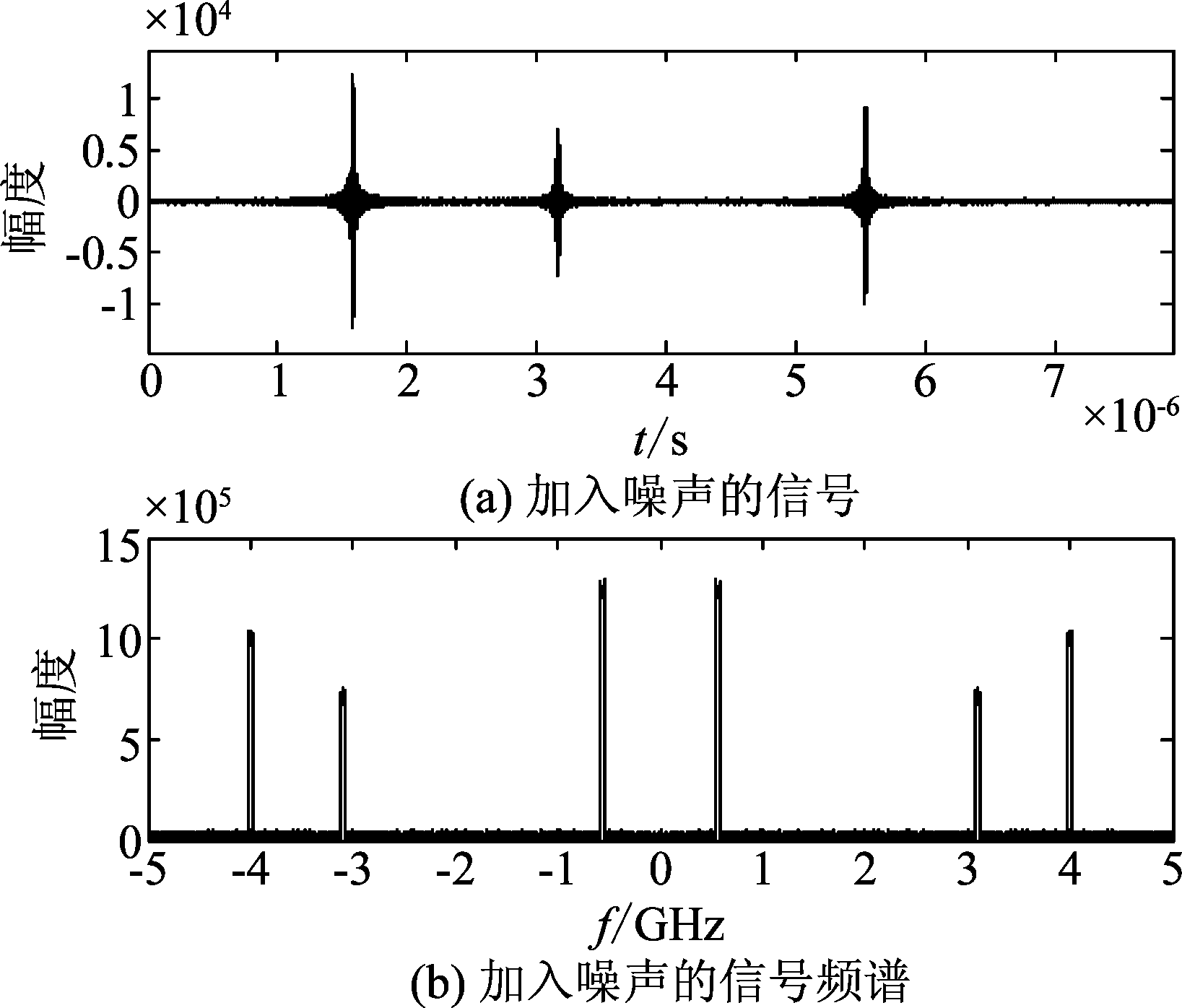
图2 加入噪声的信号及其频谱图
Fig.2 Original noisy signal and its spectrum
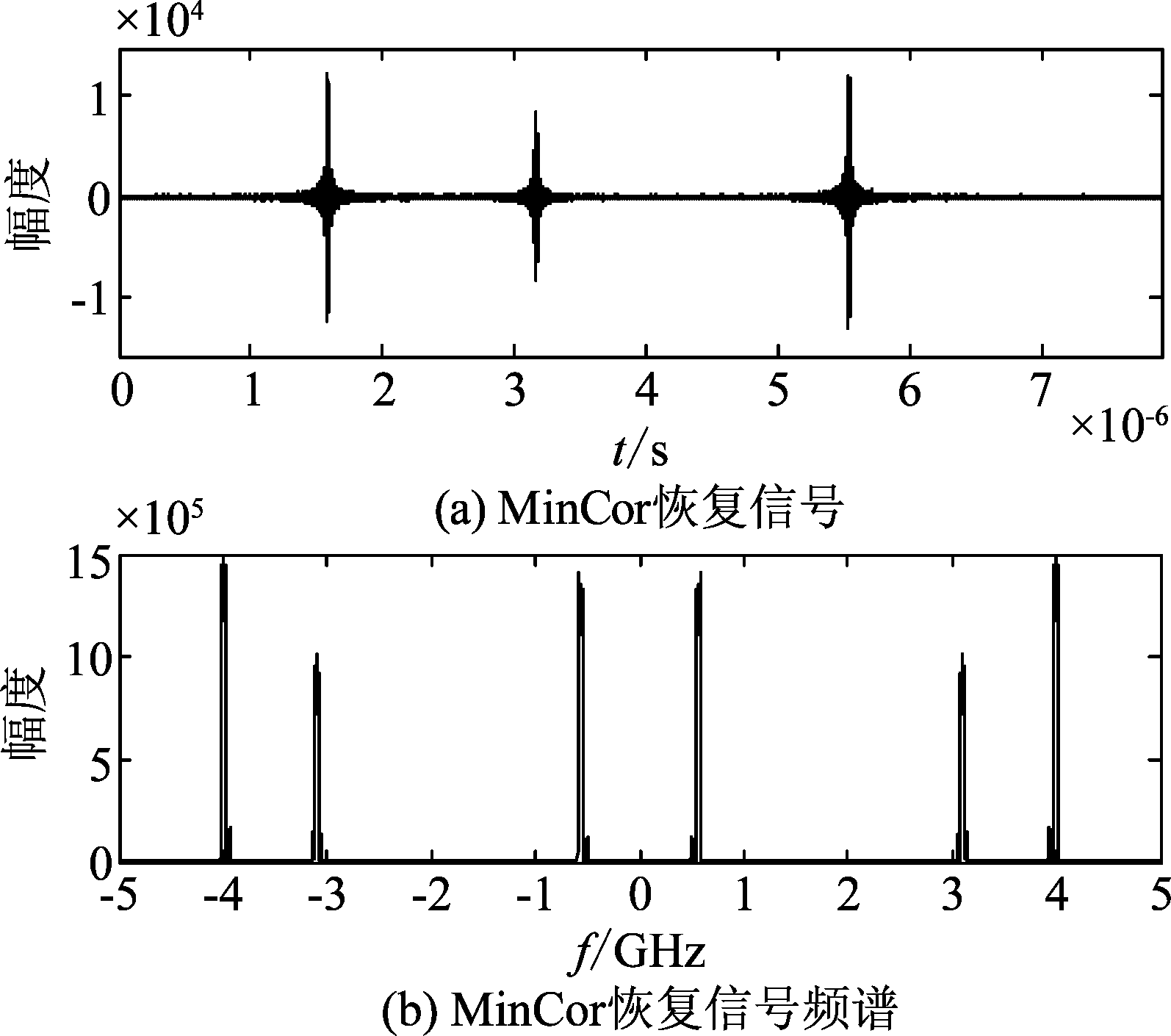
图3 MinCor恢复信号及其频谱图
Fig.3 Reconstructed signal based on MinCor and its spectrum
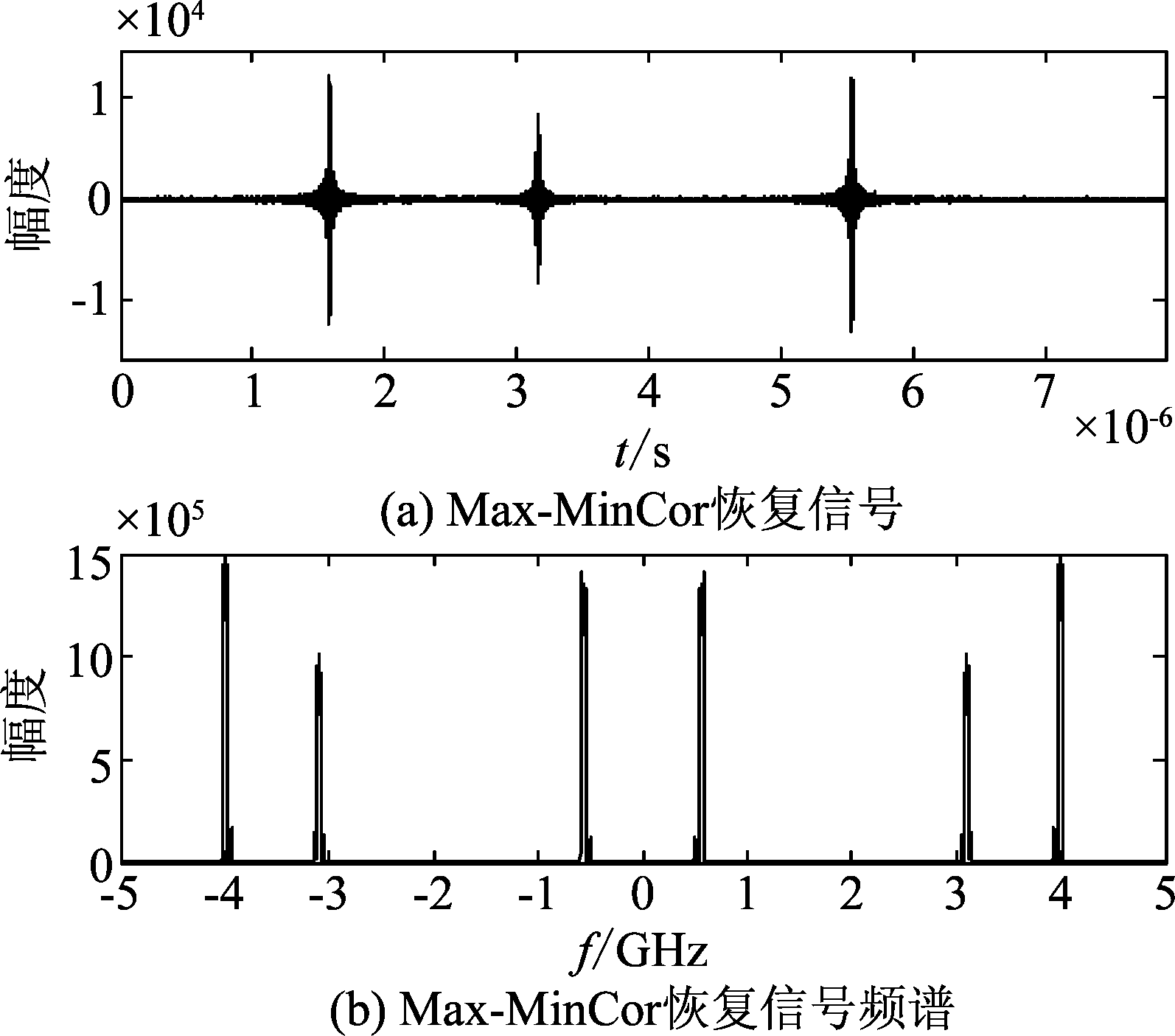
图4 Max-MinCor恢复信号及其频谱图
Fig.4 Reconstructed signal based on Max-MinCor and its spectrum
4.1 重构成功率比较
计算重构成功率时，进行500次蒙特卡罗实验，计算支撑集成功方法见文献[7]。图5给出了在不同SNR下，当通道数m∈[1,41]时Max-MinCor、MinCor、OMP、RPMB算法的重构成功率情况。可见，在没有噪声时，Max-MinCor、MinCor算法在m=K+1=13时即可实现高于99%的重构成功率。在有噪声时，以上两种算法仍然能在低通道数下实现高概率重构。在不同信噪比条件下，从实验结果可以看出，当m<22时，MinCor算法重构成功率明显高于OMP和RPMB；在信噪比较低时(<10 dB)，随着通道数的增加MinCor算法重构成功率低于OMP，此时Max-MinCor算法的恢复率在所选通道数区间高于MinCor、OMP和RPMB，稳定时恢复率可以达到96.6%，比MinCor算法稳定时的恢复率高6%左右。
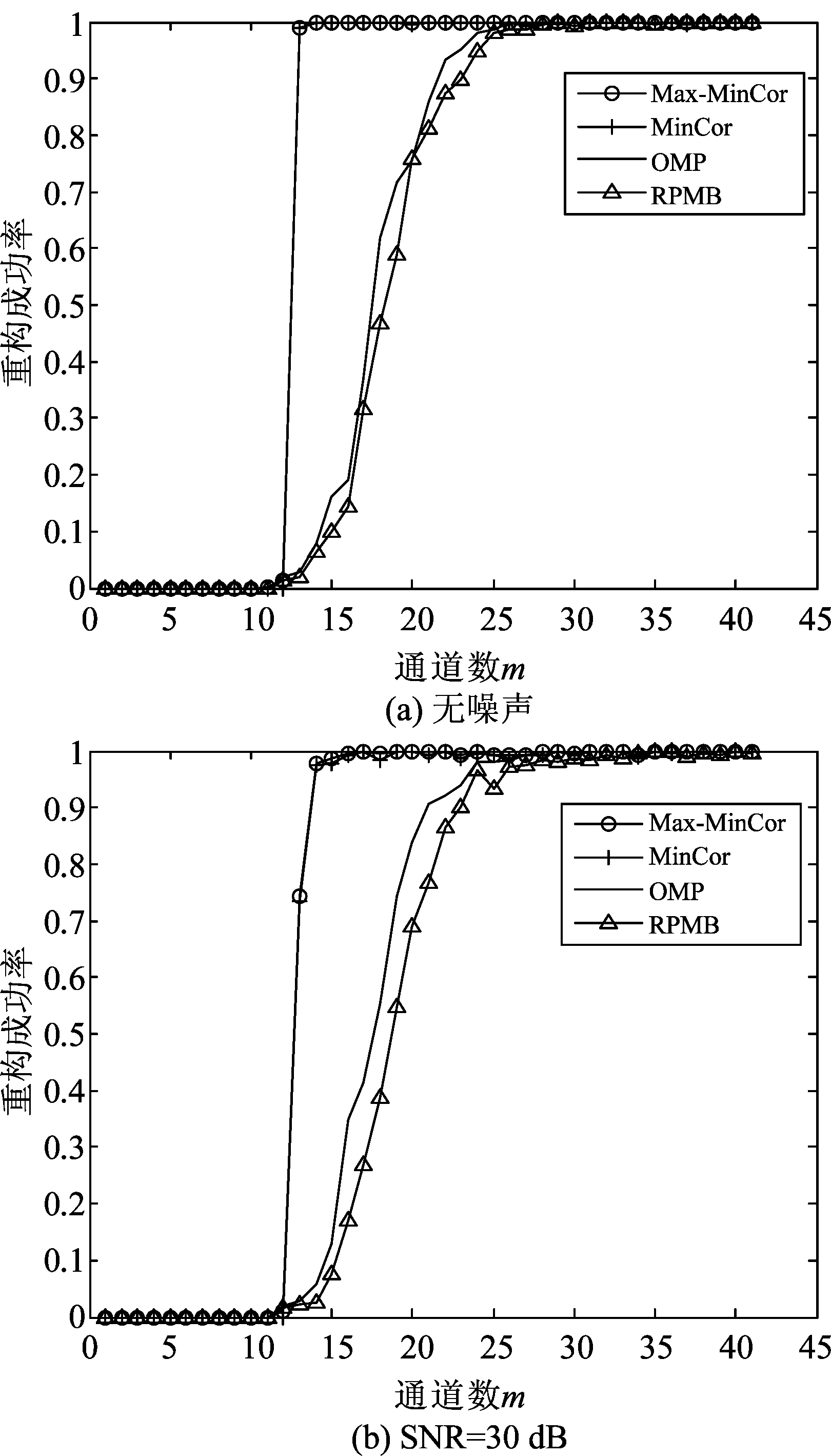
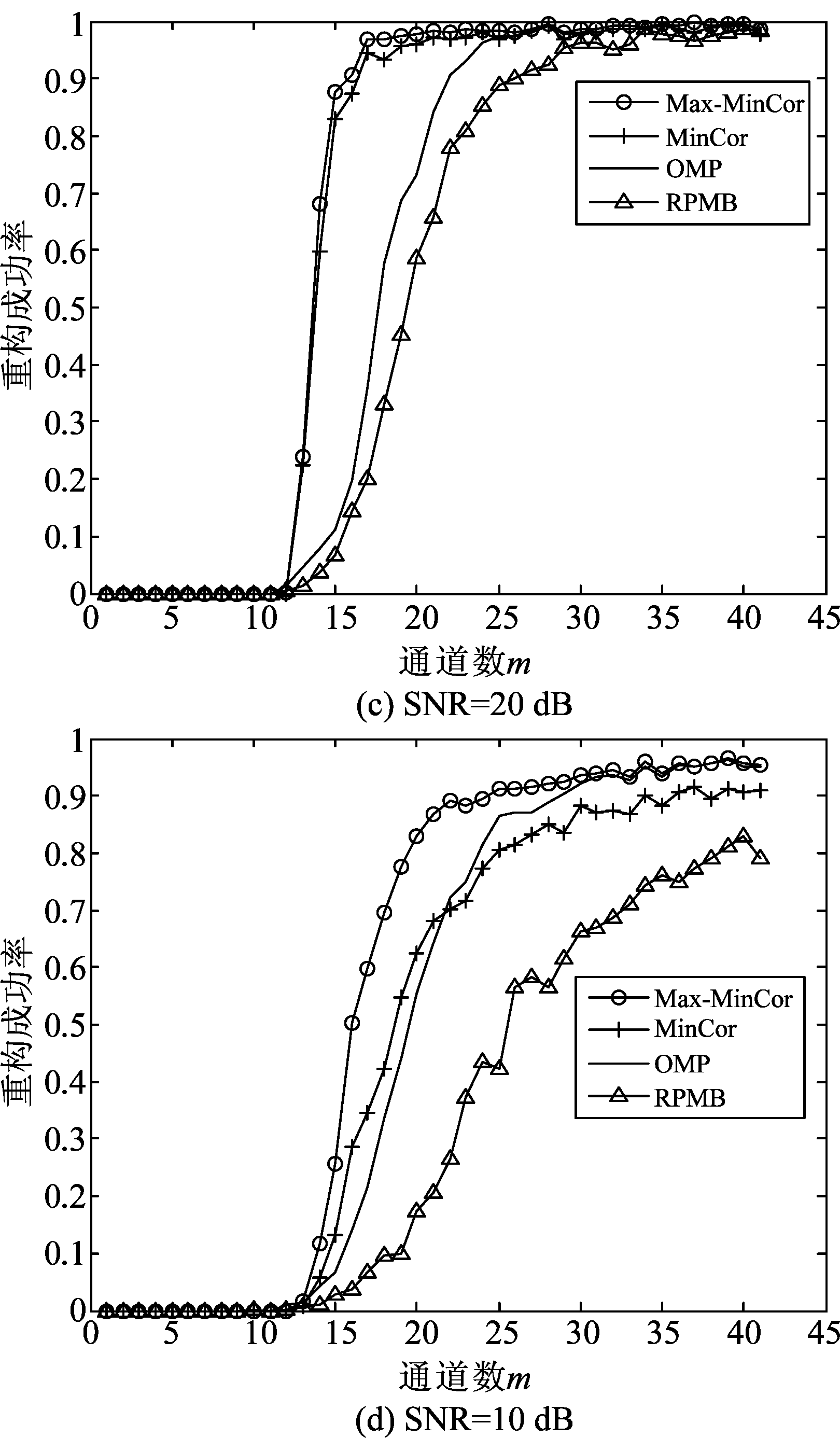
图5 不同信噪比时的重构成功率比较
Fig.5 Reconstruction success rate comparison under different SNRs
4.2 重构时间比较
MinCor算法的另一个优点是在通道数较小时，因为其测量值矩阵的维度为m×(m-2N)小于OMPMMV算法的测量值矩阵维度m×2N，所以当m在区间[2N+1,4N]取值时，MinCor算法的运行时间小于OMP、RPMB和Max-MinCor算法，这时在信噪比大于10 dB时，MinCor算法可实现快速高概率重构。
本节在4.1节的基础上，设置m∈[10,60]，SNR=30 dB，其余参数不变，得到Max-MinCor、MinCor、OMP、RPMB算法的支撑集重构所需时间对比图如图6所示。图6中重构时间等于同一个信号重复执行500次支撑集求解过程的总时间除以500，即多次重构的平均重构时间。由图6可以看出，重构时间随着样本数据量(即通道数)的增加而增加，在通道数小于35时，MinCor算法的重构时间低于以上所有算法的重构时间。
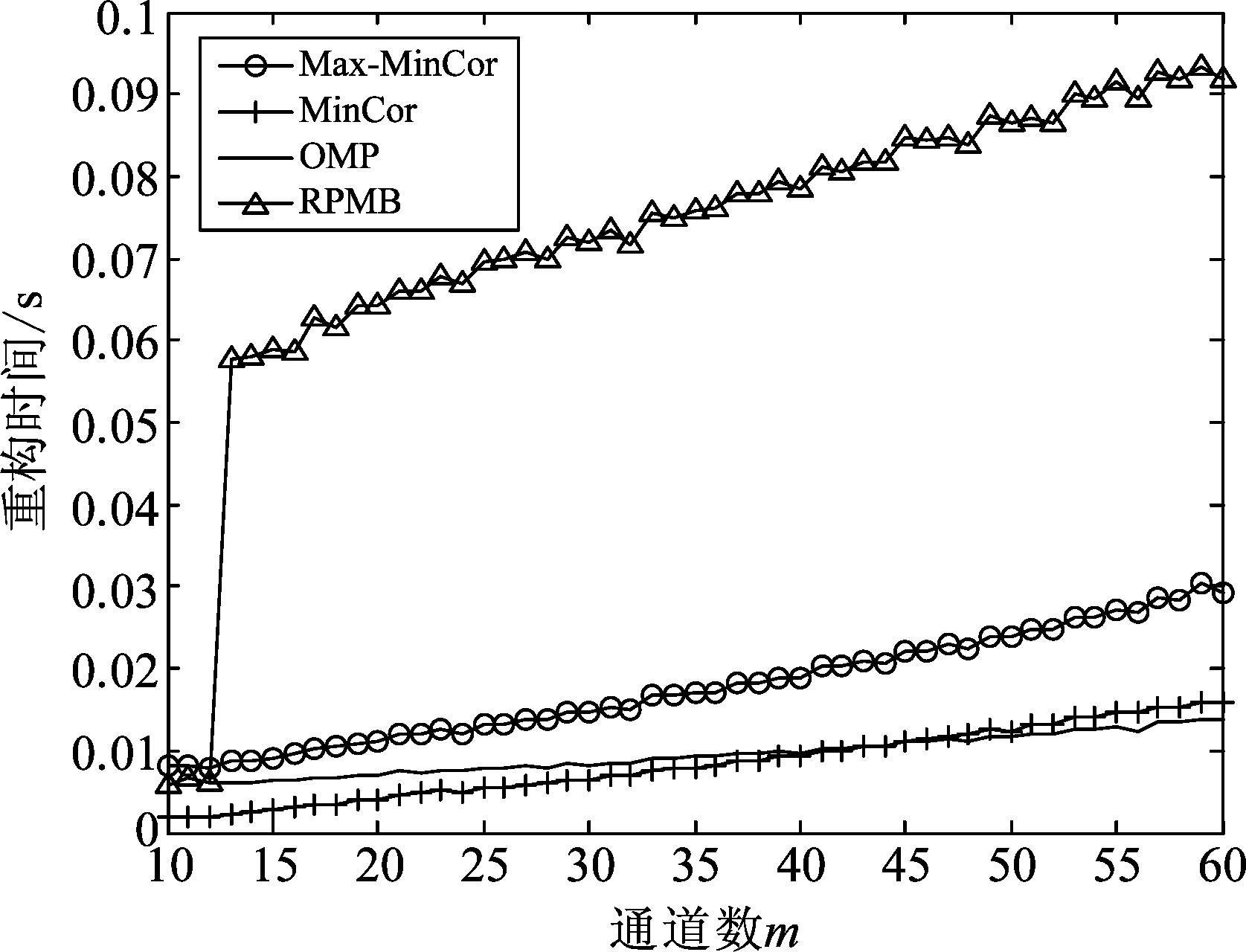
图6 重构支撑集所需时间对比
Fig.6 Reconstruction time comparison
4.3 与通道扩展复用进一步减小通道数
文章[7]提出的扩展通道的方法通过增加后端ADC采样率来达到降低通道数节约硬件成本的目的。这种方法是实用的，且与本文提出的MinCor、Max-MinCor算法并不矛盾，两者复用将达到更好的效果。MinCor、Max-MinCor算法与扩展通道复用，理论上可以将频带数为N时恢复率达到99%以上所需的最小通道数从2N+1降低到「(2N+1)/q⎤，其中q为扩展因数，「•⎤表示向上取整，更大程度上减小了硬件通道数。
本节在4.1节的基础上，设置q=3，其余参数不变。图7给出了MinCor、Max-MinCor算法与OMP、RPMB算法在不同信噪比下，当通道数m∈[1,41]时的重构成功率情况。可以看出当SNR≥20 dB时，MinCor算法重构成功率大于等于OMP和RPMB；Max-MinCor算法重构成功率高于MinCor、OMP和RPMB；且在无噪声的理论条件下，m=5时就可以达到100%的恢复率，当SNR为10 dB时，MinCor算法稳定重构率能达到95%左右，Max-MinCor算法稳定重构率能达到98%左右。从图7(a)的实验结果也可以看出，无噪声时，恢复率达到99%以上的最小通道数从扩展前的13减小到了扩展后的5。
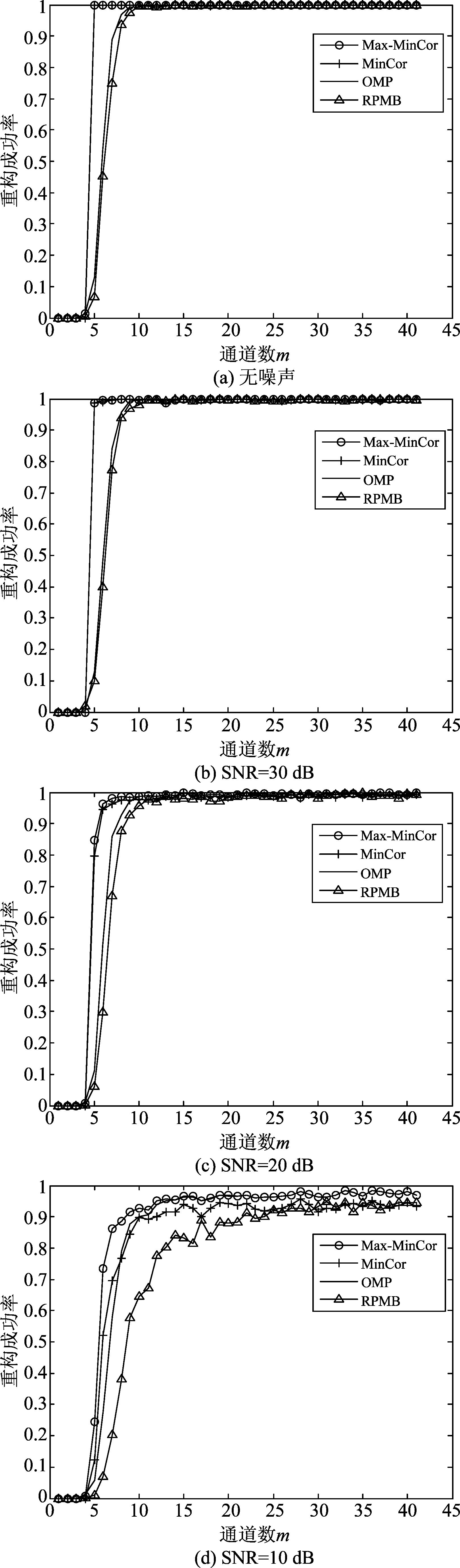
图7 扩展因数q=3，不同信噪比时的重构成功率比较
Fig.7 Reconstruction success rate comparison under different SNRs if q=3
5 结论
针对MWC中现有算法高概率恢复支撑集所需通道数高的缺陷，提出两种新的计算支撑集的方法即MinCor算法和Max-MinCor算法。实验结果表明无噪声条件下两种算法完美恢复所需的最小通道数均已接近理论极限。且MinCor算法在低通道数下恢复速率高于现有MMV算法，但该方法缺失了一定的抗噪性。Max-MinCor算法在MinCor算法的基础上提高了抗噪性能，但该算法恢复速率有降低。同时，如果有进一步降低通道数的要求，以上两种方法可以与通道扩展进行复用。在以后的研究中，可以对算法的抗噪性能和运算速率进行进一步改善。
[1] Candès E J, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction From Highly Incomplete Frequency Information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509．
[2] Donoho D L. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306．
[3] Kirolos S, Laska J, Wakin M, et al. Analog-to-Information Conversion via Random Demodulation[C]∥2006 IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software, USA,2006: 71-74.
[4] Laska J, Kirolos S, Duarte M, et al. Theory and Implementation of an Analog-to-Information Converter using Random Demodulation[C]∥2007 IEEE International Symposium on Circuits and Systems, USA, 2007:1959-1962.
[5] Tropp J, Laska J, Duarte M, et al. Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals[J]. IEEE Transactions on Information Theory, 2010,56(1): 520-544.
[6] 金磊,黄建军,高国星.多相随机子采样FFT模拟信息转换器[J].信号处理,2016,32(4):457- 462.
Jin Lei, Huang Jianjun, Gao Guoxing. Implementation for Analog-to-information Convertor via Multiphase Random Sampling and Sub-sampled FFT[J]. Journal of Signal Processing,2016,32(4):457- 462. (in Chinese)
[7] Mishali M, Eldar Y. From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J]. IEEE Journal of Selected Topics In Signal Processing, 2010, 4(2): 375-391.
[8] Mishali M, Eldar Y, Dounaevsky O, et al. Xampling: Analog to Digital at Sub-Nyquist Rates[J]. IET Circuits Devices & Systems,2011,5(1):8-20.
[9] Xu Ziyong, Li Zhi, Li Jian. Broadband Cooperative Spectrum Sensing Based on Distributed Modulated Wideband Converter[J].Sensors,2016,16(10),1602-1613.
[10] Ioushua S, Yair O, Cohen D, et al. CaSCADE: Compressed Carrier and DOA Estimation[J]. IEEE Transactions on Signal Processing,2017,65(10):2645-2658.
[11] Yao Bo, Li Zhi, Hua Wei, et al. Efficient Recovery of Support Set in Modulated Wideband Converter System[J]. Journal of Information and Computational Science,2015,12(16):6043- 6055.
[12] Mishali M, Eldar Y. Reduce and Boost: Recovering Arbitrary Sets of Jointly Sparse Vectors[J].IEEE Transactions on Signal Processing,2008,56(10):4692- 4702.
[13] 邓伯华, 李健, 李智. 基于测量向量转换的MWC支撑集恢复算法[J]. 四川大学学报:工程科学版, 2015, 47(2): 161-165.
Deng Bohua, Li Jian, Li Zhi. A Joint Support Set Recovery Algorithm of MWC Based on Measurement Vectors Transform[J]. Journal of Sichuan University: Engineering Science Edition,2015,47(2):161-165. (in Chinese)
[14] Jia Min, Shi Yao, Gu Xuemai, et al. Improved algorithm based on modulated wideband converter for multiband signal reconstruction[J].EURASIP Journal on Wireless Communication and Networking,2016,2016(1):1-9.
[15] 盖建新，付平，孙继禹，等. 基于随机投影思想的MWC亚奈奎斯特采样重构算法[J].电子学报,2014,42(9):1686-1692.
Gai Jianxin, Fu Ping, Sun Jiyu, et al. A Recovery Algorithm of MWC Sub-Nyquist Sampling Based on Random Projection Method[J]. Acta Elestronica Sinica,2014,42(9):1686-1692. (in Chinese)
[16] 盖建新，付平，付宁，等.基于SVD与MUSIC的亚奈奎斯特采样重构算法[J].仪器仪表学报,2012,33(9):2073-2079.
Gai Jianxin, Fu Ping, Fu Ning, et al. Sub-Nyquist sampling reconstruction algorithm based on SVD and MUSIC[J].Chinese Journal of Scientific Instrument,2012,33(9):2073-2079. (in Chinese)
[17] 石光明，刘丹华，高大化，等．压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.
Shi Guangming, Liu Danhua, Gao Dahua, et al. Advances in Theory and Application of Compressed Sensing[J].Acta Elestronica Sinica,2009,37(5):1070-1081．(in Chinese)
