1 引言
交叉眼干扰技术由角闪烁干扰发展而来,能够有效欺骗角跟踪雷达使其指向错误目标位置[1]。随着技术的发展,交叉眼干扰的实现逐渐成为可能,从而成为对抗单脉冲测角雷达的研究热点。
南非的W.P.du Plessis从单脉冲雷达的处理过程出发,对交叉眼干扰进行了详细推导并建立了干扰的几何模型,在此基础上就其中容限、干信比等影响干扰效果的因素进行了分析,为交叉眼干扰的研究提供了详尽的思路[3-7];国内的学者曹菲建立了交叉眼干扰的数学模型[8],并对干扰信号带来的多普勒频移进行了讨论;此外为了能够改善严苛的参数条件,国内的刘天鹏、刘松杨、王彩云等学者对多阵元反向交叉眼干扰进行了研究[2,9-12],提供了增加交叉眼容限、扩大干扰使用条件等的方案。对于干扰信号的波前相位问题,尹洪成、黄庆东等对拖曳式诱饵、闪烁干扰等样式下信号的波前相位进行了理论推导分析[13];N.M.Harwood对传统交叉眼干扰的波前相位畸变进行了研究[14],但条件设置较为简单,且没有进行详尽的数学推导。在目前较新的多元反向交叉眼干扰研究中,尚无对其波前相位畸变的分析。采用波前相位畸变的方法研究交叉眼干扰,可以只从干扰信号的角度来进行讨论[14],对于交叉眼干扰信号的调制参数优化以及多阵元干扰天线设计有重要意义。
本文推导建立干扰信号到达单脉冲雷达处的合成场模型,并提出有效相位畸变区和中心相位畸变程度这两个指标对干扰信号的波前相位畸变特性进行描述并对波前相位进行分析。同时建立以中心相位畸变程度和有效相位畸变区为目标的约束模型,采用MOEA/D算法对不同干扰系统各环路的信号幅度比、相位差等参数进行优化计算,使得干扰达到更好效果。最后通过仿真得到在一定方位和距离范围内干扰信号相位畸变并考虑到干扰信号对单脉冲雷达跟踪角的影响,对MOEA/D算法得到的不同环路的相位畸变进行验证分析。
2 多环路交叉眼干扰的相位畸变
2.1 多环路交叉眼干扰系统
多环路交叉眼干扰系统采用Van Atta天线阵构成反向天线结构,本文以线性阵列为例进行研究,如图1所示,1,2,…,2N为天线阵元,dci为不同环路的阵元间的距离。每个环路信号由两路接收发射信号构成,A、B为接收信号,A′、B′为发射信号,对其中一路信号进行幅度、相位的调制,从而得到两路相干干扰信号源对单脉冲雷达进行干扰。
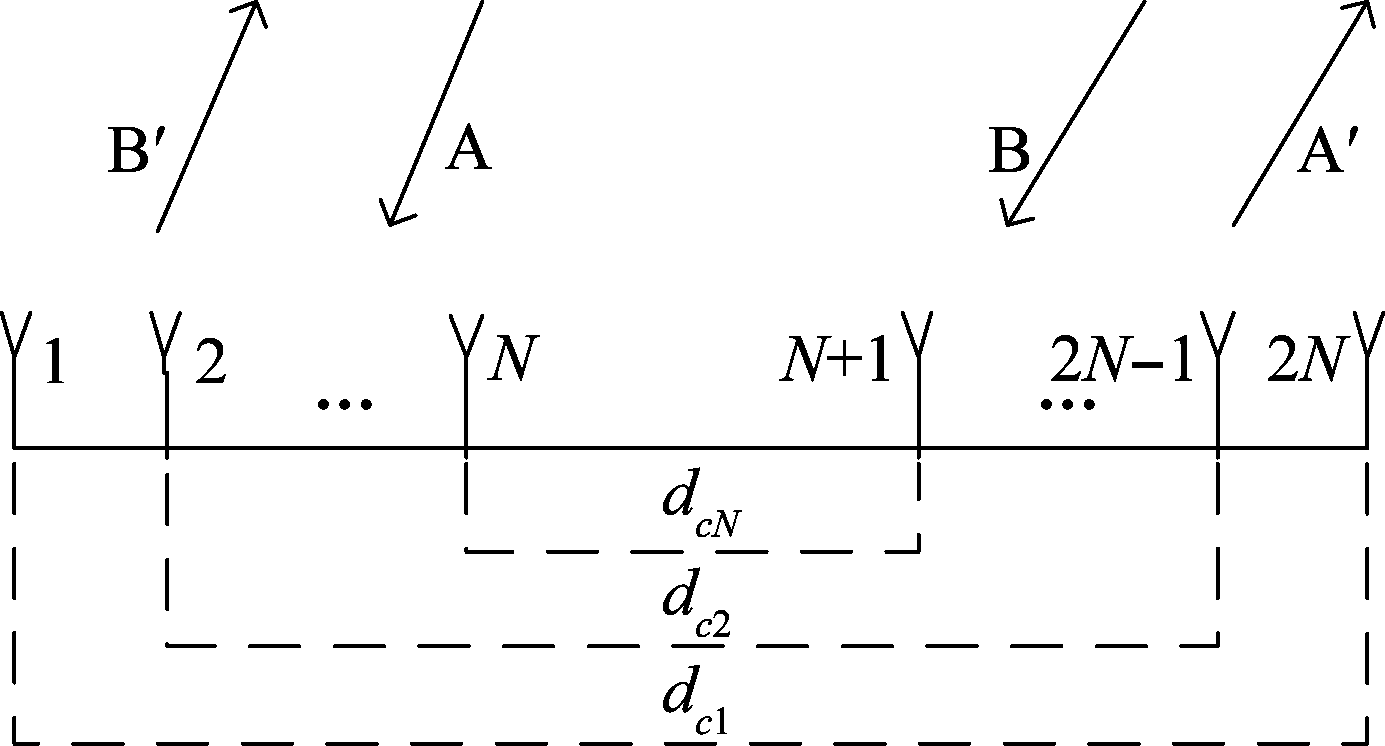
图1 多环路交叉眼干扰系统结构
Fig.1 Multi-loop cross-eye jamming system structure
2.2 数学分析
多环路反向交叉眼干扰场景如图2所示,该系统由2N个阵元组成,构成N个交叉眼干扰环路,天线i与天线2N+1-i互为一组收发天线对,为干扰环路i。多环路交叉眼干扰系统天线阵元等间隔分布,其中干扰环路1的基线长度为dc,相邻环路距离为de。干扰系统中心到达单脉冲雷达处所的P点距离为r,干扰天线连线与干扰系统中心到雷达路径的夹角为θ,天线阵元i到达P点距离为ri,干扰天线连线与干扰天线阵元i到雷达路径的夹角为θi。
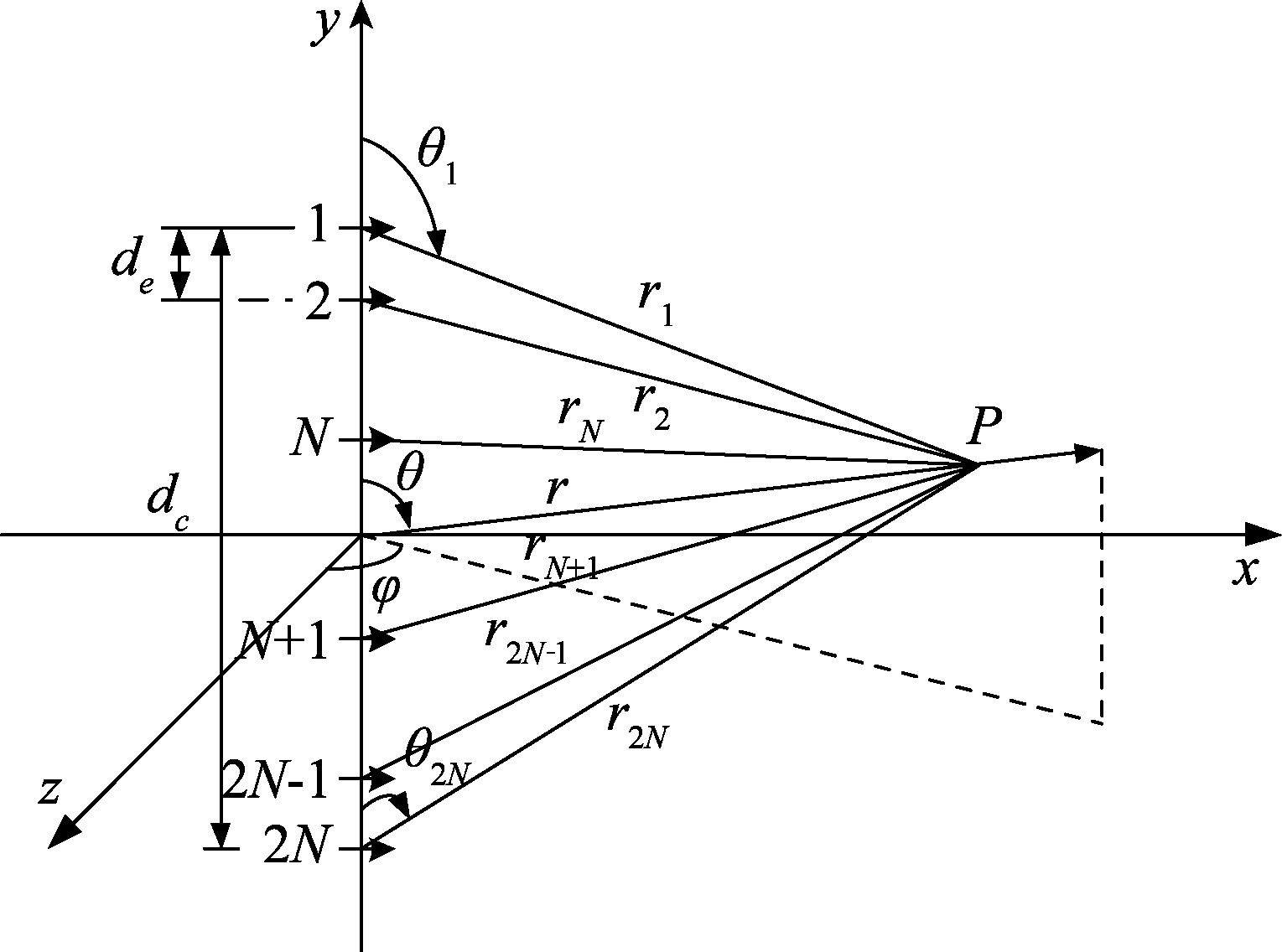
图2 多环路交叉眼干扰场景
Fig.2 Multi-loop cross-eye jamming scene
多环路交叉眼干扰系统内干扰天线发射信号幅度为Ai、相位为φi,则不同干扰环路的信号为:
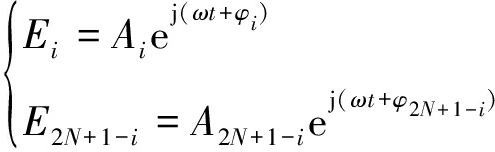
(1)
在空间中P点单脉冲雷达处,第i(i=1,2,...,N)个干扰环路波源发射的电磁波到达P点时的信号为:
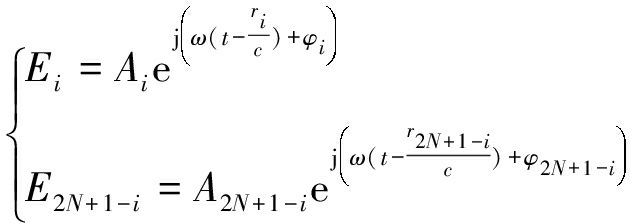
(2)
则合成波信号
(3)
其中![]()
由于r>>dc,则![]() 根据波的相干叠加原理,则有
根据波的相干叠加原理,则有
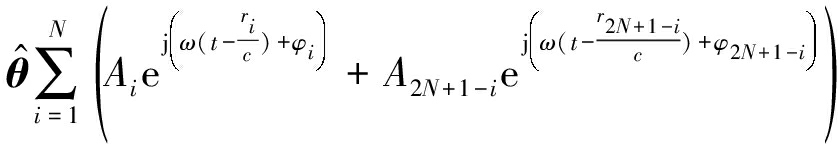
(4)
由图2中几何关系,干扰环路i上两天线到P点距离
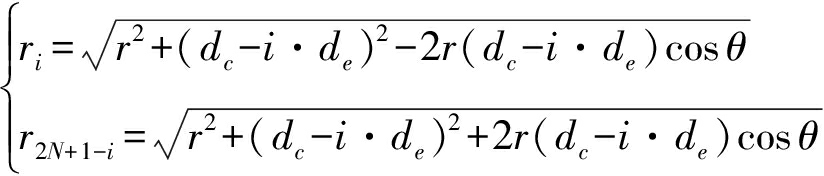
(5)
若环路i的两干扰信号Ei、E2N+1-i幅度比为ai,相位差为φi,信号E1,Ei幅度比为ci,相位差为ψi,令
An=[a1eφ1,a2eφ2,…,aNeφN]
(6)
Cn=[c1eψ1,c2eψ2,…,cNeψN]
(7)
B1n=[e-jkr1,e-jkr2,…,e-jkrN]
(8)
B2n=[e-jkr2N,e-jkr2N-1,…,e-jkrN+1]
(9)
Dn=[a1ejφ1-jkr2N,a2ejφ2-jkr2N-1,…,aNejφN-jkrN+1]
(10)
其中Dn为An与B2n各元素相乘的矩阵。
则式(4)得到的单脉冲雷达处的合成场可表示为式(11)所示,得到关于变量θ、N、An、Cn、de的函数关系。
E(θ,r,An,Cn,de,N)=E1Cn(B1n+Dn)T
(11)
式中E1=A1ej(ωt+φ1)。
根据文献[14-15],式中θ、de的取值范围为:![]()
2.3 相位畸变参量表征
根据交叉眼干扰的原理,单脉冲雷达形成角度欺骗是由干扰信号的合成场的相位畸变造成的,而畸变区的大小直接影响交叉眼干扰的使用和效果。相位畸变即是在与信号波源相同距离的圆周内相位发生变化,如图3所示,故可以将相位的变化率来反映相位畸变的程度,所以在这里使用圆周上的相位梯度κ表征相位畸变程度:
(12)
交叉眼干扰系统采用的反向结构能够保证同一环路的干扰信号传输路径相同,且只在畸变区内才可对雷达形成角度欺骗,为对该区域相位畸变进行表征,根据图2中场景,将θ=90°时相位梯度κ定义为中心畸变程度κ0,同时能够对雷达形成有效欺骗的畸变区定义为有效畸变区ρ(如图3)。
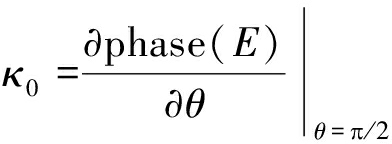
(13)
(14)
式中phase(E)为合成场的相位函数,value为有效畸变区边界的相位梯度值。
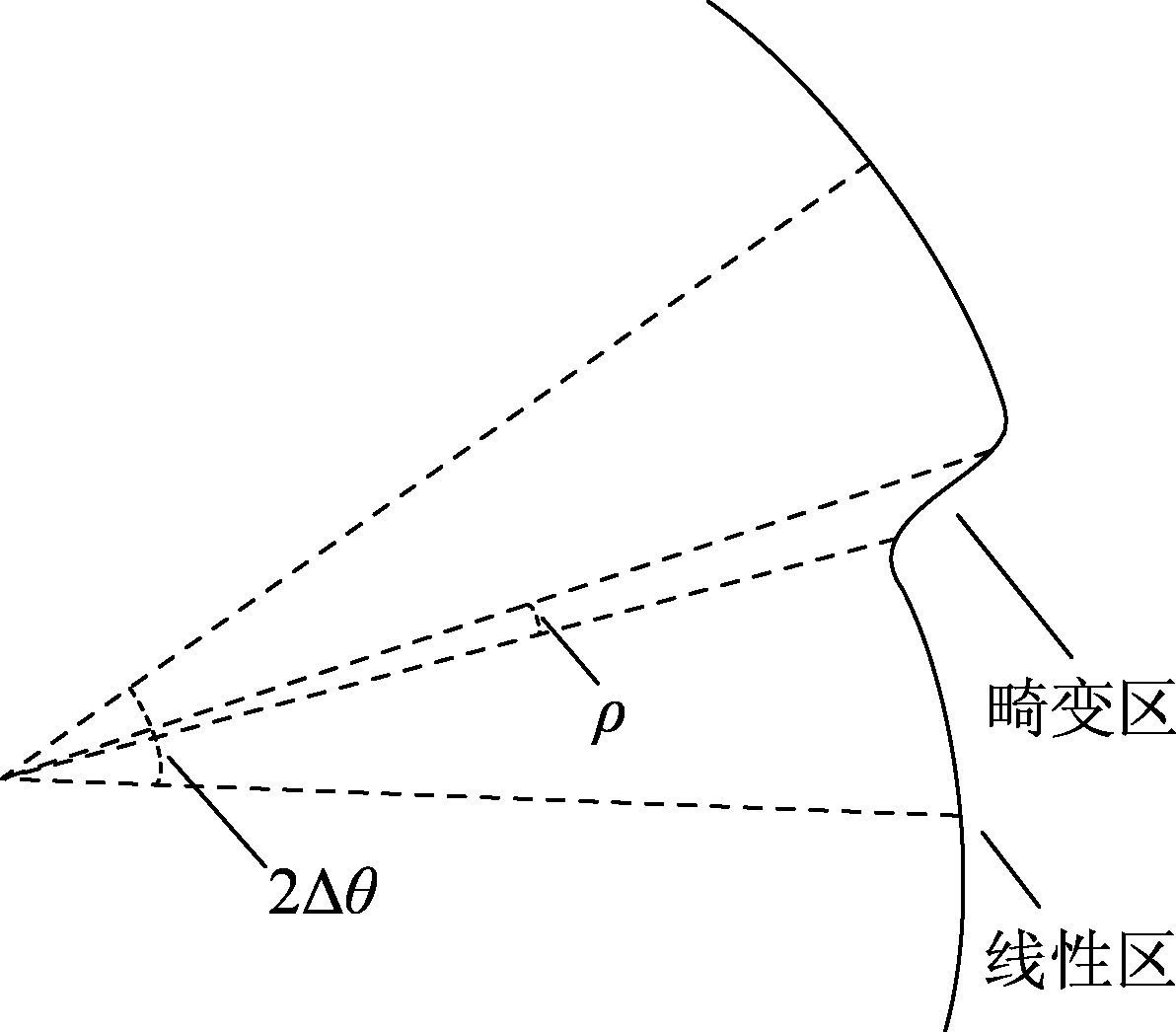
图3 波前相位畸变示意图
Fig.3 Diagram of wave-front phase distortion
3 基于相位畸变的约束优化
3.1 约束模型
根据第2节对干扰信号的相位畸变的表征,合成场的中心畸变程度应满足κ0≥κmin,其中κmin为达到欺骗效果时中心畸变程度最低要求,另一方面有效畸变区边界应大于定值梯度κmin。在对单脉冲雷达的角度欺骗,相位畸变程度越大,所造成的角度误差越大,同时干扰的作用区域越大,单脉冲雷达运动对干扰效果造成的影响越小,故为达到好的干扰效果,中心畸变程度和有效畸变区的大小均是越大越好,得到目标函数为
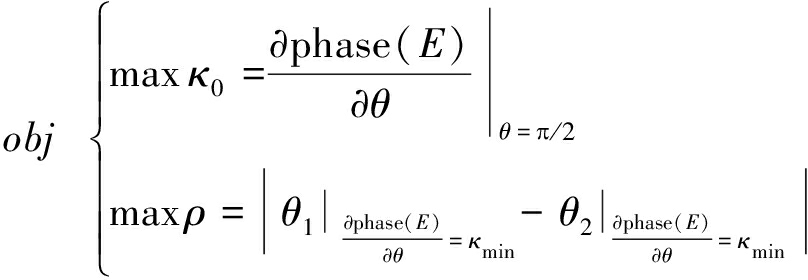
(15)
联立式(11), N、An、Cn、de为决策变量,根据文献[7]中对多环路交叉眼干扰的An中各环路两天线之间的幅度比、相位差的要求,变量的约束范围进行如下取值:
ai∈(0.5,1.5)
φi∈(90°,270°)
κmin为达到欺骗目的即干扰系统与雷达对准时使雷达指示角偏离0.5倍波束宽度达到失锁状态所需的最低中心畸变程度。
为简化分析,文中不考虑不同环路间的信号调制,故Cn=[1,1,…,1]。
该问题属于典型的多目标优化问题,为解决此类问题,本文采用基于分解的MOEA/D进化算法[15]。因为一方面MOEA/D进化算法中目标子问题可通过临近子问题的优化信息来进行优化,另一方面当目标增多的情况下求解性能没有明显下降,适用于求解多阵元交叉眼干扰系统优化这种复杂的多目标优化问题上。
3.2 MOEA/D进化算法
MOEA/D进化算法是一种基于分解技术的多目标进化算法,该算法的步骤分为初始化、进化、停机三步,该算法的输入参数及意义如表1所示,结合上述约束模型,具体步骤如下[16]:
表1 MOEA/D算法输入参数及意义
Tab.1 MOEA/D algorithm input parameters and its significance

输入意义F={f1,f2,…,fm}目标函数,m是目标个数S决策变量Np子问题的个数,即种群的规模Nnei每个权重向量Wj邻居集合的大小Tmax最大迭代次数
其中: j=1,2,…,Np。
Step1初始化
Step1.1 在决策变量S产生一个规模为Np的种群P0={X1,X2,…,XNp}。
Step1.2 产生Np个权重向量Wj, j=1,2,…,Np,其中![]()
Step1.3 计算两两权重向量之间的距离dij,然后根据距离矩阵d选择Nnei个最近邻个体作为Xi的邻居集合Bi,i=1,2,…,Np,Bi={Xi,1,Xi,2,…,Xi,Nnei},Nnei表示Bi的规模。
Step1.4 对每一个决策变量个体Xi,i=1,2,…,Np,计算目标函数值f1(Xi), f2(Xi),…, fm(Xi)。设理想点![]()
Step1.5 设外部档案S*=∅,t=1。
Step2进化
对每个i=1,2,…,Np,执行:
Step2.1 产生新决策变量个体:首先,从个体Xi的邻居集合Bi中随机选择两个体,然后执行差分进化操作,产生一个新个体Xi,new,最后,增加Xi,new到种群Pt,即Xi=Xi,new。
Step2.2 更新理想点![]() 对于每个j=1,2,…,m,如果
对于每个j=1,2,…,m,如果![]() 那么
那么![]()
Step2.3 更新个体Xi的邻居解:对于每个Xi的所有邻居Xi,k,k=1,2,…,Nnei,如果![]() 那么Xi,k=Xi,其中Wi,k表示邻居Xi,k的权重向量。
那么Xi,k=Xi,其中Wi,k表示邻居Xi,k的权重向量。
Step2.4 更新外部档案S*:去除S*中所有被个体Xi,new支配的解;如果S*中不存在支配个体Xi,new的解,那么将Xi,new加入集合S*。
Step3停机准则:如果t>Tmax,那么停机并输出外部档案S*={Xi|i=1,2,…,Np},否则转到Step2,t=t+1。
输出 外部档案S*⊂S。
根据3.1中得到的约束模型,其中的决策变量为各环路间幅度比ai、相位差φi,在决策变量的取值范围内运用随机的方法产生n×m的矩阵,其中n为决策变量的个数,m为种群的规模。
4 仿真验证
4.1 仿真实验典型参数
在交叉眼干扰过程中,主要参数有干扰环路天线基线长度、干扰信号幅度比、相位差、干扰环路数等,所要考虑的指标主要是干扰信号到达单脉冲雷达处的有效畸变区的范围以及畸变程度的大小。为使有效畸变区的范围以及中心畸变程度最大,使用MOEA/D算法进行优化设计,得到较好的干扰参数设置。进行仿真时,采用典型的多环路交叉眼干扰场景参数如表2所示,MOEA/D的参数设置如表3所示。
表2 多环路交叉眼干扰系统典型参数
Tab.2 Typical parameters of multi-loop cross-eye jamming scene
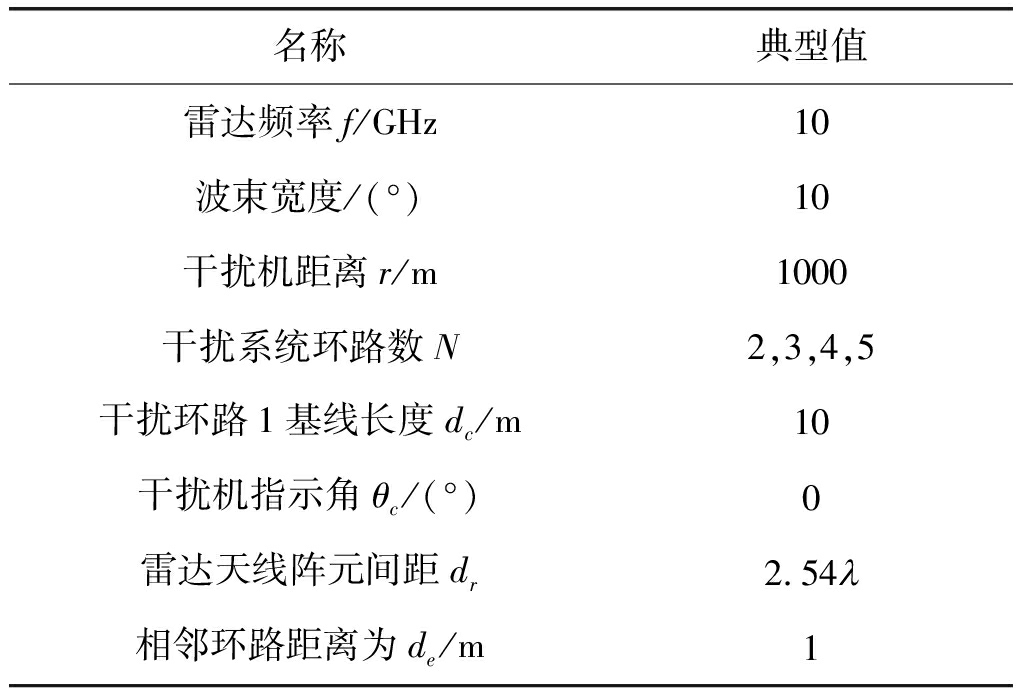
表3 MOEA/D算法参数
Tab.3 MOEA/D algorithm parameters

算法参数设置种群数量:100邻居规模:20进化代数:700目标个数:2问题维度:由干扰环路数确定
4.2 计算分析
以不同环路上干扰信号幅度比、相位差为决策变量,以有效畸变区、中心畸变程度为目标函数进行计算,得到交叉眼干扰系统不同环路下Pareto前沿解,如图4、5所示。图中左端为Pareto 最优解中有效畸变区较优的解,右端为中心畸变程度较优的解。
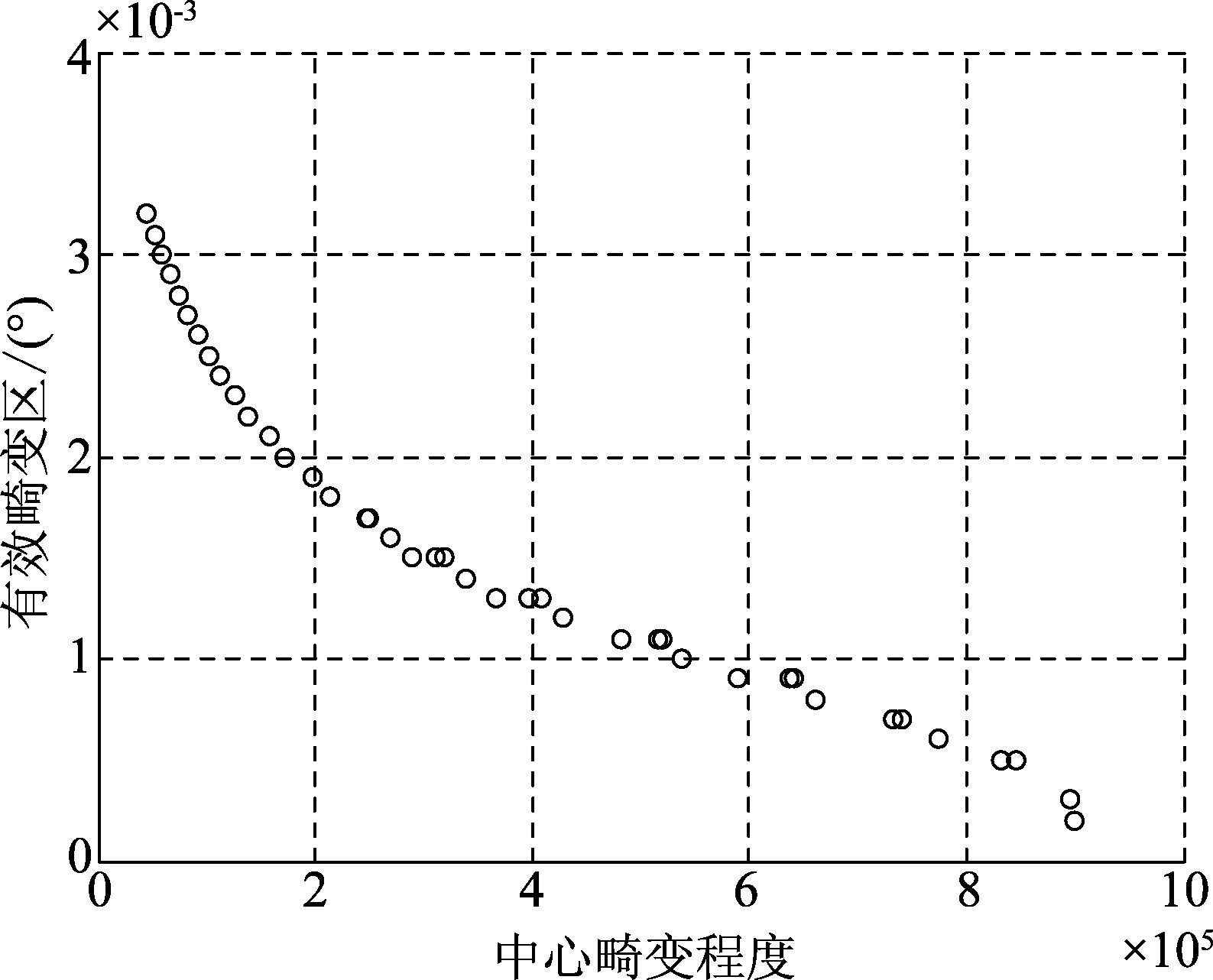
图4 单环路干扰系统Pareto前沿解
Fig.4 Pareto front solution of single loop jamming system
有效畸变区ρ较优时不同环路的相位畸变情况如表4所示,表中结果即是此时所得到决策变量(幅度比、相位差)较优解(非闭合解)下的有效畸变区、中心畸变程度以及此时的合成场中心点幅度的大小。
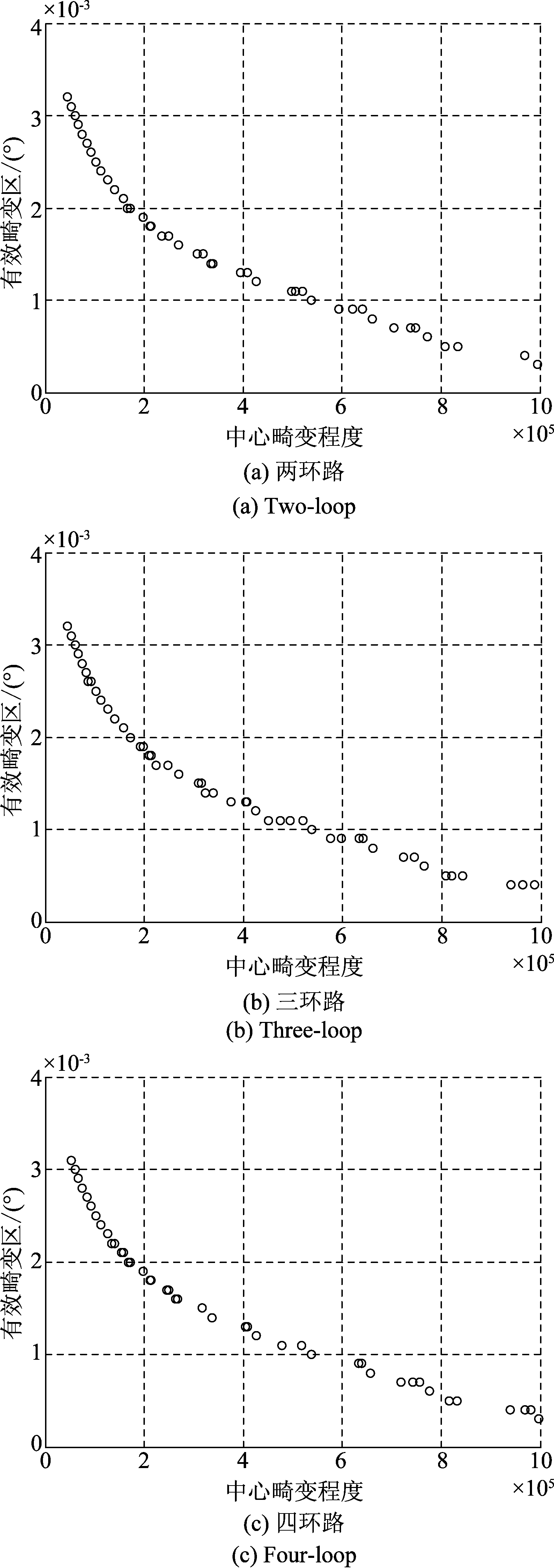
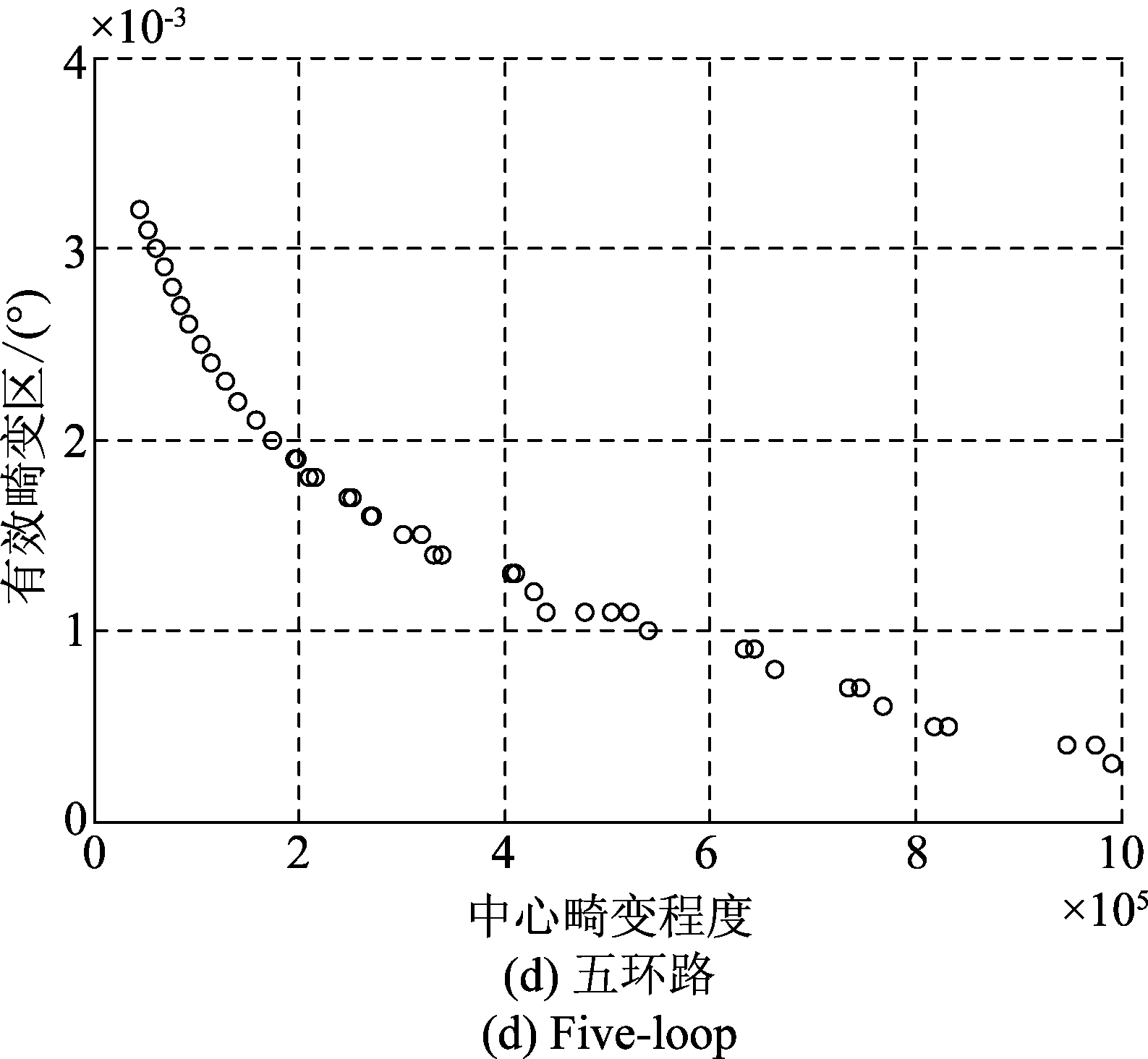
图5 多环路干扰系统Pareto前沿解
Fig.5 Pareto front solution of multi-loop jamming system
中心畸变程度κ较优时有效畸变区的大小如表5所示,表中结果此时所得到决策变量(幅度比、相位差)较优解(非闭合解)下的有效畸变区和中心畸变程度的大小。
通过表4可以看出,有效畸变区较优时,多环路系统对提升合成场中心点幅度有很大效果。在表5中也可看到,中心畸变程度较优时,多环路交叉眼干扰系统的中心畸变程度和有效畸变区均优于单环路交叉眼干扰系统,由此可以判断多阵元交叉眼干扰系统能够有效提升交叉眼干扰性能。
同时从表4发现,不同环路数的交叉眼干扰系统的较优有效畸变区基本相同,由此可见,通过增加多环路交叉眼干扰的环路数设计对消除单脉冲雷达横向运动带来的影响并不明显。
依据表4中计算的参数,得到干扰天线方位角90±0.005°和距离1000±10 m范围内的相位畸变结果,即该范围内各点的相位梯度值,如图6所示。
从图6中可以看到,两环路干扰的相位畸变在方位维上变化明显,在距离维上无明显变化,但中心相位梯度值较小;三环路和四环路干扰的相位畸变在方位维和距离维上均有明显变化,最大相位梯度值集中在90°上,不同的是三环路干扰的畸变程度最大区域远离1000 m中心点,而四环路干扰靠近1000 m中心点;五环路干扰与两环路干扰的相位畸变相似,不同的是五环路干扰的畸变程度较大的区域随着远离1000 m中心点发生偏离,且相比于三环路和四环路畸变程度较小。由此,环路数为3、4时相位畸变程度要优于环路数为2、5的干扰系统,同时,在方位角90°附近,环路数为2时的有效畸变区要大于环路为5时的有效畸变区,故环路数超过4时,干扰的效果会有明显减小。
4.3 不同环路干扰系统欺骗角度分析
为对上述得到的多环路交叉眼干扰的相位畸变进一步分析,通过4.2中所得到的干扰信号参数对多环路所带来的欺骗角度进行讨论。根据文献[3]雷达跟踪角误差与交叉眼干扰的关系,同时考虑到不同环路信号传输路径带来的相位差的影响[6],得到角误差公式:
表4 不同环路下Pareto前沿解最左端值
Tab.4 The leftmost value of Pareto front solution under different loops

环路数12345有效畸变区ρ0.0032°0.0032°0.0032°0.0031°0.0032°中心畸变程度(相位梯度)κ4.38×1044.46×1044.48×1045.25×1044.52×104中心点幅度0.0450.0870.1040.0930.097
表5 不同环路下Pareto前沿解最右端值
Tab.5 The rightmost value of Pareto front solution under different loops

环路数12345中心畸变程度(相位梯度)κ8.99×1059.94×1059.87×1059.97×1059.91×105有效畸变区ρ0.0002°0.0003°0.0004°0.0003°0.0003°

图6 多环路干扰信号相位畸变
Fig.6 Phase distortion of multi-loop jamming singal
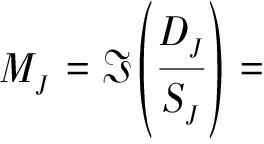
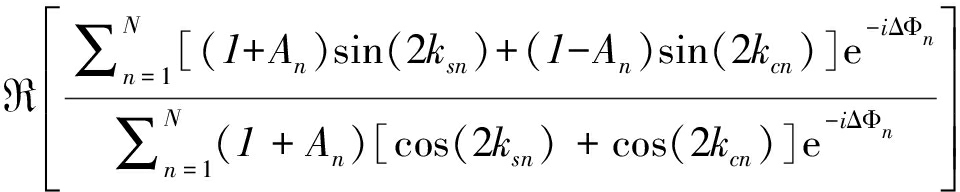
(16)
其中ΔΦn为环路n与环路1之间的干扰信号传输路径造成的相位差。
在有效畸变区较优时,一方面,对r=1000 m时不同环路下跟踪角随雷达天线旋转角的变化进行仿真,结果如图7(a)所示。另一方面,对当雷达正对干扰天线时雷达跟踪角随距离r的变化进行仿真,结果如图7(b)所示。
从图7(a)看出,对于环路数为2、3、4时,随雷达天线旋转角的变化跟踪角均大于5°,干扰效果较好。从图(b)看出,环路数2时,雷达跟踪角达到5°时距离最远,并且同一距离下随着环路数的增加雷达跟踪角减小,当环路数到达5时,跟踪角偏离程度一直小于1°,目标仍处于雷达波束范围内,干扰效果已不明显。因此,对于多环路交叉眼干扰并非环路数越多越好,随着环路数的增加,环路N的干扰天线基线长度会越来越小,从而使相位畸变程度减小,干扰系统更多表现为雷达指示器的作用,同时环路数的增加也会使系统的成本和复杂度也会大大增加。
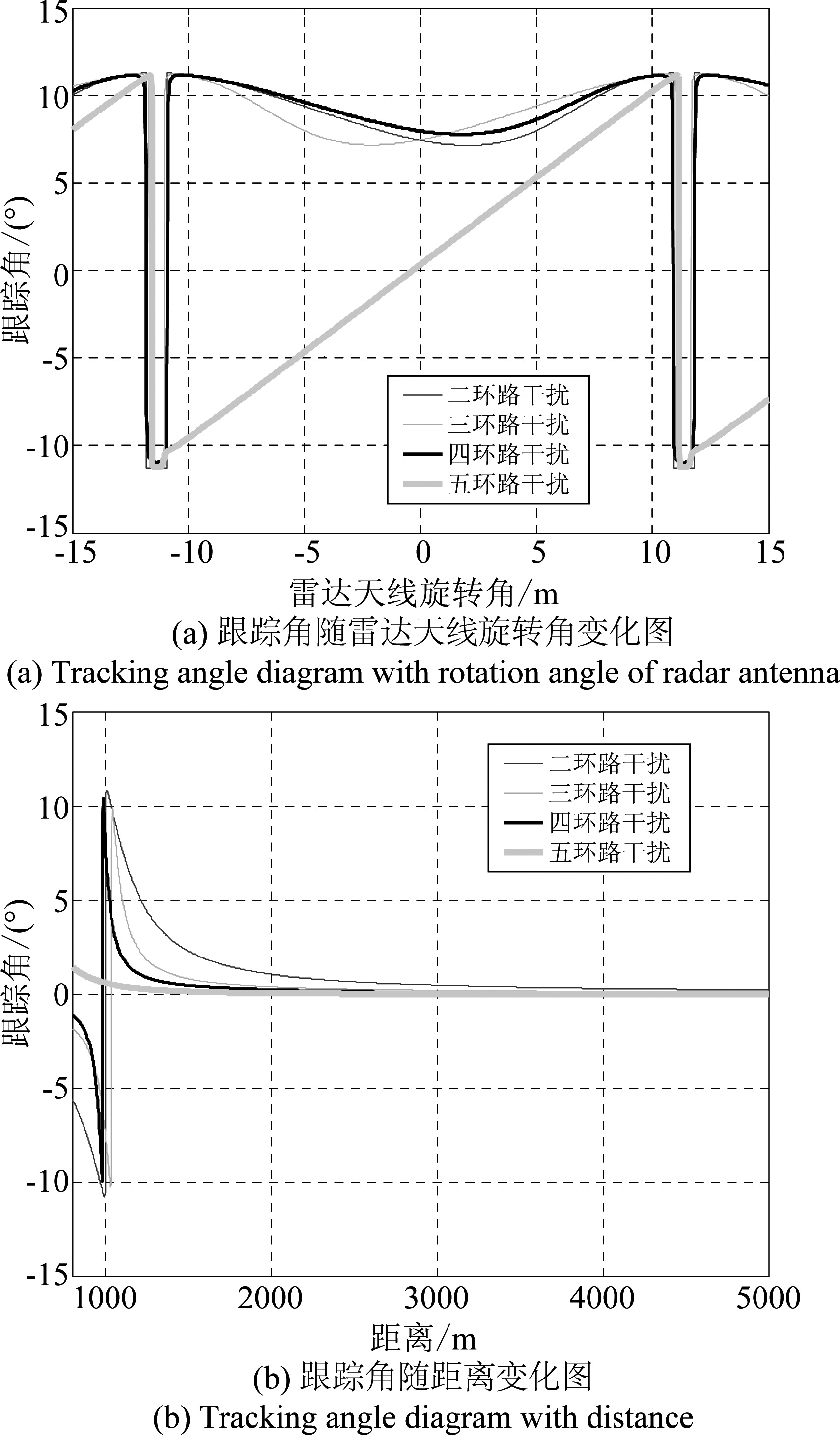
图7 不同环路干扰系统的角度偏差图
Fig.7 Angle deviation diagram of different loop jamming systems
5 结论
本文对多环路交叉眼干扰系统的波前相位畸变特性进行了研究,首先对干扰系统进行分析并建立了多元干扰合成场模型,并以中心畸变程度和有效畸变区为目标函数建立了约束模型。然后采用MOEA/D算法对约束模型进行优化计算,得到较优的干扰信号幅度比、相位差等参数,并对不同环路数的相位畸变进行比较分析。结果表明,相比于单环路交叉眼干扰系统,多环路交叉眼干扰系统的中心畸变程度和有效畸变区均有所提升。此外,对于多环路交叉眼干扰系统的区域内相位畸变进行分析发现并非环路数越多越好,结合对雷达的跟踪角欺骗效果的分析,将经过MOEA/D算法得到的幅度比、相位差等关键参数值进行仿真,表明有效畸变区较优的情况下,雷达跟踪角偏离大于0.5倍波瓣宽度,干扰效果较好,同时发现干扰环路数增加时,干扰效果也随之减弱,其中环路数达到5后对雷达角度欺骗已不明显。上述研究为多环路交叉眼干扰系统的工程应用提供理论依据。
[1] Falk L. Cross-Eye Jamming of Monopulse Radar[C]∥IEEE 2007 Waveform Diversity & Design, Pisa, Italy:IEEE Press, 2007: 209-213.
[2] 刘松杨. 基于干扰平台旋转的反向交叉眼干扰研究[D]. 西安:西安电子科技大学,2016.
Liu Songyang. Analysis of Retrodireetive Cross-eye Based on Jammer Platform Rotating[D]. Xi’an: Xidian University, 2016. (in Chinese)
[3] Du Plessis W P, Odendaal J W, Joubert J. Extended Analysis of Retrodirective Cross-Eye Jamming[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(9): 2803-2806.
[4] Du Plessis W P. Platform Skin Return and Retrodirective Cross-Eye Jamming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 490-500.
[5] Du Plessis W P, Odendaal J W, Joubert J. Tolerance Analysis of Cross-Eye Jamming Systems[J]. Transactions in Aerospace and Electronic Systems, 2011, 47(1): 740-745.
[6] Du Plessis W P. Path-Length Effects in Multi-Loop Retrodirective Cross-Eye Jamming[J]. IEEE Antennas and Wireless Propagation Letters, 2016,15: 626- 629.
[7] Du Plessis W P. Cross-Eye Gain in Multiloop Retrodirective Cross-Eye Jamming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016,52(2): 875- 882.
[8] 曹菲,刘庆云,辛增献. 交叉眼干扰数学建模[J]. 现代雷达,2013, 35(6): 69-72.
Cao Fei, Liu Qingyun, Xin Zengxian. Mathematical Modeling of Cross-eye Jamming[J]. Modern Radar, 2013, 35(6): 69-72. (in Chinese)
[9] Liu T P, Liu Z, Liao D P, et al. Platform Skin Return and Multiple-Element Linear Retrodirective Cross-Eye Jamming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(2):821- 835.
[10] 刘天鹏. 多源反向交叉眼干扰技术研究[D]. 长沙:国防科学技术大学,2016.
Liu Tianpeng. Research on Multiple-Element Retrodirective Cross-Eye Jamming[D]. Changsha: National University of Defense Technology, 2016. (in Chinese)
[11] 刘松杨, 董春曦, 董阳阳. 旋转的正交多点源反向交叉眼干扰分析[J]. 电子与信息学报, 2016, 38(6):1424-1429.
Liu Songyang, Dong Chunxi, Dong Yangyang. Analysis of rotating orthogonal multiple elements retrodirective cross-eye jamming[J]. Journal of Electronics & Information Technology, 2016, 38(6):1424-1429. (in Chinese)
[12] 王彩云,何志勇,宫俊. 多干扰机反向交叉眼干扰分析[J]. 系统工程与电子技术, 2017,39(7):1457-1463.
Wang Caiyun, He Zhiyong, Gong Jun. Analysis of retro-directive cross-eye jamming for multiple elements[J]. Systems Engineering and Electronics, 2017,39(7):1457-1463. (in Chinese)
[13] Yin H C, Huang P K. Unification and Comparison Between Two Concepts of Radar Target Angular Glint[J]. IEEE Transactions on Aerospace and Electronic Systems. 1995, 31(2):778-783.
[14] Harwood N M, Dawber W N, King D J. Multiple-element crosseye[J]. IET Radar Sonar Navig., 2007,1(1): 67-73.
[15] 谭艳艳. 几种改进的分解类多目标进化及其应用[D]. 西安:西安电子科技大学,2013.
Tan Yanyan. Several Modified Decomposition-Based Multi-objective Evolutionary Algorithms and Their Application[D]. Xi’an: Xidian University, 2013. (in Chinese)
[16] 祝华正. MOEA/D算法及其在多序列比对中的应用研究[D]. 重庆:重庆大学,2015.
Zhu Huanzheng. Research on Multi-objective Evolutionary Algorithm based on Decomposition and Its Application in Multiple Sequence Alignment[D]. Chongqing: Chongqing University, 2015. (in Chinese)


