1 引言
当前，随着社交网络(Social Networks)、物联网(Internet of Things)、车联网(Internet of Vehicles)等新兴业务的蓬勃发展，下一代移动通信网络所面临的将是海量的用户数量及数据传输量[1]。无线接入网(Radio Access Network, RAN)将面临着：复杂网络环境导致无线覆盖质量不高、网络资本支出与运维成本逐年增高、大量站点导致高能耗等前所未有的挑战。针对这些问题，IBM和中国移动提出了一种新型的接入网架构——云接入网[2](Cloud Radio Access Network, C-RAN)。C-RAN的特点是将网络中各接入点的射频拉远头(Remote Radio Head, RRH)和基带处理单元(Baseband Unit, BBU)完全地分离，将RRH更靠近用户，而各个BBU向后集中成虚拟的BBU池，BBU池和RRH通过高速链路(比如光纤，毫米波)连接。这种结构具有扩展网络节约成本，能源消耗远远小于传统蜂窝网络以及有利于干扰协调、多点协作算法的实施等优点。
相较于传统蜂窝网络，C-RAN的网络状态和信道状态更为复杂、多变，而且每个用户都可能通过多个RRH接入，导致这些用户又将互为干扰。在传输过程中，用户接入的RRH亦有可能发生变化。这些特性对传统的固定速率信道编码(比如LDPC码，Turbo码)在C-RAN中的应用提出了挑战。传统的固定速率信道编码在译码失败时使用混合重传[3] (Hybrid Automatic Repeat reQuest, HARQ)机制。HARQ是结合前向纠错(Forward Error Correction, FEC)与自动重传请求(Automatic Repeat reQuest)的混合ARQ技术，是一种传统的动态速率编码技术。信息接收端收到的数据即使在传输过程中出现差错也不会被丢弃，通过递增冗余[4]技术将重传得到的数据与先前的数据合并处理，以达到修正信息差错。在C-RAN中，由于译码在远端的BBU池进行，因此BBU池需要经由前向链路通过RRH来与用户进行ACK以及NACK信号交互。当用户数量较多的情况下，大量用户的反馈信号容易导致网络拥塞，造成通信出现异常。当RRH与BBU距离较远时，反馈信号需要经历较长的时间才能被传送到发送端，相较于传统蜂窝网，C-RAN的反馈信令交互延迟将大大增加，这将降低系统性能，抵消C-RAN所带来的优势[5]。而无速率码是一种具备良好的自适应当前网络和信道状态传输特性的高效差错控制编码技术。通过借鉴Tornado码的非规则稀疏矩阵的方式可以构造无速率码。然而，仅仅通过随机选择的方法进行编码，虽然可以逼近香农信道极限，但其编译码为多项式复杂度[6]，导致其难以应用于实际通信系统。鉴于此，Luby提出了LT码[7],通过对编码包的度数分布进行设计，使编码矩阵成为具有比较低代价的稀疏矩阵，相比于线性随机无速率码，LT码大大降低了复杂度。然而，LT码编码包的译码开销和平均度数与输入编码器的信息长度有关。为了进一步减小译码开销和编译码复杂度，Shokrollahi提出了Raptor码[8]。Raptor编码采用级联的结构，通过预编码手段减小对LT码译码性能要求，使LT码编码包的平均度数降为常数。Raptor码的译码开销为常数，与输入编码器的数据长度无关，并且其运算复杂度也降为线性复杂度。此外，在噪声信道下，LT码会出现误码平台，而Raptor码可以避免这个问题。与传统固定速率信道编码相比，无速率码发送端不预先设置固定速率，实际的传输速率由当前网络和信道状态决定[9]，传输过程中不需要任何反馈信号。接收方在译码失败时只需要继续接收更多的数据包就可以再尝试译码，一旦译码成功，接收方仅需发送一个非常简单的结束信号告知发送端停止发送即可。这样减小了信令开销，能够有效缓解ACK\NACK信号反馈延迟带来的系统损失。具有以上特性的无速率码是一种非常适合C-RAN系统中灵活传输机制的信道编码方案。
目前，已有的相关研究中针对C-RAN的物理层信道编码设计的工作还比较少。在文献[10-11]中主要的研究集中于固定速率信道编码的译码算法在BBU池的软、硬件实现问题，但对无速率码的编译码实现没有涉及。在文献[12]中主要研究了上行链路中量化/压缩技术的实现和对量化噪声的优化以及容量限制问题。当将RRH看作中继时，C-RAN网络与中继系统以及分布式多天线系统有内在的联系。Li等[13]讨论了如何构建分布式MIMO系统中基于无速率网络编码的协作通信方案，提出了基于无速率网络编码的单源和多源两种协作策略。但其并没有给出实际的编译码、信号量化方法以及针对不同信噪比下无速率码的优化方法。文献[14-16]主要研究了C-RAN网络中资源分配的算法设计问题。在双向中继和多接入中继系统的无速率网络编码[17-18]中，研究主要集中在多点协作通信中无速率网络编码设计，中继节点具备一套完整的基带信号处理和译码功能。这并不完全适用于C-RAN系统，因为C-RAN中RRH不具备或只具备有限信号处理能力，无法实现复杂信号处理及译码。
本文完成的工作主要包括以下方面：1)设计了C-RAN中单用户场景下无速率编码上行传输方案，即以LDPC码作为预编码将用户要发送的信息编成Raptor码，将码字调制后发送到覆盖该用户的各个RRH，各RRH预处理单元对收到的信号预处理得到基带信号，RRH的量化器采用基于标量量化的压缩算法对信号压缩后通过高速链路上传到BBU池，BBU池采用基于图的置信传播译码算法对所有RRH的上行信号做联合解压缩及译码恢复用户信息； 2)设计了无速率码度数分布优化算法，本文采用外信息传递分析了BBU池的联合解量化译码过程，然后以最大化系统传输速率为目标，优化度数分布，并将优化问题转化为易于求解的线性规划问题，优化得到的度数分布具有接近系统理论上限的性能。无速率码的诸多优良特性使其适合应用于C-RAN 中物理层信道编码环节，然而学界内对C-RAN中无速率编码传输机制的研究还比较少，本文对C-RAN中无速率码传输设计以及无速率码优化展开研究，是解决5G网络中密集分布条件下低差错、大容量需求的重要方向之一，对新一代5G通信技术的发展具有一定的借鉴意义。
本文的其余部分安排如下。第2节介绍系统模型。第3节给出了C-RAN上行无速率编码传输方案，包括用户无速率编码调制，RRH量化传输，BBU池联合解压缩及译码的算法实现过程。第4节中给出了设计无速率编码最优输出度数分布的方法。仿真数值结果在第5节给出。最后，第6节是总结。
2 系统模型
如图1所示，考虑一个单用户的C-RAN系统，包含一个用户S，远端单天线射频单元RRHj, j=1,2,...,L，以及BBU池。用户S到RRHj之间的链路信道增益定义为hj，服从瑞利分布，概率密度为h(x;σ)=(x/σ2)·e-x2/(2σ2),x≥0，其分布相互独立，并且假设在一轮信息传输中保持不变；各RRH处高斯噪声方差均为
用户S到RRHj的链路信噪比(SNR)表示为：
其中P是用户的发射功率，为了简单起见，将发射功率进行归一化，即P=1。
首先，用户S将长度为k比特的消息m进行无速率码编码得到码字c[i],i=1,...,k；接着对码字进行调制，为了简单起见采用BPSK(Binary Phase Shift Keying)调制，将调制后的符号x[i],i=1,...,N发送到覆盖该用户各RRH节点；各RRH的预处理单元对接收到的信号进行预处理得到基带信号：
yj[i]=hjx[i]+nj[i]
(1)
其中nj[i]是节点RRHj处的高斯白噪声；接着RRH的量化器对信号yj[i]进行量化压缩，其中RRH处量化处理器是固定的，即其量化门限不随信道的改变而改变；从各RRH量化器输出的量化信号
通过高速链路传输到BBU池，BBU池处的软解调器对各路量化信号解调输出软信息LLRj后进行联合解压缩，最后联合译码器通过置信传播(Belief Propagation, BP)算法进行联合译码，成功译码后利用下行链路通过RRH反馈ACK信号告知用户S停止发送。
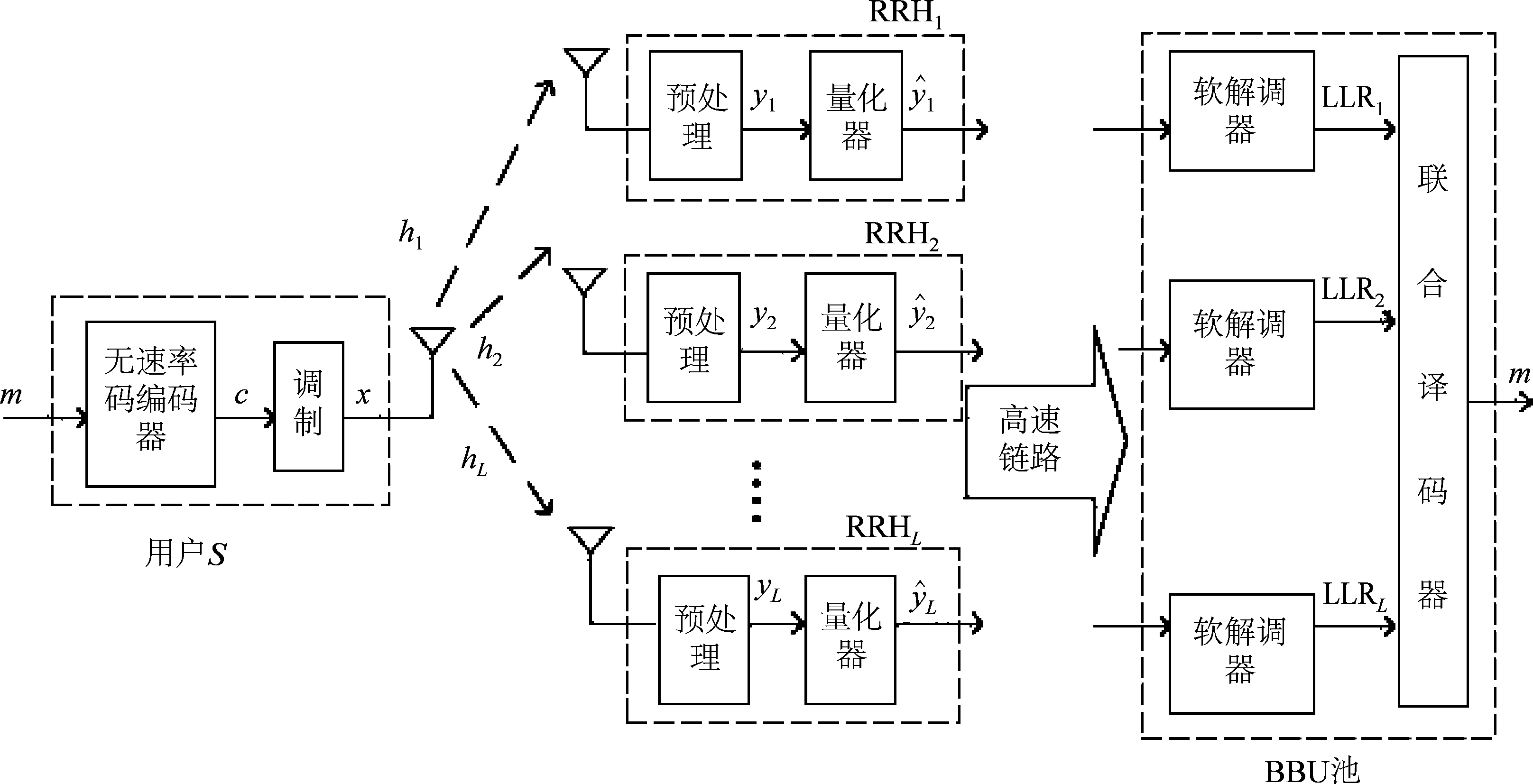
图1 C-RAN单用户上行传输系统
Fig.1 The C-RAN single user uplink transmission system
3 云接入网上行无速率编码传输方案
3.1 用户无速率码编码方案
对用户要发送的信息进行Raptor编码[8]，使用LDPC码作为其预编码。将消息m依次经过LDPC编码器和LT编码器。LDPC码编码器将k比特信息序列m=[m1,...,mk]映射为N比特码字序列u=[u1,...,uN]。具体过程表示为：u=m·G，其中G为生成矩阵，与校验矩阵H满足G×H=0的关系，生成的LDPC码字序列满足校验方程u×HT=(0,0,...,0)N-K。LT码编码器由输出节点度数分布Ω(x)来表征：
(2)
其中Ωd表示度数为d的输出节点出现的概率。对于每一个输出比特，根据度数分布确定其对应的输出节点度数。例如，对于度数为d的输出节点，从输入节点中随机等概率地选取d比特做异或运算，运算结果作为其对应的输出比特值。为保证无速率码有较好的误码率以及吞吐量性能，度数分布Ω(x)是需要优化的，依据本文所提出的优化方法得到。通过上述编码过程，源源不断地生成无速率码C。接着对无速率码进行BPSK调制，即比特0和1分别映射到1和-1。用户源源不断发送已调信号x，直到BBU正确恢复出用户消息并且反馈ACK为止。
3.2 RRH处信号量化方案
RRH对收到的信号进行预处理得到基带信号，量化器再将基带信号进行量化压缩，使其速率满足前向回传容量要求。文献[19]介绍了一种针对前向回传链路基于网络信息理论的信号压缩方案，该方案采用基于向量量化的压缩算法，执行的复杂度较高。为了减少复杂度，本文将采用基于标量量化的压缩算法。此外，本文限定RRH处量化器量化间隔、门限是固定的，不随信道变化而变化，这样可以进一步降低RRH的复杂度，便于实现。等间隔量化方案的不足之处是对小信号有不利影响，限于时间关系，作者下一阶段的工作是对量化器的间隔作优化。RRH收到的用户S发送的消息为(为了便于讨论将时间下标省去)：
y=hx+n
(3)
y(针对信道增益h，发送信号x以及噪声n的概率密度空间)的期望为：
E(y)=E(hx+n)=E(h)·E(x)+E(n)=0
(4)
方差为：
(5)
其中
为信道增益系数的方差。根据“3σ”准则[20]，可认为y的取值几乎全部集中在
区间内。量化器设计如图2所示。令量化器的量化比特数为b，则量化电平数满足2M=2b。将信号y量化得到量化信号
其中
取集合{q-M,q-M+1,..., q-1,q1,...,qM}中的值。
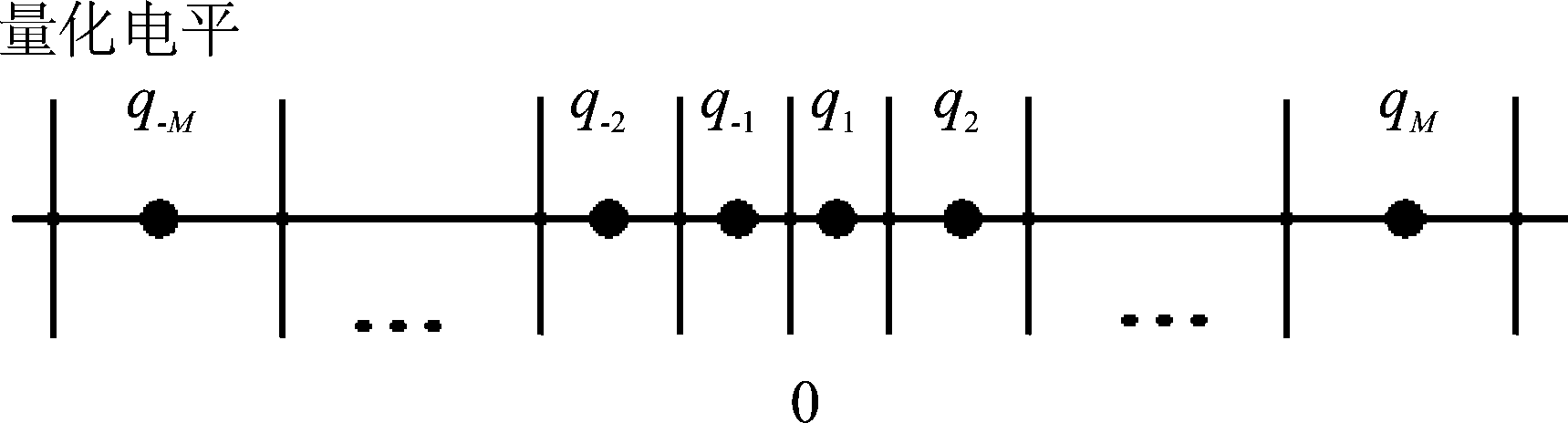
图2 2M电平的b比特量化器
Fig.2 2M level b-bit quantizer
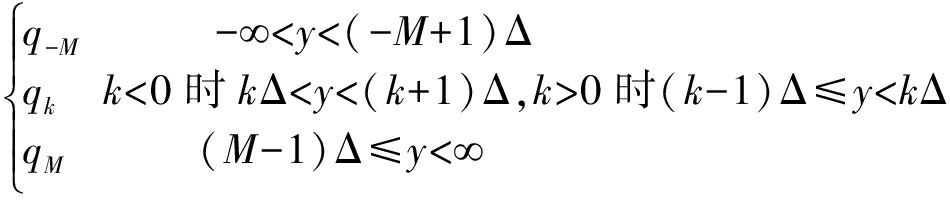
(6)
在本文中，RRH的量化器采用等间隔量化，通过公式(6)的规则将收到的信号y量化成信号其中
是量化间隔，qk=(j-sgn(j)/2)·Δ, k=±1,±2,...,±M是量化值。
3.3 在BBU池迭代译码
在BBU池进行迭代译码前首先对RRH发送来的量化信号进行软解调。用户无速率码第i个编码码比特c[i]等概率地取0和1，第j个RRH上传到BBU池的量化信号
其对应的对数似然比(Log Likelihood Ratio, LLR)为：
(7)
合并后第i比特的对数似然比为：
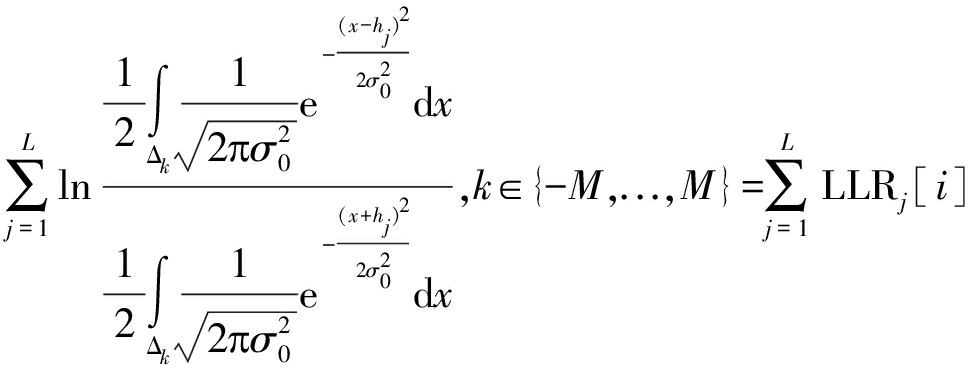
(8)
式中Δk为量化电平qk所对应的量化区间，
为各RRH处高斯噪声方差，hj为链路信道增益。
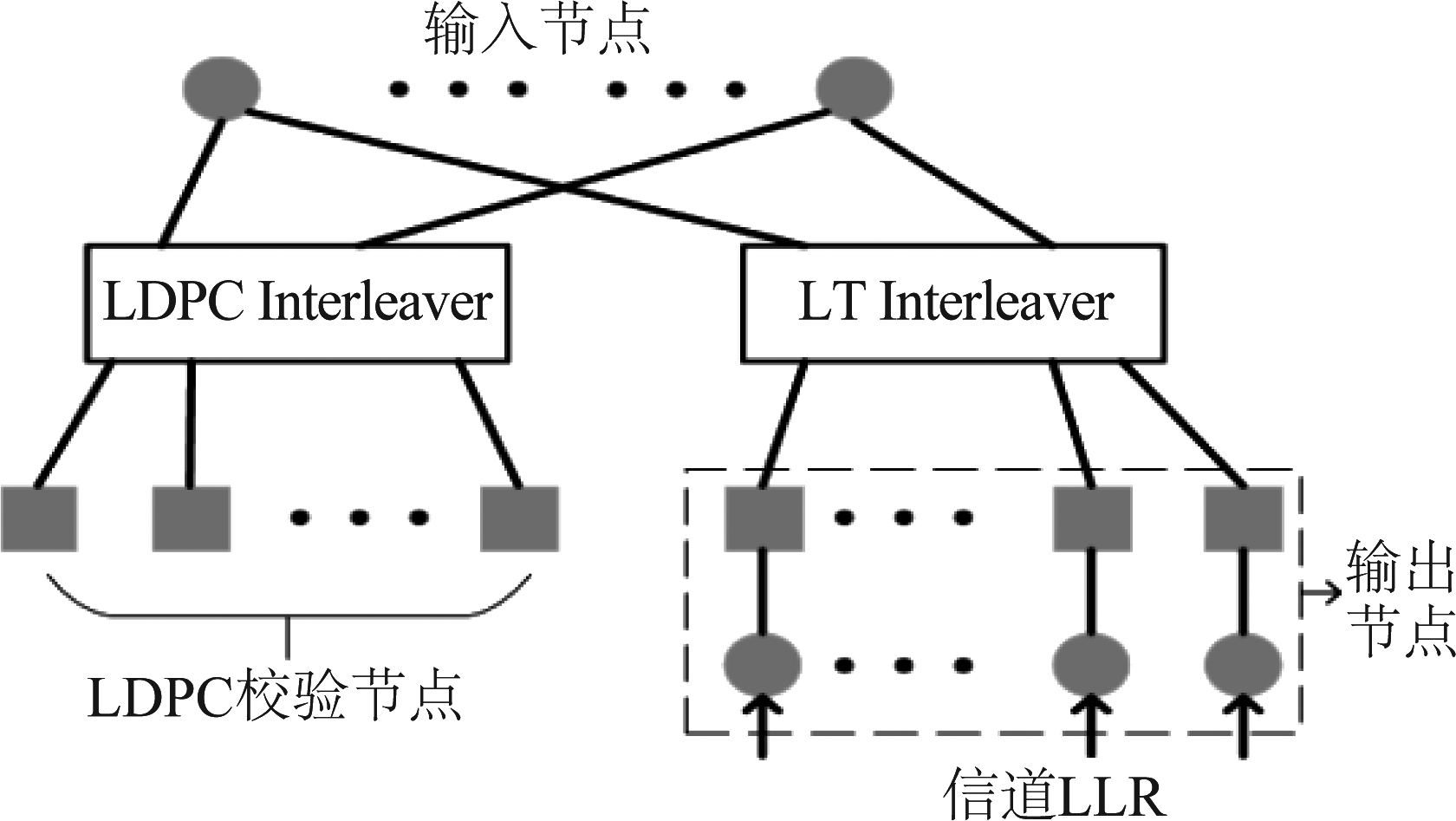
图3 无速率码译码Factor图
Fig.3 The Raptor decoding Factor graph
接下来进行迭代译码，采用基于图3所示Factor图的BP译码算法[21]。译码过程中消息的传递顺序为：先从输入节点传向LDPC校验节点，再由LDPC校验节点传回输入节点，然后从输入节点传向输出节点，最后从输出节点传回输入节点。第l轮中获取消息更新规则如下：
(9)
(10)
式中
是第l轮迭代中输出节点o传给输入节点i的消息；
是第l轮迭代中输入节点i向输出节点o发送的消息；Zo是输出节点根据对应码字比特量化值由式(8)计算得到的信道
是与输入节点i相连的输出节点(除o以外)在上一轮传给该输入节点o的消息，
是LDPC校验节点o传给输入节点i的消息。
当输入节点的LLR均值(或等价地，其对应的外信息量)超过某一门限后，单独在LDPC译码图上进行迭代。其消息的传递顺序为：先从变量节点传向校验节点，再从校验节点传回变量节点。获取消息更新规则与前面类似，这里不再赘述。完成每轮迭代之后，对LDPC变量节点ν的值进行判决。若译码成功则停止迭代，否则继续迭代。
4 无速率码输出度分布设计
本节提供了一种C-RAN系统中用户信源无速率编码输出度分布设计方法。在AWGN信道下，无速率码不存在一个统一的最优度数分布[22]，因此需要针对不同的信噪比设计最优的度数分布以逼近信道的香农容量。首先，分析在BBU池迭代译码基于高斯近似[23]的外信息传递关系[22,24](Extrinsic Mutual Information Transfer, EXIT)。然后，在BBU池联合译码器无差错译码的约束下，以最大化系统吞吐量作为目标函数，通过求解线性规划(Linear Programming, LP)问题得到最优的度数分布。
4.1 译码过程的EXIT分析
在译码迭代译码过程中将输入节点传向输出节点的消息近似为对称高斯变量(即方差为均值两倍的高斯变量)，然后分析其外信息更新过程。RRH量化器输出的量化信号为：
(11)
其中nq是量化噪声，在分析中我们将信道高斯噪声与量化噪声的和噪声近似为高斯噪声(注：由于同方差下高斯分布熵最大，因此我们考虑的实际上是对系统性能下界的优化)。输入Factor图的LLR根据式(8)计算得到，当将和噪声近似为高斯分布时，LLR服从对称高斯分布。我们仿真了RRH 3比特量化下输入Factor图的LLR概率分布直方图如图4所示，其近似服从对称高斯分布。LLR的均值τ可以由下式计算得到:
(12)
其中Δ为量化值所对应的量化区间，p(y)为发送1时(即x=1)，接收到信号y的概率密度函数，表示为：
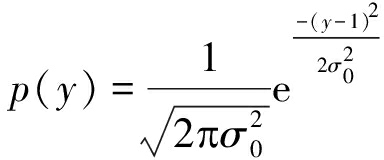
(13)
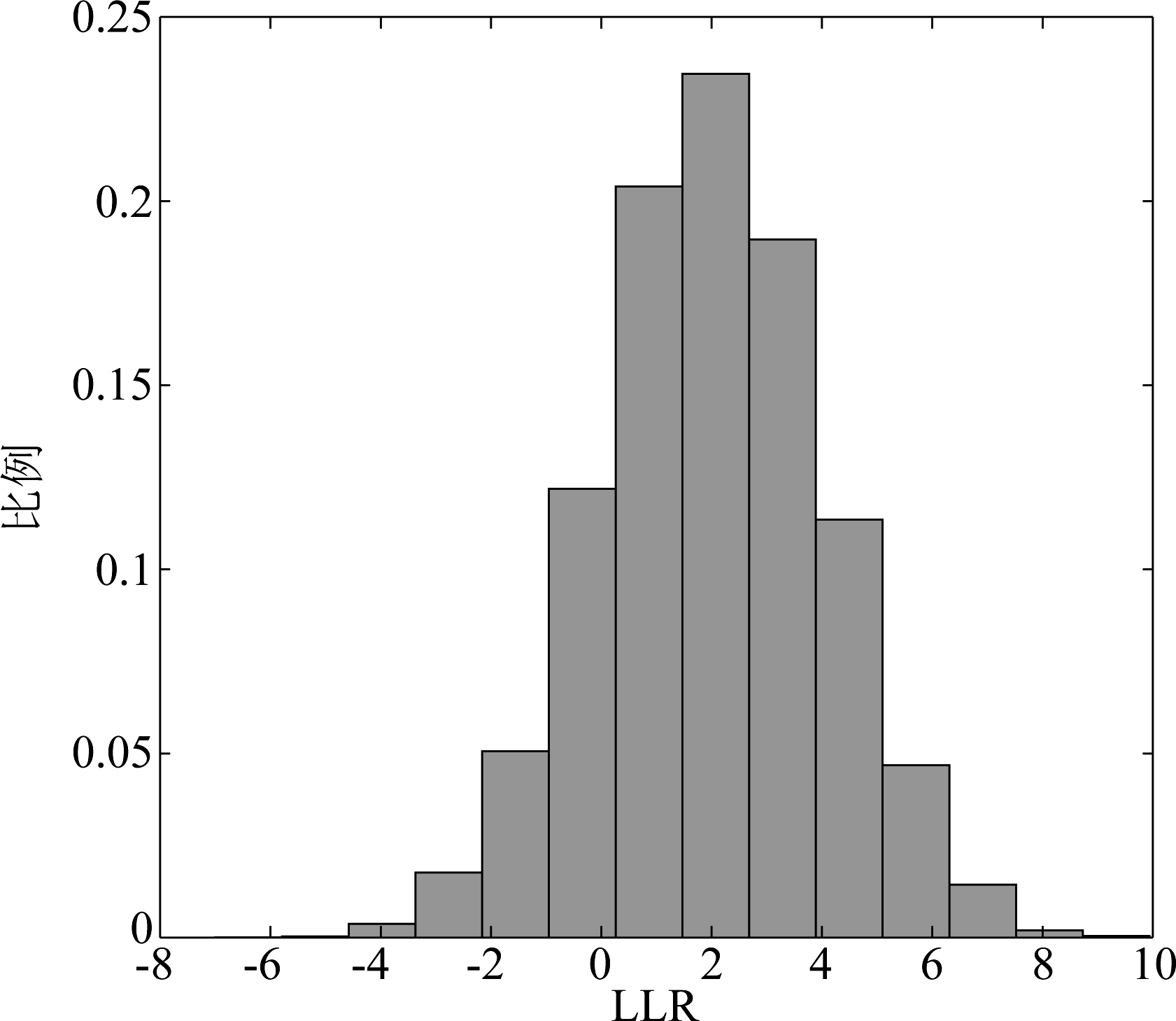
图4 RRH 3比特量化下输入LLR的分布直方图
Fig.4 LLR distribution histogram under 3-bit quantization at the RRH
对于均值为τ，方差为2τ的满足对称高斯分布的消息，其携带的外信息为[25]：
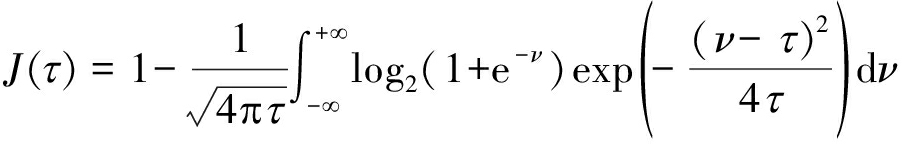
(14)
BBU池联合译码每轮迭代各节点EXIT传递过程如图5所示。LDPC码变量节点度分布定义为
其中ξd为LDPC译码图中度数为d的变量节点占所有变量节点的比例，
为变量节点最大度数。变量节点边度分布定义为
码校验节点边度分布定义为
其中
是与度数为d的校验节点相连的边占所有边的比例，
为校验节点的最大度数。输入节点的边度分布定义为
其中
表示与度数d输入节点相连的边的比例，dν表示输入节点的最大度数。输出节点边度分布定义为
其中ωd表示与度数为d的输出节点相连的边占所有边的比例，dc为最大输出节点的度数。输出节点度分布为Ω(x)，ω(x)与Ω(x)的换算关系为：
(15)
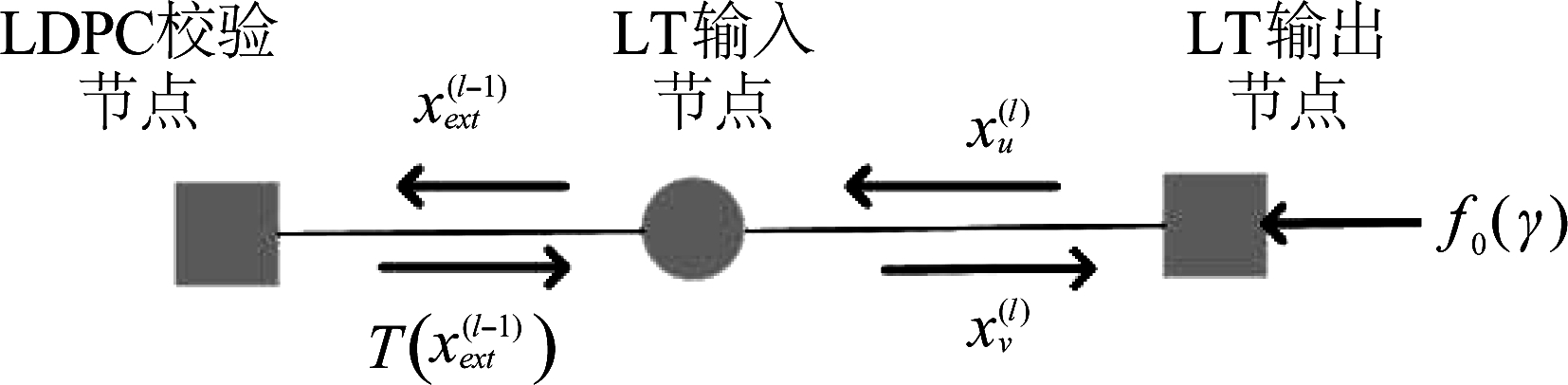
图5 BBU池处译码器中消息传递图示
Fig.5 The message passing on the factor graph in the iterative decoder at the BBU pool
首先，LLR消息由LT输入节点传向LDPC校验节点，其携带的外信息平均值为：
(16)
式中
为第l-1次迭代过程中LT输出节点在第l-1轮迭代时LT输出节点传向输入节点的外信息平均值。接着，由LDPC校验节点传回LT输入节点的消息的外信息量为[26]:
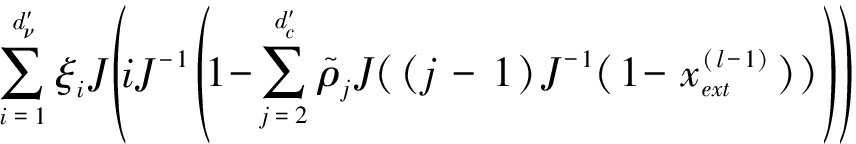
(17)
接下来是LT输入节点传向输出节点，其中包含了上一轮迭代中输出节点传给该输入节点的消息以及之前LDPC校验节点传给该输入节点的消息，其携带的外信息为：
(18)
最后，LT输出节点传向输入节点消息所携带的外信息为：
(19)
其中f0(γ)=J(2γ)表示信噪比为γ的二元输入高斯信道的输出所携带的信息量。将式(17)，(18)代入式(19)得到每轮迭代更新的
为：
(20)
显然式(20)与LT输出节点的边的度分布系数{ωd}呈线性关系。
4.2 输出度分布优化
本小节根据前面的EXIT分析，优化用户无速率码输出度分布Ω(x)。由于译码方法分为两步，即第一步先在包括LDPC子图和LT子图的整幅译码图上进行迭代，第二步在LDPC子图上单独迭代以消除剩余错误。为了保证所有的剩余错误都能在第二步被消除，需要LT子图中所有的输出节点传向输入节点的平均外信息和在最后一轮(l′)迭代高于使LDPC码能够正确译码的某一最小外信息门限xp，即
该门限根据[18]中方法得到。
本文的优化目标是最大化系统传输速率，等价于最小化系统传输速率的倒
(21)
其中
为LT输入节点平均度数，该表达式与LT输出节点边度分布系数呈线性关系。通过求解优化问题找到最优的输出节点边度数分布ω(x)使得式(21)最小，同时满足消息m能在BBU池被正确恢复。优化问题条件列出如下：
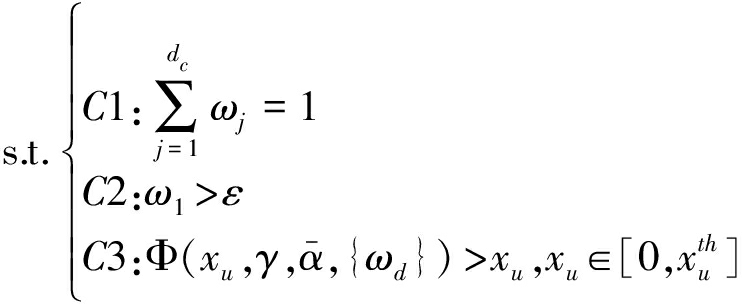
(22)
该组约束条件中，条件C1表示输出节点的边度分布系数{ωd}的和为1。条件C2表示需要一定数量的度数为1的输出节点，这是保证BP译码开始的启动条件，ε是大于零的一个小量。条件C3中变量xu都是连续的，在实际优化操作中可以将xu在其取值范围内N等分离散化，那么就可以将条件C3转化为N个等价条件：
(23)
式中xu,i是在范围
中的N个等间隔点。通过如上转化，度分布优化问题就转化为一个线性规划问题，然后根据式(15)换算即可得到输出节点最优度分布Ω(x)。最后，对于优化度数分布的计算复杂度，当前线性规划问题的求解已经非常成熟，其复杂度在最坏情况下为多项式复杂度。因此最终求解优化问题(22)的计算复杂度是线性规划问题复杂度乘以α搜索时的离散点数，所以最坏情况仍为多项式复杂度。需要注意的是，当信道不变时，只需要优化一次度数分布，所以与译码相比优化度数分布的复杂度是很小的。
5 仿真结果
5.1 理论可达速率
本文中以RRH不进行量化，直接向BBU上传基带信号(3)时理论可达速率作为系统性能上限。容易证明，当RRH处量化间隔趋向于0，量化门限趋向于无穷，BBU池的LLR合并即式(8)等价于最大比合并。因此BBU池接收信噪比为：
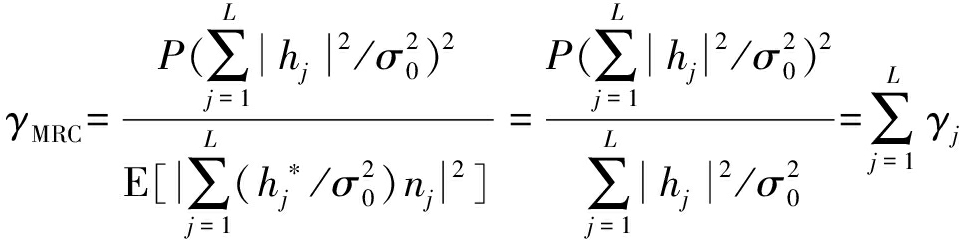
(24)
令RRH无量化时C-RAN上行单用户系统的理论信道容量为C。由于采用BPSK调制，信噪比为γMRC的二元输入对称高斯信道(BIAWGN)理论容量为[22]：
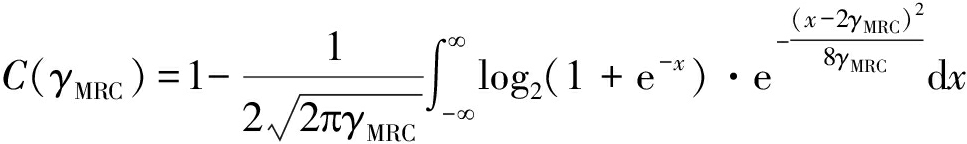
(25)
5.2 C-RAN上行单用户系统误码率性能
在仿真中，本文考虑单个用户，两个RRH场景，其中用户处采用速率为0.95，长度为10000的LDPC码作为无速率码的预编码，该LDPC码的正确译码门限xp=0.9818。令各RRH处噪声方差均为
用户S到RRH1和RRH2两条链路的信道衰落系数分别为h1=0.7，h2=1.1。译码额外开销定义为：
(26)
其中C是由式(25)计算得到的系统上行链路理论信道容量，N为译码成功时实际传输码长，k为用户原始信息长度。这里的额外开销是对于理论所需译码开销的相对值，其为0即代表达到了理论可达速率。令文献[22]删除信道下最优度数分布为ΩBEC(x)，将其与本文方法优化得到度数分布在误码率性能上进行对比，同时本文还考虑和比较了量化噪声对输出度数分布的影响。
不考虑RRH处量化器量化噪声，即对于BBU池接收信噪比为式(24)时采用本文所述方法进行优化(等效于对具有该信噪比的二元对称高斯信道进行优化)。得到的无速率码输出节点度分布为Ωopt(x)：
Ω1=0.004715,Ω2=0.436706,Ω3=0.272642,
Ω6=0.127585,Ω7=0.085293,Ω19=0.055493,
Ω20=0.011292,Ω60=0.006274
考虑RRH处量化器量化噪声时，在不同量化比特下分别对无速率码输出节点度分布做优化。当采用3比特量化时，RRH1处量化器量化噪声方差
处量化器量化噪声方差
优化得到的无速率码输出度数分布为Ωopt,3bit(x)：
Ω1=0.004699,Ω2=0.442896,Ω3=0.263535,
Ω6=0.162180,Ω7=0.050176,Ω17=0.000004,
Ω18=0.043109,Ω19=0.026503,Ω60=0.006899
当采用8比特量化时，RRH1处量化器量化噪声方差
处量化器量化噪声方差
优化得到的无速率码输出度数分布为Ωopt,8bit(x)：
Ω1=0.004716,Ω2=0.436733,Ω3=0.272578,
Ω6=0.128052,Ω7=0.084788,Ω19=0.057789,
Ω20=0.009034,Ω60=0.006233
当采用10比特量化时，RRH1处量化器量化噪声方差
处量化器量化噪声方差
优化得到的无速率码输出度数分布为Ωopt,10bit(x)：
Ω1=0.004716,Ω2=0.436727,Ω3=0.272592,
Ω6=0.127943,Ω7=0.084898,Ω19=0.057255,
Ω20=0.009558,Ω60=0.006311
在不同Overhead下，比较BEC度数分布ΩBEC(x)与以上优化得到的度分布分别达到的系统误码率，仿真结果如图6所示。
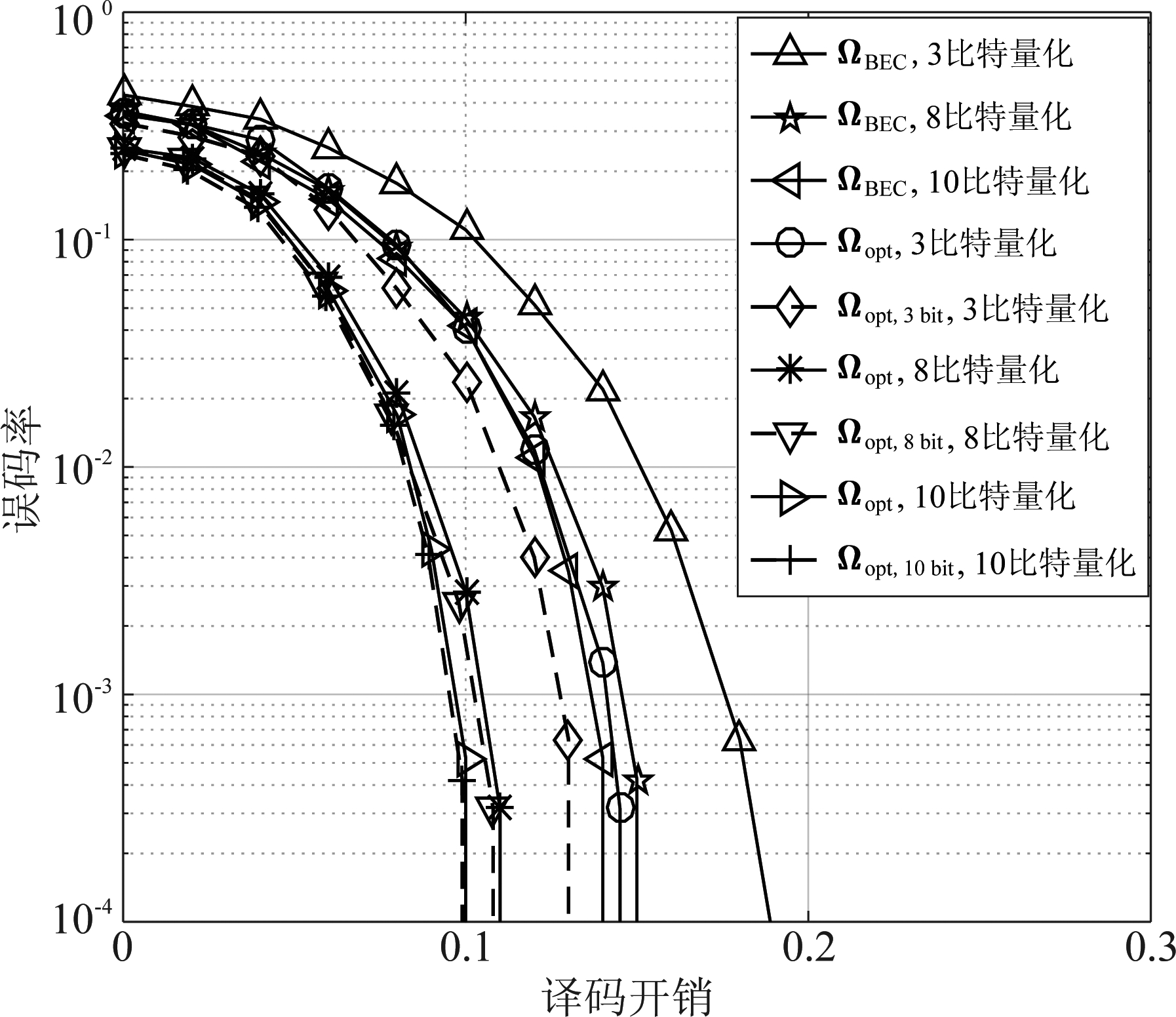
图6 不同输出度分布下系统误码率
Fig.6 Bit error rate under different output degree profiles
从仿真结果中可以看出，当RRH进行3比特量化时，考虑量化噪声优化的度数分布Ωopt,3bit(x)比不考虑量化噪声优化的度数分布Ωopt(x)的性能好2%；比BEC度数分布ΩBEC(x)的性能好5%左右。当RRH进行8比特量化时，考虑量化噪声优化的度数分布Ωopt,8bit(x)与不考虑量化噪声优化的度数分布Ωopt(x)的性能趋于接近，相差1%以内；比BEC度数分布ΩBEC(x)的性能好4%左右。当RRH达到10比特量化时，考虑量化噪声优化的度数分布Ωopt,10bit(x)与不考虑量化噪声优化的度数分布Ωopt(x)的性能基本上趋于相同，其译码额外开销仅比RRH无量化理论极限损失10%左右。以上仿真结果表明，在C-RAN上行无速率码传输系统中，可以通过适当的优化设计出更好的无速率码输出度数分布。此外，随着量化比特逐渐增大到一定的值以后，系统趋于RRH没有进行量化的上限，此时相当于单入多出MIMO系统，系统性能也就不会有明显的提升。
5.3 C-RAN上行单用户系统吐量性能
在仿真中，令各RRH处噪声方差均为
用户S到RRH1和RRH2两条链路服从方差为1的瑞利分布。我们将瑞利分布的信道增益量化为三个状态，分别对其进行度数优化。RRH进行8比特量化时，比较在不同信噪比(Signal Noise Ratio, SNR)下，采用本文所述方法优化得到的度分布Ωopt(x)与BEC度分布ΩBEC(x)在C-RAN上行单用户接入系统中达到的系统平均吞吐量。仿真结果如图7所示，仿真结果表明，本文优化的无速率码输出度数分布实现了更高的吞吐量，其与理论极限相差10%以内。
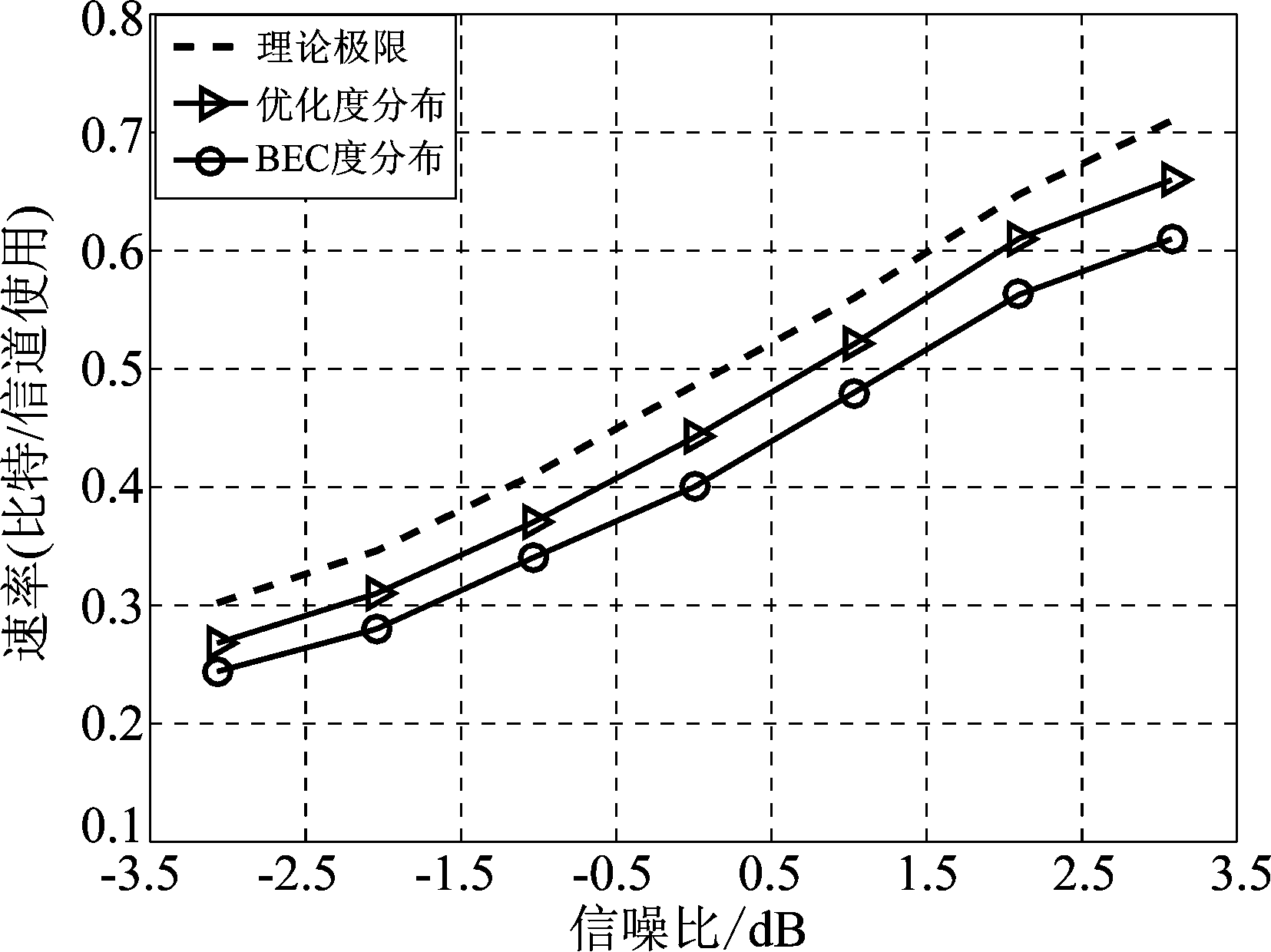
图7 不同度数分布下系统吞吐量
Fig.7 Average system throughput under different degree profiles
6 结论
本文主要研究了C-RAN中单用户上行接入场景下基于无速率码的传输机制。针对RRH对信号量化转发，BBU池集中处理的特点，设计了在RRH处复杂度较低的标量量化算法以及BBU池联合译码算法。为了进一步提升性能，本文基于EXIT分析给出了对无速率码输出度数分布优化的设计方法。仿真结果表明，在C-RAN上行接入系统中，本文优化的度数分布在误码率和吞吐量性能上相较于传统度数分布均有比较好的提升。本文中RRH量化器的设计采用等间隔量化方案，不足之处是对小信号有不利影响。下一步的工作是针对量化器的量化间隔与度数分布的联合优化。
[1] Cisco. Cisco visual networking index: global mobile data traffic forecast update, 2015-2020[R]. White Paper,2016: 1-39.
[2] Chen Kulin, Run Duan. C-RAN: the road towards green RAN[R]. China Mobile Research Institute, White Paper, 2(2011).
[3] 程宇新, 项海格.无线数据传输中的混合ARQ[J]. 电信科学, 2005, 21(2):42- 47.
Cheng Yuxin, Xiang Haige. Hybrid ARQ Techniques for Wireless Data Transmission[J]. Telecommunications Science, 2005, 21(2): 42- 47.(in Chinese)
[4] Rowitch D N, Milstein L B. On the performance of hybrid FEC/ARQ systems using rate compatible punctured turbo(RCPT) codes[J]. IEEE Transactions on Communications, 2000, 48(6): 948-959.
[5] Han Qing, Wang Chenxi, Levorato M, et al. On the effect of fronthaul latency on ARQ in C-RAN systems[J]. ArXiv Preprint ArXiv: 1510.07176(2015).
[6] Mackay, David J C. Fountain codes[J]. IEEE Proceedings Communications, 2005, 152(6): 1062-1068.
[7] Michael L. LT codes[C]∥Null. IEEE, 2002:271.
[8] Shokrollahi A. Raptor codes[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2551-2567.
[9] Castura J, Mao Yongyi. Rateless coding over fading channels[J]. IEEE Communications Letters, 2006, 10(1): 46- 48.
[10] Wang Guohui, Michael W, Sun Yang, et al. GPU accelerated scalable parallel decoding of LDPC codes[C]∥IEEE the Forty Fifth Asilomar Conference on Signal, Systems and Computers(ASIL). IEEE, 2011: 2053-2057.
[11] Wübben D, Paul H, Balleydier P, et al. Decoder implementation for cloud based architectures[C]∥European Conference on Networks and Communications (EuCNC), Bologna, Italy, 2014.
[12] Zhou Yuhan, Yu Wei. Optimized backhaul compression for uplink cloud radio access network[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1295-1307.
[13] Li Xiangming, Jiang Tao, Cui Shuguang, et al. Cooperative communications based on rateless network coding in distributed MIMO systems[J]. IEEE Wireless Communications, 2010, 17(3): 60- 67.
[14] Wu Yuan, Qian Liping, Mao Haowei, et al. Optimal Power Allocation and Scheduling for Non-Orthogonal Multiple Access Relay-Assisted Networks[J]. IEEE Transactions on Mobile Computing, 2018.
[15] Lu Weidang, Gong Yi, Liu Xin, et al. Collaborative energy and information transfer in green wireless sensor networks for smart cities[J]. IEEE Transactions on Industrial Informatics, 2018, 14(4):1585-1593.
[16] 孙远,李春国,黄永明, 等.基于云接入网络的多目标资源分配算法设计[J].信号处理,2017,33(3):294-303.
Sun Yuan, Li Chunguo, Huang Yongming, et al. Multi-Objective Resource Allocation Design Algorithm in Cloud Radio Access Network[J]. Journal of Signal Processing, 2017, 33(3): 294-303. (in Chinese)
[17] Zhang Yu, Zhang Zhaoyang, Yin Rui, et al. Joint network channel coding with rateless code in two-way relay systems[J]. IEEE Transactions on Wireless Communic-ations, 2013, 12(7): 3158-3169.
[18] Zhang Yu, Zhang Zhaoyang. Joint network-channel coding with rateless code over multiple access rely system[J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 320-332.
[19] Park S H, Simeone O, Sahin O, et al. Fronthaul compression for cloud radio access networks: signal processing advances inspired network information theory[J]. IEEE Signal Processing Magazine, 2014, 31(6): 69-79.
[20] Pukelsheim F. The three sigma rule[J]. The American Statistician, 1994, 48(2): 88-91.
[21] Venkiah A, Poulliat C, Declercq D. Analysis and design of raptor codes for joint decoding using information content evolution[C]∥Information Theory, 2007. ISIT 2007. IEEE International Symposium on. IEEE, 2007: 421- 425.
[22] Etesami O, Shokrollahi A. Raptor codes on binary memo ryless symmetric channels[J]. IEEE Transactions on Information Theory, 2006, 52(5): 2033-2051.
[23] Chung S Y, Richardson T J, Urbanke R L. Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J]. IEEE Transactions on Information Theory, 2001, 47(2): 657- 670.
[24] Richardson T J, Shokrollahi M A, Urbanke R L. Design of capacity-approaching irregular low-density parity-check codes[J]. IEEE Transactions on Information Theroy, 2001, 47(2): 619- 637.
[25] Roumy A, Guemghar S, Caire G, et al. Desifn methods for irregular repeat-accumulate codes[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1711-1727.
[26] Venkiah A, Poulliat C, Declercq D. Jointly decoded raptor codes: analysis and design for the biawgn channel[J]. EURASIP Journal on Wireless Communications and Networking, 2009, 2009(1): 657-970.
