1 引言
网络编码技术是一种融合了路由和编码的信息交换技术，由Ahlswede等人于2000年提出[1]。在网络编码系统中，中间节点不是简单的存储转发，而是将收到的信息进行线性或者非线性的处理，然后转发给下游节点，中间节点扮演着编码器或信号处理器的角色。网络编码技术可以显著提高系统容量。当网络编码技术应用在无线通信环境的双向中继系统时，由于无线网络的广播特性，物理链路的交汇为网络编码创造了条件，同时网络节点可以利用无线信道的广播特性侦听一定量的冗余数据包，也为网络译码创造了条件。因此，网络编码技术特别适合被应用于无线网络环境中产生了物理层网络编码技术[2]。
物理层网络编码应用在双向中继系统中，双向通信的双方Alice和Bob之间没有直接链路，只能通过中继节点Relay进行中继通信。在第1个时隙，Alice和Bob同时向Relay发送信号，利用无线环境下空中自然叠加的原理，中继节点Relay接收的信号是两侧用户的信息经过信道失真后电磁波的叠加。Relay将叠加后的信号进行一定的处理在第2个时隙转发出去，两侧用户接收后根据自身的发送码元推算得到对方发送的码元。物理层网络编码只用了2个时隙就完成了一次信息交换，提高了网络吞吐率[3]。
虽然物理层网络编码利用了电磁波空中自然叠加节省了一个时隙，但同时也产生了诸多问题，比如同步、信道失真的补偿和中继节点的转发模式选择等问题。由于无线通信环境的复杂性，不同的用户距离造成不同的时延，如何能保证Alice和Bob发送的信号能同时到达Relay，如果两侧信号到达时延不同如何解决，这都属于同步问题需要解决的范畴，文献[4-7]等对同步问题进行了研究。同样由于无线信道环境的复杂性，除了时延外还存在信道失真，两侧不同信道的失真给中继节点的解码带来很大的困难。为此，文献[8-12]等对信道失真的补偿问题进行了研究。另外，中继节点的转发模式选择问题也是研究热点之一，中继节点转发模式将对物理层网络编码系统性能带来很大的影响。为此，研究不同转发模式对物理层网络编码系统性能的影响具有重要的意义。在使用物理层网络编码的双向中继系统中，中继节点常用的转发模式一般分两种：放大转发(Amplify and Forward，AF)和解码转发[13]。放大转发模式下，中继节点对接收信号不做任何其他操作只是简单的放大后转发[14]；解码转发模式下，中继节点对接收信号进行解码操作后再转发。根据解码算法的不同，解码转发模式又分为去噪转发(Denoise and Forward，DnF)和去噪再编码转发(Denoise Encode and Forward，DEF)等。对于去噪转发模式，中继节点对接收信号进行判决去除噪声后直接转发[15]；而对于去噪再编码转发模式，中继节点对接收信号判决去噪后，再进行编码后转发[16]。
本文在假设系统同步和信道失真得以补偿的情况下，研究了中继节点不同转发模式下的系统抗噪声性能。针对采用正交相移键控(QPSK)调制的物理层网络编码系统，对放大转发，去噪转发和去噪再编码转发的三种转发模式进行了分析和比较。首先研究其信号星座图特性，给出了编码方法的星座图对应关系；然后推导了三种转发模式在高斯白噪声信道环境下的误码率计算公式；最后仿真验证了推导的误码率公式的正确性，并根据误码率和误比特率分析比较了三种转发模式的优劣。
本文的内容安排如下：第一部分为引言，第二部分给出了物理层网络编码系统的系统模型，分析了物理层网络编码中双向通信的基本原理；第三部分研究了中继节点的三种转发模式，对每个转发模式，分析了信号星座图，研究了中继节点的物理层网络编码算法和用户节点的解码算法；第四部分推导了三种转发模式的误码率公式；第五部分对物理层网络编码系统进行了MATLAB仿真，结果表明仿真的误码率曲线和理论推导的误码率公式曲线完全重合，验证了公式推导的正确性，进行了三种转发模式的抗噪声性能分析和比较；第六部分为总结。
2 系统模型
系统模型如图1所示，其中Alice和Bob为双向通信的双方，Relay为实施物理层网络编码的中继节点。在第1个时隙，Alice和Bob同时向中继节点Relay发送信号。Alice发送的数据cA经过QPSK调制得到信号sA，通过功率控制fA后发送，经过信道A后的信号yA到达Relay。假设信道环境是平坦衰落信道，令信道A的衰落为hA，加性高斯白噪声为nA，白噪声的方差为
则有：
yA=hAfAsA+nA
(1)
同时，Bob发送的数据cB经过QPSK调制得到信号sB，通过功率控制fB后发送，经过信道B后的信号yB到达Relay。假设信道环境是平坦衰落信道，令信道B的衰落为hB,加性高斯白噪声为nB，白噪声的方差为
则有:
yB=hBfBsB+nB
(2)
假设Alice和Bob端进行信道估计[17]后，采用相应的同步策略[4-7]和功率控制[8-12]，能保证Alice和Bob发送的信号同步Relay到达且功率一致，即有‖hAfA‖=‖hBfB‖=H，则Relay的接收信号为两侧电磁波的叠加，表示为：
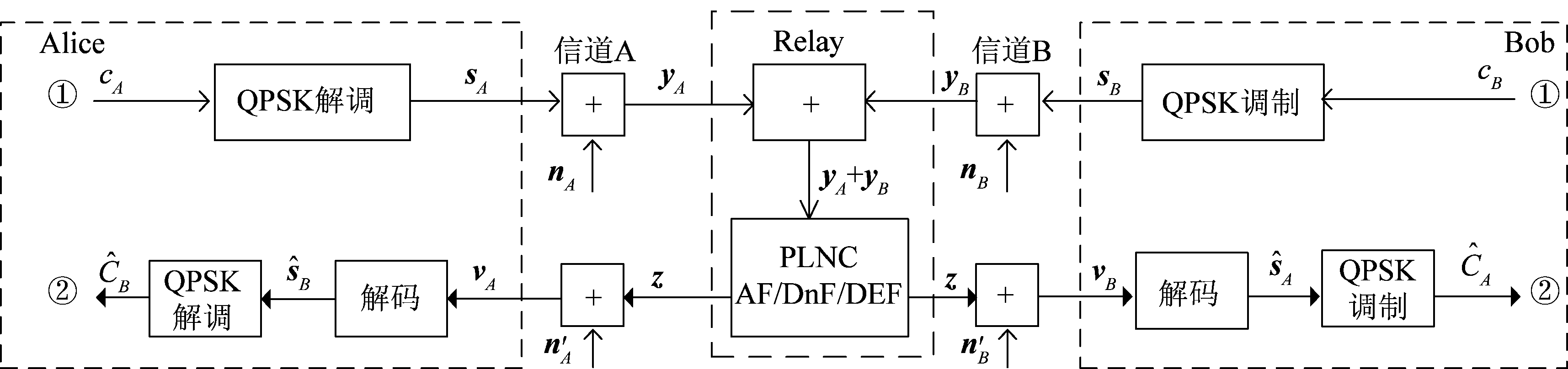
图1 物理层网络编码的双向中继系统模型
Fig.1 The two-way relay system with physical layer network coding
yA+yB=HsA+HsB+nA+nB
(3)
对于在第1个时隙接收到的叠加信号，Relay需要对其进行物理层网络编码的转发操作，可以使用三种转发模式：放大转发、去噪转发和去噪再编码转发，三种不同的转发模式将在第三节进行详细介绍。
在第2个时隙，中继节点Relay将不同转发模式产生的信号z通过下行链路分别发送给Alice和Bob。在Alice侧，z经过下行加性高斯白噪声信道A后的信号vA到达Alice，vA经过解码后再解调得到Bob发送比特的估计
同样的，在Bob侧，z经过下行加性高斯白噪声信道B后的信号vB到达Bob，vB经过解码后再解调得到Alice发送的比特的估计
这样经过两个时隙，Alice和Bob就完成了一次信息交换。
3 中继节点的转发模式
在物理层网络编码系统中，在第1个时隙，中继节点Relay接收到的信号是Alice和Bob端同时发送的两路QPSK信号(QPSK信号的星座图如图2(a)所示)的叠加。在不存在信道失真和噪声的情况下，两路QPSK信号的叠加称之为2+QPSK信号，2+QPSK信号的星座图如图2(b)所示。存在高斯白噪声的情况下，例如每比特信噪比为15 dB时，Relay接收信号的星座图如图2(c)所示。
Relay需要对接收信号进行转发操作，可以使用三种转发模式：放大转发、去噪转发和去噪再编码转发。放大转发模式下，中继节点对接收信号不做任何其他操作只是简单的放大后转发；去噪转发模式下，中继节点对接收信号进行判决去除噪声后转发；去噪再编码转发模式下，中继节点对接收信号判决去噪后再进行编码后转发。本节将对三种转发模式进行详细介绍，通过转发信号的星座图分析和对比来探讨不同转发模式的优缺点。
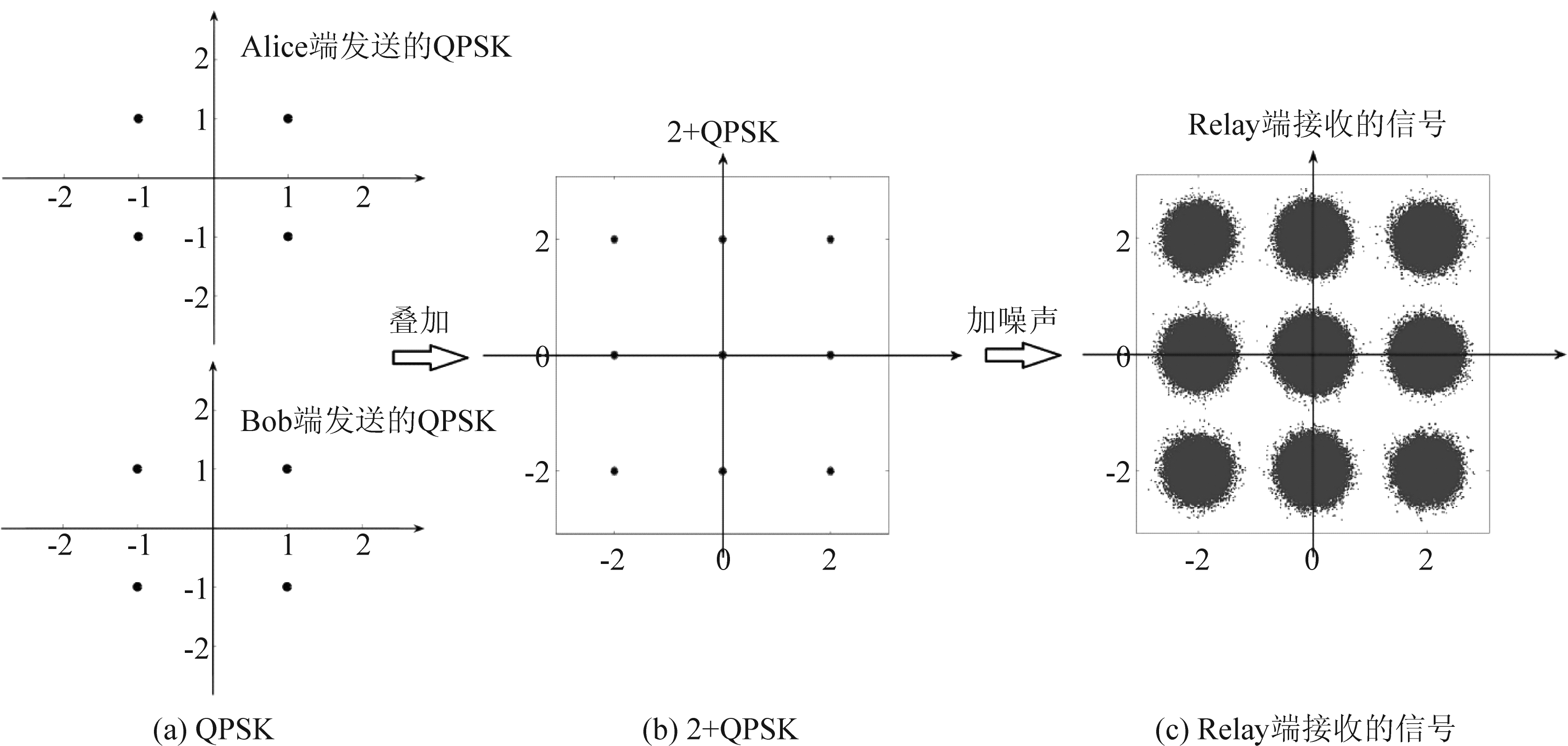
图2 三种信号的星座图
Fig.2 Constellation diagrams for three signals
3.1 放大转发模式(AF)
放大转发模式下，Relay对接收到的信号进行直接放大转发，放大目的是为了补偿传输过程中的功率损耗,令放大系数为α。放大转发的信号可以表示为：
zAF=αHsA+αHsB+αnA+αnB
(4)
当放大系数α的选择满足αH=1时，则有
zAF=sA+sB+αnA+αnB
(5)
放大转发模式下，当每比特信噪比为15 dB时，Relay转发信号的星座图如图3(a)所示。
在第2时隙，Relay转发的信号zAF经过信道A到达Alice，同时经过信道B到达Bob。令
为下行链路Relay到Alice的信道加性白噪声，
为上行链路Relay到Bob的信道加性白噪声。
在放大转发模式下，Alice得到：
(6)
Alice已知自己的发送信号sA，对vA进行解码，解码算法采用直接相减算法，得到：
(7)
同样，在放大转发模式下，Bob得到：
(8)
Bob端已知自己的发送信号sB，对vB进行解码，解码算法采用直接相减算法，得到：
(9)
Alice对vA-sA进行判决从而获得Bob的发送信号sB的估计
再经过解调获得Bob的发送比特cB的估计
对vB-sB进行判决从而获得Alice的发送信号sA的估计
再经过解调获得Alice的发送比特cA的估计
经过两个时隙Alice和Bob完成了一次信息交换。
3.2 去噪转发模式(DnF)
在放大转发模式中，Relay不仅对有用信号进行了放大转发，同时对噪声进行了放大转发，Relay转发出去的信号包含了一部分噪声功率，既浪费功率又影响性能，而去噪转发模式能有效解决这一问题。去噪转发是在Relay端对接收到的信号进行去噪判决后再转发，在去噪转发模式下，Relay转发的信号zDnF可以表示为：
zDnF=sA+sB
(10)
去噪转发是对接收信号进行去噪判决，具体去噪判决算法见算法1，其中，R{·}代表取实部，I{·}代表取虚部。
算法1:去噪转发算法(1)Relay对接收信号进行放大得到zAF;(2) 如果R{zAF}>1,则R{zDnF}=2;如果R{zAF}<-1,则R{zDnF}=-2;否则R{zDnF}=0;(3)如果I{zAF}>1,则I{zDnF}=2;如果I{zAF}<-1,则I{zDnF}=-2;否则I{zDnF}=0;(4)zDnF=R{zDnF}+I{zDnF}j。
去噪转发模式下，Relay转发信号的星座图如图3(b)所示。跟放大转发模式(图3(a))相比，去噪转发模式在Relay端增加了判决去除噪声模块，转发信号是9点的2+QPSK信号，不会放大和转发噪声。
在第2时隙，Relay转发的信号zDF经过下行信道A到达Alice，同时经过下行信道B到达Bob。Alice接收到的信号为：
(11)
Alice已知自己的发送信号sA，对vA进行解码，解码算法采用直接相减算法，得到：
(12)
同样，在放大转发模式下，Bob接收到信号为：
(13)
Bob端已知自己的发送信号sB，对vB进行解码，解码算法采用直接相减算法，得到：
(14)
Alice对vA-sA进行判决从而获得Bob的发送信号sB的估计再经过解调得到Bob的发送比特cB的估计对vB-sB进行判决从而获得Alice的发送信号sA的估计再经过解调得到Alice的发送比特cA的估计经过两个时隙Alice和Bob完成了一次信息交换。
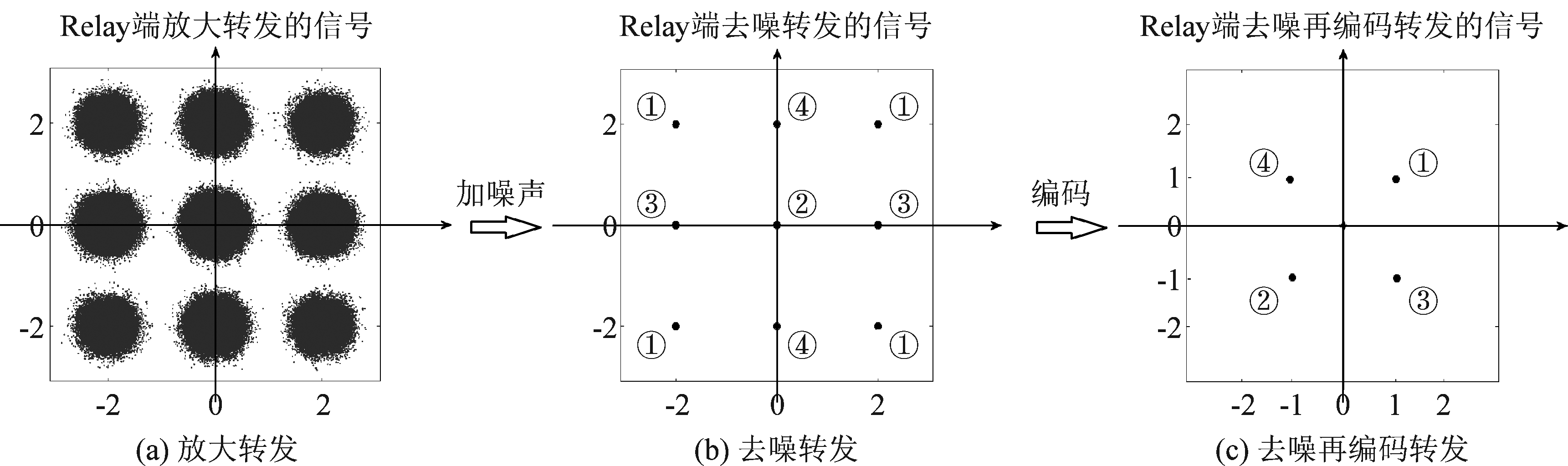
图3 三种转发模式的信号星座图
Fig.3 Constellation diagrams for signal with three forwarding modes
3.3 去噪再编码转发(DEF)
去噪转发模式下，Relay转发的信号是两路QPSK混合信号2+QPSK信号，我们参考文献[16]的编码算法并对其进行重新的星座图解释和详细的算法分析，这是一种去噪再编码转发的模式，称之为DEF模式。去噪再编码转发模式是2+QPSK信号再编码转化为QPSK信号，信号星座图由9点2+QPSK星座图转化为4点QPSK星座图，具体编码算法见算法2，其中，R{·}代表取实部，I{·}代表取虚部，‖·‖代表取绝对值。
算法2:2+QPSK信号转化为QPSK信号的编码算法(1)Relay对接收信号利用算法1得到zDF;(2)如果‖R{zDF}‖>1则R{zDEF}=1,否则R{zDEF}=-1;(3)如果‖I{zDF}‖>1则I{zDEF}=1,否则I{zDEF}=-1;(4)zDEF=R{zDEF}+I{zDEF}j。
2+QPSK信号(图3(b))转化为QPSK信号(图3(c))的编码算法2可以在星座图上进行直观的解释。图3(b)中2+QPSK星座图上的9个点可以分为四组。图3(b)中第①组的四个点对应转化为QPSK星座图(图3(c))中的①点“1+j”，图3(b)中第②组的一个点对应转化为QPSK星座图(图3(c))的②点“-1-j”，图3(b)中第③组的两个点对应转化为QPSK星座图(图3(c))的③点“1-j”, 图3(b)中第④组的两个点对应转化为QPSK星座图(图3(c))的④点“-1+j”。第①组代表Alice和Bob发送的QPSK信号实部和虚部都相同，第②组代表Alice和Bob发送的QPSK信号实部和虚部都不同，第③组代表Alice和Bob发送的QPSK信号实部相同虚部不同，第④组代表Alice和Bob发送的QPSK信号实部不同虚部相同，具体见表1所示。
在第2时隙，Relay转发的信号zDEF经过下行信道A到达Alice，同时经过下行信道B到达Bob。Alice接收到的信号为：
(15)
Alice已知自己的发送信号sA，对vA进行解码得到sB的估计值根据表1的对应关系解码算法为：
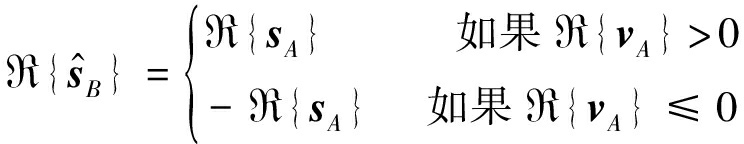
(16)
(17)
同样， Bob接收到的信号为：
(18)
表1 2+QPSK信号转化为QPSK信号的对应关系
Tab.1 The corresponding relationship with 2+QPSK signal conversion to QPSK signal
星座图的点组两路QPSK的实部两路QPSK的虚部2+QPSK信号的星座图编码后QPSK信号的星座图①组相同相同2+2j,2-2j,-2+2j,-2-2j1+j②组不同不同0-1-j③组相同不同2,-21-j④组不同相同2j,-2j-1+j
Bob已知自己的发送信号sB，对vB进行解码得到sA的估计值根据表1的对应关系解码算法为：
(19)
(20)
Alice对
解调得到Bob的发送比特cB的估计对
进行解调得到Alice的发送比特cA的估计经过两个时隙Alice和Bob完成了一次信息交换。
4 三种转发模式的误码率性能
为了分析高斯白噪声信道下三种转发模式的误码率性能，本文根据已有的正交振幅调制(QAM)误码率公式[18]推导出2+QPSK的误码率公式。下面，首先介绍QPSK和QAM调制对应的误码率公式。假设四条信道的噪声功率一样均为N0=σ2。
对于QPSK信号, QPSK信号幅度为
信号功率为2A2。由于每两个比特生成一个QPSK信号，因此每比特的信号功率为Pbit=A2，噪声功率为N0，rb为每比特信噪比rb=A2/σ2。根据文献[18]，QPSK的误码率公式为:
(21)
对于M-QAM信号, M为QAM调制的点数，dmin为QAM调制的最小距离，噪声功率为N0。根据文献[18]，M-QAM的误码率公式为：
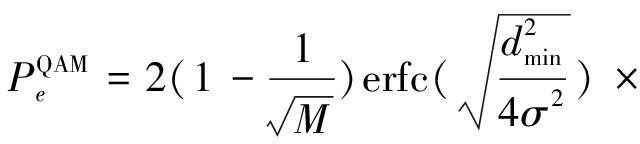
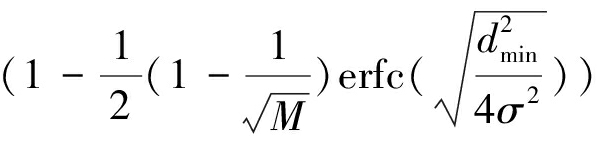
(22)
两路QPSK信号经过物理层网络编码后形成的信号为2+QPSK信号，其星座图如图2(b)所示。2+QPSK的星座图跟矩形QAM的星座图很像，因此2+QPSK信号可以看作是9个点的矩形9-QAM信号，M=9,dmin=2A。利用M-QAM的误码率公式(22)，我们推导出2+QPSK信号的误码率：
(23)
4.1 放大转发模式(AF)的误码率
在放大转发模式下，第1个时隙Relay接收到的信号是两路QPSK信号叠加，两侧信道的白噪声也进行了叠加，在第2个时隙，下行链路Relay将信号直接转发出去，Alice和Bob接收到的信号分别如式(6)和式(8)所示。Alice和Bob的接收信号中包含三路噪声信号，因此噪声总功率为3σ2，带入式(23)得到放大转发模式下，Alice端和Bob端的误码率为：
(24)
4.2 去噪转发模式(DnF)的误码率
在去噪转发模式下，Relay的接收信号如式(3)所示。由于两侧噪声是不相关的，叠加后的噪声功率为两侧噪声功率之和，因而噪声总功率为2σ2，代入式(23)得到上行链路Relay去噪判决过程的误码率：
(25)
去噪后的信号在第2时隙经过下行链路信道到达Alice或Bob(见式(11)(13))，2+QPSK信号叠加了一路噪声，噪声总功率为σ2，代入式(23)得到下行链路的误码率为：
(26)
第1时隙上行链路的正确概率为
第2时隙下行链路的正确概率为
根据联合概率计算得到，去噪转发模式的总误码率：
(27)
4.3 去噪再编码转发模式(DEF)的误码率
在去噪再编码转发模式下，第1个时隙上行链路Relay去噪过程中的误码率为
去噪的信号经过编码将2+QPSK信号编码为QPSK信号，第2时隙再经过下行链路信道到达Alice或和Bob，叠加一路的噪声，噪声总功率为σ2，因此下行链路的误码率为
(28)
上行链路的正确概率为
下行链路的正确概率为
根据联合概率计算得到，DEF的误码率：
(29)
5 仿真结果
我们使用MATLAB仿真来验证物理层网络编码系统中三种转发模式的误码率性能。仿真中，Alice和Bob同时向Relay发送2×106个数据比特，采用QPSK调制生成106个QPSK信号发送，发送信号功率为2，调制的幅度为
假设两侧上下行信道的高斯白噪声功率均为σ2，每比特信噪比rb=1/σ2，rb取值范围为-10 dB至15 dB。
经过仿真得到了三种转发模式的误码率曲线如图4所示，经对比跟推导计算的误码率公式曲线重合，验证了误码率推导式(24)、式(27)和式(29)的正确性。由图4可知，当rb<-5 dB时，AF性能最好，DEF性能次之，DnF性能最差；当-5 dB<rb<0 dB时，DEF的性能最好，AF性能次之，DnF性能最差；当rb>0 dB时，DEF性能最好，DnF性能次之,AF性能最差。
经过仿真得到三种转发模式的误比特率曲线如图5所示，从仿真误比特率曲线可以看出，当rb<-5 dB时，三种转发模式的误比特率均为50%系统无法运行，当-5 dB<rb<0 dB时，DEF的性能最好，AF性能次之，DnF性能最差；当rb>0 dB时，DEF性能最好，DnF性能次之，AF性能最差。
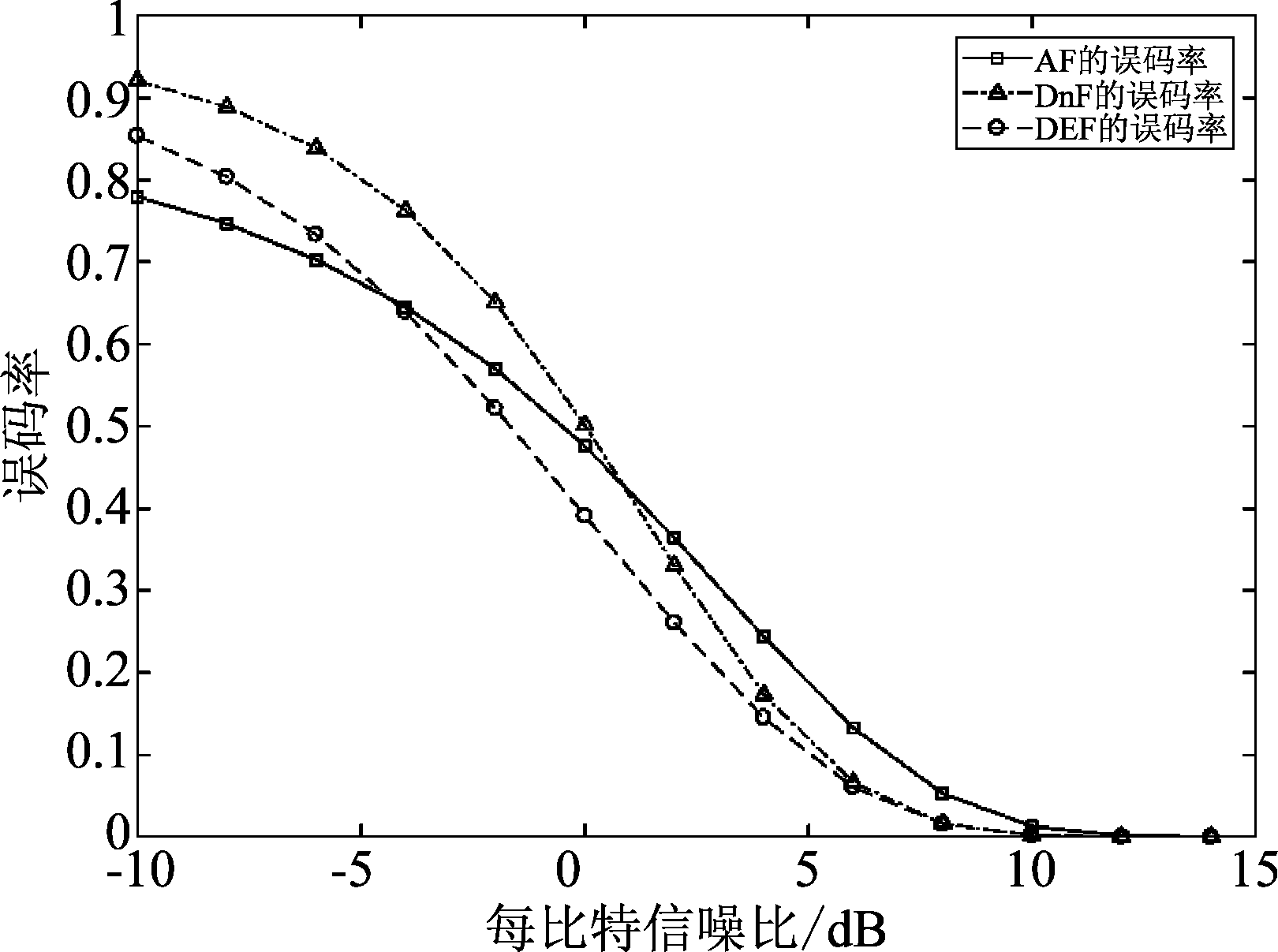
图4 三种转发模式下物理层网络编码系统的误码率性能
Fig.4 SER of PLNC system with three forward modes
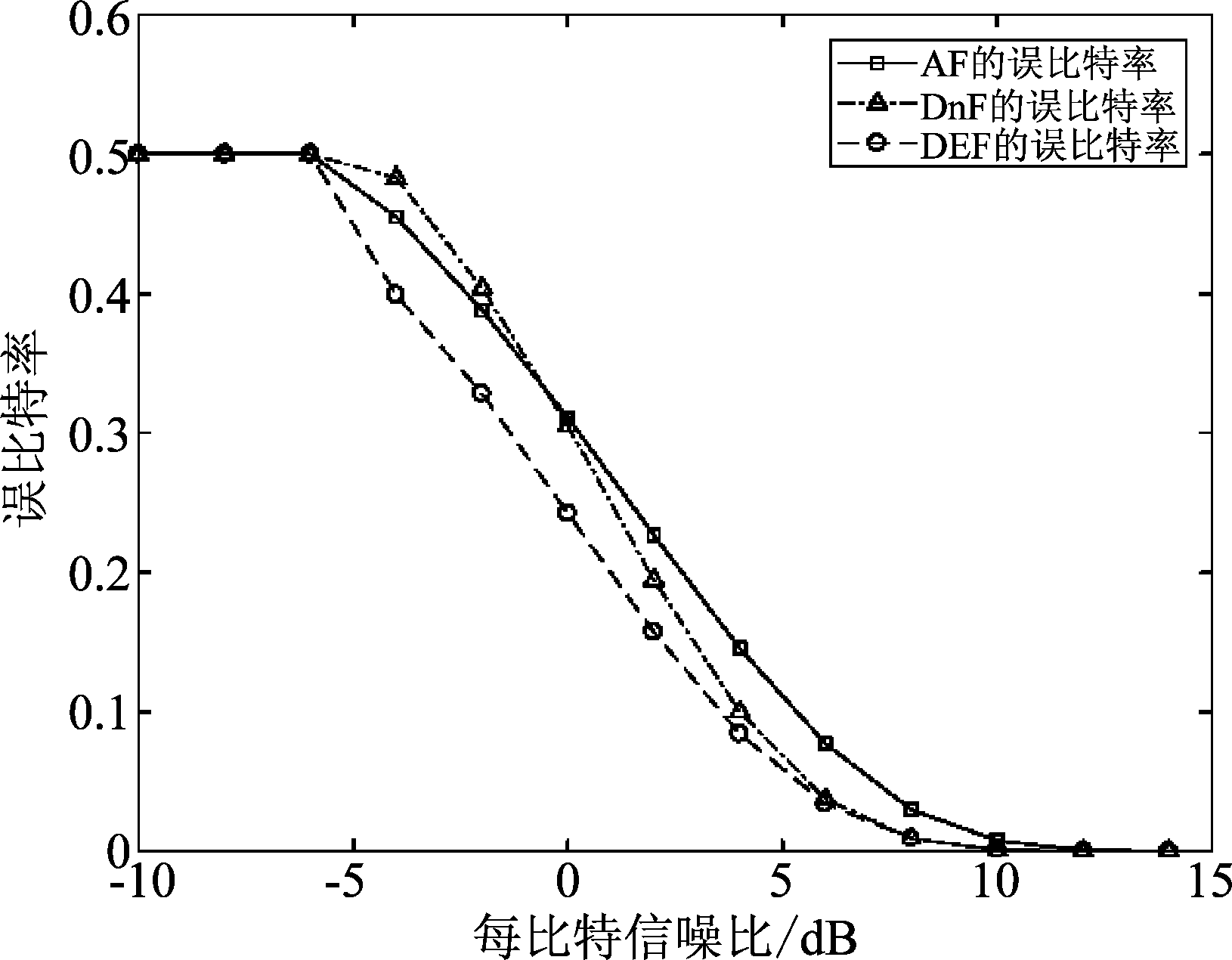
图5 三种转发模式下物理层网络编码系统的误比特率性能
Fig.5 BER of PLNC system with three forward modes
一般的通信环境下，要保证正常通信需要足够低的误码率。放大转发模式将噪声同时放大转发影响了系统性能，去噪转发和去噪再编码两种模式在中继节点进行去噪后再转发，在信噪比较好的环境下，系统性能会提高。由于有效通信环境信噪比通常满足rb>0 dB，因此去噪再编码转发模式是物理层网络编码系统中最优的转发模式。
6 结论
在无线双向中继系统中，中继节点使用物理层网络编码技术可以带来网络吞吐率的提高。物理层网络编码技术中很多问题值得研究，比如同步、信道失真补偿和中继节点的转发方式等问题。本文主要研究中继节点不同的转发方式对于系统性能的影响。我们分别研究了放大转发、去噪转发和去噪再编码转发三种转发方式在物理层网络编码的应用。在QPSK调制方式下，对三种转发方式的星座图和编码对应关系进行了深入分析，推导了三种转发方式的误码率公式，并仿真验证了公式的正确性，系统误码率和误比特率性能都说明去噪再编码转发模式是物理层网络编码系统中最优的转发模式。但是在物理层网络编码系统的某些结构下，放大转发和去噪转发模式也需要使用，比如在中继节点无法进行正确解码时或解码全部放在用户端等情形下，中继节点都只能采用放大转发或去噪转发的模式，因此本文中三种转发模式的性能分析对物理层网络编码研究有一定的指导意义。
[1] Ahlswede R, Cai N, Li S Y R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216.
[2] You L Z, Liew S C, Lu L. Reliable Physical-Layer Network Coding Supporting Real Applications[J]. IEEE Transactions on Mobile Computing, 2017, 16(8): 2334-2350.
[3] Zhang H Y, Zheng L, Cai L. Design and Analysis of Hierarchical Physical Layer Network Coding[J]. IEEE Transactions on Wireless Communications, 2017, 16(12): 7966-7981.
[4] Zhang S, Liew S C, Lam P P. On the Synchronization of Physical-Layer Network Coding[C]∥Information Theory Workshop, 2006. ITW'06 Chengdu. IEEE, 2006:404- 408.
[5] Wang H, Zhu G, Hou M, et al. Time synchronization based on multiplexing RPR channel and IRIG-B time code[C]∥International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. IEEE, 2016:869- 872.
[6] Kramarev D. Accurate symbol-level synchronization of universal software radio peripherals for physical-layer network coding applications[C]∥MILCOM 2017-2017 IEEE Military Communications Conference (MILCOM), 2017: 756-761.
[7] Chang S, Kelley B. An Efficient Time Synchronization Scheme for Broadband Two-Way Relaying Networks Based on Physical-Layer Network Coding[J]. IEEE Communications Letters, 2012, 16(9): 1416-1419.
[8] Zhang M L, Lu L, Liew S C. An Optimal Decoding Strategy for Physical-Layer Network Coding Over Multipath Fading Channels[J]. IEEE Transactions on Vehicular Technology, 2015, 64(9): 4365- 4372.
[9] Ahmed A H, Tsimenidis C C, Neasham J, et al. Dfe for Frequency Selective Pnc Channels Using Af[C]∥2015 IEEE 11th International Conference on Wireless and Mobile Computing, Networking and Communications (Wimob), 2015: 833- 838.
[10] Liew S C, Zhang S L, Lu L, et al.Physical-layer network coding: Tutorial, survey, and beyond[J]. Physical Communication, 2011, 6:4- 42.
[11] Li X, Gao Z Z, Lv G M, et al. Generalized Anti-Eavesdropping Space-Time Network Coding for Cooperative Communications[C]∥IEEE Wireless Communications and Networking Conference (Wcnc), 2013: 4163- 4168.
[12] Ndih E D N, Cherkaoui S. Statistical Modeling of the Physical-Layer Network Coding in Time-Varying Two-Way Relay Channels[C]∥2011 IEEE International Conference on Communications (Icc), 2011.
[13] Popovski P, Yomo H. Physical network coding in two-way wireless relay channels[C]∥2007 IEEE International Conference on Communications, Vols 1-14, 2007: 707-712.
[14] Li Y T, Yu Q Y, He K, et al. Apply Uniquely-Decodable Codes to Multiuser Physical-Layer Network Coding Based on Amplify-and-Forward Criterion[C]∥2015 IEEE Global Communications Conference (GLOBECOM), 2015: 1- 6.
[15] Jebur B A, Tsimenidis C C. Performance Analysis of OFDM-Based Denoise-and-Forward Full-Duplex PLNC with Imperfect CSI[C]∥2015 IEEE International Conference on Communication Workshop, 2015: 997-1002.
[16] Bartoli G, Fantacci R, Marabissi D, et al. Physical Layer Network Coding in Multipath Channel: Effective Precoding-Based Transmission Scheme[C]∥2011 IEEE Global Telecommunications Conference (Globecom 2011), 2011.
[17] 吕斌, 杨震, 冯友宏. 针对块稀疏信道的估计算法[J]. 信号处理, 2015, 31(12):1680-1687.
Lv B,Yang Z,Feng Y H. Novel Channel Estimation Algorithms for Block Sparse Channels[J].Journal of Signal Processing, 2015, 31(12):1680-1687. (in Chinese)
[18] 普罗科斯．数字通信[M]．张力军,译，第5版．北京：电子工业出版社，2012．
JohnG. Proakis．Digital Communications[M]．Zhang L J, translate,5th Edition. Beijing: Electronics Industry Press,2012.(in Chinese)
