1 引言
时延估计技术是近年来备受关注的研究热点课题，在导航定位[1]、雷达探测[2]、智能机器人控制[3]、通信系统[4]等领域得到广泛应用，尤其在目标定位中，无源时差定位技术因布站灵活、设备成本低、抗干扰能力强等优势成为最常用的定位方法之一，该方法通过检测目标信号到达监测站的时延建立双曲线方程实现定位，时延估计的精确度直接影响最终的定位性能，因此研究高精度的时延估计技术至关重要。目前，经典的时延估计方法主要有最小均方(Least mean square，LMS)自适应法[5]、子空间类时延估计方法[6]、广义互相关(generalized cross correlation，GCC)法[7]等。LMS自适应法无需信号和噪声的统计先验知识即可实现信号间时延差估计，但为达到高精度的时延估计，需要较长适应时间，难以满足实时性要求；子空间类法大多需要进行多径数目估计、特征分解、谱峰搜索等操作，计算复杂度较高；GCC方法具有原理简单、计算量小、稳定性好，适用性强等优势，在时延估计领域受到广泛关注。
GCC时延估计方法通过信号间互相关函数的峰值检测估计时延，该方法基于理想信号模型，即假设噪声与信号，噪声与噪声两两正交，对平稳随机信号，在高信噪比条件下可获得精确的时延估计值。然而，在实际中，这种假设并不成立，受各种噪声和混响的影响，GCC函数峰值不再尖锐，甚至出现伪峰值，使得时延估计出现较大偏差。为解决该问题，文献[8-10]对其进行了改进。文献[8]引入改进的小波阈值函数进行信号去噪与重构，采用GCC方法进行时延估计，这种方法克服了传统软硬阈值函数的缺点，提升了时延估计性能，然基于小波阈值的信号去噪受小波基选择、分解尺度等因素制约。文献[9]采用倒谱法分离声门脉冲机制和声道响应，并结合谱减法设计了区分含噪信号有用频段的有效方案，最后利用经验模态分解后的本征模函数谱特性，进行信号重构，该方法显著提高了时延估计算法的抗噪性能，但算法复杂，应用场景单一，还需不同场景性能检验。文献[10]通过加权欧式失真检测、话音激活检测、最小值控制递归平均等信号预处理及时延后处理，极大地提高了时延估计的准确性，然该时延后处理方式假设时延初值已知，但实际中这种假设并不能保证。
基于上述分析可知，接收信号中往往含有各种干扰噪声，使得时延估计精度下降，因此提高时延估计精度需解决的关键问题是如何降低噪声的影响。奇异值分解(Singular Value Decomposition, SVD)[11]方法具有去噪效果显著，稳定性强等优点，利用该方法进行信号预处理既可保留信号形变信息 又可较好的过滤掉噪声污染。鉴于此，本文提出了一种新的时延估计方法，即SVDHB-GCC (generalized cross correlation method with Hassab-Boucher based on singular value decomposition)时延估计法。该方法首先利用SVD进行信号预处理，提高信号的信噪比；其次，利用HB加权函数进行频域互功率谱处理，锐化GCC函数峰值；最后，在时延初值未知的情况下，提出了一种基于中位数和平均数相结合的时延后处理方法，修正了时延估计中因噪声等影响造成的异常波动，提高了时延估计的精确性。仿真实验结果显示，本文所提SVDHB-GCC方法与参考GCC和SVD-GCC(generalized cross correlation method based on singular value decomposition)方法相比，抗噪性更强，准确度更高。
2 SVD去噪机理
对任意一个矩阵P(P∈Rm×n)，且m≥n，rank(P)=r≤n，则它的奇异值分解为：
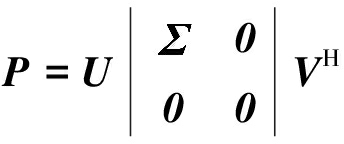
(1)
式(1)中，
=diag([σ1,σ2,...,σr])为一对角矩阵，且满足σ1≫σ2≫…≫σr>0，各个对角线元素表示矩阵P的非零奇异值；r为矩阵P的秩，U，V分别为m×m，m×n维正交矩阵；0表示元素全为0的矩阵。
剔除矩阵P中的零奇异值，得到P简化奇异值分解式为：
(2)
式(2)中，uk和vk分别表示正交矩阵U和V的第k列向量。
对于声传感器节点接收到的声源信号s(i)，(i=1,2,...,N)，构造Hankel矩阵Q：
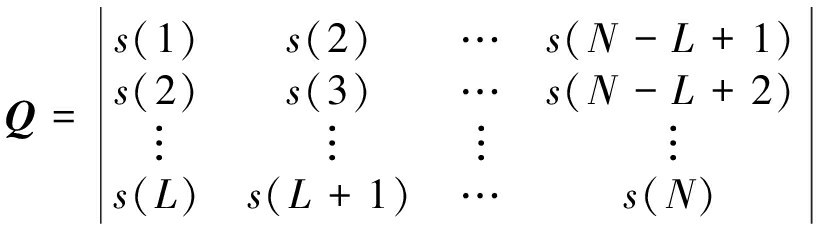
(3)
式中，1<L<N，N为采样信号的长度。
采集的声源信号中夹杂各种环境噪声干扰信号，从而构造的矩阵Q中同样包含噪声。对式(3)进行奇异值分解，得到非零奇异值矩阵，则中的元素代表了信号和噪声能量集中的分布，其中，较大的非零奇异值表示有用信号，较小为干扰噪声。将较小的归零就可达到消除噪声的目的。再利用式(2)进行矩阵重构，还原信号。本文采用文献[12]提出的奇异性检测方法确定Hankel矩阵Q的有效秩阶次及重构矩阵结构，该方法根据参与奇异值分解的信号数据自适应确定非零较大奇异值的个数，并非直接固定有效奇异值的个数，这对分帧后的不同帧平稳信号噪声抑制更为适用。其核心思想是根据奇异值分布的特点，在有效秩阶次k之前的各奇异值内部差异较小，变化较为平稳，而在第k+1个奇异值开始，奇异值序列出现明显的大幅度下降，之后奇异值序列变化趋于平缓，不存在明显波动，从而将k作为突变点，选取前k个非零较大的奇异值，其他归为零。
3 SVDHB-GCC时延估计
3.1 信号模型
假设两个传声器Sen1和Sen2接收的信号模型[13]为：
s1(t)=α1s(t-τ1)+n1(t)
(4)
s2(t)=α2s(t-τ2)+n2(t)
(5)
其中，s(t)为声源信号，n1(t)和n2(t)表示各种环境噪声，αi是声信号衰减因子，即由多路径反射噪声引起的声波在传播过程中的信号损失[14]，它的范围为0～1，τ12=τ1-τ2表示Sen2相对于Sen1接收信号的时间延迟。
3.2 GCC时延估计
信号s1和s2的互相关函数可表示为：
Rs1s2(τ)=E(s1(t)s2(t-τ))=
α1α2E(s(t-τ1)s(t-τ2-τ))+
α1E(s(t-τ1)n2(t-τ))+
α2E(s(t-τ2-τ)n1(t))+
E(n1(t)n2(t-τ))
(6)
式(6)中，E(·)表示数学期望。
因声源信号与噪声信号及噪声信号之间完全正交，则
α1E(s(t-τ1)n2(t-τ))=0
(7)
α2E(s(t-τ2-τ)n1(t))=0
(8)
E(n1(t)n2(t-τ))=0
(9)
从而可将式(6)简化为
Rs1s2(τ)=α1α2E(s(t-τ1)s(t-τ2-τ))
(10)
根据相关函数的性质可知，当且仅当τ=τ12时，Rs1s2取得最大值，即最大相关系数，τ12为接收两路信号的时延。
维纳辛钦定理指出，互相关函数与其互功率谱互为傅里叶变换[14]，因此互相关函数的计算公式可转化为：
(11)
式(11)中, Gs1s2(ω)为互功率谱密度函数，计算公式如式(12)所示。
(12)
式(12)中，(·)*为复数共轭操作，S1，S2分别为接收信号s1和s2的傅里叶变换。
在信号噪声先验知识未知的前提下，HB加权的GCC时延估计方法对提高时延估计精确度、动态跟踪时延变化等具有较好的性能[15]，同时采用HB加权函数进行互功率谱处理有两个重要优势[15-16]：1)乘以一个声源信号的功率谱密度函数，加重了信号功率谱密度中声源信号的成分；2)对互功率谱除以两个接收信号的自功率谱，本质是对Roth(roth filter)处理器仅对一个输入信号归一化处理的改进，与Roth加权类似，起到对输入声源信号白化的作用。HB加权函数的表达式：
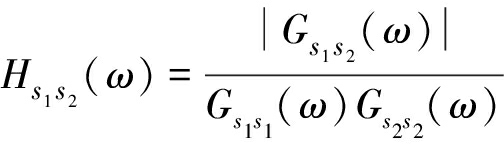
(13)
则互相关函数的计算公式为：
(14)
从而时延的估计值为：
(15)
3.3 时延后处理
因噪声、混响等因素干扰，时延估计值中有少量异常值波动，为去除该异常点，提高时延估计精度，提出一种基于中位数和平均数相结合的时延后处理方法：
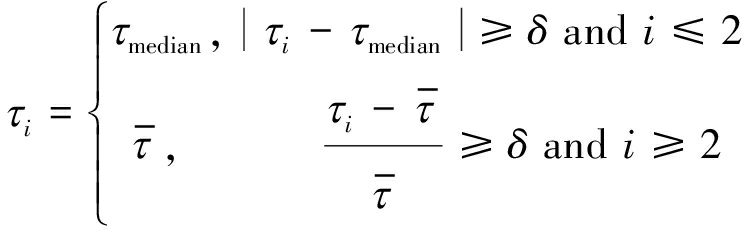
(16)
其中，τmedian表示M帧信号时延估计的中位数，δ为设定的阈值，
表示i帧的前三帧时延估计值的平均值，计算公式为
3.4 SVDHB-GCC时延估计
在GCC时延估计算法研究的基础上，针对环境噪声及异常值波动导致时延估计出现较大偏差的问题，本文提出了一种奇异值分解的HB加权广义互相关算法，图1给出了该算法的原理流程图。
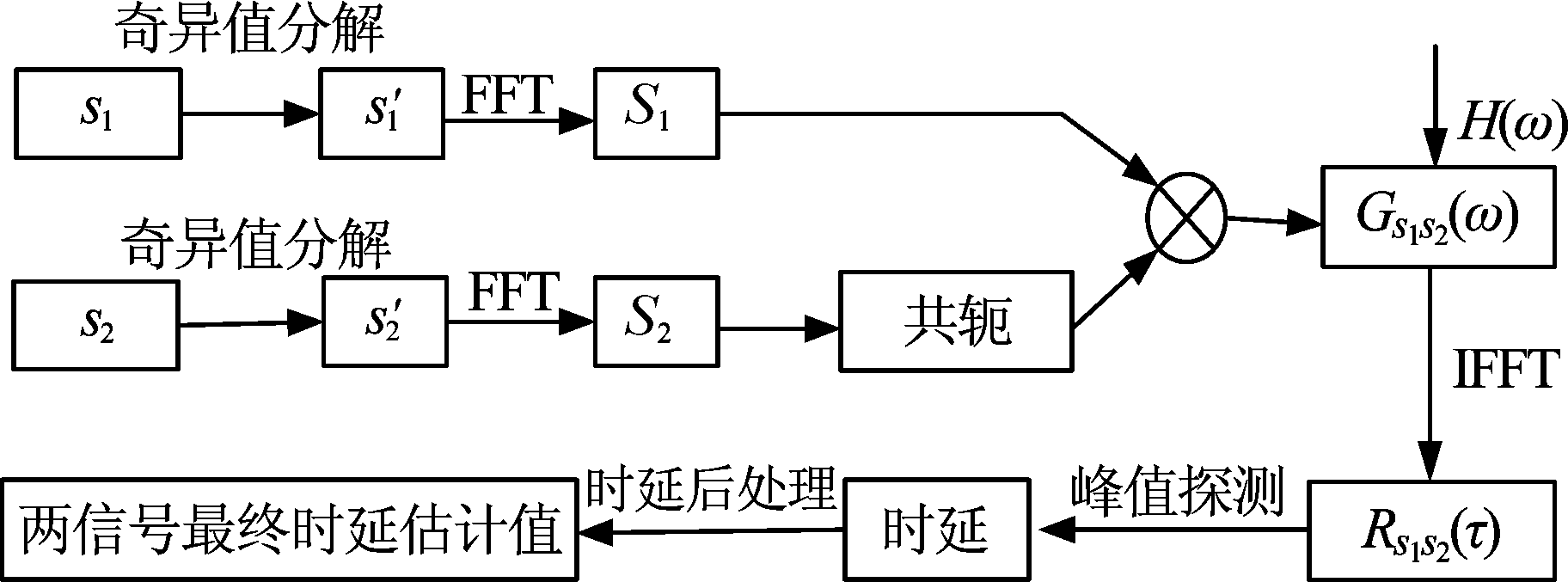
图1 本文算法流程图
Fig.1 Procedure of the proposed algorithm
SVDHB-GCC算法的实现步骤如下：
4 仿真实验与性能分析
为了验证提出算法的时延估计性能，本文进行了两组实验，第一组采用模拟信号验证算法的高效性和抗噪性，第二组采用传声器进行实际真实声源信号采集，在满足第一组实验性能的基础上，进一步验证算法的实用价值。其中，将GCC方法和SVD-GCC方法作为参考算法，比较分析了本文算法的优越性，传统GCC的加权函数为Hs1s2(ω)=1。
4.1 性能评价指标
本文中采用均方根误差(Root mean square error，RMSE)、异常点百分比(Percentage of abnormal point，PAP)和正确率(Accurate rate，AR)衡量提出算法与参考算法的时延估计性能。评价指标的表达式定义为：
(1)均方根误差
(17)
(2)异常点百分比
(18)
(19)
(3)正确率
AR=Ncorrect/Ntotal
(20)
其中，τi表示第i次实验的时延估计值，τ为时延真实值，x是时延估计值与真实值之间的偏差，本文规定时延估计结果与真实时延结果相差超过2个采样点时即视为异常点，Ncorrect表示时延估计完全正确的实验次数，Ntotal表示时延估计的总实验次数。
4.2 模拟信号实例实验
模拟信号采用余弦信号s1及其延迟信号s2，假设延迟时间t=40Ts，其中，Ts=1/fs，采样频率fs=500 Hz，采样点数N=1000，L=N/2，两个信号表示为：
s1(n)=Acos(Bπ·n/fs)
s2(n)=Acos(Bπ·(n+d)/fs)
实验中，设置系数A=20，B=20，并对s1加入信噪比SNR=-20 dB的噪声，从而原始信号、加噪信号及奇异值分解后的降噪信号比对结果见图2。从图2可以看出，基于奇异值分解的信号去噪方法有效的滤掉了噪声污染，同时保留了信号的形变信息，使降噪后的信号与原始信号更加接近，因此采用SVD方法去噪稳定可靠。
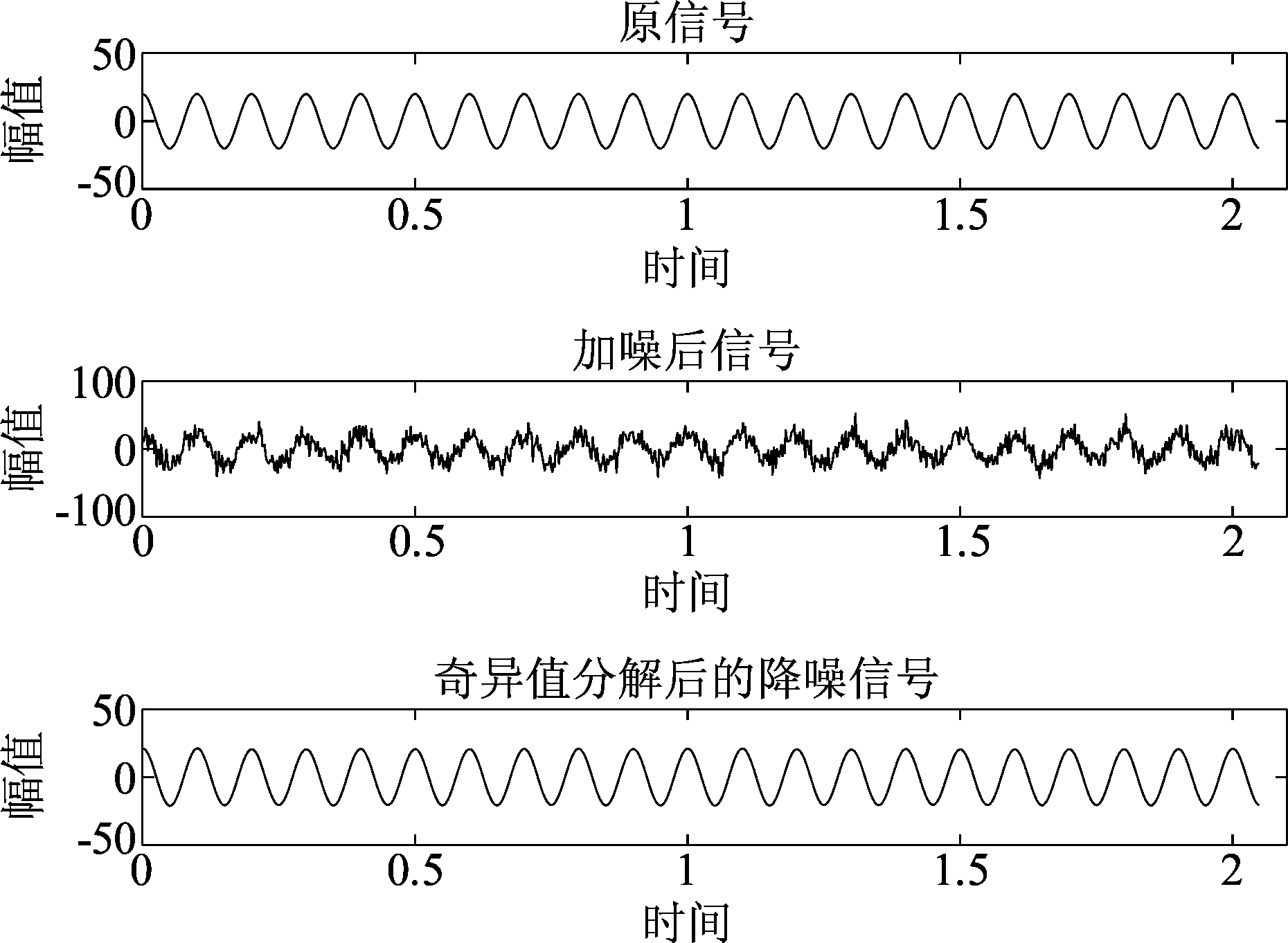
图2 原信号、加噪信号和降噪信号
Fig.2 Primary signal, noisy signal and noise reduction signal
为验证提出算法的抗噪性，对两个信号s1和s2同时加入噪声，设定信噪比变化范围为-20 dB～10 dB，GCC、SVD-GCC及SVDHB-GCC方法的时延估计结果如图3～图6所示，横坐标表示时延点数，纵坐标表示相关程度。由图3～图6可知，在高信噪比条件下，GCC、SVD-GCC及SVDHB-GCC均可准确的估计出时延，但随着信噪比的降低，GCC峰值周围逐渐出现干扰，甚至出现伪峰值，造成较大时延估计误差；SVD-GCC估计精度也逐渐出现偏差，但相比GCC方法，该方法中采用了奇异值分解方法对接收信号进行了噪声抑制，时延估计误差低于GCC方法。本文提出的SVDHB-GCC方法在既采用了SVD对接收信号进行初始降噪，又在GCC时延估计中引入HB加权处理，加强信号中的有用成分，锐化GCC函数峰值，在低信噪比条件下能够较好的估计出时延点数，展现出显著的时延估计优势。与此同时，对信噪比范围-20 dB～10 dB的含噪信号，分别采用GCC、SVD-GCC及SVDHB-GCC方法进行50次随机实验，得到不同噪声条件下评价时延估计性能的异常点百分比、准确率及均方根误差变化曲线，如图7所示。图7(a)与图7(b)反映了不同信噪比条件下，三种算法时延估计的均方根误差与异常点百分比，高信噪比情况下，三种算法的RMSE与PAP较小，波动较低，但随着信噪比的降低，尤其当信噪比低于-5 dB,本文所提SVDHB-GCC算法的RMSE与PAP明显低于传统GCC方法和SVD-GCC方法；从图7(c)可以看出，当信噪比低于0 dB时，传统GCC方法的正确率骤降，而SVD-GCC与SVDHB-GCC算法的正确率下降趋势相对平缓，且SVDHB-GCC的正确率高于SVD-GCC方法。综合图7的指标结果，本文所提算法时延估计性能更优。
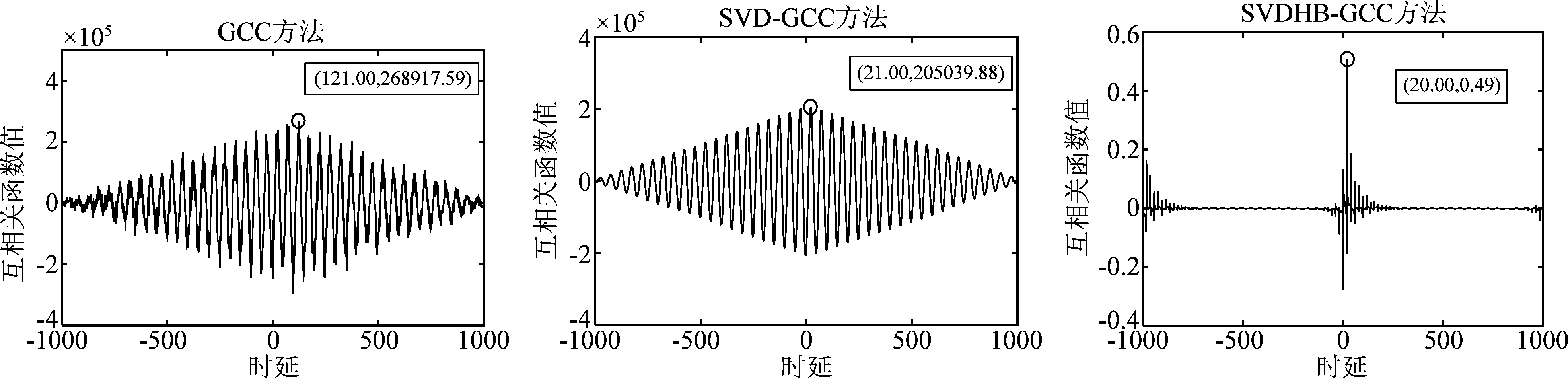
图3 信噪比SNR=-20 dB的三种算法时延估计峰值对比图
Fig.3 Comparisons of peak values of three methods in -20 dB SNR
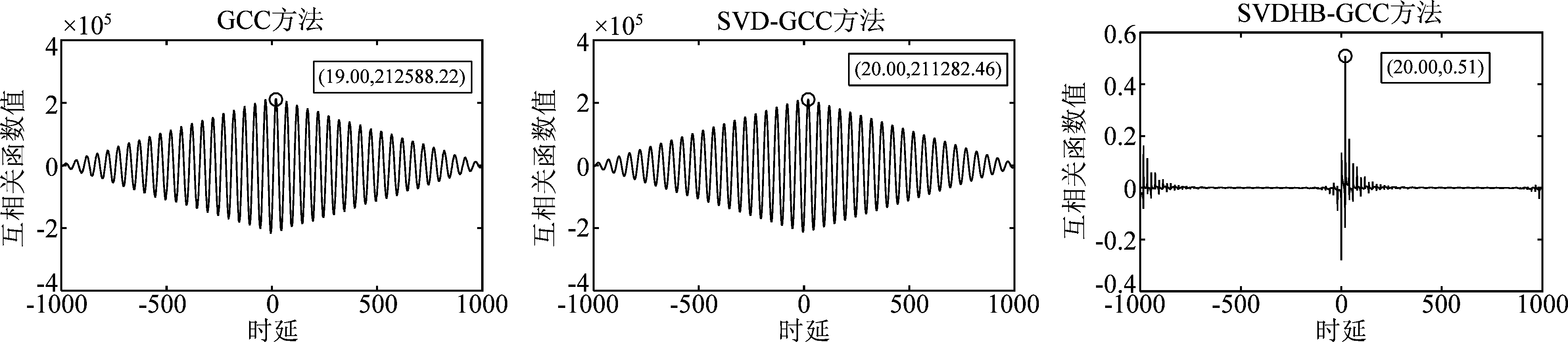
图4 信噪比SNR=-10 dB的三种算法时延估计峰值对比图
Fig.4 Comparisons of peak values of three methods in -10 dB SNR
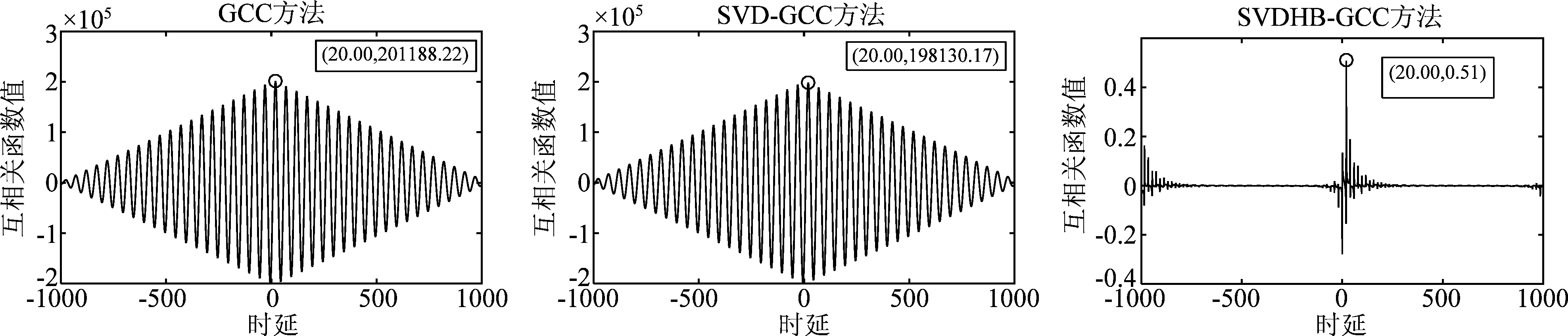
图5 信噪比SNR=0 dB的三种算法时延估计峰值对比图
Fig.5 Comparisons of peak values of three methods in 0 dB SNR
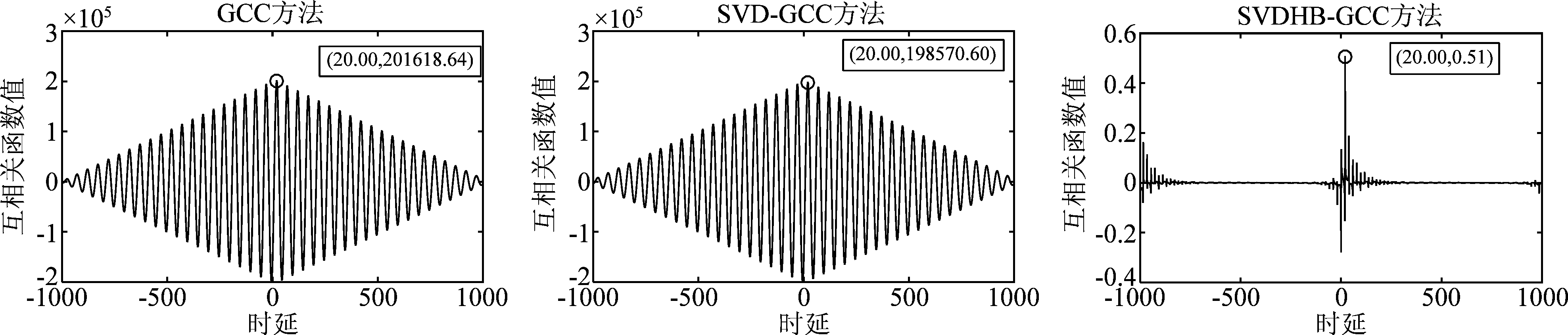
图6 信噪比SNR=10 dB的三种算法时延估计峰值对比图
Fig.6 Comparisons of peak values of three methods in 10 dB SNR
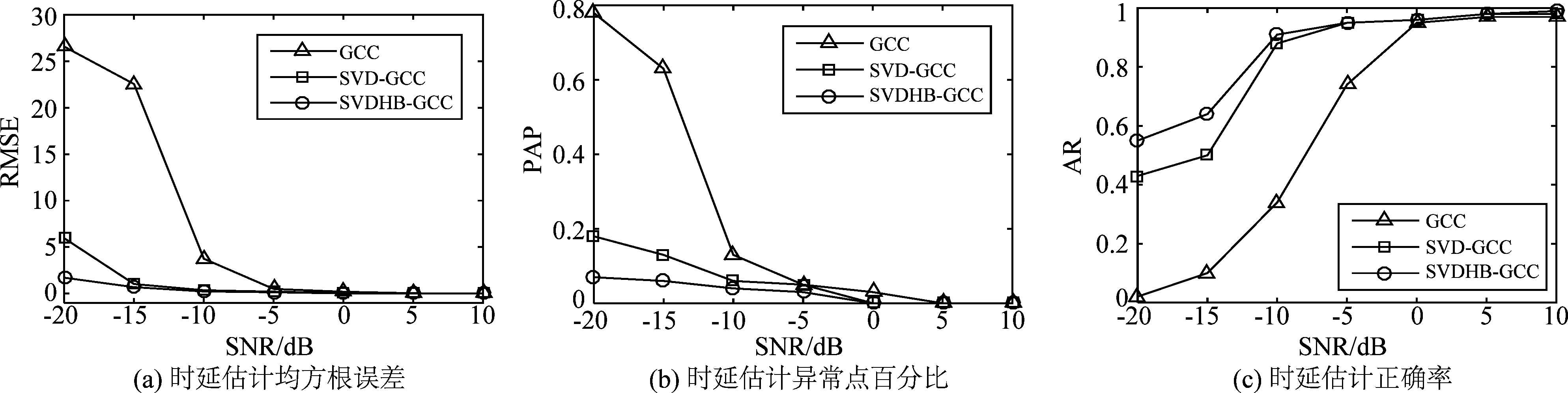
图7 三种算法时延估计性能比较
Fig.7 Performance analysis and comparison of three algorithms
采集声音信号时，因意外声源闯入等外界因素导致噪声干扰突然增强，使得接收数据在某一瞬间污染严重，进而导致最终时延估计结果出现较大偏差。针对这种情况，采用分帧处理是一种有效的信号处理方法，通过分帧的方式，可获得短时平稳信号并进行时延估计，将这种意外干扰控制在某一帧或某几帧信号中，然后利用后处理技术，可较好的处理瞬间时延估计偏差较大的问题。本文提出了一种基于中位数和平均值相结合的时延后处理方法，设置分帧大小为1024，对同一信号源的30帧信号采用SVDHB-GCC算法进行时延估计，后处理前后的时延估计结果见图8。
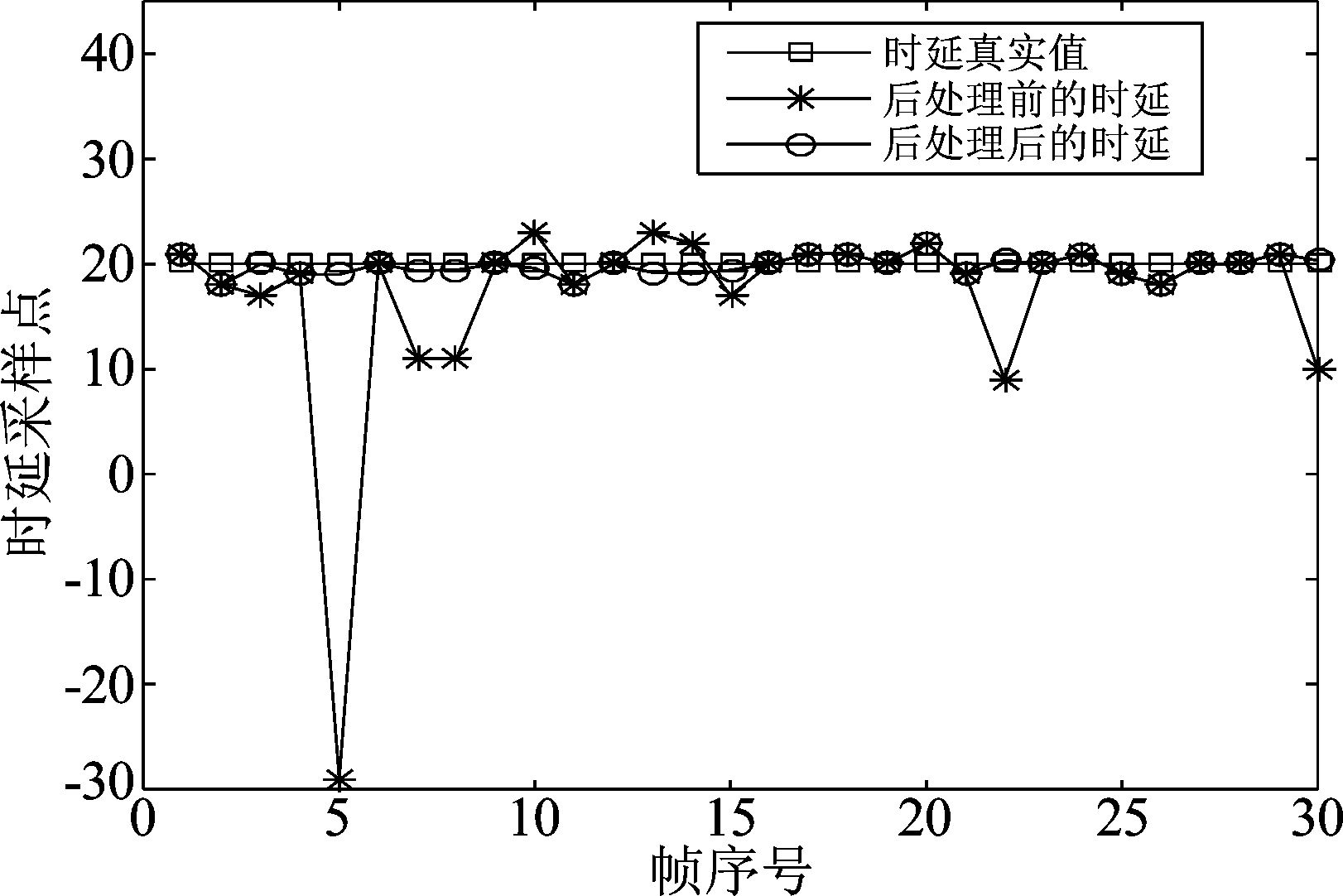
图8 时延后处理前后结果比较
Fig.8 Comparison of time delay between the proposed algorithm and the proposed algorithm without post processing
由图8的实验结果可知，在后处理前，计算得到的各帧时延中存在少量异常值波动，这些异常波动显著的降低了时延估计的精度，而采用本文所提基于中位数与平均值相结合的时延后处理技术能够有效的改善少量帧信号因噪声突然增强干扰造成时延估计误差较大的问题，使得时延估计值更接近真实值，提高时延估计精度。
4.3 实测信号实验
为了验证提出时延估计算法的实用性，进行了实际场景真实声源信号拾取，实验中，采用全指向性间距为25 cm的线性传声器阵列进行声源信号拾取，各个节点频响范围为20 Hz～20 kHz，灵敏度为-28 dB。图9给出了实测信号拾取场景及传声器节点的线性布设结构。
图9 信号收集场景
Fig.9 The environment of collecting signals
声源信号采样时设置采样率为50000 Hz。本文选取传声器节点1和节点2的接收信号进行时延估计和性能比较分析。考虑声源信号的短时平稳特性和缩短时延估计的计算时间，对信号进行分帧处理，帧长设置为102
4，声源与接收节点1和接收节点2的距离分别为2.596 m，2.426 m，从而真实时延为(2.596-2.426)/34
50000=25个采样点。两路接收信号的时域波形如图10所示。
对接收的两路信号分别采用GCC、SVD-GCC和SVDHB-GCC进行时延估计，结果见图11，从图中可以看出，本文提出的方法与GCC、SVD-GCC相比，在实测环境中，噪声类型不唯一情况下，仍能较好的估计信号时延。考虑接受信号的短时平稳特性和缩短时延估计时间，对接收到的声信号，进行分帧处理并估计时延，设置帧长为1024，图12显示了30帧信号的时延估计结果，在时延后处理前，SVDHB-GCC算法估计的时延中含有异常值波动，稳定性不高，严重影响了时延的准确性；采用本文所提时延后处理技术有效的修正了这些时延异常点波动。
图10 两路接收信号时域波形图
Fig.10 The oscillogram of time domain signals
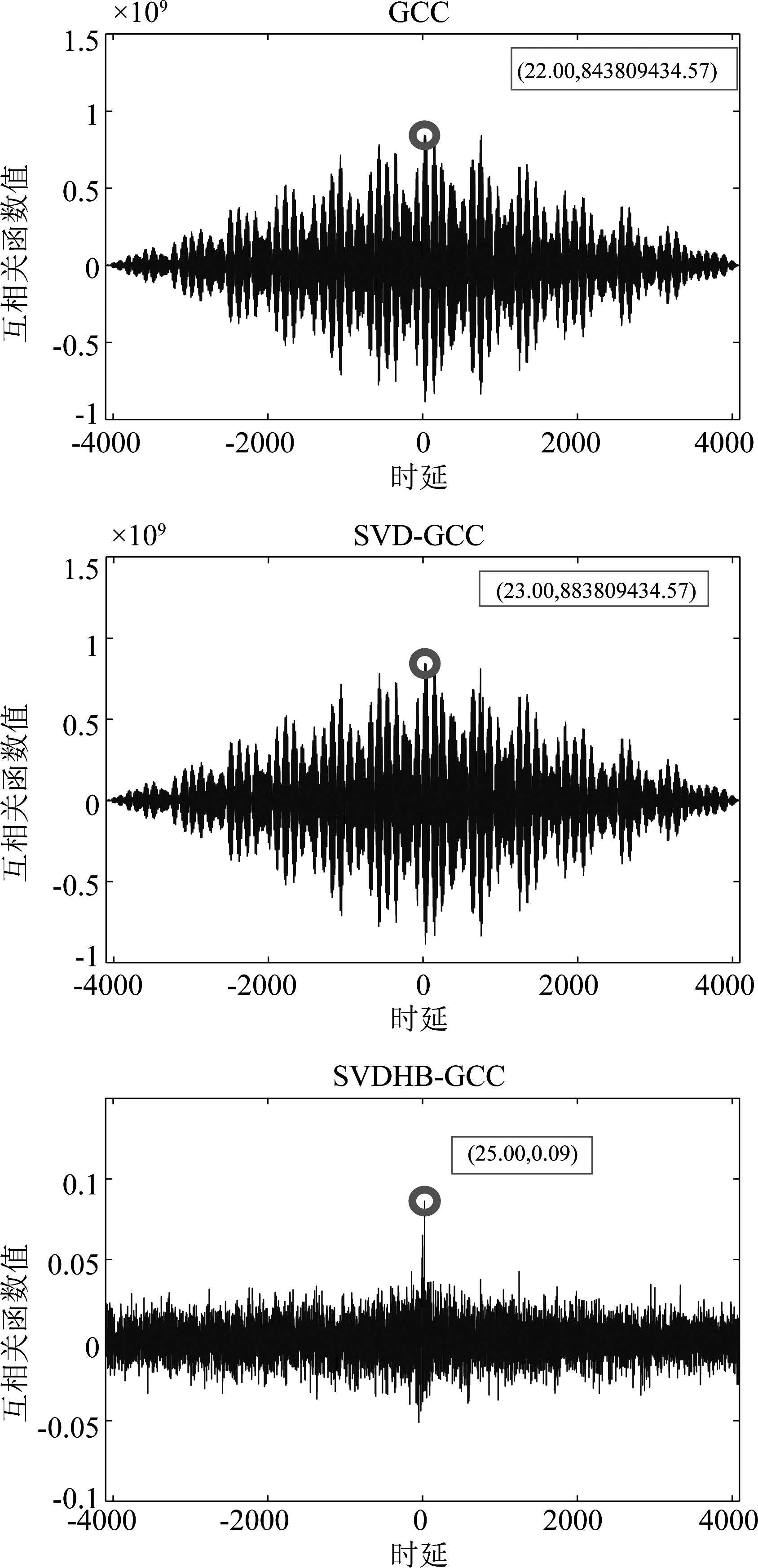
图11 三种算法时延峰值估计结果对比图
Fig.11 Comparisons of peak values of three methods
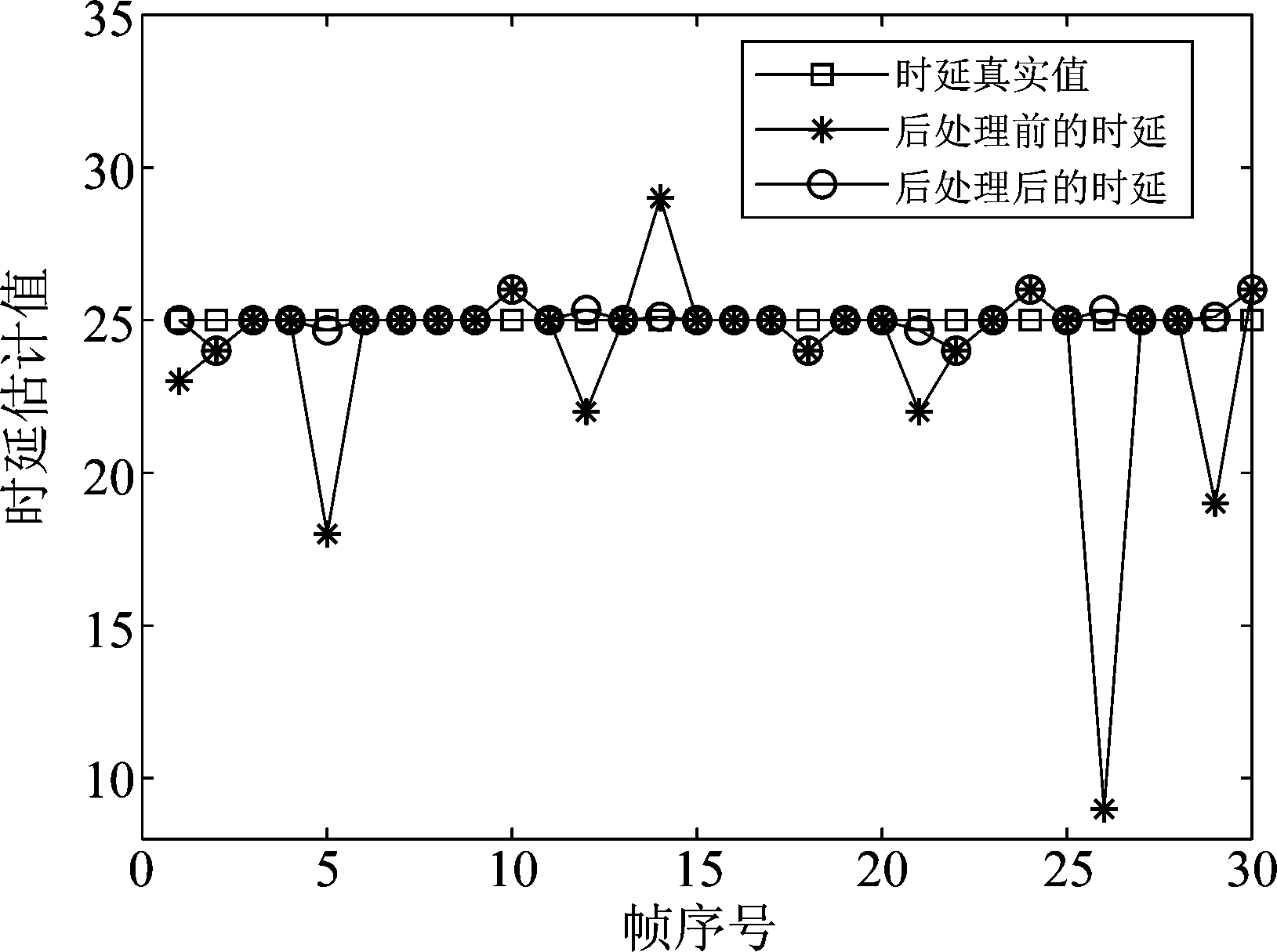
图12 时延后处理前后结果比较
Fig.12 Comparison of time delay between the proposed algorithm and the proposed algorithm without post processing
5 结论
低信噪比条件下，传统GCC方法进行时延估计会出现较大偏差，针对此问题，提出了一种新的时延估计方法，即奇异值分解的HB加权广义相关。首先，对传感器阵列接收到的声源信号作奇异值分解处理，降低环境中各种噪声的影响，提高信号信噪比；其次，采用GCC方法进行时延估计时，引入HB加权函数，通过频域互功率谱处理，达到锐化峰值的作用；最后，提出一种基于中位数和平均数的时延后处理方法，消除少量帧信号时延估计的异常波动，提高时延估计精度。仿真实验结果显示，本文所提新的时延估计算法性能明显优于传统GCC和SVD-GCC参考算法。
在实际场景中，针对固定声源目标，本文所提时延估计算法具有更高的精度和抗噪性能，这对基于时延估计的目标探测、定位、追踪等应用意义重大；下一步将本文算法应用移动声源目标，并进行优化和完善，提高算法的普适性。
[1] Daniel Valle de Lima, João Paulo C. L. da Costa, Felix Antreich, et al. Time-delay estimation via CPD-GEVD applied to tensor-based GNSS arrays with errors[C]∥Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), 2017 IEEE 7th International Workshop. Curacao, Netherlands Antilles,2017:1-5.
[2] Pan J J, Bastard C L, Wang Y D, et al. Time delay estimation using ground-penetrating radar with a support vector regression-based linear prediction method [J]. IEEE Transactions on Geoscience and Remote Sensing, 2018,56(5): 2833-2840.
[3] Lee J Y, Chang P H, Jin M L. Adaptive integral sliding mode control with time delay estimation for robot manipulators[J]. IEEE Transactions on Industrial Electronics, 2017,64(8):6796- 6804.
[4] 汪子嘉,于宏毅,胡赟鹏.面向窄带通信信号的相位谱时差估计方法研究[J].信号处理,2013,29(4):457- 465.
Wang Zijia, Yu Hongyi, Hu Yunpeng. Research on TDOA Estimation Method Based on Phase Spectrum for Narrow-Band Communication Signal[J].Journal of Signal Processing, 2013,29(4):457- 465.(in Chinese)
[5] 王鹏,张晓彤,徐丽媛,等.基于自适应时延估计的室内近场测距算法[J].计算机学报,2017,40(8): 1902-1917.
Wang Peng, Zhang Xiaotong, Xu Liyuan, et al. Indoor near field ranging algorithm based on adaptive time delay estimation[J]. Chinese Journal of Computers,2017,40(8):1902-1917.(in Chinese)
[6] 王云龙,吴瑛.改进SSMUSIC超分辨多径时延估计算法[J].信号处理,2014,30(8):979-986.
Wang Yunlong, Wu Ying. Improved SSMUSIC algorithm of super-resolution time delay estimation in multipath environments [J]. Journal of Signal Processing, 2014,30(8):979-986.(in Chinese)
[7] Yi S, Wang G, Liu F C. Effect of sound velocity on time delay estimation based on double beam forming algorithm[C]∥2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China,2017:1-5.
[8] Dong Y, Lu J Y, Zhu X J,et al. Generalized cross correlation time delay estimation based on improved wavelet threshold function[C]∥2016 Sixth International Conference on Instrumentation & Measurement, Computer, Communication and Control, Harbin, China,2016: 629- 633.
[9] 周卓伟,孙山林,李云,等.基于经验模态分解重构的二次相关时延估计[J].电讯技术,2016,56(5): 562-567.
Zhou Zhuowei,Sun Shanlin,Li Yun,et al. Second correlation time delay estimation based on empirical mode decomposition reconstruction [J]. Telecommunication Engineering, 2016,56(5):562-567.(in Chinese)
[10] 张大威, 鲍长春, 夏丙寅. 复杂环境下基于时延估计的声源定位技术研究[J].通信学报,2014, 35(1): 183-190.
Zhang Dawei, Bao Changchun, Xia Bingyin. Source localization based on time delay estimation in complex environment [J].Journal on Communications,2014,35(1):183-190.(in Chinese)
[11] Yin L L, Tian W M, Wang Z H, et al. Coupling signal suppression method of ground-based synthetic aperture radar based on singular value decomposition[C]∥Radar (RADAR), 2016 CIE International Conference, Guangzhou,China, 2016:1- 4.
[12] 查翔,倪世宏,谢川,等.奇异值分解去噪中有效秩阶次的自身辅助确定[J].计算机应用研究,2016, 33(5): 1359-1362.
Zha Xiang,Ni Shihong,Xie Chuan, et al. Self-assisting determination of effective rank degree in SVD denoising[J]. Application Research of Computers,2016, 33(5): 1359-1362. (in Chinese)
[13] 李晶,赵拥军,李冬海.基于马尔科夫链蒙特卡罗的时延估计算法[J].物理学报,2014,63(13): 67-73.
Li Jing, Zhao Yongjun, Li Donghai. Time delay estimation using Markov Chain Monte Carlo method[J]. Acta Physica Sinica, 2014,63(13): 67-73.(in Chinese)
[14] 胡小锋,刘卫东,王雷,等.广义互相关电晕放电辐射信号时延估计方法[J].强激光与粒子束,2018, 30(1):56- 60.
Hu Xiaofeng, Liu Weidong, Wang Lei, et al. Time-delay estimation of corona discharge radiation signal based on generalized cross correlation[J].High Power Laser and Particle Beams, 2018, 30(1):56- 60.(in Chinese)
[15] 李伟红,汤海兵,龚卫国.公共场所异常声源定位中时延估计方法研究[J].仪器仪表学报,2012, 33(4):750-756.
Li Weihong, Tang Haibing, Gong Weiguo.Time delay estimation method of abnormal sound source localization in public places[J]. Chinese Journal of Scientific Instrument, 2012,33(4): 750-756.(in Chinese)
[16] 孙永梅,邱天爽.分数低阶α稳定分布噪声下HB加权自适应时间延迟估计新方法[J].信号处理,2007,23(3):339-342.
Sun Yongmei, Qiu Tianshuang. The novel HB weighted adaptive time delay estimation algorithm under fractional lower order α-stable noise conditions[J]. Signal Processing, 2007, 23(3): 339-342.(in Chinese)
