1 引言
无线能量传输技术是近年来新兴的技术,可以应用在许多节点供电受限的场合[1],该技术可以有效地延长无线传感器网络的生存期,在环境监测系统、身体传感器网络或智能家居系统等,都有着很高的应用价值。目前,由于基站、WiFi热点的大量设立,无线射频信号在环境中普遍存在,可以作为能量收集的重要来源。另一方面,射频信号往往也是信息数据的载体,因此,信息和能量传输相结合产生了新的研究热点,即无线信息与能量的联合传输技术。
已经有若干文献对无线信息与能量的联合传输问题从不同的角度做了研究[2-17]。根据不同的通信系统和应用场景,相关研究经历了由简单到复杂的过程,从单天线系统扩展到多天线系统。在2008年,Lav R.Varshney[2] 首次提出了同时传输信息和能量的概念,指出在单位时间内接收端的能量获取和数据传输是一对此消彼长的矛盾,由此建立了速率-功率域函数。该文献给出了特殊离散信道下的容量-功率域数学表达式,发现并证明了该函数的若干性质,如非增性、凹性等。该项研究奠定了无线信息和能量联合传输的基础。P.Grover等[3]研究了一个基于磁共振电路的无线传输模型,将其建模为频率选择性确定信道。在接收机能量效率大于一定阈值并且发送功率受限的条件下,给出了发送端在传输频带上的最优功率分配方案。与文献[2]相比,该文献的工作基于典型的磁共振电路和连续信道模型,较为贴近实际。文献[4]研究了单天线衰落信道下的接收机设计,包括能量接收机和信息接收机。该文给出了能量与信息若干典型复用方式的电路结构,特别提及了静态功率拆分和“开关型”功率拆分方案的适用场合和优缺点。另一方面,多天线通信系统的信息-能量联合传输若干问题,如发送协方差设计、可达速率-功率域描述、结合正交时空编码的系统性能等,在文献[5-15]得到了研究。Zhang等证明了在发送端功率一定的条件下,发送信号协方差矩阵的设计将会对信息和能量接收机同时产生影响[5]。文献[7]研究了多天线放大转发通信系统的最优信息-能量可达域边界,该系统采用正交空时编码发送用户信息数据,设计联合的信源-中继预编码以达到信息-能量域边界。文献[14]研究了大规模多天线通信系统的信息-能量传输机制,该系统的接收机需要从发射机收集能量才能支持其数据接收和解码。在满足一定通信质量的条件下,该文给出了高能效的资源管理方案。还有一些研究考虑了多天线系统的用户调度、波束成形、安全通信等问题[8,13,15,17]。
在上述研究中,信道状态信息对于发送端的传输策略设计、闭环功控等是不可缺少的。现有文献大多假设信道状态信息(channel state information, CSI)对发送端是已知的,即系统可以获取完备的即时信道信息。例如,文献[5]以此为前提研究最优发送策略及不同复用方法的可达域等问题。然而,也有一些文献考虑到,由于实际通信系统中噪声、移动用户的运动等因素的影响,接收机难以获得理想的CSI,导致发送端得到的CSI存在误差。例如,Xiang等针对多发单收系统,给出了在信道信息有误下系统达到Pareto边界点时,发送端预编码向量应该满足的条件[6]。多发单收的系统假设使得优化和分析得以大大简化,同样针对该系统模型,文献[11]研究了基于有限反馈的信息和能量联合传输方案设计。
现有研究大多利用发送端获取的即时信道信息来设计传输方案,提高系统通信性能,包括理想和非理想信道信息两种情况。这种机制对于慢变信道是可行的,但是对于快速变化的信道,频繁的信道信息反馈将给系统带来较大负担,此时反馈即时信道信息不再合适。基于上述考虑,本文研究了基于统计信息反馈的传输机制,此时发送端仅能获取信道统计信息,即信道均值矩阵,系统设计不再针对即时信息传输速率,而是信息传输速率的期望值。发射端传输方案的目标是设计一种预编码使得系统通信速率期望最大,同时满足能量接收机的最低能量需求。
本文的组织结构如下:第2节介绍了系统模型;第3节提出了基于均值反馈的预编码算法;第4节是实验仿真,验证提出算法的性能;最后,第5节总结全文。
符号说明:向量用小写黑体字母表示,矩阵用大写黑体字母表示;E(·) 代表统计期望运算;![]() 代表m×n的复数矩阵集合;对于向量x, x~CN(μ,R)表示x服从均值μ、协方差R 的复高斯分布;对于矩阵X,符号X1/2, Tr(X), XH和 X*分别代表矩阵的开方、求迹、Hermitian转置和转置运算。X
代表m×n的复数矩阵集合;对于向量x, x~CN(μ,R)表示x服从均值μ、协方差R 的复高斯分布;对于矩阵X,符号X1/2, Tr(X), XH和 X*分别代表矩阵的开方、求迹、Hermitian转置和转置运算。X![]() 0表示X是正定的;Im是m×m的单位矩阵。
0表示X是正定的;Im是m×m的单位矩阵。
2 系统模型
如图1,本文考虑三节点的MIMO信息-能量联合传输系统模型,包括一个发送机TX,一个能量接收机RXE和一个信息接收机RXD。TX、RXE和RXD分别配备了NT、NE和ND根天线。系统有两种类型的通信:一种是广播,用以发送端的数据广播;另一种是反馈,用以反馈信道均值信息。用户数据![]() 由发送端发射,包括d个独立的数据子流,其自相关矩阵为E(xxH)=Id, 这里d=min{NT, ND}。在用户数据传输之前,x需要乘以预编码矩阵
由发送端发射,包括d个独立的数据子流,其自相关矩阵为E(xxH)=Id, 这里d=min{NT, ND}。在用户数据传输之前,x需要乘以预编码矩阵![]() 编码之后的数据经过平坦衰落信道到达接收端,信息接收机和能量接收机的接收信号可写成
编码之后的数据经过平坦衰落信道到达接收端,信息接收机和能量接收机的接收信号可写成
yD=HDPx+nD
(1)
yE=HEPx+nE
(2)
其中,![]() 和
和![]() 分别是发送端到信息接收机和能量接收机的MIMO平坦衰落信道。噪声
分别是发送端到信息接收机和能量接收机的MIMO平坦衰落信道。噪声![]() 和
和![]() 是 i.i.d 高斯噪声,分别服从CN(0, σ
是 i.i.d 高斯噪声,分别服从CN(0, σ![]() IND)和CN(0, σ2EINE)的分布。接下来,为了表述方便,我们称 HD和HE分别为信息信道和能量信道。
IND)和CN(0, σ2EINE)的分布。接下来,为了表述方便,我们称 HD和HE分别为信息信道和能量信道。
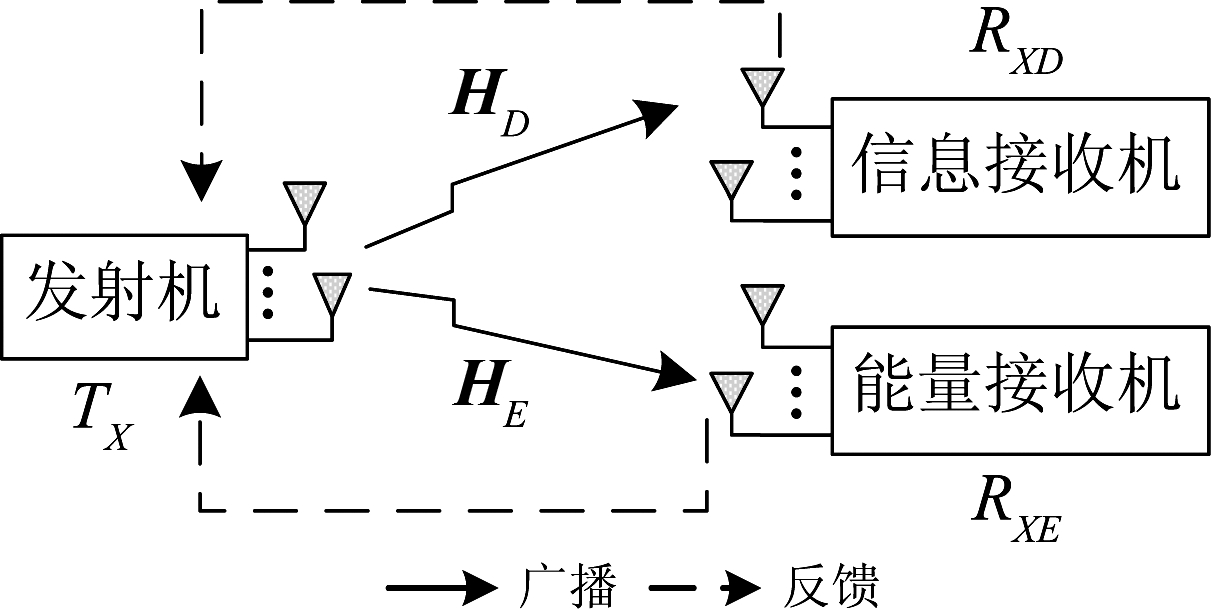
图1 三节点的MIMO信息-能量传输系统
Fig.1 A three-node MIMO information and energy transfer system
信道矩阵HD和HE可以进一步建模为
(3)
(4)
其中,Hμ,D和Hμ,E分别是信息信道和能量信道的均值信息,K1和K2分别是各自的莱斯因子。Hω,D 和Hω,E 是随机矩阵,矩阵的每个元素是零均值、单位方差的,并且元素之间是独立不相关的。
接收机经过一段时间的测量之后,通过反馈,发送端获得了信道统计信息,即均值信息Hμ,D和Hμ,E。发送端使用这些信息设计预编码矩阵,使得系统信息通信速率最大并且同时满足能量接收的最低能量需求。很明显,相比即时信道信息反馈策略,这种基于统计信息的反馈策略将减小系统开销,但是也会导致信息速率的损失。
最后,定义系统的信噪比。考虑到用户发送数据x的自相关矩阵是单位阵,发送功率可表示为:
(5)
其中PT是最大发送功率。很明显,PPH是预编码之后的发送信号协方差矩阵。因此,系统信噪比定义为:
(6)
其中, σ![]() 是信息信道的噪声功率。不失一般性,设定σ
是信息信道的噪声功率。不失一般性,设定σ![]() =1。
=1。
注:根据公式(6),信噪比定义为实际的发送功率与噪声功率σ![]() 之比。实际上,求出的最优预编码矩阵总是满足Tr(PPH)=PT,因此,信噪比也可定义为
之比。实际上,求出的最优预编码矩阵总是满足Tr(PPH)=PT,因此,信噪比也可定义为![]()
3 基于均值反馈的预编码算法
本节首先将预编码求解归纳为一个半正定规划,然后引入辅助变量和对偶函数将之转换成对偶问题。基于此,进一步提出了预编码算法求解对偶问题。
3.1 问题描述
首先,根据公式 (1),系统信息传输速率可以表示为:
(7)
其中,矩阵![]() 是发送信号的协方差矩阵,定义Q=PPH。
是发送信号的协方差矩阵,定义Q=PPH。
然后,给出能量接收机单位时间收集的能量表达式。最近,文献[18-19]提出了能量收集的非线性模型,指出,相比传统的线性模型,非线性模型更加接近实际测量结果。因此本文采用该文献提出的非线性模型。接收机单位时间内收集的能量可表示为
(8)
其中,M、a和b是模型中的常数。PER是到达接收机的信号能量,根据公式(2)可以写成
(9)
根据公式(4),公式(9)可以进一步表示为
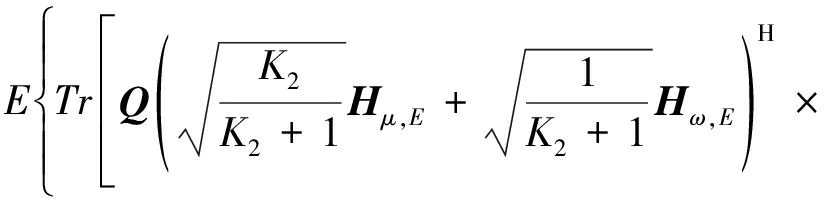
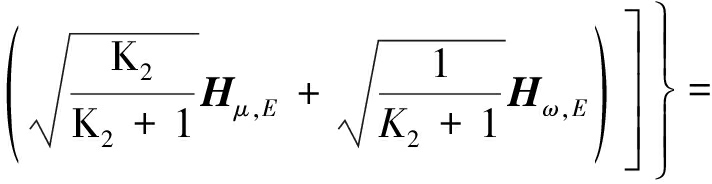
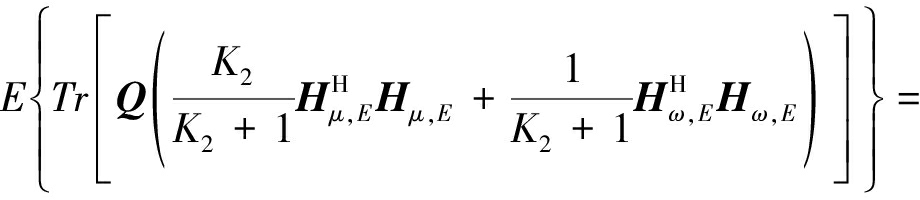
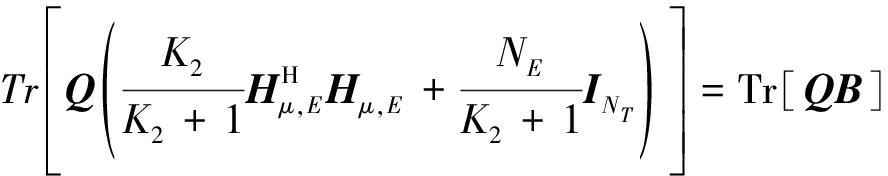
(10)
其中,![]()
最后,预编码设计准则为系统信息平均传输速率最大化,同时满足最低能量要求Eth。可以将问题归结为(P1):
s.t.Q 0
0
Tr(Q)≤PT
Erec≥Eth
(11)
注:经过简单推导,问题P1的能量约束可以写成另一种等价形式,即Tr(QB)≥b-ln(M/Eth-1)/a。
关于能量要求Eth,有如下引理(证明见附录A)。
引理1 当![]() 问题P1无解,这里λmax(B)是矩阵B的最大特征值;当
问题P1无解,这里λmax(B)是矩阵B的最大特征值;当![]() 能量约束无效,这里
能量约束无效,这里![]() 是问题
是问题![]() 的解。
的解。
s.t.Q 0;Tr(Q)≤PT
0;Tr(Q)≤PT
另外,与文献[5]类似,本文使用信息-能量域描述所有的可达信息速率和能量的数值组合, 定义如下:
Tr(QB)≥b-[ln(M/Eth-1)]/a,Tr(Q)≤PT,Q![]() 0}
0}
(12)
很明显,能量需求给定时,问题P1的速率解是信息-能量域边界点的纵坐标。
3.2 提出的预编码算法
本节提出一种基于梯度下降的数值算法求解问题P1。首先,引入问题 P1的拉格朗日函数:
[Tr(QB)-b+ln(M/Eth-1)/a]-u[Tr(Q)-PT]
(13)
其中λ≥0,u≥0,它们是引入的两个辅助变量。可见,拉格朗日函数整合了问题的目标函数和约束条件,引入该函数的目的是为了将原问题转换成一个较容易求解的问题。进一步定义对偶函数为:
(14)
则问题 P1 的对偶问题可以表示为(P2):
(15)
可见,问题P2只包括两个变量λ和u,形式比原问题P1简单许多。容易验证Slater条件成立(见附录B),因此P1和P2是等价的。
接下来,考虑求解问题P2。分成两步:第一,给定(λ, u), 求出最优的Q和g(λ, u);第二,找到g(λ, u)的最小值。函数g(λ, u)可以整理成如下形式,
Tr{CQ}+Tconst
(16)
其中,C=uINT-λB,Tconst=uPT-λ[b-ln(M/Eth-1)/a]。注意,矩阵 C必须是半正定的,否则g(λ,u)会趋于无穷大。这意味着u>λλmax(B),其中λmax(B)是矩阵B的最大特征值。
考虑到Q是半正定的,可以写成Q=PPH, 代入公式(16)得到:
(17)
对L(P,λ,u)求关于P*的偏导数,可得
(18)
从上式可见,求解![]() 是无约束的优化问题,给定(λ, u),我们提出下述算法求解g(λ, u),从而获得P和Q。
是无约束的优化问题,给定(λ, u),我们提出下述算法求解g(λ, u),从而获得P和Q。

给定(λ, u),上述算法将求出最优P和g(λ, u)。基于算法1,我们提出算法2求解问题P2,步骤归纳如下。

不难得出,算法2提及的偏导数可表示为:
gλ(λ(i),u(i))=Tr(P(i)(P(i))HB)-
[b-ln(M/Eth-1)/a]
(20a)
gu(λ(i),u(i))=-Tr(P(i)(P(i))H)+PT
(20b)
根据算法2可以得到最优P(记为POPT),也可以得到g(λ, u)的最小值。根据对偶性原理,原问题P1最优的预编码即为问题P2求出的POPT,原问题P1的最大传输速率即为g(λ, u)的最小值。
3.3 复杂度分析
本小节分析提出算法以及若干经典发送方案的运算复杂度。记一次浮点乘法或者除法运算为一次运算,其复杂度为O(1),这里不考虑加法和减法,因为相对于前者其运算量可以忽略。假设算法1和2收敛所需的循环次数为S1和S2。不难发现,算法的主要运算量在算法1的步骤2。考虑到一个m×m矩阵求逆的复杂度O(m3),容易得出,提出算法的复杂度为![]()
时分复用方法是指发送数据周期分成两个时段轮流发送信息数据和能量数据,具体描述可见文献[5]。两个时段分别需要不同的预编码矩阵,在能量发送阶段,运算量主要集中在矩阵B的特征分解,其复杂度为![]() 在信息发送阶段,若采用文献[22]的计算方法,主要运算量在于矩阵Hμ,D的奇异值分解,则预编码的计算复杂度为
在信息发送阶段,若采用文献[22]的计算方法,主要运算量在于矩阵Hμ,D的奇异值分解,则预编码的计算复杂度为![]() 因此,时分复用方法的复杂度为
因此,时分复用方法的复杂度为![]() 另外,对于各向同性发送方案,其预编码矩阵是单位阵,不需要运算。
另外,对于各向同性发送方案,其预编码矩阵是单位阵,不需要运算。
可见,在上述三种发送方案中,提出算法复杂度是最高的,时分复用方法其次,各向同性发送方案最低。
4 仿真结果
本节采用计算机仿真考察提出预编码方法的性能,并与若干经典方法进行了对比。我们采用第2节所述三节点MIMO广播系统模型,且假定节点配备的天线数目均相同;对于能量和信息信道,莱斯因子均设为1;对于非线性能量收集模型,设置参数a=0.45,b=15,最大可收集功率M=50 mW。
图2验证了提出预编码算法的收敛性。系统参数设置如下:节点配备的天线数NT=ND=NE=2;对SNR=5 dB,设定Eth=2;对SNR=6 dB,设定Eth=4;初始的(λ, u)均为(0.05, 0.5);信息信道和能量信道的均值矩阵分别为:![]() 和
和![]() 由图可见,对于上述两种情况,对偶函数g(λ, u)均收敛较快,约经过3~6次迭代即收敛到某固定值。例如,当SNR=6 dB,g(λ, u)初始值为3.808,经过5次迭代为3.723,与最终收敛值3.721相差无几。
由图可见,对于上述两种情况,对偶函数g(λ, u)均收敛较快,约经过3~6次迭代即收敛到某固定值。例如,当SNR=6 dB,g(λ, u)初始值为3.808,经过5次迭代为3.723,与最终收敛值3.721相差无几。
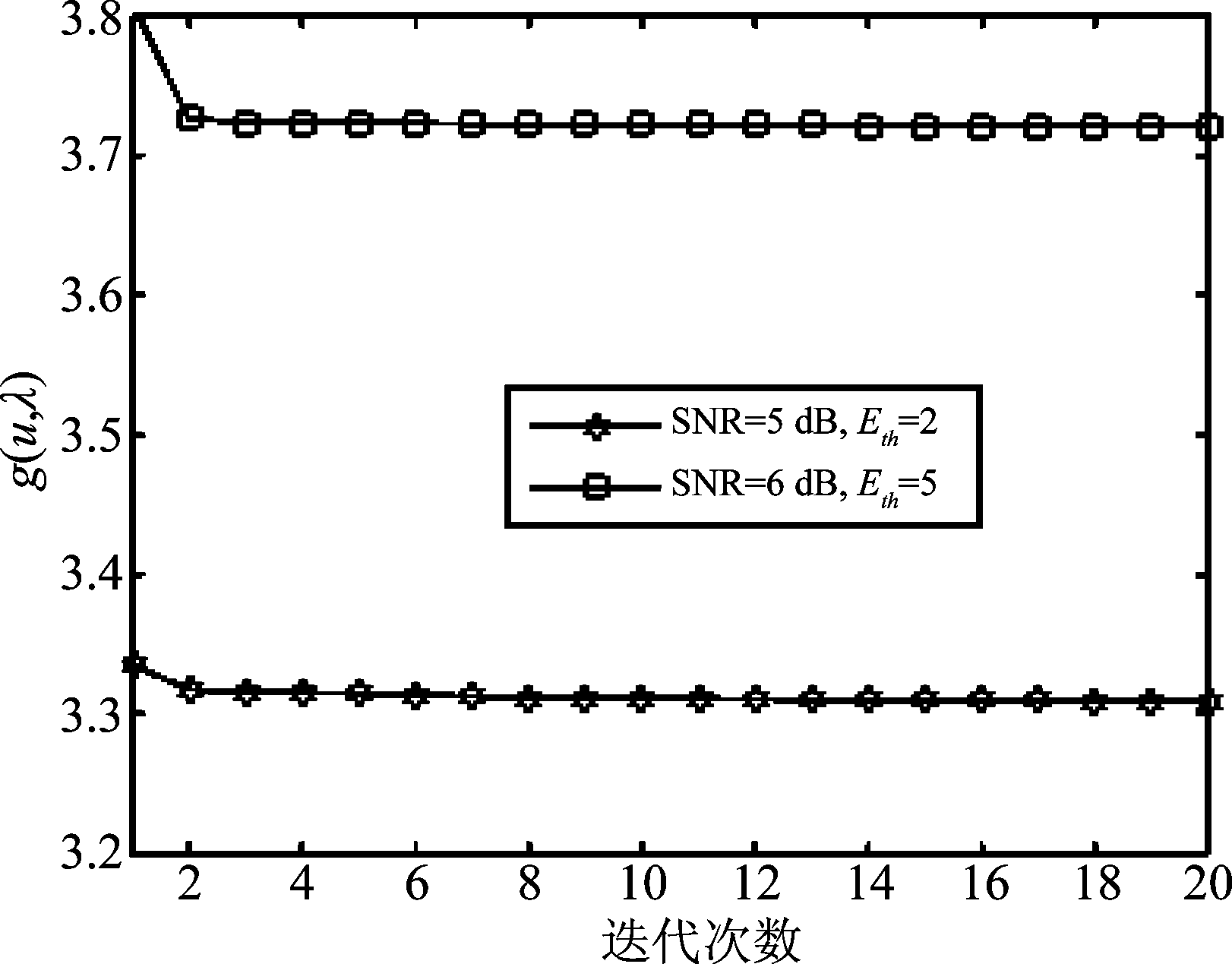
图2 提出预编码算法的收敛性
Fig.2 The convergence of the proposed precoding algorithm
图3展示了不同能量需求下的信息速率随信噪比的变化趋势。系统的天线配置、信道均值矩阵与图2相同。考虑了三种情况:能量需求Eth=6,Eth=10和无能量约束的情形。可见,系统信息速率均随着信噪比的增加而增加。无能量约束曲线是有能量约束曲线(另外两种情况)的上界。当SNR小于某数值,问题P1无解,因为最大可收集能量受限于发送功率,导致能量需求无法满足。对于Eth=6和Eth=10,所需最低信噪比分别为5.60和6.13分贝,实际上,该数值可以从引理1计算得到。另外,随着信噪比的升高,有能量约束曲线与无能量约束曲线的信息速率差距逐渐减小,直到差距为零、曲线重合。这是因为,随着信噪比的增加能量约束条件逐渐失效了。
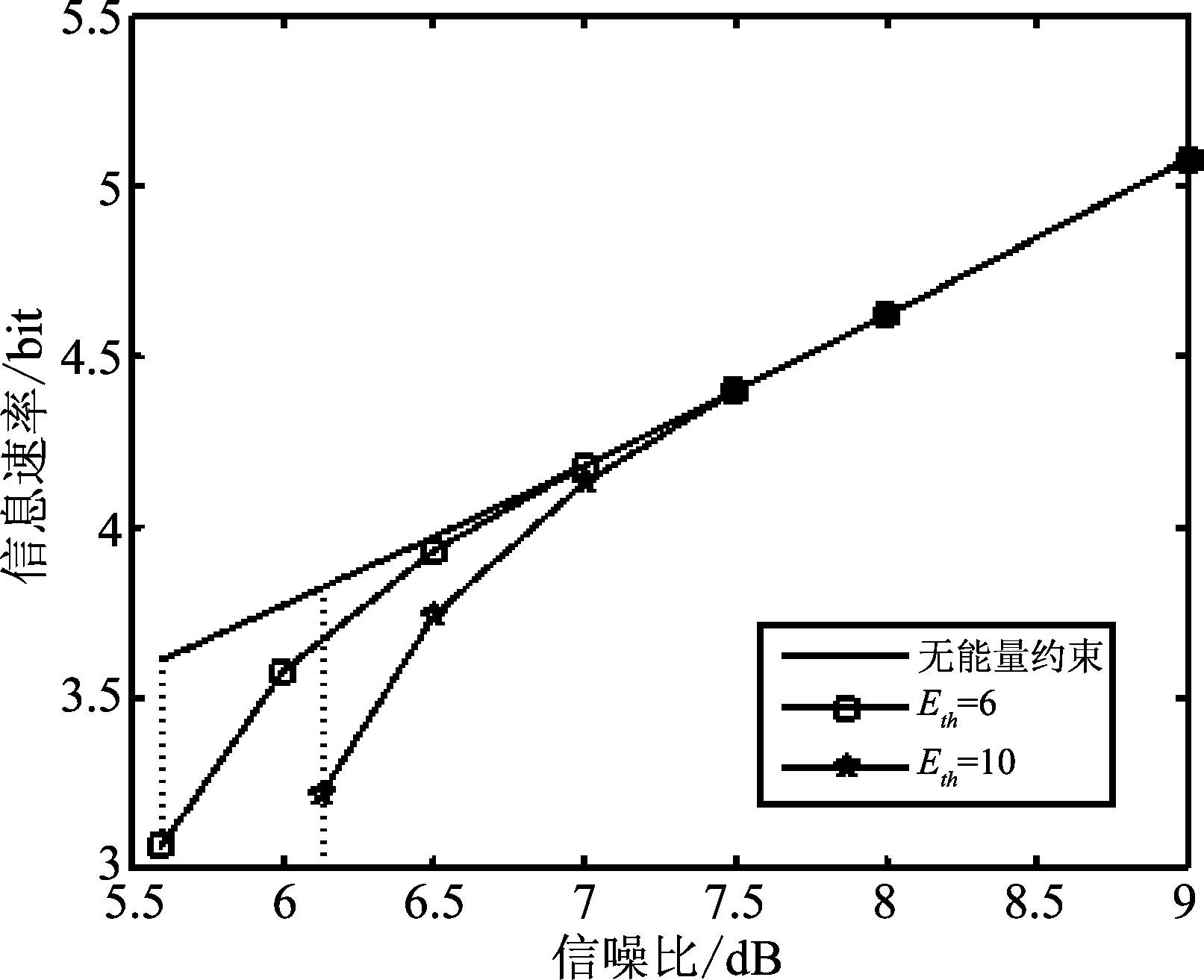
图3 不同能量需求下的信息速率随信噪比的变化趋势
Fig.3 The information rate versus SNR, with different energy requirements
图4给出了不同信噪比下的信息-能量可达域。系统的天线配置、信道均值矩阵与图2相同。考虑了三种情况:SNR=5 dB,6 dB和8 dB。可见,随着信噪比的增加,信息-能量可达域变得更加宽阔。对这三种情况,当Eth较小时,信息-能量域边界曲线是水平的,在某个拐点(如A1、A2),Eth增加会导致信息速率下降,这是因为Eth较小时,能量约束不起作用,但是Eth增加导致能量约束逐渐起作用,从而降低了信息传输速率。同样发现, 信息-能量域边界存在某截止点(如B1、B2),对应着最大可收集功率,超过该截止点,问题P1无解。实际上,拐点和截止点均可以从引理1计算得出,与数值仿真得出的结果是一致的。
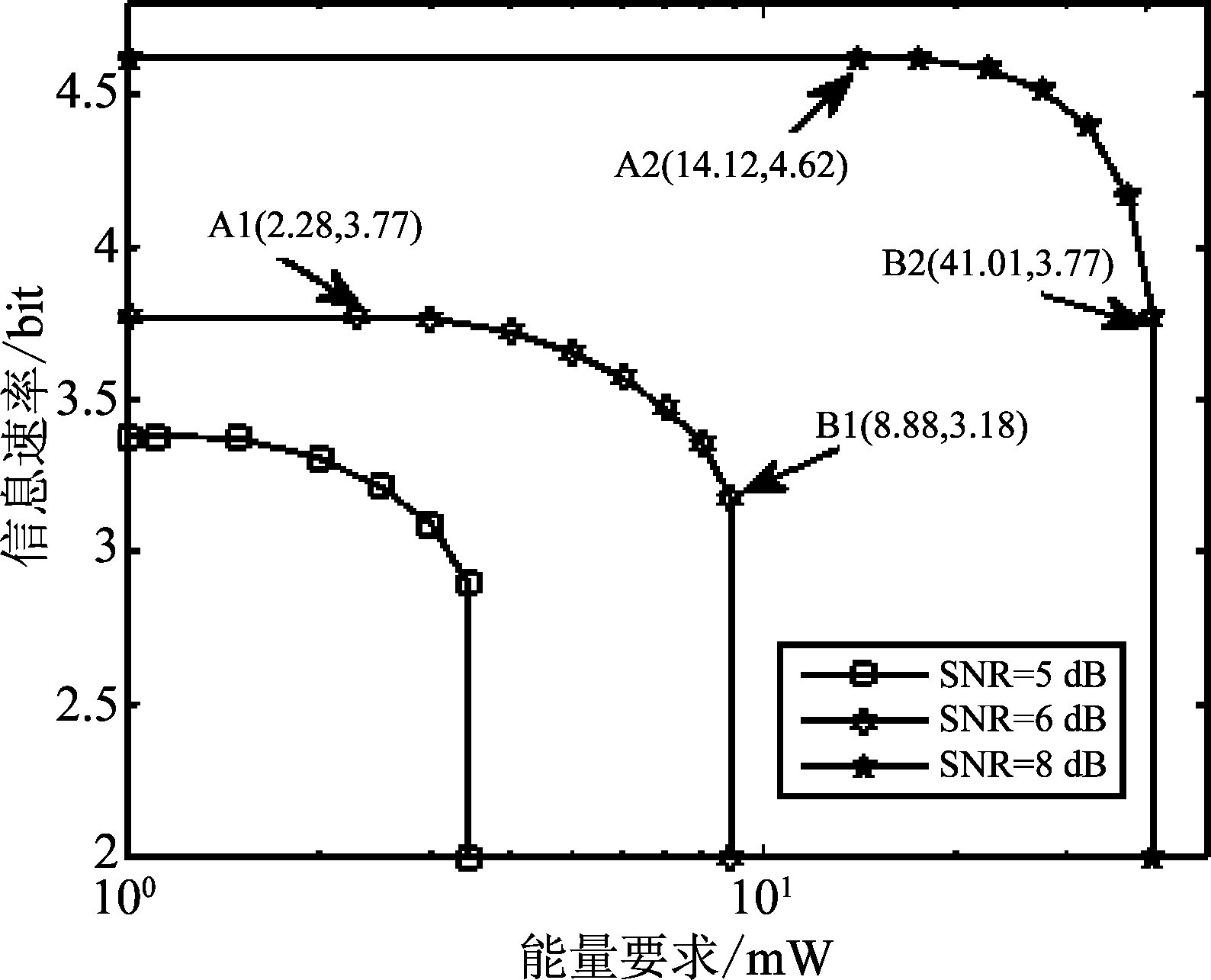
图4 不同信噪比下的信息-能量可达域
Fig.4 The achievable R-E region with different SNRs
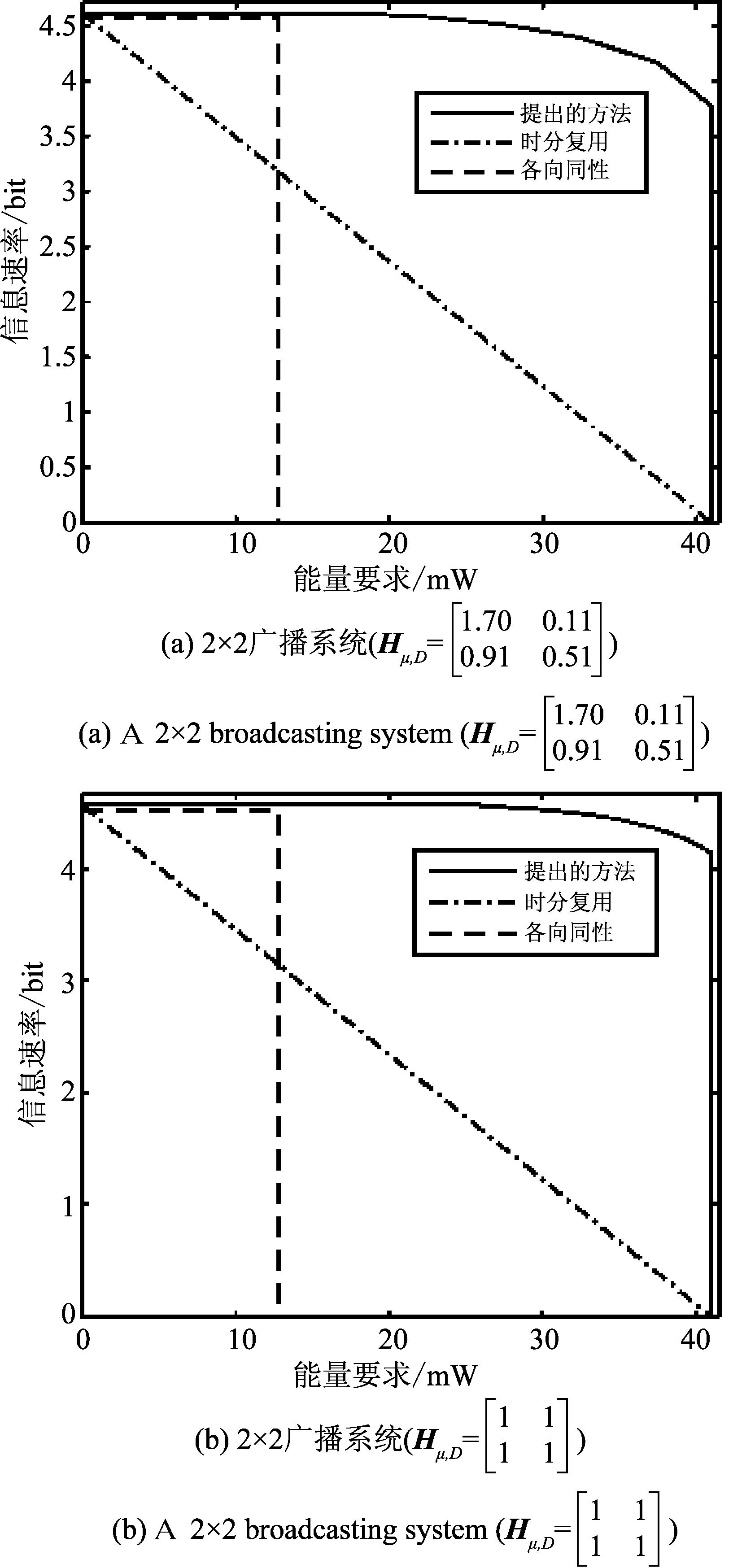
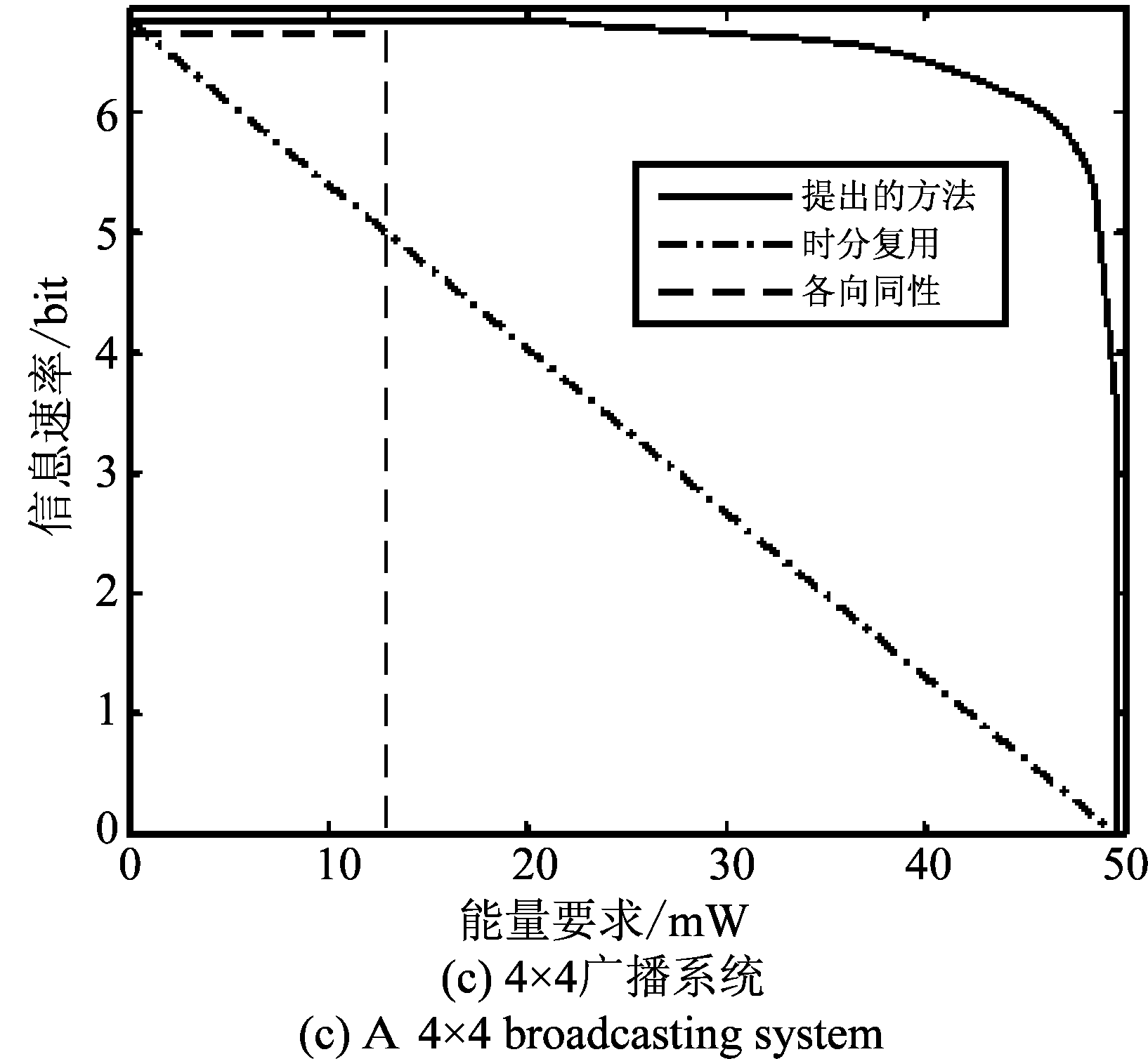
图5 不同传输方案的信息-能量可达域
Fig.5 The achievable R-E region with different transmission schemes
图5给出了不同传输方案的信息-能量可达域。对2×2广播系统,SNR=8 dB;对4×4广播系统,SNR=5 dB。对2×2广播系统,均值矩阵Hμ,E与图2设置相同,但是均值矩阵Hμ,D分成两种情况:图5(a)的Hμ,D与图2设置一致;图5(b)的![]() 对4×4广播系统,信道均值矩阵设置如下:
对4×4广播系统,信道均值矩阵设置如下:
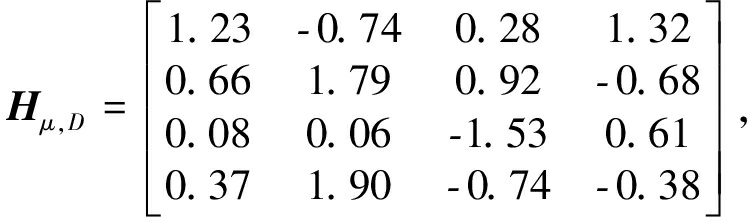

该图对比了三种发送方案:提出的预编码方法,时分复用方法和各向同性发射方案。各向同性发射是指发送端发射NT个独立的数据流,每个数据流的发射功率是相同的,其预编码矩阵可以写成:![]() 时分复用方法在3.3小节已经说明。由图可见,无论是2×2广播系统还是4×4系统,提出预编码方法的信息-能量可达域均优于其他两种方法。另外,在若干典型系统配置下,表1给出了最优协方差和预编码矩阵,其中2×2广播系统的信道均值矩阵与图2设置相同。
时分复用方法在3.3小节已经说明。由图可见,无论是2×2广播系统还是4×4系统,提出预编码方法的信息-能量可达域均优于其他两种方法。另外,在若干典型系统配置下,表1给出了最优协方差和预编码矩阵,其中2×2广播系统的信道均值矩阵与图2设置相同。
5 结论
本文研究了MIMO信息-能量广播通信系统的预编码设计问题,系统包括一个发送端,一个信息接收端和一个能量接收端共三个节点。信道建模为具备视距路径的莱斯衰落信道,发送端仅具备信道均值反馈信息,由此设计最优预编码。利用凸优化理论将原预编码设计问题转换成为一个对偶问题,Slater条件的成立表明了两个问题是等价的。基于半正定矩阵分解技术,提出了梯度下降搜索算法进行求解,并且分析了算法的计算复杂度。另一方面,信息-能量可达域通常作为衡量系统性能的指标,该文提出的引理1则刻画了可达域的边界曲线特征。实际上,引理1给出的拐点和截止点有助于快速绘制边界曲线的大致轮廓。最后,研究了若干典型发送传输方案的系统性能,仿真结果表明,提出的预编码方案优于各向同性和时分复用方案。该文提出的预编码算法和相应研究结果可为今后系统的实践应用提供参考。
表1 不同系统配置下的最优协方差和预编码矩阵
Tab.1 The optimum covariance matrices and precoders with different system configurations
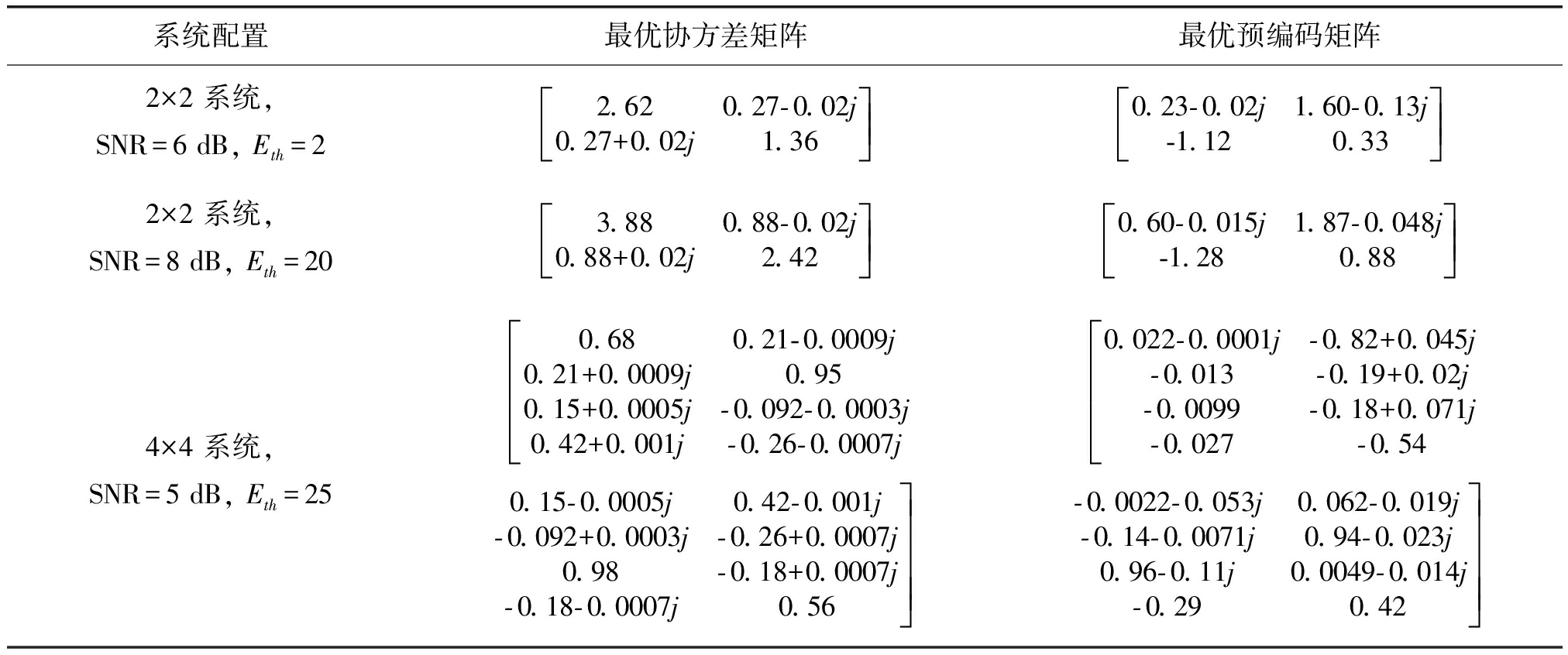
系统配置最优协方差矩阵最优预编码矩阵2×2 系统, SNR=6 dB, Eth=22.620.27-0.02j0.27+0.02j1.36éëêêùûúú0.23-0.02j1.60-0.13j-1.120.33éëêêùûúú2×2 系统, SNR=8 dB, Eth=203.880.88-0.02j0.88+0.02j2.42éëêêùûúú0.60-0.015j1.87-0.048j-1.280.88éëêêùûúú4×4 系统,SNR=5 dB, Eth=250.680.21-0.0009j0.21+0.0009j0.950.15+0.0005j-0.092-0.0003j0.42+0.001j-0.26-0.0007jéëêêêê0.15-0.0005j0.42-0.001j-0.092+0.0003j-0.26+0.0007j0.98-0.18+0.0007j-0.18-0.0007j0.56ùûúúúú0.022-0.0001j-0.82+0.045j-0.013-0.19+0.02j-0.0099-0.18+0.071j-0.027-0.54éëêêêê-0.0022-0.053j0.062-0.019j-0.14-0.0071j0.94-0.023j0.96-0.11j0.0049-0.014j-0.290.42ùûúúúú
附录A: 引理1的证明
接收信号能量PER满足:PER=Tr(QB)≤Tr(Q)λmax(B)≤PTλmax(B), 且收集的能量Ereν是参数PER的单调递增函数,因此,最大收集的能量不超过![]() 能量需求大于此数值,问题P1无解。另一方面,若能量需求小于
能量需求大于此数值,问题P1无解。另一方面,若能量需求小于![]() 这里
这里![]() 是问题
是问题![]() 的解。我们可以推断
的解。我们可以推断![]() 同样是问题P1的解,原因如下:第一,P1的目标函数是凹的,约束是线性的,因此P1是凸问题,存在一个全局最优解;第二,
同样是问题P1的解,原因如下:第一,P1的目标函数是凹的,约束是线性的,因此P1是凸问题,存在一个全局最优解;第二,![]() 使得P1的目标函数取得最大值,同时满足所有的线性约束条件。注意到,此时P1的能量约束等号不成立,约束不起作用。
使得P1的目标函数取得最大值,同时满足所有的线性约束条件。注意到,此时P1的能量约束等号不成立,约束不起作用。
综上所述,引理1成立。
附录B:Slater条件成立的证明
首先,若![]() 最优发送协方差矩阵可以表示为
最优发送协方差矩阵可以表示为
其中UB由矩阵B的特征向量组成。不失一般性,假设矩阵B的特征值按照降序排列,所以功率PT 全部分配到了第一个特征值。此时,无必要将P1转换成对偶问题。
其次,若![]() 令发送协方差矩阵
令发送协方差矩阵![]() 其中PT-{b-[ln(M/Eth-1)]/a}/λmax(B)> δ>0。此时,Tr(Q)=(PT-δ)<PT,且PER=Tr(QB)=(PT- δ)λmax(B)。不难验证Ereν>Eth。因此,当
其中PT-{b-[ln(M/Eth-1)]/a}/λmax(B)> δ>0。此时,Tr(Q)=(PT-δ)<PT,且PER=Tr(QB)=(PT- δ)λmax(B)。不难验证Ereν>Eth。因此,当![]() 问题P1存在严格可行解,Slater条件满足,对偶关系成立。
问题P1存在严格可行解,Slater条件满足,对偶关系成立。
[1] Deng Y, Wang L, Elkashlan M, et al. Modeling and Analysis of Wireless Power Transfer in Heterogeneous Cellular Networks[J]. IEEE Transactions on Communications, 2016, 64(12): 5290-5303.
[2] Varshney L R. Transporting Information and Energy Simultaneously[C]∥IEEE International Symposium on Information Theory, 2008: 1612-1616.
[3] Grover P, Sahai A. Shannon meets Tesla: Wireless Information and Power Transfer[C]∥IEEE International Symposium on Information Theory Proceedings, 2010: 2363-2367.
[4] Zhou X, Zhang R, Ho C K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff[J]. IEEE Transactions on Communications, 2013, 61(11): 4754- 4767.
[5] Zhang R, Ho C K. MIMO Broadcasting for Simultaneous Wireless Information and Power Transfer[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 1989-2001.
[6] Xiang Z, Tao M. Robust Beamforming for Wireless Information and Power Transmission[J]. IEEE Wireless Communications Letters, 2012, 1(4): 372-375.
[7] Chalise B K, Ma W K, Zhang Y D, et al. Optimum Performance Boundaries of OSTBC Based AF-MIMO Relay System with Energy Harvesting Receiver[J]. IEEE Transactions on Signal Processing, 2013, 61(17): 4199- 4213.
[8] Park J, Clerckx B. Joint Wireless Information and Energy Transfer in a Two-User MIMO Interference Channel[J]. IEEE Transactions on Wireless Communications, 2013, 12(8): 4210- 4221.
[9] Xiong K, Fan P, Zhang C, et al. Wireless Information and Energy Transfer for Two-Hop Non-Regenerative MIMO-OFDM Relay Networks[J]. IEEE Journal on Selected Areas in Communications, 2014, 33(8): 1595-1611.
[10] Asiedu D K P, Mahama S, Jeon S W, et al. Optimal Power Splitting for Simultaneous Wireless Information and Power Transfer in Amplify-and-Forward Multiple-Relay Systems[J]. IEEE Access, 2018, 6(99): 3459-3468.
[11] Chen X, Yuen C, Zhang Z. Wireless Energy and Information Transfer Tradeoff for Limited-Feedback Multiantenna Systems with Energy Beamforming[J]. IEEE Transactions on Vehicular Technology, 2014, 63(1): 407- 412.
[12] Chen X, Wang X, Chen X. Energy-Efficient Optimization for Wireless Information and Power Transfer in Large-Scale MIMO Systems Employing Energy Beamforming[J]. IEEE Wireless Communications Letters, 2013, 2(6): 667- 670.
[13] Morsi R, Michalopoulos D S, Schober R. Multiuser Scheduling Schemes for Simultaneous Wireless Information and Power Transfer over Fading Channels[J]. Wireless Communications IEEE Transactions on, 2014,14(4): 1967-1982.
[14] Su Y, Jiang L, He C. Decode-and-Forward Relaying with Full-duplex Wireless Information and Power Transfer[J]. IET Communications, 2017, 11(13): 2110-2115.
[15] Feng Y, Yang Z, Zhu W P, et al. Robust Cooperative Secure Beamforming for Simultaneous Wireless Information and Power Transfer in Amplify-and-Forward Relay Networks[J]. IEEE Transactions on Vehicular Technology, 2017, PP(99): 1-1.
[16] 刘杰群, 陈瑾, 任国春,等. 能量收集全双工中继网络中的中继选择策略研究[J]. 信号处理, 2017, 33(1): 116-125.
Liu Jiequn, Chen Jin, Ren Guochun,et al.Research on Relay Selection Strategy of Energy Harvesting Full-Duplex Relay Network[J].Journal of Signal Processing, 2017, 33(1): 116-125.(in Chinese)
[17] 秦城, 田辉. 非线性能量收集下的鲁棒性波束赋形[J]. 信号处理, 2017, 33(11): 1416-1423.
Qin Cheng, Tian Hui. Robust Beamforming under Non-Linear Energy Harvesting Model[J]. Journal of Signal Processing, 2017,33(11): 1416-1423. (in Chinese)
[18] Kang J M, Kim I M, Dong I K. Wireless Information and Power Transfer: Rate-Energy Tradeoff for Nonlinear Energy Harvesting[J]. IEEE Transactions on Wireless Communications, 2017, PP(99): 1-1.
[19] Boshkovska E, Ng D W K, Zlatanov N, et al. Practical Non-Linear Energy Harvesting Model and Resource Allocation for SWIPT Systems[J]. IEEE Communications Letters, 2015, 19(12): 2082-2085.
[20] Boyd S, Vandenberghe L. Convex Optimization[M]. Cambridge University Press, 2009.
[21] Cover T M, Thomas J A. Elements of Information Theory[M]. New York, Wiley, 1990.
[22] Li X, Jin S, Gao X, et al. Near-optimal power allocation for MIMO channels with mean or covariance feedback[J]. IEEE Transactions on Communications, 2010, 58(1): 289-300.

