1 引言
菱形中继网络通过灵活设计传输协议，利用分布在空间不同位置的用户天线来构造虚拟多天线阵列[1]，能够有效获取分级增益对抗多径衰落[2]，实现类似MIMO(Multiple-Input-Multiple-Output)的空间分集效果[3]。随着微蜂窝技术在5G通信网络中的应用，小区范围不断缩小，菱形中继网络具有中继节点发射功率小、部署灵活等特点，非常适合应用于5G网络。对于目前广泛采用的AF模式，在许多应用场景，如分集合并、最佳功率分配、最佳中继选择，分布式空时编码等[4- 6]都要求需要在获取级联信道的信道状态信息(CSI)的同时估计单跳信道，涉及到多个(级联或单跳)信道分离估计问题，带来的多训练序列优化问题更加复杂[7]。
在AF模式下的中继协作网络中关于信道估计的研究最早主要集中在级联信估计方面，文献[8]中设计了一种循环正交训练，文献[9]中，推导了MIMO系统中继放大矩阵设计的必要条件。然而，文献[8]和[9]中忽略了单跳信道估计对于系统优化的重要性[10-11]。文献[12]研究了一种多用户接收机，可以对中继链路各单跳信道进行盲估计，但是很难通过盲方法获取即时的CSI。文献[13]提出一种带内叠加训练进行单跳信道估计，通过将中继训练序列直接叠加到数据序列上，使得单跳信道和级联信道相互独立地进行，且消除了协作干扰和中继传输噪声的影响，但是由于在中继进行了干扰置零，以信号失真为代价获得信道估计的提升，降低了端节点符号检测性能。文献[14]提出时分叠加训练方案，在中继节点将自身训练叠加到源训练符号上，通过优化训练序列设计实现级联和单跳的分离估计。
本文针对单载波频域均衡系统，为了节省带宽的同时获取单跳信道的CSI，将时分叠加训练的帧结构设计思想拓展到菱形中继网络，开展高效信道分离估计理论研究。提出了一种适用于AF菱形中继网络的基于叠加训练(ST)信道估计方案，以消除多址接入干扰和训练间互干扰为目标，进行最优的多训练序列设计。新方案将中继训练叠加到源训练序列上，通过对中继识别符号以及中继训练组进行联合优化设计，设计了一种基于频域循环移位的正交扩展序列组生成算法；并且提出了一种中继噪声消除算法有效地解决了非高斯复合噪声对单跳信道估计的性能恶化问题。通过仿真实验，探究了最佳中继功率分配，并且分析验证了方案的有效性。
2 系统模型
以菱形中继协作为系统模型，如图1所示，包括源节点S，两个中继节点R1和R2以及目的节点D。
源节点S与目的节点D的通信分为两个时隙，在第一时隙内，源节点S分别向中继R1和R2广播数据；在第二时隙内，两中继放大接收数据并且转发至目的节点D，从而得到两份独立衰落的信息副本。
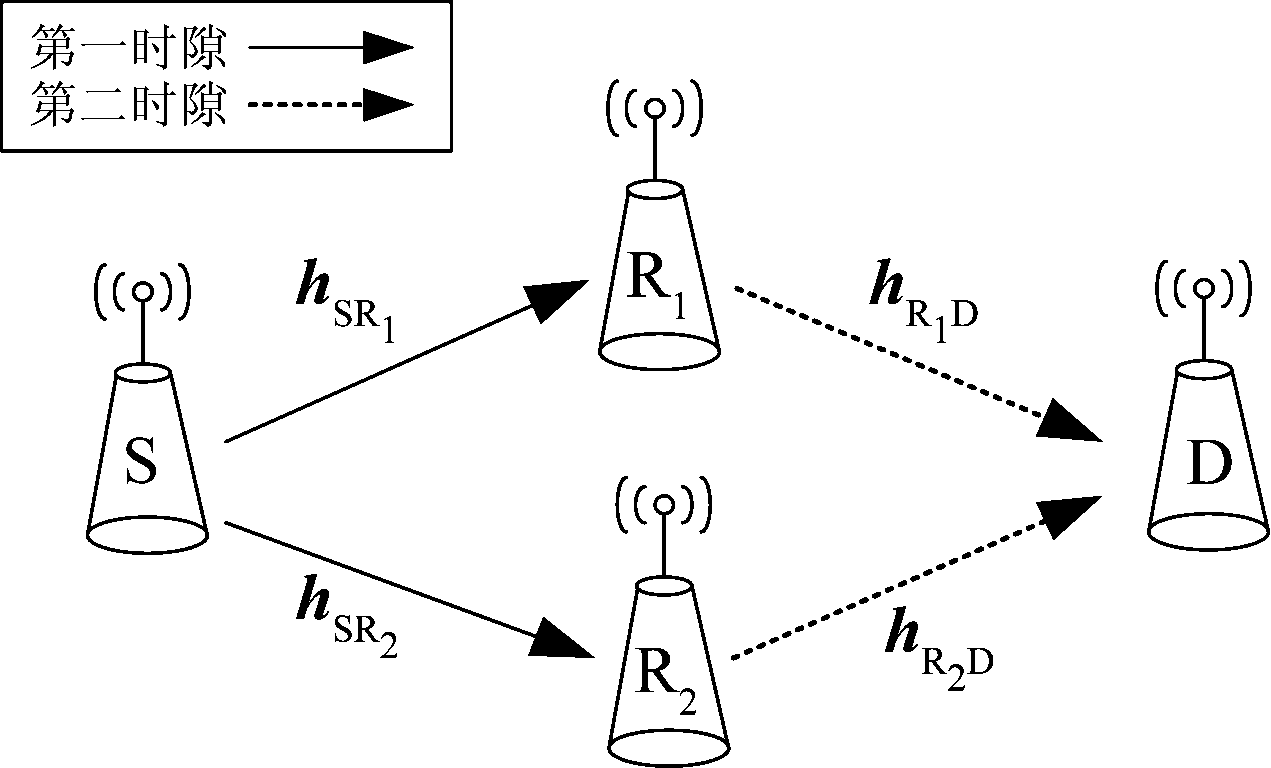
图1 菱形中继网络结构框架
Fig.1 Diagram for cooperative diversity of diamond relay network
假设菱形中继网络中，所有节点均只配备一根天线，工作在半双工模式下。在该中继网络模型中，S到R1的信道(S→R1)、S到R2的信道(S→R2)、R1到D的信道(R1→D)以及R2到D的信道(R2→D)冲激响应分别表示为
hSR1=[hSR1(0),hSR1(1),…,hSR1(LSR1-1)]T
hSR2=[hSR2(0),hSR2(1),…,hSR2(LSR2-1)]T
hR1D=[hR1D(0),hR1D(1),…,hR1D(LR1D-1)]T
hR2D=[hR2D(0),hR2D(1),…,hR2D(LR2D-1)]T
(1)
其中LSR1、LSR2、LR1D以及LR2D为对应的信道阶数，其他各项参数做如下假定：
1)信息符号d(n)为相互独立均匀分布的随机变量，取自调制信号符号集，均值E{d(n)}=0，符号功率进行归一化，即E{|d(n)|2}=1。
2)中继和目的节点噪声均为独立同分布的加性高斯白噪声(Additive White Gaussian Noise, AWGN)。
3)信道设定为准静态频率选择性衰落信道，信号包络服从瑞利分布。各个信道及信道内的各个抽头系数均相互独立。信道抽头设为零均值循环对称复高斯(Cyclic Symmetric Complex Gaussian, CSCG)随机变量，即
4)数据帧由一个训练块和一个信息块组成。
源节点训练序列和信息序列分别用tS=[tS(0),tS(1),…,tS(N-1)]T∈CN×1和d=[d(0),d(1),…,d(N-1)]T∈CN×1表示(本文为了方便描述，训练块长度Nt和信息块长度Nd都用N表述)。时分叠加训练的帧结构如图2所示。
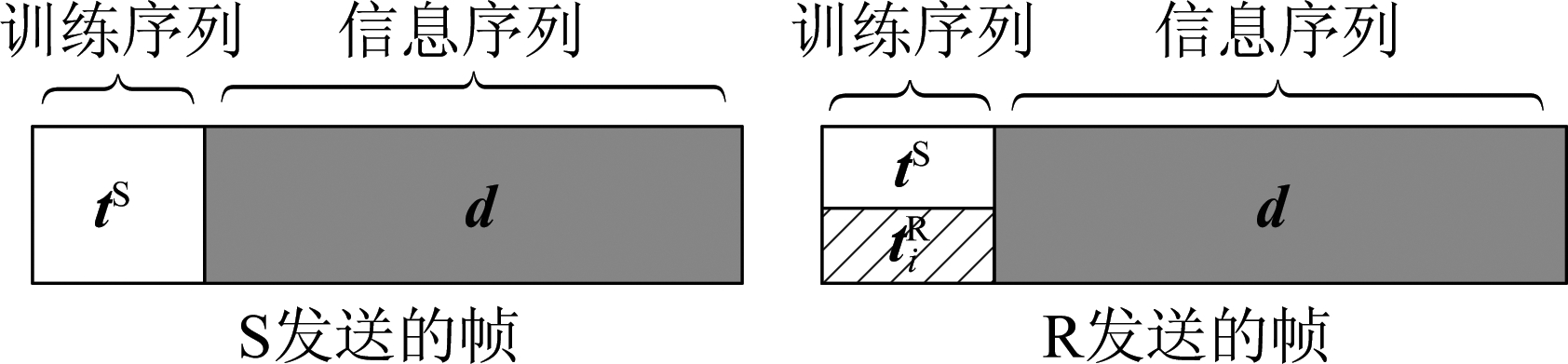
图2 时分叠加训练方案的帧结构图
Fig.2 Frame structure with relay superimposed training scheme
为了消除块间干扰(Inter-Block Interference, IBI)，通过插入和去除合适长度的循环前缀(Cyclic Prefix, CP)进行传输。不失一般性地，源节点会用全部功率Ps发送数据帧，训练序列和信息序列的平均发射功率分别为(tS)HtS/N=Ps和E{dHd}/N=Ps。
在第一时隙，在中继节点
接收的训练序列和信息序列分别为：
(2)
(3)
其中
中的元素服从AWGN分布，即
表示首列为
向下循环移位N-1次后形成的N×N维矩阵。
在第二时隙，R1和R2中继分别对接收的数据进行放大转发，由于目的节点不具备识别不同中继对应信道的能力，因此在中继对训练块增加不同的识别符号后叠加中继训练序列，中继处理后的训练序列和信息序列可以表示为：
(4)
(5)
其中Ai为中继Ri对应的中继识别矩阵，
为中继训练序列，
和
为放大因子，可以表示为：
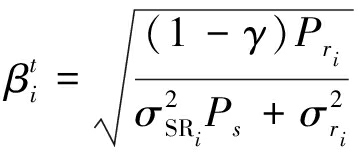
(6)
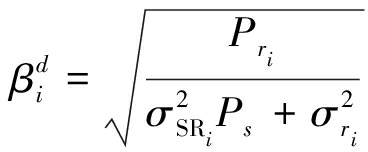
(7)
其中，
中继Ri的平均发射功率为Pri，γ为中继发射功率分配因子(0<γ<1)，分配给时分叠加训练的平均功率为
对应地，中继接收的放大的源训练信号的平均功率为(1-γ)Pri。
在第二时隙，在目的节点接收的训练序列和信息序列分别为：
(8)
(9)
其中，
为AWGN，服从
表示首列为
向下循环移位N-1次后形成的N×N维矩阵，HRi表示首列为
向下循环移位N-1次后形成的N×N维矩阵，hRi=hSRi*hRiD，LRi=LSRi+LRiD-1。
3 信道估计
为了实现分集合并，需要获得中继链路各单跳信道的CSI，根据式(8)，在目的节点接收的训练序列可以表示为：
(10)
其中，ΦL[x]是首列为x的N×L的循环矩阵，
为包含中继传播噪声和目的节点引入噪声在内的非高斯复合噪声。为了获得S→R1单跳信道的CSI，首先要依赖时分叠加训练获得R1→D单跳信道的CSI，根据式(10)可以清楚发现，在目的节点的接收的训练序列中，信道估计的干扰项包括：多址接入干扰、源训练序列与中继训练序列间的干扰以及与CSI相关的非高斯复合噪声。假设噪声相互独立，非高斯复合噪声
的协方差矩阵可以表示为：
(11)
其中，
不失一般性地，以R1中继链路为研究对象，则在基于LS的信道估计中，对应的R1→D单跳信道估计结果可以表示为
(12)
为了使得R1→D单跳信道估计的MSE最小，需要满足下列条件：
(13)
对应地，同时考虑以R2中继链路为研究对象后，在
时i=2以及
时i=1的情况下，可以将上述条件，转换为一般性的条件表述：
(14)
当C1～C4上述条件得到满足时，可以获得Ri→D单跳信道估计
根据式(10)，以R1中继链路为研究对象，则在基于LS的信道估计中，对应的S→R1单跳信道估计结果可以表示为
(15)
为了使得S→R1单跳信道估计的MSE最小，需要满足下列条件：
(16)
对应地，同时考虑以R2中继链路为研究对象后，可以将上述条件，转换为一般性的条件表述：
(17)
根据上述推导最小化信道估计MSE的条件C1～C8可以判断，要求添加识别符号后的源训练序列与不同中继对应的中继训练序列之间存在严格的正交约束关系。在进行理想的序列设计时，源训练序列tS选择具有循环特性以及在时域和频域为恒幅度的FZC序列，其自相关函数在零延时处存在波峰，而其互相关函数在所有的延时处全部为零，从而通过频域的循环移位生成一组正交扩展序列[13]，实质上，在时域增加中继识别符号(左乘中继识别矩阵Ai)即等效于在频域进行循环移位，且
即循环移位后平均功率不发生变化。训练序列的频域结构如3所示。
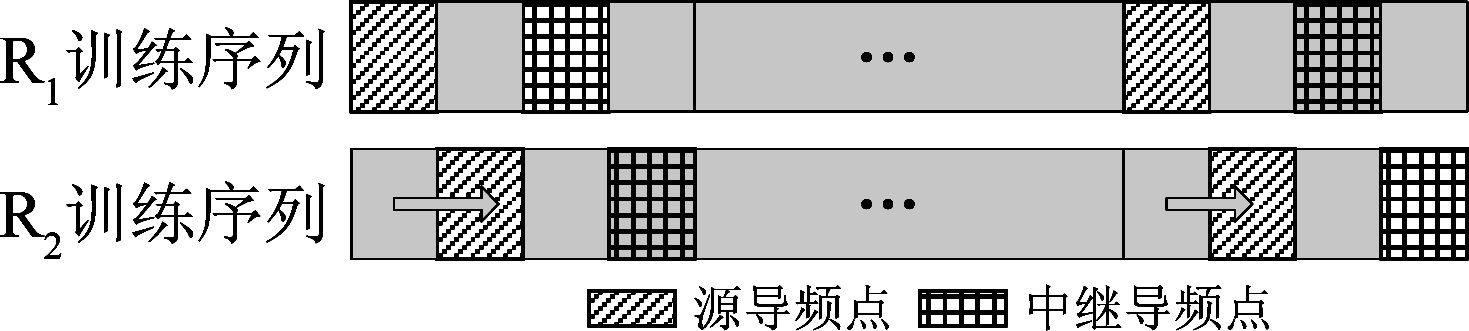
图3 训练序列的频域结构
Fig.3 Sketch for structure in frequency domain for training sequence
根据DFT圆周移位特性，中继识别矩阵Ai以及不同的中继训练序列
进行优化设计，如下：
tS(l)=ejπl(l+υ)/P, P is odd υ=1,P is even υ=2
(18)
A1=Π1
A2=Π3
(19)
其中P为训练序列的周期。
对应的Ri→D单跳信道LS估计的MSE可以表示为：
(20)
根据条件C2，最小的MSE可以进一步表示为：
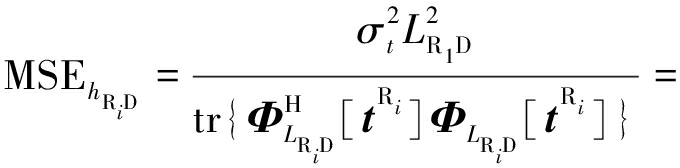
(21)
根据式(21)可以判断，对中继识别矩阵以及不同的中继训练序列优化后，Ri→D单跳信道的估计性能仅与非高斯复合噪声有关，能够消除多址接入干扰以及源训练与中继训练序列间的干扰。然而S→Ri单跳信道的估计性不仅仅与非高斯复合噪声有关，同时还受到Ri→D单跳信道的估计误差的影响。
4 中继消噪算法
根据式(21)，中继引入的噪声在中继被放大，在接收端的非高斯复合噪声实际上是本地噪声与中继传输噪声的混叠噪声，且后者恶化了单跳信道的估计性能。因此，为了消除单跳信道估计过程中前一级信道累计噪声的影响，设计了一种中继消噪算法。考虑到源训练序列与中继训练序列相互正交，频域离散且占据不同的频点的特点，对中继接收信号进行预处理，消除中继接收信号特定位置的频域幅值，用以容纳中继训练，从而消除中继传输噪声对信道估计造成的影响。
假设在中继
的中继训练序列对应的非零导频点的集合为Kr1,i∈{1,2}，大小为N×N的频域对角矩阵
中的元素可以定义为：
(22)
则对应的时域对角阵可以表示为
为N×N的傅里叶矩阵。中继首先通过预处理矩阵完成部分噪声消除的工作，接着对接收信号进行放大，最后与中继训练序列进行叠加。根据式(4)，采用中继消噪算法后，中继转发的信号可以重新表示为：
(23)
其中
为采用中继消噪算法后的放大因子，可以表示为：
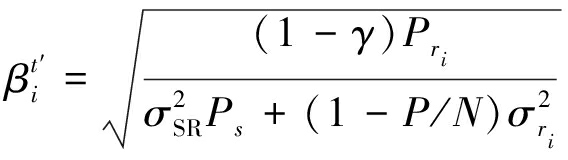
(24)
采用中继消噪算法后，单跳信道的最小MSE可以进一步表示为：
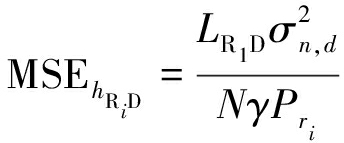
(25)
5 符号检测
获得单跳信道估计的CSI后
根据式(9)，在目的节点经过DFT处理后，接收的信息序列的频域值可以表示为：
(26)
其中对角阵
为k频点上的信道频域值，其中
和
分别为
和
的频域值。频域均衡后的信号可以表示为：
(27)
其中，
为MMSE均衡系数，且
经过MMSE频域均衡后，检测符号可以表示为：
(28)
6 仿真实验与分析
下面对本章节中的理论推导进行仿真实验，针对AF协议下的菱形中继网络，从归一化MSE和SER两方面探究时分叠加训练方案以及TM-IBST方案下的信道估计性能及符号检测性能。假定AF协作网络中信道为多径瑞利衰落信道，且具有指数功率延迟为E{|h(l)|2}=exp(-0.2l)。信息数据采用QPSK的调制方式，接收端设定为LS信道估计器以及MMSE均衡器。仿真实验中，假设源节点功率分配因子α=0.2，各级信道链路传输距离相同，训练序列和信息序列的块长度Nt和Nd由源节点功率分配因子决定，源节点和中继节点的平均传输功率设置为Ps=Pr1=Pr2=1，中继节点
和目的节点的信噪比分别定义为
且SNRr1=SNRr2=SNRd。假设信道阶数LSR1=LSR2=LR1D=LR2D=4，假设数据帧长度N=512(其中训练序列长度Nt=96，信息序列长度Nd=416)，为了获得理想的中继训练设计，时分叠加训练方案下不同信噪比下功率比γ与MSE的曲线如图4所示。
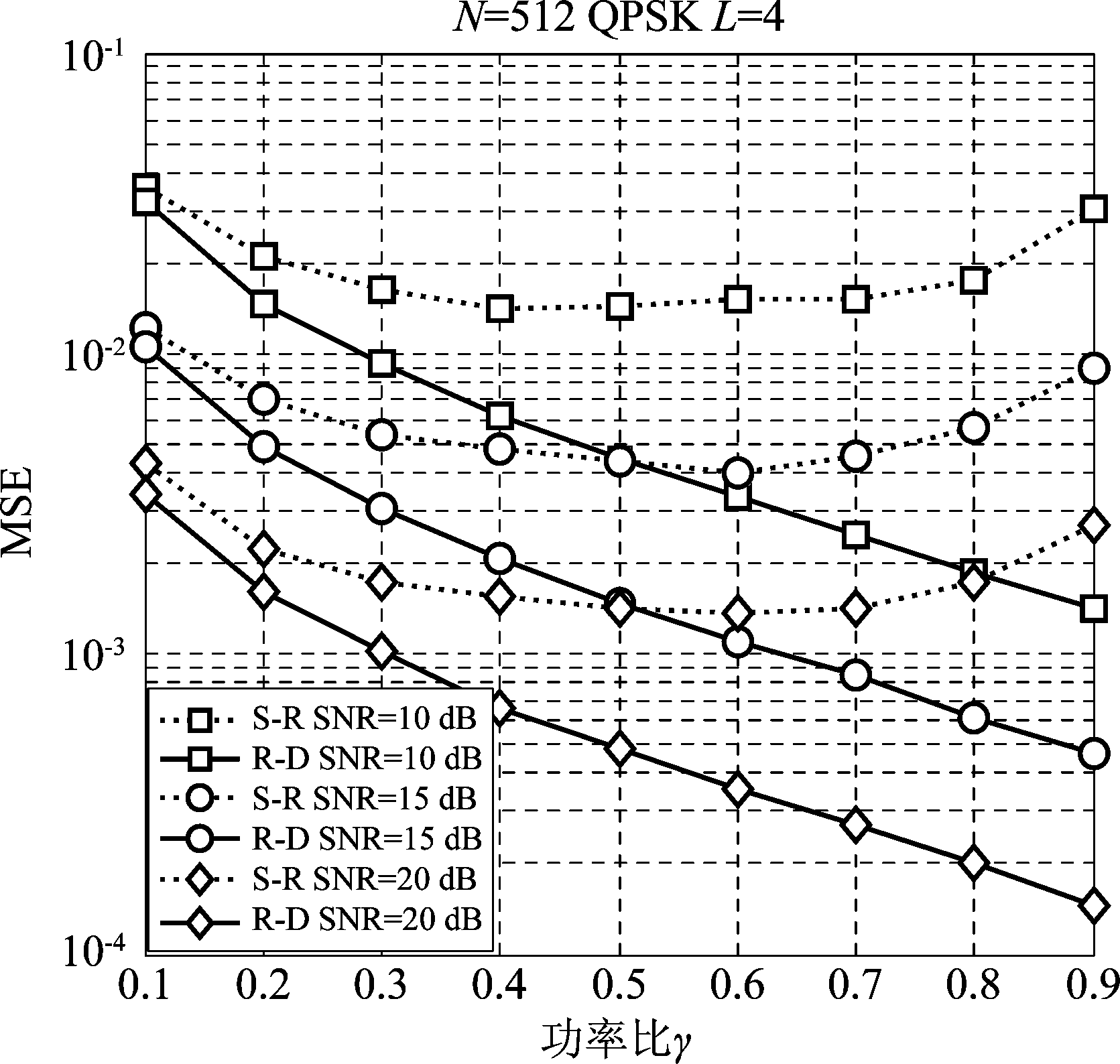
图4 时分叠加训练方案中不同信噪比下功率比与MSE曲线
Fig.4 MSE versus power allocation ratio at different SNR conditions with relay superimposed training scheme
可以明显发现，在时分叠加训练方案中，随着中继训练功率比γ增加，源训练序列功率减小，中继训练序列功率增大，Ri→D单跳信道的估计性能增加，而S→Ri单跳信道不仅受中继节点分配的功率影响，还与Ri→D单跳信道的估计性能息息相关，因此一开始由于Ri→D单跳信道的估计性能提高，S→Ri单跳信道估计性能随之提高，之后受功率因素的影响更为严重，因此S→Ri单跳信道估计性能随之下降，在0.4≤γ≤0.7之间保持稳定，获得最佳的信道估计性能。
由于γ与SER之间存在复杂的数学关系，在理论上获得最优的功率分配因子γ是极为困难的，本节采用仿真的方法探究不同功率分配因子下的SER性能。在时分叠加训练方案中，随着中继训练功率比γ增加，信息序列的在中继节点的发射功率不变，因此，与信道估计性能相对地，如图5所示，符号检测性能SER曲线大约在0.4≤γ≤0.7较大区域内相对平坦，最佳的功率分配因子存在平坦区域内。假设时分叠加训练的中继训练分配因子分别取γ=0.4，各单跳链路的信道估计性能MSE、符号检测性能SER分别与协作中继网络SNR的关系如图6和图7所示。
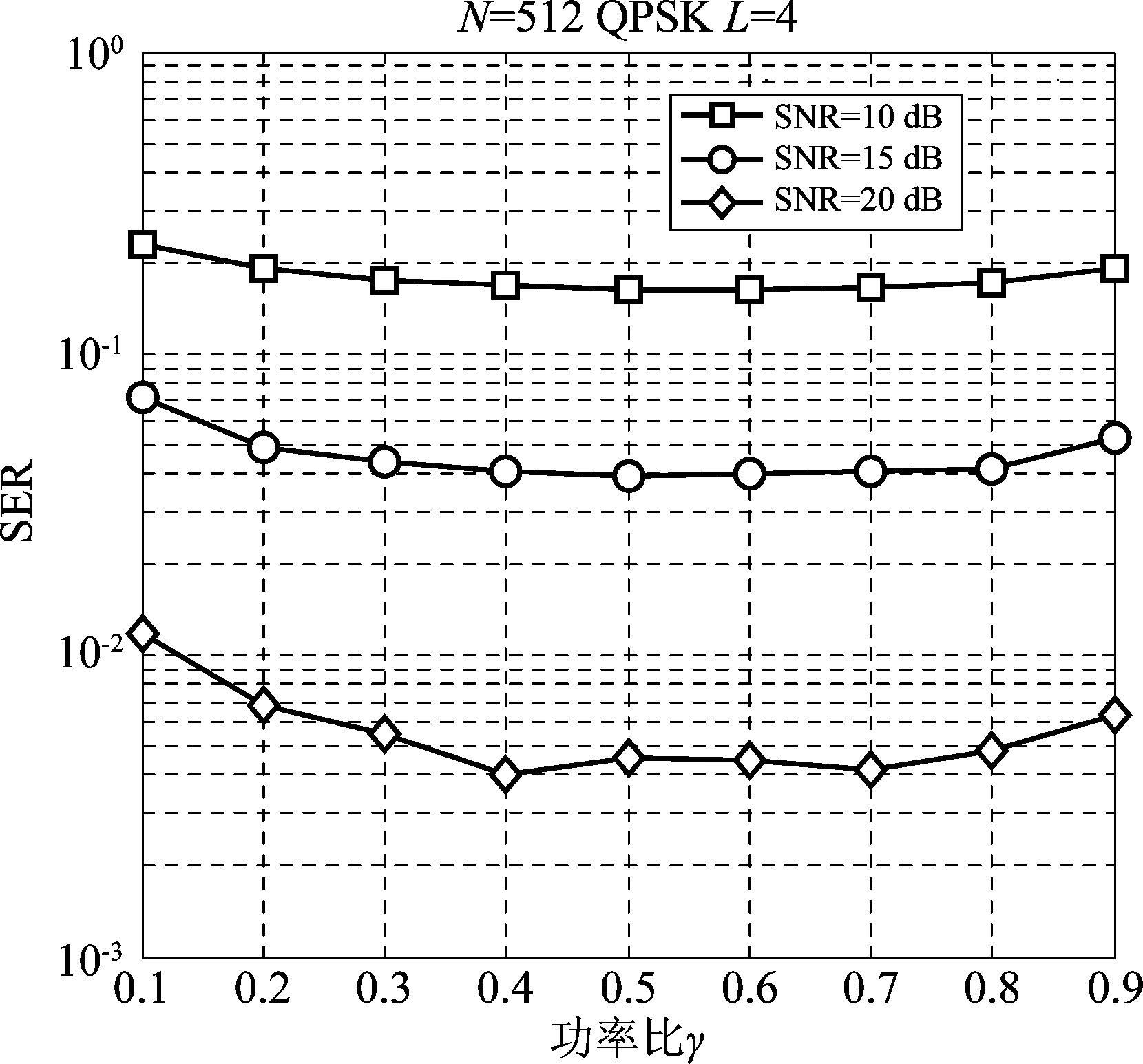
图5 时分叠加训练方案中不同信噪比下功率比与SER曲线
Fig.5 SER versus power allocation ratio at different SNR conditions with relay superimposed training scheme
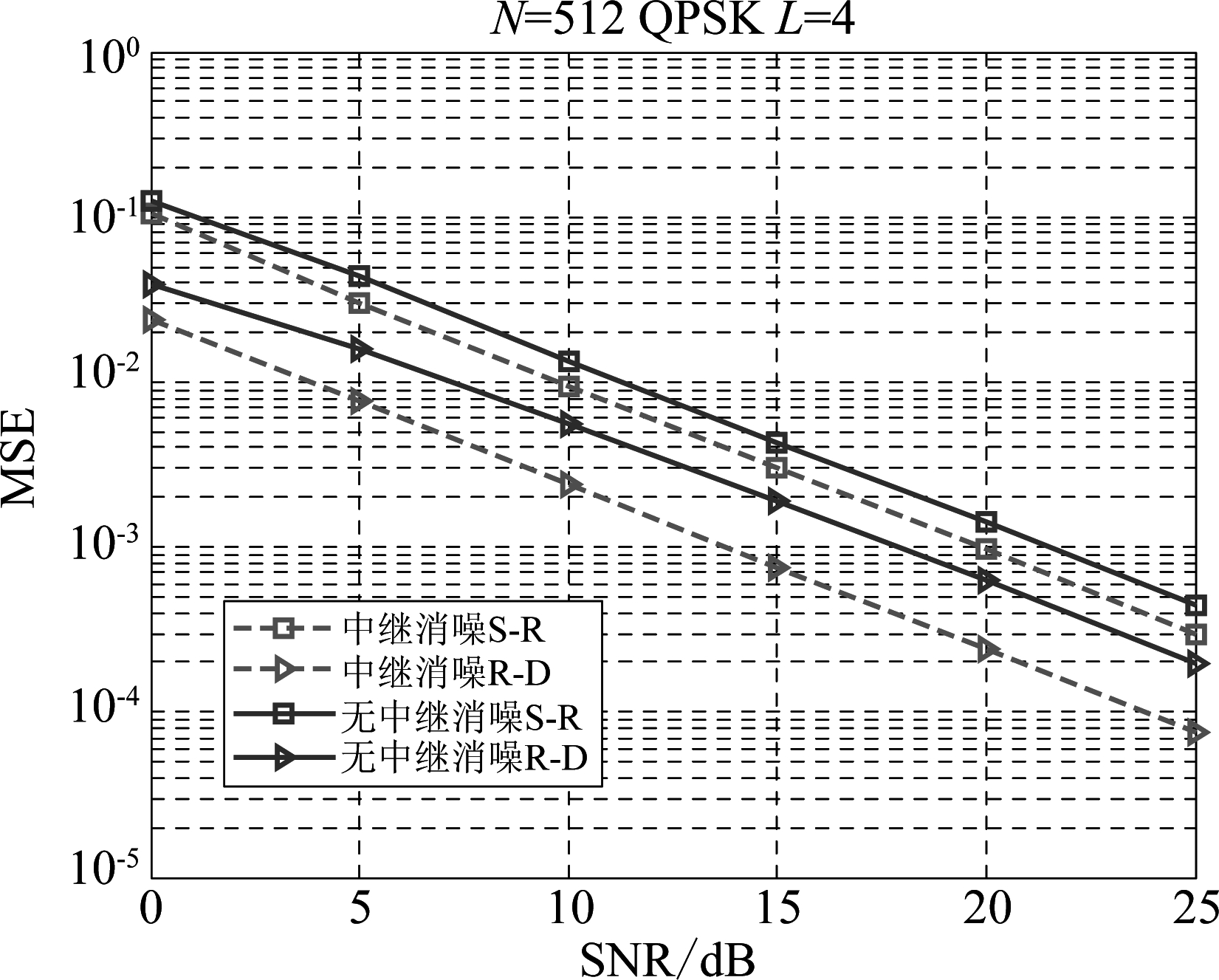
图6 信道估计均方误差与信噪比曲线
Fig.6 The curves of MSE versus SNR for channel estimation
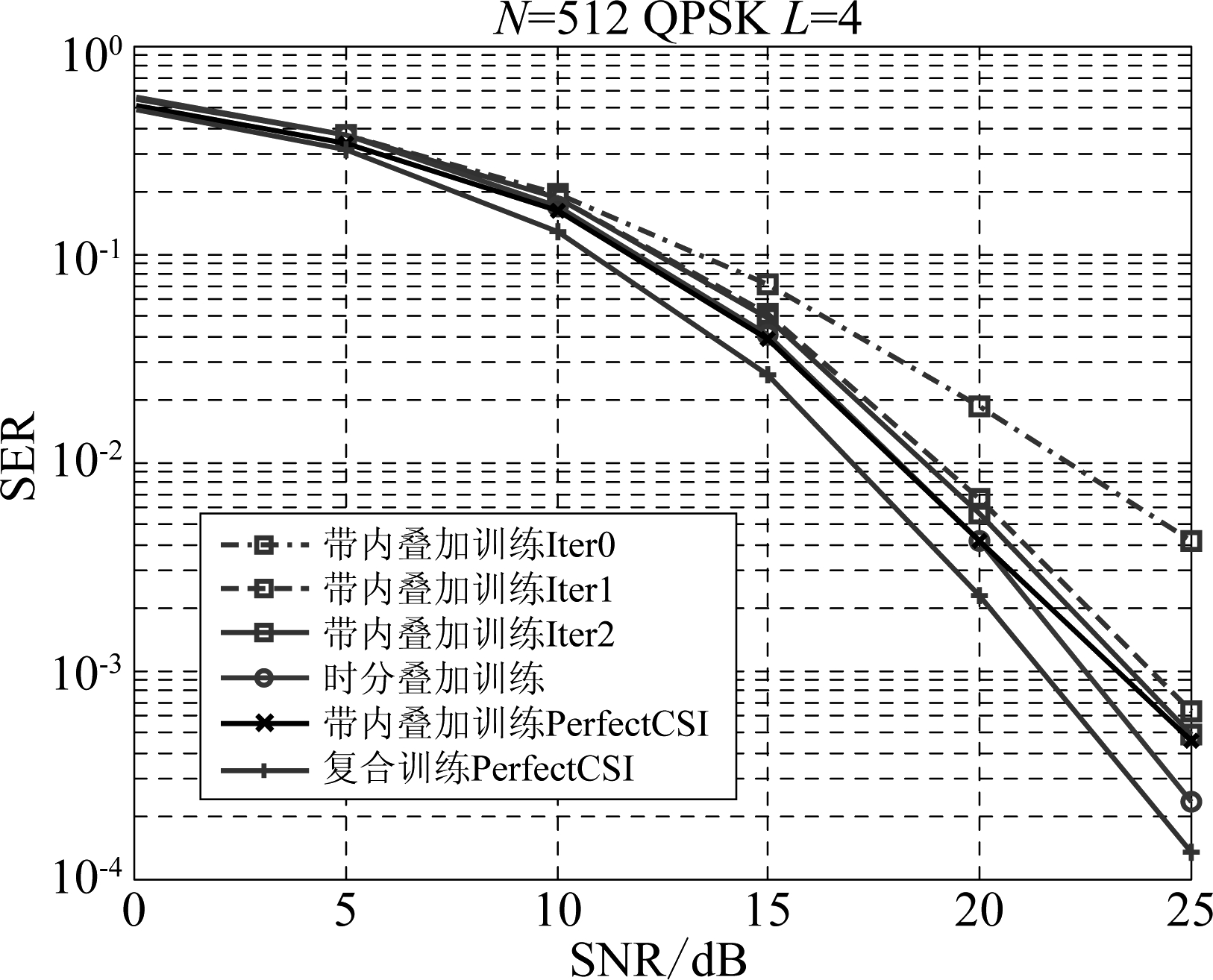
图7 符号检测误符号率与信噪比曲线
Fig.7 The curve of SER versus SNR for symbol detection
可以明显发现，如图6所示，在时分叠加训练方案中，Ri→D单跳信道的估计性能较S→Ri单跳信道更好，根据式(21)，未采用中继消噪算法的Ri→D单跳信道仅受包含中继传输噪声在内的非高斯复合噪声的影响，而S→Ri单跳信道还与Ri→D单跳信道估计误差相关；而采用中继消噪算法后，Ri→D单跳信道的估计性能提高明显，消除了中继传播噪声的影响，仅与目的节点引入的白噪声相关，即消除了非高斯复合噪声，有效地提高了估计性能；对应地其S→Ri单跳信道估计性能也相应的得到提高。
如图7所示，比较了本文中提出的基于时分叠加训练的信道估计方案以及文献[13]中的带内叠加训练方案的符号检测性能，在带内叠加训练方案中，其本质是将中继训练序列叠加到接收的信号上，以部分失真为代价换取较好的信道估计性能。由于中继干扰置零操作引入了严重的信息失真，检测性能经过1次迭代后提高效果明显，2次迭代后性能不再随之提高，是由于文献[13]迭代重构算法依赖于初始的检测性能，所以其补偿能力有限。对应地，本文提出的方案由于不存在信息失真，其符号检测性能明显高于带内叠加训练方案。相比时分叠加训练方案理想CSI下的检测性能，可以明显判断，信息失真导致了部分的性能损失，且该部分性能损失为迭代重构不能修复的性能损失。因此本文提出的时分叠加训练能够在不引入失真的情况下获得高性能的信道估计，且应用环境更加丰富。
7 结论
为了节省带宽的同时获取单跳信道的CSI，将时分叠加训练的帧结构设计思想拓展到菱形中继网络，开展高效信道分离估计理论研究。提出了一种适用于AF菱形中继网络的基于ST的单跳信道估计方案，以消除多址接入干扰和训练间互干扰为目标，进行最优的多训练序列设计。通过仿真实验，探究了最佳中继功率分配，验证了中继消噪算法能够完全消除非高斯复合噪声对单跳信道估计性能恶化，有效地提高了估计性能。对比同类型的信道估计方案，本文提出的方案能够不引入信息失真，获得更好的符号检测性能。
[1] Zhuang W, Ismail M. Cooperation in wireless communication networks[J]. IEEE Wireless Commun, 2012, 19(2): 10-20.
[2] Wang Q, Fan P, Mckay M R, et al. On the position selection of relays in diamond relay networks[J]. IEEE Trans. Commun, 2011, 59(9): 2515-2527.
[3] Laneman J N, Tse D N C, Wornell G W. Cooperative diversity in wireless networks: efficient protocols and outage behavior[J]. IEEE transactions on information theory, 2004, 12(11): 3062-3080.
[4] Huang C, Cui S. On the alternative relaying Gaussian diamond channel with conferencing links[J]. IEEE Trans. Wireless Commun, 2013, 12(2): 758-768.
[5] Dou G, He X, Deng R, et al. Individual channel estimation for AF-based relaying systems using in-band pilots[J]. IEEE Communications Letters，2016, 20(11): 2201-2204.
[6] Singh K, Ku M, Lin J. Power allocation and relay selection in relay networks: A perturbation-based approach[J]. IEEE Signal Processing Letters, 2017, 24(9): 1328-1332.
[7] 何宪文，李晓文，高俊. 基于协作干扰抑制的信道估计技术研究[J]. 信号处理, 2018, 34(3): 253-261.
He Xianwen, Li Xiaowen, Gao Jun. Channel estimation based on cooperative interference suppression[J]. Journal of Signal Processing, 2018, 34(3): 253-261. (in Chinese)
[8] Lei M, Zhao M, Zhong J, et al. Channel estimation based on cyclic orthogonal training sequence for relay-assisted cooperative communication system[C]∥Computer, Information and Telecommunication Systems(CITS), Amman, Jordan, 2012.
[9] Ma J, Orlik P, Zhang J, et al. Pilot matrix design for estimating cascaded channels in two-hop MIMO amplify-and-forward relay systems[J]. IEEE Trans. Wireless Commun, 2011, 10(6): 1956-1965.
[10] Munoz-Medina O, Vidal J, Agustin A. Linear transceiver design in nonregenerative relays with channel state information[J]. IEEE Trans. Signal Processing, 2007, 55(6): 2593-2604.
[11] Qin D, Ding Z, Dasgupta S. On Forward Channel Estimation for MIMO Precoding in Cooperative Relay Wireless Transmission Systems[J]. IEEE Trans. Signal Process, 2014, 62(5): 1265-1278.
[12] Han X, Andre L F. Multiuser receiver for joint symbol/channel estimation in dual-hop relaying systems[J]. Wireless Personal Communication, 2015, 83(2): 17-33.
[13] He X, Dou G, Gao J. Individual Channel Estimation in a Diamond Relay Network Using Relay-Assisted Training[J]. International Journal of Digital Multimedia Broadcasting, 2017(10): 1-7.
[14] Gao F, Jiang B, Gao X, et al. Superimposed Training based Channel Estimation for OFDM Modulated Amplify-and-Forward Relay Networks[J]. IEEE Transations on Signal Processing, 2011, 59(7): 2029-2039.
