1 引言
随着物联网的迅速发展,如何延长能量受限设备的使用寿命成了亟待解决的问题。无线通信技术的飞速发展使得射频能量资源变得越来越丰富,基于射频(Radio Frequency, RF)信号的无线能量传输(Wireless Power Transfer, WPT)技术为解决该问题提供了有效途径。基于此,无线能量通信网络(Wireless Powered Communication Networks, WPCNs)正日益引起学者们的关注[1]。
近年来,WPCNs得到了广泛的研究。文献[2]提出了著名的收集再传输(Harvest-then-transmit, HTT)协议,该协议是当前WPCNs运行的主要基础。该协议包含能量收集和数据传输两个阶段,在能量收集阶段,用户(无线设备)收集基站在下行链路辐射的能量信号;在数据传输阶段,用户利用先前收集的能量以时分多址(Time Division Multiple Access, TDMA)的方式向基站发送数据。在文献[2]中,基站因仅含有一根天线只能工作在半双工(Half Duplex)模式。为了提升系统容量,文献[3]将文献[2]拓展至全双工模式。在文献[3]提出的模型中,基站含有两个天线,因此可以同时发射能量信号和接收数据。
众所周知,在认知无线电网络(Cognitive Radio Networks, CRNs)中,次网络可以有效的利用主网络的空闲频谱[4],通过感知频谱来动态管理频谱资源,以此来提高频谱利用率[5]。受文献[2]启发,文献[6]提出了一个新的网络模型:认知无线能量通信网络(Cognitive WPCNs, CWPCNs)。在该网络中,当主网络忙碌时,次发射机(Secondary Transmitter, ST)可以收集主发射机(Primary Transmitter, PT)发射的能量信号;并利用收集的能量在主网络空闲时向次接收机(Secondary Receiver, SR)发送数据。在该网络中,网络的通信性能满足干扰温度约束和主网络速率约束,通过联合优化时间和功率分配来提高次网络的吞吐量。文献[7]提出了协作式的CWPCN,在该网络中提出中继协议来最大化该网络的能量效率。CWPCNs是WPCNs的有效延伸,但是CWPCNs也存在着一些问题。例如,用户间公平性的问题;CWPCNs需要专门的电力基础设施且电池需要专门的维护,带来较大的额外开销。
为了避免对基础电力设施的维护,文献[8]设计了一种新的通信协议:反向散射通信(Backscatter Communication, BackCom)协议,该通信协议使用环境射频信号作为通信设备的能量源。环境反向散射通信利用已存在环境中的射频信号来进行通信,不需要再产生专用的能量信号,相较于文献[2-3,6-7]的模型更加节能和易于部署。
BackCom利用环境信号进行通信的优势十分显著[9],文献[10-11]将BackCom与WPCN结合,提出了反向散射辅助的无线能量通信网络(Backscatter Assisted WPCNs, BAWPCNs),并考虑了多用户情况下的吞吐量优化问题。文献[12]将非正交多址接入技术首先引入了BAWPCNs。文献[13]将BackCom与CWPCN进行巧妙地结合,提出了反向散射辅助的认知无线能量通信系统(Backscatter Assisted CWPCNs, BACWPCNs)。在该网络中,含有一个主发射机和一个由次发射机和次接收机组成的次用户对。次发射机具备有工作BackCom协议和HTT协议的能力,作者通过分析这两个协议间的最优时间分配方案,最大化系统的性能容量。
相较于增加固定的中继节点来提高网络的速率,BACWPCN的提出使网络的部署更具灵活性。BackCom的引入可以充分利用主网络忙碌的时间,在BACWPCN中,当主网络忙碌时,ST可以通过BackCom与SR进行数据传输。但是,当主网络忙碌时间减少时,限于时间约束,BackCom的性能降低。当主网络空闲时,ST利用HTT协议在网络忙碌时收集到的能量来传输数据,以此来增加次网络的传输效率。故在BACWPCN中充分利用BackCom和HTT协议的优势显得尤为明显。CRNs中常常包含多个次用户。为考虑更为实用的CRNs, 受文献[13]启发,本文研究了包含两个次用户对的BACWPCNs。在文本提出的模型中,当主信道忙碌时,两个次发射机以TDMA方式工作在BackCom协议下,即分别向次接收机发射数据;当一个用户工作在BackCom协议下,另一个用户则处于HTT协议的能量收集阶段;当主信道空闲时,两个次发射机利用先前收集的能量同样以TDMA方式传输数据。考虑到收集的能量相对有限和次发射机的功耗,会存在收集的能量不足以驱动次发射机工作的现象。为此,本文根据收集的能量是否可以驱动次发射机工作考虑了三种场景,针对每种场景分别研究了其最优的时间分配方案以最大化系统容量,仿真表明其性能优于同样场景下中继协议的CWPCN。
本文的内容安排如下:第2节主要介绍系统模型,第3节主要介绍最优时间分配研究,第4节给出了仿真结果并进行分析,第5节是对本文的总结。
2 系统模型
2.1 网络模型
本文研究基于BackCom的CWPCN,该网络包含一个主发射机,两个由次发射机和次接收机组成的次用户对。系统模型如图1所示。为便于描述,两个次发射机和两个次接收机分别命名为STi和SRi(i=1,2)。STi装备有能量收集模块和BackCom模块,故STi具有工作BackCom协议和HTT协议的能力。在本文提出的模型中,当PT传输信号时,主信道被占用,STi可以利用BackCom协议反射信息给SRi或者收集能量;当主信道空闲时,STi利用先前收集的能量给SRi发送信息。不失一般性,我们假设次接收机能够自动识别次发射机的通信模式并使用相对应的解调器[13]。令1-β表示信道忙碌的时间, β表示信道空闲的时间。假设每个传输时隙为T。如图2所示,在每个传输时隙内,发射机的工作可以分为反向散射通信、能量收集和数据传输三个阶段。由于BackCom和能量收集都需要利用次用户信道,故当主用户信道忙碌时,STi只能工作在BackCom阶段或者只进行能量收集。在信道空闲时,主用户不进行数据传输,能量收集模块没有能量可以收集,故在信道空闲时,STi利用已经收集的能量向SRi传输数据。
(1)BackCom阶段:如图2(a)所示,令αi表示STi处于BackCom协议的时间,αi(1-β)表示STi利用BackCom协议将数据反射给SRi的时间。
(2)能量收集阶段:在这个阶段,能量收集模块可以收集能量并将其储存在储能器中。在此假设储能器的初始能量为零。如图2(b)所示,1-αi表示STi收集能量的时间,(1-αi)(1-β)表示一个时隙中STi收集能量的时间。
(3)数据传输阶段:如图2(c)所示,ri(i=1,2)表示STi在信道空闲时中用收集到的能量进行数据传输的时间,其中r1+r2∈[0, β]。假定一个时隙内收集到的全部能量都用于该时隙内次网络的信息传输。
在给定传输时隙中,如何选取STi的工作模式和时间分配显得尤为重要。为了最大化次网络的系统容量,在主信道忙碌时需要均衡BackCom和能量收集的时间,在主信道空闲时需要均衡各个用户数据传输的时间。
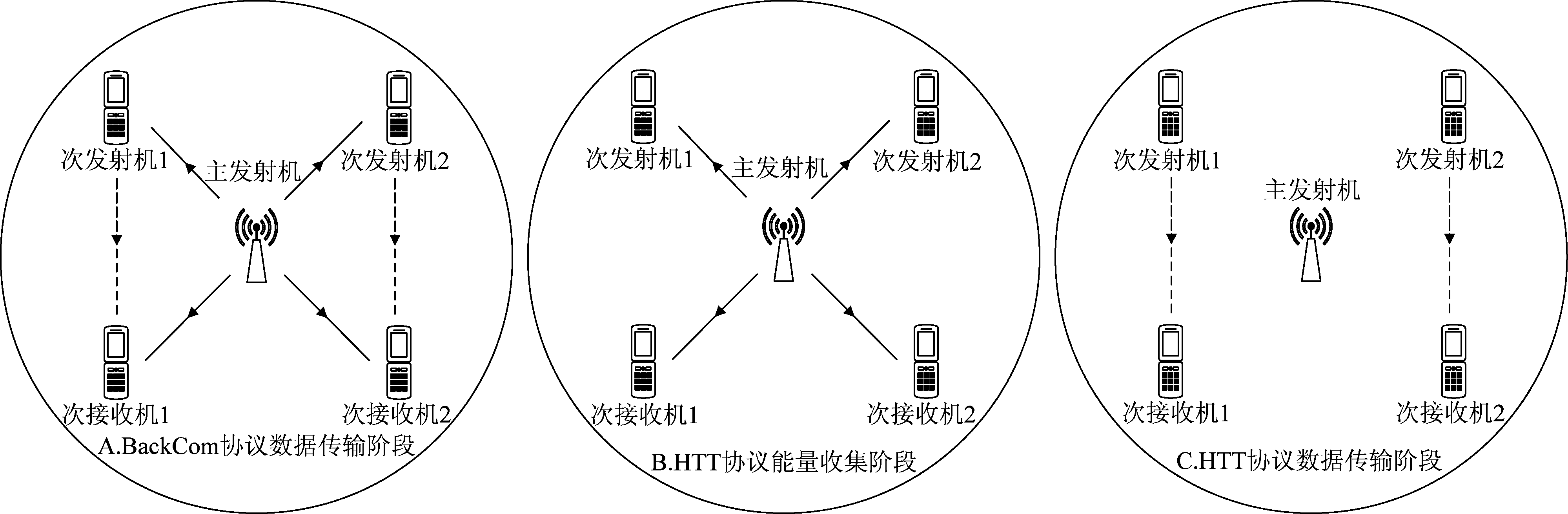
图1 反向散射通信辅助的认知无线能量网络
Fig.1 Backscatter Assisted Cognitive Wireless Powered Communication Network
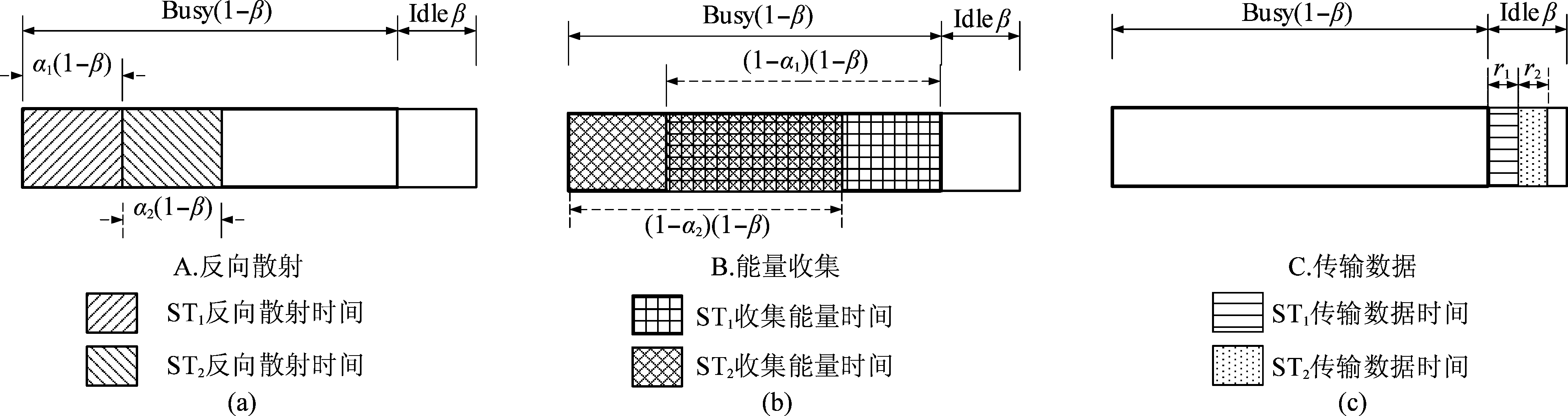
图2 BACWPCN中时间分配
Fig.2 Time Allocation in BACWPCN
2.2 信道容量模型
在次用户网络中,令R表示在给定时隙中次网络的总系统容量,R=Rh1+Rh2+Rb1+Rb2,其中,Rhi表示STi工作在HTT协议时的容量,Rbi表示STi工作在BackCom协议时的容量。下面将详细介绍各个参数的定义。
(1)HTT协议:该协议包括两个阶段,分别是能量收集阶段和数据传输阶段。在能量传输阶段,STi收集PT发送的能量信号;在数据传输阶段,STi利用收集到的能量传输数据。
a)能量收集阶段:在该阶段中,从PT到STi的射频功率可以从以下的公式得到[13]:
(1)
其中,PRi表示STi的收集能量的功率,δ是能量收集的效率,PT表示PT的传输功率, GT是PT的天线增益,GRi是STi的天线增益,λ是发送波长,di是PT与STi之间的距离。因而,在能量收集时间(1-αi)(1-β)中,STi收集的总能量为:
Ehi=(1-αi)(1-β)PRi=
(2)
b)数据传输阶段:当信道空闲时,STi用先前收集到的能量进行数据传输。考虑到STi的电路损耗,STi在空闲时段传输数据的功率为:
(3)
其中,Eci是电路消耗的能量。 如果Ptri为负数,表明收集到的能量无法满足STi的电路消耗,此时STi无法工作在HTT协议下。在Ptri非负的条件下,需要满足如下的表达式:
Ehi=(1-αi)(1-β)PRi≥Eci
(4)
由(4)可得
(5)
设![]() 表示STi反向散射通信时间的最大值,且
表示STi反向散射通信时间的最大值,且![]()
在满足![]() 且
且![]() 条件下,HTT协议下的传输速率表示为:
条件下,HTT协议下的传输速率表示为: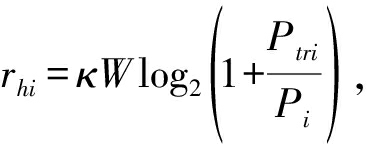 其中κ为数据传输效率,W为主信道的带宽,Pi为噪声功率与信道增益系数的比值,
其中κ为数据传输效率,W为主信道的带宽,Pi为噪声功率与信道增益系数的比值,![]() 因此,该阶段每个时隙的系统容量如下:
因此,该阶段每个时隙的系统容量如下:
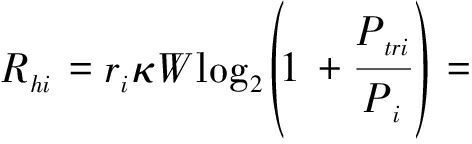
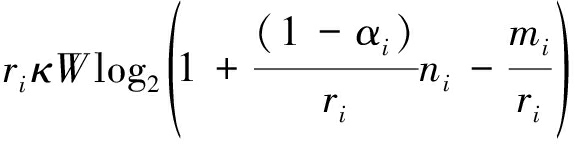
(6)
其中![]()
对于HTT协议阶段,在一个时隙中的系统容量为:
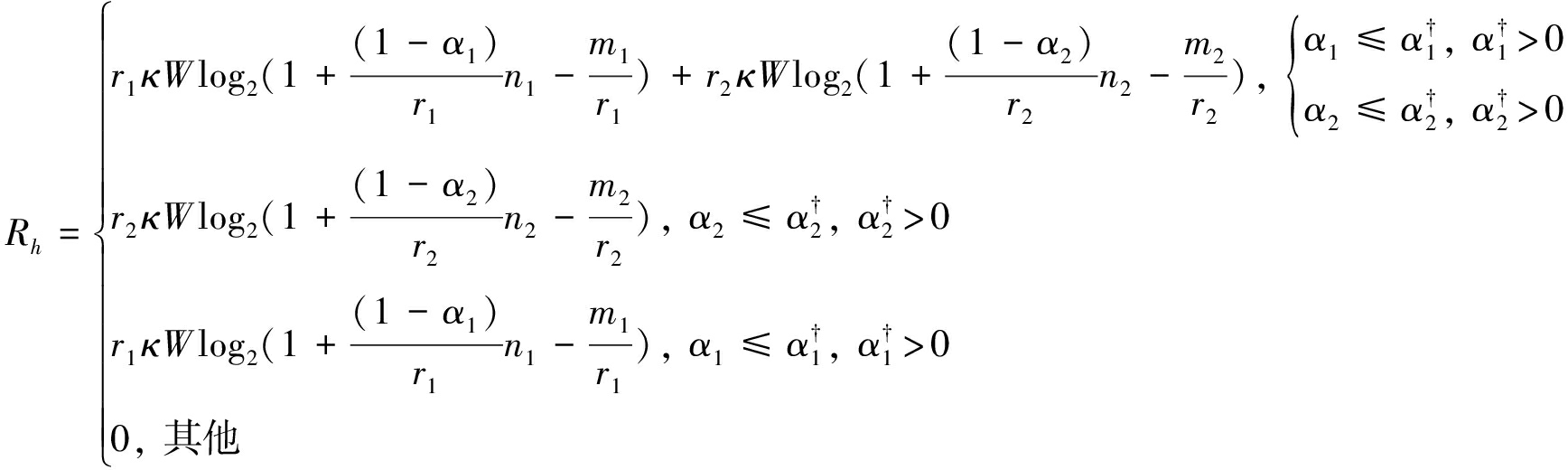
(7)
(2)BackCom协议:该通信协议利用环境反向散射(Ambient Backscatter)技术进行数据的传输,即STi实时反射PT发送的信号至![]() 文献[8]表明,环境反向散射通信的传输速率取决于反向散射电路中电路元件的设置,与环境因素无关。令Bbi表示STi反向散射通信的传输速率,那么对于BackCom协议,每个时隙的系统容量为:
文献[8]表明,环境反向散射通信的传输速率取决于反向散射电路中电路元件的设置,与环境因素无关。令Bbi表示STi反向散射通信的传输速率,那么对于BackCom协议,每个时隙的系统容量为:
Rb=α1(1-β)Bb1+α2(1-β)Bb2
(8)
综上,关于两种协议系统总容量的优化问题可以由如下的公式表示出来:
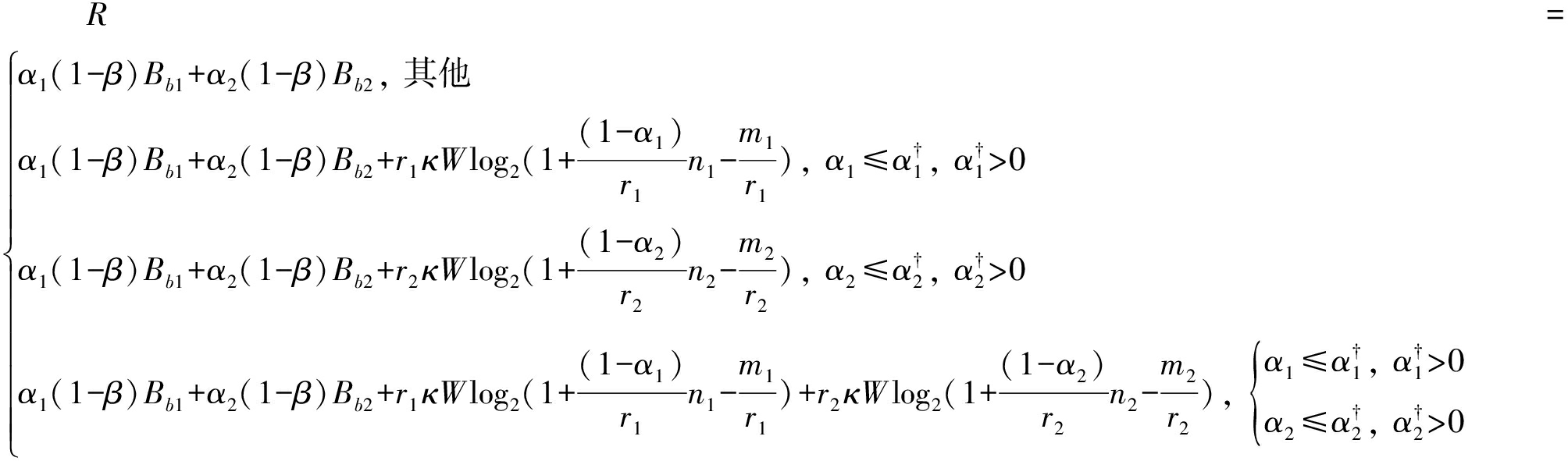
(9)
根据式(9)可知,基于BackCom和HTT协议的总容量表达式可以分为三种情况。情况1):两个ST均无法驱动HTT协议,即只能工作在BackCom协议下;情况2):其中一个ST可以驱动HTT协议,故其可工作在BackCom和HTT协议下,而另一个ST只能工作在BackCom协议下;情况3):两个ST均可工作在BackCom和HTT协议下。
3 最优时间分配研究
根据上述描述的三种情况,分别建立优化问题,求解对应问题的最优解,即最优时间分配方案。针对情况1),α1,α2有以下四种可能的取值范围:
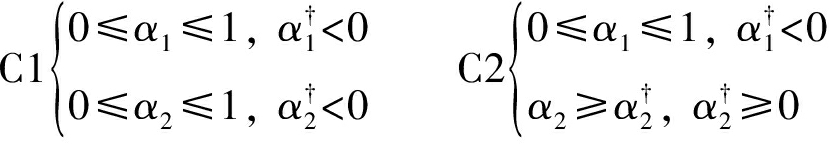
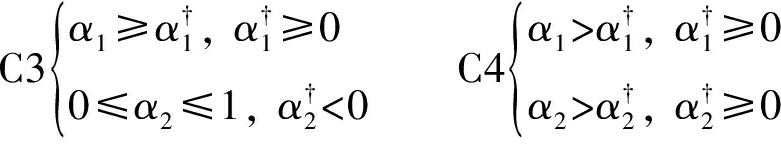
对于第一种取值范围C1,对应总容量R(α1,α2)=α1(1-β)Bb1+α2(1-β)Bb2,很容易建立一个优化问题:
![]() s.t. 0≤α1≤1 0≤α2≤1
s.t. 0≤α1≤1 0≤α2≤1![]() α1+α2≤1
α1+α2≤1
(10)
该优化问题是一个凸优化问题,其中目标函数是线性的,该优化问题的最优解为![]()
对于C2、C3和C4,可以建立与(10)类似的优化问题,并得到最优解。受限于文章篇幅,这里不再赘述。
对于情况2),假设只有ST1能满足HTT协议通信条件,ST2只能进行反向散射通信。此时对应的约束条件存在如下两种可能:
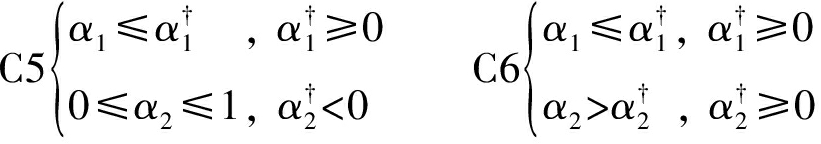
对于约束条件C5,对应的总容量为:
R(α1,α2,r1)=α1(1-β)Bb1+α2(1-β)Bb2+
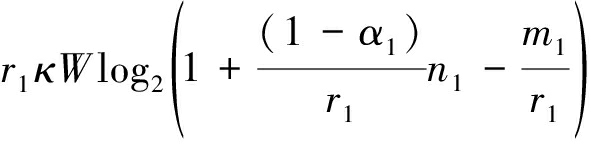
(11)
该种情况下的优化问题为:
0≤α2≤1
α1+α2≤1
0≤r1≤β
(12)
引理1 优化问题(12)是一个凸问题,且![]()
证明1 请参照附录1。
根据引理1,问题(12)可以转换成以下凸优化问题:
0≤α2≤1
α1+α2≤1
(13)
定理1 针对优化问题(13),该问题的最优解为:
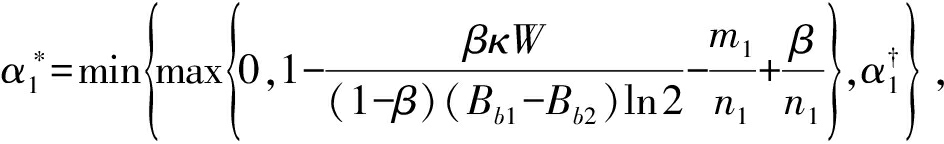
(14)
证明2 请参照附录2。
对于约束条件C6,可以建立与(13)类似的优化问题,由于受![]() 的限制,此时
的限制,此时![]() 利用定理1中的方法同样可得到该约束条件下的最优解。
利用定理1中的方法同样可得到该约束条件下的最优解。
针对情况2),若ST2能满足HTT协议通信,ST1只能工作在BackCom协议下,此时约束如下:
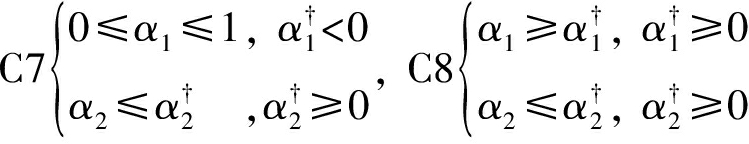
在这种情况下,对α1,α2的数值最优化分析与前文的优化算法相同,此处不做过多阐述。
在情况3)中,ST1,ST2均能满足BackCom协议和HTT协议通信条件,需要满足如下的条件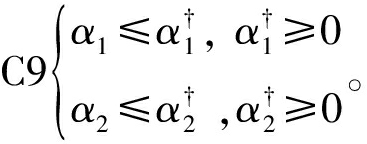
基于此,建立的优化问题如下:
α1+α2≤1, r1+r2≤β
(15)
优化问题(15)是一个凸优化问题,证明过程与优化问题(12)相类似,此处不再证明。针对α1,α2的最优化求解,用内点法(Interior-point method),构造罚函数来描述可行区域,通过遍历内部可行区域对优化问题进行求解。用内点法直接求解连续线性规划问题的主要优点是其计算时间对问题的规模不敏感,故其时间复杂性在计算大规模优化问题时很有优势。
4 仿真结果分析
本节通过数值仿真对提出的最优的时间分配方案进行验证。环境参数设置如下:假设信号的带宽和频率分别为100 kHz和100 MHz,ST的传输速率为Bb1=33 kbps, Bb1=55 kbps, 主次发射机的接收天线均为6 dbi,电路中的损耗功率为-20 dBm,数据传输效率与能量收集效率均为60%。与文献[13]相同,主发射机与次发射机的距离为6.7英里,同时次发射机与次接收机之间的距离为1 米。本文提出的模型将与如下三个参照系做对比:即只工作在BackCom协议下,只工作在HTT协议下以及文献[7]的协作式CWPCN。
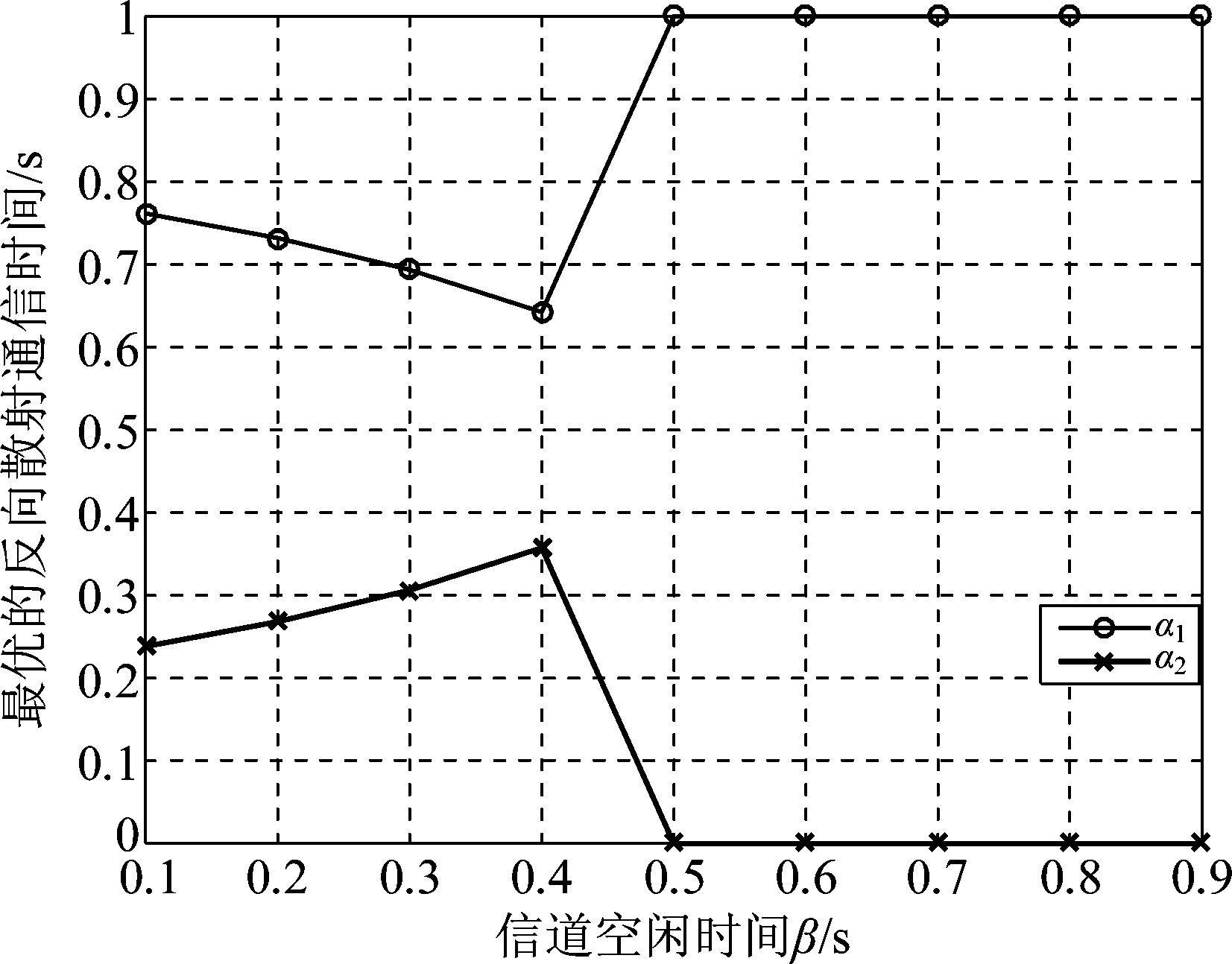
图3 不同信道空闲时间下的最优反向散射通信时间
Fig.3 The optimal time of BackCom versus channel idle time
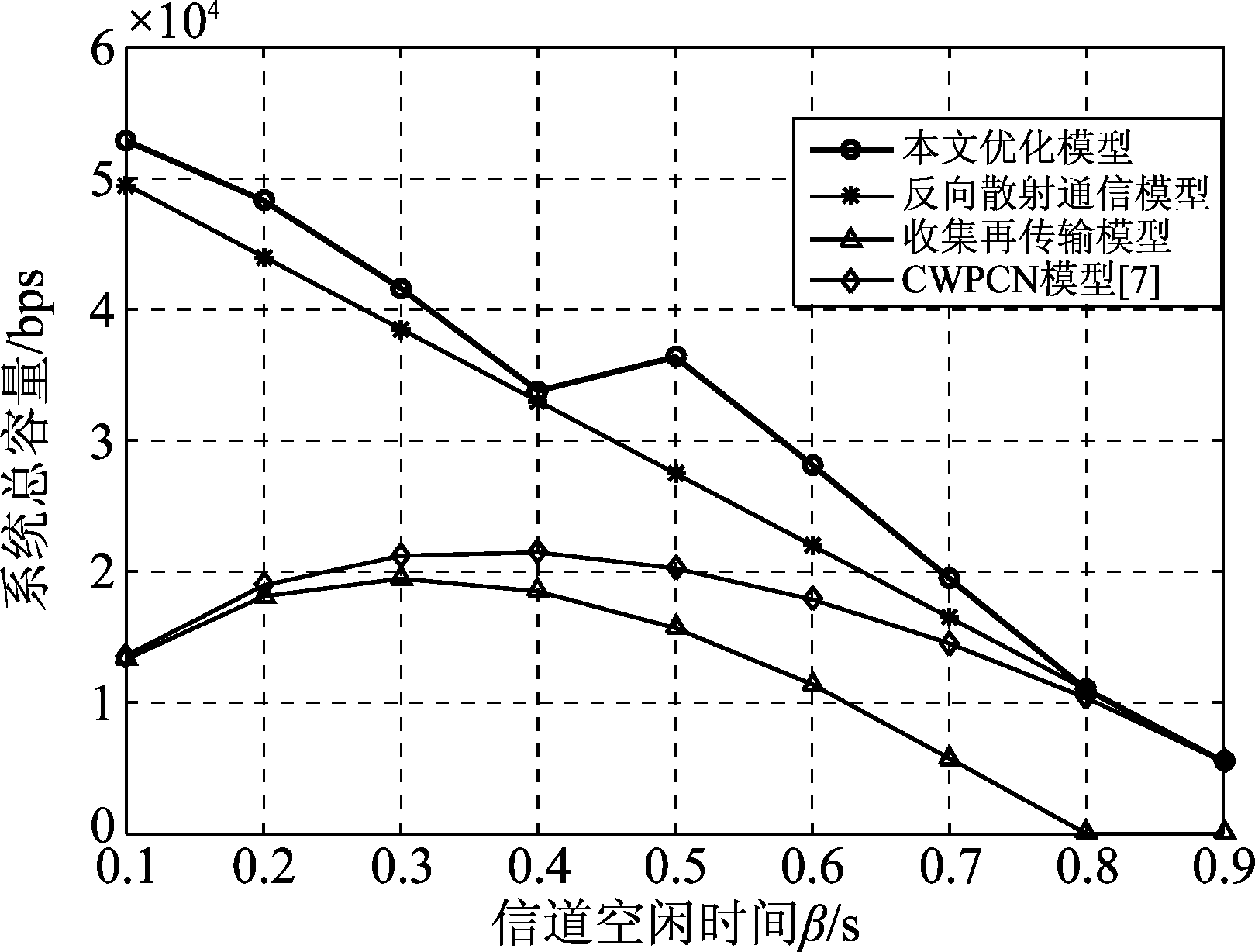
图4 不同信道空闲时间下的系统总容量
Fig.4 The system throughput versus channel idle time
图3研究了在不同信道空闲时间条件下STi最优的BackCom时间。不失一般性,将发射机的传输功率设置为10 kW。当信道空闲时间β从0.1上升到0.4时,两个ST均能驱动HTT协议,满足上文情况3)。这种情况下,ST1的BackCom时间呈递减趋势,ST2的BackCom时间呈递增趋势,这是由于当β增大时,![]() 会减小,又因两个ST的BackCom时间和为1,故ST2的BackCom时间呈递增趋势。当信道空闲时间为0.5至0.8时,收集的能量无法驱动ST1进行HTT协议通信,此时 ST1用全部时间进行BackCom,ST2用全部时间进行HTT协议通信,对应上文情况2)。当β增大到0.8时,ST1、ST2均不能满足HTT协议通信,对应上文情况1),此时ST1用全部时间来进行BackCom,ST2不进行通信。
会减小,又因两个ST的BackCom时间和为1,故ST2的BackCom时间呈递增趋势。当信道空闲时间为0.5至0.8时,收集的能量无法驱动ST1进行HTT协议通信,此时 ST1用全部时间进行BackCom,ST2用全部时间进行HTT协议通信,对应上文情况2)。当β增大到0.8时,ST1、ST2均不能满足HTT协议通信,对应上文情况1),此时ST1用全部时间来进行BackCom,ST2不进行通信。
图4描述了在不同信道空闲时间下各个模型的系统总容量。当信道空闲时间小于0.7时,本文提出模型的总容量始终优于BackCom协议模型,HTT协议模型和协作式CWPCN模型,且当信道空闲时间较低时,本文提出的模型明显优于协作式CWPCN。当信道空闲时间大于0.8时,ST1和ST2均不能进行HTT协议通信,此时提出模型的总容量与只利用BackCom模型容量相同。此时信道空闲时间较大,主用户传输信息时间较少,各个模型次网络的系统容量相差不大,本文优化模型的系统容量略大于协作式CWPCN。
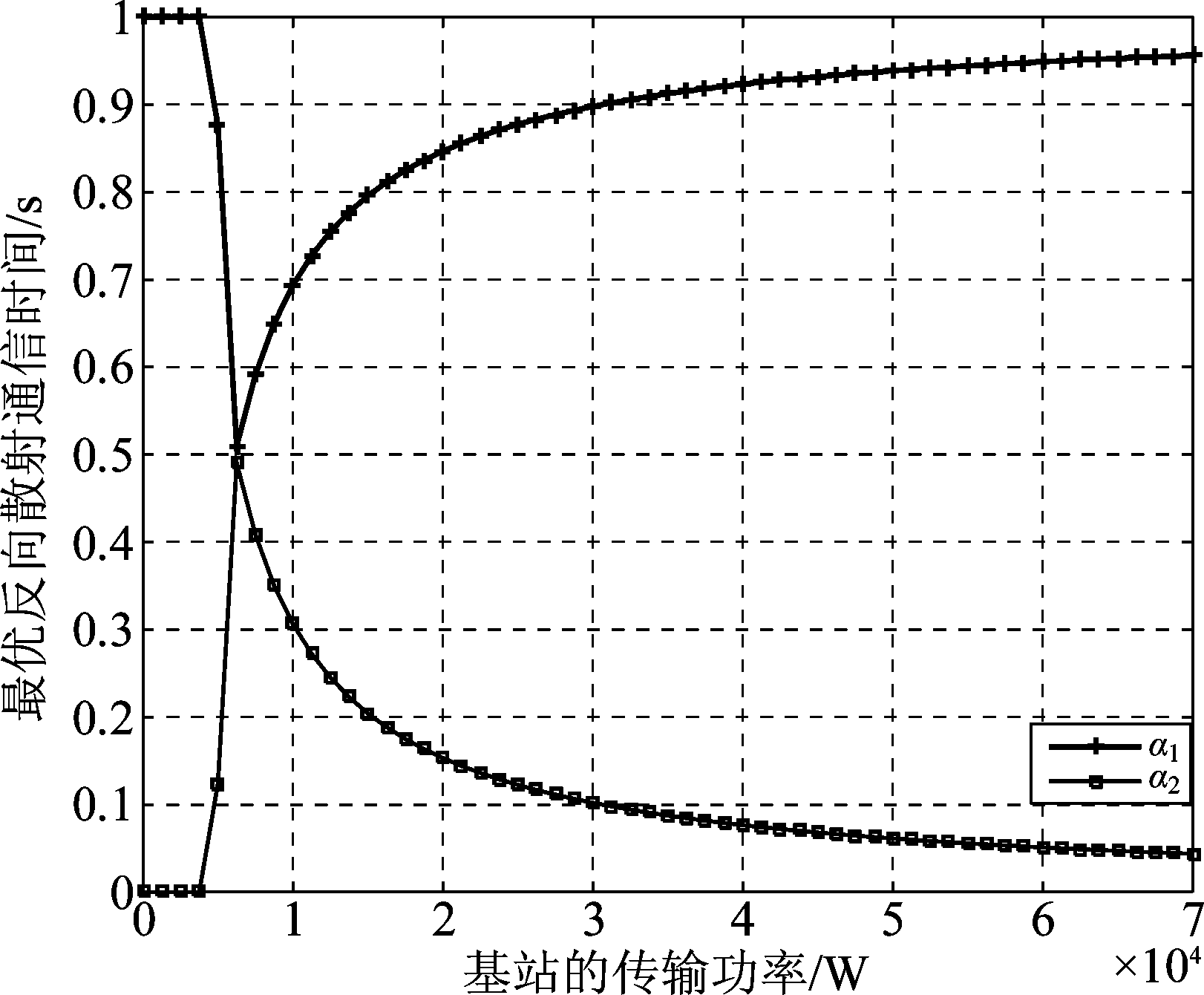
图5 不同传输功率下的最优反向散射通信时间
Fig.5 The optimal time of BackCom versus transmission power
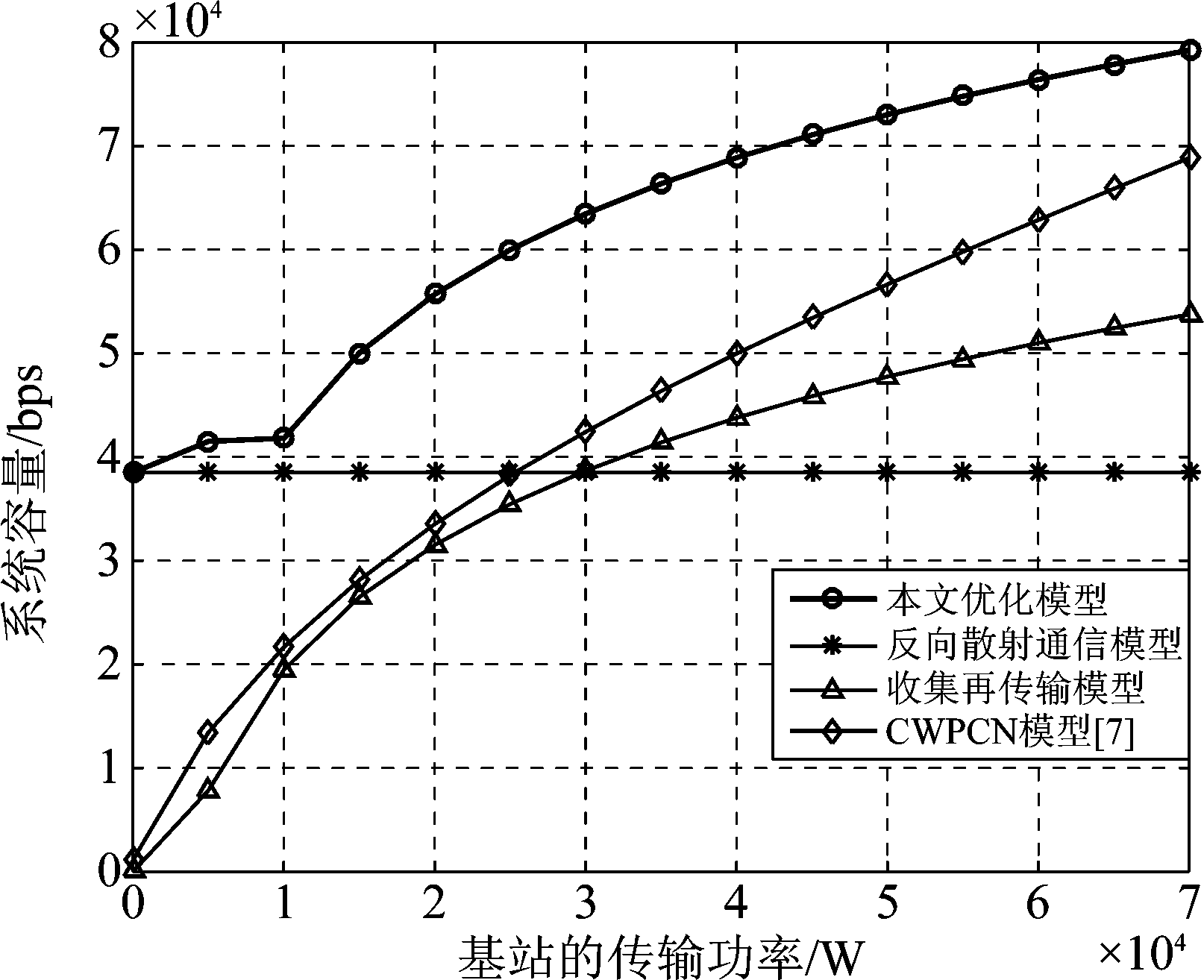
图6 不同传输功率下的系统总容量
Fig.6 The system throughput of versus transmission power
图5说明了基站传输功率对于BackCom时间的影响。设空闲信道时间为β=0.3。从图中可见,当基站的传输功率小于5000 W时,ST1和ST2均不能满足HTT协议通信的条件,对应情况1),此时ST1用全部时间来进行BackCom,而ST2不进行通信。当基站传输功率等于5000 W时,ST1不能满足HTT协议通信的条件,ST2能满足HTT协议通信,对应情况2)。当基站传输功率大于5000 W时,ST1、ST2均满足条件可以进行HTT传输,对应情况3),此时ST1的反向散射时间与传输功率呈单调递增关系,ST2的反向散射时间与传输功率呈单调递减关系。
图6表示了在不同基站传输速率下各个模型的系统总容量。由图6可以看出,本文提出的模型相比于单独利用BackCom和HTT协议性能更佳,同时本文的模型明显优于协作式CWPCN的系统容量。
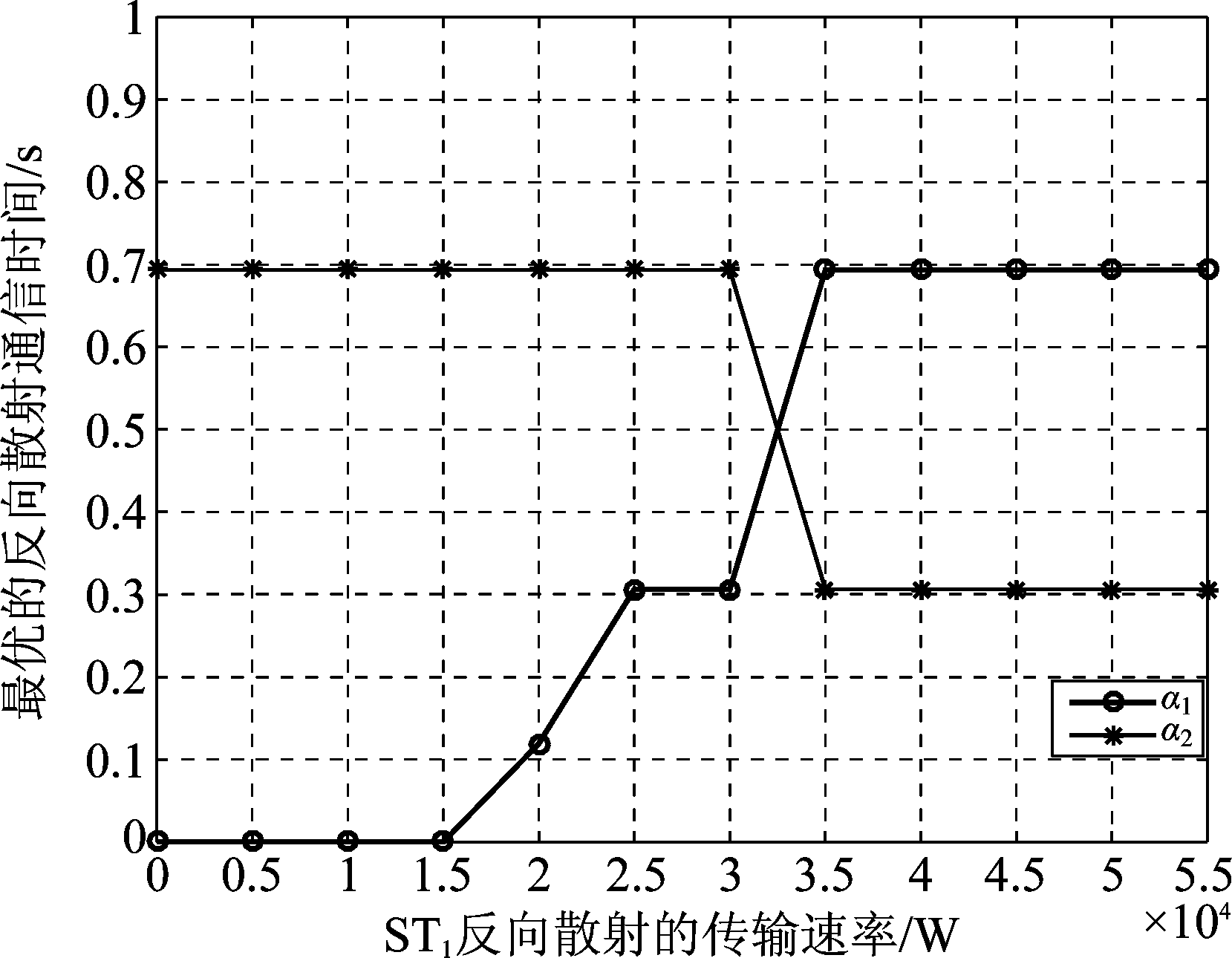
图7 不同ST1反向散射传输速率下的最优反向散射通信时间
Fig.7 The optimal time of BackCom versus ST1’s BackCom transmission rate
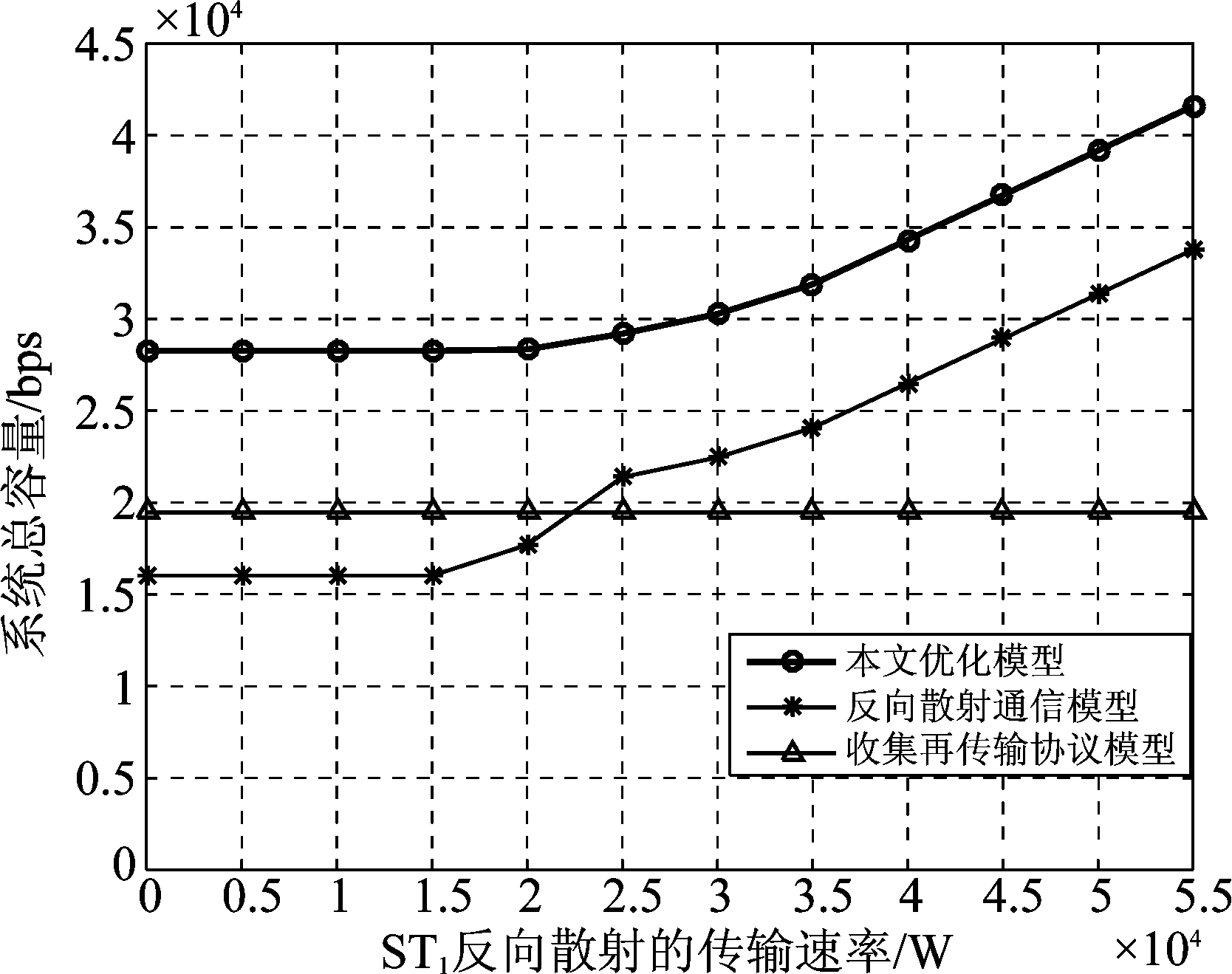
图8 不同ST1反向散射传输速率下的系统总容量
Fig.8 The system throughput of versus ST1’s BackCom transmission rate
图7表示在ST2的BackCom速率固定为33 kbps,ST1的BackCom速率从0至55 kbps变化的情况下,两个ST最优的反向散射时间。设置空闲信道时间为β=0.3,当β固定时,αi的最大上限也固定。从图中看出,无论ST2的反向散射速率如何变化,两个发射机均能满足HTT协议通信,对应情况3)。由于ST2的反向散射速率固定为33 kbps,在ST1 小于33 kbps时,ST1的BackCom时间较短,反之,ST1的BackCom时间变大。在ST1传输速率为25 kW时,α1已达到上限![]() 故α1不再上升。在ST1等于ST2的反向散射速率这种特殊情况下,两个ST的反向散射时间都为0.5,使得总容量达到最大。在ST2反向散射速率为33 kbps,ST1反向散射传输速率从0至55 kbps变化的情况下,图8比较了各个协议模型的系统总容量,图中可以看出,本文提出的模型相比于单独利用BackCom和HTT协议性能更佳。
故α1不再上升。在ST1等于ST2的反向散射速率这种特殊情况下,两个ST的反向散射时间都为0.5,使得总容量达到最大。在ST2反向散射速率为33 kbps,ST1反向散射传输速率从0至55 kbps变化的情况下,图8比较了各个协议模型的系统总容量,图中可以看出,本文提出的模型相比于单独利用BackCom和HTT协议性能更佳。
5 结论
本文研究了反向散射通信辅助的认识无线能量通信网络。在该网络中,含有一个主发射机和两个由次发射机和次接收机组成的次用户对。为了最大化系统总容量,根据收集的能量是否驱动次发射机,分别研究了三种工作场景下的最优时间分配方案。相较于传统的单独利用反射散射通信协议或者单独利用收集再传输协议的工作模式,本文提出的模型具有更大的系统容量。相较于传统的协作式CWPCN,本文提出的模型也具有很好的传输性能。
附录1
R(α1,α2,r1)是一个实值多元函数,该函数的Hessian矩阵为:
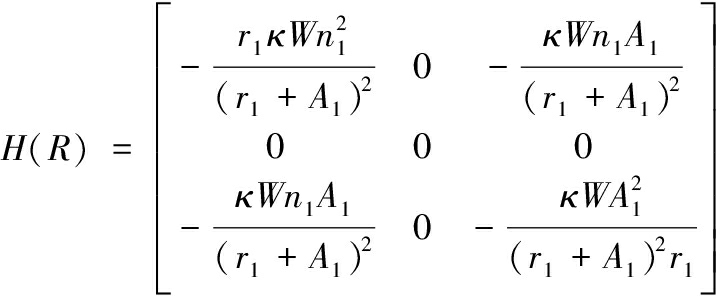
(16)
H(R)是3阶实对称矩阵,对于任意一个非零向量A=(x,y,z),都有
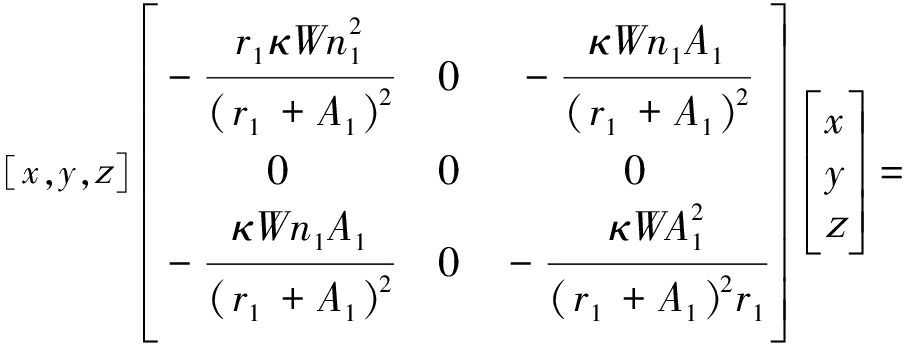
(17)
故该二阶导矩阵为负正定矩阵。因此R(α1,α2,r1)是一个凸优化问题。
由于![]() 为递减函数,
为递减函数,![]() 故R′(r1)>0,因此R(α1,α2,r1)为关于r1的单调递增函数,在最大点处求得最优解,在该问题的最优情况下
故R′(r1)>0,因此R(α1,α2,r1)为关于r1的单调递增函数,在最大点处求得最优解,在该问题的最优情况下![]() 可以得到
可以得到![]()
根据以上公式,引理1可以直接证明出来。
附录2
![]() 故R(α1,α2)是关于α2的单调递增函数,故可得
故R(α1,α2)是关于α2的单调递增函数,故可得![]() 即α2=1-α1,所以R(α1,α2)可以简化为:
即α2=1-α1,所以R(α1,α2)可以简化为:
R(α1)=(1-β)Bb2+α1(1-β)(Bb1-Bb2)+
(18)
对于R(α1)的拉格朗日函数为:
(19)
根据其拉格朗日函数,可以求出α1的极值。当![]() 时,
时,![]() 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() 由此可得该优化问题的最优解为:
由此可得该优化问题的最优解为:
![]()
参考文献
[1] Bi S, Zeng Y, Zhang R. Wireless powered communication networks: An overview[J]. IEEE Wireless Communications, 2016, 23(2): 10-18.
[2] Ju H,Zhang R.Throughput maximization in wireless powered communication networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 418- 428.
[3] Kang X, Ho C K, Sun S. Full-duplex wireless-powered communication network with energy causality[J]. IEEE Transactions on Wireless Communications,2015,14(10): 5539-5551.
[4] Mitola J, Maguire G Q. Cognitive radio: making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18.
[5] 吕斌, 杨震, 林畅. 采用支持向量机的宽带频谱感知算法[J]. 信号处理, 2014, 30(12):1502-1509.
Lv Bin, Yang Zhen, Lin Chang. Broadband Spectrum Sensing Algorithms Using SVM[J]. Journal of Signal Processing, 2014, 30(12):1502-1509. (in Chinese)
[6] Lee S,Zhang R.Cognitive wireless powered network: Spectrum sharing models and throughput maximization[J]. IEEE Transactions on Cognitive Communications and Networking, 2015, 1(3): 335-346.
[7] Yin S, Qu Z, Wang Z, et al. Energy-efficient cooperation in cognitive wireless powered networks[J]. IEEE Communications Letters, 2017, 21(1): 128-131.
[8] Liu V, Parks A, Talla V, et al. Ambient backscatter: wireless communication out of thin air[J]. ACM SIGCOMM Computer Communication Review, 2013, 43(4): 39-50.
[9] Kellogg B, Parks A, Gollakota S, et al. WI-FI backscatter: internet connectivity for RF-powered devices[C]∥ACM Conference on SIGCOMM. ACM, 2015:607- 618.
[10] Lyu B, Yang Z, Gui G, et al. Wireless Powered Communication Networks Assisted by Backscatter Communication[J]. IEEE Access, 2017,PP(99):1-1.
[11] Lyu B, Yang Z, Gui G, et al. Throughput Maximization in Backscatter Assisted Wireless Powered Communication Networks[J]. IEICE Transactions on Fundamentals, 2017,100(6):1-5.
[12] Lyu B, Yang Z, Gui G. Backscatter Assisted Wireless Powered Communication Networks with Non-Orthogonal Multiple Access[J]. IEICE Transactions on Fundamentals, 2017,100(8):1-5.
[13] Hoang D T, Niyato D, Wang P, et al. The tradeoff analysis in RF-powered backscatter cognitive radio networks[J]. arXiv preprint arXiv:1608.01789, 2016.


