1 引言
干扰是移动通信系统面临的主要挑战之一，为解决干扰问题，由Cadambe 和 Jafar等人提出了干扰对齐技术[1-2]，干扰对齐可以在接收端重叠干扰信号，压缩干扰信号所占用的资源，减弱干扰信号对有用信号的影响，能更好的管理干扰，使得有用信号获得更高的和速率。对于全联通K用户MIMO干扰信道，每个发射机配备M根天线与此同时每个接收机也配备M根天线，那么该系统的自由度为
自由度可以视为在干扰网络上无干扰信号的维度，也可以作为评估无线网络潜在吞吐量的关键度量值之一。
在文献[1-2]中，Cadambe和Jafar在时变单输入单输出K用户干扰信道中用干扰对齐技术建立了以自由度为变量的方程，并解出它的解为
这与正交发射方案相比自由度有了很大的提升。然而，在常系数MIMO干扰信道中，只有在少数特殊情况下才能求出它的封闭解[3]。为解决这一问题，在常系数MIMO干扰信道中提出了分布式干扰对齐算法，大部分分布式干扰对齐算法需要全局信道状态信息[4-7]，文献[4]提出了一种分布式干扰对齐算法，它只需要接收端信道的局部状态信息，并将这些接收端信道的局部状态信息反馈到发射端，将这些反馈回来的矩阵组合在一起，使用标量加权，以确定下一组要发送的预编码矩阵。文献[5]分析了在发射端发送相同数据流，接收端用迫零法接收时，特征波束成形算法和迭代算法相比自由度的差异。文献[6]提出了一种新的分布式干扰对齐算法，它适用于部分连接的干扰网络，且在发射端不需要完整的拓扑信息。文献[7]提出了一种新的分布式干扰对齐算法，在发射端和接收端分别设计预编码矩阵和干扰消除矩阵，预编码矩阵和干扰消除矩阵不断变换角色，直到找到合适的预编码矩阵，虽然这样做可以找出合适的预编码矩阵，但是这需要极大的开销。文献[8]没有利用信道的互易性假设，而是将矩阵距离作为目标表达式来重叠接收端的干扰信号空间，在文献[9-10]中提出了收发端联合干扰对齐算法，文献[9]中的收发端联合干扰对齐算法，它不仅使得溢出干扰信号子空间的干扰功率最小，而且使得溢出有用信号子空间的有用功率最小。文献[10]分别以最小干扰泄露(MIL)、最大信干燥比(Max-SINR)和最大总速率(Max-SR)为准则，提出了三种新的收发端联合干扰对齐算法，这三种算法在有总功率限制的条件下，对所有的用户基站对可以实现最优的功率分配。仿真结果表明，文献[10]中提出的三种算法与高信噪比和高维信号相比能获得更令人满意的和速率增益。虽然以上提出的收发端联合干扰对齐算法只需要局部的信道状态信息，但是，此类算法要应用到实际中开销依然很大。为了减小开销，单边干扰对齐算法应运而生[11]。单边干扰对齐算法是指仅仅只需要发射端参与的干扰对齐算法，不需要进行迭代，这样能显著的减小开销。本文在干扰子空间弦距离最小化的单边干扰对齐算法[12]的基础上，将预编码矩阵利用Stiefel流形进行建模求解。
目前干扰对齐预编码矩阵的求解，大多还是基于传统的最优化理论，虽然它们在求解时利用了不同的方法，但是这些方法都是基于传统的优化理论，这样设计出的干扰对齐预编码算法无论在性能还是在复杂度上都很难令人满意，不能发挥出干扰对齐的优势。在文献[13]中，将流形应用到预测量化中，它利用源信号的相关性，与传统无记忆预测量化方案相比可以显著的降低量化码本的大小。在文献[14-15]中，分别将流形应用到预编码预测和信道预测，虽然文献[13-15]都应用到流形，但是都是将流形应用于预测中。文献[16]中提出了一种针对多个主用户和多个次用户的多输入多输出认知网络，先利用编码的方法消除主次用户之间的干扰，在此基础上建立等效模型，在等效模型的基础上以总容量最大化为目标函数设计预编码矩阵，对于预编码矩阵的求解利用了Grassmann流形上的梯度法。然而，在利用Grassmann流形上的梯度法时要使得目标表达式满足酉不变性，本文将Stiefel流形应用到多用户MIMO系统的干扰对齐预编码矩阵设计中，它不仅不需要满足酉不变性，能够简化约束条件将有约束的预编码矩阵优化问题转化为无约束的预编码矩阵优化问题进行求解，同时也继承了单边干扰对齐技术上的优势。本文利用文献[17]给出的Stiefel流形上的一阶偏导，梯度方向表达式，流形测地线轨迹曲线和平行传输切矢量，最终设计出Stiefel流形上的单边干扰对齐最速下降预编码算法和Stiefel流形上的单边干扰对齐共轭梯度预编码算法，通过设计出的算法求出干扰对齐预编码矩阵。仿真结果表明，相比最优化方法[12]优化的单边干扰对齐预编码算法，本文设计出的Stiefel流形上的单边干扰对齐预编码算法的收敛速度更快、系统容量更高。
本文的符号说明：大写和小写粗体分别表示矩阵和列向量。对于任意一般矩阵X,XT、X*、XH分别代表转置，共轭，共轭转置。span(X)代表矩阵X的列空间。IN代表N×N单位阵。Cm×n代表m×n复矩阵。‖.‖和tr(.)分别代表Frobenius范数和矩阵的迹。
2 系统模型
在本文中，我们考虑平坦衰落K用户MIMO复高斯干扰信道，信道模型如图1所示。假设在连续发射数据期间信道系数保持不变。第k个用户分别配备Mk根发射天线和Nk根接收天线，发射信号sk∈Cdk×1(dk≤Mk)，同时传输dk路数据流，预编码矩阵Vk∈CMk×dk(dk≤Mk)，满足
第k个接收器的接收信号为：
(1)
Hk,l∈CNl×Ml为发射器l到接收器k的复信道增益矩阵，Hk,l独立同分布。wk∈CMk×1是均值为0，方差为1的加性高斯白噪声。
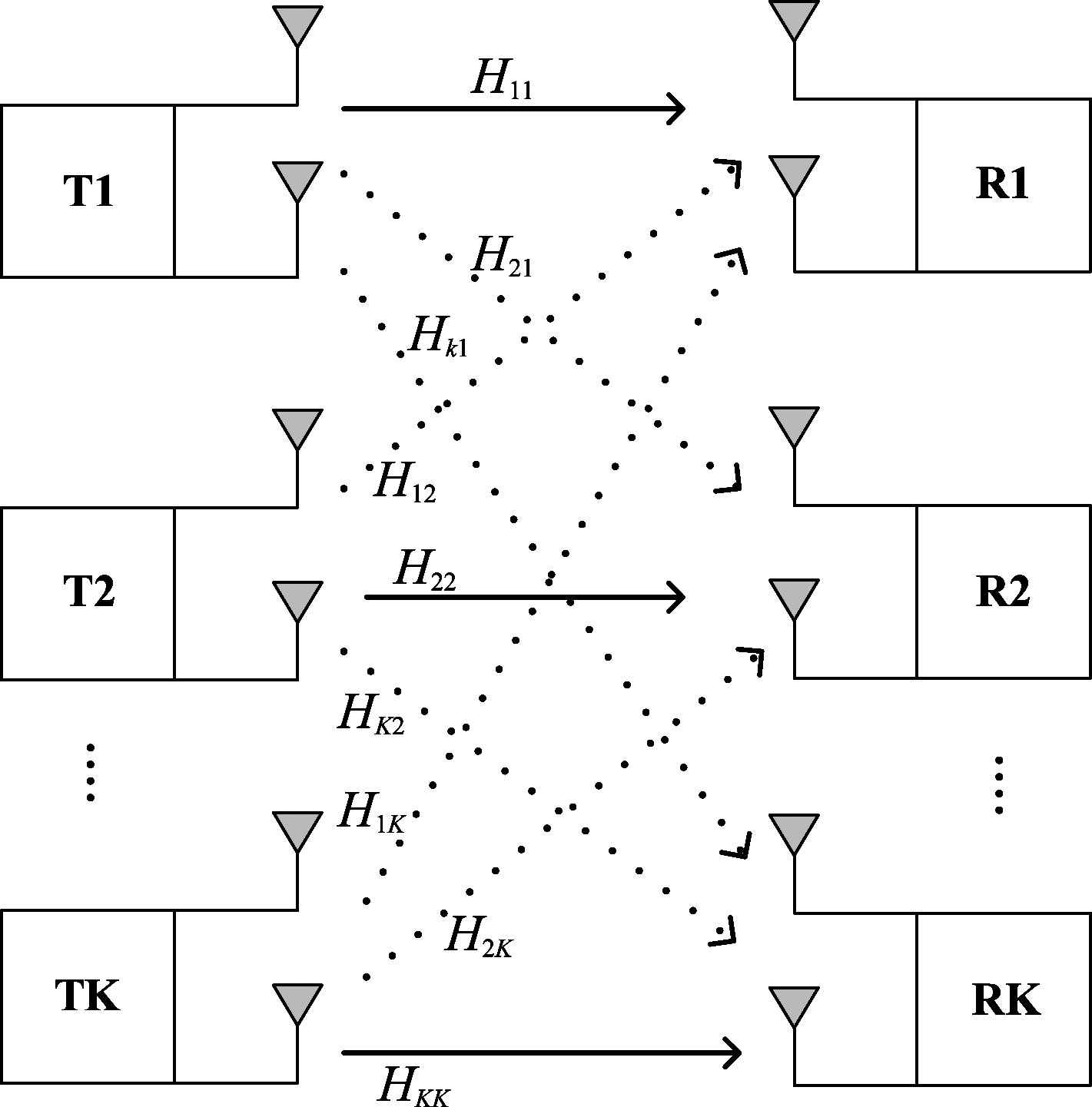
图1 K用户MIMO干扰信道模型
Fig.1 K user MIMO interference channel model
经过干扰消除矩阵Uk∈CMk×dk处理以后，得到的接收信号yk如下所示：
(2)
是接收端k的期望信号，
是接收端k,除了k以外其他用户的干扰。完美干扰对齐的条件为：
(3)
(4)
接下来，每个接收器对准不同的干扰子空间距离，那么不同干扰子空间的总和距离为：
(5)
3 单边干扰对齐预编码
为了方便讨论，假设(Mk,Nk,dk)=(M,N,d),1≤k≤K，干扰信道是对称信道。干扰对齐是在接收端对齐多用户干扰，假设有用信号占据d维空间，那么干扰信号占据(N-d)维空间。为实现干扰对齐，最重要的是要找到一个合适的指标，用以指示不同干扰子空间的相对位置。在文献[12]中，将不同干扰子空间的总和距离作为干扰对齐的指标，当不同的干扰子空间相互重叠时，这时可以认为它们之间的空间距离近似为零，也就可以认为实现了干扰对齐。
S1和S2是维度相同的两个空间，定义S1和S2之间的弦距离为：
(6)
假设S1和S2是接收端干扰信号子空间，如果d(S1,S2)=0，这两个干扰信号对齐。其中Pi是空间Si的正交投影，有：
(7)
其中si是Si空间内任意满秩矩阵，即Si是si的列向量张成的空间，
是si的共轭转置矩阵。用Hk, jVj∀j,k≠j表示发射端j到接受端k的干扰信号所张成的空间。由上式可知，Pk, j为列向量Hk, jVj所张成空间的正交投影：
(8)
接下来为方便描述，我们假设在干扰信道中存在三个收发器，即k=3。在三用户干扰信道中，接收器1将发射器2和发射器3发射的信号视为干扰，接收器2将发射器1和发射器3发射的信号视为干扰，接收器3将发射器1和发射器2发射的信号视为干扰，因此，由以上可知每个接收器的干扰子空间弦距离可以表示为:
接收端1干扰子空间的弦距离为：
P1=‖P12-P13‖
(9)
接收端2干扰子空间的弦距离为：
P2=‖P21-P23‖
(10)
接收端3干扰子空间的弦距离为：
P3=‖P31-P32‖
(11)
记
表示接收端干扰子空间的弦距离之和，因此得出需要优化表达式为：
(12)
在需要优化的干扰子空间弦距离给出之前，先给出一些正交投影矩阵的知识，设X的列向量所张成空间的正交投影为A，由文献[18]知，A具有如下的一些性质：
AH=A
(13)
A×A=A
(14)
tr(In)=n
(15)
由于
则T可以表示为：
T=tr{(P12-P13)(P12-P13)H}+tr{(P21-P23)
(P21-P23)H}+tr{(P31-P32)(P31-P32)H}=
(16)
又因为tr(Pi, j)=d，1≤i, j≤3，d为发射端发射的空间数据流，经过转换后，T可表示为：
T=6d-2tr(P12P13)-2tr(P21P23)-2tr(P31P32)
(17)
假设f=tr(P12P13)+tr(P21P23)+tr(P31P32)，则干扰子空间弦距离之和T最小化等价于f最大化，即：
max f=tr(P12P13)+tr(P21P23)+tr(P31P32)
(18)
4 Stiefel流形上的单边干扰对齐方案
4.1 Stiefel流形的基本概念
Stiefel流形[19]是嵌入在欧氏空间里的微分流形，它是一个紧凑流形，可定义为满足以下条件的矩阵集合：
St(n,p)={X∈Cm×p;XHX=Ip}
(19)
Stiefel流形的维度为：
(20)
由前文可知，本文需要设计预编码矩阵Vk，且
满足Stiefel流形上的约束条件，因此可以将预编码矩阵在Stiefel上建模，又由于(18)是可微函数，从而可以设计出Stiefel流形上的预编码算法。由文献[17]可知，Stiefel流形上的最陡下降沿表达式为：
Zj=Gj-YjGjYj
(21)
其中，Gj为目标表达式在Yj处的梯度即一阶导数。要使得代价函数的自变量始终在流形内沿着最陡下降沿方向移动，那么它必须遵循某种轨迹曲线运动，这种轨迹曲线就是流形的测地线[20]。它表示在局部范围内长度最短的曲线，对于Stiefel流形，可以将(21)做SVD分解：
(22)
其中Uj和Vj分别为左右酉矩阵，Σj为对角阵，假设每次迭代的步长为t，由文献[17]可得出自变量Yj沿测地线的迭代轨迹为：
(23)
由前文可知，本文需要设计预编码矩阵Vk，且满足Stiefel流形上的约束条件，可以将预编码矩阵在Stiefel上建模，设计出Stiefel流形上的预编码算法。
4.2 Stiefel流形上的最速下降干扰对齐算法
前文得到了代价函数f的表达式，将(8)带入代价函数(18)中，对代价函数f分别关于
进行微分运算，由文献[18]可以求得
的具体表达式如下所示：
令HH21=(H21V1)HH21V1；HH31=(H31V1)HH31V1
(24)
令HH12=(H12V2)HH12V2；HH32=(H32V2)HH32V2
(25)
令HH13=(H13V3)HH13V3；HH23=(H23V3)HH23V3
(26)
假设在对称3用户MIMO干扰信道中，发射端和接收端分别配备M根天线，每个发射端发射d个数据流，可以设计出Stiefel流形上的最速下降干扰对齐算法，Stiefel流形上的最速下降干扰对齐算法的具体设计步骤如表1所示。
表1 Stiefel流形上的最速下降干扰对齐算法
Tab.1 Steepest descent interference alignment algorithm on Stiefel manifold
算法设计流程:1.设定任意的预编码矩阵Vi,满足VHiVi=Id,i=1,…,3计算T。2.当T≥ε(ε为任意小的值)时,i=1,…,3,计算式(18)中的f,否则Vi为所求预编码矩阵,执行步骤7。3.计算式(18)中的f在V∗i处的导数Gi=∂f∂V∗i,切向量Zi=Gi-ViGHiVi。4.令H=Zi,在Vi处沿着方向H发出的测地线轨迹曲线为:Vi(t)=ViM(t)+QN(t),M(t)N(t)()=exptA-RTR0()I0(),A=VHiH,Q和R分别为矩阵(I-ViVHi)H的QR分解所得到的矩阵。5.对更新得到的预编码矩阵Vi(t),使得Vi=Vi(t),计算T。6.重复步骤2～5,直到T<ε,即收敛,得到Vi,i=1,…,3。7.以下步骤用于计算接收滤波器矩阵Ui,i=1,…,3,计算矩阵Hk,jVj,i,j=1,…,3,i≠j的SVD分解。[Xi,Li,Mi]=SVD(Hk,jVj) i,j=1,…,3,i≠j8.接收滤波器矩阵为U∗i=X∗li‖X∗li‖F。
4.3 Stiefel流形上的共轭梯度干扰对齐算法
当代价函数需要利用Stiefel流形上的共轭梯度算法进行求解时，不仅要利用以上介绍的关于Stiefel流形的梯度沿方向，沿测地线运动的轨迹曲线，还需要利用到沿着测地线方向的平行传输方向。由文献[17]可知，在Stiefel流形上，沿着测地线方向不能得出平行传输方向的简单通式，但是，由于测地线的切方向是平行的，可以得出沿着测地线平行传输方向的简单通式为[17]：τHi=HiM(ti)-ViRTN(ti)，其中，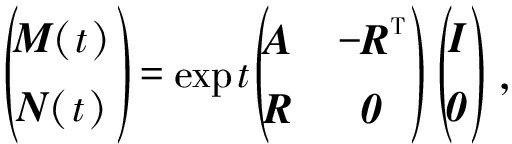
为在Vi处的导数，R为矩阵
的QR分解中的R，Hi为搜索方向，求出平行传输方向的通式后，可以设计出Stiefel流形上的共轭梯度干扰对齐算法，Stiefel流形上的共轭梯度干扰对齐算法的具体设计步骤如表2所示。
表2 Stiefel流形上的共轭梯度干扰对齐算法
Tab.2 Conjugate gradient interference alignment algorithm on Stiefel manifold
算法设计流程:1.设定任意的预编码矩阵Vi,满足VHiVi=Id,i=1,…,3计算T。2.计算式(18)中f在起始V∗0处的导数和切向量分别为G0=∂f∂V∗0、Z0=G0-V0GH0V0,初始平行传输方向H0=-Z0。3.当T≥ε(ε为任意小的值)时,i=1,…,3,由测地线的轨迹曲线为Vi(t)=ViM(t)+QN(t),其中Vi(t)为Vi沿测地线的下一个更新点,M(t)N(t)()=exptA-RTR0()I0(),A=VHiH,Q和R分别为矩阵(I-ViVHi)H的QR分解中的Q和R,Hi为搜索方向。否则Vi为所求预编码矩阵,执行步骤8。4.计算式(18)中的f在V∗i处的导数Gi=∂f∂V∗i,求出切向量Zi=Gi-ViGHiVi,在Vi(t)处的平行传输切向量为:葳Hi=HiM(ti)-ViRTN(ti),Hi为上一次的搜索方向,M(t),N(t)和R为经过第3步更新后的M(t),N(t)和R。5.计算新的搜索方向:Hi+1=-Zi+γi葳Hi,其中,γi=〈Zi+1-葳Zi,Zi+1〉〈Zi,Zi〉,令葳Zi=0,可以得到Fletcher-Reeves方程γi=〈Zi+1,Zi+1〉〈Zi,Zi〉,[Δ1,Δ2]=tr ΔT1Δ2-12ΔT1VVHΔ2()。6.对更新得到的预编码矩阵Vi(t),使得Vi=Vi(t),Hi=Hi+1,计算T。7.重复步骤3～6,直到T<ε,即收敛,得到Vi,i=1,…,3。8.以下步骤用于计算接收滤波器矩阵Ui,i=1,…,3,计算矩阵Hk,jVj,i,j=1,…,3,i≠j的SVD分解。[Xi,Li,Mi]=SVD(Hk,jVj),i,j=1,…,3,i≠j9.接收滤波器矩阵为U∗i=X∗li‖X∗li‖F。
5 数值仿真和收敛性及复杂度分析
5.1 数值仿真
这一部分我们给出仿真结果，通过仿真结果比较了本文提出的Stiefel流形上的共轭梯度算法、Stiefel流形上的最速下降算法与最速下降算法的和速率与收敛性。和速率的计算公式可以表示为:
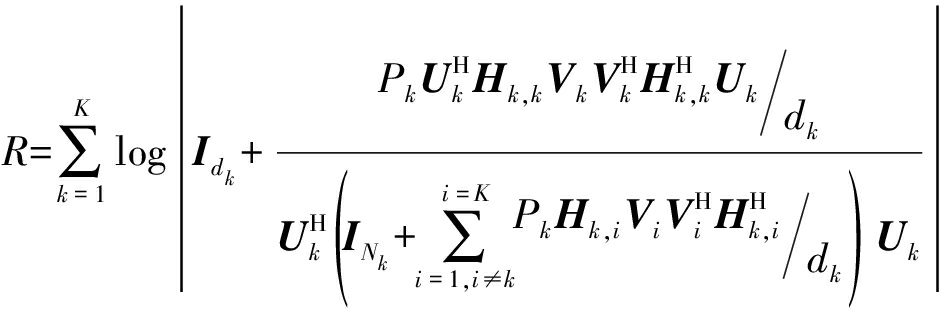
(27)
我们考虑系统(M,N,d)K，发射端和接收端分别配备K个发射器和接收器，每个发射器和接收器分别配备M根天线和N根天线，每个用户期望发送d个数据流。每个用户对有完全相同的发射功率，即Pk=P, k=1,…,K。在接收端对噪声进行归一化处理后，功率P就代表SNR，所有信道之间相互独立，在本文提供的所有算法中，设置步长t为0.05。
在图2和图3中， 我们画出了在(4×4,2)3和(6×8,2)4干扰信道中三种算法的代价函数和迭代次数的收敛曲线，式(20)中的f为代价函数，从仿真结果可以看出，Stiefel流形上的共轭梯度算法收敛速度最快，Stiefel流形上的最速下降算法次之，普通的最速下降算法的收敛速度最慢，在Stiefel流形上建模求最优化问题的收敛性比普通优化算法的收敛性更好。
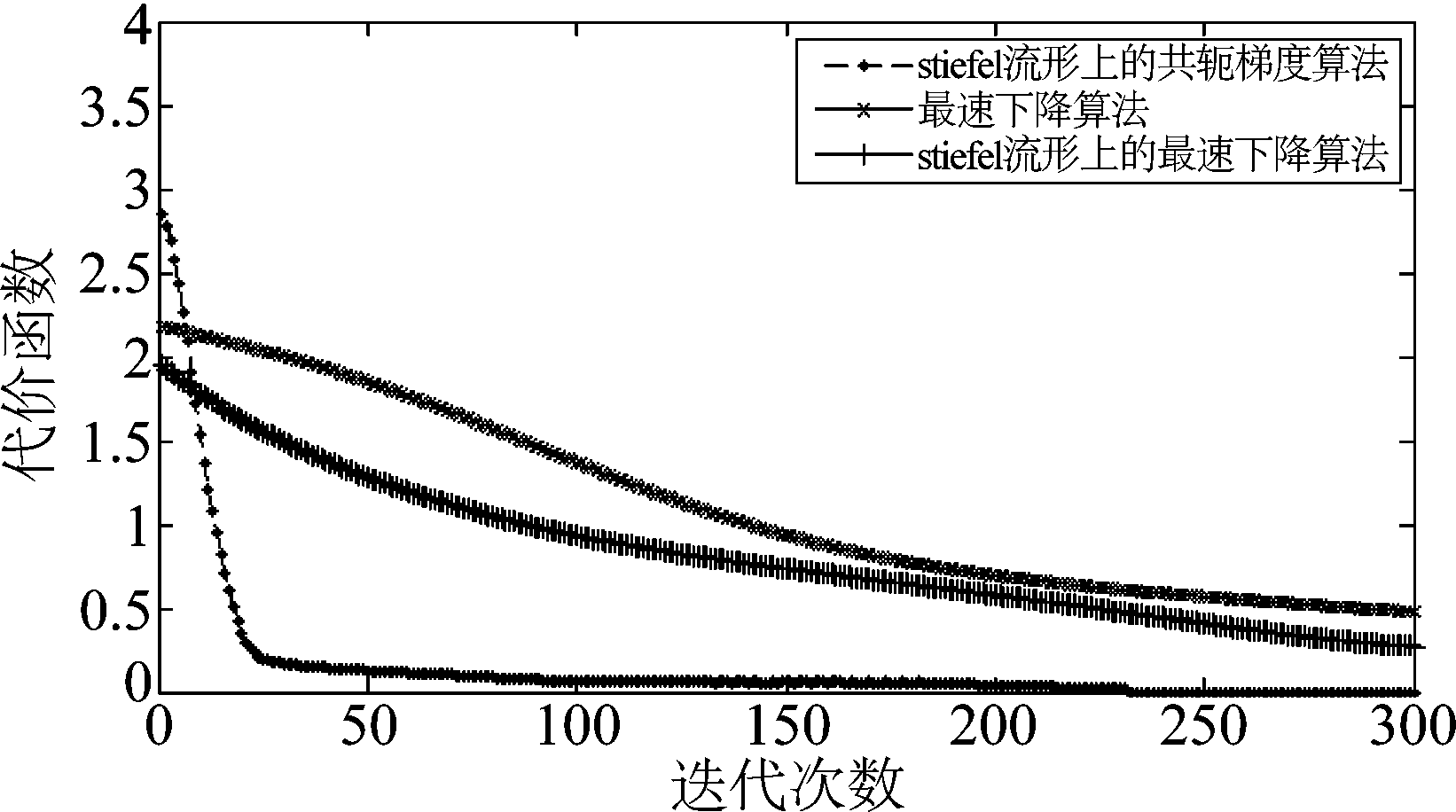
图2 在(4×4,2)3干扰信道中的收敛曲线
Fig.2 Convergence curve in interference channel (4×4,2)3
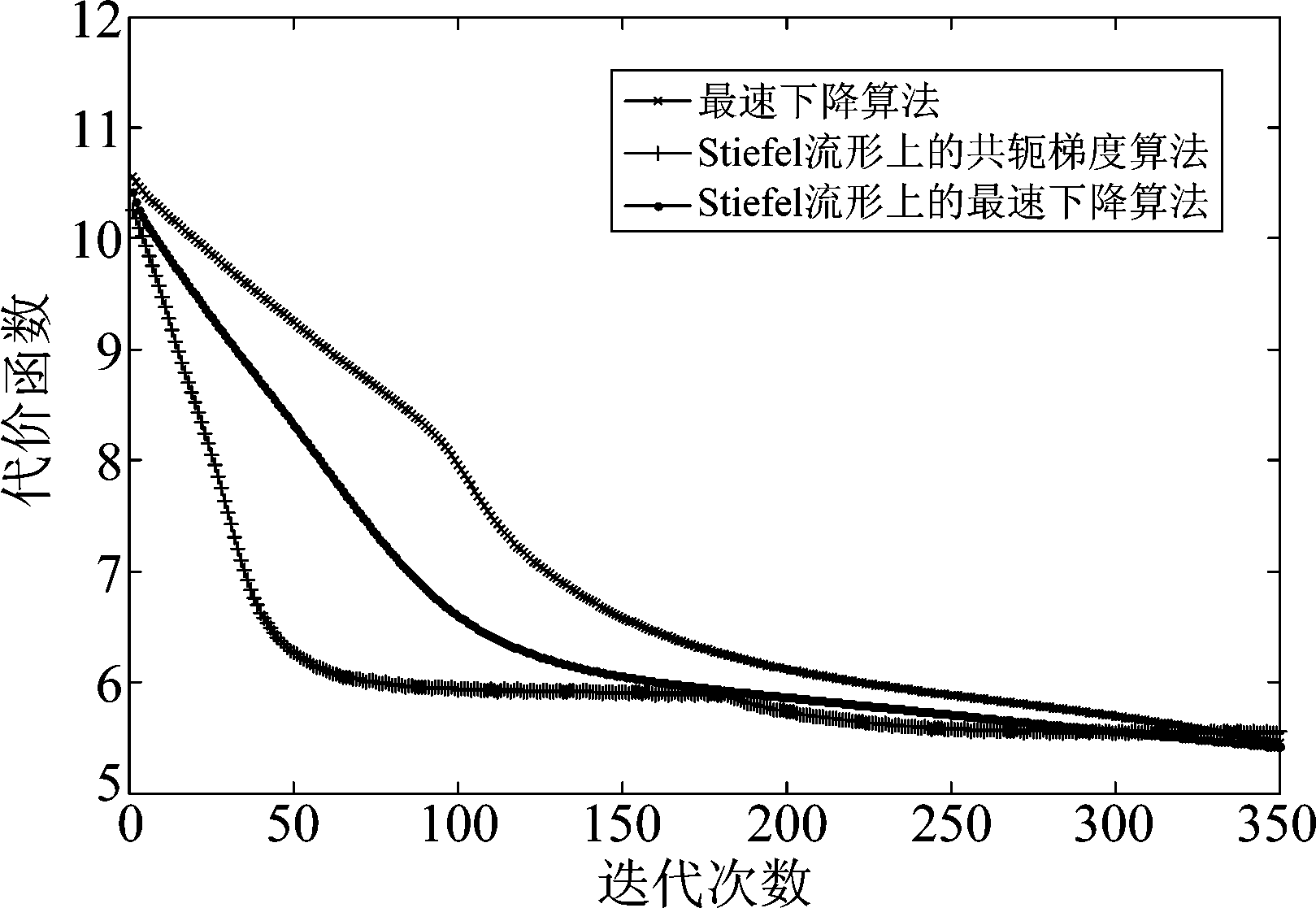
图3 在(6×8,2)4干扰信道中的收敛曲线
Fig.3 Convergence curve in interference channel(6×8,2)4
在图4和图5中，我们分别画出了在(4×4,2)3和(6×6,2)4干扰信道中四种算法的和速率曲线，从图4和图5中可以看出，在相同SNR条件下，Stiefel流形上的共轭梯度算法的和速率最大，同时，随着用户数的增加和速率也在不断的增加。
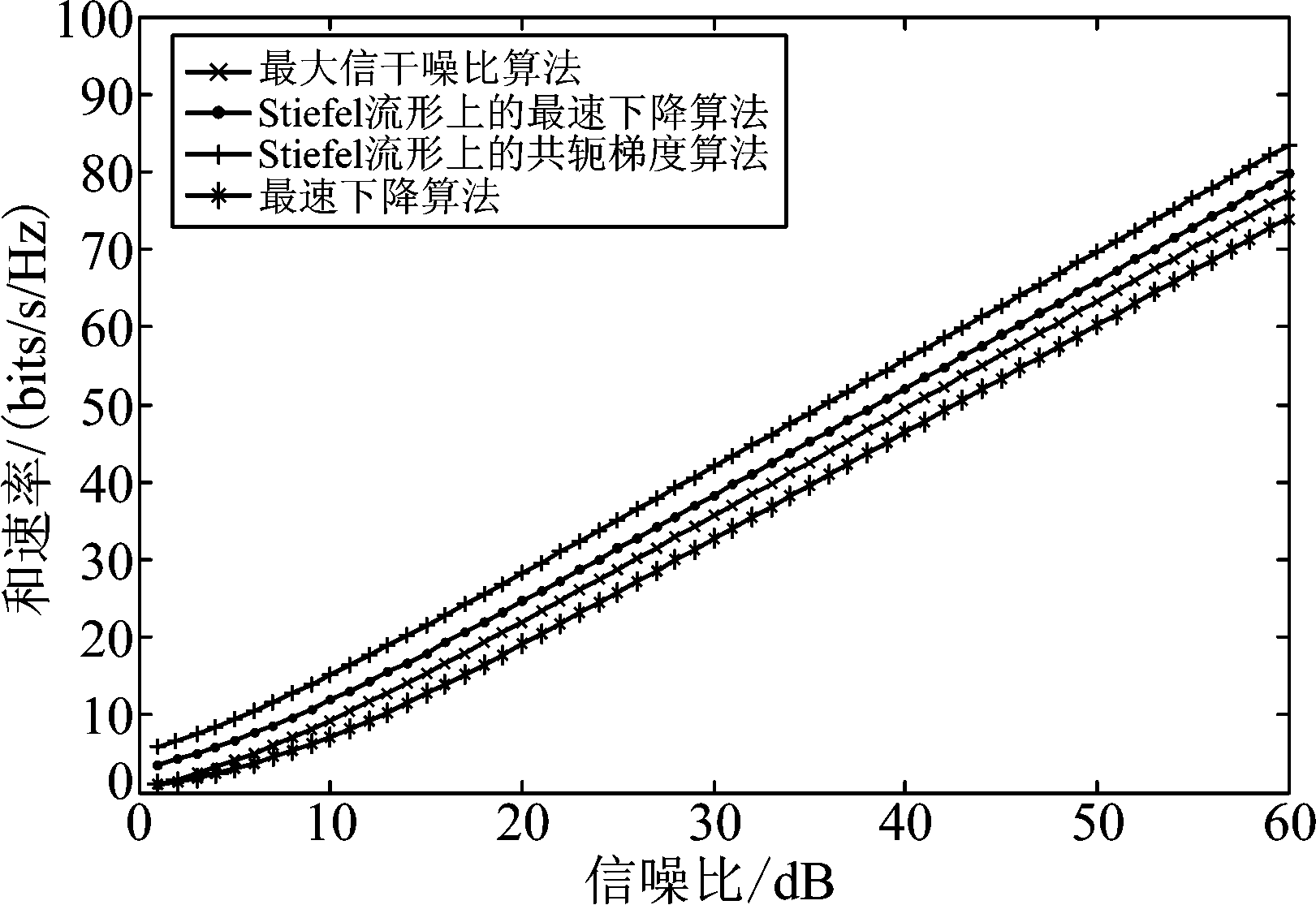
图4 在(4×4,2)3干扰信道中的和速率曲线
Fig.4 Sum rate curve in interference channel (4×4,2)3
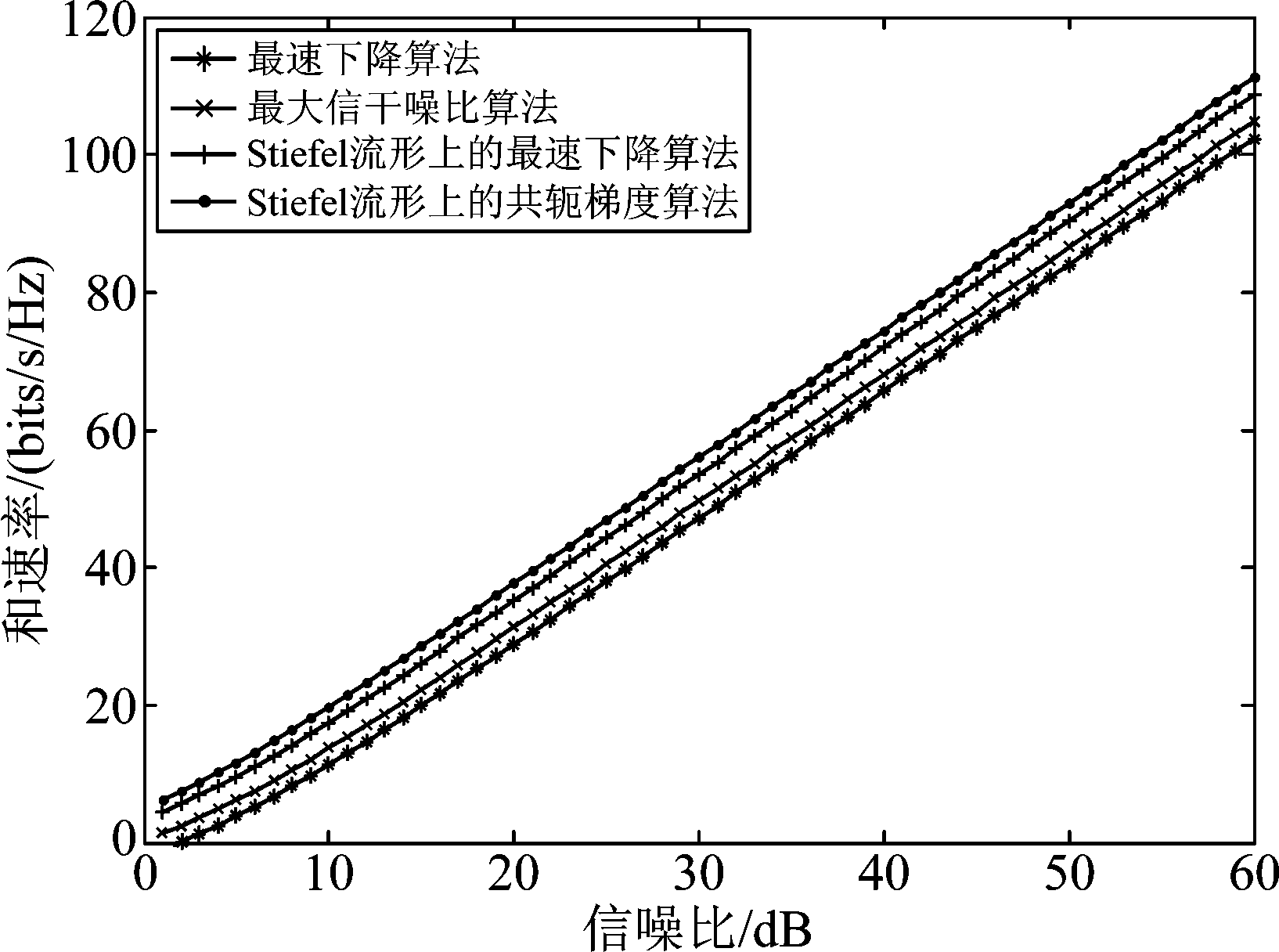
图5 在(6×6,2)4干扰信道中四种算法的和速率曲线
Fig.5 Sum rate curve in interference channel (6×6,2)4
5.2 收敛性及复杂度分析
由以上图2和图3的仿真可以看出，Stiefel流形上的干扰对齐预编码算法的收敛性要好于优化理论条件下的干扰对齐预编码算法。这是因为优化理论条件下的干扰对齐预编码算法的维度为：dim(Cn×p)=np，而Stiefel流形上的干扰对齐预编码算法的维度为：
后者的维度要小于前者的维度，因此后者解空间的搜素维度小于前者解空间的搜索维度，从而，在Stiefel流形上的干扰对齐预编码算法的收敛速度要快于优化理论条件下的干扰对齐预编码算法。
迭代算法总的复杂度是由迭代次数和每次迭代复杂度的乘积共同决定的，由文献[21]可知，Stiefel流形上的复杂度和一般优化理论的算法复杂度，都和矩阵的维度M成渐进3次方关系。由以上的分析可知，Stiefel流形上的干扰对齐预编码算法的迭代复杂度要远远小于一般优化理论的干扰对齐预编码算法且Stiefel流形上的干扰对齐预编码算法的迭代次数要小于或者近似等于一般优化理论的干扰对齐预编码算法，所以Stiefel流形上的干扰对齐预编码算法的复杂度要低。
6 结论
本文由单边干扰对齐技术设计出了Stiefel流形上的单边干扰对齐预编码算法，利用了干扰子空间的弦距离，将干扰子空间的弦距离之和是否为零作为接收端干扰子空间是否对齐的度量标准，并将子空间弦距离用函数表达式的形式给出，该函数表达式一阶可导，这样干扰对齐条件下的预编码矩阵求解问题，转化为如何利用最优化的方法求解预编码矩阵问题。一般求最优化问题都是利用最优化知识进行求解，然而本文将Stiefel流形模型应用于预编码矩阵的求解，这样可以将有约束的预编码矩阵求解问题转化为无约束的预编码矩阵求解。从仿真结果可以看出，Stiefel流形上的共轭梯度算法与Stiefel流形上的最速下降算法和最速下降算法相比和速率提高了且收敛速度加快了。
参考文献
[1] Cadambe V R, Jafar S A. Interference alignment and degrees of freedom of the K-user interference channel[J]. IEEE Transactions on Information Theory, 2008, 54(8):3425-3441.
[2] Jafar S A, Fakhereddin M J. Degrees of freedom for the MIMO interference channel[C]∥IEEE International Symposium on Information Theory, IEEE, 2006:1452-1456.
[3] Yetis C M, Gou T, Jafar S A, et al. On feasibility of interference alignment in MIMO interference networks[J]. IEEE Transactions on Signal Processing, 2009, 58(9):4771- 4782.
[4] Colman G W K, Muruganathan S D, Willink T J. Distributed interference alignment for mobile MIMO systems based on local CSI[J]. Communications Letters IEEE, 2014, 18(7):1206-1209.
[5] Xu Tianyi, Xia Xianggen. A diversity analysis for distributed interference alignment using the max-SINR algorithm[J]. IEEE Transactions on Information Theory, 2014, 60(3):1857-1868.
[6] Farka P, Staron M, Schindler F. Distributed interference alignment in partially connected networks without preliminary topological knowledge[C]∥IEEE International Conference on Future Internet of Things and Cloud Workshops, IEEE, 2016:103-108.
[7] Gomadam K, Cadambe V R, Jafar S A. Approaching the capacity of wireless networks through distributed interference alignment[C]∥IEEE Global Telecommunications Conference, IEEE, 2008:1- 6.
[8] Peters S W, Heath R W. Interference alignment via alternating minimization[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE Computer Society, 2009:2445-2448.
[9] Raj Kumar K, Xue Feng. An iterative algorithm for joint signal and interference alignment[C]∥IEEE International Symposium on Information Theory Proceedings, IEEE, 2010:2293-2297.
[10] Panahi F H, Ohtsuki T, Jiang Wenjie, et al. Joint interference alignment and power allocation for multi-user MIMO interference channels under perfect and imperfect CSI[J]. IEEE Transactions on Green Communications and Networking，2017:131-144.
[11] Ghauch H G, Papadias C B. Interference Alignment: A one-sided approach[C]∥Global Telecommunications Conference, IEEE, 2011:1-5.
[12] Wang Chao, Zhang Bohan, Zhang Xiaodan, et al. Linear precoder designs for interference alignment in constant MIMO interference channels[C]∥Wireless Communications and NETWORKING Conference, IEEE, 2013:3573-3578.
[13] Schwarz S, Rupp M. Predictive quantization on the Stiefel manifold[J]. IEEE Signal Processing Letters, 2015, 22(2):234-238.
[14] Li Ting, Li Fei, Li Chunguo. Manifold-based predictive precoding for the time-varying channel using differential geometry[J]. Wireless Networks, 2016, 22(8): 2773-2783.
[15] 李汀. Grassmannian流形上基于高分辨率动态聚焦码本的MIMO信道预测[J]. 信号处理, 2016, 32(6):724-732.
Li Ting. MIMO channel prediction based on the dynamic focused codebook with high resolution on the Grassmannian manifold[J]. Journal of Signal Precessing, 2016, 32(6):724-732. (in Chinese)
[16] 聂俊美, 谢显中, 张森林,等. 多用户认知网络中基于Grassmann流形梯度法的干扰对齐算法[J]. 信号处理, 2016, 32(3):362-369.
Nie Junmei, Xie Xianzhong, Zhang Senlin, et al. Multi-user interference alignment using gradient method on Grassmann manifold in cognitive radio networks[J]. Journal of Signal Precessing, 2016, 32(3):362-369.(in Chinese)
[17] Edelman A, Arias T A, Smith S T. The geometry of algorithms with orthogonality constraints[J]. Siam Journal on Matrix Analysis & Applications, 1998, 20(2):303-353.
[18] 张贤达. 矩阵分析与应用[M]. 北京：清华大学出版社, 2013.
Zhang Xianda. Matrix analysis and applications[M]. Beijing: Tsinghua University Press, 2013. (in Chinese)
[19] Absil P A, Mahony R, Sepulchre R. Optimization algorithms on matrix manifolds[M]. Princeton University Press, 2009.
[20] Yilmaz S A, Kerimoglu O S, Pekin A T, et al. On gradient adaptation with unit-norm constraints[J]. Signal Processing IEEE Transactions on, 1999, 48(6):1843-1847.
[21] 王存祥, 邱玲. 协作多点传输中一种基于特征子信道的干扰对齐预编码矩阵优化方案[J]. 信号处理, 2011, 27(3):395-399.
Wang Cunxiang,Qiu Ling.An optimized precoding scheme based on eigen-channel in interference alignment for coordinated multi-point transmission systems[J]. Signal Processing, 2011, 27(3):395-399.(in Chinese)
