1 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种基于宽带信号匹配滤波及回波信号相干累积的二维高分辨率成像雷达,由于其具备全天时、全天候获取数据的能力,因而成为军事侦察、资源监视等的重要手段,是现代雷达技术的重要发展方向之一[1]。变化检测作为SAR图像的一种重要应用,目的是通过SAR数据研究固定场景在一段时间内的变化情况,在军事领域常常被用来进行战场态势感知、军事目标侦察以及打击效果评估[2]。在民用领域,SAR图像变化检测在森林环境监测、灾情估计、城市变迁及农作物生长状况监测等领域也同样起到了重要作用。
基于差异图的检测方法是目前SAR图像变化检测中应用较为广泛的方法,即首先对不同时相的图像进行逐像素比较,再采用某种方法对像素点差异程度进行度量,并将其映射到灰度上,生成差异图。最后对差异图进行分割,即可得到结果二值图,区别变化区域与未变化区域[3]。
基于差异图的变化检测方法性能主要受SAR图像固有的相干斑噪声影响,研究人员已经证明其为服从瑞利分布的乘性随机噪声[1]。经典的差值法与比值法获取差异图无法有效抑制乘性噪声,而对数比(Log-Ratio, LR)算子计算过程简单,将乘性相干斑噪声转换为加性噪声,并且对差异图像素灰度级进行了非线性变换,抑制了差异图中畸变点的灰度,是目前较为常用的差异图获取方法。差异图生成后,需要对其进行分析,分割变化区域与未变化区域,模糊C均值聚类(Fuzzy C-Means Clustering, FCM)方法作为经典的聚类分割方法被广泛应用在这一环节中[4]。但由于FCM方法并未考虑局部信息与邻域信息,对噪声较为敏感,易产生大量虚警[5]。针对这种情况,研究者们提出了大量改进算法,包括空间约束FCM(Fuzzy C-Mean with Spatial constraints, FCMS)及快速广义FCM(Fast Generalized Fuzzy C-Mean, FGFCM)等,然而这些算法依赖人工参数,并不适用于快速无监督的SAR图像变换检测。局部信息FCM算法(Fuzzy Local Information C-Means Clustering, FLICM)在目标函数中加入了一个模糊因子,体现邻域窗内像素集合的同质程度[6],引入了邻域信息。相对于传统的FCM算法,FLICM对于含有噪声图像的分割效果有了极大地改善,且无需人工设置参数,因而得到了广泛的使用。综上所述,基于LR差异图与FLICM的变化检测方法有效抑制了相干斑噪声的影响,提高了结果精度。但是对于灰度变化程度较弱的场景以及变化细节区域,该方法依然存在一些不足:
(1)LR差异图依然存在加性噪声,灰度分布集中在低灰度区域,弱变化区域易被湮没。
(2)对邻域信息的利用不足,使FLICM算法中当邻域窗移动至边缘区域时,变化区域细节信息易被作为噪点平抑,从而造成漏警[7]。
针对以上问题,本文提出了一种利用二进小波增强和边缘局部信息FCM的模糊聚类方法,首先利用二进小波对LR差异图进行变换,通过不同尺度上的小波系数间的相关性来区分噪声和真实信号,在此基础上自适应选定阈值完成差异图增强;利用指数加权均值比(Ratio of Exponentially Weighted Average, ROEWA)算子对差异图进行边缘信息提取,修正局部信息FCM算法中邻域窗内像素点权值,使邻域窗滑动至变化区域边缘部分时能够对噪声切向平抑,对差异图完成分割得到变化检测结果。实验结果表明,本文方法能够有效抑制相干斑噪声的影响,同时对变化区域的细节保持效果较好。
2 基于二进小波的差异图增强
LR差异图由于灰度的非线性变化在视觉上偏暗,并且由于在SAR图像变化检测中,变化区域面积一般占比较小,因此差异图灰度分布往往较为集中[8]。图1为利用实测SAR图像获得的LR差异图及其灰度直方图,可以看出其受噪声影响较为严重,变化区域灰度较低,轮廓不明显,在灰度直方图上体现为在低灰度区域有较高的峰,并向高灰度区域陡变。

图1 LR差异图及直方图
Fig.1 LR different image and gray histogram
LR差异图对比度较弱,像素主要集中在低灰度区域的特点为进一步的聚类分割造成了较大的困难。对于这一问题,可以利用图像增强算法对差异图进行处理,增强数据的可分性。
考虑到LR差异图依然受噪声影响,传统的灰度直方图均衡和空域滤波方法在处理时往往效果不佳[9]。本文采用二进小波对LR差异图进行分解,利用不同尺度下小波系数的相关性区别噪声和变化细节信息,达到自适应增强的效果,在保留变化细节的同时抑制噪声。设LR差异图为
I′=I+n
(1)
其中I为真实差异图,n为加性噪声。对其进行k级二进小波分解,获得低频分量I′k与一系列高频子带![]() 为分解层数,d表示子带方向。小波分解后,图像细节与噪声往往都对应在高频子带中,如何对其进行区分是增强算法的关键[10]。
为分解层数,d表示子带方向。小波分解后,图像细节与噪声往往都对应在高频子带中,如何对其进行区分是增强算法的关键[10]。
多尺度方法是通过多个尺度之间分量的相关性对噪声与图像细节进行区分,这是因为真实信号各尺度上的系数之间一般呈强相关,而噪声对应系数之间呈弱相关或不相关。记![]() 为两个相邻尺度的小波系数
为两个相邻尺度的小波系数![]() 和
和![]() 的乘积。对
的乘积。对![]() 进行尺度变换,得到相关性系数
进行尺度变换,得到相关性系数![]()
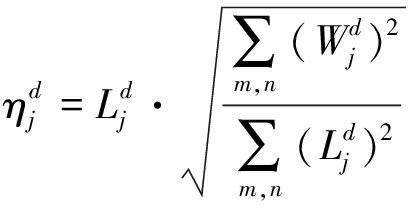
(2)
当![]() 则表明通过乘积小波系数在(x,y)处得到了增强,呈强相关关系,认为其对应真实信号,此时利用函数
则表明通过乘积小波系数在(x,y)处得到了增强,呈强相关关系,认为其对应真实信号,此时利用函数
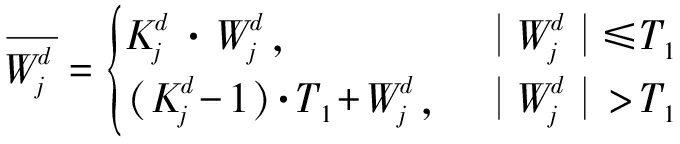
(3)
对![]() 进行变换,认为区间[-T1,T1]内为弱边缘进行增强;区间[-T1,T1]外为原本较强的边缘,避免形变失真。其中增益
进行变换,认为区间[-T1,T1]内为弱边缘进行增强;区间[-T1,T1]外为原本较强的边缘,避免形变失真。其中增益![]() 一般取
一般取![]() 为小波系数模的均值。
为小波系数模的均值。
反之若![]() 此时(x,y)处的小波系数可能对应噪声,且
此时(x,y)处的小波系数可能对应噪声,且![]() 越小,对应噪声可能性越大。此时利用函数
越小,对应噪声可能性越大。此时利用函数
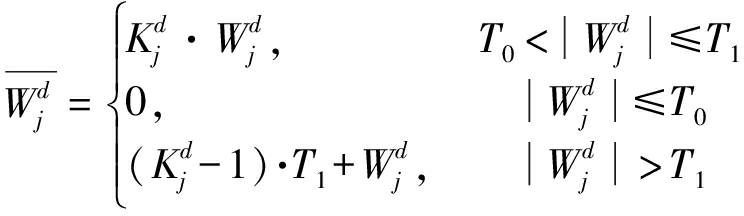
(4)
对![]() 进行变换,其中T0为噪声门限,对[-T0,T0]间的小波系数进行抑制,而[-T1,-T0],[T0,T1]内的系数放大,从而达到去噪增强的效果。
进行变换,其中T0为噪声门限,对[-T0,T0]间的小波系数进行抑制,而[-T1,-T0],[T0,T1]内的系数放大,从而达到去噪增强的效果。
由于用于变化检测的图像成像环境、参数各异,噪声的污染程度也存在差别,软门限较之硬门限具有更好地去噪效果。一般认为图像小波变换的高频子带系数可以被Laplacian分布很好地描述,在此基础上,文献[11]给出了最小均方误差原则下的最优阈值估计:
(5)
其中ζj,σj分别为第j层小波分解得到的子带![]() 和低频分量I′j的标准差。
和低频分量I′j的标准差。
3 结合边缘局部信息的差异图分析
3.1 FLICM算法
传统FCM算法的目标函数定义为
(6)
其中c为聚类数目,n是图像中像素的数量,μij是第j个像素隶属于第i类的隶属度,满足0≤μij≤1且![]() 是算法的相似性度量,最常采用欧几里得距离即欧氏距离,用νi表示第i类的聚类中心,式中欧式距离表示为
是算法的相似性度量,最常采用欧几里得距离即欧氏距离,用νi表示第i类的聚类中心,式中欧式距离表示为
(7)
隶属度μij和聚类中心νi的迭代式为
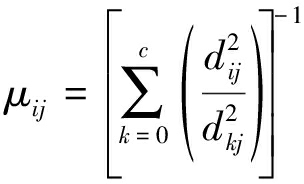
(8)
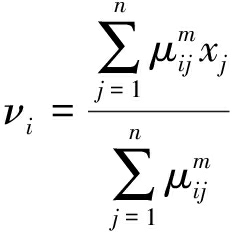
(9)
为最小化目标函数,迭代过程中距离聚类中心近的像素将被赋予较大的隶属度,而与聚类中心距离较远的像素隶属度较小[12]。然而,FCM算法的目标函数中仅考虑了像素的灰度值,并没有考虑其他信息,因此对噪声敏感。
针对这一问题,Krinidis等提出了FLICM算法[5]。FLICM算法中目标函数定义为:
(10)
其中Gij为模糊因子,表示邻域窗Nk内像素与聚类中心νi的欧氏距离加权和,反映了FLICM算法中对邻域信息的利用,定义为:
(11)
算法的聚类中心和隶属度的更新式如下:
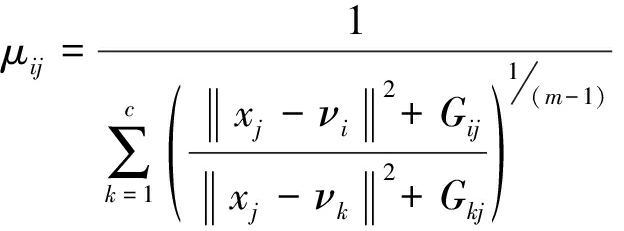
(12)
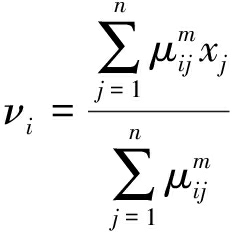
(13)
从上式可以看出,当中心像素与邻域像素点灰度趋近于不同聚类中心时,模糊因子Gij 值较大,进而在迭代过程中影响隶属度与聚类中心,使同一邻域窗内的像素点趋近于同一类别,由此对畸变的噪声点产生平抑效果[13]。
3.2 边缘局部信息FCM算法
当邻域窗移动至边缘时,会包含有大量与中心像素不同类别的像素点,如图2所示,左图为仿真图像LR差异图,右图为差异图最外层边框边缘位置3×3像素大小邻域窗灰度示意图。红框标出邻域窗内部分点属于非变化类,中心像素属于变化类。在迭代过程中,邻域窗内异类的像素点致使中心像素隶属度向非变化类偏移,从而在分割判决中遭到误判,导致变化区域的细节丢失。
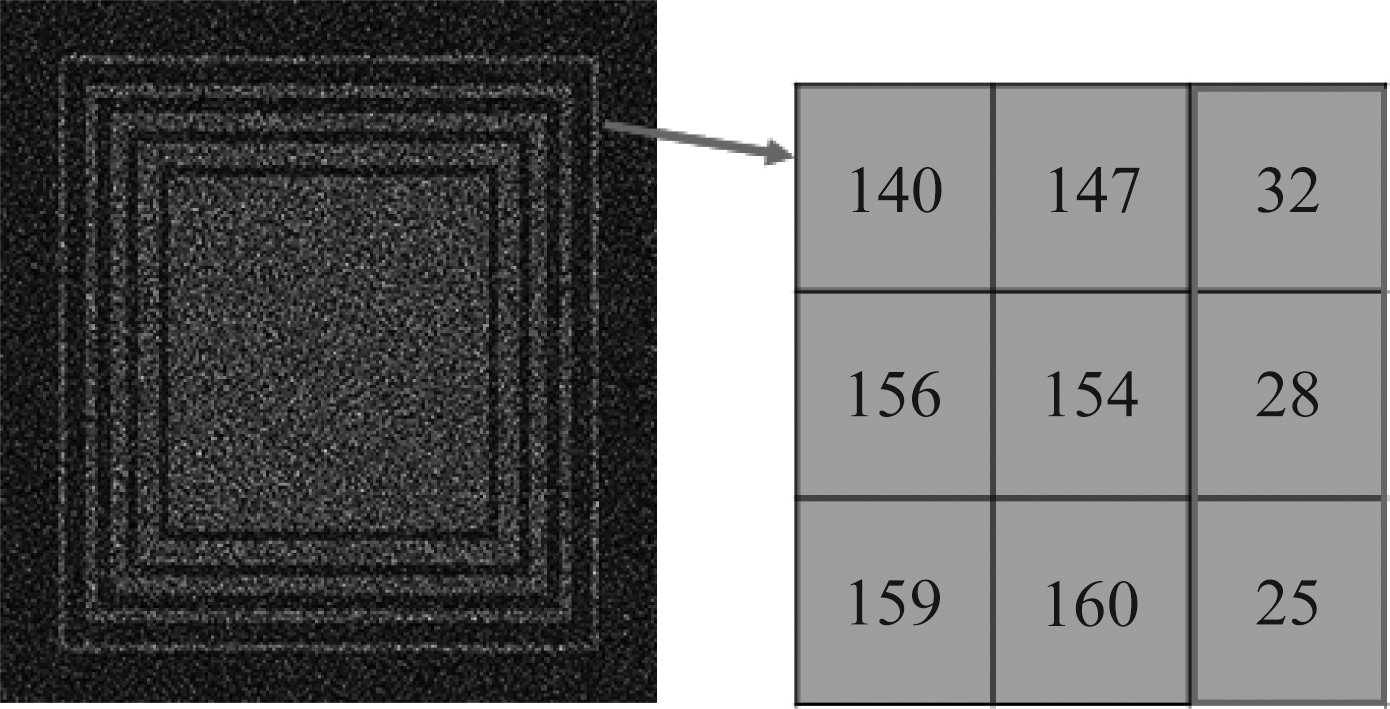
图2 边缘灰度示意图
Fig.2 Gray level of edge region
针对这一问题,本文利用ROEWA算子提取边缘信息并引入到邻域窗内,对窗内各像素点在模糊因子Gij中的权重进行修正。ROEWA检测器是一种具有线性最小均方误差的指数加权滤波器,抗噪性能良好,且具有恒虚警特性,计算简单、实用性强,被广泛应用于图像边缘检测[14]。使用ROEWA算子对差异图进行边缘信息提取,得到各像素点的边缘强度|r(x,y)|,归一化并非线性拉伸:
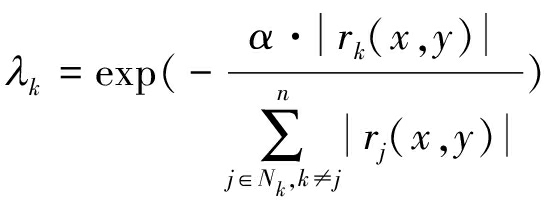
(14)
其中α为常数,用于控制拉伸强度,多次实验表明α=3时,拉伸效果较为理想,且可以有效限制虚假边缘的影响。代入到式(11)中,对邻域窗内权值进行修正,得到新的模糊因子如下式:
(15)
通过加权修正,邻域窗内边缘区域的像素点在模糊因子中权重降低,非边缘区域像素点的权重提高,从而消除边缘像素对中心像素的影响,使邻域窗在同质区域时对中心像素全向平抑,在边缘区域时沿边缘区域切向平抑,在平抑噪声的同时尽可能的保持图像细节。
综上所述,利用二进小波增强与边缘局部信息FCM进行SAR图像变化检测,具体流程如下:
步骤1 获取LR差异图;
步骤2 对LR差异图进行二进小波分解,计算相关系数并进行自适应变换,重构得到增强差异图;
步骤3 利用ROEWA算子提取差异图边缘强度,对邻域窗权值进行修正;
步骤4 设定分类数c,阈值ε,初始化FLICM隶属度函数uij与聚类中心νi;
步骤5 更新聚类中心;
步骤6 更新隶属度矩阵;
步骤7 重复步骤4、5共k次,直至![]() 获取结果二值图。
获取结果二值图。
4 实验结果及分析
为验证本文算法的有效性,对带噪声的仿真SAR图像、实际SAR图像开展变化检测实验。FLICM及本文改进算法邻域窗口均设置为5×5像素,实验环境为Intel Core i5-3770U,内存4G的计算机,实验软件为Matlab R2012a。
仿真SAR图像噪声视数越小,噪声干扰越强。图3(a)和图3(b)为添加视数为5的瑞利分布噪声的合成SAR图像,图3(c)和图3(d)为添加视数为3的瑞利分布噪声的合成SAR图像,尺寸均为500×500像素,可以看出变化区域是最内层正方形及由内至外逐渐变窄的四层矩形边框。图3(e)与图3(g)分别为5视与3视情况下的LR差异图,图3(f)与图3(h)为对应的经过二进小波增强后的差异图,经过增强去噪后变化区域更加清晰。图3(i)与图3(j)分别为LR-FLICM算法与本文算法对图3(f)的分割结果,黑色表示变化区域,白色为未变化区域。可以看出,传统FLICM算法虽能消除噪声的影响,但最外层边缘几乎完全被作为噪声平抑掉,如右侧矩形框处所示;其余部分产生了断裂或粘连,边缘较为粗糙,如正下方矩形框内所示;而本文算法能够对变化区域进行精确地分割,外部边缘保持较为完整,内部边缘更为平滑,在平抑噪声的同时尽可能地保留了变化区域的细节信息。图3(k)与图3(l)分别为LR-FLICM算法与本文算法对图3(h)的分割结果,在噪声污染更为严重的情况下,本文算法相对于传统FLICM,更好地保留了最外层与最内层的细长变化区域,依然具有较好的精度。
图4(a)和图4(b)为尺寸为800×800像素的实测SAR数据,可以看出变化区域主要包括:(1)人工修建的正方形道路A;(2)道路下方的大量强散射体B;(3)左侧大面积不规则区域C。图4(e)和图4(f)分别为LR差异图与经过增强处理后的差异图,可以看出经过二进小波的分解重构,差异图对比度得到了明显提升。图4(i)和图4(j)分别为LR-FLICM与本文方法的变化检测结果。相比较而言,LR-FLICM算法有效地抑制了噪声,但SAR图像中较为狭窄的道路、施工区域的较小的强散射点等细节信息没有得到保留。与之相对,在本文算法分割结果中,道路与左侧不规则变化区域保留的更为完整。
图4(c)和图4(d)为尺寸为500×500像素的实测SAR数据,变化区域主要为右侧人工道路;图4(g)和图4(h),分别为LR差异图与经过增强处理后的差异图,差异图增强处理后变化区域更加明显;图4(k)和图4(l)分别为LR-FLICM与本文方法的变化检测结果,可以看出本文方法更加完整的提取了变化道路的结构。

图3 仿真SAR图像变化检测结果图
Fig.3 Result of change detection of simulation SAR images
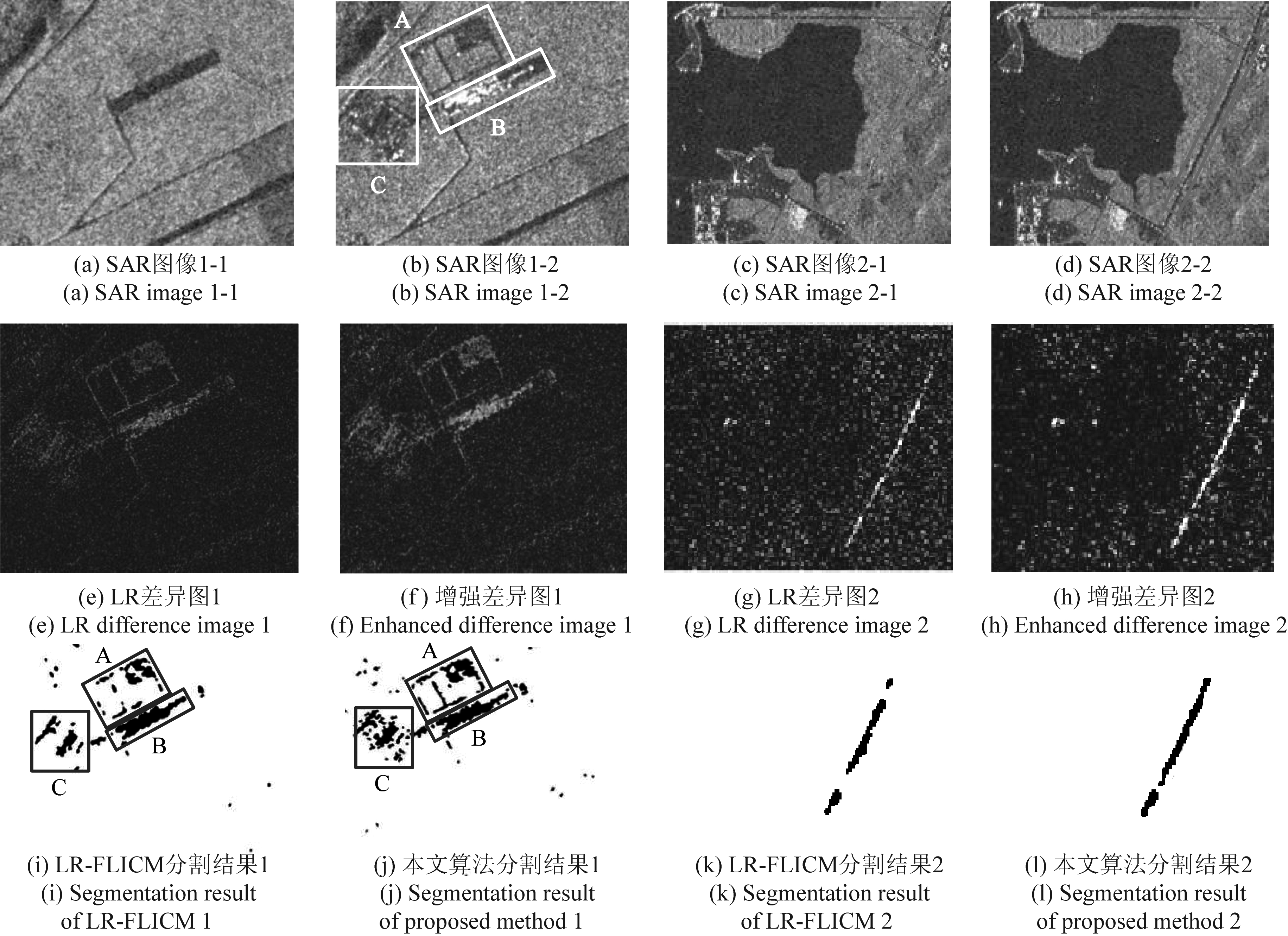
图4 真实SAR图像变化检测结果图
Fig.4 Result of change detection of real SAR images
表1 差异图增强实验结果
Tab.1 Experimental results of difference image enhance

仿真图像实验5视差异图增强前增强后3视差异图增强前增强后实测图像实验差异图1增强前增强后差异图2增强前增强后对比度49.7454.8650.1054.8730.8638.3141.3347.10
表1给出了差异图增强前后,基于灰度共生矩阵得到的对比度变化情况。对比度是衡量图像增强效果的重要指标,差异图对比度越高,说明数据可分性越好;可以看出经过差异图增强后,对比度都得到较大提升,体现了本文方法的有效性。
表2 实验结果对比分析
Tab.2 Comparative analysis of experimental results
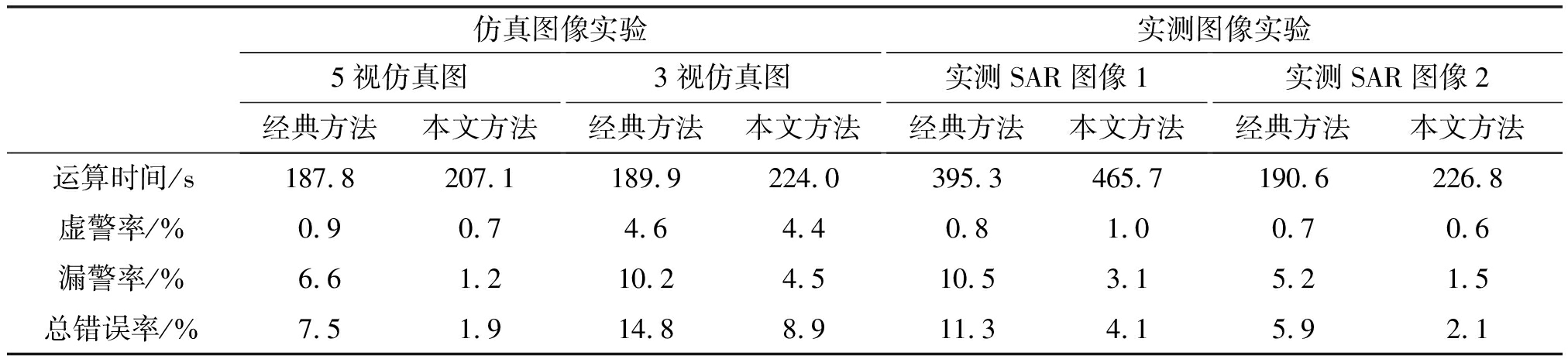
仿真图像实验5视仿真图经典方法本文方法3视仿真图经典方法本文方法实测图像实验实测SAR图像1经典方法本文方法实测SAR图像2经典方法本文方法运算时间/s187.8207.1189.9224.0395.3465.7190.6226.8虚警率/%0.90.74.64.40.81.00.70.6漏警率/%6.61.210.24.510.53.15.21.5总错误率/%7.51.914.88.911.34.15.92.1
表2为定量分析,比较方法为经典的LR-FLICM算法。从运行效率角度来看,由于增加了差异图增强与边缘局部信息提取等步骤,本文算法较之LR-FLICM算法运行耗时略有增加。噪声视数为5的仿真实验中,本文方法较之经典的LR-FLICM算法虚警率与漏警率均有优势,其中漏警率变化更为显著,这是由于对邻域窗权值修正使算法能够自适应的在边缘区域对噪声切向平抑,起到了较好的效果;噪声视数为3的仿真实验中,由于高强度的噪声,两种算法效果较之5视条件下均有不同程度恶化,相比较而言本文算法在漏警率指标优势明显,且整体准确率优于90%,取得了较好的效果;实测图像实验中,由于环境更为复杂,在边缘强度提取时不可避免的存在虚假边缘的影响,从而致使本文方法的虚警率较之LR-FLICM方法略微升高,但漏警率大幅下降,整体准确率得到了明显提升。
5 结论
针对传统的基于差异图的SAR图像变化检测方法存在的问题,本文利用二进小波对经典LR差异图进行分解,利用不同尺度间的相关性区分真实信号与噪声,自适应地增强图像。在提升对比度的同时抑制噪声,增强数据可分性。针对传统FLICM算法在边缘区域易丢失图像细节的问题,利用ROEWA算子的恒虚警特性,对增强后的差异图进行边缘信息提取。利用得到的边缘强度对FLICM算法中邻域窗内各点的权值进行修正,减弱边缘部分像素对中心像素的影响,使算法在边缘区域时对噪声切向平抑,在同质区域时全向平抑,尽可能地保留图像细节。实验证明,本文方法显著提高了变化检测准确率,对噪声污染严重及细微变化区域的SAR图像具有较好的效果。
参考文献
[1] 公茂果,苏临之,李豪,等. 合成孔径雷达影像变化检测研究进展[J]. 计算机研究与发展,2016(1):123-137.
Gong M G, Su L Z, Li H, et al. A survey on change detection in synthetic aperture radar imagery[J]. Journal of Computer Research and Development, 2016(1):123-137.(in Chinese)
[2] 陈富龙,张红,王超. SAR变化检测技术发展综述[J]. 遥感技术与应用,2007,22(1):109-115.
Chen F L, Zhang H, Wang C. The Art in SAR Change Detection-A Systematic Review[J]. Remote Sensing Technology and Application,2007,22(1):109-115. (in Chinese)
[3] Bruzzone L, Prieto D F. An adaptive semiparametric and context-based approach to unsupervised change detection in multitemporal remote-sensing images[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2002, 11(4):452- 466.
[4] 李玉峰,李景芳. 基于FCM算法的SAR图像相干斑噪声滤波算法研究[J]. 计算机应用研究, 2016,33(8):2496-2499.
Li Y F, Li J F. Coherent noise filtering algorithm in SAR images based on FCM algorithm[J]. Application Research of Computers, 2016,33(8):2496-2499. (in Chinese)
[5] 万红林,汪洋,江凯,等. 基于模糊贴近度和非紧凑邻域的变化检测[J]. 雷达科学与技术, 2014(3):229-234.
Wan H L, Wang Y, Jiang K, et al. Fuzzy Neartude and Information in a Non-Compact Neighborhood Based Change Detection[J]. Radar Science and Technology, 2014(3):229-234.(in Chinese)
[6] Krinidis S, Chatzis V. A robust fuzzy local information C-Means clustering algorithm[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2010, 19(5):1328-1337.
[7] Gong M, Liang Y, Shi J, et al. Fuzzy C-means clustering with local information and kernel metric for image segmentation[J]. Image Processing IEEE Transactions on, 2013, 22(2):573-584.
[8] 刘妍, 徐德伟, 李立,等. 结合强度和相干信息的多阈值SAR影像变化检测[J]. 信号处理, 2015, 31(11):1531-1538.
Liu Y, Xu D W, Li L, et al. Multi-thresholds Fusion Based Change Detection of SAR Images by Combining the Intensity and Coherence Information[J]. Journal of Signal Processing, 2015, 31(11):1531-1538. (in Chinese)
[9] 王红霞,成礼智,吴翊. 基于二进小波变换的噪声图像自适应增强新算法[J]. 国防科技大学学报, 2005, 27(1):51-54.
Wang H X, Cheng L Z,Wu Y. An Adaptive Strategy for Image Enhancement Based on the Dyadic Wavelet Transform[J]. Journal of National University of Defense Technology, 2005, 27(1):51-54.(in Chinese)
[10] Chang G, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2000, 9(9):1532.
[11] Chang G, Yu B, Vetterli M. Image denoising via lossy compression and wavelet thresholding[C]∥International Conference on Image Processing, 1997. Proceedings. IEEE, 1997:604- 607.
[12] Li H, Gong M, Wang Q, et al. A multiobjective fuzzy clustering method for change detection in SAR image[J]. Applied Soft Computing, 2016, 46(C):767-777.
[13] Jia L, Li M, Zhang P, et al. SAR Image Change Detection Based on Multiple Kernel K-means Clustering With Local-Neighborhood Information[J]. IEEE Geoscience & Remote Sensing Letters, 2016, 13(6):856- 860.
[14] 曾阳帆,刘伟,陈建宏. SAR图像启发式搜索直线提取[J]. 信号处理, 2015, 31(3):282-289.
Zeng Y F, Liu W, Chen J H. Straight Line Extraction by Heuristic Search for SAR Images[J]. Journal of Signal Processing, 2015, 31(3):282-289.(in Chinese)
