1 引言
无线通信技术的应用范围愈来愈广,频谱资源需求量不断扩增,正是这些巨大的需求导致频谱资源由充足状态逐渐趋于短缺状态,同时早期频谱分配方式采取固定分配,导致部分频段利用率很低。因此,为了满足大量用户对于频谱的需求并且保证频谱资源高效利用,认知无线电技术[1-2]应运而生。认知无线电的首要任务就是频谱感知(SS,Spectrum Sensing)[3- 4],感知过程中发现未使用频谱并合理利用空闲频谱。最终,实现频谱的动态分配和共享。
现有算法包括基于特征结构的感知算法和基于协方差阵的算法、基于功率谱的算法[5]、基于最大相关系数算法[6]、拟合优度(GOF,Goodness of Fit)算法等。采用接收信号协方差阵进行特征分解的感知算法,利用特征值性质进行感知,其中主要有最大最小特征值之比(MME,maximum-minimum eigen-value)和最大特征值与迹之比(MET,maximum eigen-value trace),两种算法需要进行特征分解,复杂度高,且判决门限由近似理论分布得到,精确性不好;根据采样协方差阵构造频谱感知所需检验统计量的算法有方差绝对值算法(CAV,covariance absolute value),其检测门限需要渐近得到; GOF算法从不同的角度对频谱感知问题做出诠释, PU(Primary User)不存在时,接收信号服从某一特定分布;PU存在时接收信号将不再服从特定分布,产生偏离。在SS中,当PU信号为窄带信号时文献[7]结合AD(Anderson-Darling)准则提出GOF算法并表明其性能优于能量检测,缺陷是噪声方差必须已知。文献[8]和[9]将CM(Cramer-von Mises)准则和KS(Kolmogorov-Smirnov)准则应用于GOF算法,使拟合度检验适应于更多拟合对象,从而可以进一步提高检测性能。文献[10]对GOF算法中信号类型和分布应用进行了扩展,算法感知过程中信号不仅可以是实信号,也可以是复信号,并且PU信号不存在时采样数据能量服从卡方分布,可以替代正态分布进行拟合度检验。文献[11]采用单边检验进行检测,在计算复杂度和检测性能两方面对文献[10]进行改进,缺陷是需要知道噪声方差。文献[12]采用似然比检验对检验统计量进行改进,从而在一定程度上提高文献[10]的检测性能,缺点是仍受噪声方差影响。
上述所提算法,在高信噪比时均可以达到相对很好的检测效果,而在低信噪比以及采样数较少时检测效果相对很低。然而在认知无线电系统中,通常为了减小认知用户对PU的干扰,采用降低认知用户发射功率的方法,使得认知用户处于低功率高噪声环境工作。因此,如何提高低信噪比时的感知能力是认知无线电系统中必须解决的问题之一。针对上述问题,本文应用样本特征和广义T2统计量构造新的检验统计量,频谱空闲时,该检验统计量服从贝塔分布。从而提出了基于贝塔分布的盲频谱感知算法(BSB,Blind spectrum sensing based the B-distribution)。然而,该算法在采样数较少时检测性能相对较差且判决门限受采样点数的影响,因此本文根据BSB 算法在频谱空闲时服从贝塔分布,并结合 AD 准则提出了基于贝塔分布的拟合优度检验算法(GOF-B,Goodness of Fit Based on the B-distribution)。所提两种算法均无需PU信号和噪声的任何参数,从而解决了MME算法、MET算法和CAV算法门限不精确的问题以及噪声影响,提高了低信噪比时的检测性能。同时,GOF-B算法也无需噪声的相关信息,并不受噪声方差影响,消除了已有GOF算法中方差带来的影响,提高了低信噪比、采样数少时的检测性能。
2 信号模型
多用户系统相当于无线通信中的基站,系统中的次级用户相当于基站中的手机用户,多个手机用户同时感知每个授权频段是否正在使用。H0表示PU不存在,次级用户可进入授权频段;H1当PU存在,次级用户必须马上撤离授权频段以确保PU可以正常通信。因此,得到频谱感知的二元假设为:
(1)
式中:s(α)=[s1(α) s2(α) … sP(α)]T为主用户信号矢量;n(α)=[n1(α) n2(α) … nP(α)]T为噪声向量,P为阵元个数,ni(α)表示均值为零,方差为![]() 的独立同分布加性高斯白噪声。在实际通信中,传输PU信号可以存在很多形式,一般表示为复信号。
的独立同分布加性高斯白噪声。在实际通信中,传输PU信号可以存在很多形式,一般表示为复信号。
3 检验统计量的确定
3.1 构造检验矩阵
接收信号的协方差阵为:
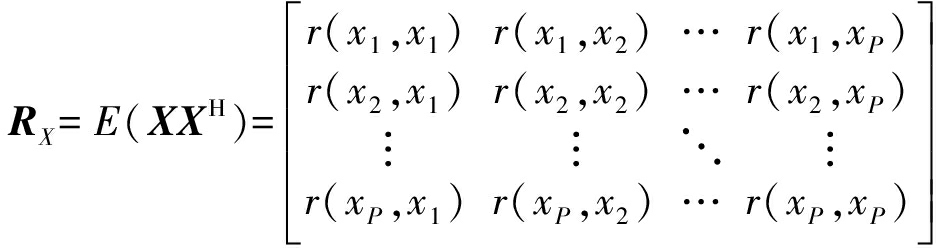
(2)
其中:X为接收信号的采样矩阵,r(xi,xj)为接收信号采样矩阵X中的第i个接收信号与第j个接收信号的协方差。
为了构造样本检验矩阵,需要得到两个新的矩阵RXX和RXK。RXX是RX在的基础上去除其主对角线元素,得到的一个新的非对称矩阵即为:
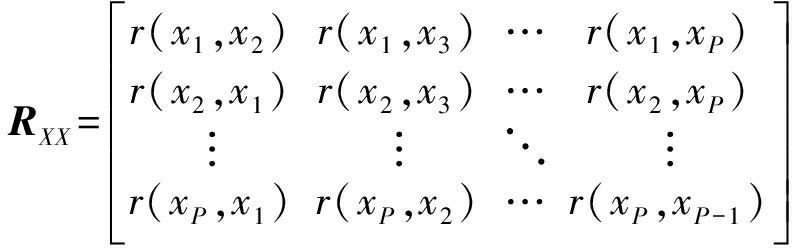
(3)
RXK(K<M)则是选取矩阵X的前M-K列和后M-K列来构建协方差阵,此时RXK为空时矩阵。RXK即为:

(4)
其中:rXK(xi,xj)为矩阵X的前M-K列中第i个接收信号与后M-K列中第j个接收信号的协方差。
构建得到样本检验矩阵RZ:
RZ=[RXXRX1RX2 … RXK]
(5)
由文献[13],在H0情况下, RXK中的元素服从均值为0的正态分布,即:
E(rXK(xi,xj))=0 i, j=1,2,…,P;K=1,2,…,Q
(6)
在H1情况下,RXK中的元素服从正态分布且均值E(rXK(xi,xj))=μ;同理,RXX中的元素rXX(xi,xj)(i≠j)与RXK中的元素同分布。在H0情况下,E(RXX)=0,E(RXK)=0,则E(RZ)=0,RZ服从均值为0的正态分布;在H1情况下,RZ服从正态分布且E(RZ)=μ,其中μ为未知向量。
由此可以根据均值μ进行判断,当μ=μ0时,频谱空闲;当μ≠μ0时, 频谱被占用。其中样本检验矩阵RZ服从N(μ,Σ )分布,其中μ0=0。
3.2 构造检验统计量
根据多元统计学中T2统计量的定义得到:![]() 其中
其中![]() 是N个样本的均值向量,S是样本协方差阵。在本文中,基于来自N(μ,Σ )的样本(即样本检验矩阵RZ)的假设检验H0: μ=μ0,其似然比检验就是基于T2统计量的。假设RZ中每个次级用户的N个观测值为x1,x2,…,xN(N>P),似然比函数是:
是N个样本的均值向量,S是样本协方差阵。在本文中,基于来自N(μ,Σ )的样本(即样本检验矩阵RZ)的假设检验H0: μ=μ0,其似然比检验就是基于T2统计量的。假设RZ中每个次级用户的N个观测值为x1,x2,…,xN(N>P),似然比函数是:
(7)
根据似然比准则:![]() 分子是μ,Σ的似然函数在原假设限制的参数空间(μ=μ0,Σ正定)上的极大值;分母是似然函数在整个参数空间(Σ正定的)上的极大值。参数无限制条件下,根据极大似然估计求得μ和Σ的极大估计值
分子是μ,Σ的似然函数在原假设限制的参数空间(μ=μ0,Σ正定)上的极大值;分母是似然函数在整个参数空间(Σ正定的)上的极大值。参数无限制条件下,根据极大似然估计求得μ和Σ的极大估计值![]() 和
和![]() 在H0假设下,即μ=μ0时,似然函数在
在H0假设下,即μ=μ0时,似然函数在![]() 处有极大值,而且极大值为:
处有极大值,而且极大值为:

(8)
在H1假设下,即μ≠μ0时,似然函数在![]() 处有极大值,极大值为:
处有极大值,极大值为:
(9)
因此得到似然比为:
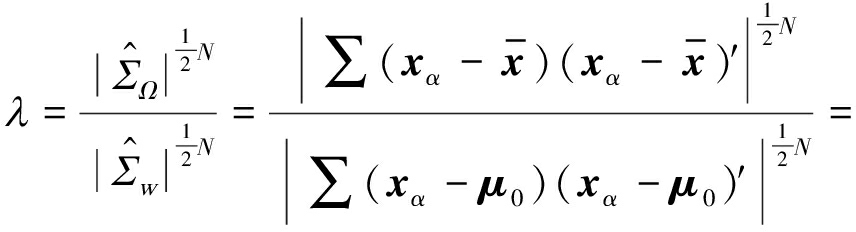
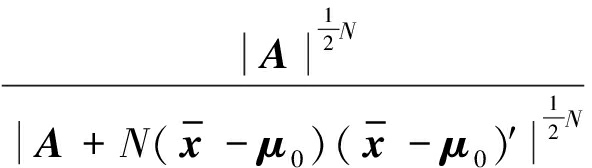
(10)
其中,A为样本协方差矩阵S的极大似然估计,![]() 推导可得检验统计量为:
推导可得检验统计量为:
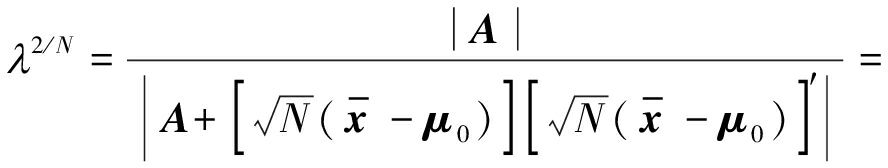
(11)
其中,![]()
当PU不存在时,采样点数N趋于无穷大,此时![]() 因此λ2/N=1;当PU信号存在时,随着采样点数的变化,样本均值
因此λ2/N=1;当PU信号存在时,随着采样点数的变化,样本均值![]() 均不会等于总体均值μ0,因此λ2/N<1。然而,在实际感知过程中,由于采样点数有限,只能通过有限样本计算得到,即H0时,λ2/N近似等于1。因此,H0假设下,λ2/N实际值与理想值有偏差,但其服从一定分布。
均不会等于总体均值μ0,因此λ2/N<1。然而,在实际感知过程中,由于采样点数有限,只能通过有限样本计算得到,即H0时,λ2/N近似等于1。因此,H0假设下,λ2/N实际值与理想值有偏差,但其服从一定分布。
3.3 检验统计量λ2/N的分布
根据文献[14],当空假设为真时,令n=N-1,采样点数有限时,T 2/n有分布![]() 则对应式(11)中λ2/N的分布为
则对应式(11)中λ2/N的分布为![]() 令a=n-p+1,b=p,当
令a=n-p+1,b=p,当![]() 和
和![]() 独立时,
独立时,![]() 的密度是:
的密度是:

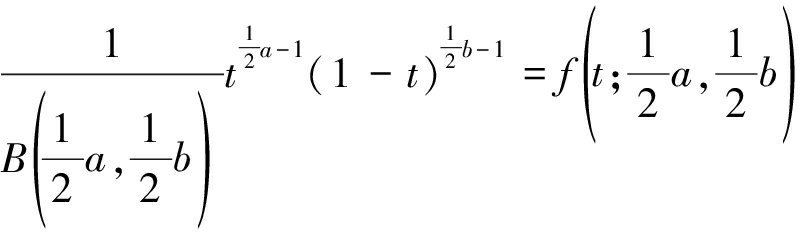
(12)
其中,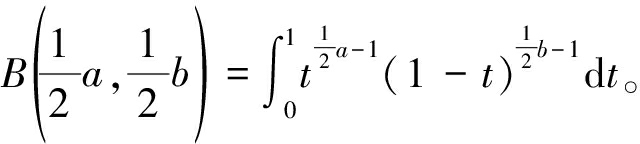
这实际上是β分布的概率密度函数,其参数为a/2和b/2。因此,λ2/N服从参数为![]() 和
和![]() 的β分布。
的β分布。
4 基于贝塔分布的盲频谱感知算法(BSB)
基于上述分析,利用式(11)的检验统计量判断PU是否存在,提出基于贝塔分布的盲频谱感知算法。令检测门限为γBSB,当λ2/N小于等于γBSB,判断H1成立,否则判断H0成立。因此,BSB算法的判决准则为:
(13)
从而根据给定的虚警概率Pf计算对应的检测门限,表达式如下:
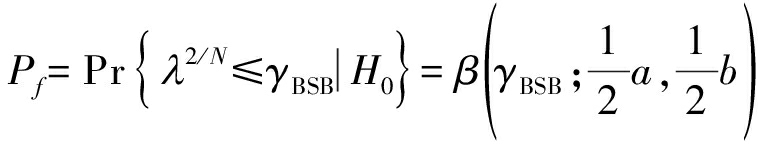
(14)
其中 为贝塔分布的累积分布函数。因此,得到γBSB为
为贝塔分布的累积分布函数。因此,得到γBSB为
γBSB=β-1(Pf)
(15)
由式(11)、(15)可知,λ2/N和γBSB均与噪声参数无关,且完全不需要先验信息,因此BSB算法是一种盲频谱感知算法。因此,下节以BSB算法为基础构造新的检验统计量提出基于贝塔分布的拟合优度检测算法。
5 基于贝塔分布的拟合优度检验算法(GOF-B)
GOF算法利用H0和H1条件下λ2/N概率分布函数的差异进行感知。在H1假设下,由于PU存在,λ2/N分布函数不服从特定分布。而依据式(12),在H0条件下,接收数据λ2/N服从贝塔分布。其分布函数为
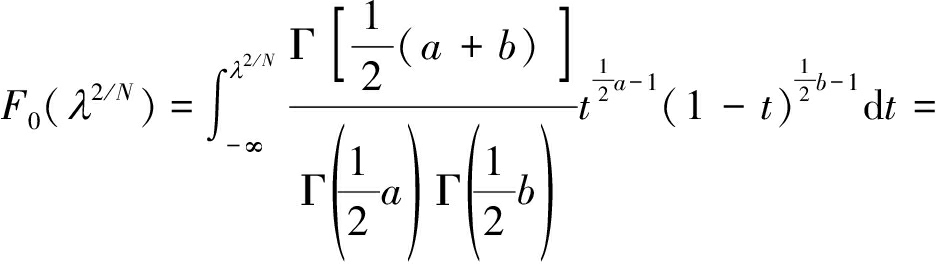
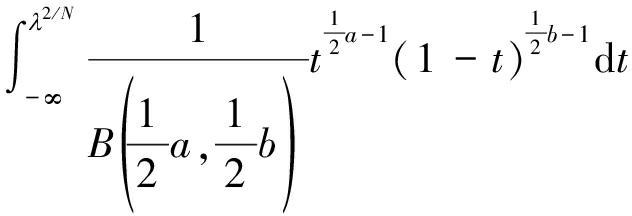
(16)
因此,基于贝塔分布的拟合度检验也可以感知授权用户存在与否。
将接收信号x1,x2,…,xN等分为L(L<N)段,则每段有m=N/L个数据。因此,依据式(11) 可以形成第l段接收信号的![]() 对其进行升序排列,即
对其进行升序排列,即![]() 得到检验统计量的经验谱分布FL(λ2/N)为:
得到检验统计量的经验谱分布FL(λ2/N)为:
(17)
当假设H0成立,分段数L→∞时,FL(λ2/N)依概率1收敛于F0(λ2/N);当假设H1成立,由于PU存在,随着L的增大,FL(λ2/N)也会始终偏离F0(λ2/N)。因此,计算F0(λ2/N)与FL(λ2/N)之间的距离,判断PU是否存在,将频谱感知问题转化为拟合优度检验问题:
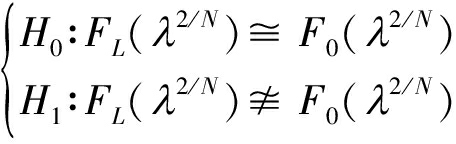
(18)
依据AD准则进行拟合优度检验,FL(λ2/N)与F0(λ2/N)之间的距离![]() 为:
为:
(19)
文献[15]将![]() 简化为:
简化为:
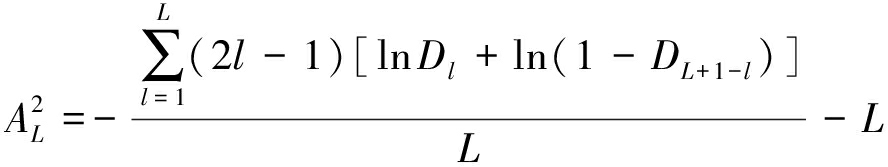
(20)
其中![]() 因此,式(18)中的感知问题转化为比较
因此,式(18)中的感知问题转化为比较![]() 和检测门限γGOF-B大小的问题。当
和检测门限γGOF-B大小的问题。当![]() 大于γGOF-B时,判断H1成立,反之认为H0成立。γGOF-B可由下式推导得出:
大于γGOF-B时,判断H1成立,反之认为H0成立。γGOF-B可由下式推导得出:
(21)
H0假设下,由贝塔分布形成的![]() 的极限分布函数为:
的极限分布函数为:
(22)
其中aj=(-1)jΓ(j+0.5)/(Γ(0.5)j!),Γ为Gamma函数。事实上,当l→∞时,![]() 的极限分布是收敛的。于是Pf已知时,依据式(22)便可求得相应的γGOF-B。由于极限分布计算复杂,也可以根据文献[16]查表获得检测门限。
的极限分布是收敛的。于是Pf已知时,依据式(22)便可求得相应的γGOF-B。由于极限分布计算复杂,也可以根据文献[16]查表获得检测门限。
由式(21)、式(22)可知,γGOF-B仅仅与Pf有关,检验统计量![]() 与噪声参数、采样点数无关,且完全不需要先验知识。因此,说明GOF-B算法不受噪声方差和采样数影响,符合盲频谱感知的要求。
与噪声参数、采样点数无关,且完全不需要先验知识。因此,说明GOF-B算法不受噪声方差和采样数影响,符合盲频谱感知的要求。
综上,GOF-B算法步骤如下:
(1)Pf给定条件下,根据式(21)、(22)求得检测门限γGOF-B;
(2)获取接收数据,根据式(11)得到![]() 并对其进行升序排列;
并对其进行升序排列;
(3)根据式(20)得到检验统计量![]()
(4)当![]() 判决H1成立,否则判决H0成立。
判决H1成立,否则判决H0成立。
6 算法仿真结果与分析
为了验证上述分析,现给出在瑞利衰落信道和均值为零,噪声方差![]() 的高斯信道下,BSB算法、GOF-B算法、MME算法、MET算法、CAV算法、MPS(the Maximum value of Power Spectrum)算法、MCC(the Maximum value of Correlation Coefficient)算法以及GOF-T(Goodness of Fit Based on the B-distribution)算法的仿真结果。仿真中,蒙特卡罗仿真次数设置为10000次,PU信号为采用采样频率fs=100 s的QPSK调制信号,虚警概率设置为Pf=0.01,采样点数N=40,GOF-B算法中进行的数据分段每段长度m=5。
的高斯信道下,BSB算法、GOF-B算法、MME算法、MET算法、CAV算法、MPS(the Maximum value of Power Spectrum)算法、MCC(the Maximum value of Correlation Coefficient)算法以及GOF-T(Goodness of Fit Based on the B-distribution)算法的仿真结果。仿真中,蒙特卡罗仿真次数设置为10000次,PU信号为采用采样频率fs=100 s的QPSK调制信号,虚警概率设置为Pf=0.01,采样点数N=40,GOF-B算法中进行的数据分段每段长度m=5。
表1说明了所提两种算法的复杂度,由表1知,BSB算法和GOF-B算法复杂度分别为O(N)和O(L)(L<N),然而GOF-B算法需要进行排序,因此两种算法的运算量需要分情况分析。当采样数较多时,两种算法的复杂度基本可以趋于一致,而GOF-B算法需要进行排序,因此在大样本情况下,选择BSB算法更为适合;当采样数较少时,GOF-B算法进行排序的时间几乎可以忽略,同时GOF-B算法的复杂度也相对较低,因此小样本时,选择GOF-B算法更为适合。
表1 BSB算法与GOF-B算法的复杂度分析
Tab.1 Computational complexity analysis of BSB and GOF-B

算法检验统计量的运算复杂度是否需要排序BSB算法O(N)否GOF-B算法O(L)是
图1(a)、图1(b)分别为在高斯信道下,采样点数N=40和20,虚警概率Pf=0.01,阵元数P=8时,BSB算法与GOF-B算法的检测性能。由图1(a)可以看到,采样点数较多时,GOF-B算法得到的检测概率明显高于BSB算法,且在低信噪比时,其性能仍明显优于BSB算法,弥补了BSB算法在低信噪比性能较差的不足之处。由图1(b)可以看到,采样点数较少时,GOF-B算法得到的检测概率在信噪比低于-9 dB时相比BSB算法检测性能优势显著,当信噪比大于-9 dB时性能又相对低于BSB算法的检测性能。因此,GOF-B算法在低信噪比,小采样时,检测性能相对更好。如图1(b)中,信噪比RSN分别为-14 dB,-6 dB时,GOF-B算法的检测概率分别为0.5,0.8,BSB算法的检测概率为0.1,0.98。
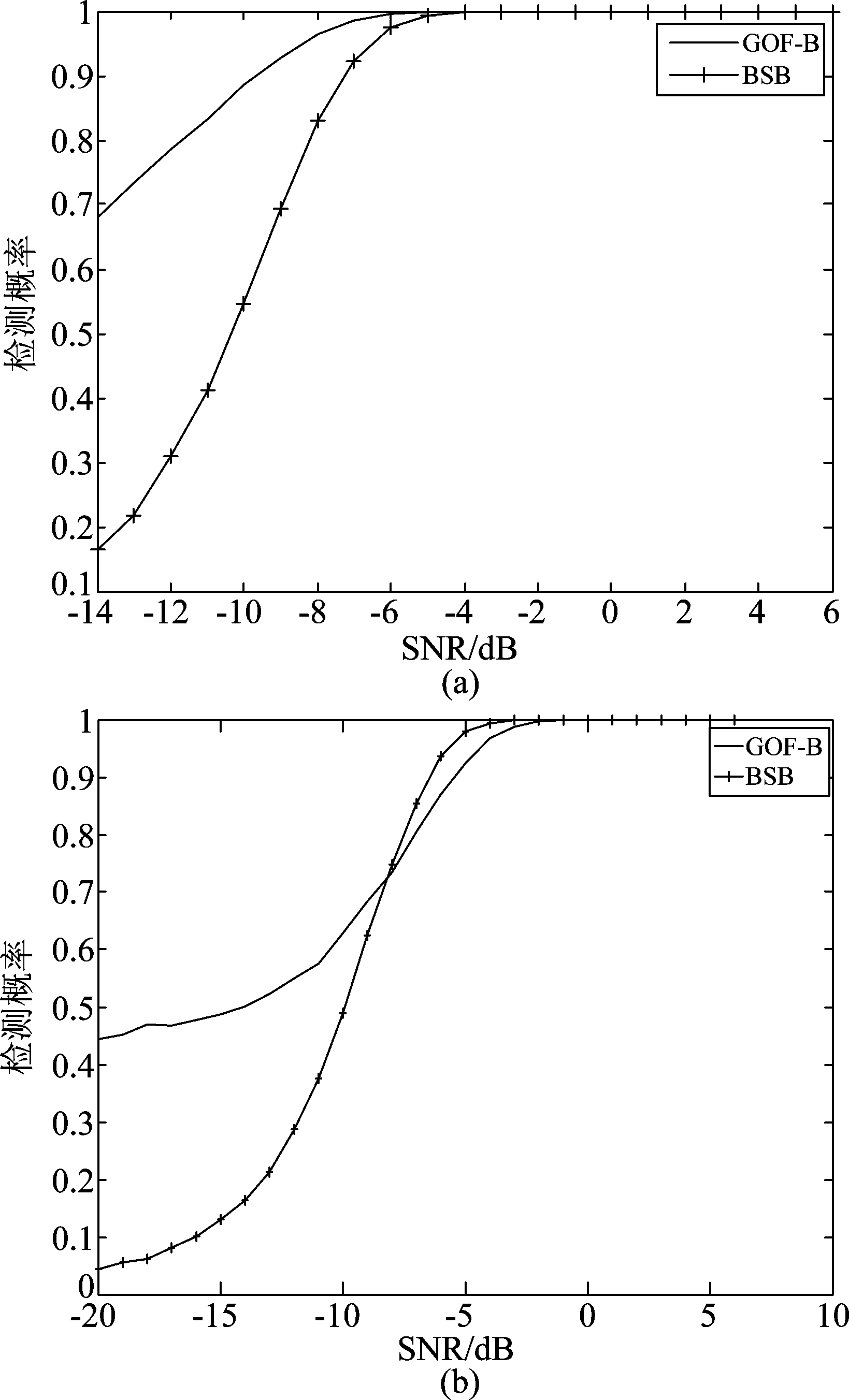
图1 不同采样点数时BSB算法、GOF-B算法检测性能
Fig.1 The performance of BSB and GOF-B for different samples
图2是噪声方差未知,采样点数N=40,信噪比RSN=-8 dB时,BSB算法、GOF-B算法检测性能图。由图可见,当噪声方差改变时,BSB算法、GOF-B算法得到的检测概率以及虚警概率几乎趋于一条直线,这说明了BSB算法、GOF-B算法不受噪声方差的影响。同时,GOF-B算法在信噪比较低时,依然保持较高的检测概率和较低的虚警概率。
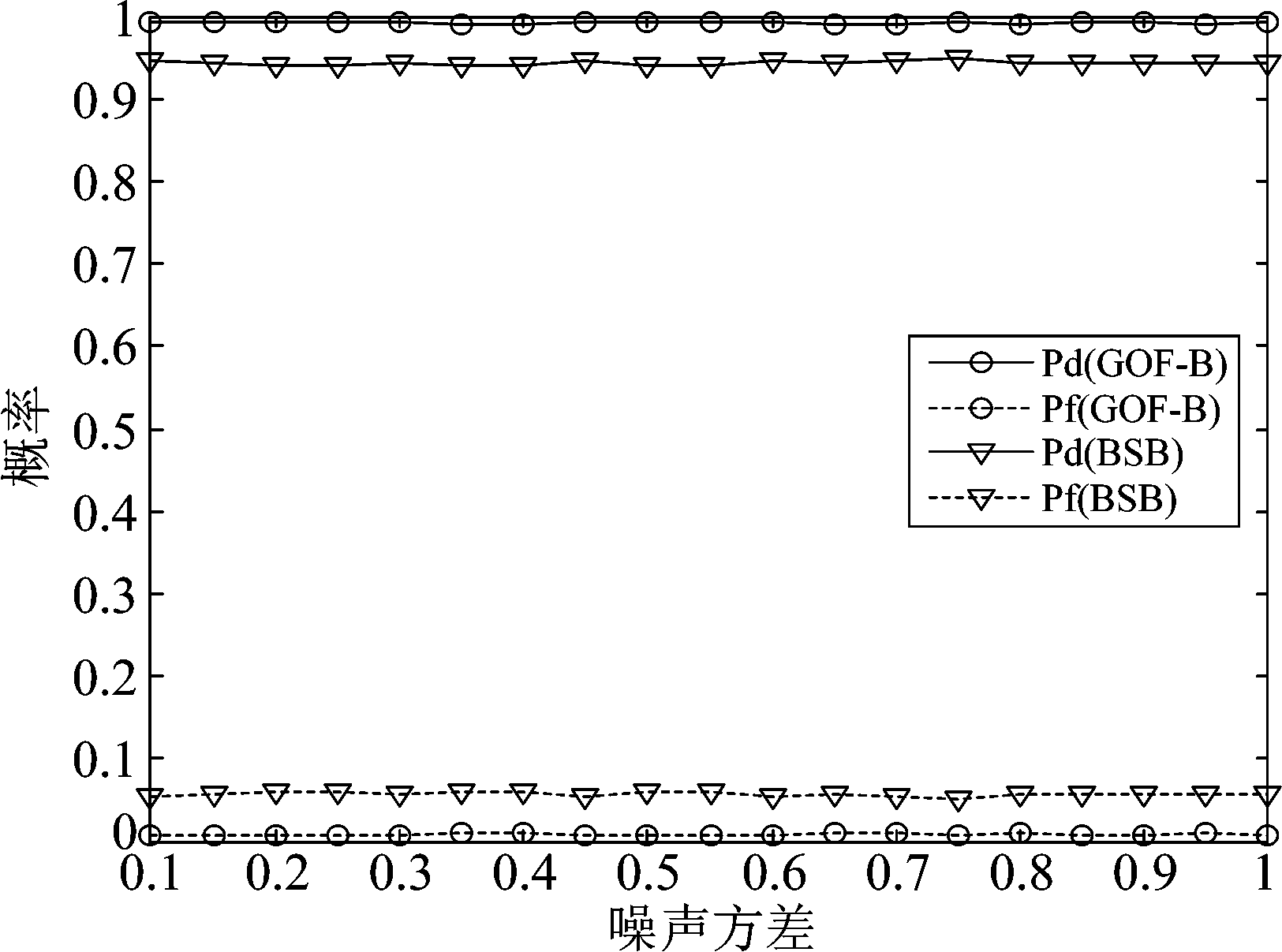
图2 噪声方差未知时两种算法性能
Fig.2 The performance for two methods with the unknown noise variance
图3(a)、图3(b)分别是在高斯信道下,PU信号为采样频率fs=100 Hz的QPSK信号,虚警概率Pf=0.01和0.1,阵元个数P=8,采样点数N=40时,所提算法与经典算法的检测性能对比图。图3(c)、图3(d)分别为在高斯信道下,PU信号是采样频率fs=100 Hz的BPSK信号,Pf=0.01,采样数N=40时,所提算法和经典算法的检测性能对比图以及所提算法与最近的盲频谱感知算法的检测性能对比图。由图3(a)、图3(b)对比知,在相同频谱检测条件下,当给定的Pf较小时,GOF-B算法、BSB算法的检测性能仍优于其他三种算法,且所提两种算法几乎在RSN=-8 dB时检测概率趋于1。由图3(a)、图3(c)对比知,当PU信号为同频率的BPSK信号时,GOF-B算法、BSB算法的检测性能仍优于其他三种算法,且当主PU信号为QPSK信号时的检测性能更好。由图3(d)知,本文所提算法的检测性能优于MCC算法和MPS算法,但相比GOF-T算法检测性能相对较差。
图4(a)、4(b)分别为在瑞利衰落信道下,PU信号分别为采样频率fs=100 Hz 的BPSK调制信号,虚警概率Pf=0.01,采样点数N=40和20时,所提算法与经典盲频谱感知算法的仿真对比图。对比图4(a)、图4(b)可知,当检测环境相同时,随着采样数的增多,算法性能也随之提高,且所提算法检测性能优于其他算法。同时对比图4(a)和图3(c)在低信噪比时,瑞利信道中GOF-B算法的检测性能优于高斯信道中算法性能,BSB算法的检测性能有所下降,但依然优于其他算法。
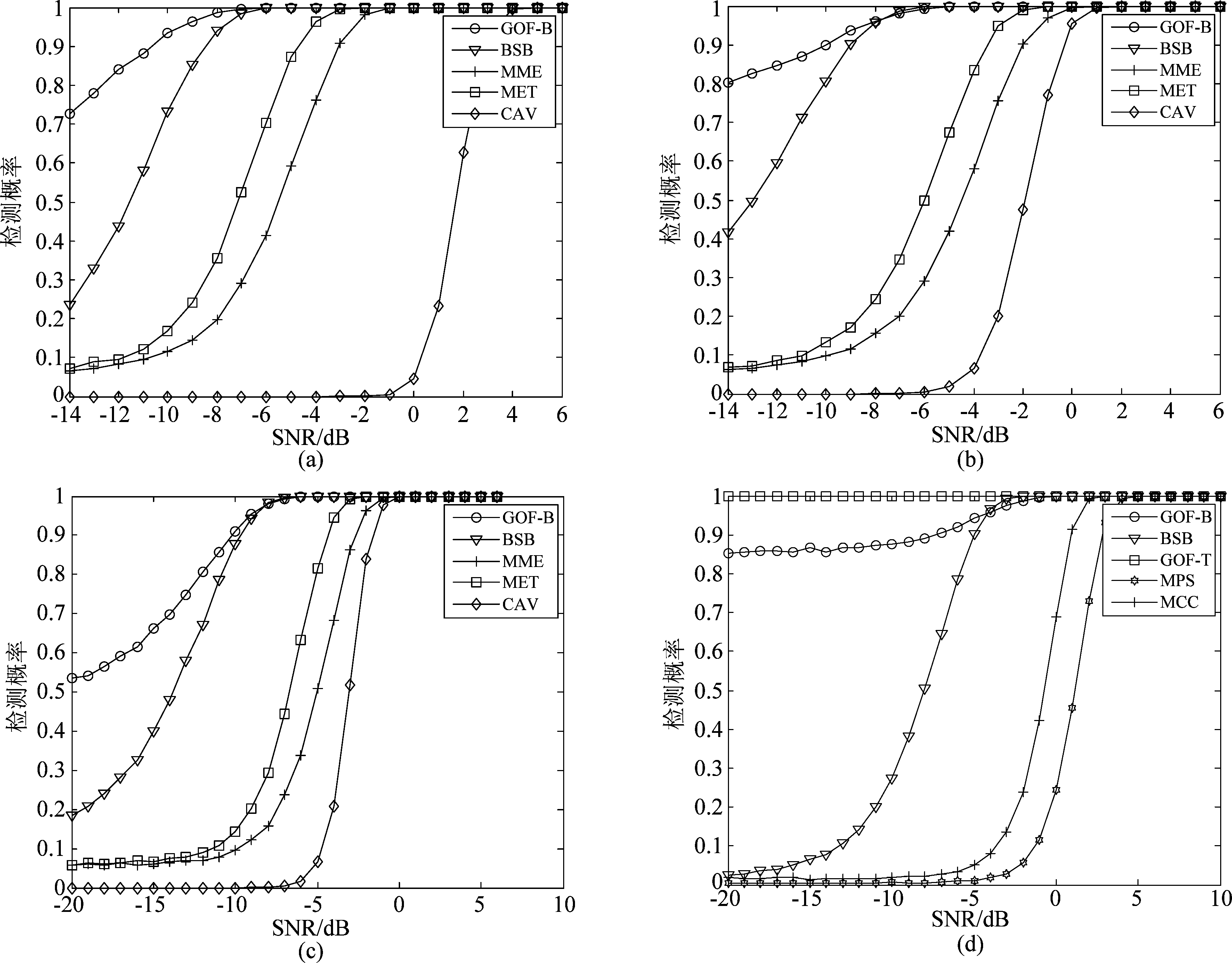
图3 不同虚警概率,不同PU信号时五种算法的检测性能
Fig.3 The performance for five methods with different False alarm probability and PU signals
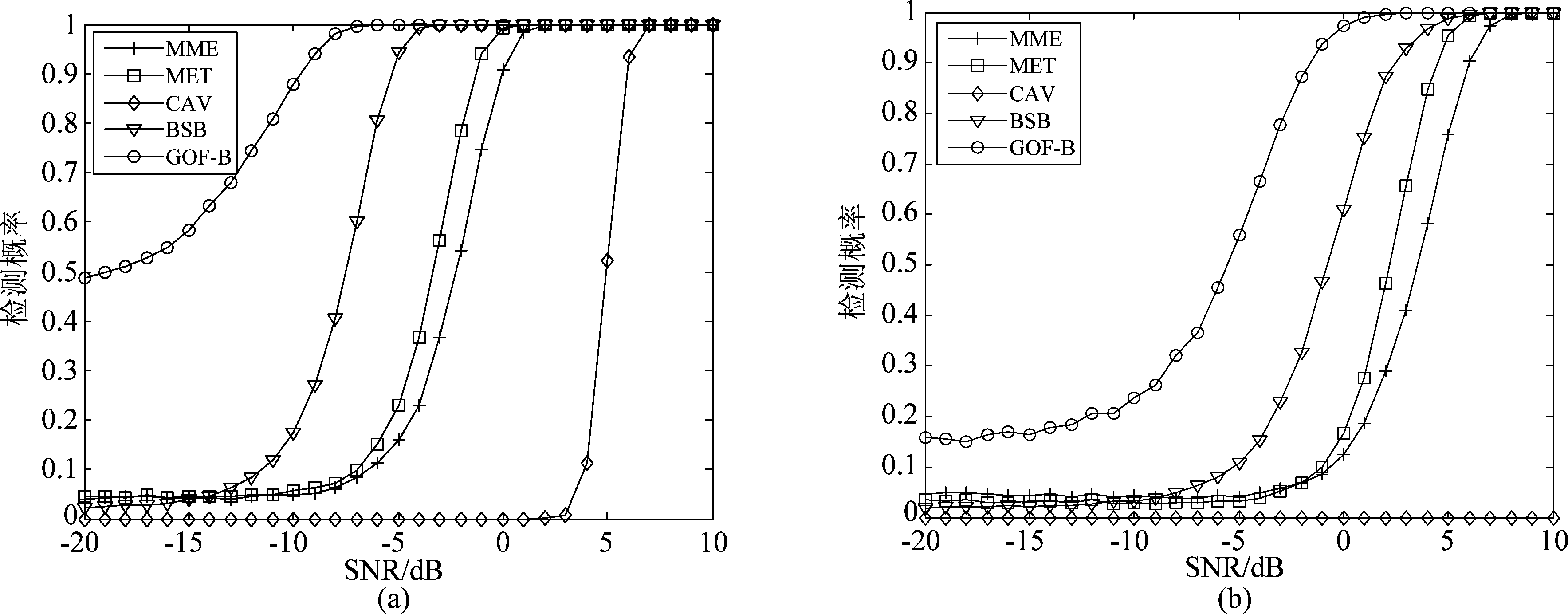
图4 瑞利慢衰落信道中采样数不同时五种算法检测性能
Fig.4 The performance for five methods in Rayleigh channel with different samples
7 结论
本文通过多元统计学中的广义T2统计量与AD准则,提出了BSB算法与GOF-B算法。BSB算法以T2统计量为基础,并以极大似然比准则为依据推导出了判决门限的理论分布,得到非渐近的检测门限。所以相比MME、MET算法,所提算法可以精确区分主用户是否存在;相比CAV算法,所提算法的检测门限和检验统计量均与噪声方差无关,不受噪声方差影响,且在低信噪比时检测性能稳定。同时,GOF-B算法既不受噪声方差影响,又可以弥补小采样时BSB算法的性能劣势。但GOF-B算法也有不足之处,就是其检测门限由极限分布统计得到,存在一定误差。因此,在以后基于拟合度检验的算法中需要对检测门限的获得方式进行改进。
参考文献
[1] Hattb G, Ibnkahala M. Multiband spectrum access: great promises for future cognitive radio networks[J].Proceedings of the IEEE, 2014, 102(3): 282-306.
[2] Masonta M T, Mzyece M, Ntlapa N. Spectrum decision in cognitive radio networks: A survey[J].IEEE Communication Surveys & Tutorials, 2013, 15(3):1088-1107.
[3] Chen Y, Wang C, Zhao B. Performance comparison of feature-based detectors for spectrum sensing in the presence of primary user traffic[J]. IEEE Signal Processing Letters, 2011, 18(5): 291-294.
[4] Bokharaiee S, Nguyen H H, Shwedyk E. Blind spectrum sensing for OFDM-based cognitive radio systems[J]. IEEE Transactions on Vehicular Technology, 2011, 60(3):858- 871.
[5] 赵知劲,吕曦,尚俊娜,等.利用功率谱最大最小值的频谱感知算法[J].信号处理, 2017,33(2):152-157.
Zhao Zhijin, Lv Xi, Shang Junna, et al. The spectrum sensing algorithm using the maximum value and minimum value of the power spectral density[J].Journal of Signal Processing, 2017, 33(2):152-157.(in Chinese)
[6] 叶迎晖,卢光跃.采用相关系数和拟合优度的频谱盲检测[J]. 信号处理,2016,32(11):1363-1368.
Ye Yinghui, Lu Guangyue. Employing correlation coefficient and goodness of fit for blind spectrum sensing[J]. Journal of Signal Processing, 2016,32(11):1363-1368.(in Chinese)
[7] 叶迎晖,卢光跃,弥寅.利用样本特征的盲频谱感知算法[J].信号处理,2016,32(4):444- 450.
Ye Yinghui, Lu Guangyue, Mi Yin. Blind spectrum sensing algorithm using sample features[J]. Journal of Signal Processing, 2016, 32(4):444- 450.(in Chinese)
[8] 徐偲,卢光跃,叶迎晖. 利用CM分量的无噪声不确定度频谱感知算法[J]. 信号处理, 2016,32(8):945-950.
Xu Cai, Lu Guangyue, Ye Yinghui. No noise uncertainty spectrum sensing algorithm using CM component[J]. Journal of Signal Processing, 2016, 32(8):945-950.(in Chinese)
[9] Lekomtcev D,Marsalek R.Evaluation of Kolmogorov-Smirnov test for cooperative spectrum sensing in real channel conditions[C]∥2014 22nd Telecommunications Forum Telfor, Belgrade, 2014:557-560.
[10] Teguig D, Nir V L, Scheers B. Spectrum sensing method based on goodness of fit test using chi-square distribution[J]. Electronics Letters, 2014, 50(9):713-715.
[11] Jin M, Guo Q H, Xi J T, et al. Spectrum sensing based on goodness of fit test with unilateral alternative hypothesis[J]. Electronics Letters, 2014,50(22):1645-1646.
[12] Teguig D, Le Nir V, Scheers B. Spectrum sensing method based on likelihood ratio goodness-of-fit test[J]. Electronics Letters, 2015, 51(3):253-255.
[13] Zeng Y, Liang Y C. Spectrum-Sensing Algorithms for Cognitive Radio Based on Statistical Covariannces[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4):1804-1815.
[14] Anderson T W. An Introduction to Multivariate Statistical Analysis[M]. 3th Edition. US Wiley-Interscience, 2003:127-129.
[15] Laio F. Cramer-von Mises and Anderson-Darling goodness of fit tests for extreme value distributions with unknown parameters[J]. Water Resources Research, 2004, 40(9):333-341.
[16] Stephens M A. EDF Statistics for Goodness of Fit and Some Comparisons[J]. American Statistical Association, 1974,69(347):730-737.


