1 引言
自适应波束形成技术起源于二十世纪,现已被广泛应用于雷达、声呐、无线通信等多个领域[1-3]。由于其能在多个期望信号方向形成波束增益,在多个干扰方向自适应形成零陷进行抑制的特性,现已被推广至自适应多波束形成领域[4-5]。在实际应用中,由于受到载体位置、速度快速变化以及姿态变化的影响,自适应多波束形成只能采用较少采样快拍数进行权值更新训练。在快拍数较少时,大多数自适应多波束形成算法特征值分解较不稳定,极易发生各波束主波束畸变的情况[6]。另一方面,当多个输入期望信号功率差异较大时,大多数自适应多波束形成算法对强期望信号波束形成效果会明显下降,此时强期望信号极易发生波束畸变、自适应零陷深度恶化甚至零陷方位错乱[7- 8]。
针对以上提出的两方面问题,有大量学者已经做了相关研究。文献[9]中运用的对角加载方法可有效降低多波束形成对快拍数的依赖度,但其对强期望信号波束稳健性的提升不明显。文献[10]中运用的非凸约束可提升多波束形成中弱期望信号波束稳健性,但是其对强期望信号波束稳健性的提升较有限。文献[11-12]中运用的协方差矩阵修正的思想可有效提高自适应多波束形成中强期望信号波束的稳健性,但是其会降低弱期望信号自适应波束形成效果。文献[13]提出的高效快速稳健自适应波束形成算法可有效提高强弱期望信号自适应波束的稳健性,但是该方法无法运用于小型阵列。以上算法均无法同时提高强弱期望信号的波束稳健性,所以实际应用中常对强弱期望信号分别采用不同的自适应波束形成算法进行多波束合成,这将极大耗费硬件计算资源。
针对此现象,本文结合子空间变换以及对角加载技术对协方差矩阵进行了重构,然后运用此协方差矩阵进行多波束权值训练。首先,通过子空间变换对信号子空间和干扰子空间进行向量化分析,然后结合对角加载技术重构出一个新的协方差矩阵,最后通过重构协方差矩阵训练出的多波束权值形成稳健自适应多波束。通过与其他多个算法波束图的对比分析可知本文算法在较少快拍数且多个输入期望信号功率差异较大的情况下,能够保持各波束主波束无畸变且提升各波束零陷的稳健性。随着期望信号功率的增强,本文算法输出信干噪比更优。
2 数学模型
假设已知有P个干扰信号和S个期望信号分别从不同的方向到达均匀线阵,N为阵元个数,λ为工作波长,阵元间距 d=λ /2,期望信号与干扰信号入射角度分别为![]() 和
和![]() 期望信号入射角已知,干扰信号入射角未知,则阵列输出可以表示为:
期望信号入射角已知,干扰信号入射角未知,则阵列输出可以表示为:
(1)
式中,sl(t)和v(θsl)分别为期望信号和期望信号阵列响应,zi(t)和v(θji)分别为干扰信号与干扰信号阵列响应,n(t)为噪声矢量。期望信号,干扰信号与噪声信号皆互不相关。阵列响应又称导向矢量,可表示为
(2)
式中θ为信号的入射角。期望信号导向矢量矩阵为V(θs)=[v(θs1),v(θs2),…,v(θsS)]N×S,干扰信号导向矢量矩阵为V(θj)=[v(θj1),v(θj2),…,v(θjP)]N×P,则多波束形成的输出信号可表示为
y(t)=WHx(t)
(3)
式中,y(t)和W分别为多波束形成输出矢量与多波束形成权矩阵,![]() 为N×1维列向量,代表每个波束的权矢量,(·)H代表矩阵的共轭转置。根据文献[14]中提出的线性约束最小方差(LCMV:Linearly Constrained Minimum Variance)自适应波束形成器,并结合以上多波束形成数学模型,可将自适应LCMV多波束形成表示为以下优化问题
为N×1维列向量,代表每个波束的权矢量,(·)H代表矩阵的共轭转置。根据文献[14]中提出的线性约束最小方差(LCMV:Linearly Constrained Minimum Variance)自适应波束形成器,并结合以上多波束形成数学模型,可将自适应LCMV多波束形成表示为以下优化问题
subject to (W∘V(θs))T![]() =f
=f
(4)
式中,∘代表矩阵Hadamard积,aνν为矩阵WHRW中对角元素,R=E{x(t)xH(t)}为理想协方差矩阵,![]()
![]() 为多波束线性约束矢量, f1, f2,…, fs均为固定值,具体设置方法文献[14]已有讨论,但在实际情况中很难获得理想协方差矩阵,所以根据文献[14]多波束形成器的权矢量可表示为
为多波束线性约束矢量, f1, f2,…, fs均为固定值,具体设置方法文献[14]已有讨论,但在实际情况中很难获得理想协方差矩阵,所以根据文献[14]多波束形成器的权矢量可表示为
(5)
式(5)中,dig表示将矩阵对角元素的倒数排列N行所得新矩阵,F为fT排列N行所得新矩阵,
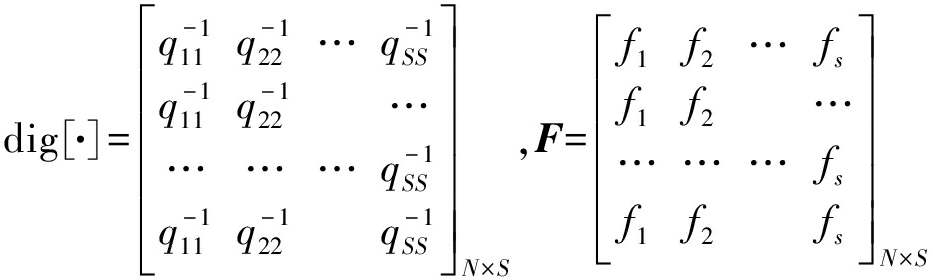
其中![]() 为矩阵
为矩阵![]() 的对角元素,
的对角元素,![]() 为采样协方差矩阵,M为采样快拍数。
为采样协方差矩阵,M为采样快拍数。
3 联合对角加载与子空间变换的协方差矩阵重构
3.1 对角加载
当采样快拍数较少时,采样协方差矩阵特征分解所得主特征值及所对应的特征向量能较快收敛,而噪声矢量对应的特征值则不能较快收敛,这将降低特征分解的有效性,影响后续子空间变换的性能,因此对采样协方差矩阵先进行对角加载,保证特征分解的有效性是极其必要的。本文针对此情况,讨论了一种动态自适应加载值选取方法,首先定义对角加载为
(6)
式中,λd是对角加载值,![]() 是对角加载后协方差矩阵,I为单位矩阵。
是对角加载后协方差矩阵,I为单位矩阵。
根据文献![]() 可表示为
可表示为
(7)
式中,B代表协方差矩阵的估计误差矩阵,ε为误差系数,因此对角加载后的协方差矩阵可以表示为
(8)
经文献[15]证明得λd的取值范围为
(9)
式中diag表示将矩阵对角元素依次排列组成的向量,std表示向量中各元素的标准差,trace表示矩阵的迹,由于加载值过大或过小都不利于波束稳健性,所以实际应用中可以选取式(9)中最大值与最小值的平均值进行对角加载,即
(10)
可见λd的选取不需要任何先验信息,其随着采样协方差矩阵的变化进行动态调整,便于工程应用。
3.2 子空间变换
假设S个期望信号中含有K个功率较强信号,即其功率强于噪声功率或与干扰功率相近,针对此类信号须先对协方差矩阵进行重构。上一节通过对角加载有效提升特征值分解收敛速度,此时对对角加载后采样协方差矩阵进行特征值分解,分解后所得主特征值对应的特征向量代表期望信号与干扰信号导向矢量子空间,则期望信号与干扰信号真实协方差矩阵(SPI矩阵:signals-plus-interferences 矩阵)可表示为
(11)
式中![]() 和
和![]() 分别为R的特征值由大到小排列,前P+S个较大特征值及对应的特征向量。则Rsj的估计
分别为R的特征值由大到小排列,前P+S个较大特征值及对应的特征向量。则Rsj的估计![]() 可通过文献[7]、[16]中约束条件得到
可通过文献[7]、[16]中约束条件得到
(12)
式中![]() 表明
表明![]() 是半正定矩阵。
是半正定矩阵。
如果接收信号之间互不相关,则真实SPI矩阵可以写为
(13)
式(13)中![]() 代表期望信号的功率,
代表期望信号的功率,![]() 代表干扰信号的功率。
代表干扰信号的功率。
本文定义关于方向θ的相关向量为
c(θ)=vec(v(θ)vH(θ))
(14)
式中vec(·)是将矩阵的每一列堆叠起来组成的列向量,因此,真实SPI协方差矩阵又能被表示为
(15)
根据式(15)可以得出vec(Rsj)位于相关向量的子空间,定义
(16)
T=[r1,r2,…,rc]
(17)
式(16)、(17)中,根据文献[17],定义S为相关矩阵,相关向量子空间可由矩阵S的特征向量构成,![]() 是矩阵S的非零特征值对应的特征向量,矩阵T的每一列相互正交且构建了相关向量子空间。此时我们添加一个约束条件重新定义式(12)
是矩阵S的非零特征值对应的特征向量,矩阵T的每一列相互正交且构建了相关向量子空间。此时我们添加一个约束条件重新定义式(12)
(18)
式(18)中第二个约束条件能够保证协方差矩阵估计误差在相关向量子空间的补空间中的投影消失。
为简化式(18)本文定义
(19)
根据式(19)可以将式(18)重新写为
(20)
由于向量![]() 与vec(R⊥)相互正交,所以式(20)可以被写为
与vec(R⊥)相互正交,所以式(20)可以被写为
(21)
式(21)可以被简化为
(22)
由于此时RT已为![]() 相关向量子空间投影所得结果,所以式(22)可写为
相关向量子空间投影所得结果,所以式(22)可写为
(23)
观察式(23)可得,式(23)的优化问题模型与式(12)完全相同,此时可用文献[7]、[16]中式(12)的最优解求解方法对式(23)进行求解。
根据式(23)可以获得估计SPI矩阵,采样协方差矩阵可以表示为
(24)
式中Rsj为真实SPI矩阵,Rτ为估计误差矩阵,![]() 为噪声方差。Rsj在采样协方差矩阵投影时能保持无失真。当Rτ投影到相关向量子空间时,其在相关向量子空间的补空间的投影消失[18]。本文算法类似于子空间投影算法,但是对子空间维度进行了扩展,通过式(22)中第二个约束条件
为噪声方差。Rsj在采样协方差矩阵投影时能保持无失真。当Rτ投影到相关向量子空间时,其在相关向量子空间的补空间的投影消失[18]。本文算法类似于子空间投影算法,但是对子空间维度进行了扩展,通过式(22)中第二个约束条件![]() 在扩展子空间中降低Rτ对子空间的影响,对于N阵元均匀线阵,矩阵T的秩为2N-1,则Rτ在N2-2N+1维子空间的投影消失,相较文献[10]、[19]中算法,不受估计误差影响的子空间维度有明显提升。另外,随着阵元数的增加,误差消失的子空间维度将远大于相关向量子空间维度。因此,本文算法将减少大部分强期望信号所带来SPI矩阵估计误差所造成的影响。
在扩展子空间中降低Rτ对子空间的影响,对于N阵元均匀线阵,矩阵T的秩为2N-1,则Rτ在N2-2N+1维子空间的投影消失,相较文献[10]、[19]中算法,不受估计误差影响的子空间维度有明显提升。另外,随着阵元数的增加,误差消失的子空间维度将远大于相关向量子空间维度。因此,本文算法将减少大部分强期望信号所带来SPI矩阵估计误差所造成的影响。
根据式(23)获得的估计SPI矩阵![]() 可以将重构的协方差矩阵训练所得强期望信号多波束权值W'表示为
可以将重构的协方差矩阵训练所得强期望信号多波束权值W'表示为
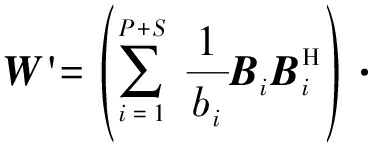
(25)
式中bi和Bi分别为![]() 的P+S个主特征值与对应的特征向量,V(θsk)为K个强期望信号导向矢量构成方向矢量, FK为K个强期望信号波束的约束条件矢量。当计算第k个强期望信号的权值wk时,自适应波束形成会将其他k-1个强期望信号视为强干扰信号形成零陷对其进行抑制,所以会形成k-1+P个自适应零陷,所以强期望信号与干扰信号的个数必须满足k-1+P<N。
的P+S个主特征值与对应的特征向量,V(θsk)为K个强期望信号导向矢量构成方向矢量, FK为K个强期望信号波束的约束条件矢量。当计算第k个强期望信号的权值wk时,自适应波束形成会将其他k-1个强期望信号视为强干扰信号形成零陷对其进行抑制,所以会形成k-1+P个自适应零陷,所以强期望信号与干扰信号的个数必须满足k-1+P<N。
针对剩下的S-K个功率较弱期望信号,即其功率与噪声功率相近或弱于噪声功率,因为其功率与噪声相近,所以前P+S个非零特征值中最小的S-K个特征值未必代表的是弱期望信号,此时需对上文得到的矩阵![]() 进行再处理,得
进行再处理,得
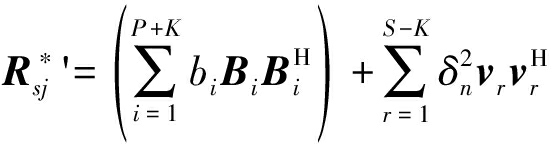
(26)
式中vr为S-K个功率较弱期望信号的导向矢量,则弱期望信号多波束权值W ''表示为
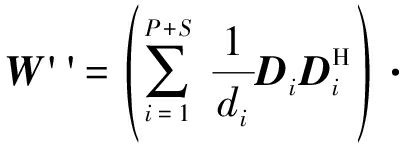
(27)
式中di和Di分别为![]() 的P+S个主特征值与对应的特征向量,V(θse)为S-K个弱期望信号导向矢量构成的方向矩阵,FS-K为S-K个弱期望信号波束的约束条件矢量,可见弱期望信号波束形成只需在重构协方差矩阵上替换若干子空间,这样就避免了针对强弱期望信号需要采用不同的自适应波束形成算法。在实际应用中,首先可运用对角加载后的采样协方差矩阵进行空间谱估计[20],由于一般情况下干扰信号功率较强且干扰信号与期望信号同方向到达的概率较小,所以可通过空间谱估计的办法进行干扰信号个数P的估计;其次,由于期望信号参数皆已知,所以要求在对各期望信号进行自适应多波束合成前对各信号进行简单的测幅判断其功率大小,也可以直接求
的P+S个主特征值与对应的特征向量,V(θse)为S-K个弱期望信号导向矢量构成的方向矩阵,FS-K为S-K个弱期望信号波束的约束条件矢量,可见弱期望信号波束形成只需在重构协方差矩阵上替换若干子空间,这样就避免了针对强弱期望信号需要采用不同的自适应波束形成算法。在实际应用中,首先可运用对角加载后的采样协方差矩阵进行空间谱估计[20],由于一般情况下干扰信号功率较强且干扰信号与期望信号同方向到达的概率较小,所以可通过空间谱估计的办法进行干扰信号个数P的估计;其次,由于期望信号参数皆已知,所以要求在对各期望信号进行自适应多波束合成前对各信号进行简单的测幅判断其功率大小,也可以直接求![]() 然后用
然后用![]() 对所有期望信号进行波束形成,此时强信号波束形成效果会有少许下降。最后通过本文方法可得自适应多波束形成的权矢量W为
对所有期望信号进行波束形成,此时强信号波束形成效果会有少许下降。最后通过本文方法可得自适应多波束形成的权矢量W为
W=[W ',W '']
(28)
下面通过仿真实验进一步验证本文算法对自适应多波束形成稳健性的提升。
4 仿真分析
本文设定一个阵元数为16的均匀线阵,阵元间距λ/2。干扰信号到达方向为70°,干噪比为30 dB。期望信号、干扰信号和噪声三者相互独立且噪声为高斯白噪声,蒙特卡罗次数设定为200次。
(1)仿真1
设定采样快拍数为10~100,仅考虑一个期望信号,到达方向为10°,信噪比为12 dB,画出对角加载前后本文算法的输出信干噪比对比图。
从图1可以看出,当快拍数较少时,通过子空间变化重构所得协方差矩阵波束形成性能有明显下降,随着快拍数的增加性能逐渐提升并收敛。本文算法结合对角加载的子空间变换在快拍数较少时性能更优且收敛速度较快,证明对角加载有效的降低了子空间变换对快拍数的依赖度。
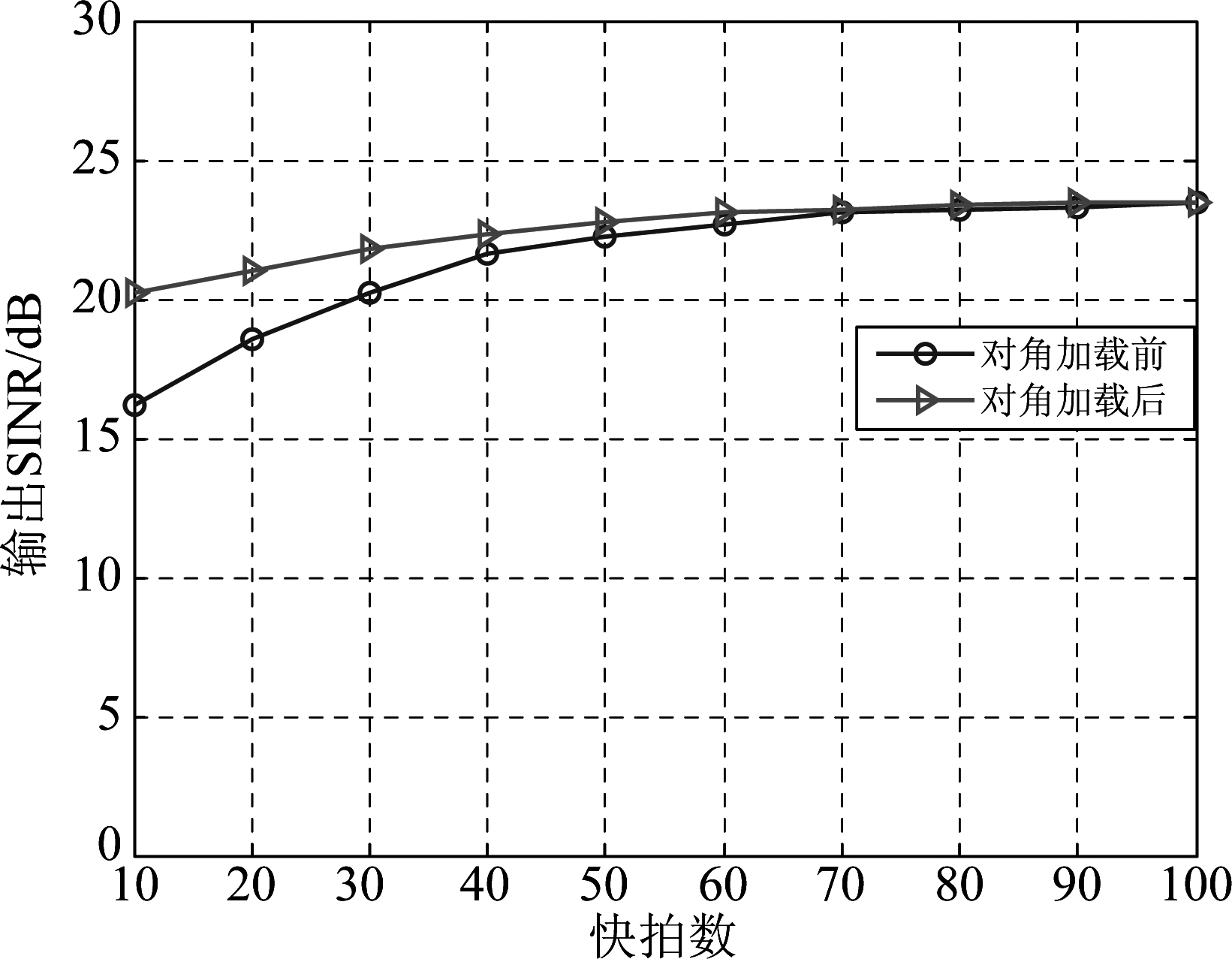
图1 对角加载前后本文算法的输出信干噪比对比图
Fig.1 Comparison of output SINR between the proposed algorithm and the proposed algorithm without diagonal loading
(2)仿真2
设采样快拍数为16,期望信号到达方向分别为-30°和10°,信噪比分别为-30 dB和25 dB,比较几种不同算法的归一化强期望信号波束图。
从图2可以看出,在期望信号较强且快拍数较少的情况下,文献[14]经典算法主波束消失,文献[9]、[12]算法主波束保持稳定但干扰方向零陷严重偏移,本文算法不仅主波束稳定且在干扰方向零陷依然存在,波束旁瓣较其他算法更低,虽然本文算法稳健性有所提升,但是当期望信号功率与干扰信号功率强度越接近时,本文算法性能也将快速下降。
(3)仿真3
设定采样快拍数为16,期望信号到达方向分别为-30°和10°,信噪比分别为-30 dB和25 dB,比较几种不同算法的归一化弱期望信号波束图。
从图3可以看出,在期望信号较弱且快拍数较少的情况下,文献[14]算法主波束偏移且零陷深度明显恶化,文献[9]、[12]算法与本文算法均能保持主波束恒定且干扰方向零陷稳定存在,但是本文算法的自适应零陷更深,另一方面也可看出针对弱期望信号波束形成,强期望信号已被视为干扰信号在其方向形成零陷对其进行抑制,与前文分析一致。
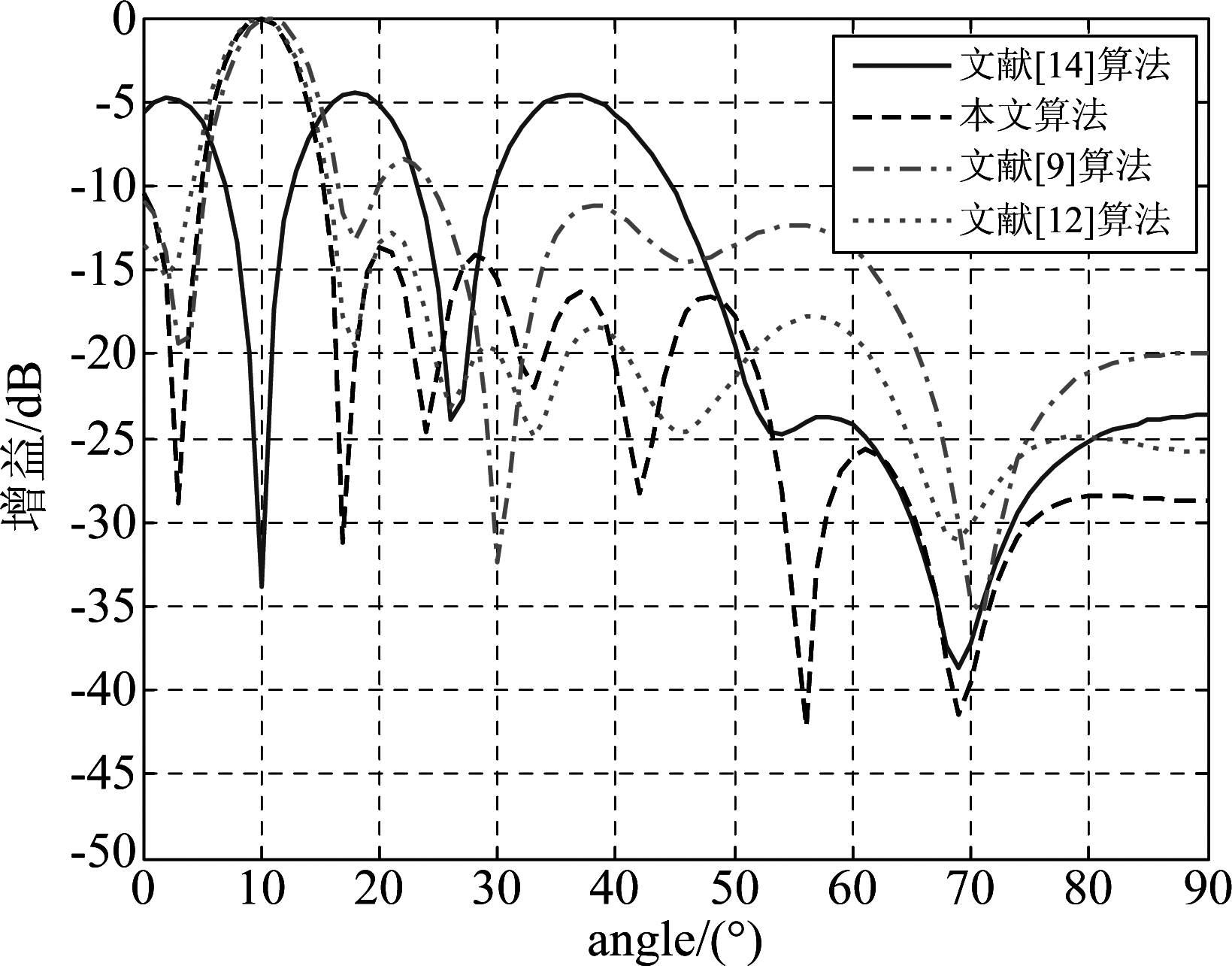
图2 快拍数较少情况下不同算法强期望信号波束图
Fig.2 The multi-beam pattern of the strong desired signal between different algorithms with a small number of snapshots
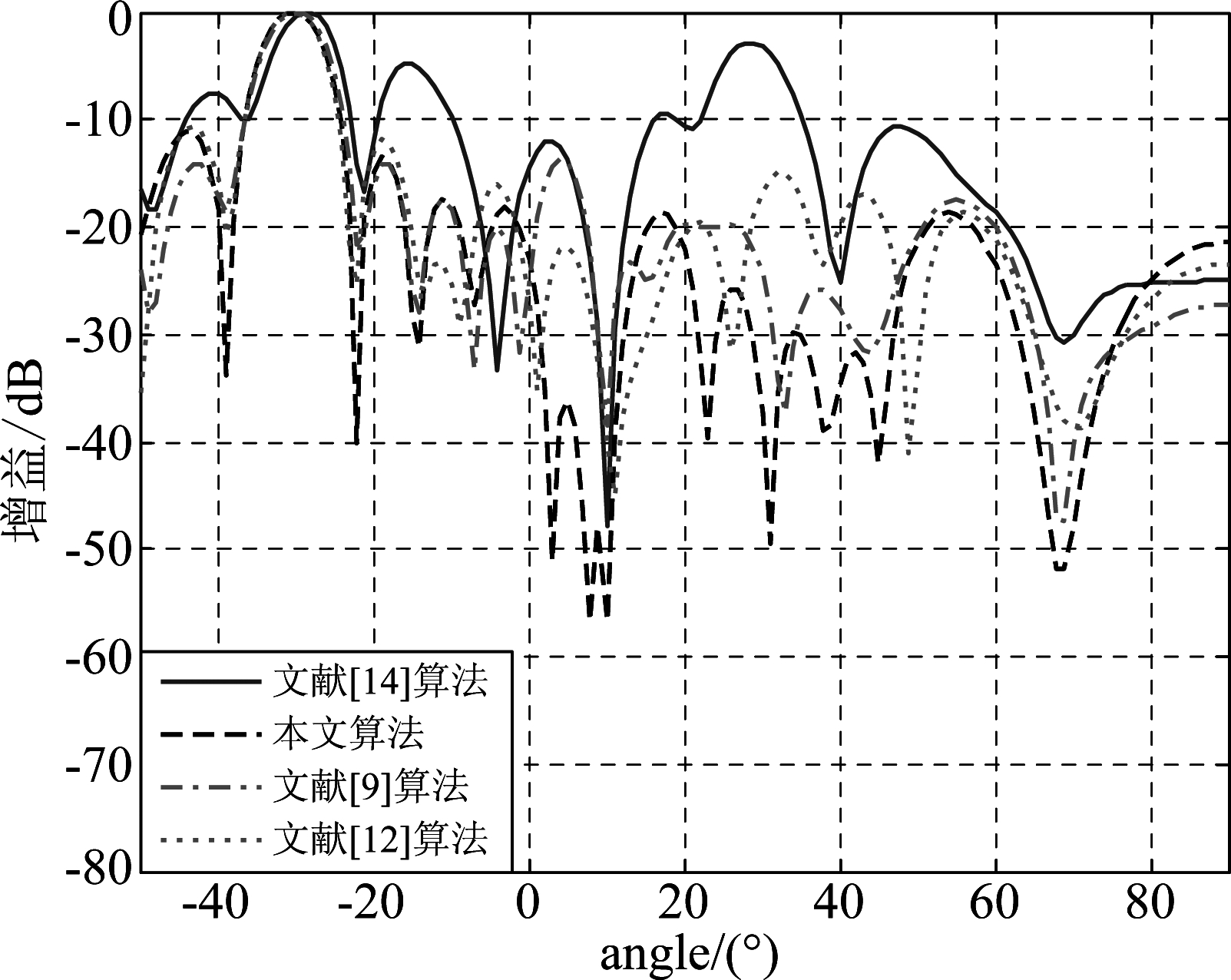
图3 快拍数较少情况下不同算法弱期望信号波束图
Fig.3 The multi-beam pattern of the weak desired signal between different algorithms with a small number of snapshots
(4)仿真4
设定采样快拍数为16,仅考虑一个期望信号,到达方向为10°,信噪比为-25~25 dB,比较几种不同算法的输出信干噪比对比图。
从图4可以看出,随着期望信号信噪比的提升,文献[14]经典算法在期望信号较强时性能下降最快;文献[9]算法对强期望信号波束形成效果有所提升,但是当期望信号信噪比大于10 dB时,性能也开始下降;文献[12]算法在期望信号信噪比大于10 dB时,性能开始快速下降,且在期望信号信噪比较低时性能低于其他算法;本文算法在期望信号由弱到强期间一直保持输出信干噪比的稳定性,抗干扰性能较其他三种算法更优。
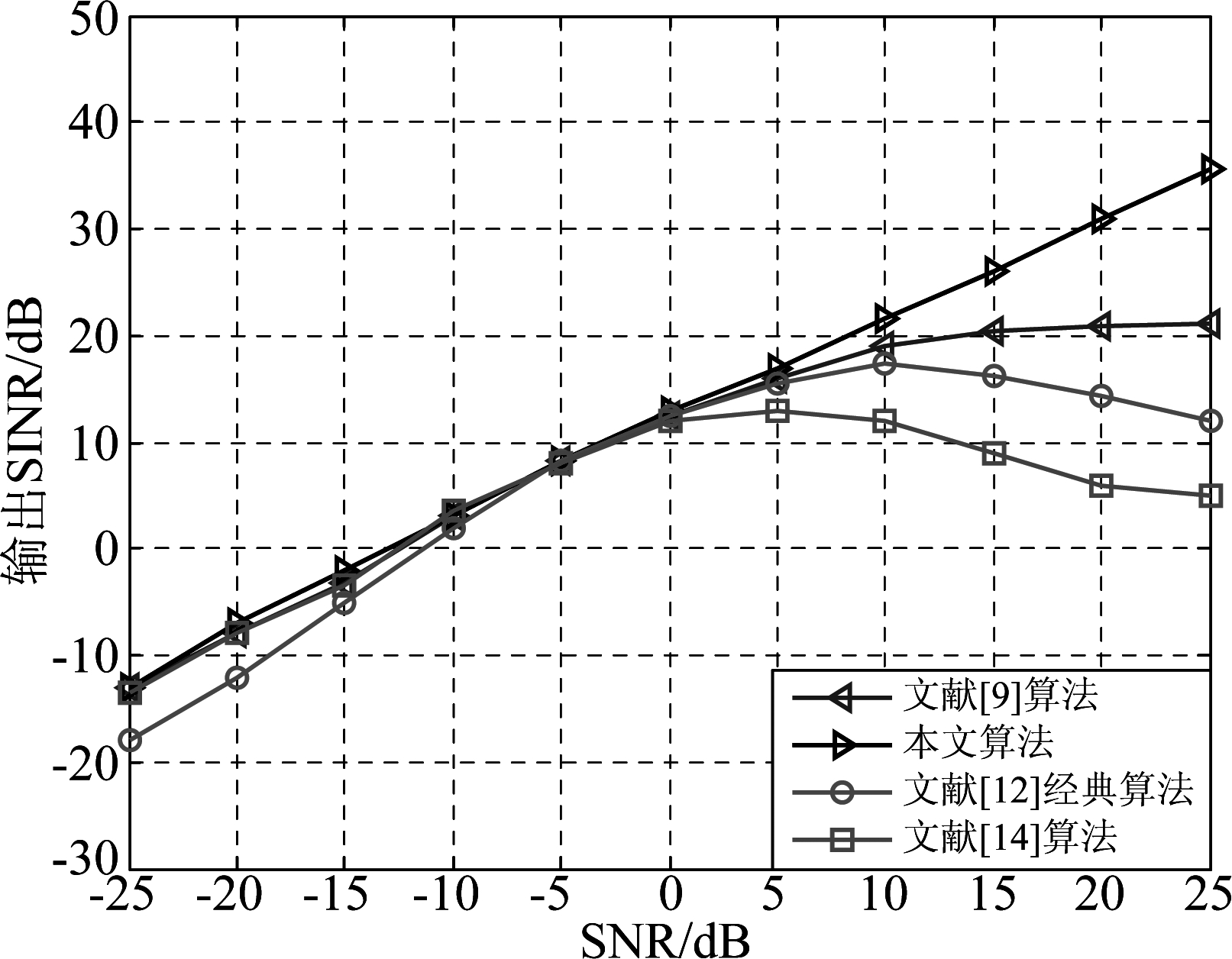
图4 不同算法的输出信干噪比对比图
Fig.4 Comparison of output SINR of different algorithms
(5)仿真5
设定采样快拍数为16,仅考虑一个期望信号,已知期望到达方向为10°,信噪比为-25~25 dB,期望信号实际到达方向与已知方向存在5°的偏差,画出本文算法的输出信干噪比图。
从图5可以看出,当期望信号到达角存在偏差时,本文算法性能有明显下降,且随着期望信号信噪比的提升,性能恶化越严重。由于期望信号到达角存在偏差,当期望信号较强时,本文算法会将此强期望信号视为干扰信号对其进行抑制,导致主波束发生严重畸变。由于此类情况在实际应用中常有发生,所以可运用文献[16]中的迭代算法对期望信号导向矢量进行迭代修正,以此获得最优的波束形成效果,可见,在实际应用中,本文算法尚需进一步的完善与改进。
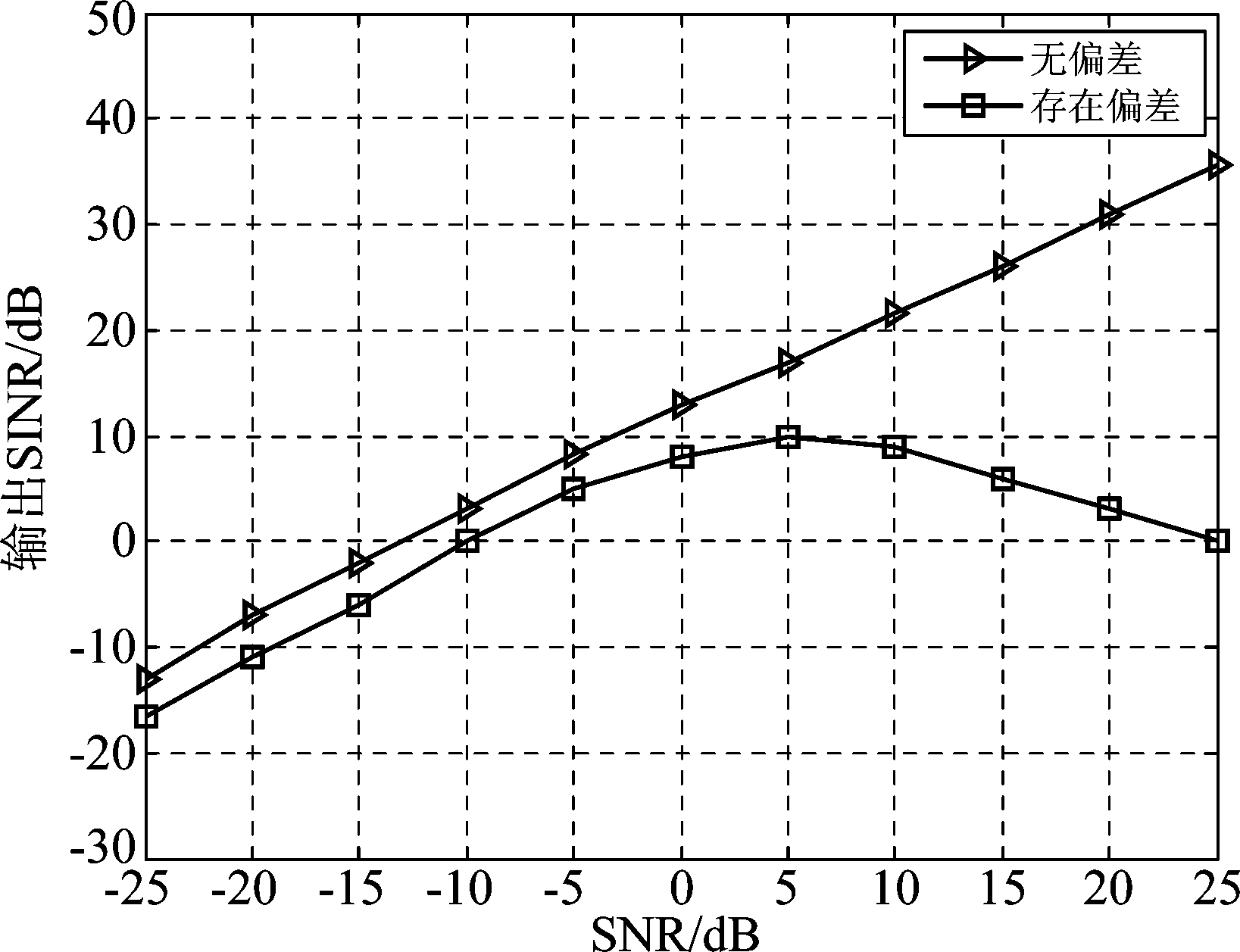
图5 期望信号到达方向存在偏差时本文算法输出信干噪比对比图
Fig.5 Comparison of output SINR of the proposed algorithm when the arrival direction of the desired signal has error
综上所述,本文算法波束方向图可同时保持强弱期望信号主波束与干扰方向零陷的稳健性且通过对比不同算法的输出信干噪比可得本文算法的抗干扰性能更优,所以本文算法较好的解决了在快拍数较少情况下,同时对强弱期望信号进行波束形成的问题,但是针对期望信号导向矢量存有误差等实际情况,本文算法尚有不足。
5 结论
本文提出了一种基于协方差矩阵重构的稳健自适应多波束形成算法,该算法结合子空间变换与对角加载技术,降低了自适应多波束形成对采样快拍数的依赖性,并且在多个输入期望信号功率差异较大情况下,有效的抑制多波束畸变零陷偏移等多波束恶化情况的发生,提高了多波束的稳健性。通过多个对比实验验证了本文算法较其他多个稳健多波束形成算法稳健性更优,抗干扰性能更好。本文算法可同时提高多个强弱期望信号自适应波束的稳健性,有广阔的工程应用前景,但是针对期望信号到达方向未知或者存有偏差的情况,本文算法尚需进一步改进和完善。
参考文献
[1] Brennan L E, Mallet J D, Reed I S. Adaptive arrays in airborne MTI radar[J]. IEEE Transactions Antennas & Propagation, 1976, 24(5): 607- 615.
[2] Kim S M, Baek M W, Nahm S H. Visible light communication using TDMA optical beamforming[J]. EURASIP Journal on Wireless Communications and Networking, 2017, 56.
[3] Agrawal S, Rana V, Jagannatham AK. Queuing analysis for multiple-antenna cognitive radio wireless networks with beamforming[J]. IEEE Signal Processing Letters, 2017, 24(3): 334-338.
[4] 李鹏程,田玉坤,杨峰,等. 基于LCMV的卫星导航多波束形成抗干扰技术[J]. 电子信息对抗技术, 2016, 31(4): 47-51.
Li Pengcheng, Tian Yukun, Yang Feng, et al. Anti-jamming technology of satellite navigation multiple beam forming based on LCMV[J]. Electronic Information Warfare Technology, 2016, 31(4): 47-51. (in Chinese)
[5] 林森. 伪随机码加权的自适应多波束形成新方法[J]. 无线电通信技术, 2015, 41(1): 35-37.
Lin Sen. Novel adaptive multibeam forming method based on pseudo-random noise codes weighting[J]. Radio Communication Technology, 2015, 41(1): 35-37. (in Chinese)
[6] Habets E, Benesty J, Naylor P A. A speech distortion and interference rejection constraint beamformer[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2012, 20(3): 854- 867.
[7] Feldman D D, Griffiths L J. A projection approach for robust adaptive beamforming[J]. IEEE Transactions on Signal Processing, 1994, 42(4): 867- 876.
[8] Widrow B, Duvall K M, Gooch R P, et al. Signal cancellation phenomena in adaptive antennas: causes and cures[J]. IEEE Transactions Antennas & Propagation, 1982, 30(3): 469- 478.
[9] Carlson B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace & Electronic Systems, 1988, 24(4): 397- 401.
[10] Vorobyoy S A, Gershman A B, Luo Z Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313-324.
[11] Hassanien A, Vorobyoy S A, Wong K M. Robust adaptive beamforming using sequential quadratic programming: an iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters, 2008, 15: 733-736.
[12] Khabbazibasmenj A, Vorobyoy S A, Hassanien A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE Transactions on Signal Processing, 2012, 60(6): 2974-2987.
[13] Rahmani M, Bastani M H, Shahraeeni S. Two layers beamforming robust against direction-of-arrival mismatch[J]. IET Signal Processing, 2014, 8(1): 49-58.
[14] Lorenz R, Boyd S P. Robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2005, 53(5): 1684-1696.
[15] Ma N, Goh J T. Efficient method to determine diagonal loading value[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Hong Kong, 2003, 5(5): 341-344.
[16] Zhuang J. Robust adaptive array beamforming with subspace steering vector uncertainties[J]. IEEE Signal Processing Letters, 2012, 19(12): 785-788.
[17] Khabbazibasmenj A, Vorobyov S A, Hassanien A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE Transactions on Signal Processing,2012,60(6):2974-2987.
[18] Mostafa R, Mohammad H B. Robust and rapid converging adaptive beamforming via a subspace method for the signal-plus-interferences covariance matrix estimation[J]. IET Signal Processing, 2014, 8(5): 507-520.
[19] 关刚强,聂俊伟,黄仰博,等. 子空间投影后波束形成的导航接收机抗干扰性能分析[J]. 国防科技大学学报, 2016, 38(3): 50-54.
Guan Gangqiang, Nie Junwei, Huang Yangbo, et al. Performance analysis of anti-jamming algorithm in GNSS receiver utilizing subspace projection and beamforming[J]. Journal of National University of Defense Technology, 2016, 38(3): 50-54. (in Chinese)
[20] 鲍晓红,黄绣坤. 一种新的二维空间谱估计方法—二维组合阵列ESPRIT[J]. 信号处理, 1992, 8(1): 24-30.
Bao Xiaohong, Huang Xiukun. A new method of two-dimensional spatial spectrum estimation based on ESPRIT using combined array[J]. Signal Processing, 1992, 8(1): 24-30. (in Chinese)

