1 引言
跳频通信是一种抗干扰性强且具有低截获概率的通信技术,其在军事和民用通信中有着广泛的应用。对跳频信号进行参数估计是一个十分重要的课题,比如在民用通信中,对跳频信号进行参数估计可以估计出特定频段用户数,以避免频率碰撞影响通信的质量;在军事通信中,对跳频信号进行参数估计可以对敌方的跳频电台实施干扰从而破坏敌方的通信[1- 4]。在众多的跳频信号参数估计的方法中,时频分析是一种直观有效的工具,近年来受到了广泛的关注。目前已有的时频分析方法包括线性和非线性变换。线性时频分析方法主要是短时傅里叶变换(STFT, short time Fourier transform)、Gabor变换、小波以及s变换[5]。线性时频分析方法由于不确定原则,其时间分辨率和频率分辨率相互制约。非线性时频分析主要是Wigner-Ville分布、平滑伪Wigner-Ville分布[6]。Wigner-Ville分布具有很好的时频分辨率,但是存在交叉项,平滑伪Wigner-Ville分布不存在交叉项,但是由于在时域和频域加窗使得时频分辨率降低。所以,现有的时频分析方法在分析跳频信号时存在诸多的局限。
文献[7]利用近似l0算法对跳频信号时频图进行重构,但是算法的收敛性不高。文献[8]利用稀疏贝叶斯学习算法对信号进行稀疏重构,但是只针对于单测量向量模型(SMV, single measurement vector)。本文利用文献[7,9]中对接收信号的处理得到的观测矩阵类似于多测量向量模型(MMV, multiple measurement vector),利用块贝叶斯学习(bSBL, block sparse Bayesian learning)框架,将MMV转换为SMV,并利用观测矩阵的每一列在时间上的相关性提出TBSBL算法,利用该算法可以得到精度较高的跳频信号时频图,但是由于算法计算过程在一个高维的参数空间,计算量巨大[10],因此根据文献[11]的思想对TBSBL算法进行改进利用近似算法将高维空间变换到原始空间进行处理,改进后的TBSBL算法性能基本保持不变但是算法的收敛速度却大大的增加。
2 跳频信号时频稀疏模型
2.1 跳频信号模型
根据跳频信号的产生原理,在单天线接收的情况下,观测时间T内M个跳频信号同时进入接收机的接收信号表达式为:
(1)
其中,sm(t)表示的是接收机接收到的第m个跳频信号,ν(t)表示的是均值为0,方差为σ2的加性高斯白噪声,y(t)表示的是接收机接收到的M个跳频信号与噪声的叠加。其中
(2)
其中t′=t-(k-1)Tm-αTm,am是单个跳频信号sm(t)的幅度,K表示的是在观测时间T内的跳数,第k跳所对应的频率为fmk,第一跳的持续时长为αTm,φmk是第k跳的初相,rect表示的是单位矩形脉冲。对式(1)进行离散采样得到:
(3)
n∈{0,1,...,N-1},N为时间T内的采样点数,wmk=2πfmkTs,式(3)的矢量形式为:
(4)
2.2 跳频信号时频分析的稀疏模型
根据时频处理机制,将接收到的信号y分割成有重叠的M段,按照时间精度的要求,每段包含P个数据,那么每段信号的表达式为[7]:
yi=y(i![]() iL+P-1)
iL+P-1)
(5)
其中1≤i≤M,L表示的是分段间隔,M=![]()
![]()
![]() ,从而构造出观测矩阵:
,从而构造出观测矩阵:
(6)
假设频率集ω=[f1:Δf: fN]中包含跳频信号的所有频率,Δf为频率集中频率间隔,Δf越小那么稀疏后的时频图频率分辨率就越高,N为频率集中频率的个数,那么可以构造傅里叶正交基矩阵Φ。
(7)
其中:φ(fi)=[ej2πfi/fs,...,ej2πfiP/fs]T,P<N,那么跳频信号的稀疏模型为:
Y=ΦX+V
(8)
X=[x1,...,xM],其中![]() 代表的是第i段观测数矩的时频图。V是未知的噪声矩阵。
代表的是第i段观测数矩的时频图。V是未知的噪声矩阵。
由式(8)可以看出,时频图的稀疏模型属于MMV模型,文献[12-14]证明对于该模型在求解的过程中其收敛速度明显的快于SMV模型。
3 块稀疏贝叶斯学习(bSBL)框架下TBSBL算法
首先,假设所有的Xi·,(∀i)是相互独立的,而且X的每一行密度均服从高斯分布,则:
p(Xi·;γi,Bi)~N(0,γiBi),i=1,...,M
(9)
其中γi是非负超参数控制X的行稀疏,在SBL算法中当γi=0时,Xi·=0。Bi是正定矩阵,用来捕捉X的相关结构。通过矢量化,即![]() 处理,这样MMV就转化为bSMV模型
处理,这样MMV就转化为bSMV模型
y=Dx+v
(10)
假设v中的元素独立且服从高斯分布,那么p(vi)~N(0,λ),vi表示v中的第i个元素,λ是方差,那么对于该模型满足:
p(y|x;λ)~N(Dx,λI)
(11)
x的先验概率为:
p(x;γi,Bi,∀i)~N(0,![]() 0)
0)
(12)
其中:
![]() 0=diag(γ1B1,…,γMBM)
0=diag(γ1B1,…,γMBM)
(13)
由贝叶斯定理可以得到x的后验概率:
p(x|y;λ,γi,Bi,∀i)=N(ux,![]() x)
x)
(14)
均值和方差分别为:
![]()
![]() xDTy
xDTy
(15)
![]() x=
x=![]() 0-
0-![]() 0DT(λI+D
0DT(λI+D![]() 0DT)-1D
0DT)-1D![]() 0
0
(16)
因此,一旦给定所有的超参数λ,γi,Bi,∀i,x的最大后验估计即为:
x* ux=
ux=![]() 0DT(λI+D
0DT(λI+D![]() 0DT)-1y
0DT)-1y
(17)
3.1 超参数的估计
超参数的估计方法一般采用Evidence最大化或者Type-II最大似然的方法。通过求接收数据y的边缘概率密度,进行最大似然估计,从而估计出超参数。注意,文献[15]证明了如果X的每一行都对应一个矩阵Bi,那么将导致计算结果的过拟合,同时证明了用一个正定矩阵B来替代Bi,其全局最下值并不受到影响,所以本文要估计的超参数为Θ=[γ1,...,γM,B,λ]。
为了计算出超参数,利用Evidence最大化算法(EM)最大化边缘似然函数p(y;Θ)其等同于最小化lg p(y;Θ),可得到有效的代价函数:
![]()
![]() y|
y|
(18)
其中![]() y
y λI+D
λI+D![]() 0DT,EM算法将x看作隐藏的变量,并求Q(Θ)的最大化:
0DT,EM算法将x看作隐藏的变量,并求Q(Θ)的最大化:
Q(Θ)=Ex|y[lg p(x,y;Θ)]=Ex|y[lg p(y|x;λ)]+
Ex|y[lg p(x;γ1,...,γM,B)]
(19)
可以看出在式(19)中第一项与γ和B均不相关,所以为了估计γ和B,式(19)可以简化为Q(γ,B)=Ex|y[lg p(x;γ1,...,γM,B)],其中:
(20)
其中Γ diag(γ1,...,γM),那么:
diag(γ1,...,γM),那么:
(21)
其中ux和![]() x通过式(15)和式(16)求出,对Q(γ,B)中γ求偏导可得:
x通过式(15)和式(16)求出,对Q(γ,B)中γ求偏导可得:
(22)
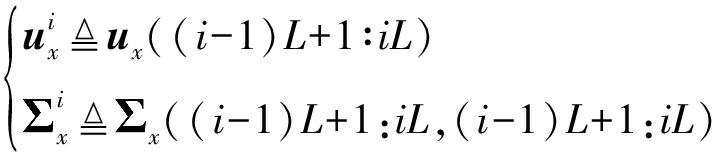
可以推导出:
(23)
同理对B求偏导推出:
(24)
为了得出超参数λ,对式(19)中的第一项进行分析即:
(25)
其中![]() 为上一次迭代得到的估计值,那么可以得到:
为上一次迭代得到的估计值,那么可以得到:
(26)
那么式(16)、(17)、(23)、(24)、(26)本文称之为TBSBL算法。
4 对TBSBL算法改进
上述算法具有很好的性能,但是算法的收敛速度不快,因为该算法在求解超参数时其过程属于高维参数求解,而不是原始空间中。比如,在bSBL框架下字典矩阵的维数为NL×ML,但是在原始的MMV模型中,字典矩阵的大小为N×L,其算法的复杂度可见一般。因此,本文利用一个近似的算法将TBSBL算法转换到原始空间进行计算。
文献[11]介绍了MSBL算法,该算法在估计超参数时并不会出现TBSBL算法的缺点,于是根据TBSBL算法的特点并结合MSBL算法中的思想引入近似替换的方法将高维矩阵变换到原始的矩阵中进行计算,其具体过程如下:
首先采用以下近似[10]:
(λINL+D![]() 0DT)-1=(λINL+(ΦΓΦT)⊗B)-1≈
0DT)-1=(λINL+(ΦΓΦT)⊗B)-1≈
(λIN+ΦΓΦT)-1⊗B-1
(27)
利用式(27)来简化γi的迭代(式(23)):
(λINL+D![]() 0DT)-1·(φi⊗IL)B]≈
0DT)-1·(φi⊗IL)B]≈
(28)
那么利用式(27)进行简化可得:
ux≈(Γ⊗B)(ΦT⊗I)[(λI+ΦΓΦT)-1⊗B-1]
vec(YT)=[ΓΦT(λIN+ΦΓΦT)-1]⊗I·vec(YT)=
vec(XT)
(29)
所以式(23)经过简化可以得到:
(30)
同样利用式(27)对超参数B进行估计,具体的过程如下:
![]() x=
x=![]() 0-
0-![]() 0DT(λI+D
0DT(λI+D![]() 0DT)-1D
0DT)-1D![]() 0=
0=
Γ⊗B-(Γ⊗B)(ΦT⊗I)(λI+D![]() 0DT)-1·
0DT)-1·
(Φ⊗I)(Γ⊗B)≈Γ⊗B-[(ΓΦT)⊗B]·
[(λIN+ΦΓΦT)-1⊗B-1]·[(ΦΓ)⊗B]=
(Γ-ΓΦT(λIN+ΦΓΦT)-1ΦΓ)⊗B
(31)
根据对![]() 的定义,可以得到
的定义,可以得到![]() 因此式(24)可以改为:
因此式(24)可以改为:
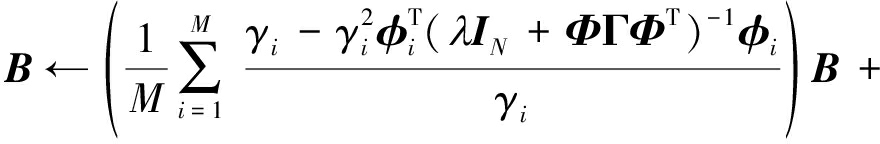
(32)
从上面的分析,本文直接构建一个参数矩阵B的计算方法:
(33)
其中![]() 为了增加算法的稳健性,对式(33)进行改进:
为了增加算法的稳健性,对式(33)进行改进:
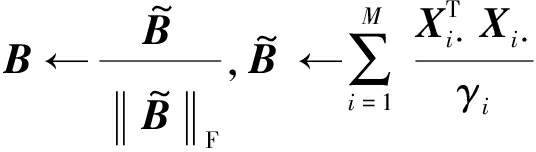
(34)
但是由于对γi和Xi·的估计存在误差,所以为了使得算法更加的精确,引入正参数η用来修正![]()
(35)
类似的对λ进行近似处理得到:
(36)
通过对(30)、(34)、(35)、(36)观察发现,经过处理后的算法,其计算过程都是在Φ所属的原始空间中进行,这样就避免了处理高维矩阵D,大大的节省了算法的开销。对于文中的算法复杂度进行分析,可以得出本文算法的复杂度主要集中于超参数的估计,两种算法的计算复杂度主要体现在式(23)、(24)、(26)和式(30)、(34)、(36)中。在TBSBL算法中,![]() 对角元素计算的运算复杂度为O(KN2P),其余超参数估计的复杂度分别为O(PM)、O(PN)、O(KPMN),其中K为迭代的次数,这样对于TBSBL算法其总的运算复杂度为O(KN2P)。改进TBSBL算法后,由于字典矩阵的维度降低,在迭代的过程中由于搜索范围的降低,其运算复杂度为O(N2L),可以看出O(N2L)≪O(KN2P),所以改进后的算法复杂度将减少。
对角元素计算的运算复杂度为O(KN2P),其余超参数估计的复杂度分别为O(PM)、O(PN)、O(KPMN),其中K为迭代的次数,这样对于TBSBL算法其总的运算复杂度为O(KN2P)。改进TBSBL算法后,由于字典矩阵的维度降低,在迭代的过程中由于搜索范围的降低,其运算复杂度为O(N2L),可以看出O(N2L)≪O(KN2P),所以改进后的算法复杂度将减少。
下面对算法的步骤进行总结:
(1)对观测信号y进行变换,构造跳频时频图的稀疏模型;
(2)设置贝叶斯学习过程中的超参数的初始值B,γi,λ,以及迭代次数的最大值;
(3)利用贝叶斯定理,求得X的最大后验概率,以及其分布的均值ux和协方差![]() x;
x;
(4)利用式(30)、(34)、(35)、(36)对超参数进行估计。
5 仿真结果以及性能分析
为了验证本文算法的有效性,仿真以单跳信号和多跳信号为例。假设信号的采样频率fs=20 MHz,观测时间T=0.02 s,跳速fh=200,在观测时间段内一共发生了4次频率跳变,其频率分别为[7 MHz,2 MHz,4 MHz,1 MHz],频率集ω=[1![]() 100
100![]() 10M],接收信号的分段间隔L=10。超参数的初始值γ0=0.01,λ0=0.01,B0=4eye(L)。该跳频信号的重构的时频图如图1所示。
10M],接收信号的分段间隔L=10。超参数的初始值γ0=0.01,λ0=0.01,B0=4eye(L)。该跳频信号的重构的时频图如图1所示。
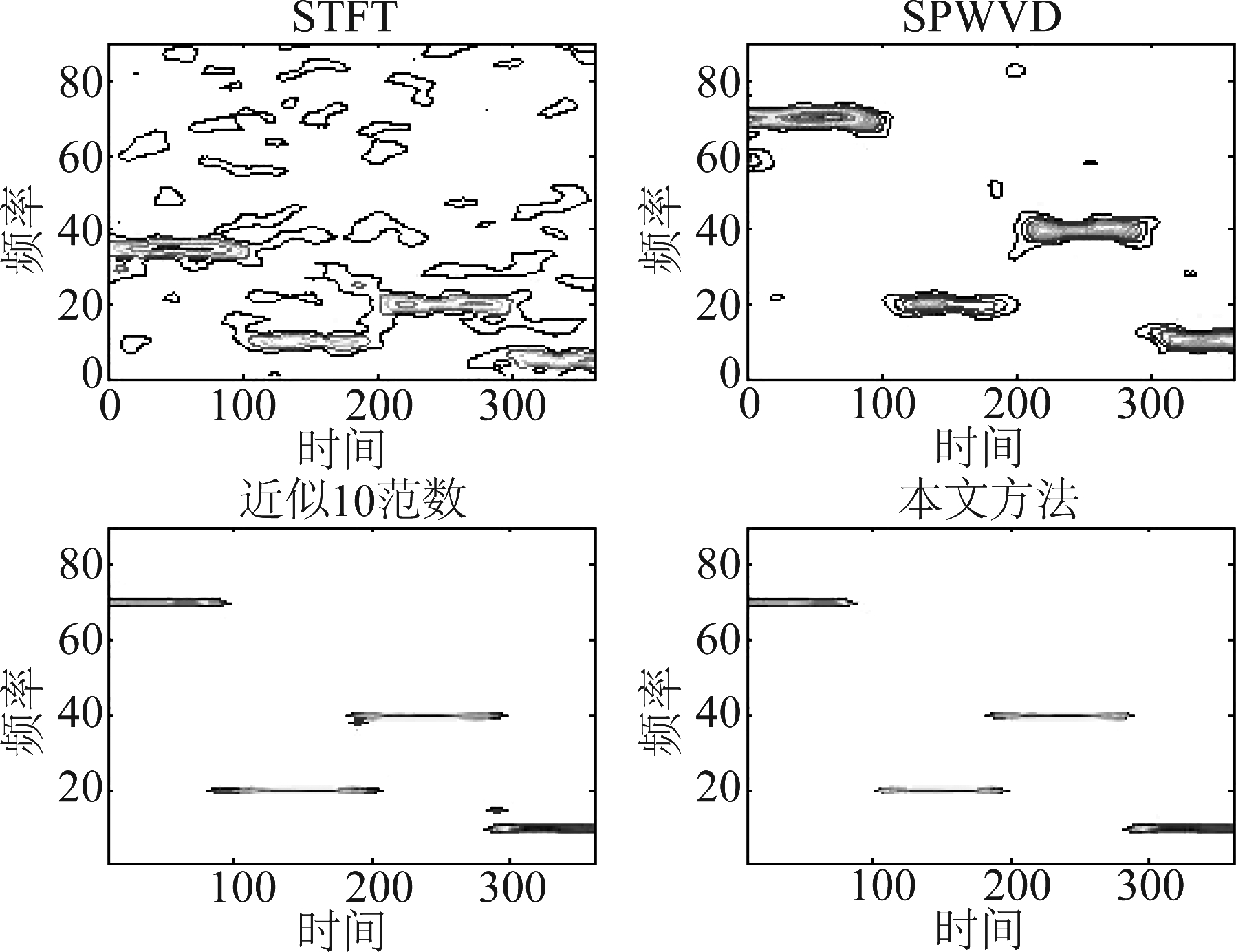
图1 信噪比为-5 dB时单跳信号的时频图
Fig.1 The time-frequency diagram of single FH signal with SNR of -5 dB
对于多跳系统而言,在上述仿真的基础上再加一个跳频信号,其频变频率分别为[8 MHz,5 MHz,8 MHz,5 MHz],那么同步多跳频信号在SNR=0 dB时的时频图为图2。若第二个跳频信号起跳时刻相比于第一个跳频晚0.5个跳变周期,那么该多跳系统属于异步多跳频信号,其在SNR=0 dB时的时频图为图3。
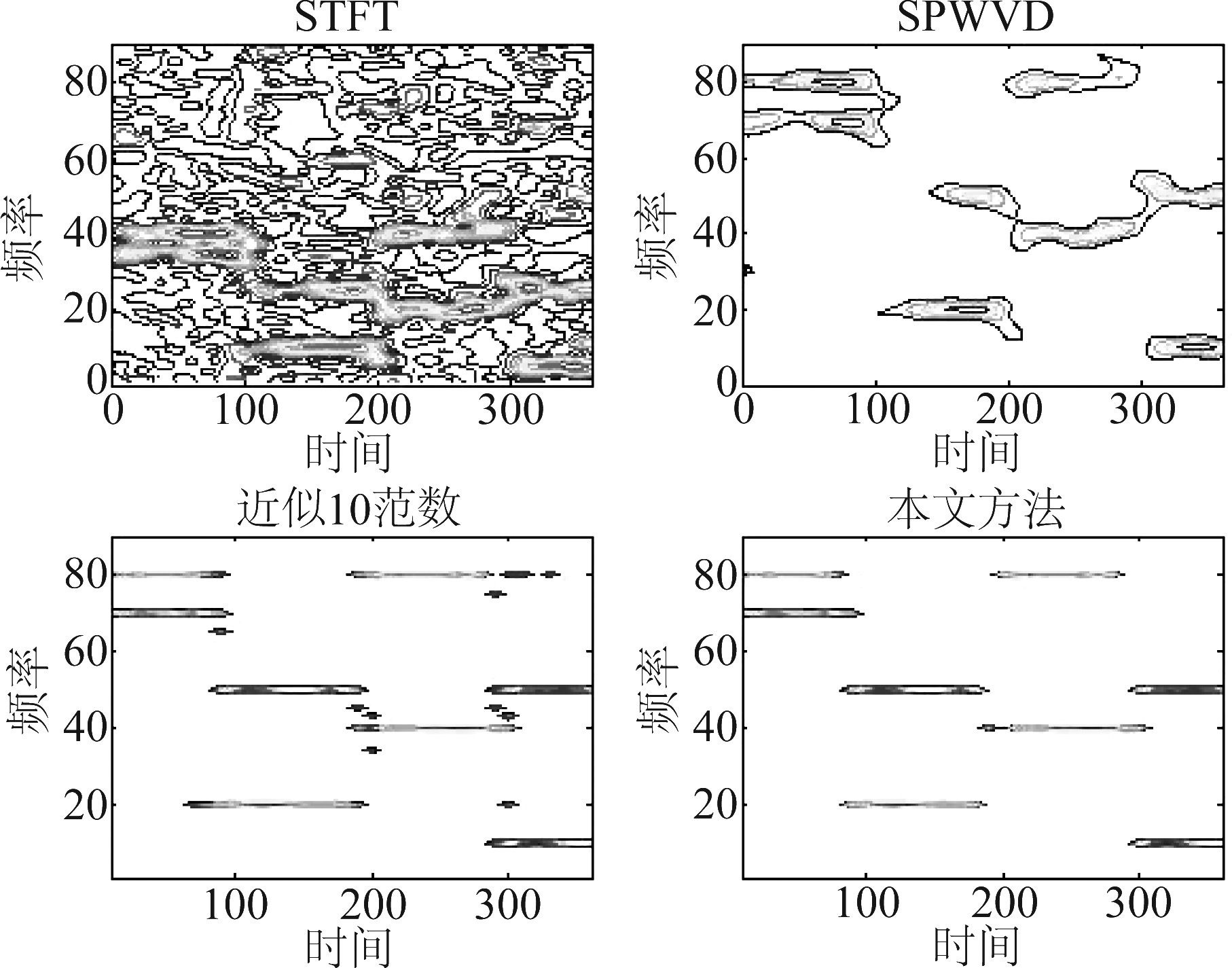
图2 信噪比为0 dB时同步多跳信号时频图
Fig.2 The time-frequency diagram of synchronous multi FH signal with SNR of 0 dB
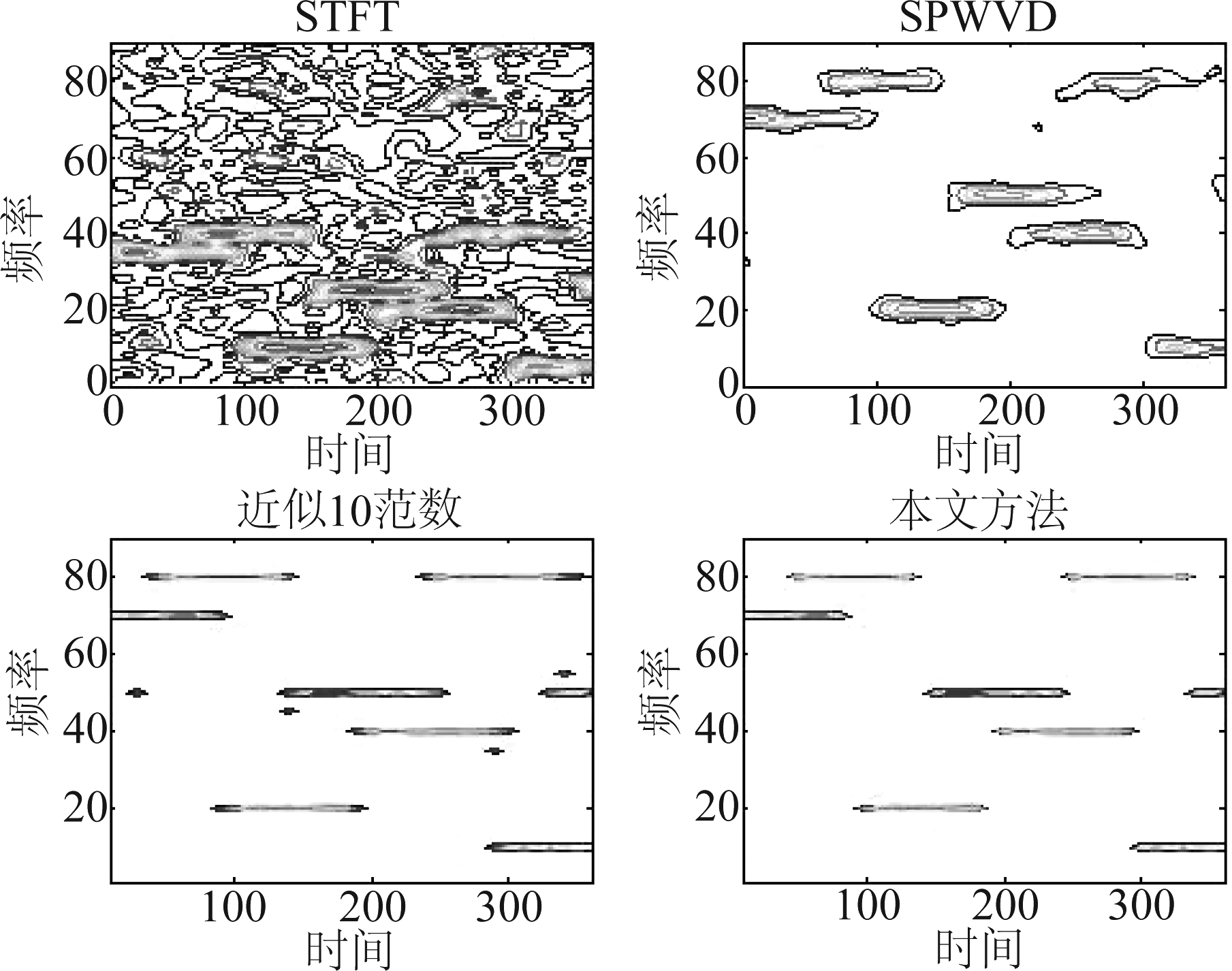
图3 信噪比为0 dB时异步多跳信号时频图
Fig.3 The time-frequency diagram of asynchronous multi FH signal with SNR of 0 dB
从上面的仿真中可以看出,本文方法得到的跳频信号的时频图,无论是时间分辨率还是频率分辨率都十分清晰,也不会产生交叉项,从时频图上就可以准确的估计跳频信号的频率和跳时刻。同时本文算法还适用于多跳频系统。
在噪声环境下,为了验证算法的可靠性引入均方误差(Mean Square Error, MSE)作为衡量的标准,其定义为![]() 其中
其中![]() 为估计出的时频矩阵,Xtrue为真实的时频矩阵。考虑信噪比从5 dB到15 dB变化,分别进行500次实验,比较各个算法的性能。其性能图如图4。
为估计出的时频矩阵,Xtrue为真实的时频矩阵。考虑信噪比从5 dB到15 dB变化,分别进行500次实验,比较各个算法的性能。其性能图如图4。
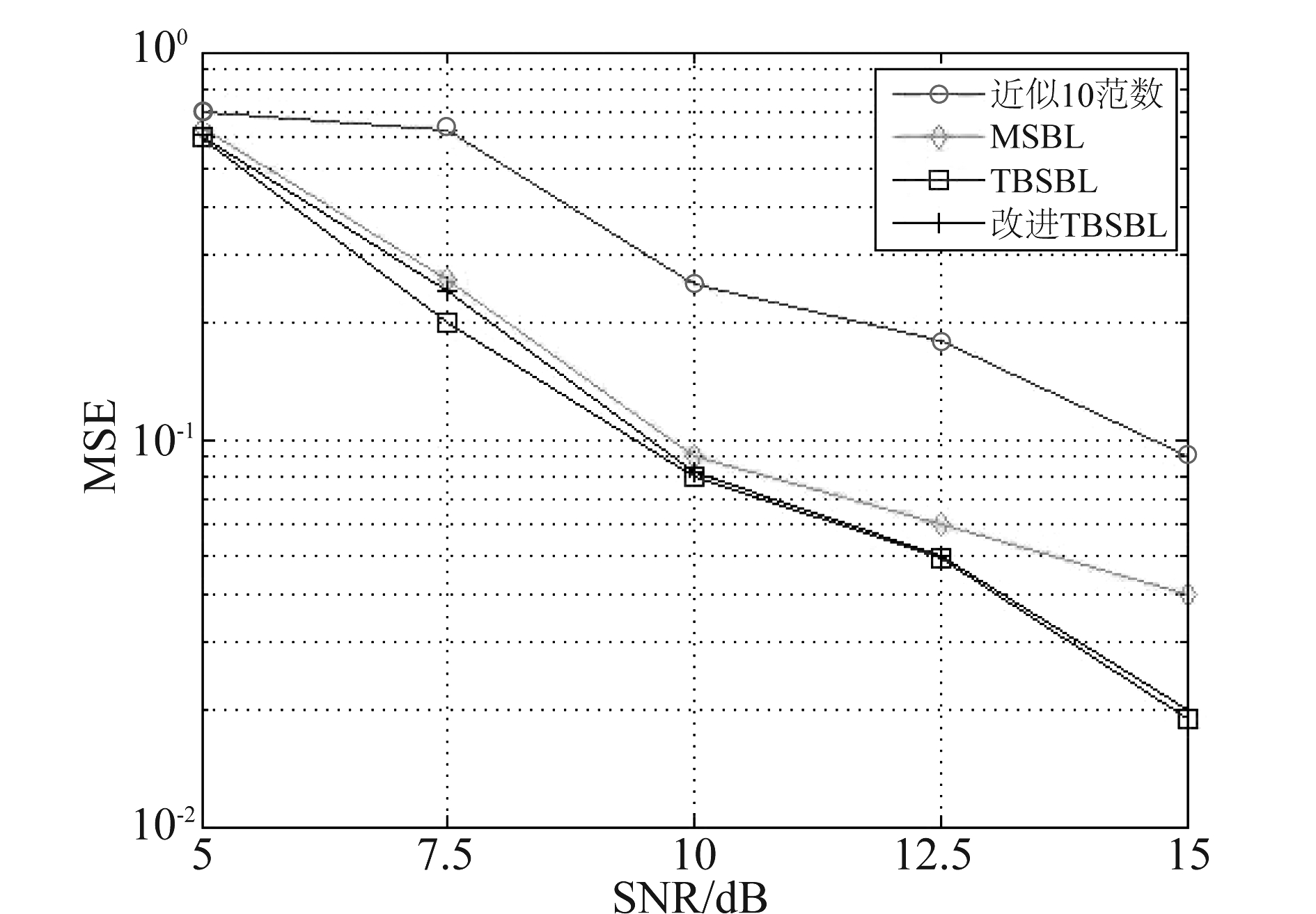
图4 不同信噪比条件下算法性能比较
Fig.4 Performance of various algorithms at different noise levels
6 结论
本文主要利用块稀疏贝叶斯学习算法进行跳频信号的时频分析,由于块稀疏使得字典矩阵维数扩大,在进行超参数估计时运算量增大,因此利用近似替换的方法将高维参数空间转换到原始参数空间计算,降低运算量。实验结果表明,本文的方法不仅能够克服交叉项的干扰同时在低信噪比下能够得到高精度的时频图,而且算法也适用于多跳频信号的时频分析。
参考文献
[1] Torrieri D, Talarico S, Valenti M C. Analysis of a Frequency-Hopping Millimeter-Wave Cellular Uplink[J].IEEE Transactions on Wireless Communications, 2016, 15(10):7089-7098.
[2] Zhang L, Wang H, Li T. Anti-Jamming Message-Driven Frequency Hopping—Part I: System Design[J]. IEEE Transactions on Wireless Communications, 2013, 12(1):70-79.
[3] Chen T C. Joint signal parameter estimation of frequency-hopping communications[J]. Iet Communications, 2012, 6(4):381-389.
[4] 张坤峰, 郭英, 齐子森,等. 基于稀疏贝叶斯重构的多跳频信号参数估计[J]. 华中科技大学学报:自然科学版, 2017, 45(1):97-102.
Zhang Kunfeng, Guo Ying, Qi zishen, et al. Parameter estimation of multiple frequency hopping signals based on sparse Bayesian reconstruction[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2017, 45(1):97-102.(in Chinese)
[5] 赵俊, 张朝阳, 赖利峰,等. 一种基于时频分析的跳频信号参数盲估计方法[J].电路与系统学报, 2003, 8(3):46-50.
Zhao Jun, Zhang Chaoyang, Lai Lifeng, et al. A blind estimation method for frequency hopping signals based on time frequency analysis[J]. Journal of Circuits and Systems, 2003, 8(3): 46-50.(in Chinese)
[6] 张曦, 杜兴民, 朱礼亚. 基于重排SPWVD的跳频信号参数提取方法[J]. 计算机工程与应用, 2007, 43(15):144-147.
Zhang Xi, Du Xingmin, Zhu Liya. Parameter extraction method of frequency hopping signals based on SPWVD[J].Computer Engineering and Applications, 2007, 43(15):144-147.(in Chinese)
[7] 沙志超, 黄知涛, 周一宇,等. 基于稀疏重构的跳频信号时频分析方法[J]. 通信学报, 2013(5):107-112.
Sha Zhichao, Huang Zhitao, Zhou Yiyu, et al. Frequency domain analysis method of frequency hopping signals based on sparse reconstruction[J]. Journal on Communications, 2013(5): 107-112.(in Chinese)
[8] Wipf D P, Rao B D. Bayesian learning for sparse signal reconstruction[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. Proceedings. IEEE, 2003:VI- 601- 4 vol.6.
[9] ![]() S, et al. Compressive Sensing Based Separation of Nonstationary and Stationary Signals Overlapping in Time-Frequency[J]. IEEE Transactions on Signal Processing, 2013, 61(18):4562- 4572.
S, et al. Compressive Sensing Based Separation of Nonstationary and Stationary Signals Overlapping in Time-Frequency[J]. IEEE Transactions on Signal Processing, 2013, 61(18):4562- 4572.
[10] Zhang Z, Rao B D. Sparse Signal Recovery With Temporally Correlated Source Vectors Using Sparse Bayesian Learning[J]. Selected Topics in Signal Processing IEEE Journal of, 2011, 5(5):912-926.
[11] Wipf D P, Rao B D. An Empirical Bayesian Strategy for Solving the Simultaneous Sparse Approximation Problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7):3704-3716.
[12] Lorintiu O, Liebgott H, Friboulet D. Compressed Sensing Doppler Ultrasound Reconstruction Using Block Sparse Bayesian Learning[J]. IEEE Transactions on Medical Imaging, 2016, 35(4):978-987.
[13] Zou Y, Gao X, Li X. A Block Sparse Bayesian Learning based ISAR imaging method[C]∥IGARSS 2016-2016 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2016:1011-1014.
[14] Zhao L, Wang L, Bi G, et al. Robust Frequency-Hopping Spectrum Estimation Based on Sparse Bayesian Method[J]. IEEE Transactions on Wireless Communications, 2015, 14(2):781-793.
[15] Cawley G C, Talbot N L C. Preventing overfitting during model selection via Bayesian regularization of the hyper-parameters[J]. J.Mach.Learn.Res.,2007,8: 841- 861.






