1 引言
与集中式多传感器多目标跟踪技术相比,分布式多传感器多目标跟踪技术(distributed multi-sensor multi-object tacking, DMMT) 具有通信代价低、容错率高等优势,因此在理论研究和实际工程应用中都具有重大意义。分布式多传感器多目标融合所面临的一个挑战是不同传感器节点间量测存在未知的相关性信息。文献[1]提出了解决该问题的最优解,然而由于最优解需要计算不同传感器节点间的公共信息,计算量大,实际中通常难以实现。Mahler在[2]中提出了一种易于实现的次优解,称之为广义协方差交集(Generalized Covariance Intersection, GCI)融合。GCI融合是协方差交集(Covariance Intersection, CI)准则[3]的推广。相比于CI融合准则,GCI融合准则放松了高斯分布假设,适用于服从任意分布的后验概率密度函数。另外,文献[4]证明了GCI融合准则能够规避公共信息的重复计算,因此适用于存在未知相关性的多目标后验分布间的信息融合。
基于Mahler的研究工作[2],Clark等人推导得出了几种类型的多目标概率分布的GCI融合解析表达式,包括泊松(Poisson),独立同分布簇(independent identically distributed clusters), 伯努利(Bernoulli)等分布[5]利用GCI融合的这些解析表达式,2013年,M.Uney等人采用序贯蒙特卡罗(Sequential Monte Carlo,SMC)滤波技术实现了基于GCI融合准则的概率假设密度(Probability Hypothesis Density,PHD)滤波器的分布式融合[6];同一时期,G.Battistelli等人也发表了利用混合高斯(Gaussian Mixture,GM)技术,并结合网络共识理论实现的基于GCI融合准则的基数化概率假设密度(Cardinalized Probability Hypothesis Density,CPHD)滤波器的分布式融合[7]; 随后,M.B.Guldogan等人于2014年实现了基于GCI融合准则的分布式伯努利滤波器的融合算法,并将该融合技术成功应用到了多普勒传感器网络中[8]。
事实上,在基于随机集(Random finite set, RFS)理论的多目标跟踪领域,相比PHD、CPHD滤波器[19- 22]只传递后验分布的一阶/二阶统计特性,多目标伯努利(Multi-Bernoulli, MB)滤波器[9-10]直接传递后验分布参数,因此性能更优、鲁棒性更强,并且已经被成功应用到许多实际问题中,如雷达目标跟踪、视频跟踪、传感器管理等[9, 11-18]。受到多目标伯努利滤波器的优良的性能和广泛应用的激励,2016年,本研究团队首次基于GCI融合准则研究了多目标伯努利滤波器的分布式融合技术[23],该融合技术简称为GCI-MB融合。在文献[23] 中,作者们首先基于两步合理近似推导得出多目标伯努利分布的GCI融合表达式;其次给出了基于SMC滤波的GCI-MB融合的实现方法。
网络共识技术被认为是为实现传感器网络中分布式计算的一个强大工具,该技术广泛应用于分布式参数估计、分布式目标状态估计等[7- 8]。从本质上讲,网络共识的目的是实现整个网络信息的分布式平均计算,具体来讲,首先通过每一个传感器节点实现本地节点的区域计算,进而各个传感器节点采用序贯迭代方法实现信息的交互与本地节点的区域计算以达到整个网络的全局计算目的。然而这种迭代的共识方式会增大不同节点间先验信息的相关性。如果融合算法无法避免公共信息的重复计算,其相应的共识算法将会随着共识步骤的增加而增加公共信息的计算次数,从而会导致目标状态估计不收敛,融合性能下降等问题。
考虑网络共识技术具有的以上优势,本文在先前工作[23]基础上进一步研究基于网络共识的分布式GCI-MB融合技术,以避免公共信息被重复计算问题,并达到提高系统的鲁棒性和稳定性目的。本文的贡献如下:
1)基于GCI-MB 融合算法,本文首次提出了网络共识-GCI-MB (Consensus-GCI-MB,C-GCI-MB)融合技术,并给出了C-GCI-MB融合权重的选择策略;
2)本文通过数学理论证明了C-GCI-MB融合可以避免传感器节点间公共信息的重复计算;
3)本文给出了基于混合高斯技术的C-GCI-MB融合算法的实现方法。
最后,在典型仿真场景下,设计仿真实验验证了C-GCI-MB融合算法的有效性及其性能优势。
2 随机集理论基础
Mahler提出了一种有限集合统计理论(Finite Set Statistics, FISST)。该理论为多目标检测、多目标跟踪和多目标分类等问题提供了一种完备的严谨的统一的数学理论框架[24]。
2.1 多目标贝叶斯滤波器
为了准确的刻画一组个数时变且未知的多目标状态的统计特性,我们将多个目标将建模成集合的形式,采用FISST理论来建立多目标跟踪问题。k时刻,多目标状态![]() 其中
其中![]() 表示单目标状态空间, 维度为
表示单目标状态空间, 维度为![]() 表示
表示![]() 的所有有限子集的集合。 每个单目标状态
的所有有限子集的集合。 每个单目标状态![]() 包括二维的目标位置
包括二维的目标位置![]() 和二维的目标速度
和二维的目标速度![]() 其中“T”表示矩阵的转置。
其中“T”表示矩阵的转置。
我们用Zk表示k时刻某个传感器提供的量测,![]() 表示1到k时刻所有量测的集合。最优集合贝叶斯滤波器是以迭代递归的方式计算集合后验概率密度函数
表示1到k时刻所有量测的集合。最优集合贝叶斯滤波器是以迭代递归的方式计算集合后验概率密度函数![]() 递归方程如下:
递归方程如下:
(1)
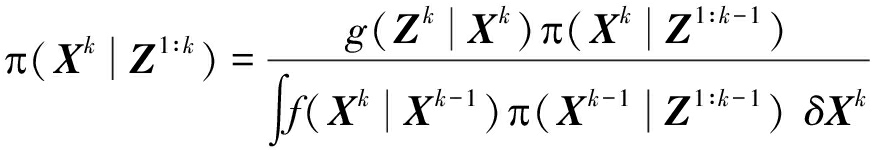
(2)
其中, f(Xk|Xk-1)表示多目标马尔可夫转移概率密度函数, g(Zk|Xk)表示多目标似然函数,![]() 表示集合积分, 其定义如下:
表示集合积分, 其定义如下:
(3)
2.2 多目标伯努利滤波器
多目标伯努利随机集合X是M个独立伯努利随机集合X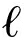 ,
,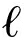 =1,...,M的并集[24],即
=1,...,M的并集[24],即
(4)
多目标伯努利分布可以完全由一组参数集合来刻画![]() 其中r(
其中r(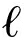 )第
)第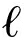 个伯努利随机集的存在概率,和p(
个伯努利随机集的存在概率,和p(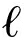 )表示该伯努利分量所对应的概率密度函数。根据[24],对任意多目标伯努利随机集合的多目标概率分布函数由下式给出,
)表示该伯努利分量所对应的概率密度函数。根据[24],对任意多目标伯努利随机集合的多目标概率分布函数由下式给出,
(5)
其中
(6)
MB分布可以等价的表示为
(7)
这里
(8)
和σ表示{1,...,n}的的一个排列,![]() 为多个伯努利分量的标号集合,称之为多目标伯努利分布的标号集合。
为多个伯努利分量的标号集合,称之为多目标伯努利分布的标号集合。
本文中,我们将在多目标后验分布服从多目标伯努利分布假设下推导得出的多目标贝叶斯滤波器的解统称为多目标伯努利滤波器。目前应用最广泛的两种多目标伯努利滤波器为:基数均衡的多目标伯努利滤波器(适用于标准点迹量测模型)[10];基于图像数据的多目标伯努利滤波器(适用于可分离的多目标似然函数)[9]。
3 基于网络共识的GCI-MB分布式融合技术
3.1 分布式融合准则
传统多传感器分布式目标跟踪往往假设传感器间量测信息相互独立。然而,在实际应用场景中,由于,不同传感器因监测同一批目标存在公共的过程噪声;量测信息经过通信链路在传感器间进行传输等原因导致传感器后验分布间存在未知相关性。如果直接采用传统方法,理论上将会存在缺陷,导致多传感器融合结果不可信等问题。针对传感器后验间存在未知相关性问题,本文采用GCI融合准则进行分布式多传感器融合。假设某传感器网络拥有![]() 个节点
个节点![]() 时刻,各节点经过本地滤波得到的后验概率分布分别为
时刻,各节点经过本地滤波得到的后验概率分布分别为![]() 融合准则[2]为
融合准则[2]为

(9)
其中![]() 为节点s的权重,各节点权重满足
为节点s的权重,各节点权重满足![]() 融合准则具有以下优势:
融合准则具有以下优势:
1)考虑多传感器后验信息间存在相关性。该准则可以实现传感器后验间存在未知相关性信息的多目标后验概率密度函数的融合。
2)规避公共信息“重复计算(double-counting)”。 较简单凸组合融合方式[25],即各节点的融合权重均为1,GCI融合准则有效避免了量测间公共信息被重复计算的问题,得到了一致收敛的融合结果[4]。
3)适用于任意分布。传统CI融合准则仅利用均值和方差信息进行融合,因此仅适用于高斯分布,而GCI融合准则适用于服从任意分布的后验概率密度函数的融合。
为了阐述方便,接下来,我们省略公式中涉及滤波时刻的上标“k”或者“![]() k”。
k”。
3.2 GCI-MB分布式融合算法
基于GCI融合准则进行MB滤波器的分布式融合,推导融合后的后概率密度函数的解析解是首要任务,然而多目标伯努利分布的GCI融合很难得到解析解。根据GCI融合准则(9),多目标伯努利分布的分数阶指数次幂项(即π(X)ω)的计算问题是面临的主要挑战,因此我们需要寻找一种误差小且易于实现的近似来解决该问题。 在前期工作[23]中, 我们对多目标伯努利分布进行了深入理论分析,得出:当不同伯努利分量的最大后验(highest posterior density, HPD)区域[26]没有交集的条件下,对于任意节点的MB后验分布πs, 如下近似成立:
(10)
详细理论分析请参考[23]中的定理1和2。
为了引出多目标伯努利滤波器的分布式融合,我们首先介绍融合映射的定义。
定义 不失一般性, 假设多目标伯努利分布标号集合![]() 定义融合映射
定义融合映射![]() 当θ(
当θ(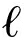 )=θ(
)=θ(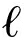 *)>0成立时,
*)>0成立时,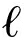 ≠
≠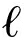 *成立。所有标号子集I可能的映射函数被称为融合映射空间,用符合ΘI表示。为了后续方便, 我们定义符号θ(I)={θ(
*成立。所有标号子集I可能的映射函数被称为融合映射空间,用符合ΘI表示。为了后续方便, 我们定义符号θ(I)={θ(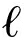 ),
),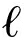 ∈I}。
∈I}。
基于多目标伯努利分布的分数阶指数次幂的近似(公式(10)),[23]经过两步合理近似得出了多目标伯努利形式的融合后的后验概率密度函数的表达式,具体推导请参见[23]中的定理3和4。这里,我们仅简要给出其推导结果。
融合后的后验概率分布推导:利用融合映射θ,并将(10)代入GCI准则(9)中,得到融合后的后验概率分布为GMB分布。
(11)
其中
(12)
(13)
和
(14)
(15)
(16)
基于一阶矩匹配原理的近似:得到(11)解析解形式后验概率分布表达式后,我们便可以实现两个传感器节点间分布式融合。然而,在传感器网络中,常常存在如下需求:
1)序贯融合。为了实现融合后的后验概率分布与其他传感器(s>2)的后验分布进行序贯融合,融合后的后验概率分布应与本地后验概率分布属于相同的类型。
2)网络共识。传感器网络各节点间的信息共识需要将融合后的后验概率分布反馈相邻各节点,作为其本地滤波的先验分布。因此,融合后的后验概率分布应与本地后验概率分布属于相同的类型。
基于以上两点实际需求,我们根据一阶矩统计特性匹配原理,将(11)近似为多目标伯努利分布πω(X),其参数化表征为![]() 其中
其中
(17)
(18)
其中1I1(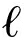 )为指示函数,其定义如下,
)为指示函数,其定义如下,
(19)
3.3 网络共识GCI-MB分布式融合算法
网络共识技术是为传感器网络分布式计算的一个强大工具,该技术广泛应用于分布式参数估计、分布式目标状态估计[7-8]等。从本质上讲,网络共识的目的是实现整个网络信息的分布式平均计算。具体来讲,首先通过每一个传感器节点实现本地节点的区域计算,进而各个传感器节点采用序贯迭代方法实现信息的交互与本地节点的区域计算以达到整个网络的全局计算目的。由于网络共识技术具有的以上优势,本文在先前工作[23]基础上将进一步研究基于网络共识的分布式GCI-MB融合技术,以提高系统的鲁棒性和稳定性。
为了清晰简洁的数学表达,我们首先介绍两种数学运算符号⊕和⊙,定义如下:
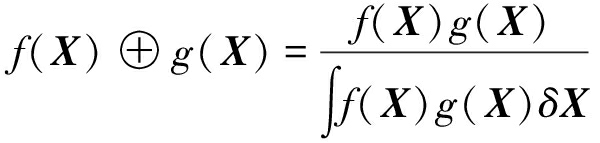
(20)
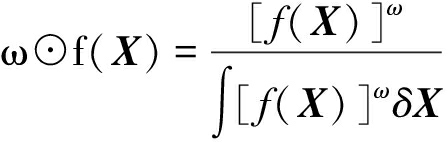
(21)
当融合权重![]() 时,采用上述两种运算符号的数学表征形式,GCI融合式(9)可以表征为:
时,采用上述两种运算符号的数学表征形式,GCI融合式(9)可以表征为:
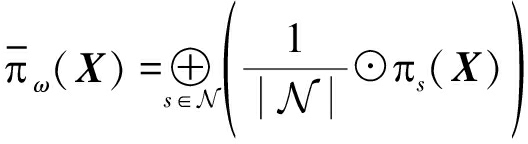
(22)
整个网络所有节点的后验分布![]() 的融合结果(22)被称为是全局融合结果。为了在分布式网络拓扑结构下实现全局融合,我们可以采用分布式结构的、融合尺度可变的融合方式来计算(22), 即所谓的共识算法。具体来讲,在多传感器网络内,各本地节点收集其相邻节点的多目标后验分布信息,并通过多步迭代技术计算并逐步更新其局部的GCI融合信息,其采用的迭代共识算法如下:令πs,t(X)表示第t步共识的融合后的后验概率密度函数,
的融合结果(22)被称为是全局融合结果。为了在分布式网络拓扑结构下实现全局融合,我们可以采用分布式结构的、融合尺度可变的融合方式来计算(22), 即所谓的共识算法。具体来讲,在多传感器网络内,各本地节点收集其相邻节点的多目标后验分布信息,并通过多步迭代技术计算并逐步更新其局部的GCI融合信息,其采用的迭代共识算法如下:令πs,t(X)表示第t步共识的融合后的后验概率密度函数,![]() 表示节点j的邻近节点集合, 则第t+1步共识的融合后的后验概率密度函数可以由下式进行计算:当t≥1时,
表示节点j的邻近节点集合, 则第t+1步共识的融合后的后验概率密度函数可以由下式进行计算:当t≥1时,
(23)
当t=1时
πj,0=πs
其中共识权重满足
(24)
令符号Ω表示共识矩阵,其第(s,s')个元素与共识权重ωs,s'保持一致(该共识权重满足:如果![]() 根据运算符⊕和⊙的运算性质, 我们可以进一步得出
根据运算符⊕和⊙的运算性质, 我们可以进一步得出
(25)
其中![]() 为第t步共识矩阵Ωt的第(s,h)个元素。当选择的共识权重
为第t步共识矩阵Ωt的第(s,h)个元素。当选择的共识权重![]() 可以保证矩阵Ωt是本原性矩阵[27]和双随机性矩阵[28]的特点时,我们可以得到如下结论,
可以保证矩阵Ωt是本原性矩阵[27]和双随机性矩阵[28]的特点时,我们可以得到如下结论,
(26)
这就意味着随着共识步数的增多,本地的多目标后验趋近于整个网络融合后的密度函数(22),最终达到了信息共享,网络共识的目的。
为了满足矩阵Ωt的双随机性,共识权重ωj,h的一种可能选择Metropolis权重[25],
由(23)和(24)可以看出,C-GCI-MB融合是基于GCI-MB融合进行有限步迭代地信息交互与信息融合来实现的。特别的,当进行t=1步共识算法时,式(23)和(24)退化为GCI-MB融合。
3.4 公共信息“重复计算”问题分析
文献[4]指出共识算法需要迭代的进行信息交互与信息融合,因此会增大不同节点间先验信息的相关性。如果融合算法无法避免公共信息的重复计算,其相应的共识算法将进一步增大该公共信息计算的次数导致融合性能发散。文献[4]已经证明GCI融合准则可以有效规避公共信息重复计算问题,因此本文提出的C-GCI-MB融合算法将继承GCI融合准则的这一优势。为了更清晰的阐明C-GCI-MB融合算法能够有效规避公共信息重复计算的优势,我们以一个仅有两个节点的传感器网络为例进行说明。
例1 假设这两个传感器节点的量测信息分别为Z1 和Z2, 且其对应输出的多目标伯努利后验概率密度函数为πs(X|Zs)对于s=1,2。不失一般性,这两个节点收集的量测信息Z1∪Z2可以被分解为由三个互不相关的量测集合,即Z1∪Z2=(Z1/Z2)∪(Z2/Z1)∪(Z1∩Z2)。因此,当以公共信息(Z1∩Z2)为条件的概率密度函数π(X|Z1∩Z2)已知时,π1(·)和π2(·)的最优融合[1]可以通过下式得出
∝π(X|Z1∪Z2)
∝π(X|Z1/Z2)π(X|Z2/Z1)π(X|Z1∩Z2)
(27)
然而,在一个既定的传感器网络架构下,其各节点的任务往往仅是不断重复地对来自于其相邻节点的后验信息进行融合,却不具备实时共享整个网络的拓扑结构的能力,所以剔除掉公共信息在实际分布式网络中是难以实现的,进而应用式(27)进行最优融合在实际的网络共识技术中难以实现。因此为了实现网络共识技术下不同节点信息的分布式融合,我们退而求其次的选用一些鲁棒性较高的次优融合策略。[25,29] 提出了基于简单凸组合准则的多节点信息融合方法,本文称之为Naive融合算法,并由下式给出,
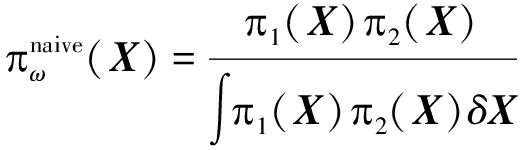
∝π(X|Z1/Z2)π(X|Z2/Z1)[π(X|Z1∩Z2)]2
(28)
观察式(28), 可以看出公共量测信息Z1∩Z2被计算了两次,因此Naive分布式融合算法会陷入公共信息的重复计算问题。
另外一种次优的分布式融合是基于GCI融合准则的GCI-MB融合算法, 即
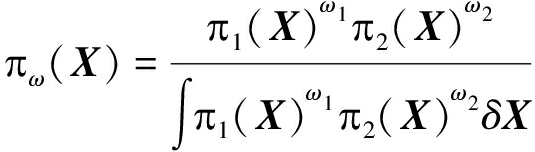
∝π(X|Z1/Z2)ω1π(X|Z2/Z1)ω2π(X|Z1∩Z2)
(29)
从式(29)可以看出,公共量测信息Z1∩Z2仅计算了1次。因此,GCI-MB融合不会存在公共信息的重复计算问题。基于式(29) 我们初步得出,针对不同节点间存在的未知水平相关性的问题,GCI-MB融合在满足式(24) 的条件下具有鲁棒性。
例1证明了在两个传感器节点情况下,GCI-MB融合算法可以避免传感器间公共信息的重复计算。接下来,本文将GCI-MB融合算法的这一特性推广到任意个数的传感器节点。考虑到各节点量测间存在未知相关性信息,我们首先作如下定义:令Y{s}表示受且仅受传感器节点s影响的量测信息,![]() 表示受且仅受传感器节点集合
表示受且仅受传感器节点集合![]() 影响的量测信息。以传感器节点个数
影响的量测信息。以传感器节点个数![]() 为例Y{1,2}=Z1∩Z2-Z3, Y{1}=Z1/(Z2∪Z3)。根据以上定义,任意两个量测集合
为例Y{1,2}=Z1∩Z2-Z3, Y{1}=Z1/(Z2∪Z3)。根据以上定义,任意两个量测集合![]() 间是相互独立的,其满足如下关系,
间是相互独立的,其满足如下关系,
![]() 和
和![]()
(30)
依据![]() 间相互独立特性,
间相互独立特性,![]() 可以解释为是对量测集合
可以解释为是对量测集合![]() 进行的一种分组。同时令
进行的一种分组。同时令![]() 表示以量测信息
表示以量测信息![]() 为条件的服从MB分布的多目标后验概率密度函数。因此, 对于节点
为条件的服从MB分布的多目标后验概率密度函数。因此, 对于节点![]() 其MB后验概率密度函数π(X)可以被分解为:
其MB后验概率密度函数π(X)可以被分解为:
(31)
定理1 假设传感器网络中各节点均进行多目标伯努利滤波,且输出多目标伯努利后验概率密度函数![]() 令所有
令所有![]() 的本地多目标伯努利后验分布均被分解为式(31)所示形式,则基于GCI融合准则(9), 各节点本地后验概率密度函数的融合结果πω(X)具有如下表达形式,
的本地多目标伯努利后验分布均被分解为式(31)所示形式,则基于GCI融合准则(9), 各节点本地后验概率密度函数的融合结果πω(X)具有如下表达形式,
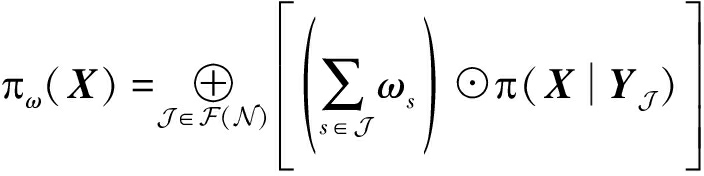
(32)
将式(31)带入式(9)中,我们得出,
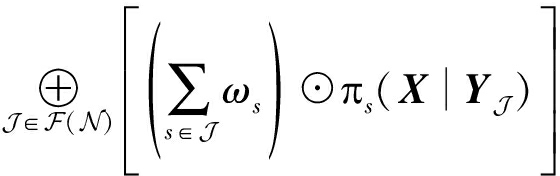
(33)
因此,定理1成立。
依据GCI融合准则权重约束条件:![]() 因此由式(32)可以得出,任意量测信息YJ均避免了重复计算。进一步可以得出, C-GCI-MB融合在进行(23)和(24)迭代计算时可以保证公共信息只计算
因此由式(32)可以得出,任意量测信息YJ均避免了重复计算。进一步可以得出, C-GCI-MB融合在进行(23)和(24)迭代计算时可以保证公共信息只计算![]() 次。同时所付出的代价是各相互独立信息
次。同时所付出的代价是各相互独立信息![]() 的计算偏保守,因为
的计算偏保守,因为![]() 的计算权重同样需满足
的计算权重同样需满足![]()
4 基于混合高斯技术的C-GCI-MB算法实现
混合高斯(Gaussian Mixture, GM)技术和粒子滤波(particle filter)技术是随机集中两种常见的后验概率密度函数近似方法。相比于粒子滤波技术,GM技术仅需要较小的高斯分量个数便可以准确的近似多目标后验概率密度分布,从而使得该技术所需计算资源更少,通信代价更低。因此,本文采用GM技术来实现C-GCI-MB融合算法。每个时刻,各节点本地滤波器输出后验多目标伯努利分布的参数集![]() 其中每个密度函数
其中每个密度函数![]() 由混合高斯分布近似表征,
由混合高斯分布近似表征,
(34)
其中![]() 为第
为第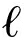 个伯努利分量所对应密度函数的高斯分量个数;
个伯努利分量所对应密度函数的高斯分量个数;![]() 表示第j个高斯分量的权重;
表示第j个高斯分量的权重;![]() 表示第j个高斯分量的均值;
表示第j个高斯分量的均值;![]() 表示第j个高斯分量的协方差矩阵。
表示第j个高斯分量的协方差矩阵。
根据公式(23)和(24),C-GCI-MB融合算法的基础是GCI-MB融合。因此,本节首先给出了基于混合高斯技术的GCI-MB融合算法的实现方法;然后以GCI-MB融合算法为基础,给出了基于混合高斯技术的C-GCI-MB融合算法的实现方法。
4.1 基于混合高斯技术的GCI-MB融合算法实现
GCI-MB融合算法的实现等价于计算融合后的多目标伯努利分布的参数集合![]() 在这些参数的过程中,公式(14)中的积分
在这些参数的过程中,公式(14)中的积分![]() 的计算是关键。由于该积分涉及到混合高斯分布的分数阶指数次幂,其计算需要引入合理的近似。为了解决该积分计算难题,我们首先引入高斯分量幂运算和高斯分量乘积运算[7]。
的计算是关键。由于该积分涉及到混合高斯分布的分数阶指数次幂,其计算需要引入合理的近似。为了解决该积分计算难题,我们首先引入高斯分量幂运算和高斯分量乘积运算[7]。
高斯分量的幂次运算后仍然为高斯分量,具体如下,
(35)
其中
(36)
高斯分量的乘积运算仍然为高斯分量,具体如下,
(37)
其中
P(1,2)=([P(1)]-1+[P(2)]-1)-1
(38)
m(1,2)=P(1,2)([P(1)]-1m(1)+[P(2)]-1m(2))
(39)
(40)
[30]建议混合高斯的幂指数运算采用如下近似,
(41)
实际情况表明,当混合高斯分布中任意两个高斯分量构成的交叉乘积项可以忽略时,式(41)中的近似是合理的。因此,为了保证这一点,不同高斯分量的均值m(i)和m(j)(i≠j), 需满足以其对应协方差矩阵P(i)和P(j)进行度量时是相互远离的条件。
利用式(35)和(37),公式(13)中的参数![]() 的分子部分
的分子部分![]() 的计算如下:
的计算如下:
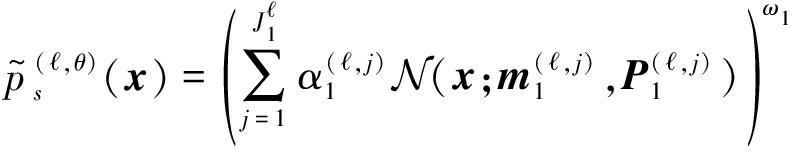
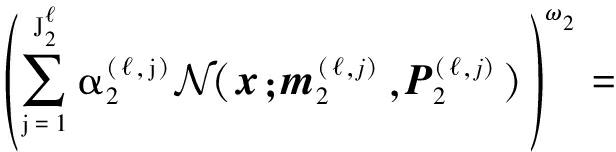
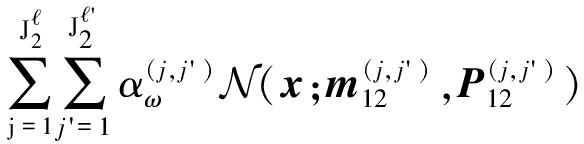
(42)
其中
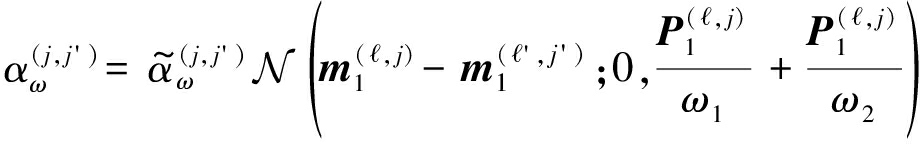
其中
进一步,积分![]() 可以进行如下计算:
可以进行如下计算:
(43)
将公式(42)和(43)带入式(13)中,我们得到参数![]() 的计算表达式,
的计算表达式,
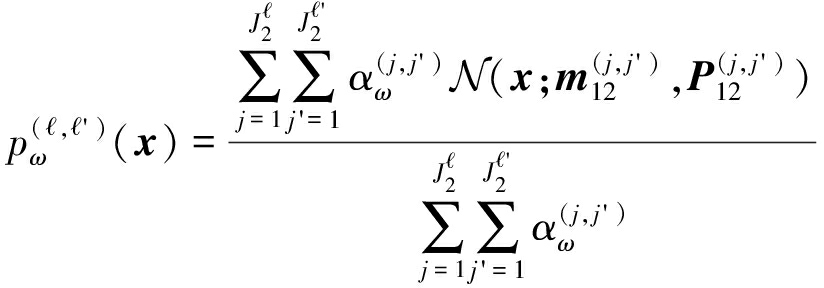
(44)
通过利用参数![]() 与积分
与积分![]() 我们可以继续计算出参数
我们可以继续计算出参数![]() 和归一化因子C,进而根据式(17)和(18),计算出多目标伯努利参数集合。
和归一化因子C,进而根据式(17)和(18),计算出多目标伯努利参数集合。
4.2 基于混合高斯技术的C-GCI-MB融合算法实现
考虑一个传感器网络, 假定每一个节点都具有监测目标以及与临近节点交换信息的能力。当传感器网络内所有节点接收到邻近节点的后验概率密度函数后,整个网络开始进行C-GCI-MB融合。C-GCI-MB融合的基础是GCI-MB融合,因此我们首先给出基于混合高斯技术的GCI-MB融合算法的伪代码,如算法1所示。

其次, 基于GCI-MB融合算法,整个传感器网络的C-GCI-MB融合算法的伪代码在算法 2中给出。
5 算法性能分析
本节在一个复杂的多目标监视场景中,通过仿真实验验证了C-GCI-MB融合算法相对现有网络共识算法的性能优势。传感器的监视区域[-1,1]×[-1,1]km2,监视时间为T=100 s,8个目标依据其各自出生和死亡时刻在整个监视场景中活动,具体监视场景如图1所示。本节将C-GCI-MB融合算法性能与另外一种经典的分布式融算法,即共识CPHD滤波器分布式融合(C-GCI-CPHD)算法[7]性能进行了对比分析。性能评估指标采用optimal sub-pattern assignment (OSPA)[31]误差。C-GCI-MB融合算法的实现采用上一节给出的基于混合高斯技术的C-GCI-MB融合算法实现方案。

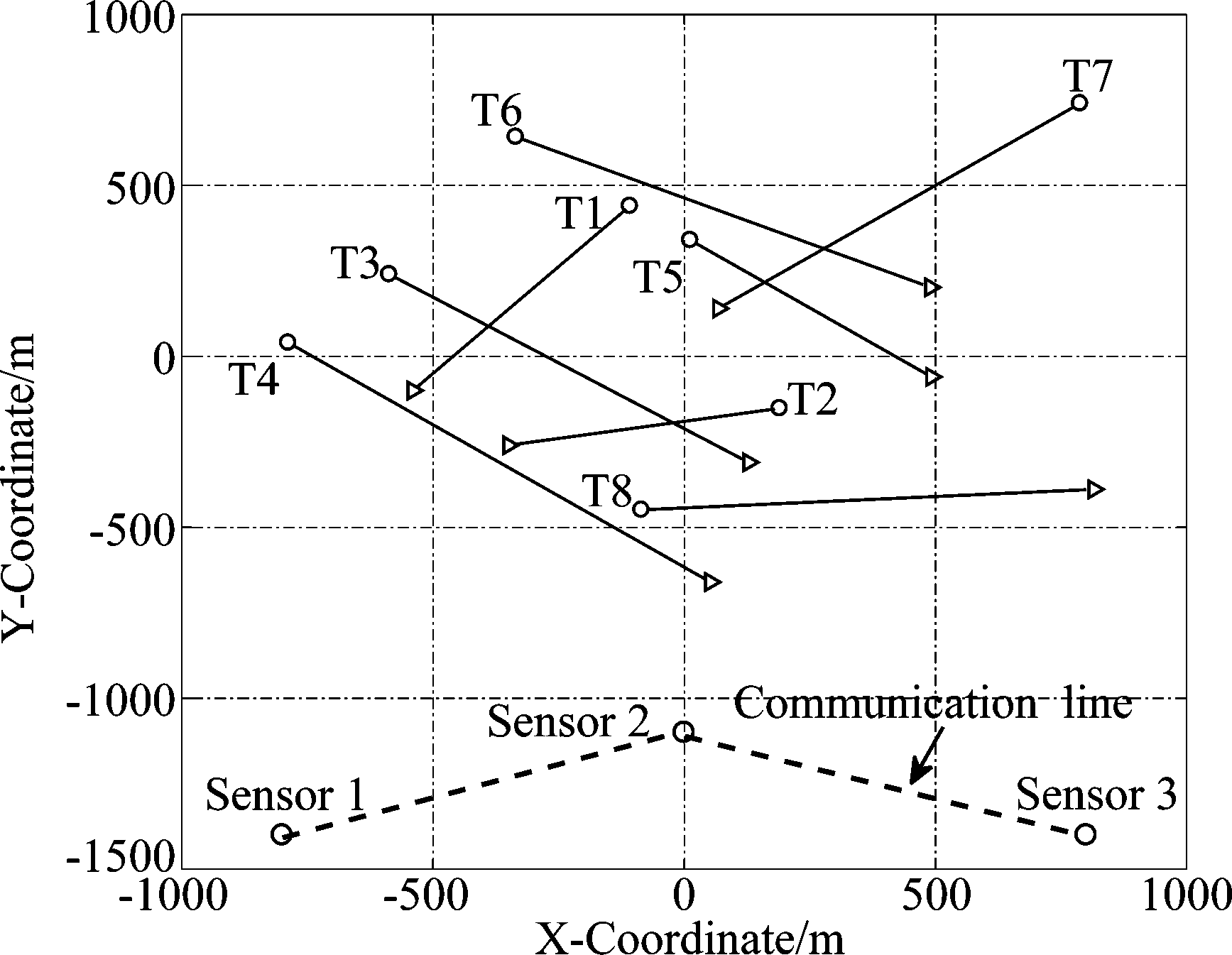
图1 多目标监视场景,其中Ti,i=1,...,8分别表示8个目标的真实航迹
Fig.1 The scenario of distributed sensor network with three sensors tracking eight targets, where Ti,i=1,...,8 denotes the true track of the i th target
C-GCI-CPHD融合算法同样采用[7] 给出的混合高斯实现方法。C-GCI-MB 和C-GCI-CPHD融合算法均采用“标准”目标运动模型和“标准”点迹量测模型[10]。假设目标服从匀速直线运动模型,其状态由目标所在二维平面位置及其运动速度构成![]() 目标状态转移模型假设为高斯模型,相应的转移矩阵Fk和过程噪声强度Qk为,
目标状态转移模型假设为高斯模型,相应的转移矩阵Fk和过程噪声强度Qk为,
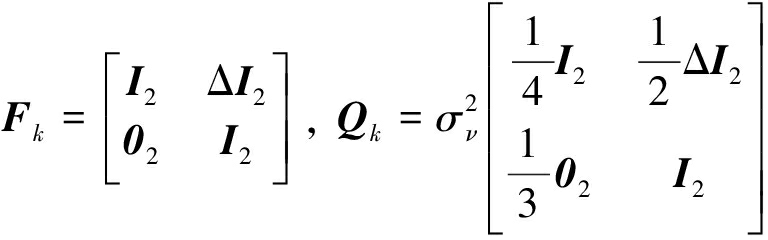
其中In和0n分别表示n×n维度的单位矩阵和零矩阵,Δ=1 s表示采样间隔,σν=5 m/s2表示过程噪声的标准差。目标继续生存概率为PS,k=0.99; 目标检测概率为PD=0.99,且其在各传感器间相互独立。8个目标的出生与死亡时刻如表1所示,由于对目标出生位置未知,本文采用了[32]所给出的自适应目标出生策略。
表1 仿真场景中目标出生与死亡时间表
Tab.1 Target birth and death times
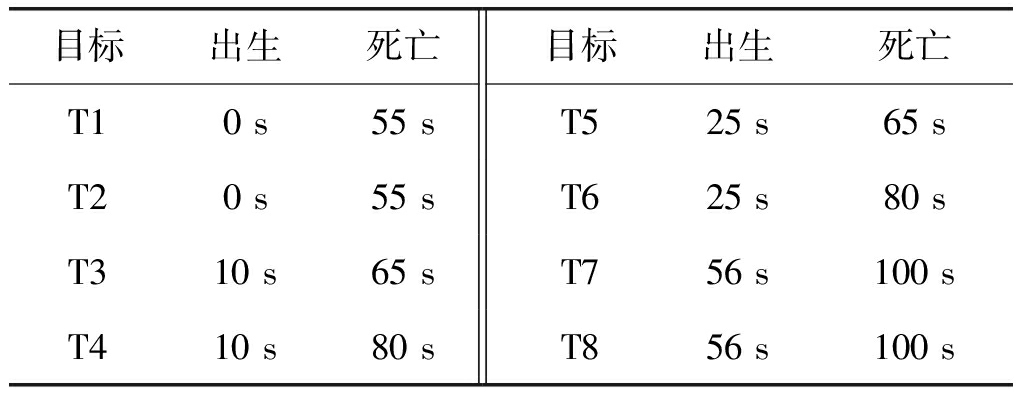
目标出生死亡目标出生死亡T10 s55 sT525 s65 sT20 s55 sT625 s80 sT310 s65 sT756 s100 sT410 s80 sT856 s100 s
单个目标的似然函数为线性高斯,由下式给出:
其中量测矩阵与量测协方差矩阵分别为
其中σε为标准量测协方差矩阵。每一个扫描间隔杂波集合服从柏松过程,其中柏松过程参数λ=10。
C-GCI-MB融合算法的本地滤波器采用基数均衡多目标伯努利滤波器[10], 参数选择如下: 伯努利分量的截断门限为γt=10-4; 每一个伯努利分量下高斯分量的截断与合并门限分别为γp=10-5和γm=10-4; 高斯分量的最大个数限制为Nmax=10。这里需要强调指出的是,上述参数设置中合并门限γm=10-4的选择满足了高斯分量间相互分离条件,相关理论分析其是否满足高斯分量间相互分离条件请参见[7]。
图2(a)和(b)给出了C-GCI-MB融合算法(一次共识)与单个传感器MB滤波算法的单次蒙特卡罗实验的航迹估计对比结果。从仿真结果中可以看出,C-GCI-MB融合算法在航迹估计精度、航迹完整度、以及虚假航迹等方面都要明显优于单传感器MB滤波器。具体来讲,C-GCI-MB融合可以在整个场景范围内连续估计目标位置,且保持较高精度。另外比较两种算法航迹估计结果,C-GCI-MB融合算法的虚假航迹较MB滤波器明显减少。
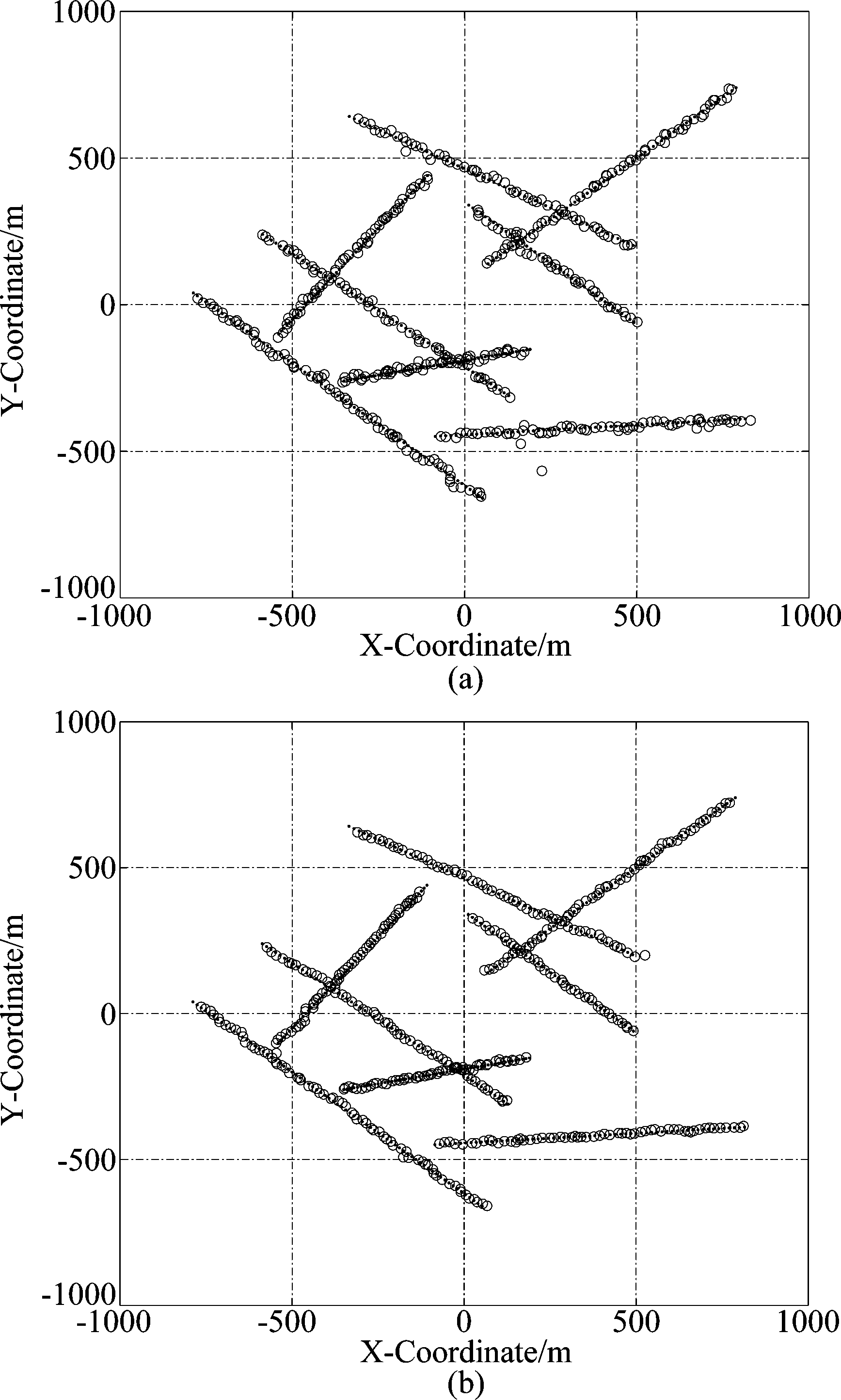
图2 (a) MB滤波器的目标状态估计结果(单次蒙特卡罗实验); (b) C-GCI-MB共识1步下的目标状态估计结果(单次蒙特卡罗实验)
Fig.2 (a) The target state estimation result of MB filter (single Monte Carlo run); (b) The target state estimation result of C-GCI-MB with 1 consensus step (single Monte Carlo run)
为了从统计角度来分析本文提出C-GCI-MB融合算法性能的优势,图3给出了C-GCI-MB融合算法与C-GCI-CPHD融合算法在不同共识步数下(i.e., 1步和5步)的平均OSPA误差(100次蒙特卡罗平均结果)。仿真结果表明:C-GCI-MB融合算法性能会随着共识步骤次数的增加而提升;其次,C-GCI-MB较C-GCI-CPHD融合算法存在显著的性能优势。
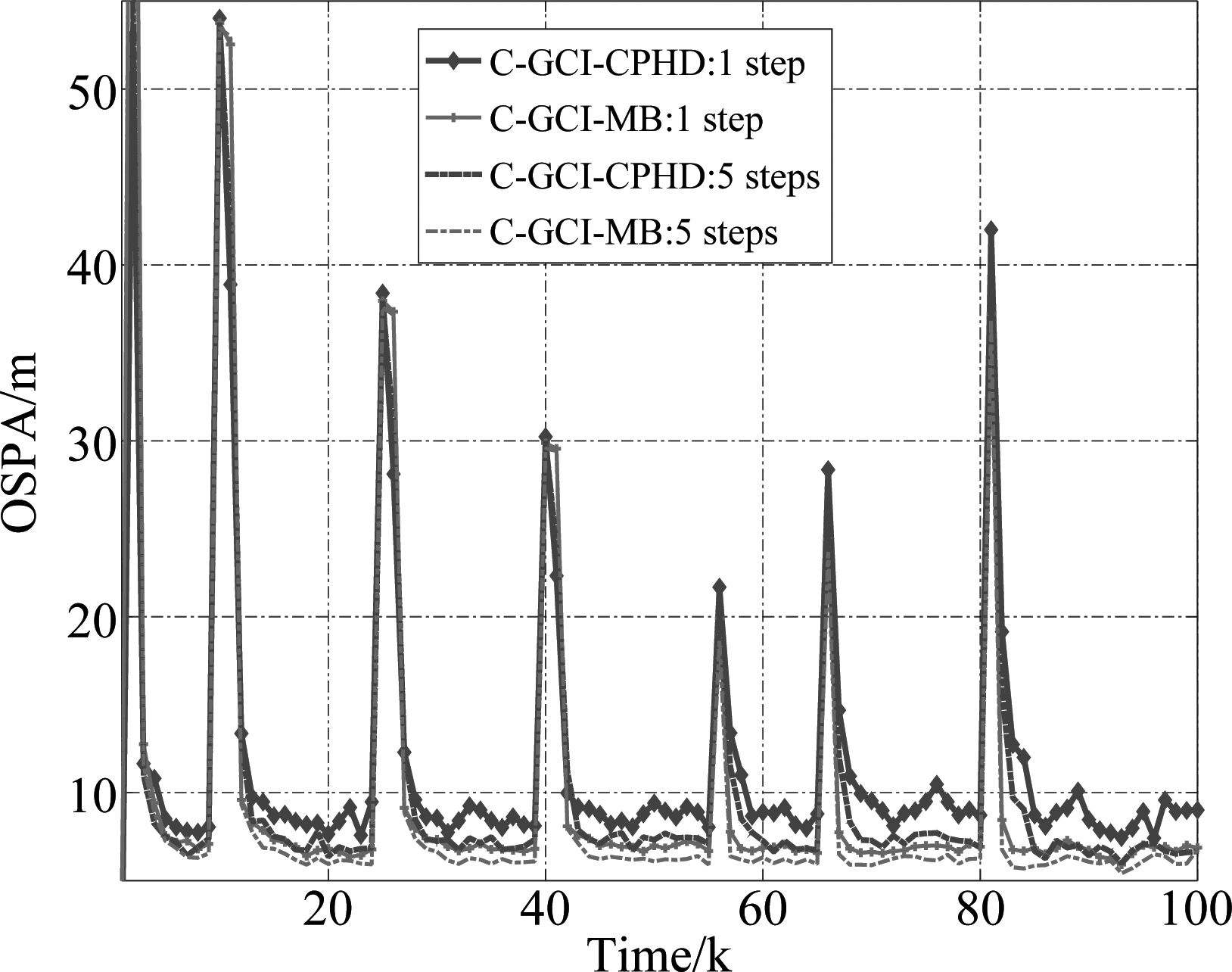
图3 在不同共识步数下,C-GCI-MB与C-GCI-CPHD两种融合算法的OSPA估计误差性能对比, OSPA误差参数为:c=100, p=1(仿真结果为100次蒙特卡罗实验的平均值)
Fig.3 The performance of OSPA error comparison between C-GCI-MB and C-GCI-CPHD algorithms for different consensus steps. The parameters of OSPA error:c=100, p=1(averaged over 100 Monte Carlo runs)
为了进一步分析C-GCI-MB融合算法性能,图4和图5分别给出了在共识1步与共识5步下两种共识融合算法的基数估计及其相应的基数估计标准差。仿真结果表明:在给定共识步数下(1步共识或者5步共识),C-GCI-MB融合算法的基数估计较C-GCI-CPHD更准确,且其基数估计的统计偏差较小;随着共识步数从1步(图4)增加到5步(图5),两种算法的基数估计与估计标准差都进一步收敛,但是C-GCI-CPHD融合算法基数估计标准差的收敛速度明显慢于C-GCI-MB融合算法。这也从侧面反映出,在较小共识步数下C-GCI-MB融合算法性能较C-GCI-CPHD融合算法性能更快的收敛。
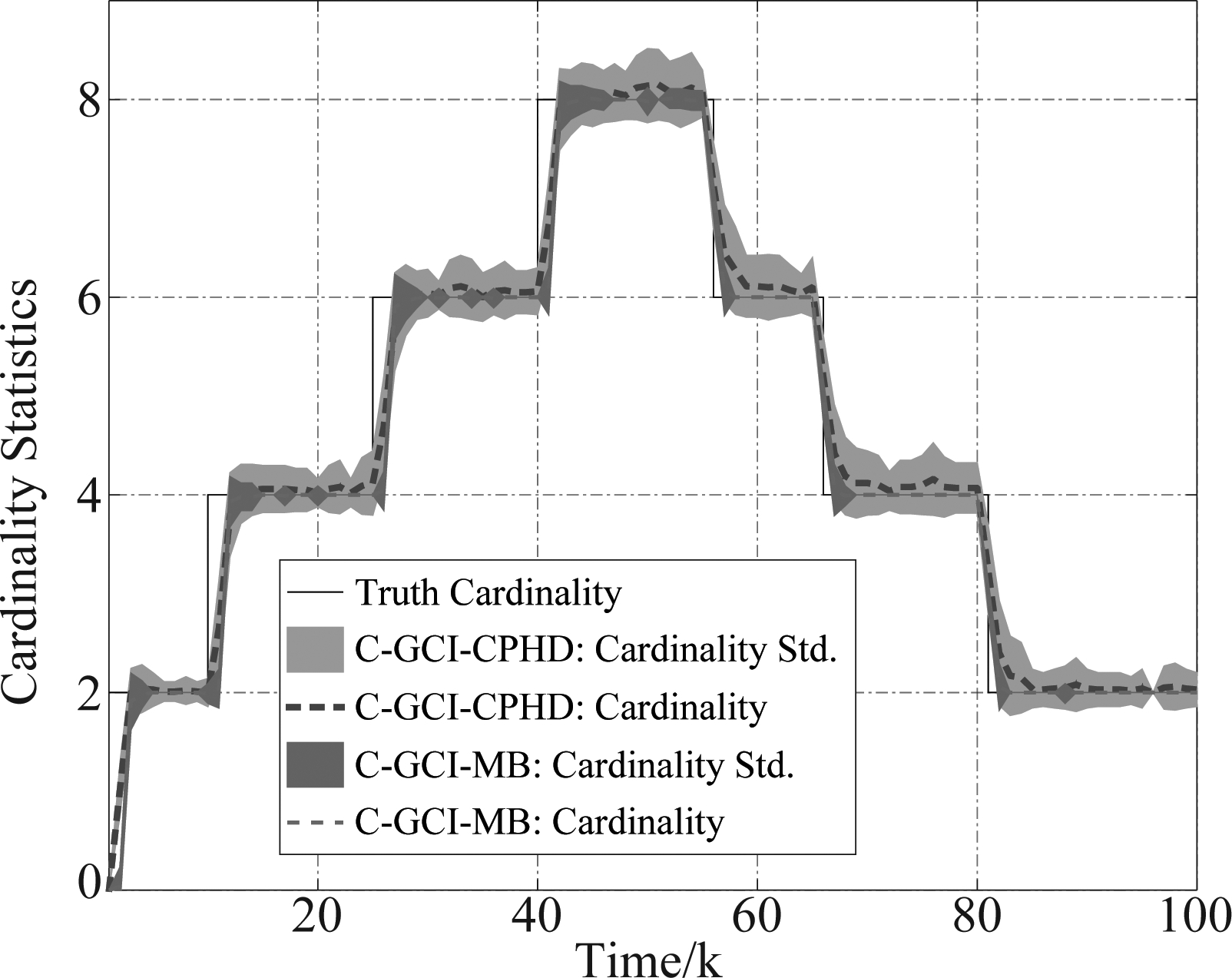
图4 在同共识1步数下,C-GCI-MB与C-GCI-CPHD两种融合算法的基数估计性能对比(仿真结果由100次蒙特卡罗统计平均得到)
Fig.4 Under 1 consensus step: the performance of cardinality estimation comparison between C-GCI-MB and C-GCI-CPHD algorithms for different consensus steps (averaged over 100 Monte Carlo runs)
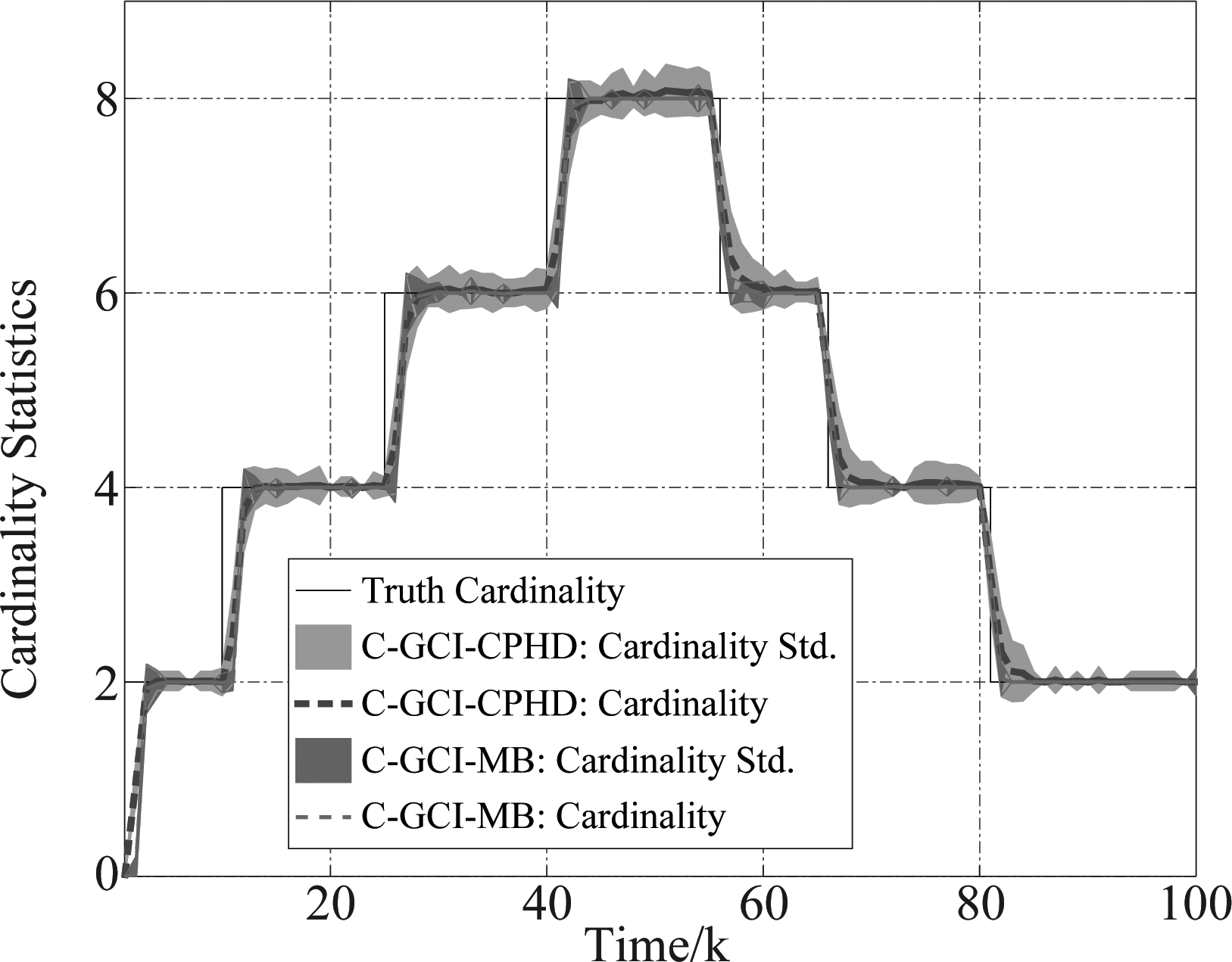
图5 在同共识5步数下,C-GCI-MB与C-GCI-CPHD两种融合算法的基数估计性能对比(仿真结果为100次蒙特卡罗实验的平均值)
Fig.5 Under 5 consensus steps: the performance of cardinality estimation comparison between C-GCI-MB and C-GCI-CPHD algorithms for different consensus steps (averaged over 100 Monte Carlo runs)
6 结论
本文研究了基于网络共识的分布式多目标伯努力(Multi-Bernoulli-MB)滤波器的目标跟踪技术。网络共识技术是实现传感器网络中分布式计算的一个强大工具,但同时对传感器间公共信息被“重复计算问题”尤为敏感。为解决该问题,本文首先在基于广义协方差交集(GCI)的分布式多目标伯努利滤波器(简称GCI-MB融合算法)基础上,通过采用序贯信息交互-本地融合的策略提出网络共识-GCI-MB融合算法,简称C-GCI-MB融合;其次,通过数学理论分析了C-GCI-MB融合可以有效的避免“重复计算问题”的特性;最后给出了 C-GCI-MB 融合算法的混合高斯(Gaussian Mixture)实现方法,并通过典型场景仿真验证了该算法的有效性及性能优势。目前本文提出的C-GCI-MB融合算法当面对大量目标时,会存在计算量随目标个数呈超指数增长的问题,因此未来工作中会继续研究C-GCI-MB融合算法的快速实现方法,例如基于分组滤波的C-GCI-MB融合算法,可以实现多个相互独立组间的C-GCI-MB融合算法的并行运算,可以极大的提高运算效率。
参考文献
[1] Chong C Y, Mori S, Chang K C. Distributed multitarget multisensor tracking[M].Multitarget Multisensor Tracking: Advanced Application, Y.Bar shalom,Ed. Norwood, MA: Artech House, 1990: 247-295.
[2] Mahler R P. Optimal/robust distributed data fusion: a unified approach[C]∥in Proc. SPIE Defense and Security Symp. Orlando, FL, United States, 2000:128-138.
[3] Uhlmann J. Dynamic map building and localization for autonomous vehicles[D]. Unpublished doctoral dissertation, Oxford University, vol.~36,1995.
[4] Battistelli G, Chisci L, Fantacci C, et al. Distributed fusion of multitarget densities and consensus PHD/CPHD filters[C]∥in Proc. SPIE 9474, Signal Processing, Sensor/Information Fusion, and Target Recognition, Baltimore, MD, USA, 2015:1-15.
[5] Clark D, Julier S, Mahler R, et al. Robust multi-object sensor fusion with unknown correlations[C]∥in Proc. Sensor Signal Process. for Defence (SSPD'10). IET, 2010:1-5.
[6] Uney M, Clark D E, Julier S J. Distributed fusion of PHD filters via exponential mixture densities[J]. IEEE Journal Select Topics on Signal Processing, 2013,7(3):521-531.
[7] Battistelli G, Chisci L, Fantacci C, et al. Consensus CPHD filter for distributed multitarget tracking[J]. IEEE Journal Select Topics on Signal Processing, 2013,7(3): 508-520.
[8] Guldogan M B. Consensus Bernoulli filter for distributed detection and tracking using multi-static doppler shifts[J]. IEEE Signal Processing Letter, 2014,6(21): 672- 676.
[9] Vo B N, Vo B T, Pham N T, et al. Joint detection and estimation of multiple objects from image observations[J]. IEEE Transactions on Signal Processing, 2010,58(10):5129-5141.
[10] Vo B T, Vo B N, Cantoni A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations[J]. IEEE Transactions on Signal Processing, 2009,57(2): 409- 423.
[11] Vo B T, Vo B N, Hoseinnezhad R. Robust multi-bernoulli filtering[J]. IEEE Journal Select Topics on Signal Processing, 2013,7(3): 399- 409.
[12] Wong J, Vo B T, Vo B N, et al. Multi-Bernoulli based track-before-detect with road constraints[C]∥in Proc. 15th of International Conference Information Fusion. IEEE, 2012: 840- 846.
[13] Gostar A K, Hoseinnezhad R, Hadiashar A B. Multi-Bernoulli sensor control via minimization of expected estimation errors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015,51(3): 1762-1773.
[14] Gostar A K, Hoseinnezhad R, Hadiashar A B. Robust multi-Bernoulli sensor selection for multi-target tracking in sensor networks[J]. IEEE Signal Processing Letter, 2013,20(12): 1167-1170.
[15] Hoseinnezhad R, Vo B N, Vo B T, et al. Bayesian integration of audio and visual information for multi-target tracking using a CB-MeMBer filter[C]∥in ICASSP'2011, Prague, Czech Republic, 2011: 2300-2303.
[16] Hoseinnezhad R, Vo B N, Vo B T. Visual tracking in background subtracted image sequences via multi-Bernoulli filtering[J]. IEEE Transactions on Signal Processing, 2013,61(2): 392-397.
[17] Dunne D, Kirubarajan T. Multiple model multi-Bernoulli filter for manoeuvring targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013,49(4): 2679-2692.
[18] Williams J L. Hybrid Poisson and multi-Bernoulli filters[C]∥in Proc. International Conference Information Fusion, Singapore, Singapore, 2012: 1103-1110.
[19] Liu Weifeng, Han Chongzhao, Lian Feng, et al. Multitarget state extraction for the probability hypotheses density using mcmc approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010,46(2): 864- 883.
[20] Liu Weifeng, Wen Chenglin, Han Chongzhao, et al. A Bayesian estimation for single target tracking based on state mixture models[J]. Signal Processing,(Elsevier), 2012(92): 1706-1714.
[21] 龙建乾, 杨威,付耀文. 基于改进的PHD粒子滤波多目标跟踪技术[J]. 信号处理, 2011,27(9):1296-1300.
Long Jianqian, Yang Wei, Fu Yaowen. A modified PHD particle filter for multi-target tacking technology[J]. Signal Processing, 2011,27(9): 1296-1300. (in Chinese)
[22] 章涛,来燃,吴仁彪,等. 观测最优分配的GM-PHD多目标跟踪方法[J]. 信号处理, 2014,30(12):1419-1426.
Zhang Tao, Lai Ran, Wu Renbiao, et al. Optimal assignment of observation based GM-PHD multi-target tacking method[J]. Journal of Signal Processing, 2014,30(12):1419-1426. (in Chinese)
[23] Wang Bailu, Yi Wei, Hoseinnezhad R, et al. Distributed fusion with multi-Bernoulli filter based on generalized Covariance Intersection[J]. IEEE Transactions on Signal Processing, 2017,65: 242-255.
[24] Mahler R. Statistical Multisource-Multitarget Information Fusion[M]. Norwell, MA, USA: Artech House, 2007:1- 856.
[25] Xiao L, Boyd S, Lall S. A scheme for robust distributed sensor fusion based on average consensus[C]∥in Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN), Boise, ID, USA, 2005: 63-70.
[26] Box G E, Tiao G C. Bayesian Inference in Statistical Analysis[M]. MA:Addison-wesley, John Wiley & Sons, 1973:1-589.
[27] Horn R A, Johnson C R. Matrix Analysis[M]. Cambridge University Press, 1985:1-563.
[28] Sinkhorn R. A relationship between arbitrary positive matrices and doubly stochastic matrices[J]. The Annals of Mathematical Statistics, 1964,35(2): 876- 879.
[29] Olfati-Saber R. Distributed Kalman filtering for sensor networks[C]∥in Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 2007: 5492-5498.
[30] Julier S J. An empirical study into the use of Chernoff information for robust, distributed fusion of Gaussian mixture models[C]∥in Proc. 9th Internation Conference Information Fusion, Florence, Italy, 2006:1- 8.
[31] Schuhmacher D, Vo B T, Vo B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008,56(8): 3447-3457.
[32] Reuter S, Vo B T, Vo B N, et al. The labeled multi-Bernoulli filter[J]. IEEE Transactions on Signal Processing,2014,62(12): 3246-3260.